0 引 言
我国煤炭开采正在向安全、智能、精准、无人化开采模式转型[1],巷道安全维稳是现代化矿井智能精准开采的保障。随着矿井开采深度增加,巷道围岩受深部高地应力、采动动载应力、采动支承应力、渗流水化等共同作用,极易出现岩体大变形破坏、支护体破断失效等煤岩动力灾害,掌握围岩结构的承载能力及弱化机理对于维护巷道在服务期内的整体稳定性至关重要[2]。文献[3-7]对煤巷道顶板围岩承载结构做了系统的研究,建立了特定条件下围岩承载结构的物理模型、力学模型、数值模型,揭示了特定条件下巷道围岩的稳定原理,但围岩结构多被简化为二维问题,无法解释沿巷道轴向方向出现的岩性变化、应力变化的时间和空间问题。随着开采深度和强度的日益增加,高地应力场、高地温、高扰动、复杂裂隙及渗流场耦合作用下,巷道围岩结构承载能力面临新的挑战,原有的模型适用性有待进一步验证[8]。文献[9-10]提出沿巷道轴向的围岩结构,揭示了局部软弱围岩大变形对周围岩体的影响规律。在实际生产过程中,巷道将穿越不同岩性的岩体,局部将穿越弱结构岩体,且弱结构岩体沿巷道轴向和径向上的分布也存在差异,同时,工程开挖扰动使巷道围岩多个方向的应力状态发生变化,其稳定性属于三维问题,弱结构岩体附近围岩的力学响应对周围岩体的影响及相互作用规律值得深入探讨。以淮南张集煤矿近水平分布的厚及特厚煤层为地质背景,矩形巷道为工程条件,建立了厚煤层巷道顶板围岩的三向承载梁结构物理和力学模型,揭示了巷道层状顶板围岩结构承载能力弱化的本质。
1 三向承载梁结构模型
1.1 三向承载梁结构物理模型
根据巷道开挖前后附近煤系地层赋存特征,假定沿巷道轴向方向为Y轴,垂直于巷道轴向的水平方向为X轴,铅垂方向为Z轴。为了简化计算,多数学者将各地层假定为一个二维平面应变问题f(x,z)。然而巷道围岩内任意一点均处于三向应力状态,即采动支承应力导致巷道顶板的垂直应力不同,进而相邻断面的顶板具有相对运动的趋势,产生了静摩擦力,而断面上的法向应力是水平应力,一般不会变化,当遇到断层、陷落柱等卸压区域,水平应力会减小。基于此,提出考虑巷道围岩轴向的三维结构承载分析模型,即认为反映巷道围岩稳定性的参量是x,y和z的函数f(x,y,z)。巷道顶板围岩结构物理模型,如图1所示,呈现层状分布、相互作用、分区承载的三维长板结构。垂直Z方向的顶板由n层不同岩性、不同厚度的层状岩层以及层间结构面组成,各个岩层承载着其上方岩层部分重量及自身的重量,并向下方传递作用力。巷道横向水平X方向上的顶板由同一岩性的岩层组成,分别由帮部煤体、顶煤、帮部煤体支撑;巷道轴向水平Y方向上的顶板由同一岩性的岩层组成,呈无限长板状分布,两侧由下方岩体支撑,并承载上方岩层及自身重量。
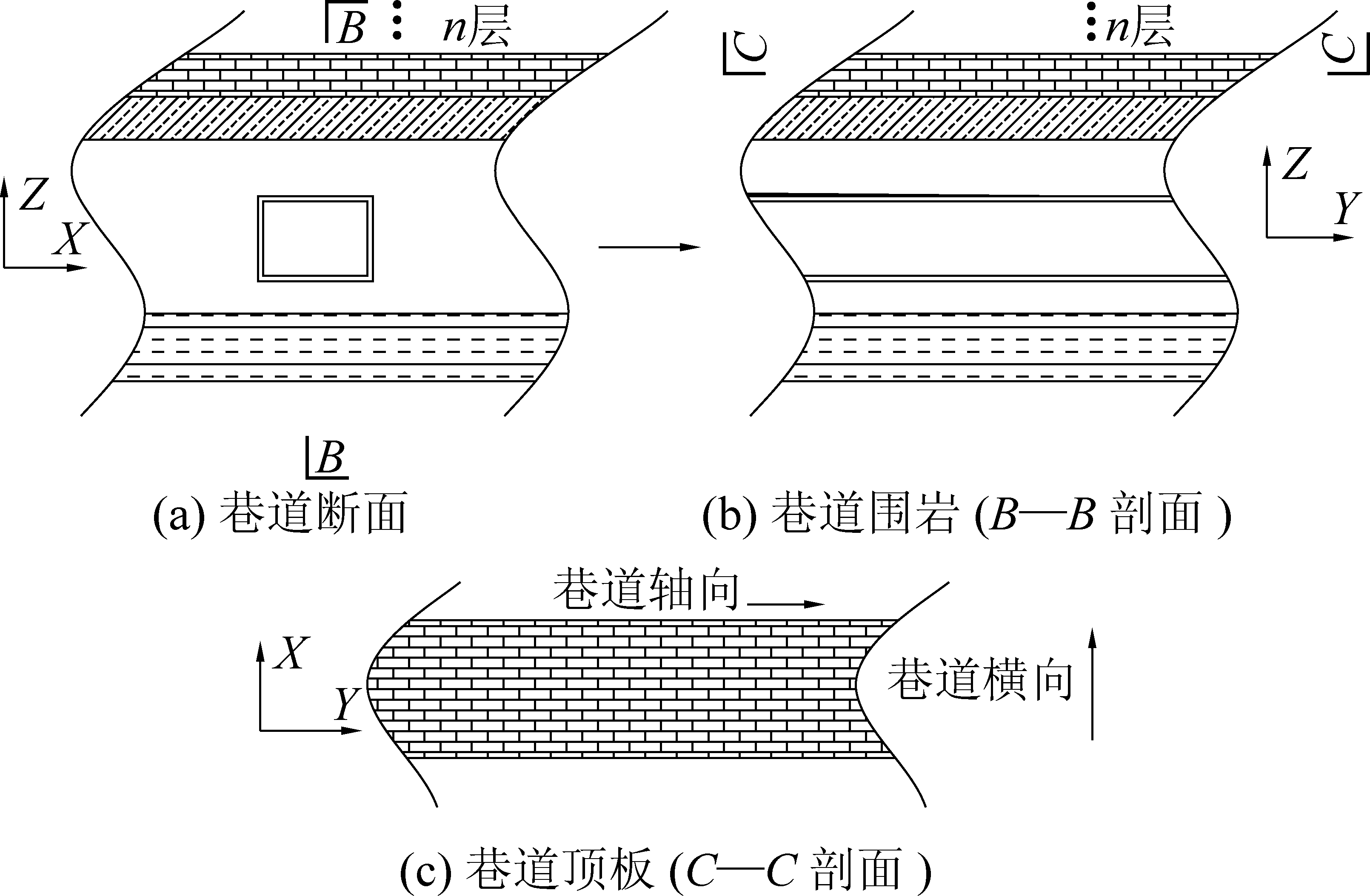
图1 巷道顶板围岩结构物理模型
Fig.1 Physical model of the roadway roof structure
1.2 三向承载梁结构力学模型
1.2.1 结构力学模型的建立
基于巷道顶板围岩承载结构的物理模型,结合影响围岩承载结构稳定性的主要影响因素,建立巷道顶板围岩承载结构的力学模型。考虑无限长板结构力学解析及其应用过程的复杂度,依据板的Marcus简算法[11],将无限长板视为分条的梁,梁间相互作用简化为法向应力σy和摩擦应力Fm,轴向不同位置处的Fm可能不同。简化后的巷道顶板三向承载梁结构力学模型如图2所示,模型的两端(X轴方向)为固支结构,上部岩层的作用应力及岩层自重应力组成的承载应力简化为均布应力σz,作用于三向承载梁结构的上表面,可由式(1)计算获得,模型的下表面由支护应力p支撑,模型的侧面(Y轴方向)承载法向应力σy和摩擦应力Fm,梁的宽度为Ly,高度为岩层厚度Lz,长度为结构的实际跨度Lx。
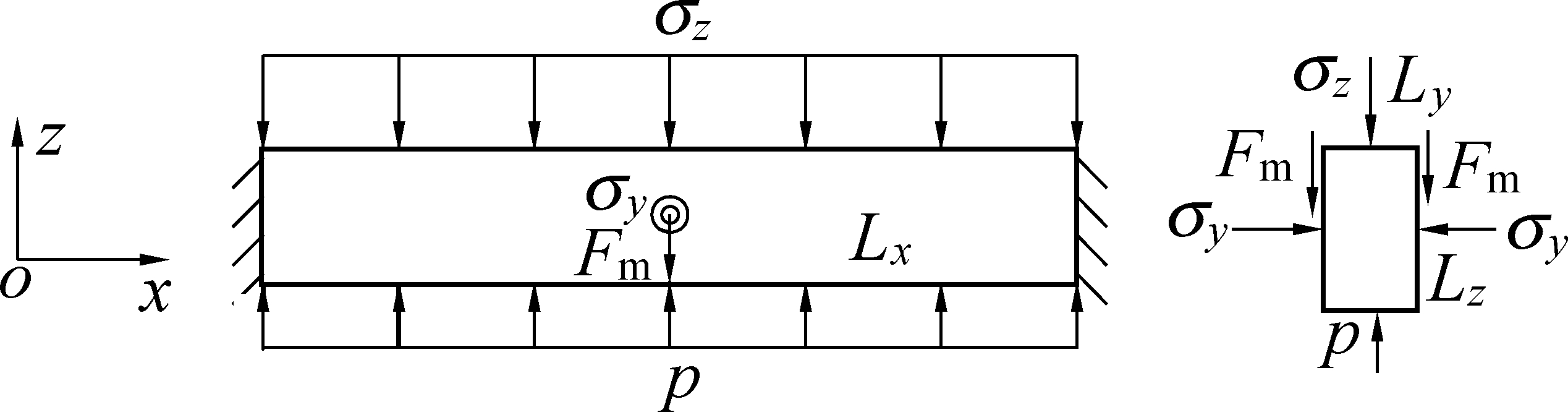
图2 巷道顶板三向承载梁力学模型
Fig.2 Mechanical model of triaxial beam structure of
the roadway roof
煤系地层呈现显著的非均质和各向异性的分布形态,各岩层承载后的力学行为存在差异,基于应力通过岩层逐层传递这一属性(图3),可求解出a层岩层当中任意岩层上的作用应力,如式(1)[2]。

图3 沉积地层静载应力传递模型
Fig.3 Static stress transmiting model of sedimentation layer
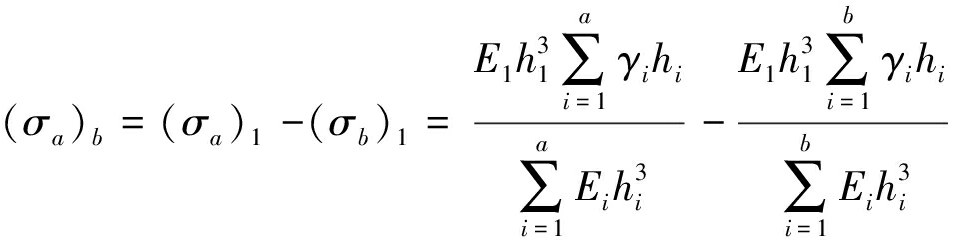
(1)
式中:(σa)b为上方a层岩层对第b层岩层的作用应力,MPa;(σa)1、(σb)1为上方a-1、b-1层岩层对第1层岩层的作用应力,包含第1层岩层的自重,MPa;E1,E2,…,Ea为各岩层的弹性模量,MPa;h1,h2,…,ha为各岩层的厚度,m;γ1,γ2,…,γa为各岩层的容重,N/m3。
1.2.2 结构的挠曲变形
以图2中的固支梁为研究对象,梁的前后(Y方向)、左右(X方向)受力对称,上下(Z方向)不对称,将在外载应力(σz、σy、Fm、p)作用下产生Z轴负方向上的挠度,叠加原理表明可以单独考虑每个载荷对梁作用后产生的挠度。依据式(2),可得上部岩层作用应力和岩层自重应力σz作用时固支梁的挠度公式(3)。固支梁间的法向应力σy对称作用于前后2个面上,与Z轴方向垂直,对梁的Z向挠度没有直接作用,可影响截面上的摩擦应力,当沿Y轴方向的各物理力学参量没有变化时,所有的固支梁在外载荷作用下运动同步,没有相对运动的趋势,摩擦应力应取0;当相邻两固支梁间存在相对运动的趋势时,摩擦应力应介于零和最大摩擦应力之间,当相邻两固支梁发生剪切滑动时,摩擦力达到最大,见式(4),该摩擦应力可影响梁的挠度,见式(5)。支护应力p产生的挠度见式(6)。基于式(3)、(5)和(6)可得固支梁的弯曲挠度解见式(7)。
(2)
(3)
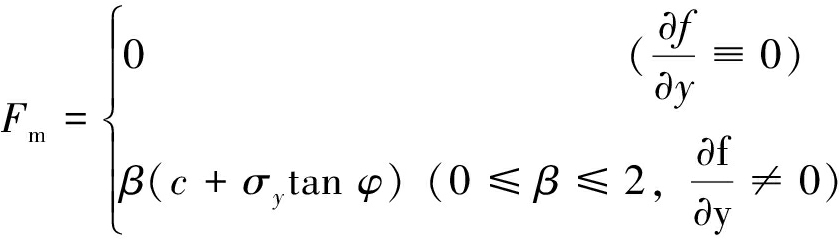
(4)
(5)
(6)
(7)
然而,外力作用下固支梁的两端将产生应力集中,产生较大的剪应力和拉应力[12],剪应力和拉应力很容易达到许用应力,进而造成固支梁在两端发生拉破坏,转而成为简支梁,同样的方法可获得简支梁在外载作用下的挠度解,见式(8)。
(8)
式中:ωb为第b层岩层的弯曲挠度,m;σb为第b层岩层的垂向载荷,MPa;x为距梁板一侧端面的距离,m; Ib、Lb分别为第b层岩层的惯性矩、横向跨距,m4、m;β为静摩擦力与滑动摩擦力的比值系数;ω1、ω2、ω3分别为各个外载应力产生的挠度解,m;ωF为固支梁的挠度,m;ωS为简支梁的挠度,m;c为岩层的黏聚力,MPa;φ为岩层的内摩擦角,(°)。
1.2.3 结构内的应力求解
原岩煤系地层处于三向应力作用下的静力平衡状态,可用6个应力分量来表达(σu、σv、σw、τuv、τuw、τvw),将该6个分量代入到相应的岩石材料屈服破坏准则,即可判定该点的弹塑性承载状态。巷道开挖后,顶板铅垂方向的部分应力被解除,平衡状态被打破,不平衡的外载应力作用引起顶板固支梁弯曲产生沿X方向的附加应力,见式(9),因此固支梁内任意一点X方向的法向应力需要考虑固支梁弯曲带来的附加效应。在上部岩层和承载应力σz与支护应力p的作用下,固支梁内任意一点Z方向的法向应力应为两者之间的较小值,即自重应力与支护应力两者中的较小者是结构内Z方向上的法向应力,两者的差值由端部下方煤体支撑力抵消,或者由端部上方顶板抵消。基于此可获得固支梁内任一点的6个应力分量的解,见式(10)。基于式(10),可求解出梁内任意一点的主应力,如式(11)[13],式中各中间参数求解见式(12)。与固支梁相比,简支梁内任一点沿X方向的法向应力即为简支梁弯曲引起的附加应力,见式(13)。
(9)

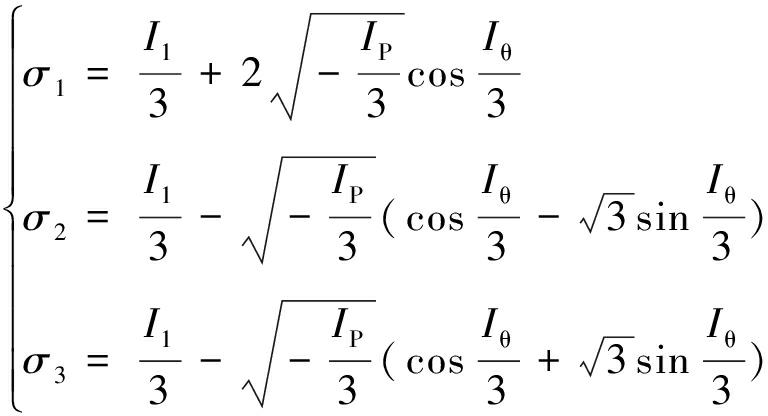
(11)
(13)
式中:σu、σv、σw、τuv、τuw、τvw为原岩煤系地层处于三向应力作用下的静力平衡状态的6个应力分量,MPa;z为距梁板中心的垂直距离,m;σ1、σ2、σ3分别为第1、2、3主应力,MPa;I1、I2、I3分别为第1、2、3应力不变量,MPa、MPa2、MPa3。
1.2.4 板梁的破坏准则
常用屈服破坏准则有Mohr-Coulomb[14]、Drucker-Prager[15]、Hoek-Brown[16]、Griffith[17]和统一强度准则[18]、拉应力准则[19]等,应结合工程实际问题选择强度准则,或对其针对性的修正。梁板结构内任一点均处于三向应力加载状态,应考虑第2主应力σ2和静水压力的作用时的剪切破坏,故而选择Drucker-Prager强度准则,见式(14),其中未知参数的求解见式(15)。考虑模型的精准性,选择Mohr-Coulomb等面积圆对应的参数解[21]。
(14)
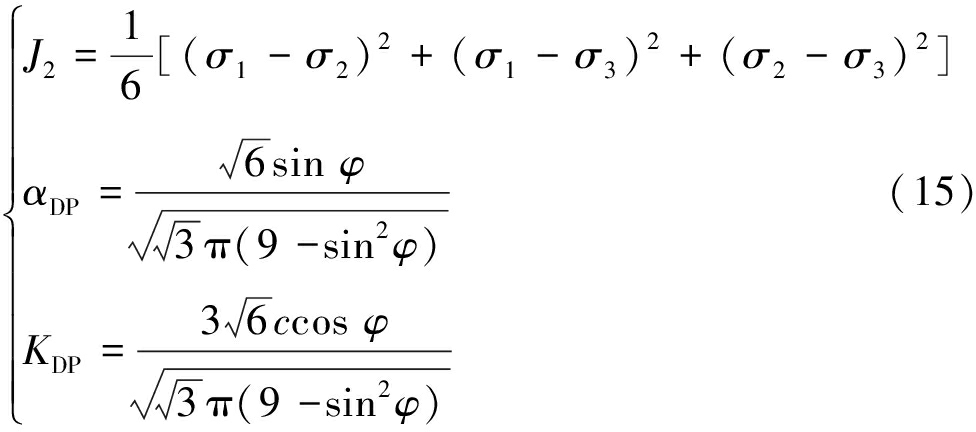
式中:f为压剪破坏判断值;J2为应力偏量第2不变量,MPa2;αDP和KDP分别为与岩石强度参数有关的试验常数[20]。
f<0,说明该点进入压剪破坏状态,且值越小预示该点越容易发生压剪破坏;f=0,说明该点达到压剪破坏的临界状态;f>0,说明该点仍处于弹性承载状态。得到巷道顶板三向承载梁结构的弹塑性分析方法,见表1。将式(12)代入到式(14)可获得固支梁弯曲压缩区域内的弹塑性压剪破坏状态。
表1 三向承载梁结构弹塑性分析方法
Table 1 Elastic and plastic analysis method of triaxial beam structure

2 三向承载梁结构承载能力衰减规律
工程材料微观裂隙扩展、颗粒脱黏过程中引起细观强度参数的弱化是导致工程材料强度弱化的根本原因,利用损伤力学、塑性力学、室内试验、数值模型的方法求解细观强度参数的弱化模型是目前应用最为广泛、直接的方法,形成了解决特定工程承载弱化的材料应变软化模型[22]、链式渐进损伤模型[23]、系列脆塑性破坏模型[24]、微裂隙渐进损伤模型等[25]。
基于三向承载梁结构的承载机理,结合极限平衡理论,假定三向承载梁结构在峰后软化和残余阶段均满足Drucker-Prager强度准则,在已知支护阻力p、梁间摩擦阻力Fm、原岩作用应力σx、σy、τxy、τxz、τyz的情况下,可求解三向承载梁结构的极限承载应力σz,其中支护阻力p根据现场锚杆(索)支护参数及实际的工作载荷确定,梁间摩擦阻力Fm根据公式(4)确定,原岩应力一般通过现场地质力学测试,或者来源于矿区地质报告。根据式(13)可获得结构内等效附加X方向的均布应力Δσxq,见式(16),基于此可获得极限平衡状态下结构的极限承载应力,见式(17),将式(17)代入到式(11)和式(12)可获得结构内主应力的大小,将主应力大小代入式(15)中,可获得应力偏量第二不变量J2的大小,从而可获得Drucker-Prager强度准则中的所有参数,将这些参数代入到式(14)的等式当中,求解该等式,即可获得结构峰后极限承载状态下的承载应力σz,由于公式的解析复杂度,此处没有列出具体的显示解析表达,但该过程可通过Matlab等数值计算软件编程实现,求解特定工程地质条件下三向承载梁结构峰后极限承载状态下的承载应力σz。
(16)
(17)
材料塑性变形积累的过程中,强度参数逐渐衰减,导致结构承载能力下降,是宏观煤岩工程结构失稳的必经过程,以最大塑性剪应变和主应力差值为基础,建立等效宏观强度参数衰减的分析模型,如图4所示。

图4 等效宏观强度参数解析模型
Fig.4 Analytical model of the equivalent macroscopic strength parameters
横坐标为最大塑性剪应变γ,纵坐标为随最大塑性剪应变增加而变化的主应力差值(σ1-σ3)。得到该类加载条件下的强度参数弱化区间[γA,γB],考虑围压不同时的强度参数弱化区间存在差异,将该区间减去γA后再除以γB-γA,建立材料强度弱化的归一化区间δ邻域[0,1],简称δ区间,δ=(γn-γA)/(γB-γA)。
3 工程应用
巷道顶板围岩的稳定性由围岩强度、围岩应力和支护强度决定,应基于巷道顶板围岩承载结构的力学模型,结合某矿具体的工程地质条件,解析巷道顶板承载结构的变形破坏规律,揭示巷道顶板承载结构稳定性的主要影响因素和影响规律。为了更直观的反映巷道开挖后顶板结构的变形及弹塑性破坏状态,以淮南张集矿17246工作面轨道巷顶板为计算分析对象,分析该巷道顶板的变形破坏规律。
3.1 工程地质概况
淮南张集矿17246工作面的标高为-517.3—-626.0 m,对应的地面标高为+18.0—+27.0 m,平均埋深约为590 m,走向长为1 879 m,倾斜长270 m。煤厚为1.8~8.0 m,平均4.0 m,倾角为2°~8°,平均4°,为近水平煤层。工作面布置在6号煤层北一采区南翼,东面以Fw2断层保护煤柱为界,南侧为17256采空区,北侧为尚未开采的17236工作面,西面为6号煤工业广场保护煤柱。17246工作面运输巷和轨道巷均沿着煤层底板掘进,掘进断面均为5 200 mm×3 400 mm,采掘工程平面,如图5所示,局部综合钻孔岩性及参数见表2。
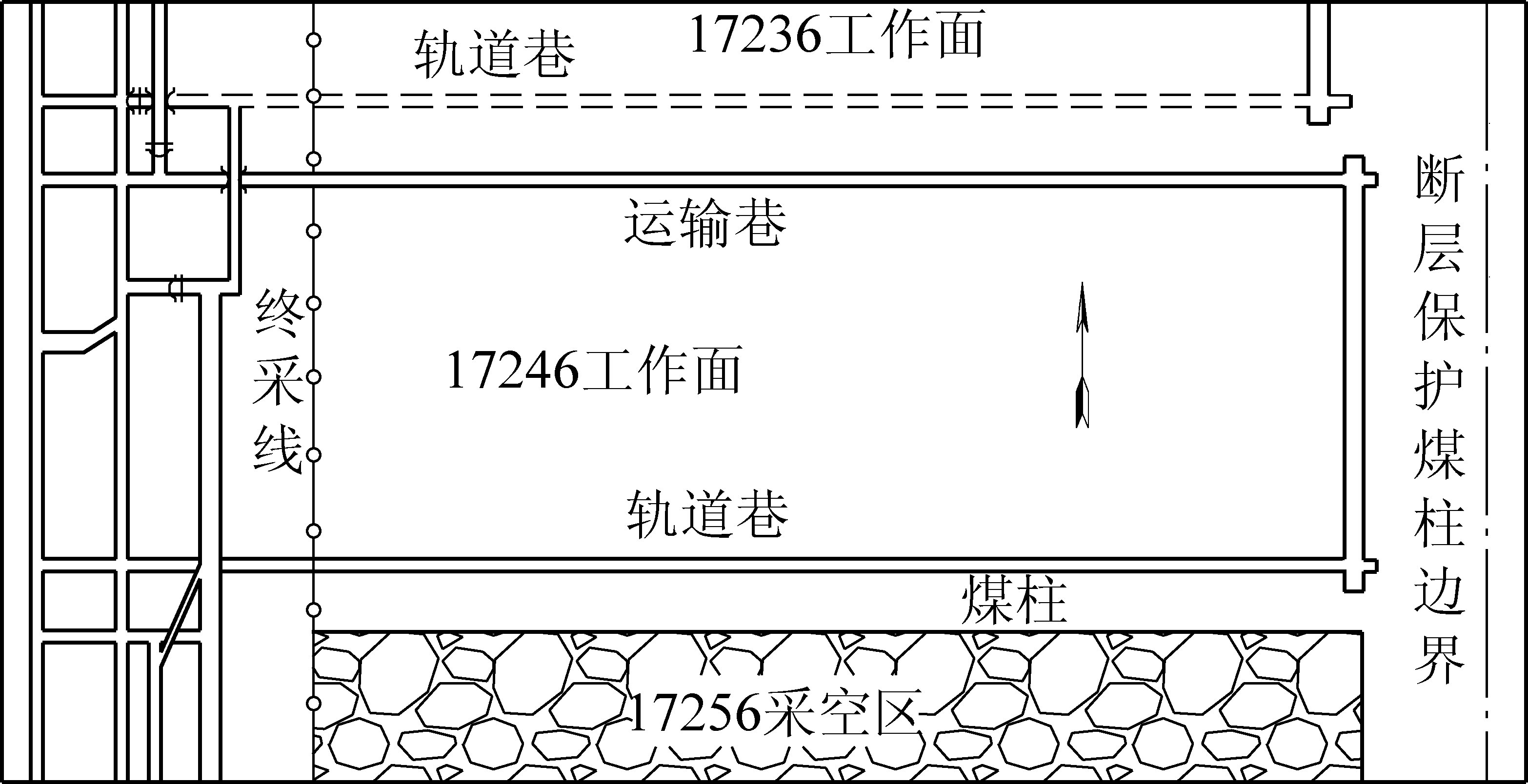
图5 17246工作面示意
Fig.5 Diagram of No.17246 coal mining face
3.2 模型参数输入
基于淮南张集矿现场地质报告、原位地质力学测试结果,将顶板三向承载梁结构力学模型的物理力学参数总结为表3,其中σz是按照式(1)计算获得[26]。
表2 17246工作面局部钻孔岩性及参数
Table 2 Local borehole lithology and parameters of No.17246 coal mining face

3.3 模拟结果分析
基于以上求解方法,结合淮南张集矿17246工作面轨道平巷的具体条件(表3),可求解出峰后泥岩顶板的极限承载应力随塑性剪应变归一化区间δ的衰减规律,如图6所示。该类条件下,上方岩层的作用应力达到5.1 MPa左右,泥岩顶板达到极限承载状态,随着塑性剪应变的增加,泥岩顶板进入峰后软化阶段,承载能力呈逐渐减小并趋于稳定的变化趋势,煤巷开挖后的泥岩顶板经历弹性承载、弹塑性承载、塑性承载后,其残余承载能力约为2.9 MPa,当处于峰后残余承载平衡状态的结构受到外界应力扰动时,结构会发生大变形灾害,甚至冒顶事故等。

图6 巷道层状顶板三向承载梁结构峰后承载能力
Fig.6 Bearing capacity after peak of the roadway roof triaxial beam structure

3.4 相似模拟结果分析
为了验证淮南张集矿17246工作面轨道平巷的泥岩顶板变形破坏规律,通过弱结构岩体相似试件单轴压缩试验,揭示弱结构岩体承载能力弱化的本质规律。选择细河沙为骨料、石膏为胶结剂、水为溶解剂制作相似模拟材料,石膏、河沙质量比分别为1∶1、1∶2、1∶3、1∶4、1∶5五组材料配比方案,将配比的河沙、石膏、水进行混合搅拌,适当添加少量的硼砂作为缓凝剂,将搅拌均匀的混合材料放入事先准备好的模具,并用工具捣实(可施加2 MPa的压力进行压实),将模型表面处理平整,将该5组材料制作成直径为50 mm、高为100 mm的试样,每种配比方案制作3个试样,共计15个岩石试样,待模型晾干后进行分组编号处理,采用RMT加载试验机进行单轴试验,加载速率设置为0.01 mm/s,记录并计算加载过程中的应力、应变曲线,其中配比1∶1、1∶3和1∶5的结果如图7所示。
随着石膏胶结剂质量浓度的减小(从50.00%减小到16.70%),试样的单轴抗压强度呈增加的变化规律,峰值强度从1.68 MPa增加到2.57 MPa,残余强度从0.81 MPa增加到1.46 MPa,增幅显著。此结果证实,颗粒间胶结的力学本质是,颗粒间存在相互作用力,即颗粒间的黏聚力和内摩擦角,所有颗粒通过胶结剂凝固在一起组成一个完整的试块。该试块的强度对胶结剂浓度非常敏感,胶结剂浓度过高时,在单轴试验过程中首先进入屈服破坏状态,是试块抗压承载的薄弱部位,进而引起试块整体破坏,抗压强度呈减小的变化趋势。

图7 单轴加载试验结果
Fig.7 Test results of the uniaxial compression test
河沙、石膏相似材料配置成的试块强度较小,无法正常开展试块的变围压三轴压缩试验。为了探讨围压对弱结构岩石的强化作用,采用已有的研究成果进行分析,基于沉积地层三轴压缩应力应变曲线[27-29],可绘制煤层、页岩、泥岩等的变围压三轴抗压强度曲线,如图8所示。
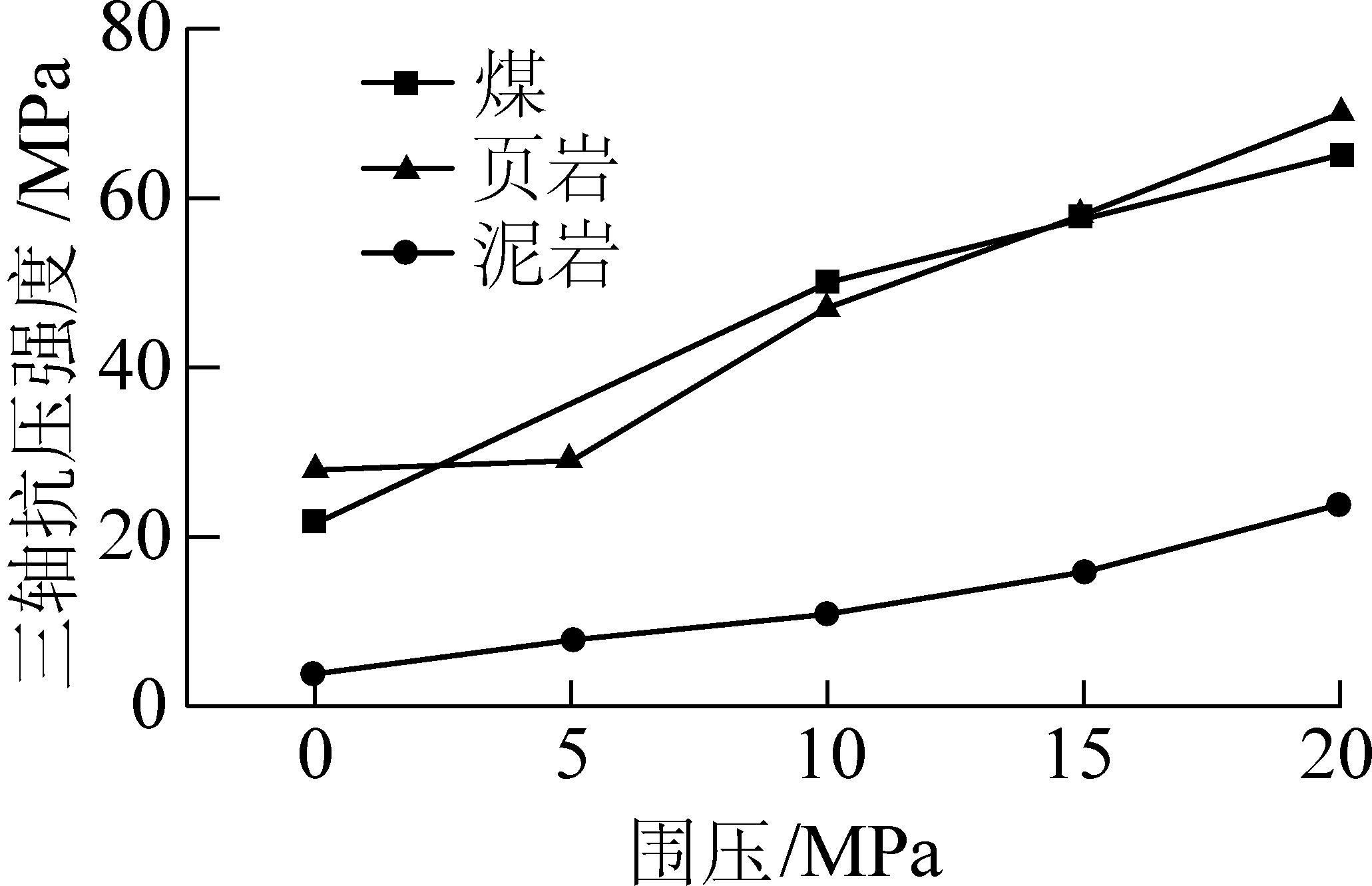
图8 围压对试样强度的作用规律
Fig.8 Effect of confining pressure on strength of specimen
随着围压的增加,试块三轴抗压强度(轴压与围压的差值)呈类似线性增加的变化规律,岩石抗压强度显著提高,页岩的三轴抗压强度显著小于煤和泥岩的三轴抗压强度。相似模拟结果与数字模拟计算结果相符。
4 结 论
1)通过建立巷道层状顶板三向承载梁结构物理和力学模型,将结构承载划分为固支承载阶段和简支承载阶段,确定了两阶段内结构弯曲变形引起的附加应力解析解,并基于Drucker-Prager强度准则和拉应力强度准则,提出了巷道顶板三向承载梁结构的弹塑性分析方法,f<0表示该点进入压剪破坏状态,f=0表示该点达到压剪破坏的临界状态,f>0表示该点仍处于弹性承载状态。
2)推导了峰后软化阶段和残余承载阶段的极限承载应力,发现进入峰后残余阶段的巷道层状顶板仍然具有一定的承载能力,实例计算试验巷道泥岩顶板的极限承载应力为5.1 MPa左右,残余承载应力为2.9 MPa左右。
3)相似模拟结果表明,增加颗粒间的黏聚力和内摩擦角,具有一定的抗压强度,该强度对胶结剂浓度有一定的适用范围;随着围压的增加,试块的抗压强度、残余强度均呈增加趋势。
参考文献:
[1] 袁 亮.煤炭精准开采科学构想[J].煤炭学报,2017,42(1):1-7. YUAN Liang.Scientific conception of precision coal mining[J].Journal of China Coal Society,2017,42(1):1-7.
[2] 周 波,袁 亮,薛俊华,等.巷道顶板三维板梁结构的传力机制研究[J].中国安全生产科学技术,2017,13(12):131-137. ZHOU Bo,YUAN Liang,XUE Junhua,et al.Study on force transfer mechanism of roadway roof with three-dimensional plate girder structure[J].Journal of Safety Science and Technology,2017,13(12):131-137.
[3] 李树清,王卫军,潘长良.深部巷道围岩承载结构的数值分析[J].岩土工程学报,2006,28(3):377-381. LI Shuqing,WANG Weijun,PAN Changliang.Numerical analysis on support structure of rock around deep roadway[J].Chinese Journal of Geotechnical Engineering,2006,28(3):377-381.
[4] 李树刚,成小雨,刘 超,等.破碎围岩动压巷道锚索支护与注浆加固技术研究[J]. 煤炭科学技术,2016,44(1):67-72. LI Shugang,CHENG Xiaoyu,LIU Chao,et al.Research on technology of anchor cable supporting and grouting reinforcement for dynamic pressurized tunnel with crushed surrounding rock[J].Coal Science and Technology,2016,44(1):67-72.
[5] 马振乾, 姜耀东, 吴桂义,等.厚层泥质顶板巷道支护难度分级研究与应用[J].中国安全科学学报,2017,27(11):121-125. MA Zhenqian,JIANG Yaodong,WU Guiyi,et al.Research on support difficulty classification for roadways with thick mudstone roof and its application[J].China Safety Science Journal,2017,27(11):121-125.
[6] 辛亚军,安定超,李梦远.巷道围岩再造承载层机理及数值模拟[J].中国安全生产科学技术,2016,12(6):36-41. XIN Yajun,AN Dingchao,LI Mengyuan.Mechanism and numerical simulation of renewable bearing stratum in roadway surrounding rock[J].Journal of Safety Science and Technology,2016,12(6):36-41.
[7] 王 猛,柏建彪,王襄禹,等.迎采动面沿空掘巷围岩变形规律及控制技术[J].采矿与安全工程学报,2012,29(2):197-202. WANG Meng,BAI Jianbiao,WANG Xiangyu,et al.The surrounding rock deformation rule and control technique of the roadway driven along goaf and heading fore adjacent advancing coal face[J].Journal of Mining and Safety Engineering,2012,29(2):197-202.
[8] 周 波,袁 亮,薛 生.巷道围岩结构稳定性控制机理研究综述[J].煤矿安全,2018,49(5):214-217,221. ZHOU Bo,YUAN Liang,XUE Sheng.Study review on sructural stability control mechanism of roadway surrounding rock[J].Safety in Coal Mines,2018,49(5):214-217,221.
[9] KONTOGIANNI V A,STIROS S C.Induced deformation during tunnel excavation:evidence from geodetic monitoring[J].Engineering Geology,2005,79(1/2):115-126.
[10] STIROS S C,KONTOGIANNI V A.Coulomb stress changes:From earthquakes to underground excavation failures[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(1):182-187.
[11] 钱鸣高,石平五,许家林.矿山压力与岩层控制[M].2版.徐州:中国矿业大学出版社,2010:145-151.
[12] 马肖彤,包 超,王秀丽,等.冲击荷载下固支梁弹塑性动力响应分析[J].兰州理工大学学报,2017,43(3):133-139. MA Xiaotong,BAO Chao,WANG Xiuli,et al.Dynamic response analysis of elasticity-plasticity of clamped beam subjected to impact load[J].Journal of Lanzhou University of Technology,2017,43(3):133-139.
[13] 王 凯.主应力的计算公式[J].力学与实践,2014,36(6):783-785. WANG Kai.Calculation formulas for principal stresses[J].Mechanics in Engineering,2014,36(6):783-785.
[14] QIN C B,CHIAN S C,YANG X L.3D limit analysis of progressive collapse in partly weathered Hoek-Brown rock banks[J].International Journal of Geomechanics,2017,17(7):04017011.
[15] ALEJANO L R,BOBET A.Drucker-Prager criterion[M].Berlin:Springer International Publishing,2015.
[16] 刘泉声,魏 莱,刘学伟,等.基于Griffith强度理论的岩石裂纹起裂经验预测方法研究[J].岩石力学与工程学报,2017,36(7):1561-1569. LIU Quansheng,WEI Lai,LIU Xuewei,et al.A revised empirical method for predicting crack initiation based on Griffith strength criterion[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(7):1561-1569.
[17] LABUZ J F,ZANG A.Mohr-Coulomb failure criterion [M].Berlin:Springer International Publishing,2015.
[18] 俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报,1994,16(2):1-10. YU Maohong.Unified strength theory for geomaterials and its applications[J].Chinese Journal of Geotechnical Engineering,1994,16(2):1-10.
[19] 郭明伟,邓 琴,李春光,等.巴西圆盘试验问题与三维抗拉强度准则[J].岩土力学,2008,29(11):545-549,554. GUO Mingwei,DENG Qin,LI Chunguang,et al.Brazilian disc test and 3-D tensile strength principle[J].Rock and Soil Mechanics,2008,29(11):545-549,554.
[20] 陈 梁,茅献彪,李 明,等.基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报,2017,42(2):484-491. CHEN Liang,MAO Xianbiao,LI Ming,et al.Elastoplastic analysis of cracked surrounding rock in deep roadway based on Drucker-Prager criterion[J].Journal of China Coal Society,2017,42(2):484-491.
[21] 张信贵,许胜才,严利娥,等.Drucker-Prager准则参数有效性及第二主应力对强度的影响分析[J].应用力学学报,2015,32(5):810-816. ZHANG Xingui,XU Shengcai,YANG Li’e,et al.Drucker-Prager criterion parameter validation and second principal stress effect on the strength analysis[J].Chinese Journal of Applied Mechanics,2015,32(5):810-816.
[22] 王水林,郑 宏,刘泉声,等.应变软化岩体分析原理及其应用[J].岩土力学,2014,35(3):609-622,630. WANG Shuilin,ZHENG Hong,LIU Quansheng,et al.Principle of analysis of strain-softening rock mass and its application[J].Rock and Soil Mechanics,2014,35(3):609-622,630.
[23] 余 俊,李 真,潘伟波,等.考虑黏聚力弱化的岩石软化模型研究[J].铁道科学与工程学报,2016,13(6):1039-1045. YU Jun,LI Zhen,PAN Weibo,et al.Research on softening model of rock with the weakening of cohesion[J].Journal of Railway Science and Engineering,2016,13(6):1039-1045.
[24] 袁 超,王卫军,赵延林,等.考虑岩体塑性硬化与软化特性的巷道围岩变形理论分析[J].煤炭学报,2015,40(S2):311-319. YUAN Chao,WANG Weijun,ZHAO Yanlin,et al. Theoretical analysis on roadway surrounding rock deformation based on the properties of rock plastic hardening and softening[J].Journal of China Coal Society,2015,40(S2):311-319.
[25] 张 平,李 宁,贺若兰.含裂隙类岩石材料的局部化渐进破损模型研究[J].岩石力学与工程学报,2006,25(10):2043-2050.ZHANG Ping,LI Ning,HE Ruolan.Research on localized progressive damage model for fractured rockike materials[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(10):2043-2050.
[26] 周 波,袁 亮,薛 生.煤巷顶板围岩结构承载能力弱化分析[J].中国安全生产科学技术,2018,14(9):122-128. ZHOU Bo,YUAN Liang,XUE Sheng.Analysis on bearing capacity weakening of surrounding rock structure at roof of coal roadway[J].Journal of Safety Science and Technology,2018,14(9):122-128.
[27] 黄 兴,刘泉声,康永水,等.砂质泥岩三轴卸荷蠕变试验研究[J].岩石力学与工程学报,2016,35(S1):2653-2662. HUANG Xing,LIU Quansheng,KANG Yongshui,et al.Triaxial unloading creep experimental study of sandy mudstone[J]Chinese Journal of Rock Mechanics and Engineering,2016,35(S1):2653-2662.
[28] 解廷堃,李二利,刘如成.炭质页岩常规三轴试验和本构方程的研究[J].露天采矿技术,2008,(6):7-10,12. XIE Tingkun,LI Erli,LIU Rucheng.Research on carbonaceous shale general tri-axial test and costitutive equation[J].Opencast Mining Technology,2008,(6):7-10,12.
[29] 刘泉声,刘恺德,朱杰兵,等.高应力下原煤三轴压缩力学特性研究[J].岩石力学与工程学报,2014,33(1):24-34. LIU Quansheng,LIU Kaide,ZHU Jiebing,et al.Study of mechanical properties of raw coal under high stress with taiaxial compession[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(1):24-34.