0 引 言
煤层厚度(简称“煤厚”)及其变化不仅影响工作面采煤方法的选择,也是煤炭资源安全高效开采的重要地质参数,对于今后智能化、无人化开采工作面尤为如此。如果能够超前准确预测工作面的煤厚变化,智能化、无人化开采工作面则可以通过采煤机摇臂的自动控制,避免截齿切割煤层顶板、保护采矿设备、提高开采效率、降低矸石率、规避瓦斯事故等[1]。
围绕煤厚变化的预测,国内外学者开展了大量的研究工作,主要包括:①基于地面钻孔的煤厚空间内插方法。它主要采用地面地质钻孔煤厚信息进行空间插值,该方法简单易行,但是受制于地面钻孔数量偏少、非沉积因素造成的煤厚异常变化难以甄别、不同插值方法的预测结果差别较大等原因,导致其煤厚预测精度偏低,仅可作为煤炭地质资源量估算的依据[2-5];②基于三维地震资料的煤厚变化趋势预测。以地面钻探控制的煤厚信息为约束,利用三维地震属性解释[6-8]、波阻抗反演预测[9-10]等方法,将地面稀疏的钻孔煤厚数据与密度较大的三维地震数据相融合,采用多项式回归、神经网络、遗传算法等数学方法,开展煤厚变化趋势预测,该方法的预测精度受三维地震数据采集质量、资料处理保真度等影响较大[11];③基于矿井物探方法的煤厚预测。无线电波坑透技术、槽波地震探测技术可以有效地圈定工作面内煤层变薄带的范围,结合巷道揭露信息可以对工作面煤厚变化加以预测,其中槽波地震对工作面内煤厚变化的预测精度相对较高[12-15];④基于煤岩识别技术的煤厚预测方法研究。近年来,围绕智能开采工作面的煤厚预测,一些学者开展了基于放射性、弹性波、电磁波、视频图像识别、截齿阻力等煤岩识别技术的研究,并取得了一定的进展,但是尚未实现技术突破[16]。总体来看,钻探手段直接获取的煤厚数据是最可靠的第一手数据,属于“硬数据”,如果实际控制的煤厚数据密度满足要求,则可以采用空间内插的方法进行煤厚预测;而以物探手段间接获取的煤厚信息是第二手数据,属于“软数据”,在已知煤厚点数量偏少的情况下,以钻孔数据为约束、利用物探资料开展煤厚预测,不失为一个较好的选择。煤矿回采工作面具备地面钻探、井下回风巷、运输巷及开切眼揭露的大量已知煤厚数据,如何开展回采工作面内部煤厚变化的高精度预测,相关的研究工作相对偏少。
在前人研究成果的基础上,笔者提出回采工作面煤层厚度递进式预测的思路和方法,即以地面钻探、井下回风巷、运输巷及开切眼揭露的煤厚数据为基础,随着回采工作面的推进,不断动态融入回采过程中揭露的煤厚数据,采用克里格空间估值技术,对回采工作面前方未采区段的煤厚变化进行递进式、超前、动态预测,并以某矿已经完成回采的S1工作面为例进行了试验研究,取得了较好的煤厚预测效果。
1 常用煤厚插值方法的筛选
在不同的煤田地质勘查阶段,通过在地面布置一定网度的钻孔,可以对煤层厚度及其赋存状态加以控制。但是,对于钻孔之间煤厚变化的推断,实际上是通过人为提出一些区域性假设,构建不同的地质模型,采用数学地质方法进行空间插值得到的。无论哪种煤厚空间插值方法,都必须与已知煤厚点的实际数据相吻合,也要符合对煤层空间赋存规律的主观认识,这就是对不同数学插值方法进行筛选的约束条件。
Surfer地质绘图软件提供了12种常用的地质数据空间插值计算方法,包括距离反比法、自然邻点插值法、最近邻点插值法、线性插值法、改进的谢别德法、移动平均法、多项式插值法、最小曲率法、局部多项式法、径向基函数法、数据度量法和克里格估值技术[17]。按照上述煤厚预测的方法要求,对12种煤厚空间插值方法分析认为[18-20]:
1)空间距离插值方法:线性内插法、距离反比法、改进的谢别德法、自然邻点法与最近邻点法,均是基于空间距离的数学插值方法,其基本原理是按照待插值点与已知点之间距离的不同,采用不同的数学算法计算权重值,以实现未知点煤厚的插值,且能保证已知煤厚点的数据稳定。但是,这些方法均不考虑不同煤厚点空间上的相关性和空间分布密度的不均匀问题,如线性内插法受已知点分布疏密不均的影响很大。众所周知:工作面回采前,已知煤厚点主要分布在回风巷、运输巷和开切眼地段,呈“U”型分布特征,数据空间分布很不均匀,因此上述5种插值方法的适用条件受到限制。
2)空间曲面插值方法:多项式插值法、局部多项式法与最小曲率法,都是基于空间趋势面分析的数据内插方法,插值结果以数学曲面反映空间分布数据的变化情况。主要优点是可以从宏观角度整体上反映煤厚变化的大致趋势;主要不足是尽管拟合出的空间曲面光滑,但是在已知煤厚点的插值结果容易失真,且趋势面的拟合次数难以确定等。因此,这3种插值方法也不适于回采工作面的煤厚预测。
3)其他插值方法:数据度量法并不是一种插值方法,它根据度量所得的数据资料,可以找到比较合适的插值方法;径向基函数是多个插值方法的组合,在数据分布不均匀时易于出现局部聚集,且运算速度最慢;移动平均法的平滑效应较强,预测结果的精度较差。
与其他常规的插值方法不同的是:克里格空间估值技术是一种线性、无偏、最优的地质数据空间预测方法。对于既有区域性结构变化又有局部性异常变化的煤厚数据而言,克里格空间估值技术通过构建实验变差函数的预测模型,考虑了地质变量的空间相关性,能够实现分布疏密不均煤厚数据的空间估值。
2 克里格空间估值预测技术
20世纪50年代,南非工程师克里格为了估计金矿的品位,综合考虑了已知样品的品位、空间位置及其与待估点的距离,提出给每个已知点赋予一定的加权系数、将各已知点品位线性加权之和作为待估点的品位值;法国的马特隆教授将上述经验和方法上升为理论,提出了线性回归系数的求取方法,形成一套最佳、线性、无偏估计的克里格估值方法[21-24],成为地质统计学中经典的估值算法。
2.1 实验变差函数的计算
变差函数是代表空间变量随距离变化的函数。在一维情况下,假设煤层厚度Z(x)满足下列二阶平稳假设的2个条件:
1)在整个研究区内Z(x)的数学期望存在,且等于常数,即
E[Z(x)]=E[Z(x+h)]=m(常数)
(1)
即变量在空间上不同位置的变化围绕m值上下波动,h为Z(x)与Z(x+h)的距离。
2)在整个研究区内,Z(x)的协方差函数Cov(Z(x),Z(x+h))存在且平稳,即
Cov{Z(x),Z(x+h)}=C(h)
(2)
即协方差C(h)不依赖于空间变量的绝对位置Z(x),而依赖于Z(x)与Z(x+h)的相对距离h,具有空间的平稳不变性。
基于二阶平稳假设,设Z(x)在x、x+h两点处的煤厚值为Z(x)和Z(x+h),其中h为Z(x)和Z(x+h)两点之间的距离,即滞后距,则Z(x)在x轴方向上的变差函数定义为
(3)
其中,Var[Z(x)-Z(x+h)]为Z(x)与Z(x+h)的方差;C0为块金值。
按照实际数据计算的变差函数称为实验变差函数。对于不同的煤厚点,可以计算不同滞后距h相应的实验变差函数。一维实验变差函数的计算公式为
![]()
(i=1,2,3,…,N)
(4)
其中,N(h)代表滞后距为h的点对数量。如果有N个已知煤厚点,则可以计算任意2点之间的滞后距h,从而能够得到N(h)×(N(h)-1)/2个点上的变差值;以点间距离h为X轴、以变差γ*为Y轴,把每一个点对投影到所建立的坐标系中,可以得到变差函数点云图;把X轴分成固定间隔的区间,对落入每个区间段的变差γ*求平均,将求取的平均值作为相应区段中点的γ*值,然后将这些不同“h~γ*”的点连接起来,所得的折线即为实验变差函数曲线(图1)。

图1 实验变差函数示意
Fig.1 Schematic diagram of experimental variation function
2.2 变差函数的理论模型
由于实际数据存在观测误差,实验变差曲线并不光滑,需要根据地质变量的特点和实验变差曲线的特征,采用球状模型、指数模型、高斯模型或立方模型,对实验变差曲线进行拟合,形成变差函数理论模型。
一般情况下,采用球状模型作为理论模型:
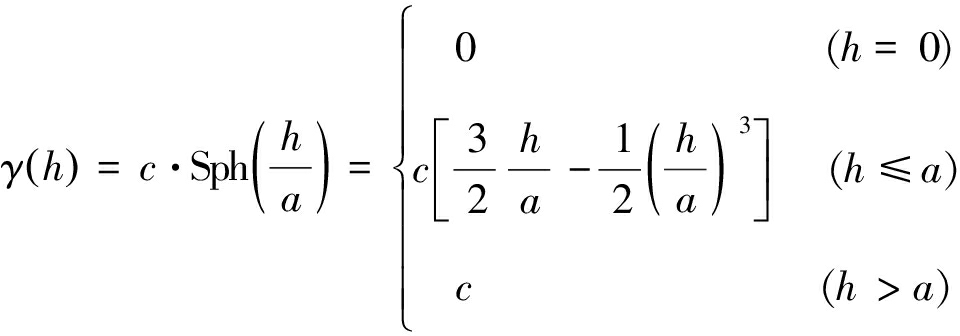
(5)
其中:c为拱高;a为变程;h为滞后距。对于空间任意一个估值点,只要求取该点与其他已知点的滞后距h,即可利用式(5)计算它的变差值γ(h)。块金值C0是滞后距h趋于0时两点之间的方差,它表征了小于观测点最小间距的数据中存在的不相关随机噪声;块金值C0越大,说明煤厚变化越大;拱高c是表征煤厚变异性的主要参数,它是煤层厚度的先验方差(图1)。在煤层厚度一定的条件下,拱高越大,表明煤厚的变化性强,稳定性差;反之,拱高越小,表明煤厚的变化性弱,稳定性强。变程a表征一个煤厚点在其邻域内的影响半径或最大影响距离。一般来说,距离小于变程a的2点间存在一定的相关性,而且距离越近相关性越强;当2点间距离大于变程a时,二者之间的相关性减弱而随机性增强。
2.3 克里格空间估值方法
克里格方法为所有已知煤厚点计算一个加权系数,最后利用加权平均法,计算每个待估点处的煤厚值:
(6)
式中:Z*(x0)为待估点的煤厚值;Z(xi)、λi分别为第i个点实际煤厚值及其权重,N为样本点数量。
由此可以看出:克里格煤厚预测并不是简单地利用已知煤厚数据点内插,而是利用已知煤厚点构建了实验变差函数和预测模型,在线性、无偏、最优估计的约束条件下,求取各已知煤厚点参与待估点煤厚计算的权重系数,进而预测空间任意一点的煤厚估计值。
即便如此,对于煤矿回采工作面煤厚预测而言,如果仅利用回风巷、运输巷和开切眼的已知煤厚数据,开展工作面未采区段的煤厚预测,其预测精度仍然偏低。表1给出了采用克里格空间估值方法,仅利用回风巷、运输巷与开切眼控制的306个已知煤厚数据,对彬长矿区某矿S1工作面的煤厚预测结果与S1工作面回采后揭露的204个煤厚点的误差统计,其中最大负误差是指预测结果小于实际煤厚的最大偏差,最大正误差是指预测结果大于实际煤厚的最大偏差,平均绝对误差是预测结果与实际煤厚之差绝对值的平均值。
表1 S1工作面内240个煤厚点预测误差统计
Table 1 Prediction error statistics of 240 verification points in S1 working face

该工作面“U”型巷道上306个已知煤厚的数学分布近似服从正态分布,其实验变差函数拟合的块金值C0=0、拱高c=5、变程a=200 m。表1的统计结果表明:仅利用回风巷、运输巷和开切眼获得的306个已知煤厚点信息,对工作面内部的煤厚进行克里格预测,经过工作面回采控制的204个煤厚点检验,其中煤厚预测误差绝对值≤0.10 m占25.98%,≤0.50 m占74.50%,≤1.00 m占90.73%。
实际上,尽管克里格空间估值技术是一种最佳的线性、无偏空间估值技术,但其估值精度与变差函数的预测模型有关。如果已知的样本数量越多,已知样本与待估数据点的距离越近,则利用实验变差函数构建的预测模型精度越高,煤厚空间估值误差则越小。因此,将工作面递进式回采过程中揭露的煤厚信息作为已知点,动态优化煤厚的预测模型,无疑将显著提高煤厚预测的精度。
3 递进式煤厚动态预测方法
3.1 递进式煤厚预测方法
图2a为工作面煤厚预测的初始阶段,此时工作面还未进行回采作业,只有回风巷、运输巷和开切眼的煤厚“静态数据”(图2a的“▲”);图2b为工作面的第一回采阶段,其中“+”代表第一回采阶段揭露的实际煤厚点。
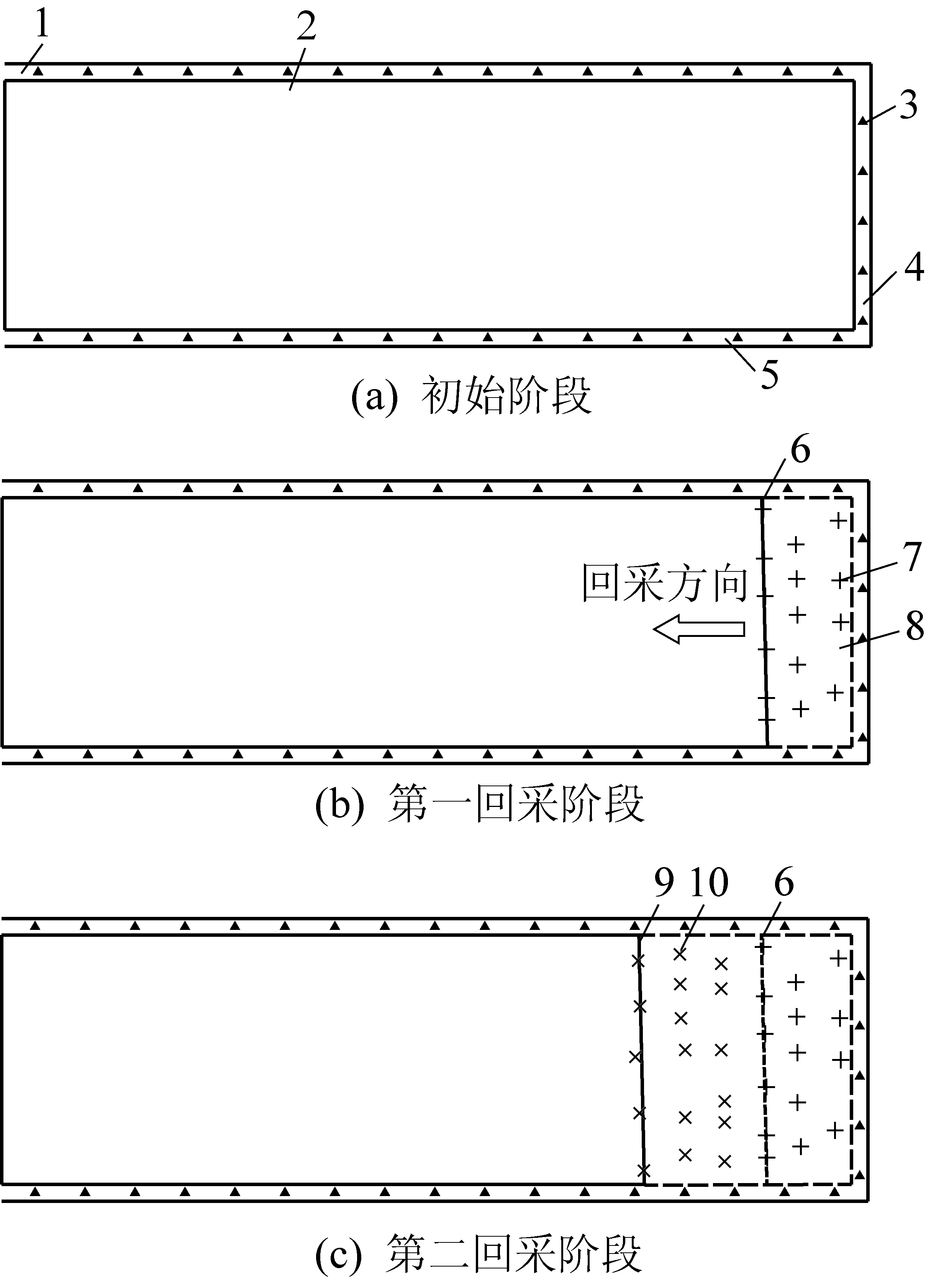
1—回风巷;2—未采煤层;3—U型回采巷煤厚测点;4—开切眼;
5—运输巷;6—第一阶段回采线;7—回采煤厚测点;
8—采空区;9—第二阶段回采线;10—第二阶段回采揭露的煤厚测点
图2 工作面煤厚递进式动态预测示意
Fig.2 Schematic diagram of coal thickness progressive prediction on working face
图2c表示工作面的第二回采阶段,与图2b相比,回采线又往前推进了一段距离,图2c中“×”表示本阶段回采新获得的煤厚点;以此类推,可以获取递进式回采过程中不断揭露的煤厚“动态数据”。
每次利用克里格估值技术进行未采区域煤厚的空间估值时,可以利用上一回采阶段新揭露的煤厚数据与前期其他已知的煤厚数据,通过煤厚“静态数据”与“动态数据”的相互融合,优化克里格估值模型,开展回采线前方的煤厚预测;如此反复迭代下去,逐步求精,可以明显提升煤厚预测的精度,这一思路和做法称为递进式煤厚动态预测。
3.2 递进式煤厚动态预测步骤
以彬长矿区某矿S1工作面为例(图3):S1工作面走向长1 650 m(横坐标x)、倾向宽180 m(纵坐标y),终采线在x=150 m处,回采方向为从右至左,该工作面已经完成回采。按照推采距离50 m作
为一个阶段,由右向左模拟回采过程,可以将S1回采工作面划分为29个递进阶段(图3)。回采工作面递进式煤厚动态预测的步骤如下:
1)递进阶段1:S1工作面推采前,已知煤厚数据仅有回风巷、运输巷和开切眼的煤厚点,以此作为输入数据,对工作面内未采区段的煤厚变化进行克里格估值,将预测结果与实际煤厚数据进行误差分析,重点分析推采距离0时开切眼前方50 m范围内(即1 600~1 650 m回采区间)的煤厚预测精度。
2)递进阶段2:S1工作面推采距离50 m、完成1 600~1 650 m的回采,在此区间实测了3个回采揭露点的煤厚数据;这时,利用1 600~1 650 m回采区间新揭露的3个煤厚点,与原有巷道、开切眼控制的306个煤厚点一起,重新拟合实验变差曲线,构建理论变差函数模型,求取空间各点的加权系数,对工作面的煤厚加以预测,重点对回采线1 600 m前方未采区段1 550~1 599 m的预测煤厚进行误差分析。
3)递进阶段3:S1工作面推采距离达到100 m、完成1 550~1 650 m的回采,在1 550~1 599 m又有回采揭露点的煤厚数据,即回采工作面新增已知煤厚点6个;这时利用1 550~1 650 m回采区间的9个煤厚点,与原有巷道、开切眼控制的306个煤厚点一起,拟合实验变差曲线,构建理论变差函数模型,求取空间各点的加权系数,对工作面范围内的煤厚变化加以预测,重点对回采线1 550 m前方未采区段1 500 ~1 549 m的预测煤厚进行误差分析。
随着模拟开采的向前推进,其他递进阶段的做法与此类似,不再赘述。

图3 S1巷道与工作面内煤厚点分布示意
Fig.3 Schematic diagram of known coal thickness points distribution in No.S1 roadway and working face
4 回采工作面煤厚预测试验
4.1 试验工作面地质概况
陕西彬长矿区某矿S1工作面的主采煤层为侏罗纪延安组的4号煤层,煤层赋存稳定,产状近乎水平;煤层结构简单,一般含2层夹矸,夹矸位于煤层的中上部,夹矸厚度一般小于0.3 m。S1工作面没有断层,但在运输巷1 079 m位置处揭露1条古河床冲刷带,对煤层回采会造成了一定的影响(图4)。S1工作面的煤厚变化范围为14.20~ 30.17 m,平均厚度24.39 m,煤厚的中值24.99 m,平均绝对误差1.49 m、标准差2.04 m、变异系数8.4%;煤厚统计直方图符合正态分布。
4.2 S1工作面的已知煤厚信息
1)巷道的煤厚静态数据。在S1工作面回采前,回风巷、运输巷及开切眼等实际控制了306个煤厚数据(图3中“▲”),其中回风巷已知煤厚点158个、运输巷已知煤厚点140个、开切眼中有8个煤厚点。
2)工作面的煤厚动态数据。在S1工作面推采过程中,不断有大量的煤厚信息被揭露,将随着工作面推采新取得的煤厚数据称为“动态数据”,图3中“+”为回采过程中揭露的204个煤厚点。如果将S1回采工作面煤厚的“静态数据”和“动态数据”不断融合,就可以对回采工作面前方未采区域的煤厚变化做出动态预测。特别需要说明的是:无论是回采工作面煤厚的“静态数据”还是“动态数据”,都是采掘工程实际揭露的可靠信息,其在煤厚预测上的价值与地质钻探控制的煤厚信息同等重要。
4.3 递进式煤厚预测的误差分析
为了对回采工作面递进式煤厚动态预测的精度进行测试,综合利用S1工作面“U”型巷道、回采工作面实际控制的510个已知煤厚点,建立S1工作面煤厚变化的实际模型。因为按照上述煤厚控制点的数量,S1工作面煤厚点的密度接近25 m×25 m,达到地面钻探控制网度的200~400倍,因此可以将此模型视为实际的煤厚模型。
按照回采工作面递进式煤厚预测的实施步骤,依次计算当前回采线前方50 m区域内煤厚预测值与实际值的误差;以回采工作面实际控制的煤厚数据为依据,计算不同递进阶段所有未采区段的煤厚预测值与实际值的误差,对递进式煤厚预测的精度进行分析。
S1工作面29个推采阶段、每次推进50 m时递进式煤厚动态预测的误差统计结果见表2。
表2 S1工作面煤厚预测精度统计
Table 2 Coal thickness prediction error statistics of S1 working face

图4给出了S1回采工作面实际的煤厚模型(图4a)、递进式煤厚的预测结果(图4b)以及预测结果与实际煤厚的误差分布图(图4c)。结果表明:S1工作面煤厚误差绝对值≤0.10 m的煤厚点数量占48.01%、≤0.50 m的煤厚点数量占85.51%、≤1.00 m的煤厚点数量占94.86%。因为S1工作面平均煤厚24.39 m,因此S1工作面的煤厚预测相对误差低于5%(即1.20 m)的点数超过95%。由此可见:基于克里格的递进式煤厚动态预测精度较高,可以为回采工作面高效开采提供可靠的地质依据。

图4 S1工作面煤厚预测结果对比
Fig.4 Results contrast of coal thickness prediction in S1 working face
5 结 论
1)针对回采工作面煤厚数据“U”型分布、疏密不均的问题,克里格估值技术通过构建空间变差函数模型,可以实现线性、无偏、最优的煤厚预测,相对于其他插值方法具有明显的优势。
2)如果仅利用“U”型巷道控制的煤厚点,开展基于克里格空间估值的工作面煤厚预测,其煤厚预测误差绝对值小于0.10、0.50、1.00 m的煤厚点数量分别占25.98%、74.50%和90.73%。
3)如果同时采用“U”型巷道和回采工作面动态揭露的煤厚数据,开展基于克里格空间估值的递进式煤厚动态预测,则煤厚预测误差绝对值小于0.10、0.50、1.00 m的煤厚点数量分别提高到48.01%、85.51%和94.86%,表明回采工作面递进式煤厚动态预测的精度显著提高。为了进一步提高回采工作面递进式煤厚动态预测的精度,今后还应加强对原始煤厚数据的校验,优化空间采样间隔、克里格预测模型和搜索半径等参数,并对薄煤层、中厚煤层工作面的适应性进行测试。
参考文献:
[1] 王国法,张德生.煤炭智能化综采技术创新实践与发展展望[J].中国矿业大学学报,2018,47(3):459-467. WANG Guofa,ZHANG Desheng.Innovation practice and development prospect of intelligent fully mechanized technology for coal mining[J].Journal of China University of Mining & Technology,2018,47(3):459-467.
[2] 孟凡刚,马亚杰,王国华,等.基于钻孔勘探数据的煤层厚度分布与构造预判[J].煤炭科学技术,2017,45(8):233-238. MENG Fangang,MA Yajie,WANG Guohua,et al.Seam thickness distribution and tectonic prediction based on exploration data from drilling[J].Coal Science and Technology,2017,45(8):233-238.
[3] 杜文凤,彭苏萍.利用地质统计学预测煤层厚度[J].岩石力学与工程学报,2010,29(S1):2762-2767. DU Wenfeng,PENG Suping.Coal seam thickness prediction with geostatistics [J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S1): 2762-2767.
[4] 何亚群,左蔚然,张书敏,等.基于地质统计学的煤田煤质插值方法比较[J].煤炭学报,2008,33(5):514-517. HE Yaqun,ZUO Weiran,ZHANG Shumin,et al.Comparison of interpolations for coal nature of coalfield based on geological statistics [J].Journal of China Coal Society,2008,33(5):514-517.
[5] 张琳娜,樊隽轩,侯旭东,等.地层数据的常用空间插值方法介绍和比较分析:以上扬子区宝塔组厚度重建为例[J].地层学杂志,2016,40(4):420-428. ZHANG Linna,FAN Junxuan,HOU Xudong,et al.Comparison of common spatial interpolation methods in stratigraphic data analysis: a case study of the stratigraphic thickness of the Ordovician pagoda formation in the upper YANGZE region[J].Journal of Stratigraphy,2016,40(4): 420-428.
[6] 孟召平,郭彦省,王 赟,等.基于地震属性的煤层厚度预测模型及其应用[J].地球物理学报,2006,49(2):512-517. MENG Zhaoping,GUO Yansheng,WANG Yun,et al.Prediction models of coal thickness based on seismic attributions and their applications[J].Chinese Journal of Geophysics,2006,49(2):512-517.
[7] 李启成,郭 雷,孙颍川,等.地震属性融合技术在煤层厚度预测中的研究[J].地球物理学进展,2017,32(5):2014-2020. LI Qicheng,GUO Lei,SUN Yingchuan,et al.Seismic attributes fusion and its research in predicting thickness of coal [J].Progress in Geophysics,2017,32(5): 2014-2020.
[8] 崔辉霞,杨文强,赵牧华.钻孔约束频域定量预测煤厚方法研究与应用[J].煤炭科学技术,2006,34(2):6-8. CUI Huixia,YANG Wenqiang,ZHAO Muhua.Research and application of seam thickness prediction method with borehole restrained frequency area quantified [J].Coal Science & Technology,2006,34(2):6-8.
[9] 李 红,吕进英,王宏友.波阻抗约束反演技术预测煤层厚度[J].煤田地质与勘探,2007,35(1):74-77. LI Hong,LYU Jinying,WANG Hongyou.Exploration logging-constrained inversion technique predicting coal-thickness [J].Coal Geology & Exploration,2007,35(1):74-77.
[10] 师素珍,李赋斌,梁 平,等.多井约束反演在煤层厚度定量预测中的应用[J].采矿与安全工程学报,2011,28(2):328-332. SHI Suzhen,LI Fubin,LIANG Ping,et al.Application of multi-well constrained seismic inversion in quantitative prediction of coal seam thickness[J].Journal of Mining & Safety Engineering,2011,28(2): 328-332.
[11] 陈优阔,杨永国,张 鑫,等.基于粗糙集及最小二乘支持向量机的煤层厚度预测[J].地球物理学进展,2015,30(5):2136-2141. CHEN Youkuo,YANG Yongguo,ZHANG Xin,et al.Forecasting of coal thickness based on rough set and LS-SVM[J].Progress in Geophysics,2015,30(5): 2136-2141.
[12] 王 伟,高 星,李松营,等.槽波层析成像方法在煤田勘探中的应用:以河南义马矿区为例[J].地球物理学报,2012,55(3):1054-1062. WANG Wei,GAO Xing,LI Songying,et al.Channel wave tomography method and its application in coal mine exploration: an example from Henan Yima Mining Area[J].Chinese Journal of Geophysics,2012,55(3):1054-1062.
[13] 程建远,江 浩,姬广忠,等.基于节点式地震仪的煤矿井下槽波地震勘探技术[J].煤炭科学技术,2015,43(2):25-28. CHENG Jianyuan,JIANG Hao,JI Guangzhong,et al.Channel wave seismic exploration technology based on node digital seismograph in underground mine [J].Coal Science and Technology,2015,43(2): 25-28.
[14] 李松营,廉 洁,滕吉文,等.基于槽波透射法的采煤工作面煤厚解释技术[J].煤炭学报,2017,42(3):719-725. LI Songying,LIAN Jie,TENG Jiwen,et al.Interpretation technology of coal seam thickness in mining face by ISS transmission method[J].Journal of China Coal Society,2017,42(3):719-725.
[15] 冯 磊,杜艳艳,李松营,等.煤层厚度地震槽波层析成像分辨率分析[J].地球物理学进展,2018,33(1):197-203. FENG Lei,DU Yanyan,LI Songying,et al.Resolution analysis of in-seam seismic tomographic inversion for coal thickness [J].Progress in Geophysics,2018,33(1):197-203.
[16] 宋庆军.综放工作面放煤自动化技术的研究与应用[D].徐州:中国矿业大学,2015.
[17] 陈欢欢,李 星,丁文秀.Surfer 8.0 等值线绘制中的十二种插值方法[J].工程地球物理学报,2007,4(1):52-57. CHEN Huanhuan,LI Xing,DING Wenxiu.Twelve kinds of gridding methods of Surfer 8.0 in isoline drawing[J].Chinese Journal of Engineering Geophysics,2007,4(1): 52-57.
[18] 靳国栋,刘衍聪,牛文杰.距离加权反比插值法和克里金插值法的比较[J].长春工业大学学报,2003,24 (3):53-57. JIN Guodong,LIU Yancong,NIU Wenjie.Comparison between inverse distance weighting method and Kriging[J].Journal of Changchun University of Technology,2003,24 (3):53-57.
[19] 张艳伟,屠世浩,王 沉,等.基于趋势面分析的煤层厚度变化规律研究[J].西安科技大学学报,2015,35(1):21-27. ZHANG Yanwei,TU Shihao,WANG Chen,et al.Research on coal seam thickness changing law based on trend surface analysis [J].Journal of Xi’an University of Science and Technology,2015,35(1): 21-27.
[20] 李晓军,胡金虎,朱合华,等.基于Kriging方法的煤层厚度估计及三维煤层建模[J].煤炭学报,2008,33(7):765-769. LI Xiaojun,HU Jinhu,ZHU Hehua,et al.The estimation of coal thickness based on Kriging technique and 3D coal seam modeling [J].Journal of China Coal Society,2008,33(7):765-769.
[21] 刘俊杰.地质统计学在预测煤层冲刷带中的应用研究[J].煤炭学报,2004,29(1):49-52. LIU Junjie.Application study of geostatistics to predicate washout zone in coal seam[J].Journal of China Coal Society,2004,29(1): 49-52.
[22] 崔洪庆,张振文,张平安.煤厚半变差函数的结构分析[J].辽宁工程技术大学学报,2003,22(3):310-312. CUI Hongqing,ZHANG Zhenwen,ZHANG Pingan.Structural analysis of half variation function of coal thickness[J].Journal of Liaoning Technical University,2003,22(3): 310-312.
[23] 科瓦列夫斯基E B.基于地质统计学的地质建模[M].刘应如,曹正林,郑红军,等,译.北京:石油工业出版社,2014.
[24] 王家华,高海余,周 叶.克里金地质绘图技术[M].北京:石油工业出版社,1999.