0 引言
大型设备是露天矿不可或缺的重要组成部分,设备利用效率直接决定了露天矿的生产效率和经济效益。电铲、卡车作为电铲—卡车间断开采工艺系统[1]和半连续开采工艺系统[1-2]的典型设备,在我国各大露天矿中使用广泛。在实际生产过程中,由于受外部环境的影响,电铲、卡车的故障频繁,维修费用高,占据整个生产成本的60%左右[3-4],同时设备故障也易引发安全事故。因此做好露天矿典型设备的维修管理具有十分重要的现实意义[5]。但就目前国内企业对露天矿典型设备的故障维修管理方法来看,现有的故障预测技术几乎都应用于设备故障诊断,即在设备发生故障后,利用相关理论与经验结合,快速推断故障部位,从而进行维修。这种后效性的故障诊断方法虽然能在一定程度上降低露天矿山的开采成本,但对降低设备故障率,保障矿山开采的安全性没有实质性效果。随着GB/T34679—2017《智慧矿山信息系统通用技术规范》的正式颁布实施,标志着我国智能化矿山[6-8]建设已开始正式落地。在矿山设备智能化发展领域,寻求更为科学有效的方法预测露天矿典型设备的故障发生时间和故障发生类型已经成为了当前亟待解决的科学问题。
近年来,随着人工智能技术的飞速发展,机器学习[9]技术得到了广泛应用,其预测准确率高,可靠性强的特点更适于解决复杂条件下露天矿各种大型设备的故障分析、预测等问题。诸多学者开展了一系列富有成效的工作,在卡车故障预测方面,白润才等[10]就矿用卡车的故障率问题,综合运用机器学习方法,提出了基于小波分析和ARMA模型的矿用卡车故障率预测方法;杨欢等[11]基于BP神经网络针对卡车齿轮箱的故障数据进行了仿真,提出了诊断卡车齿轮箱故障类型的有效方法,并给出了齿轮箱安全隐患的预判准则。H. Hu等[12]利用神经网络分类算法对矿用卡车数据进行分析建模,提出了卡车状况和性能的预测方法,显著提高了矿用卡车的效率。在电铲故障预测方面,邓正义[13]从经验出发,总结并归纳了电铲常见故障的发生原因,提出了相应的诊断方法和处理措施;王清心[14]针对WK-35电铲运行过程中的4个典型疑难故障进行了分析,并给出了相应的处理方案,为研究分析电铲故障提供了有效的实践参考。DINDARLOO等[15]利用数据挖掘技术对电铲故障数据进行了分析,通过分类和聚类算法,使故障预测精度超过75%,并将分析预测结果成功运用于设备的分配和维护计划。
上述研究各有所长,但在露天矿典型设备的故障预测研究方面还仅局限在以经验分析和故障诊断为主,得到的结果往往具有主观局限性和后效性,所采用的以机器学习技术为主的故障分析预测方法,也只能针对某一设备的故障率或设备的某一类型故障,不能兼而有之,且不能有效预测设备的故障发生时间。马尔科夫蒙特卡罗方法(Markov Chain Monte Carlo,称MCMC)是统计机器学习领域的一个重要分支,在故障数据分析和预测方面有着显著效果[16-20],因此,笔者提出了一种基于MCMC算法的露天矿典型设备故障预测方法,实践应用表明,该方法能有效应用于露天矿典型设备的故障预测分析。
1 MCMC理论
MCMC是一种可在样本不独立的条件下从任意分布中进行抽样的重要算法。MCMC可以理解为使用了“马尔科夫链”的“蒙特卡罗”方法,其核心思想[20]是构造一条马尔科夫链,使其平稳分布为待估参数的后验分布,当马尔科夫链达到平稳分布后,其时间序列上各个时刻的状态便可作为后验分布的样本。其主要过程包括以下2个部分[21]。
1.1 构造符合要求的马尔科夫链
马尔科夫链是指具有马尔科夫性质(某一时刻状态转移的概率只依赖于前一个状态)且存在于离散的指数集和状态空间内的随机过程。马尔科夫链的2个重要性质:
1)非周期不可约马尔科夫链一定可以收敛到唯一的平稳分布[22];
2)马尔科夫链在某一时刻的分布π为平稳分布的一个充分不必要条件(细致平稳条件)为
π(i)Pij=π(j)Pji
(1)
其中:π(i)表示处于状态xi的概率;Pij表示由状态xi转移到状态xj的概率,即Pij=p(j|i)。所以当给定目标分布函数p(x)时,所构造的用于在时间序列上进行抽样的马尔科夫链需具备上述2个性质。
对于不满足细致平稳条件的马尔科夫链可采用如下方法进行改造:
1)设马尔科夫链的转移矩阵为G,处于状态xi的概率为p(i),由状态xi转移到状态xj的概率为g(j|i);
2)引入条件概率α(j|i)=p(j)g(i|j)与α(i|j)=p(i)g(j|i),使得下式成立,即
p(i)g(j|i)α(j|i)=p(j)g(i|j)α(i|j)
(2)
3)令g′(j|i)=g(j|i)α(j|i),那么有
g′(i|j)=g(i|j)α(i|j),构造新的转移矩阵G′。
这样,就可将不满足细致平稳条件的马尔科夫链转变为满足细致平稳分布的新的马尔科夫链(转移矩阵由G变为G′),新马尔科夫链的平稳分布函数就是p(x)。改造过程中引入的α(j|i)一般称为接受率,可以理解为在原来的马尔科夫链中,由状态xi以概率g(j|i)转移到状态xj时,以概率α(j|i)接受这个转移,以1-α(j|i)拒绝这个转移,称拒绝率,于是新马氏链的转移概率为g(j|i)α(j|i)[23]。
上述基本MCMC抽样算法能够获得符合实际要求的样本,但马尔科夫链在转移的过程中接受率α(j|i)可能偏小,易使抽样过程原地踏步,拒绝大量跳转,导致马尔科夫链遍历状态空间时需要大量的时间,收敛到平稳分布π的速度太慢[24]。因此,在实际操作时常采用一定的策略加速收敛过程,目前常用算法主要有Metropolis-Hasting(M-H)算法和Gibbs算法,其中M-H算法多适用于低维空间,而Gibbs算法多适用于高维空间[25]。
M-H算法的设计思想是将细致平稳条件中的α(j|i)和α(i|j)同比例放大,使得2个值中较大的一个放大到1,这样就能够提高跳转接受率。同时引进一个容易抽样的提议分布g(x),在每次抽样过程中从函数g(x)中获得一个候选样本y,然后按照“保证得到的分布恰好相似于给定目标分布函数p(x)”的原则决定是否接受该样本。M-H算法的实现步骤如下:
步骤1:初始化马尔科夫链,令初始状态X0=x0。
步骤2:对于t=0,1,2,…,2n,循环执行以下过程。
步骤3:第t时刻马尔科夫链的状态为:Xt=xt,从提议分布中抽样:y~g(x|xt)。
步骤4:计算接受率α(y|xt),即
(3)
步骤5:从均匀分布中抽样:u~U(0,1)。
步骤6:若u<α(y|xt),则接受转移xt→y,Xt+1=y;否则不接受转移,即Xt+1=xt。
1.2 判断构造的马尔科夫链是否收敛
采用Gelman-Rubin判断法(方差比法)进行马尔科夫链收敛性判断。其判别原理为:当初始值分散的m条马尔科夫链平行运行达到收敛时,这些链的推断结果应该非常接近,其比值将趋近于1。Gelman- Rubin判断法的主要步骤如下:
步骤1:从目标分布p(x)中选取比较分散的初值,建立m条目标分布的马尔科夫链,对m条链分别迭代2n次,丢弃前n次迭代结果,保留并分析后n次迭代结果。
步骤2:计算多条马尔科夫链之间的方差B/n:设目标统计量为θ,第i条链的第t个样本的θ值为![]() 则
则
(4)
其中:![]()
步骤3:计算单条马尔科夫链内的方差W为
(5)
其中:![]()
步骤4:构造诊断指标![]() 为
为
(6)
其中:![]()
步骤5:根据诊断指标![]() 进行收敛性判断:当
进行收敛性判断:当![]() 时,马尔科夫链不收敛,迭代次数不够,需要增加迭代次数或重新构造马尔科夫链。当
时,马尔科夫链不收敛,迭代次数不够,需要增加迭代次数或重新构造马尔科夫链。当![]() 时,马尔科夫链收敛。
时,马尔科夫链收敛。
2 基于MCMC的设备故障预测算法
由浴盆曲线[26]性质可知,设备故障发生次数会随着设备使用时间的推移而发生变化,并在设备进入偶然失效期后呈现出稳定性。因此,设备故障发生次数所服从的泊松分布的参数λ可以通过MCMC方法抽样获得。笔者提出了一种用于系统可靠性仿真的设备故障发生时间仿真算法:首先利用MCMC算法按年度对设备故障数据进行抽样估计,获得设备故障发生次数对应的齐次泊松过程的参数λ,再根据浴盆曲线对每一年度的λ值进行修正和曲线拟合,确定设备当前状态下故障发生次数的泊松分布参数的值λc,然后再利用齐次泊松过程中随机点的点间间距是相互独立的指数分布随机变量序列的性质,将λc的倒数作为指数分布参数的估计值,确定设备故障发生时间间隔所服从的指数分布,最后利用指数分布预测设备故障发生时间。整个过程的试验设计步骤如下:
步骤1:从现场采集电铲、卡车设备月故障发生次数数据;
步骤2:(历史数据学习过程)假设设备每月故障发生次数为齐次泊松过程,采用MCMC方法抽样估计齐次泊松过程参数λ(为满足系统可靠性仿真需要,假设设备故障分布在一年内不发生显著变化,即每一年度产生一个λ值,若对s年的数据进行分析,将产生λ1,λ2,...,λs,共计s个λ),其中检验使用的马尔科夫链条数m=5,收敛性检验方法采用Gelman-Rubin判断法,提议分布选取自由度为λt的卡方分布为

(7)
步骤3:(未来数据预测过程)由步骤2获得每一年度的设备故障发生次数泊松分布参数序列λ1,λ2,…,λs,根据浴盆曲线判断设备当前状态:若λ1,λ2,…,λs中初值与其他值差距较大,说明设备已由早期失效期逐渐进入偶然失效期,可剔除掉初值,对剩下的数据进行曲线拟合,以确定λc;若λ1,λ2,…,λs中终值与其他值差距较大,说明设备已由偶然失效期逐渐进入损耗失效期,可对终值附近的数据进行曲线拟合,以确定λc;若λ1,λ2,…,λs中初值与终值均未呈现出显著波动,则说明设备正处于偶然失效期,可对所有数据进行曲线拟合,以确定λc;
步骤4:确定设备故障发生时间间隔所服从的指数分布的参数λe为
λe=30×24×60/λc
(8)
样本数据为每个月的故障发生次数,因此参数λc的时间单位是月,由于系统可靠性仿真需要以分钟为单位进行仿真钟推进,所以转换为指数分布的参数时需要扩大30×24×60倍(每月按30 d计算);
步骤5:预测设备故障发生时间。设仿真开始时间为ts,仿真结束时间为te,从设备故障发生时间间隔所服从的指数分布中进行抽样,以获得统计意义上设备故障发生时间间隔值:w1,w2,…,wk,令t1=ts+w1,t2=t1+w2,…,tk=tk-1+wk,直至tk>te,则时间序列t1,t2…,tk即为设备故障发生时间的预测值(此方法获得的设备故障发生时间与实际故障发生时间不能保证完全一致,但两者的统计特性相同,即从长期观测的角度来看,两者具有相同的频率变化趋势)。
3 应用实例
3.1 试验数据及过程说明
从神华宝日希勒能源有限公司露天煤矿大型设备维修管理系统提取了1#WK35电铲(2015—2018年)、1#TR100卡车(2010—2018年)的维修数据用于仿真预测。具体试验环境如下:
操作系统:Windows 10;环境管理器:Anaconda3;编程语言:Python3.7;核心包:pymc3、numpy、pyplotz、matplotlib、pandas、scipy、pylab、math。
仿真试验共分为2个部分,第1部分以单台卡车(1#TR100)为例,第2部分以单台电铲(1#WK35)为例。每一部分均根据设备故障持续时间(即维修时间,由设备维修记录中出厂时间减去入厂时间获得)长短将故障分为5类,分类规则见表1,分别采用MCMC方法对5类故障进行设备故障发生次数泊松过程参数抽样估计和设备故障发生时间预测。
表1 故障分类规则
Table 1 Fault classification rule

故障持续时长区间/min故障类型[0,30]1(30,60]2(60,120]3(120,480]4(480,+∞)5
3.2 试验结果与分析
1)1#TR100卡车。提取1#TR100卡车2010至2018年的故障维修记录作为观测数据。采用第2节的预测算法进行数值试验,具体结果见表2和如图1所示。
表2 1#TR100卡车5类故障发生次数泊松分布参数λ估计值和CSRF检验值
Table2 2 Estimate of parameter λ and test value of CSRF for 1#TR100 truck
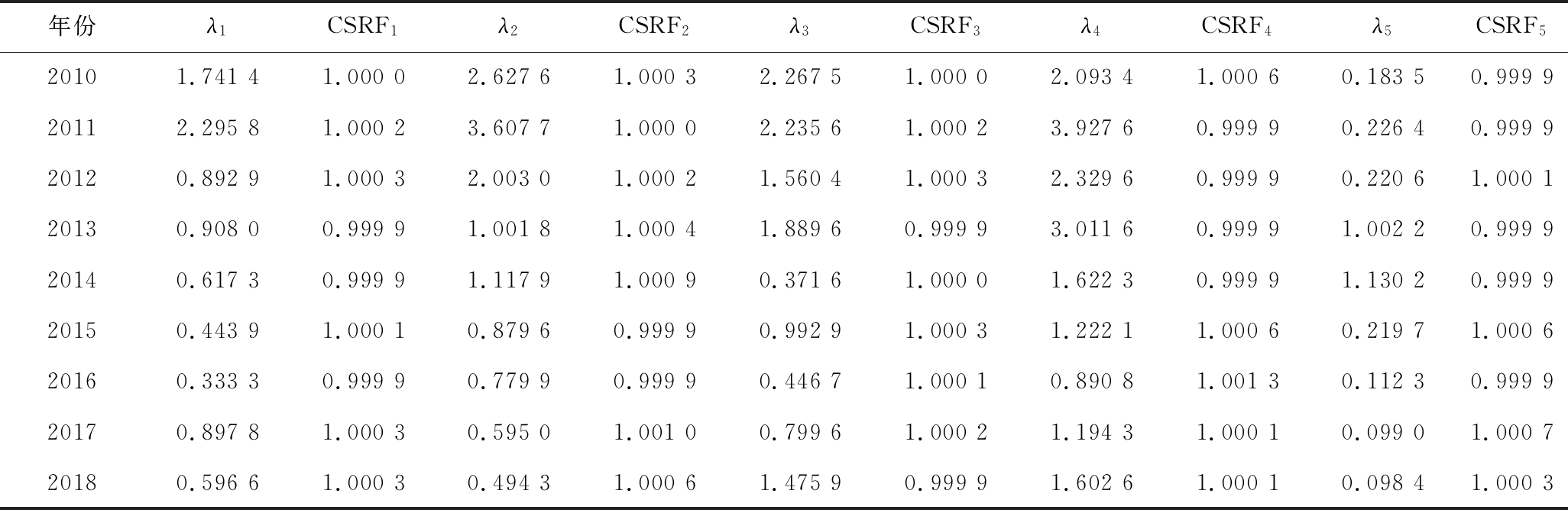
年份λ1CSRF1λ2CSRF2λ3CSRF3λ4CSRF4λ5CSRF520101.74141.00002.62761.00032.26751.00002.09341.00060.18350.999920112.29581.00023.60771.00002.23561.00023.92760.99990.22640.999920120.89291.00032.00301.00021.56041.00032.32960.99990.22061.000120130.90800.99991.00181.00041.88960.99993.01160.99991.00220.999920140.61730.99991.11791.00090.37161.00001.62230.99991.13020.999920150.44391.00010.87960.99990.99291.00031.22211.00060.21971.000620160.33330.99990.77990.99990.44671.00010.89081.00130.11230.999920170.89781.00030.59501.00100.79961.00021.19431.00010.09901.000720180.59661.00030.49431.00061.47590.99991.60261.00010.09841.0003

图1 1#TR100卡车的5类故障发生次数泊松分布参数λ趋势
Fig.1 Trend graph of fault parameter λ for 1#TR100 truck
由表2可知,1#TR100卡车2010—2018年5类故障发生次数泊松分布参数λ的CSRF值都小于1.2,且十分接近1,因此MCMC抽样获得的λ值可靠。
从图1中参数λ的变化趋势知:1#TR100卡车在2010年和2011年时前4类故障发生次数均较高,结合浴盆曲线性质可认为该设备自2012年开始进入偶然失效期,因此在设备故障发生次数泊松分布参数预测时,剔除掉2010年和2011年的数据,对2012—2018年的λ值进行线性拟合,并根据拟合结果预测参数λ的2019年取值。曲线拟合结果如图2所示,2019年5类故障发生次数泊松分布参数λc的预测值分别为λc1=0.501 3,λc2=0.176 8,λc3=0.757 5,λc4=0.767 6,λc5=0.044 2。

图2 1#TR100卡车的5类故障发生次数泊松分布参数λ拟合曲线
Fig.2 1#TR100 fault parameter λ fitting curve
将参数λc1、λc2、λc3、λc4、λc5分别代入相应的设备故障发生时间间隔指数分布,对1#TR100五类故障进行故障发生时间仿真抽样,可获得用于系统可靠性仿真的设备故障发生时间预测结果(仿真时间为六个月)见表3。
表3 1#TR100卡车的故障发生时间预测结果
Table 3 Predicted time of failure for 1# TR100
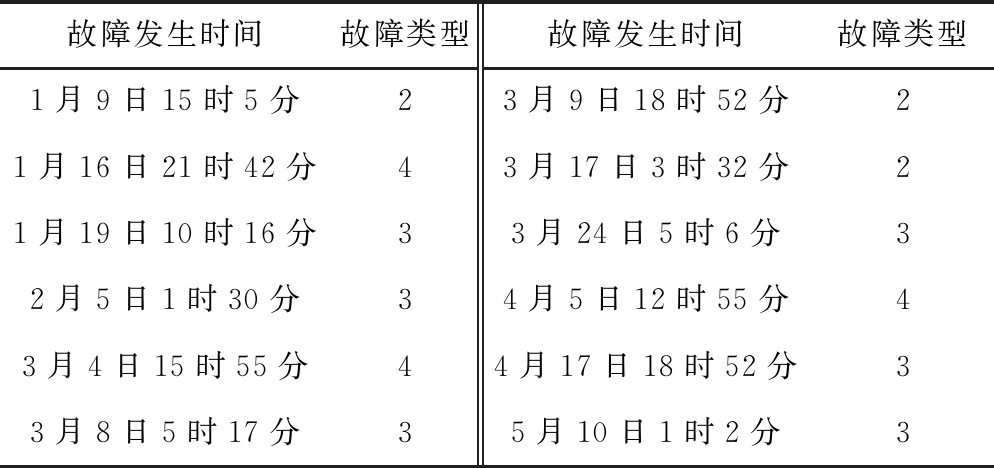
故障发生时间故障类型故障发生时间故障类型1月9日15时5分23月9日18时52分21月16日21时42分43月17日3时32分21月19日10时16分33月24日5时6分32月5日1时30分34月5日12时55分43月4日15时55分44月17日18时52分33月8日5时17分35月10日1时2分3
2)1#WK35电铲。提取1#WK35电铲2015年—2018年的维修数据记录作为观测数据。采用设计的仿真算法进行数值试验,具体结果见表4和如图3所示。
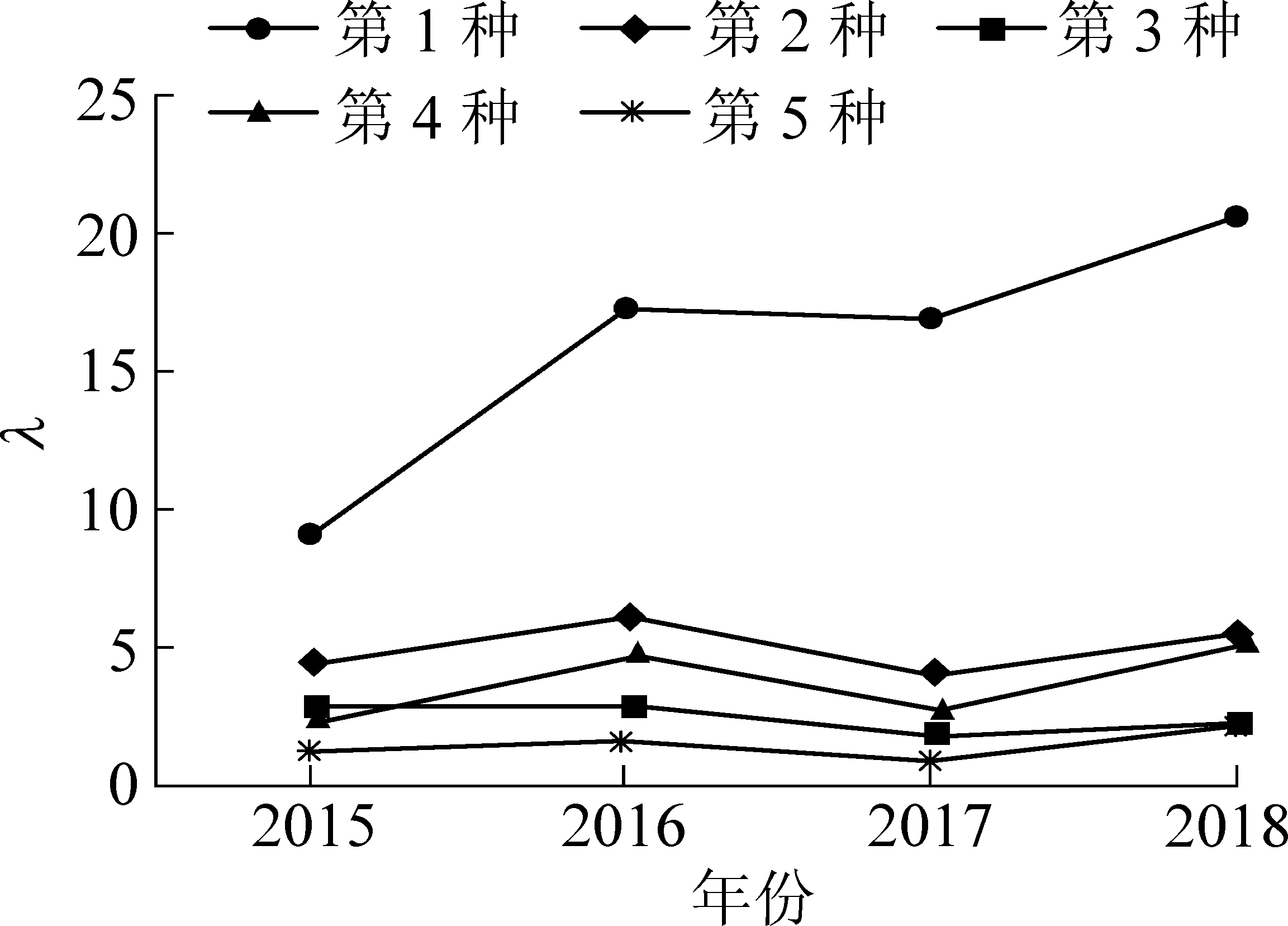
图3 1#WK35电铲5类故障发生次数泊松分布参数λ趋势
Fig.3 Trend graph of fault parameter λ for 1#WK35 shovel
由表 4可知,1#WK35电铲2015—2018年五类故障发生次数泊松分布参数λ的CSRF值都小于1.2且十分接近1.0,因此MCMC抽样获得的λ值可靠。
表4 1#WK35电铲5类故障发生次数泊松分布参数λ估计值和 CSRF检验值
Table 4 Parameter λ estimate and test value CSRF for 1#WK35 shovel

年份λ1CSRF1λ2CSRF2λ3CSRF3λ4CSRF4λ5CSRF5201513.89450.99997.31291.00073.53500.99993.69890.99990.23070.9999201617.23081.00157.53141.00003.45780.99993.38571.00020.22901.0001201717.59471.00007.24040.99993.39541.00023.99471.00030.22801.0000201819.64541.00085.12410.99994.11270.99993.86561.00090.37520.9999
对1#WK35电铲2015—2018年的故障发生次数泊松分布参数λ进行线性拟合,如图4所示。

图4 1#WK35电铲5类故障发生次数泊松分布参数λ拟合曲线
Fig.4 1#WK35 shovel fault parameter λ fitting curve
表5 1#WK35电铲故障发生时间预测结果
Table 5 Predicted time of failure for 1#WK35 shovel

故障发生时间故障类型故障发生时间故障类型1月2日10时25分41月17日2时44分11月2日22时12分11月19日19时5分31月4日3时37分11月19日19时13分31月4日8时40分11月21日17时57分41月4日20时13分11月21日23时53分11月5日2时54分11月22日0时24分31月5日15时28分11月23日20时59分11月6日0时41分11月25日21时57分11月6日1时35分11月26日11时5分31月10日7时19分11月26日23时9分11月10日9时32分11月27日13时31分11月11日23时26分11月28日0时8分11月12日1时30分11月29日11时55分31月13日15时4分21月29日18时17分21月14日22时51分11月29日23时52分21月15日6时32分21月30日6时4分1
并预测5类故障发生次数泊松分布参数λc的结果依次为
λc1=21.4955,λc2=5.0879,λc3=4.0429,λc4=4.0135,λc5=0.3739。
将参数λc1、λc2、λc3、λc4、λc5分别代入相应的设备故障发生时间间隔指数分布,对1#WK35五类故障进行故障发生时间仿真抽样,可获得用于系统可靠性仿真的设备故障发生时间预测结果(仿真时间为1个月)见表 5 。
4 结论
1)从数据驱动的角度出发,采用以机器学习为主的数据分析手段,提出了一种基于MCMC算法的露天矿典型设备故障预测方法,修正尺度简缩因子(CSRF)验证结果表明:该方法具有合理性和有效性,能够用于对露天矿典型设备的故障预测。
2)通过预测算法得到2019年露天矿典型设备故障预测结果与设备实际运行结果的对比可知,本文提出的方法能够从统计意义上对露天矿典型设备的故障发生规律进行揭示,并进一步验证了设备故障发生次数所服从的泊松分布参数随时间动态变化、设备故障维修时长随设备使用年限的增长而逐渐变长(设备发生中型及以上故障次数增多)等经验性结果。
3)在外部环境不发生明显变化时,笔者提出的方法能够有效预测露天矿典型设备的故障发生时间和故障类别,其研究成果不仅能为企业科学制定设备的预防性维修计划提供依据,而且能为露天开采工艺系统智能仿真、露天矿生产智能管控等智慧露天矿建设综合解决方案提供有效的基础决策数据。
[1] 骆中洲.露天采矿学:上册[M].徐州:中国矿业大学出版社,1986.
[2] 陈树召.大型露天煤矿他移式破碎站半连续工艺系统优化与应用研究[D].徐州:中国矿业大学,2011.
[3] 骆中洲,王连印.露天矿汽车运输的故障与维修[J].有色金属:矿山部分,1989(5):1-6.
LUO Zhongzhou,WANG Lianyin. Troubles and maintenance of truck transportation in open pit mine[J].Non-ferrous Metals:Mine Part,1989(5):1-6.
[4] 田凤亮,孙效玉,张 航.一种露天矿卡车故障的NLP技术挖掘与分析方法[J].金属矿山,2017(7):138-142.
TIAN Fengliang,SUN Xiaoyu,ZHANG Hang.A mining and analyzing methodof truck fault in open-pit mine based on NLP technology[J].Metal Mine,2017(7):138-142.
[5] 贾美青.露天矿运输机械设备如何加强设备管理与维修[J].矿业装备,2019(1):86-87.
JIA Meiqing. How to strengthen equipment management and maintenance of transportation machinery and equipment in open-pit mine[J]. Mining Equipment,2019(1):86-87.
[6] 王国法,刘 峰,孟祥军,等.煤矿智能化(初级阶段)研究与实践[J].煤炭科学技术,2019,47(8):1-36.
WANG Guofa,LIU Feng,MENG Xiangjun, et al.Research and practice on intelligent coal mine construction (primary stage)[J]. Coal Science and Technology,2019,47(8):1-36.
[7] 王国法,刘峰,庞义辉,等.煤矿智能化:煤炭工业高质量发展的核心技术支撑[J].煤炭学报,2019,44(2):349-357.
WANG Guofa,LIU Feng, PANG Yihui, et al. Coal mine intellect- tuallization:the core technology of high quality development [J].Journal of China Coal Society,2019,44(2): 349-357.
[8] 王国法,杜毅博.智慧煤矿与智能化开采技术的发展方向[J].煤炭科学技术,2019,47(1):1-10.
WANG Guofa,DU Yibo. Development direction of intelligent coal mine and intelligent mining technology[J]. Coal Science and Technology,2019,47(1):1-10.
[9] MURPHY K P. Machine learning: a probabilistic perspective[J]. Chance, 2012, 27(2):62-63.
[10] 白润才,柴森霖,刘光伟,等.基于Mallat算法与ARMA模型的露天矿卡车故障率预测[J].中国安全科学学报,2018,28(10): 31-37.
BAI Runcai,CHAI Senlin,LIU Guangwei, et al. Method for predicting truck’s failure rate in open-pit mine based on Mallat algorithm and ARMA model[J]. China Safety Science Journal, 2018,28(10): 31-37.
[11] 杨 欢,刘永刚,徐 博,等.基于BP神经网络的重型卡车齿轮箱故障诊断方法研究[J].机械研究与应用,2017,30(4):20-21,26.
YANG Huan,LIU Yonggang,XU Bo, et al. Research on fault diagnosis method of heavy truck gear box based on BP neural network[J].Mechanical Research & Application,2017,30(4):20-21,26.
[12] HU H,GOLOSINSKI T S. Early detection of mining truck failure by modelling its operation with neural networks classification algorithms[J]. Application of Computers and Operations Research Minerals Industries,2002, 29: 1-3.
[13] 邓正义.浅析电铲设备的故障诊断与处理[J].中国金属通报, 2017(7):138,137.
DENG Zhengyi. Analysis on fault diagnosis and treatment of electric shovel equipment[J].China Metal Bulletin, 2017(7): 138,137.
[14] 王清心.WK-35电铲疑难故障及维护[J].煤炭工程,2017,49 (7):84-86,89.
WANG Qingxin.WK-35 electric shovel troubles and maintenance [J].Coal Engineering,2017,49(7):84-86,89.
[15] DINDARLOO S R,Siami-Irdemoosa E. Data mining in mining engineering: results of classification and clustering of shovels failures data[J].International Journal of Mining Reclamation and Environment, 2016, 31(2):105-118.
[16] 张 颖,傅 强.GJR-CAViaR模型的贝叶斯分位数回归:基于Gibbs抽样的MCMC算法实现[J].中央财经大学学报,2017(7):87-95.
ZHANG Ying,FU Qiang.Bayesian Quantile Regression of GJR-CAViaR Model: an implementation of MCMC Algorithm based on Gibbs sampling and its associated empirical analysis [J]. Journal of Central University of Finance & Economics,2017 (7):87-95.
[17] CHEN Changyou,WANG Wenlin,ZHANG Yizhe, et al. A convergence analysis for a class of practical variance-reduction stochastic gradient MCMC[J]. Science China:Information Scien-ces,2019,62(1):67-79.
[18] LARS Holden. Mixing of MCMC algorithms[J].Journal of Statistical Computation and Simulation,2019,89(12):5-20.
[19] GOLSA Moayeripour,AMIRHOSSEIN Aghakhani,MEISAM Nesary Moghadam,et al. Reducing bandwidth allocation delay in a DVB-RCS network using Bayesian Neural Network[C],Advanced Communication Technology,11th International Conference 2009:2185-2190.
[20] 朱新玲.马尔科夫链蒙特卡罗方法研究综述[J].统计与决策, 2009(21):151-153.
ZHU Xinling. Summary of research on Markov Chain Monte Carlo Method[J].Statistics & Decision, 2009(21):151-153.
[21] RUBINSTEIN R Y, KROESE D P. Simulation and the Monte Carlo method[M].Hoboken: John Wiley & Sons, 2016.
[22] BRÉMAUD P. Markov chains: Gibbs fields, Monte Carlo simulation, and queues[M].Berlin: Springer Science & Business Media, 2013.
[23] DOUCET A,PITT M K,Deligiannidis G, et al. Efficient implementation of Markov chain Monte Carlo when using an unbiased likelihood estimator[J].Biometrika,2015,102(2):295-313.
[24] ANARI N, GHARAN S O, REZAEI A.Monte carlo markov chain algorithms for sampling strongly rayleigh distributions and deter- minantal point processes[C].Conference on Learning Theory,2016:103-115.
[25] CHO W K T,LIU Y Y.Sampling from complicated and un- known distributions: Monte Carlo and Markov chain Monte Carlo methods for redistricting[J]. Physica A: Statistical Mechanics and its Applications, 2018, 506: 170-178.
[26] 陈伟波,范 韬,叶 欣,等.基于浴盆曲线的整车耐久试验故障曲线[J].武汉理工大学学报:信息与管理工程版,2019,41(3):312-315,344.
CHEN Weibo,FAN Tao,YE Xin, et al.Vehicle durability test incident rate curve based on bathtub curve[J]. Journal of Wuhan University of Technology:Information & Management Engineering,2019,41(3): 312-315,344.
