移动扫码阅读
采矿与井巷工程
移动扫码阅读
随着全国煤炭资源的逐步开采，各地区涌现出已建或待建的各类矿井工程，在冻结法施工过程中，其冻结井筒的可靠性仍是决定工程安全的重要参数指标[1-3]。而在传统的可靠性计算过程中，无论结构抗力或荷载都是用确定值表示，但根据长期工程实践总结，深冻结工程中井筒所处的外部环境变幻莫测，导致井壁外荷载和极限抗力表现出明显的模糊随机性，故整体冻结井筒的可靠性显示出强烈的不确定性[4]。
国内外学者在结构模糊随机可靠性方面进行一些探索：肖尊群等[5]通过一次二阶矩法建立模糊随机可靠性分析模型，利用模糊随机分解定理获得重力挡土墙结构的模糊随机可靠性。吕玺琳等[6]将模糊性和随机性结合分析，以L-R型模糊随机模型为基础求解边坡的模糊随机可靠性。舒苏荀等[7]针对岩土参数的时空变异性，将其视为模糊数，利用各向异性随机场模拟土性参数的空间变异性，将有限元法和蒙特卡洛法相结合，计算各参数组合对应的可靠性指标。虽然目前模糊随机可靠性理论在少数工程中得到部分应用，但总体来说还处于初步阶段，尤其在深冻结井整体结构模糊随机可靠性方面的研究未曾报道。此外，前期的模糊随机可靠性算法基于概论统计理论，样本空间小却计算繁、精度低，工程应用较困难。
为此，在大数据环境下，将深冻结立井冻结壁和井壁视为模糊随机力场，研究井筒外荷载和极限抗力的模糊随机表达式，建立整体结构的大数据模糊随机可靠性模型，对井筒设计的合理性，提高深部地下采矿的安全性和指导后续的深部地下矿业工程实践都有重要的参考价值和指导意义。
以往既有结构的可靠性算法通过结构的抗力减去荷载为零定义极限状态方程，这就意味着零点成为整个结构有效和无效的分界点。而大量的实践工程告诉我们结构从有效到无效是个模糊渐变的过程，为此，可将传统的可靠性状态方程Z进行模糊随机化处理[8-9]：
(1)
式中：
分别为模糊随机化的整体结构抗力和荷载；
为一个很小的模糊随机阈值；g为
函数形式；
为各模糊随机参数;l为状态方程参数数量。
为尽量接近工程实况，通常采用零点附近的有界闭模糊随机数来表征模糊随机阀值
该模糊数的隶属函数
表示为[10]
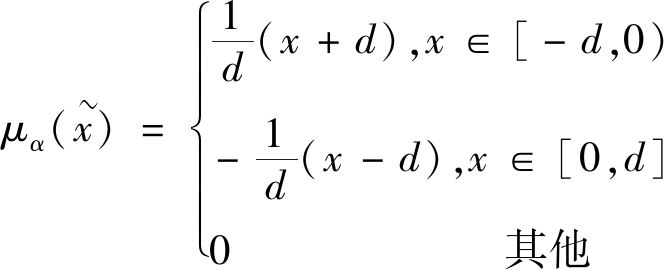
(2)
其中：常量α∈(0，1]为阀值的模糊随机约束水平；d为对应的水平截集区域范围。因此，式(1)模糊随机化后变成
(3)
其中，右下标α为相应约束水平(相应值同前)，按模糊区间运算法，则变换式(3)，有
(4)
其中，右上标-、+分别表示各变量相应的极小值、极大值。
根据可靠性定义和模糊集合的分解定理，结构模糊随机可靠性指标
可表示为
(5)
其中：μR、μS分别为
和
的均值；σR、σS分别为和的标准差；∪表示其约束水平下的截集区间。同理，模糊随机失效概率
和模糊随机可靠性
分别为
(6)
(7)
其中，Pf为随机失效概率。可见，在传统状态方程中引入约束水平和模糊随机阀值，将可靠性算法模糊随机化处理，获得相应可以求解的区间方程。
大数据挖掘的主要目标是以有效的信息手段和计算方法，获取未知且潜在的信息样型和规则，提取数据的深度价值，为行业决策和工程实践提供有效资料。
隐马可夫模型(HMM)是一个双重的随机过程，它的状态不能直接观察得到，但能通过观察向量隐式推导获得[11-12]。
隐马尔科夫模型的主要构成要素如下：
1)模型的状态，设状态集合为s={s1,s2,…,sn}，时刻t时所处的状态为qt∈s，n为初始集状态数。状态间可以相互转移。
2)状态转移矩阵，描述状态之间如何进行转移的状态矩阵A=(aij)n×n,aij表示状态转换的概率，i≤n，j≤n。
3)模型的观察值，设观察值集合V={v1,v2,…,vm}，当t时刻的状态转换完成的同时，模型都产生一个可观察输出yt∈V，m为观察集元素的个数，即观察集状态数。
4)输出的概率分布矩阵，描述产生输出的概率分布函数矩阵E=(eij)n×m。其中，eij=ei(j)=ei(vj)=P(yt=vj|qt=si)表示t时刻状态为si时输出为vj的概率。
5)初始状态分布，设η={η1,η2,…,ηn}为模型的初始状态分布。其中，ηi=P(q1=si)。因此，完整的隐马尔科夫模型可以用λ={A,E,η}表示所有的参数其中，A为转换矩阵。
以往可靠性一次二阶矩法利用Taylor级数展开其状态方程，进而用一次矩表示均值，二次矩表示方差，故近似算法整体结构的可靠性指标为两者的商，见式(8)：
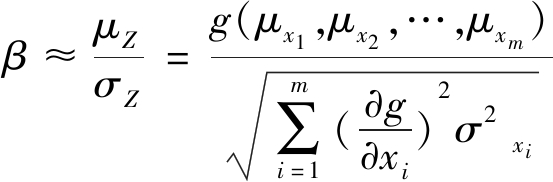
(8)
其中：μZ、σZ分别表示状态方程Z的均值和标准差；μxi、σxi分别为各分变量对应的均值和标准差；为此，基于大数据HMM模型，采用最大期望算法(EM)改进传统的可靠性计算方法，整个EM算法步骤如下：
1)E步骤：根据参数初始值或者上次迭代的模型参数θ(n)来计算极大似然估计值，如式(9)所示。
Qi(z(i)):=P(z(i)|x(i);θ)
(9)
式中：Qi为参数极大似然估计值；z(i)表示样本隐含的类别；P(z(i)|x(i))为x(i)条件下z(i)的概率；∶=为对参数的定义符号。
2)M步骤：固定Q(z)，当数据的似然性最大时候，计算参数期望估计，如式(10)所示。
(10)
式中：θ为参数期望估计值；arg max为使函数值取最大时所对应的变量θ；P(x(i)，z(i)，θ)为当参数为θ时，x(i)和z(i)的联合分布概率。
3)重复上述步骤，直到收敛，算法流程如图1所示。
图1 大数据可靠性算法优化
Fig.1 Reliability optimizatiom with big data algorithm
我国深厚冲积层冻结井筒冻结段均为双层井壁结构，根据大量的工程实践数据，施工阶段冻结井筒内外壁分别主要承受冻结压力和静水压力。在运营期通常在内外层井壁间进行注装加固，此时可以把双层井筒看成一个整体。由于壁厚冻土融沉和后期土层排水沉降产生的摩擦力直接作用在井壁整体上，井壁整体进行安全性验算时一般将永久地压考虑为设计控制荷载。
可将深冻结立井内外壁整体受力视为模糊随机力场，考虑到矿井运营期可靠性的重要性，综合以上大数据模糊随机化算法分析深厚冲积层静土压力和钢筋混凝土双层井壁整体抗力，推导获得模糊随机方程如式(11)和式(12)所示[13-15]。
(11)
其中：
为双层井筒整体在运营期间所受的静土压力；
为不同井段的土层埋深，鉴于深厚冲积层各参数的不确定性，均属模糊随机变量。
(12)
其中：
为钢筋混凝土双层井壁整体极限承载力；
为计算模式不定系数；
分别为内、外层井壁混凝土轴心抗压强度；
分别为内、外层井壁的环向配筋率；
分别为内、外层井筒的厚径比；以上均为模糊随机变量。mN、mW分别为内、外层井壁混凝土强度提高系数；RgN、RgW分别为内、外层井壁的钢筋强度；考虑到对整体极限承载力的影响程度，采用确定值形式表示。
以此为基础，将荷载式(11)和抗力式(12)代入模糊随机化的可靠性方程式(3)中，利用大数据算法建立深厚冲积层钢筋混凝土双层井筒整体结构的模糊随机功能函数。
(13)
工程实例大数据表明，采用三角型模糊因子(图2)表征模糊随机阀值更贴近实际工况的不确定性，故整体结构的模糊随机状态方程写成：
(14)
同理，对应的结构有效状态和失效状态的模糊随机方程分别为
(15)
(16)
图2 三角型模糊因子
Fig.2 Triangular fuzzy factor
根据大数据可靠性算法， 针对整体结构的模糊随机状态方程(14)作约束水平α的截集区域，其区间方程表示为
(17)
式中，
根据模糊区间运算法则，可得功能函数的模糊区间为
(18)
(19)
按照大数据分析建立HMM模型，采用改进的可靠性算法流程，将整体井壁的模糊随机功能函数展开为泰勒级数，代入相应变量的偏导数[16-18]，可得：
(20)
则相应的大数据可靠性指标表达式为
(21)
式中：
为功能函数
在均值点处对其参数变量的偏导数。
两淮矿区某深厚冲积层矿井采用立井开拓，冻结法施工，整体结构为典型的钢筋混凝土双层井壁。其井筒直径为10 m，冲积层厚度为564.73 m，冻结深度608 m，其余工程参数见表1。
表1 井筒各段工程参数
Table 1 Engineering parameters of shaft various segments
深度/m混凝土等级内壁厚度/mm外壁厚度/mm内、外壁配筋率/%318～378C60135014000.415/0.533378～426C65135014000.426/0.480426～483C65135014500.514/0.609483～521C70110010500.473/0.592521～564C70120011000.628/0.747
假设冻结时间为250 d，模糊随机阀值
约束水平α=0.75(工程惯例取值介于0.6～0.8)，鉴于工程各变量均具有不确定性，故进行模糊随机化
将各参数代入整体井筒可靠性大数据模糊随机解析模型，按照优化后的大数据可靠性算法求解，对比井筒各段的传统可靠性和大数据模糊随机可靠性，具体数据见表2。
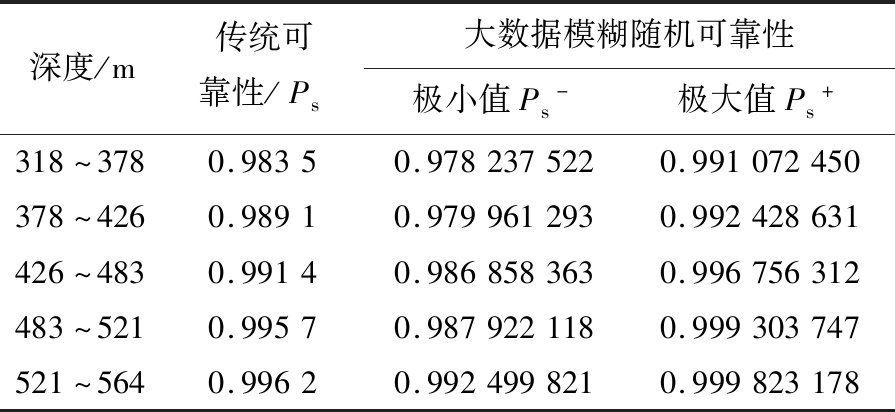
表2 不同算法可靠性对比
Table 2 Reliability compared with different algorithms
深度/m传统可靠性/Ps大数据模糊随机可靠性极小值Ps-极大值Ps+318～3780.98350.9782375220.991072450378～4260.98910.9799612930.992428631426～4830.99140.9868583630.996756312483～5210.99570.9879221180.999303747521～5640.99620.9924998210.999823178
由表2数据可知，算法综合以往的工程数据资料进行大数据分析，计算考虑到各参数变量的工程不确定性，故获得的大数据模糊随机可靠性更加合理准确，表2中其值是一组区间，相比传统的可靠性单值计算方法更有说服力。在具体的工程应用中，若计算所得可靠性区间与规范安全范围不重叠时，应引起高度重视，需重新设计或改进井壁结构参数，避免事故发生。该方法既丰富了工程技术人员对结构模糊随机性可靠性的认识，又可为今后深部地下结构工程的安全施工提供更全的资料和参考。
1)针对传统可靠性在表征深部地下结构稳定性时的不足，分析更加符合工况的模糊随机可靠性，进而对可靠性一次二阶矩法进行模糊随机改进。
2)以两淮矿区钢筋混凝土冻结井筒数据作为样本集，通过大数据HMM模型和EM算法，研究井筒整体外荷载和抗力的模糊随机表达式，建立整体井筒结构可靠性大数据模糊随机解析模型。
3)工程算例表明通过大数据模糊随机算法获得的可靠性区间比传统可靠性更加准确，取值形式更加合理。故该方法可为今后深部地下结构工程的安全施工提供更有效的参考和借鉴。
[1] 刘 春. 边坡工程中岩石力学参数随机模糊选取研究[J]. 岩土力学, 2004, 25(8): 1327-1329.
LIU Chun. Research on random-fuzzy method for selecting rock parameters in slope engineering[J]. Rock and Soil Mechanics, 2004, 25(8): 1327-1329.
[2] MA W, CHANG X X.Analyses of strength and deformation of an artificially frozen soil wall in underground engineering[J]. Cold Regions Science and Technology, 2002, 34(11): 11-17.
[3] 姚直书,程 桦,荣传新. 西部地区深基岩冻结井筒井壁结构设计与优化[J]. 煤炭学报, 2010, 35(5): 760-764.
YAO Zhishu, CHENG Hua, RONG Chuanxin. Shaft lining structural design and optimization of deep freezing bedrock shaft in west area[J]. Journal of China Coal Society, 2010, 35(5): 760-764.
[4] 荣传新,王秀喜,程 桦,等. 深厚冲积层高强钢筋混凝土井壁力学特性研究[J]. 岩石力学与工程学报, 2008, 27(S1): 2841-2847.
RONG Chuanxin, WANG Xiuxi, CHENG Hua,et al. Research on mechanical characteristics of high-strength concrete shaft lining in deep alluvium[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1):2841-2847.
[5] 肖尊群, 刘宝琛, 乔世范, 等. 重力式挡土墙结构模糊随机可靠性分析[J]. 中南大学学报, 2010, 41(4): 1522-1527.
XIAO Zunqun, LIU Baochen, QIAO Shifan,et al.Analysis of fuzzy reliability for gravity retaining wall structure[J]. Journal of Central South University, 2010, 41(4): 1522-1527.
[6] 吕玺琳, 钱建固, 吕 龙, 等. 边坡模糊随机可靠性分析[J]. 岩土力学, 2008, 29(12): 3437-3442.
LYU Xilin, QIAN Jiangu, LYU Long,et al.Fuzzy stochastic reliability analysis of slopes[J]. Rock and Soil Mechanics, 2008, 29(12): 3437-3442.
[7] 舒苏荀, 龚文惠, 王 佳, 等. 各向异性随机场下的边坡模糊随机可靠性分析[J]. 岩土工程学报, 2015, 37(7): 1204-1210.
SHU Suxun, GONG Wenhui, WANG Jia,et al.Fuzzy-random reliability analysis of slope stability in anisotropic random fields[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1204-1210.
[8] SAMIR A A, KHALID M, FAISAL F W. Influence of steel fibers and compression reinforcement on deformation of high-strength concrete beams[J].American Concrete Institute Structural Journal, 1997, 94(6): 611-624
[9] 李 贵. 结构模糊可靠性分析的模糊有限元法[D]. 南宁: 广西大学, 2004.
[10] 谭晓慧, 王建国, 胡晓军, 等. 边坡稳定的模糊随机有限元可靠性分析[J]. 岩土工程学报, 2009, 31(7): 991-996. TAN Xiaohui, WANG Jianguo, HU Xiaojun,et al.Fuzzy random finite element reliability analysis of slope stability[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 991-996.
[11] 潘 勉, 王鹏辉, 杜 兰, 等. 基于TSB-HMM模型的雷达高分辨距离像目标识别方法[J]. 电子与信息学报, 2013, 35(7): 1547-1554.
PAN Mian, WANG Penghui, DU Lan,et al. Radar HRRP target recognition based on truncated stick-breaking hidden Markov model[J]. Journal of Electronics & Information Technology, 2013, 35(7): 1547-1554.
[12] 任彦龙, 杨维好, 韩 涛. 基于不同强度准则的井壁极限承载力研究[J]. 中国矿业大学学报, 2011, 40(4): 540-543.
REN Yanlong, YANG Weihao, HAN Tao. Study of the ultimate bearing capacity of a shaft lining based on different failure criteria[J]. Journal of China University of Mining & Technology, 2011, 40(4): 540-543.
[13] 姚直书,程 桦,荣传新. 深冻结井筒内层钢板高强钢筋混凝土复合井壁试验研究[J]. 岩石力学与工程学报, 2008, 27(1): 153-160.
YAO Zhishu, CHENG Hua, RONG Chuanxin. Experimental study on composite shaft lining of inner steel plate cylinder and high strength reinforced concrete in deep frozen shaft[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(1): 153-160.
[14] 程 桦, 姚亚锋, 荣传新, 等. 深厚土层冻结法凿井过程中外层井壁模糊随机可靠性分析[J]. 煤炭学报, 2017, 42(5):1099-1107.
CHENG Hua, YAO Yafeng, RONG Chuanxin,et al.Fuzzy random reliability analysis on outer shaft lining in the process of freezing method sinking for deep alluvium[J].Journal of China Coal Society, 2017, 42(5):1099-1107.
[15] 徐鹏飞, 李耀良, 徐 伟. 压入式沉井施工对环境影响的现场监测研究[J]. 岩土力学, 2014, 35(4): 1084-1094.
XU Pengfei, LI Yaoliang, XU Wei.Field measurement and analysis of influence of jacked open caisson construction on environments[J]. Rock and Soil Mechanics, 2014, 35(4): 1084-1094.
[16] G Masrouri F. Stochastic finite element method applied to non-linear analysis of embankments[J]. Probabilistic Engineering Mechanics, 2001, 15(3): 251-259.
[17] 姚亚锋, 程 桦, 荣传新, 等. 基于RBF模糊神经网络模型的深厚冲积层立井冻结压力分析与预测[J]. 采矿与安全工程学报, 2016, 33(1): 70-77.
YAO Yafeng, CHENG Hua, RONG Chuanxin,et al.Analysis and prediction of vertical shaft freezing pressure in deep alluvium based on RBF fuzzy neural network model[J]. Journal of Mining & Safety Engineering, 2016, 33(1): 70-77.
[18] MELCHERS RE,AHAMMED M. A fast approximate method for parameter sensitivity estimation in Monte-Carlo structural reliability[J]. Computers and Structures, 2004, 82(1): 55-61.