
移动扫码阅读
露天矿边坡发生滑坡灾害会对矿区周边设备及人员造成威胁,造成生命财产损失。要做好露天矿边坡的防灾减灾工作,首先要对可能发生的滑坡灾害进行空间预测研究。
对于滑坡滑距的预测方法,国内外学者提出了多个模型并不断修正改进,但大多计算模型考虑因素一般为滑坡前后缘高差、滑坡体积或者坡度,虽然计算快捷,并因考虑因素不全面,并不能非常广泛有效地应用于实际。Heim在1932年提出了雪橇模型来预测滑距,由于假设简单合理,至今仍被很多研究人员沿用[1];1985年,Sassa在雪橇模型的理论基础上建立了三维滑坡运动模型 [2]; Scheidegger在1973年提出根据视摩擦因数预测滑坡的滑距[3];王家鼎[4]对滑坡体滑动轨迹进行了研究;文献[5-7]在单体滑坡预测方面也做了很多研究工作。随着计算机技术的发展,数值计算开始应用于滑坡预测的研究工作。文献[8-10]先后通过数值模拟对滑坡、泥石流的运动情况进行了研究,分析结果与实际情况相差不大。国内研究人员殷坤龙等[11]采用非连续变形方法(DDA)对滑坡运动的全过程进行了数值模拟;刘朋辉等[12]基于离散元方法(UDEC)模拟了滑坡各阶段的滑坡变形体的运动状态和解体过程;孙书勤等[13]利用有限元方法(FLAC3D)对滑坡体的变形状况进行了三维数值模拟分析,为滑坡体变形的发展趋势和稳定程度的评价预测提供依据;王宇等[14]运用颗粒流离散元法对滑坡运动渐进全过程进行数值模拟;张龙等[15]利用三维颗粒流软件研究滑坡体在关键块体失稳后沿着滑动面在视倾向滑动力主导下的运动过程;有些学者利用颗粒流离散元的方法对滑坡的发生、发展、破坏及运动过程进行了模拟,为研究滑坡全过程的空间预测提供了新的手段[16-17]。各研究方法从不同假设出发,针对特定的滑坡,得出了比较合理的结论,但地质条件及影响因素发生变化时,这些方法适用性存在一定的缺陷。
在当今科技发展背景下,为探求一种更精确更合理的预测边坡滑距的方法,笔者以魏家峁露天矿工作帮滑坡为例进行了模拟计算,分析顺层蠕滑型工作帮滑坡的发展规律及影响范围。魏家峁工作帮边坡属于典型的顺层蠕滑型边坡,由于发生破坏多属于大变形,因此选用颗粒流离散单元法,可直观反映滑体上颗粒的分布、运移过程。
魏家峁露天煤矿工作帮边坡地层主要由第四系粉砂与粉土、新近系粉质黏土、黏土组成,下伏二叠系的泥岩和砂岩;地下水补给主要由大气降水补给及侧向补给。研究区赋存厚度不大的泥岩,作为隔水层,其接触面长期受到地下水的浸泡,形成了露天煤矿典型的“演化弱层”。
对于受演化弱层控制的边坡来说,边坡的变形破坏特征主要取决于弱层的蠕变特征,其变形动态曲线可划分为3个阶段:初始变形阶段、等速变形阶段和加速变形阶段(图1)。初始变形阶段的特征是变形速度逐渐降低,最后变形速度基本上稳定在某一定值,此时即进入等速变形阶段。当变形累积到破坏变形量时,边坡变形将过渡到加速变形阶段,直至滑坡。
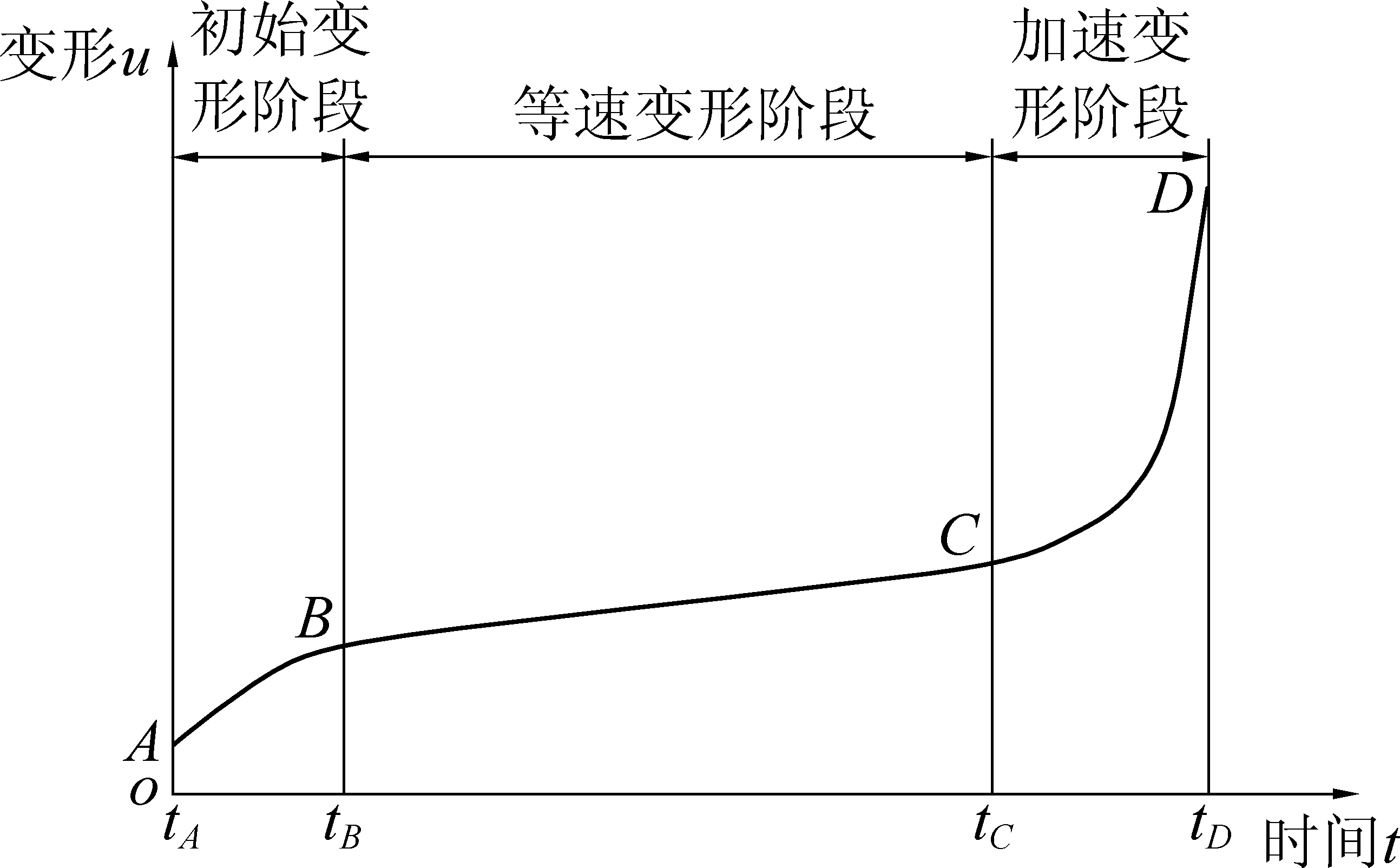
图1 典型蠕变边坡变形-时间曲线
Fig.1 Deformation-time curve of typical creep slope
根据现场GPS监测显示,魏家峁露天煤矿工作帮边坡在2018年11月以前滑坡体处于初始变形阶段,11月15日以后处于匀速变形阶段,其水平位移和竖直位移均稳定缓慢增长。分析原因如下:前期由于外界水渗入基底,弱化基底土体强度,基底抗滑力降低,使得边坡变得不稳定,随着被浸润基底土体的饱和,基底土体强度不再降低;而滑坡体在变形的过程中,坡脚逐渐产生底鼓,底鼓区起到阻滑的作用,增加了滑体的抗滑力,当抗滑力可以抵消部分潜在滑体的下滑力时,滑坡体变形移动减缓。结合边坡地层分布特征,魏家峁工作帮呈典型的顺层蠕滑型边坡。根据工程地质剖面计算,平均滑体截面积2 800 m2,滑坡平均宽度120 m,滑体体积约为3.36×105 m3(图2)。

图2 魏家峁工作帮滑坡
Fig.2 Landslide of Weijiamao working slope
颗粒流程序数值模拟作为一种新技术,其理论基础是Cundall 等 [18]提出的离散单元法,可用于颗粒材料力学性态分析,如颗粒团粒体的稳定、变形及本构关系,专门用于模拟固体力学大变形问题。通过圆形(或异型)离散单元来模拟颗粒介质的运动及其相互作用。根据平面内的平动和转动运动方程来确定每一时刻颗粒的位置和速度。
1)力-位移定律。颗粒流模型中,接触形式包括颗粒-颗粒(ball-ball)和颗粒-墙体(ball-wall)。接触力Fi为矢量,依据矢量分解规则,可分解为法向接触力和切向接触力即
式中:![]() 为法向接触力;
为法向接触力;![]() 为切向接触力。
为切向接触力。
法向接触力的表达式为
![]() =KnUnni
=KnUnni
式中:Kn为接触点处的法向刚度,通常用割线模量表达;Un为法向位移量,是指颗粒与颗粒之间,或者颗粒与墙体之间的变形重叠量;ni为接触面上的单位法向向量。
切向接触力以增量的形式计算,即
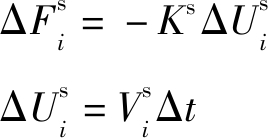
式中:Ks为接触点切向刚度;Δ![]() 为计算时步内接触位移增量的切向分量;
为计算时步内接触位移增量的切向分量;![]() 为接触点速度的切向分量;Δt为计算时步。
为接触点速度的切向分量;Δt为计算时步。
2)运动定律。不平衡力与平移运动的关系为
不平衡力矩与转动的关系
Mi=Hi
式中:F为颗粒的不平衡力;m为颗粒实体的总质量;xi为颗粒的重心位置的法向位移;gi为颗粒体积力加速度;Mi为颗粒的不平衡力矩;Hi为颗粒的角动量。
颗粒边界、墙体边界和混合边界是模型中包括的3种边界条件。用wall命令,生成边坡模型与颗粒区域,然后生成为无规则排列颗粒。首先采用半径扩展法和挤压排斥法2种方法进行试算,随后根据模拟坡体的孔隙度、含水率及计算效率等,确定模型的颗粒数。最终采用自重沉降法方法建立颗粒流模型。
研究选取P1剖面进行数值模拟。本次野外勘察及测斜工作已查明滑坡的滑带,根据工程地质钻探结果可知,该区域泥岩层赋存厚度较小,从滑动规模上看,对滑体的移动范围影响很小,而是其强度参数控制上覆岩土体的变形。因此,本次计算采用接触面代替泥岩层以简化模型的计算量,接触面测参数(KN、KS)采用泥岩层参数。初始模型如图3所示,由于砂岩为不动层,本次建模仅至粉质黏土层。根据室内试验及类比分析确定岩体物理力学参数选取见表1。
表1 岩体物理力学参数
Table 1 Physical and mechanical parameters of rock mass
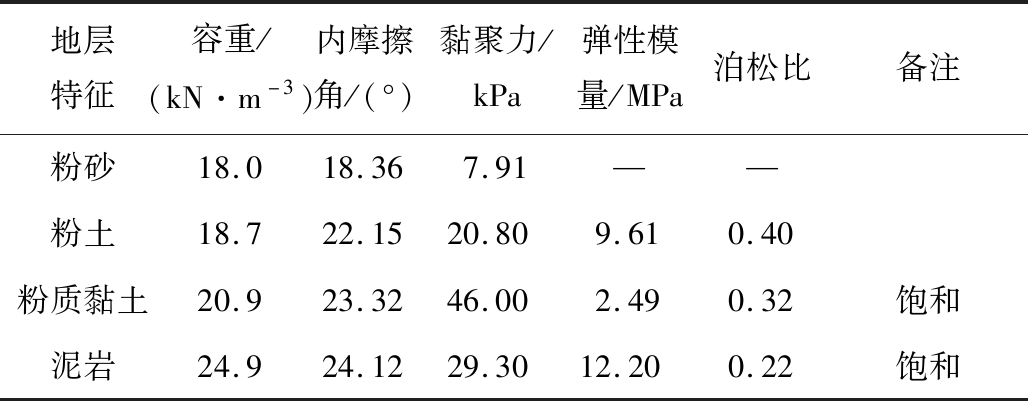
地层特征容重/(kN·m-3)内摩擦角/(°)黏聚力/kPa弹性模量/MPa泊松比备注粉砂18.018.367.91——粉土18.722.1520.809.610.40粉质黏土20.923.3246.002.490.32饱和泥岩24.924.1229.3012.200.22饱和
注:黏聚力c值对应n_bond 与s_bond所定义的粘结参数;tan φ对应于fric定义的粒间内摩擦力大小。

图3 工作帮滑坡区边坡模型
Fig.3 Slope model of landslide area
模型运行5 000时步后,粉质黏土底部颗粒与墙体间的黏聚力减小,粉质黏土从底部沿演化弱层顺层蠕滑,继而引发上覆粉土和粉砂层的滑动(图4),在重力作用下,颗粒开始向下滑落,在重力势能减小的同时速度逐渐增大,随着颗粒与地面的接近,颗粒的滑落速度逐渐减小。同时由于颗粒在坡脚堆积,坡脚产生了一定的压脚区域,坡体颗粒在黏聚力和坡脚反力的双重作用下,滑落的趋势受到阻碍,自然就导致了颗粒的运动速度变慢。在坡体后缘,临空面范围加大,形成拉张应力(图5)。

图4 5 000时步时边坡变形特征
Fig.4 Deformation characteristics of slope in 5 000 step

图5 边坡力链分布特征
Fig.5 Distribution characteristics of slope force chain
随着计算时步的持续进行,粉质黏土层沿着演化弱层向临空方向继续滑移,但速度进一步降低,在+1 112 m水平平盘逐渐堆积,伴随弯曲、隆起、强烈隆起过程中,岩体松动、破裂,伴随局部崩落、滑塌,后缘拉张变形也趋于稳定,后缘坡体倾角近于其残余内摩擦角。

图6 7 000时步时边坡变形特征
Fig.6 Deformation characteristics of slope in 7 000 steps
当模型计算结束,不平衡力趋于0时(图8),粉质黏土层向前滑动的趋势已经停止,但堆积厚度稍微增加,此时边坡总计滑动距离约54 m。

图7 系统平均不平衡力随时间变化曲线
Fig.7 System average imbalance force versus time curve
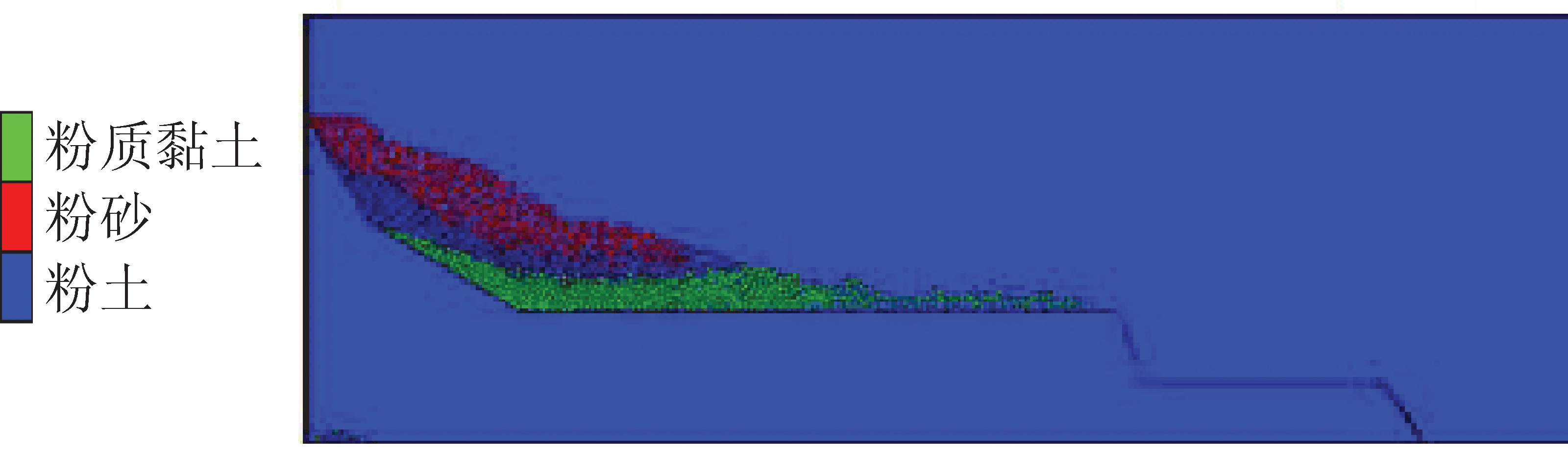
图8 模型达到平衡时边坡的滑动范围特征
Fig.8 Sliding range characteristics of the slope when the model reaches equilibrium
考虑滑坡滑动的极限位置,根据滑坡滑距为54 m,假定滑坡坐落范围与底鼓范围基本一致,边坡滑动后的状态如图9所示,此时,土质边坡局部边坡角为13°,由于滑坡的发生,岩土体结构全部发生破坏,此时,对岩土体强度参数进行极大的弱化,经极限平衡计算,边坡的稳定系数仍大于1.2(图10),在此情况下,边坡滑动后达到稳定状态。
为不影响采煤接续,需在下部台阶开展剥离工作,实际工作中,建议将剥离停采线设置为滑坡影响范围基础上额外再增加20 m的位置。

图9 边坡滑动后假定形态
Fig.9 Assumed shape after slope sliding
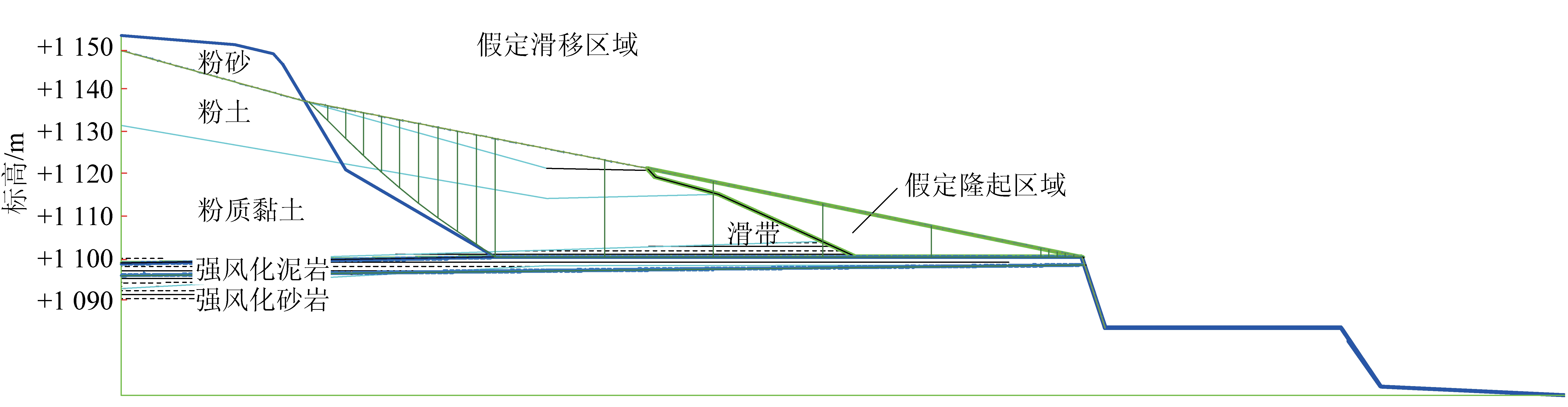
图10 边坡滑动稳定性
Fig.10 Slope sliding stability
根据现有的滑坡滑距预测公式对魏家峁露天煤矿工作帮边坡进行计算和对比,主要选取模型[19-20]为
1)前后缘高差公式为
S=2(H1-H2)
式中:S为滑坡滑动距离,m;H1、H2为滑坡后缘高程、前缘高程,m。
2)舒德格尔公式为
lg(H/S)=alg V+b
式中:H为滑坡垂直滑落高度,即坡高,m;V为滑坡体积,m3;a、b分别为系数,其中a=-0.156 66,b=0.624 19。
3)森协·宽公式为
lg(H/S)=-0.094lg V+0.1
其中,前后缘高差为46 m,滑坡体积为3.36×105m3。根据计算模型得出滑动距离。
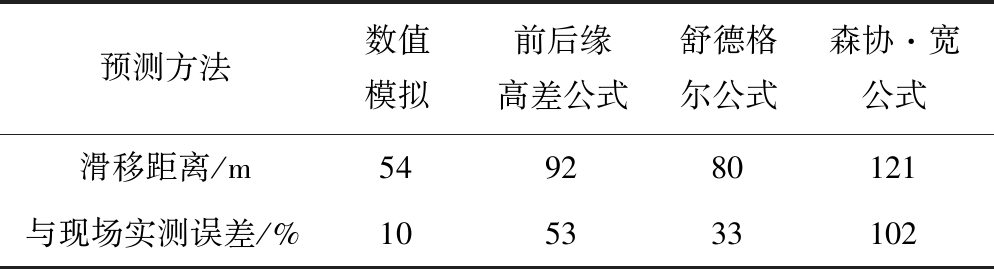
根据现场观测,在距离坡脚约60 m的地方有部分隆起和底鼓,将数值模拟结果、滑坡滑距预测公式计算结果一同与现场实测结果进行对比。计算结果对比见表2。
表2 滑坡滑移距离计算结果对比
Table 2 Comparison of calculation results of
landslide slip distance
预测方法数值模拟前后缘高差公式舒德格尔公式森协·宽公式滑移距离/m549280121与现场实测误差/%105333102
通过计算结果可以看出:数值模拟方法结果与现场实测的误差最小。前后缘高差公式只考虑前后缘高程,并不能反应所有滑坡滑动距离的实际情况;舒德格尔公式以不同类型、大型高速远程滑坡为基础资料,建立同类滑坡的回归统计公式,针对性很强,对于顺层蠕变型滑坡的适用性尚需研究改进;森协·宽公式主要针对小规模滑坡比较适用。因此,各数学模型由于考虑因素不全面,针对性较强,所以改变滑坡类型时与实际情况误差较大。而数值模拟方法因为考虑因素更全面,更能符合现场实际。
1)魏家峁露天矿工作帮滑坡为顺层蠕滑型边坡,采用颗粒流离散元数值模拟方法对其进行模拟分析,计算得出的滑坡滑距与现场实测误差为10%。由于此方法综合考虑滑体形态、物理参数以及滑坡体内部颗粒受力等诸多因素,其计算结果更符合实际情况,误差较小,在露天矿顺层蠕变边坡滑距研究中具有较好的应用。
2)应用前后缘高差公式、舒德格尔公式、森协·宽公式3种传统的滑坡滑距预测公式对魏家峁露天矿工作帮滑坡进行滑距计算,计算误差为33%~102%。由于数学预测模型考虑因素相对简单且不全面,造成计算结果误差较大,并不能非常广泛有效地应用于实际工程当中。
3)颗粒流离散元数值模拟方法具有更高的普适性,可为类似滑坡的预测提供参考。
[1] 刘朋辉.滑坡滑动机理及风险评价研究[D].北京:北京工业大学,2007.
[2] 张克亮.滑坡运动学模型及其应用研究[D].西安:长安大学,2011.
[3] SCHEIDEGER A E. On the prediction of the research and velocity of catastrophic landslide [J]. Rock Mechanics, 1973,5(4):231-236.
[4] 王家鼎.滑坡体滑动轨迹的研究[J].中国地质灾害与防治学报,1991,2(2):1-10.
WANG Jiading. Research on sliding track of landslide[J]. The Chinese Journal of Geological Hazard and Control,1991, 2(2):1-10.
[5] 文宝萍.滑坡预测预报研究现状及发展趋势[J].地学前缘,1996,3(1/2):86-91.
WEN Baoping.The state of the art and trend of the landslide predictions[J].Earth Science Frontiers, 1996, 3(1/2):86-91.
[6] 许 强,黄润秋,李秀珍.滑坡时间预测预报研究进展[J].地球科学进展,2004,19(3):478-483.
XU Qiang,HUANG Runqiu,LI Xiuzhen. Research progress in time forecast and prediction of landslides[J]. Advance in Earth Sciences,2004,19(3):478-483.
[7] 龙建辉.高速远程黄土滑坡预测预报方法研究[D].西安:长安大学,2008.
[8] REVELLINO P, HUNGR O, GUADAGNO R M,et al. Velocity and run-out simulation of destructive debris flows and debris avalanches in pyro-elastic deposits Campania region Italy[J].Environmental &Geology,2004,45:295-311.
[9] SOSIO R, CROSTA G B,HUNGR O . Complete dynamic modeling calibration for the Thurwieser rock avalanche(Italian Central Alps) [J].Engineering Geology,2008,100:11-26.
[10] CAMPBELL C S, CLEARY P W M. HOPKINS. Large-scale landslide simulations: global deformation velocities arid basal friction[J].Journal of Geophysical Research,1995,100(B5):8267-8283.
[11] 殷坤龙,姜清辉,汪 洋.新滩滑坡运动全过程的非连续变形分析与仿真模拟[J].岩石力学与工程学报,2002,21(7):959-962.
YIN Kunlong,JIANG Qinghui,WANG Yang.Numerical simulation on the movement process of Xintan landslide by DDA method[J].Chinese Journal of Rock Mechanics and Engineering,2002,21(7):959-962.
[12] 刘朋辉,魏迎奇,杨昭冬.贵州印江岩口滑坡过程的数值模拟分析[J].中国水利水电科学研究院学报,2007,5(2):115-119.
LIU Penghui,WEI Yingqi, YANG Zhaodong. Numerical simulation analysis of the process of Yankou landslide in Yinjiang River of Guizhou[J].Journal of China Institute of Water Resources and Hydropower Research,2007,5(2):115-119.
[13] 孙书勤,黄润秋,丁秀美.天台乡滑坡特征及稳定性的FLAC3D分析[J].水土保持研究, 2006,13(5): 30-32.
SUN Shuqin,HUANG Runqiu,DING Xiumei.Tiantai landslide and its stability analysis with FLAC3D[J].Research of Soil and Water Conservation, 2006,13(5): 30-32.
[14] 王 宇,李 晓,王声星,等.滑坡渐进破坏运动过程的颗粒流仿真模拟[J].长江科学院院报,2012,29(12):46-52.
WANG Yu,LI Xiao,WANG Shengxing, et al.PFC simulation of progressive failure process of landslide[J].Journal of Yangtze River Scientific Research Institute,2012,29(12):46-52.
[15] 张 龙,唐辉明,熊承仁,等.鸡尾山高速远程滑坡运动过程PFC3D模拟[J].岩石力学与工程学报.2012,31(S1):2601-2612.
ZHANG Long,TANG Huiming,XIONG Chengren,et al.Movement process of high-speed long-distance Jiweishan landslide with PFC3D[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S1):2601-2612.
[16] 吴顺川,张晓平,刘 洋.基于颗粒元模拟的含软弱夹层类土质边坡变形破坏过程分析[J].岩土力学,2008,29(11):2899-2904.
WU Shunchuan,ZHANG Xiaoping,LIU Yang. Analysis of failure process of similar soil slope with weak intercalated layer based on particle flow simulation [J]. Rock and Soil Mechanics,2008,29(11):2899-2904.
[17] 马秋娟,唐 阳,宿 辉.泥石流启动过程试验与数值模拟研究[J].科学技术与工程,2015,25(15):7-10.
MA Qiujuan,TANG Yang,SU Hui. The initiation process test of debris flow and numerical simulation researching[J].Science Technology and Engineering,2015,25(15):7-10.
[18] 马栋和.黄土公路边坡坡面冲刷的水-土力学耦合机制及模型研究[D].长春:吉林大学, 2012.
[19] 吴钟腾.云南彝良麻窝滑坡失稳后的运动危险区预测研究[D].成都:成都理工大学, 2014.
[20] 陈 达.刘涧滑坡变形破坏机理及运动过程研究[D].西安:西安科技大学,2018.