
移动扫码阅读
煤矿机电与智能化
采煤工作面的瓦斯涌出量是决定矿井通风、制定安全技术措施的重要指标,能否准确的预测涌出量,对于矿井设计和煤矿安全开采具有重要的现实意义。影响采煤工作面的瓦斯涌出量通常包含煤层埋藏深度、煤层厚度、煤层瓦斯含量、煤层间距、日进度、日产量等诸多因素[1],这些因素之间往往存在着复杂的、动态的非线性关系[2],用一般的线性模型难以保证预测精度。
传统的瓦斯涌出量预测方法可分为3 类:矿山统计法[3]、分源计算法[4]和瓦斯地质数学模型法[5]。但是这些方法的预测过程均表现为静态,难以动态的模拟瓦斯涌出量的实时变化。随着人工智能技术的兴起,不少机器学习方法被应用到瓦斯涌出量预测领域,包括CART[6]、神经网络[7-8]、线性回归[9]、支持向量机(SVM)[10]、遗传规划法[11]、基因表达式程序设计法[12]等,但这些方法都存在不足之处,譬如,神经网络法适用于样本数量极大丰富的场景,当样本数量有限时效果不理想,易陷入局部最优。线性回归法适合特征之间高度线性相关的场景,而影响瓦斯涌出量各因素之间存在着复杂的、动态的非线性关系,导致模型拟合效果不理想。SVM相比于线性回归法预测精度高,能拟合线性与非线性的数据,比较符合瓦斯涌出量的预测场景,但是在高维数据的情况下,SVM算法建模效率较低,预测精度不高。遗传规划法和基因表达程序设计法虽然能够实现全局搜索,但这2种方法的随机性很难保证模型搜索到最优解。经典CART回归算法[13]建立决策树的过程简单易理解,预测结果准确度较高,总体效果不错,但仍存在以下不足:①预测值计算方法不合理。将预测值设定为叶子节点训练样本的均值,导致该算法从本质上变成了离散性质的分类算法,大幅降低了连续回归预测结果的准确度;②稳定性差。数据发生很小的改动都会导致生成一个完全不同的树;③泛化性能差,容易过拟合。
通过文献研究分析,特别受启发于决策树M5’算法思想,笔者认为采取分区域法拟合数据,对于不同的子区域选择相应的最优参数逼近数据特性曲线,以实现高精度的瓦斯涌出量预测结果,将是一种行之有效的方法。结合SVM和M5’算法思想,提出一种增强CART回归算法,利用SVM在回归树的叶节点部分建模,以提高模型稳定性、预测精度及防止过拟合的发生,并将增强CART回归算法用于建立预测采煤工作面瓦斯涌出量的量化模型。
经典CART算法[13]最初是由Breiman等于1984年提出的一种机器学习算法,广泛应用于分类与回归问题。CART回归算法规定,树中各叶节点的输出部分选取该节点中样本数据目标属性的均值,即树中叶节点的输出部分永远为定值,导致该算法从本质上来讲属于分类而非回归算法。Quinlan于1992年提出M5算法[14],使用线性回归算法对树中叶节点建模,改善CART回归算法中叶节点的输出部分为定值的缺陷。WANG等[15]于1997年提出改进的M5算法,即M5’算法,树的结构更简洁,预测精度更高,实现了真正意义上的回归预测。自M5’算法提出以来,广泛应用于机组耗汽量预测[16]、感觉评估[17]、城市不透水面百分比预测[18]、洪涝灾害预测[19]等。
M5’算法[15]虽然解决了CART回归算法中叶节点输出部分为定值的缺陷,但是叶节点处使用的线性回归算法相较于SVM回归算法,数据拟合度较差,预测精度低,容易产生过拟合[20]。为解决上述问题,笔者提出一种增强CART回归算法,该算法将样本空间划分为多个互不相交的子样本空间,对各子样本空间应用SVM建立相应的回归模型。算法具体的执行步骤如下:
1)生成增强回归树T。增强CART回归算法根据样本属性差异化原则(standard deviation reduction, SDR)[16]递归地划分样本空间,以图1的二维样本空间为例,可以将划分操作看作一个递归二分化样本空间的问题。首先根据SDR值的大小确定划分X1、X2维度的优先顺序,即先划分X1还是X2;其次确定具体的划分位置,即某一维度中的属性值。按照上述方式递归地划分样本空间,直到满足停止条件。在这里设置2个停止条件:①子样本空间包含的样本数量小于预设值n;②子样本空间内样本目标属性的标准差与总样本目标属性标准差的比例小于给定阈值ε。满足其中任一停止条件,停止划分过程。回归树停止生长的结点为叶节点,在每个叶节点处使用SVM回归算法进行建模,生成增强回归树T。
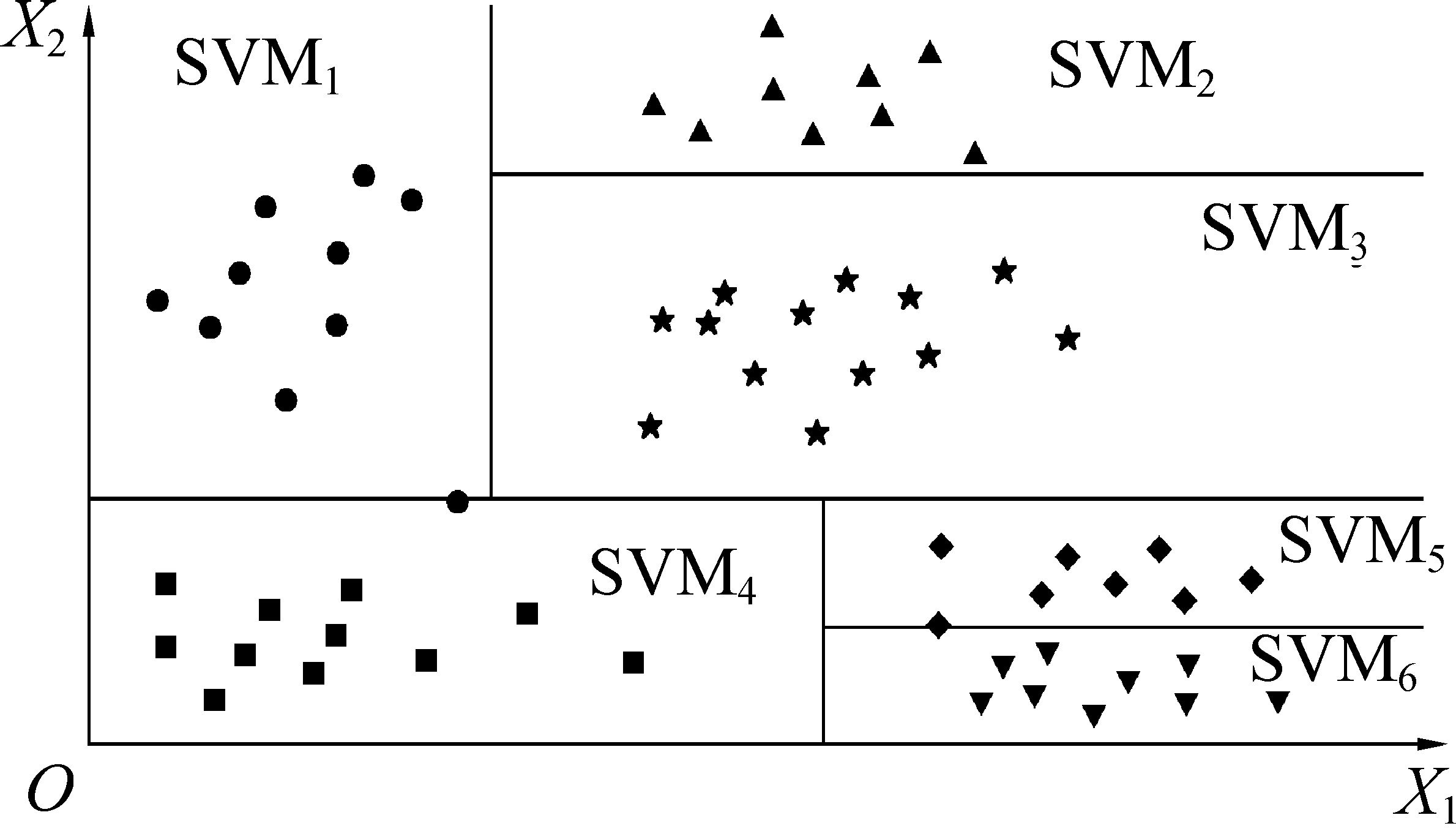
图1 样本空间划分
Fig.1 Partition sample space
SDR表示为
(1)
式中:N为总样本空间,总样本数为|N|;N1、N2为N被划分为2个子样本空间,样本数分别为|N1|、|N2|;sd(N)为总样本目标属性的标准差,sd(N1)、sd(N2)为划分后2个子样本空间内样本目标属性的标准差。
在对叶节点使用SVM回归算法建模的过程中,假设某一叶节点空间含有j个样本数据,表示为X=[X1,X2,X3,…,Xj],其中Xi=[x1,x2,x3,…,xm]由m个影响因素组成,Yi为目标属性值,建立的回归方程f(Xi)表示为式(2),并根据结构风险最小化准则将式(2)转换为式(3)的最优化问题,利用拉格朗日对偶性,将式(3)转换为对偶形式进行求解,得到最优平面f(x),即相应叶节点的回归方程,表示为式(4)。
f(Xi)=Wφ(Xi)+b
(2)
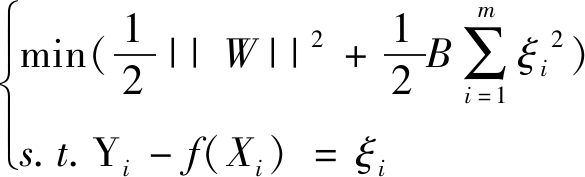
(3)
f(x)=Aφ(X)+b*
(4)
式中:φ(Xi)为核函数;b为偏置项;b*为优化偏置项;松弛变量ξi≥0 ;惩罚参数B>0;A为拉格朗日乘子。
2)对增强回归树T进行修剪操作,生成最优决策树T0。
树的修剪操作是指根据预测误差的减少程度,从增强回归树T的底端递归地裁去冗余子树,并用相应的叶节点替代。修剪后树结构更为简洁,能够有效缓解过拟合带来的影响,提高模型对未知数据的预测能力。预测误差减少量的计算为
ER=|N|RMSE-|N1|RMSE1-|N2|RMSE2
(5)
式中:RMSE为该节点处的预测均方误差;RMSE1、RMSE2分别为该节点划分为2个子节点N1、N2处的预测均方误差。
具体修剪操作为:从树T底端的子树开始,依次计算各子树的预测误差减少量ER,当ER大于0时,该子树能够降低预测误差,说明该子树不为冗余子树,因此不需要修剪操作,否则该子树为冗余子树,需要进行修剪操作,并转化为一个叶节点。
3)对最优决策树T0进行平滑处理。对增强回归树T进行修剪操作后,最优决策树T0中相邻的叶节点部分可能出现一定程度的不连续性。因此,QUINLAN[14]提出平滑方法,将子节点与相应父节点的方程合并为一个新的回归方程为
(6)
式中:fp为叶节点相应父节点处的回归方程;fc为叶节点处的回归方程;i为叶节点处样本数量;k为常数项。
若子节点采用新函数后,RMSE的变化小于一定的阈值,则将取代子节点的回归方程,否则不进行平滑处理。增强CART回归算法实现流程如图2所示。

图2 增强CART回归算法流程
Fig.2 Flow chart of enhanced CART regression algorithm
采煤工作面瓦斯涌出量是指单位时间内从煤(岩)层涌入矿井的气体总量。矿井中瓦斯赋存分布不均衡,瓦斯涌出量随着开采过程的不断推进,不断产生相应的变化。预测模型选取特征属性Xi为回归树节点处的划分依据,对瓦斯涌出量Y(即目标属性)进行预测。根据笔者提出的增强CART回归算法,采煤工作面瓦斯涌出量预测模型的建模过程可分为数据预处理、生成回归树、树的修剪操作、平滑处理以及最终的预测过程。
1)数据预处理。从实际场景中采集到数据集往往都含有一定的噪声数据,这些数据最终会影响模型预测结果的精确度。因此,在使用这些数据建模前,必须对采集的数据进行预处理,以去除噪声偏差的影响。首先剔除缺失属性值的数据,保证每个样本数据特征值完整。然后采用极差化的处理方法,对剔除缺失值后的数据进行归一化操作,归一区间为[0,1],具体方式表示为式(7)。划分预处理操作后的数据集,随机选取其中70%的数据为训练样本集,剩余的30%作为测试样本集,用于评估模型的预测精度。
(7)
式中:Xi为样本集中特征i的数据;Xi,min为特征i中数值最小的数据;Xi,max为特征i中数值最大的数据;Xi,out为归一化后的数据。
2)生成增强回归树T。根据式(1)所示的SDR原则[16],选择最优切分特征属性与相应的切分位置划分预处理后的训练数据,并将该特征属性设置为父节点,划分出的2个空间为子空间。不断重复上述过程,直到满足任一停止条件,结束划分过程,生成多个互不相交的子空间。再使用SVM回归算法对各子空间建模,生成增强回归树T。
3)修剪、平滑过程。从增强回归树T底端的节点开始,利用第1.2小节中步骤2,递归地判断哪些节点需要进行修剪操作。并利用步骤3对修剪后的回归树进行平滑操作,生成最优决策树T0。
4)预测涌出量及评估模型性能。使用最优决策树T0预测采煤工作面的瓦斯涌出量,并将预测结果用式(8)进行反归一化处理,计算实际瓦斯涌出量。
Xi,fin=Xi,min+Xi,out(Xi,max-Xi,min)
(8)
式中:bi,fin为反归一化后的数据。
笔者选用测试样本集评估模型性能,具体的评估指标为平均绝对误差(MAE)、平均方差(MSE)、R平方值(R2)。其中,平均绝对误差(MAE)就是评估预测值与真实值之间相差的程度,该值越小说明模型对试验数据集外的样本具有较好的预测性能,反映预测值误差的实际情况,体现模型的泛化能力,具体计算为式(9)。均方根误差(MSE)和平均绝对误差(MAE)类似,是指预测值与真实值之差平方的期望值,该值越小说明预测模型对试验中的样本数据具有越高的预测精度,具体计算为式(10)。R平方值(R2)评估模型对各个特征属性的拟合程度,或者说模型与真实情况的相似程度,R2值越接近1说明模型预测效果越接近真实情况,具体计算为式(11)。
(9)
(10)
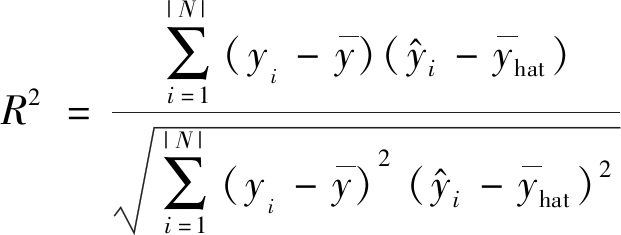
(11)
式中:|N|为测试样本的数量;yi为第i个测试样本真实涌出量;yi为模型预测第i个测试样本的涌出量;![]() 为测试样本中涌出量的平均值;
为测试样本中涌出量的平均值;![]() 为模型预测涌出量的平均值。
为模型预测涌出量的平均值。
针对文献[20]中新安煤矿12241采煤工作面2013年9月至2014年8月共365组瓦斯涌出量历史监测数据(部分数据见表1)进行建模分析,随机选取其中256组数据为训练样本集,剩余的109组数据作为测试样本集。模型的特征属性为Xi,其中X1为煤层深度、X2为煤层厚度、X3为煤层瓦斯压力、X4为煤岩层瓦斯含量、X5为日进度、X6为日产量[20],实际瓦斯涌出量为Y(即目标属性)。
表1 部分瓦斯涌出量历史监测数据
Table 1 Historical monitoring data of partial gas emission

序号X1/mX2/mX3/MPaX4/(m3·t-1)X5/(m·d-1)X6/(t·d-1)Y/(m3·min-1)14212.000.492.924.3120803.5624081.800.323.584.6721725.1234562.200.473.204.6120274.2345392.800.514.133.2622434.9655172.600.573.613.6822194.78︙︙︙︙︙︙︙︙3626232.600.614.673.2732156.633636404.300.694.952.6933405.613645442.700.524.873.8124186.953655733.800.474.174.2119906.77
对这256组数据使用增强CART回归算法构建瓦斯涌出量预测模型,模型的具体参数情况设置如下:子空间的最少样本数量n为35;阈值ε为0.5;SVM中的核函数采用泛化能力较强的径向基函数(RBF)。由图3可以看出最优决策树T0叶节点数为6,煤层深度X1、煤层厚度X2、日进度X5为主要影响因素。
当X1≥544 m and X5≥4.13 m/d and X2≥2.80 m时,回归模型为SVM1;当X1≥544 m and X5≥4.13 m/d and X2<2.80 m时,回归模型为SVM2;当X1≥544 m and X5<4.13 m/d and X2≥2.27 m时,回归模型为SVM3;当X1≥544 m and X5<4.13 m/d and X2<2.27 m时,回归模型为SVM4;当X1<544 m and X2≥4.50 m时,回归模型为SVM5;当X1<544 m and X2<4.50 m时,回归模型为SVM6。

图3 最优决策树T0
Fig.3 Optimal decision tree T0
试验采用增强CART、SVM、M5’三种回归模型对样本数据进行分析、建模,评估模型的性能。
表2为测试样本集中任意6个样本点的预测情况,以及各模型的MAE、MSE和R2值。由表2中的结果不难发现,增强CART模型的R2值高于M5’模型1.1%,高于SVM模型3.7%,并且6个样本点的相对误差均有不同程度的下降,说明增强CART回归模型的预测精度得到明显的提升。从MAE和MSE两个指标来看,增强CART模型相比于M5’模型,MAE值降低了1.1%,MSE降低了1.9%,相比于SVM模型来讲,MAE值降低了3.3%,MSE降低了3.1%,说明增强CART回归模型保证较高的预测精度同时具有较好的泛化能力,模型稳定性强,能够较为准确地预测采煤工作面的瓦斯涌出量,达到较为理想的预测效果。
为了能够更加直观地观察模型的预测值与真实样本点目标属性值之间的差异,表1中的6个样本数据,以折线图的形式绘制模型真实值-预测值对比图(图4),从图4可知,图4a中涌出量预测值的折线图和真实值的折线图很相近,上下浮动范围较小,说明模型的预测值与真实值之间的差异小,而图4b和图4c中2个折线图差异较大,上下浮动范围比图4a 大,说明增强CART回归模型能够最大限度地逼近真实场景的变化曲线,具有较高的实用价值。


图4 不同模型真实值-预测值对比
Fig.4 Comparison of real values and predicted values of different models
针对CART和M5’回归算法的缺陷,提出了一种增强CART回归算法并应用于采煤工作面瓦斯涌出量的预测场景,通过MAE、MSE、R2三个指标评价增强CART回归算法性能,可得出以下结论(在试验样本集范围内):
1)影响采煤工作面瓦斯涌出量的诸多因素中,煤层深度、煤层厚度、煤岩层瓦斯含量和日进度为主要影响因素。
2)增强CART回归模型结构简单、稳定性好,能够最大限度地逼近实际数据,弥补了CART回归算法中输出值为定值以及容易过拟合的缺陷,同时改进了M5’算法预测精度不高的问题,对应用于采煤工作面瓦斯涌出量预测具有一定的现实意义。
3)未来笔者打算在增强CART回归算法叶节点建模方面继续开展深入研究。
[1] 何 清.工作面瓦斯涌出量预测研究现状及发展趋势[J].矿业安全与环保,2016,43(4):98-101.
HE Qing.Present research situation on gas emission prediction of working face and its developing trend[J].Mining Safety & Environmental Protection, 2016,43(4):98-101.
[2] 俞启香,王 凯,杨胜强.中国采煤工作面瓦斯涌出规律及其控制研究[J].中国矿业大学学报,2000,29(1):9-14.
YU Qixiang, WANG Kai, YANG Shengqiang.Study on pattern and control of gas emission at coal face in China[J].Journal of China University of Mining & Technology, 2000,29 (1):9-14.
[3] 俞启香.矿井瓦斯防治[M].徐州:中国矿业大学出版社,1992:40-52.
[4] 崔洪庆,樊帅帅,关金锋.采煤工作面瓦斯涌出量分源计算[J].中国安全科学报,2015,25(10):78-82.
CUI Hongqing, FAN Shuaishuai, GUAN Jinfeng.Calculation of methane emission from different sources at coal mining face based on monitoring data [J].China Safety Science Journal,2015,25(10):78-82.
[5] 张子戌,袁崇孚.瓦斯地质数学模型法预测矿井瓦斯涌出量研究[J].煤炭学报,1999,24(4):368-372.
ZHANG Zixu, YUAN Chongfu.Study on mathematical model of coalbed gas geology used to prediction of mine gas emission[J].Journal of China Coal Society,1999,24(4):368-372.
[6] 李超群, 李宏伟.一种基于支持向量机和模型树的回归模型及其在采煤工作面瓦斯涌出量预测中的应用[J].应用基础与工程科学学报, 2011,19(3):371-377.
LI Chaoqun, LI Hongwei.A SVM and model tree based regression model and its applicationin predicting the amount of gas emitted from coal face[J].Journal of Basic Science and Engineering, 2011,19(3):371-377.
[7] 付 华,谢 森,徐耀松,等.基于ACC-ENN 算法的煤矿瓦斯涌出量动态预测模型研究[J].煤炭学报,2014,39(7):1297-1301.
FU Hua, XIE Sen, XU Yaosong, et al.Gas emission dynamic prediction model of coal mine based on ACC-ENN algorithm[J].Journal of China Coal Society,2014,39(7):1297-1301.
[8] 李振兴,王小研.基于BP 神经网络的采煤工作面瓦斯涌出量预测[J].煤炭工程,2016,48(3):99-103.
LI Zhenxing, WANG Xiaoyan.Gas emission prediction of coal mining face based on BP neural network[J].Coal Engineering,2016,48(3):99-103.
[9] 黄政祥,公衍伟,王怀勐. 黔北煤田绿塘井田瓦斯赋存的地质控制因素研究[J].煤炭科学技术, 2018, 46(7): 213-217.
HUANG Zhengxiang,GONG Yanwei,WANG Huaimeng. Study on geologic control factors of gas occurrence in Lyutang Minefield of Qianbei Coalfield[J].Coal Science and Technology, 2018, 46(7): 213-217.
[10] 任志玲,林 冬,夏博文,等.基于GASA-SVR的矿井瓦斯涌出量预测研究[J].传感器学报,2017,30(2):248-252.
REN Zhiling, LIN Dong, XIA Bowen,et al.Research on prediction of mine gas emission quantity based on GASA-SVR[J].Chinese Journal of Sensors and actuators,2017,30(2):248-252.
[11] 赵朝义,袁修干,孙金镖.遗传规划在采煤工作面瓦斯涌出量预测中的应用[J].应用基础与工程科学学报,1999,7(4):389-392.
ZHAO Chaoyi, YUAN Xiugan, SUN Jinbiao.Application of genetic programming to predicting the amount of gas emitted from coal face[J].Journal of Basic Science and Engineering,1999,7(4):389-392.
[12] 李 曲,蔡之华,朱 莉.基因表达式程序设计方法在采煤工作面瓦斯涌出量预测中的应用[J].应用基础与工程科学学报,2004,12(1):50-54.
Ll Qu,CAI Zhihua,ZHU Li.Application of gene expression programing in predicting the amount of gas emitted from coal face[J].Journal of Basic Science and Engineering, 2004,12(1):50-54.
[13] BREIMAN L, FRIEDMAN J, STONE C.Classification and regression trees[J].Wadsworth,1984,40(3):874-881.
[14] QUINLAN R J.Learning with continuous classes[C]//5th Australian Joint Conference on Artificial Intelligence, Singapore, 1992:343-348.
[15] WANG Y, WITTEN I H.Induction of model trees for predicting continuous classes[C]//Poster Papers of the 9th European Conference on Machine Learning,1997.
[16] 章坚民,刘登涛,吴光中,等.采用M5’模型树和测量数据识别抽汽式机组汽耗量特性[J].中国电机工程学报, 2011,31(23):22-26.
ZHANG Jianmin, LIU Dengtao, WU Guangzhong,et al.Working condition characteristics identification for extraction unit by using M5’ model tree and measured data[J].Proceedings of the CSEE, 2011,31(23):22-26.
[17] 王 涛.M5算法在感觉评估中的应用[J].微计算机信息息,2010,26(11):229-231.
WANG Tao.Application on M5 algorithm in sensory evaluation[J].Microcomputer Information,2010,26(11):229-231.
[18] 戴 舒,付迎春,赵耀龙.基于Cubist模型树的城市不透水面百分比遥感估算模型[J].地球信息科学,2016,18(10):1401-1409.
DAI Shu, FU Yingchun, ZHAO Yaolong.The remote sensing model for estimating urban impervious surface percentage based on the cubist model tree[J].Journal of Geo-information Science,2016,18(10):1401-1409.
[19] SOLOMATINE D P,YUNPENG X.M5 model trees and neural networks:application to flood forecasting in the upper reach of the huai river in China[J].Journal of Hydrologic Engineering,2004,9(6):491-501.
[20] 王 宁,谢 敏,邓佳梁,等.基于支持向量机回归组合模型的中长期降温负荷预测[J].电力系统保护与控制,2016,44(3):92-97.
WANG Ning, XIE Min, DENG Jialiang,et al.Mid-long term temperature-lowering load forecasting based on combination of support vector machine and multiple regression[J].Power System Protection and Control, 2016,44(3):92-97.
[21] 王艳晖,李国勇,王炳萱.MFOA-SVM在采煤工作面瓦斯涌出量预测中的应用[J].矿业安全与环保,2016,43(2):54-58.
WANG Yanhui, LI Guoyong, WANG Bingxuan.Application of MFOA-SVM in coalface gas emission prediction[J].Mining Safety & Environmental Protection,2016,43(2):54-58.