移动扫码阅读
移动扫码阅读
截齿作为掘进机、刨煤机以及采煤机等重要矿山机械设备的煤岩截割刀具，在煤矿采掘及巷道建设等工程中得到广泛应用[1]。由于作业环境条件错综复杂，在破岩的过程中，截齿要承受如压应力、摩擦力等多种作用力，复杂多变的冲击载荷、煤岩的腐蚀作用以及温升等因素影响，导致截齿材质软化，磨损速率加剧，截齿消耗量不断增大[2]。截齿的磨损主要包括磨粒磨损和热疲劳磨损，现有数据显示，磨损失效在截齿失效形式中比例高达75%～90%[3]。截齿作为掘进机截割过程中的重要零部件，其磨损程度直接影响其截割性能、采煤效率及设备关键部件的可靠性。截齿磨损对设备的工作效率、安全可靠性、使用寿命等都会产生巨大影响[4]。因此，实时监测截齿磨损情况，了解截齿的工作情况，预测截齿的剩余寿命，掌握截齿的维护周期与最佳更换时机，对提高机械设备的工作效率以及延长使用寿命具有重要意义。
近年来，一些专家学者针对截齿磨损相关问题进行了研究。张景异等[5]采用统计学与图像处理技术相结合的方法对截齿磨损进行研究试验，得出了截齿的磨损规律。DEWANGAN等[6]采用显微观察X射线能量色散对磨损图像进行分析，得到了镐型截齿7种不同的磨损机理。张建广[7]通过人工模拟的方法对截齿截割进行研究试验，得到了截齿的磨损特性、磨损机理及影响磨损的主要因素。张强等[8-12]采用多种神经网络的截齿磨损程度多特征信号融合的检测方法，建立了截齿磨损程度的识别模型，实现截齿磨损程度在线监测与精确识别。袁一鸣[13]通过采用小波变换技术和统计分析的方法分析截齿的振动信号，再通过信号进行融合的方法实现对截齿磨损状态更为可靠的识别。
对于Gamma过程，是一个多应用于平稳退化的随机过程，有很多学者应用此方法并结合贝叶斯公式应用于寿命预测模型的建立。朱贝蓓等[14]通过对碳化钨涂层磨损数据的分析，引用Gamma过程，提出了一种融合监测数据与先验历史数据的磨损剩余寿命预测方法，实现碳化钨涂层磨损剩余寿命预测。王浩伟等[15-17]为了提高剩余寿命预测的可信度，针对进行过加速老化试验的产品，提出利用Gamma过程参数的非共轭先验分布进行Bayesian统计推断的剩余寿命预测方法。谷玉波等[18]通过研究产品故障机理，建立了基于Gamma退化过程的模型，并运用EM-PF参数估计方法求解模型参数，最后用轴承寿命试验所得到的数据对模型进行了验证，实例结果证明该模型是可行有效的。孙中泉等[19]给出了一个随机Gamma过程模型，通过求解该过程的首达时分布即可获得产品的失效分布。李常有等[20]提出了一种基于退化数据的特定系统或元件的实时可靠性评估方法。采用平稳Gamma过程描述系统或元件的退化过程，并使用贝叶斯估计方法来实时更新其参数，在此基础上推导出精确检测和有误差检测下的系统或元件可靠度表达式。在此基础上，结合掘进机截齿的磨损特性，应用Gamma过程对截齿磨损失效进行建模，结合试验数据，完成对截齿磨损剩余寿命的预测。
在实际的工作过程中，多种磨损状态通常同时存在，互相影响，因此应用一个磨损公式无法描述这一复杂问题难于采用某一特定磨损公式进行简单描述。目前针对这一的问题，国内外多名学者已经建立了多种模型研究退化过程。鉴于截齿磨损是一种单调的退化过程，被广泛应用于此种研究，且Gamma过程是一个独立、增量非负的随机过程恰好适用于截齿磨损退化的研究，为此，采用Gamma过程对截齿磨损失效进行建模，结合截齿磨损实时磨损监测数据，进行截齿磨损实时剩余寿命预测研究。
将t时刻的磨损退化量定义为X(t)，X(t)随时间t增加不断增大；失效时，X(t)=r0，达到最大，符合Gamma过程的特点。Gamma过程{X(t)，t≥0}一般具有如下性质：
1)随机增量。X(ti)-X(ti-1)为Gamma分布，即X(ti)-X(ti-1)～Ga[v(ti)-v(ti-1),u]。其中：Ga为Gamma函数；v(t)>0为形状参数；u>0为尺度参数；ti为时刻，i=1,2,…，n。
2)具有独立增量。不相交时间区间上的随机参数相互独立。
3)X(0)=0，概率为1。
在Gamma过程的建模框架下，利用首达时间的概念，tk时刻设备的剩余寿命Lk为
Lk=inf{t:X(tk+lk)≥ω|X(tk)<ω}= {t:X(tk+lk)≥ω|X(tk)<ω}
(1)
式中：ω为失效阈值；lk为故障前的任意时刻系统退化量(lk<Lk)。
由于截齿磨损的增量是非负的，所以其磨损过程是一个平稳的Gamma过程，通常记作 Γ(ct),因此,令v(t)=ct,常数c>0，所以，X(t)的概率密度函数FX(t)(x)为
(2)
同时，可以得到磨损退化量X(t)的期望E[X(t)]=
xFX(t)(x)dx=ct/u，方差Var[X(t)]=E{[X(t)-E(X(t))]2}=ct/u2。
如果在时刻ti，并且0=t0<t1<t2<…<tn，对应的磨损退化数据xi,且0=x0≤x1≤x2≤…≤xn。考虑磨损的增量δi=xi-xi-1(i=1,2,…,n)的似然函为
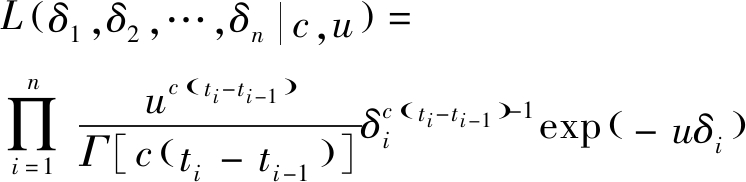
(3)
分别对式中c和u求导，可以得到对于c和u的估计值
和
的方程组，其中，φ为t的最小二乘估计参数。
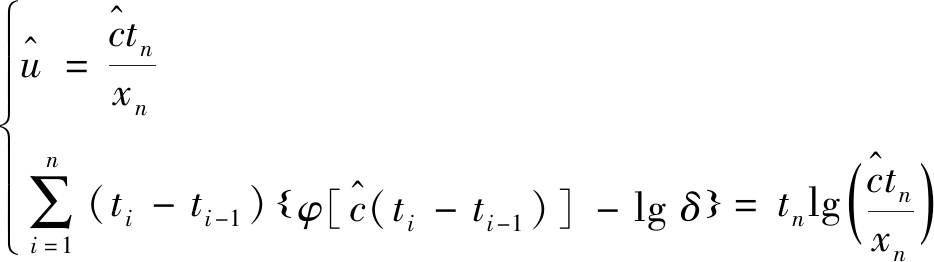
(4)
求解方程组得到c和u的估计值和
也可根据截齿的磨损量退化数据xi,i=1,2，…,n，得到各检测时间退化量的均值和方差的估计值
(5)
对式(5)两端求对数后，通过线性回归的方法，解得未知参数c和u的估计值和
设Tr0表示截齿磨损退化量X(t)首次达到磨损阈值r0的时刻，根据Gamma过程定义可知截齿磨损失效时间的分布函数为
F(t)=
FX(t)(x)dx=
(6)
其中，对于不同时刻，如果能确定参数c和u的估计值
和
就可以得到此时截齿磨损的可靠性。如果截齿磨损失效时间的分布函数F(t)可导，可得到截齿磨损失效时间的概率密度f(t),令
即
(7)
如果v(t)可导，则有
(8)
由于在建模过程中，截齿磨损失效阈值的首达时间无法准确得到，因此为了便于验证采用给定可靠度阈值为0.8的方法，再根据Gamma过程的截齿磨损失效建模反求出此时的剩余寿命。
在试验初期，磨损数据量过少，若按照原有的方法来推算新的Gamma过程的参数c和u，由于要求解答的过程过于复杂，且数据少，误差大。因此考虑利用已有的样本数据作为正在进行试验的截齿磨损退化机制的先验经验，再通过贝叶斯方法更新Gamma过程的参数c和u，既能够提高预测效率，又可提高参数精度。此外，由于此过程中形成了一个前一组的后延分布作为下一组的先验分布的先验链，因此先验分布和后验分布需要满足形式相同的要求，所以这里定义先验分布与似然函数是共轭的。
根据贝叶斯原理可以得到
π(c,u|δ1,δ2，…，δn)=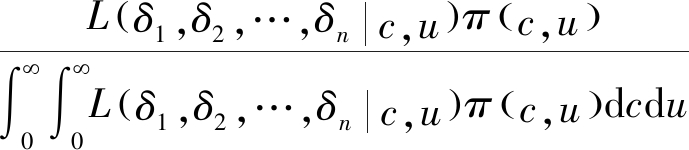
(9)
其中，π(c,u|δ1,…,δn)为向量(c，u)的后验分布。L(δ1，δ2，…，δn|c,u)为当给定量(c，u)，是退化增量δ1,δ2，…,δn的似然函数；π(c，u)为向量(c、u)的先验分布；根据贝叶斯公式，当磨损监测数据有更新时，可以根据新的退化数据来更新(c，u)的后验分布，从而得到实时正在试验的截齿磨损可靠性评估。对于先验分布π(c，u)，可以考虑先固定c，并假设u的先验分布π(u|c)是形状参数为α、尺度参数为β的Gamma分布，由Gamma分布性质可知：u的后验分布是形状参数为 (α+ctn)、尺度参数为(β+xn)的Gamma分布。由此，贝叶斯公式可以改写成:
π(c,u|δ1,…,δn)=
π(u,c|δ1,…,δn)π(c|δ1,…,δn)∝
(10)
当参数c未知时，u的先验分布π(u|c)可以认为是形状参数为α(c)、尺度参数为β(c)的Gamma分布。由于先验分布和似然函数符合共轭条件，从而u的后验均值可以写成：
(11)
根据贝叶斯公式更新的c和u的估计值和
得到截齿磨损可靠性函数为
(12)
在得到性能可靠性函数的基础上，对于给定可靠性阈值(取0.8)，可以求出此时截齿磨损剩余寿命，从而实现截齿磨损剩余寿命的预测。
为研究截齿磨损的退化机制，通过试验测得不同时刻，截齿磨损量的大小，选用精度等级为0.1 g的电子天平测量磨损量，每次测量3次，取平均值。总共进行了10组次试验，分别在40、80、…、1 920 min时，记录磨损量，磨损数据见表1。
表1 截齿的磨损量数据
Table 1 Wear data of pick
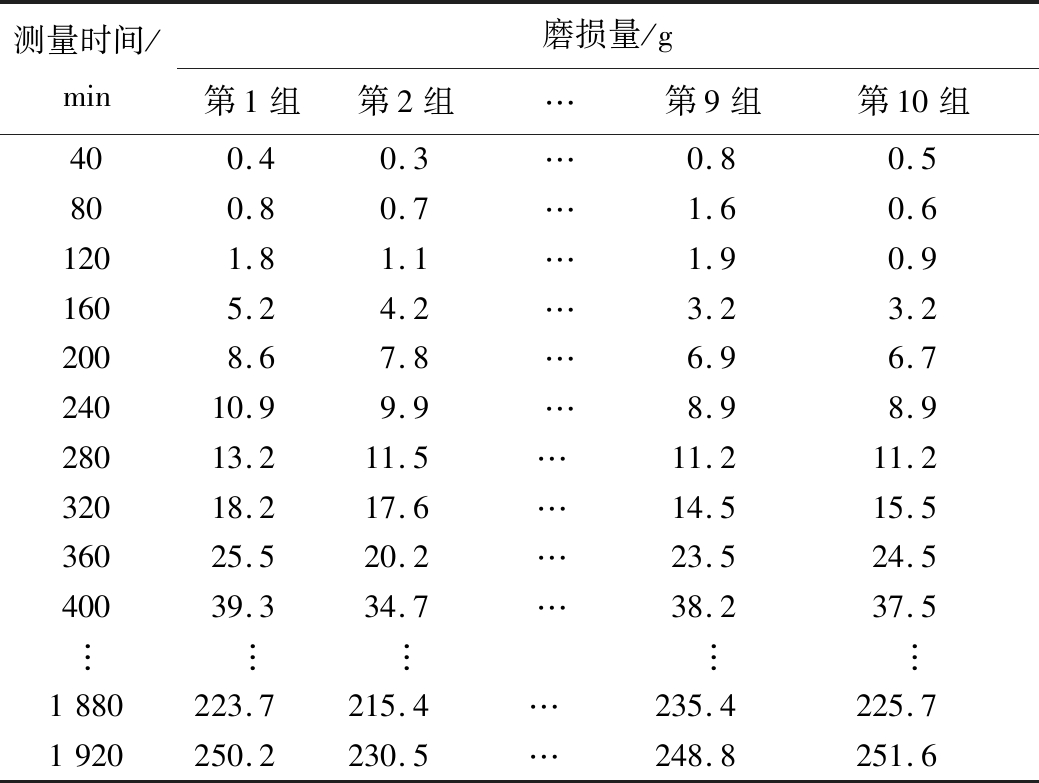
测量时间/min磨损量/g第1组第2组…第9组第10组400.40.3…0.80.5800.80.7…1.60.61201.81.1…1.90.91605.24.2…3.23.22008.67.8…6.96.724010.99.9…8.98.928013.211.5…11.211.232018.217.6…14.515.536025.520.2…23.524.540039.334.7…38.237.5︙︙︙︙︙1880223.7215.4…235.4225.71920250.2230.5…248.8251.6
由于所得数据均来自不同截齿，具有样本独立性，且初始量满足过程的定义，利用Matlab软件的ks检验进行验证，其他数据经均满足Gamma过程的要求。
计算得出，第1组磨损增量服从Ga(x|0.745,41.38)分布，对应的拟合曲线如图1所示。
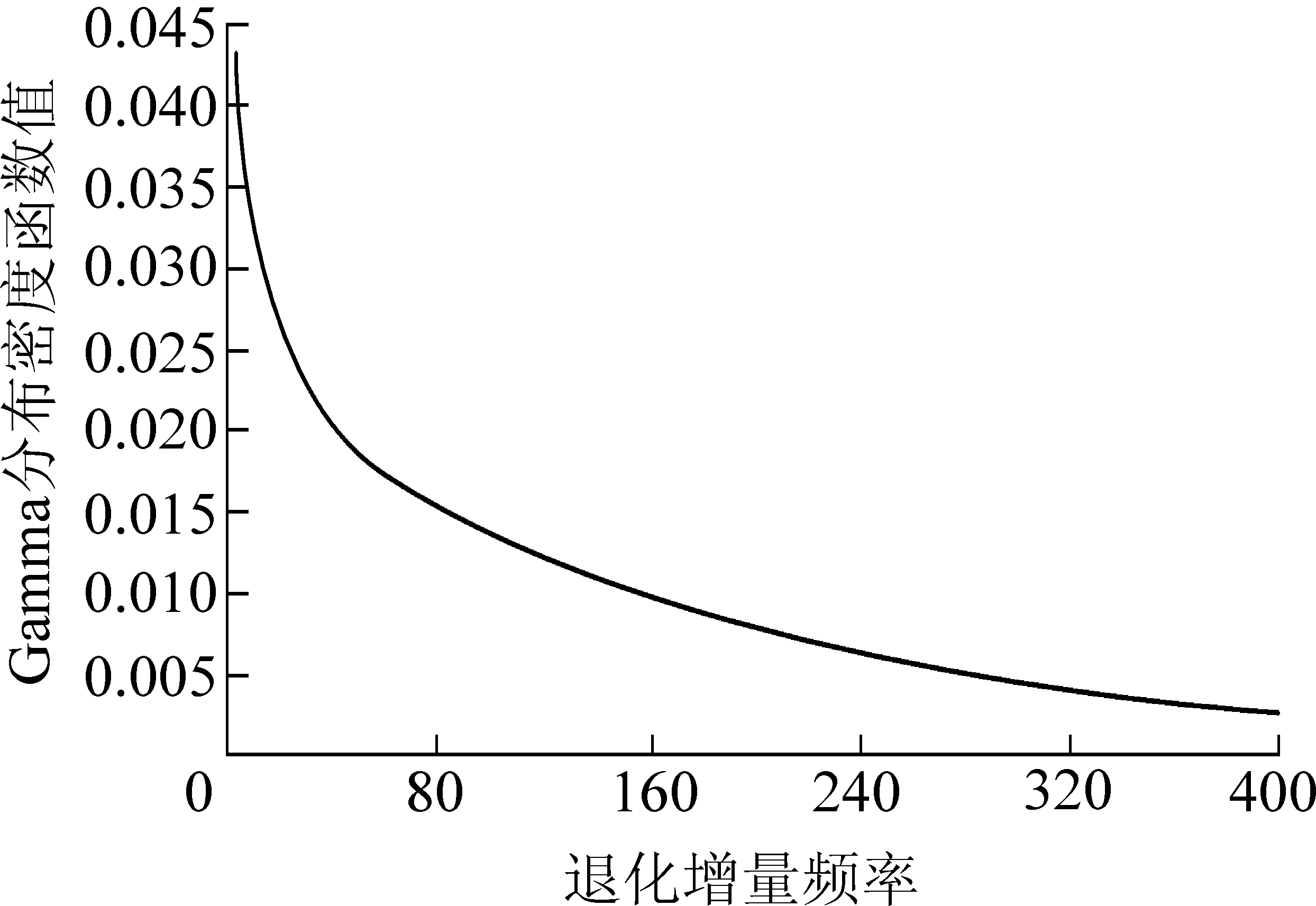
图1 截齿磨损退化增量与Gamma概率密度
Fig.1 Wear degradation increment of pick and Gamma probability density
应用此方法计算得到各组数据的参数估计值，见表2。
基于表2的计算结果，以的均值0.759作为c的初始值，选择3组数据分别利用贝叶斯方法更新Gamma过程参数u的估计值见表3。
按照式(11)计算80、160、240、320 min时的可靠度，其中第1组可靠度曲线如图2所示。
表2 各组截齿数据的参数估计值
Table 2 Parameter estimates for datas of each group pick
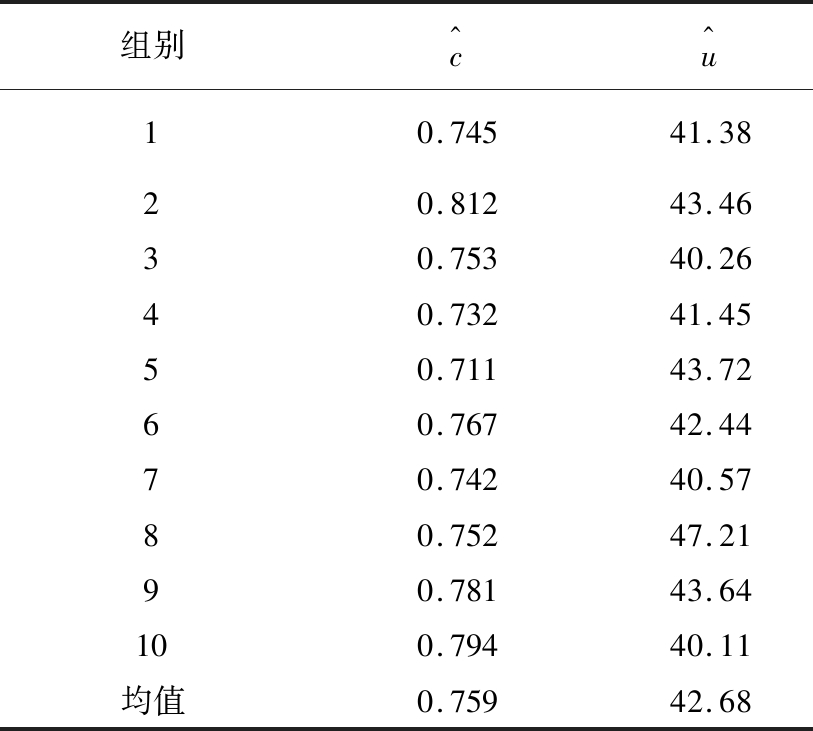
组别c^u^10.74541.3820.81243.4630.75340.2640.73241.4550.71143.7260.76742.4470.74240.5780.75247.2190.78143.64100.79440.11均值0.75942.68
表 3 Gamma过程参数u的估计值
的更新结果
Table 3 Update results of estimated value 
of Gamma process parameters u
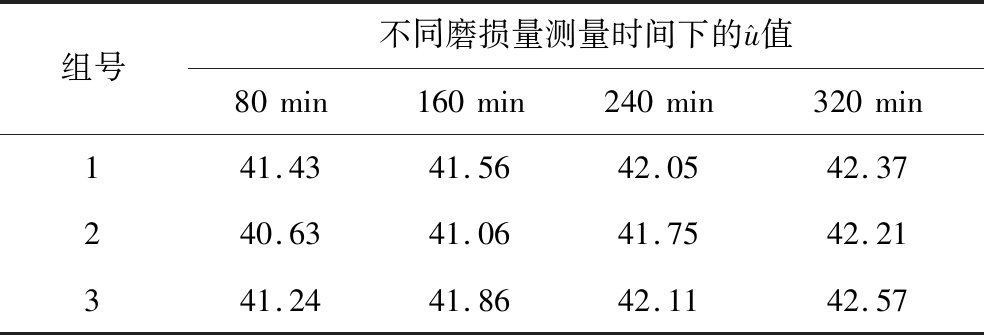
组号不同磨损量测量时间下的u^值80min160min240min320min141.4341.5642.0542.37240.6341.0641.7542.21341.2441.8642.1142.57
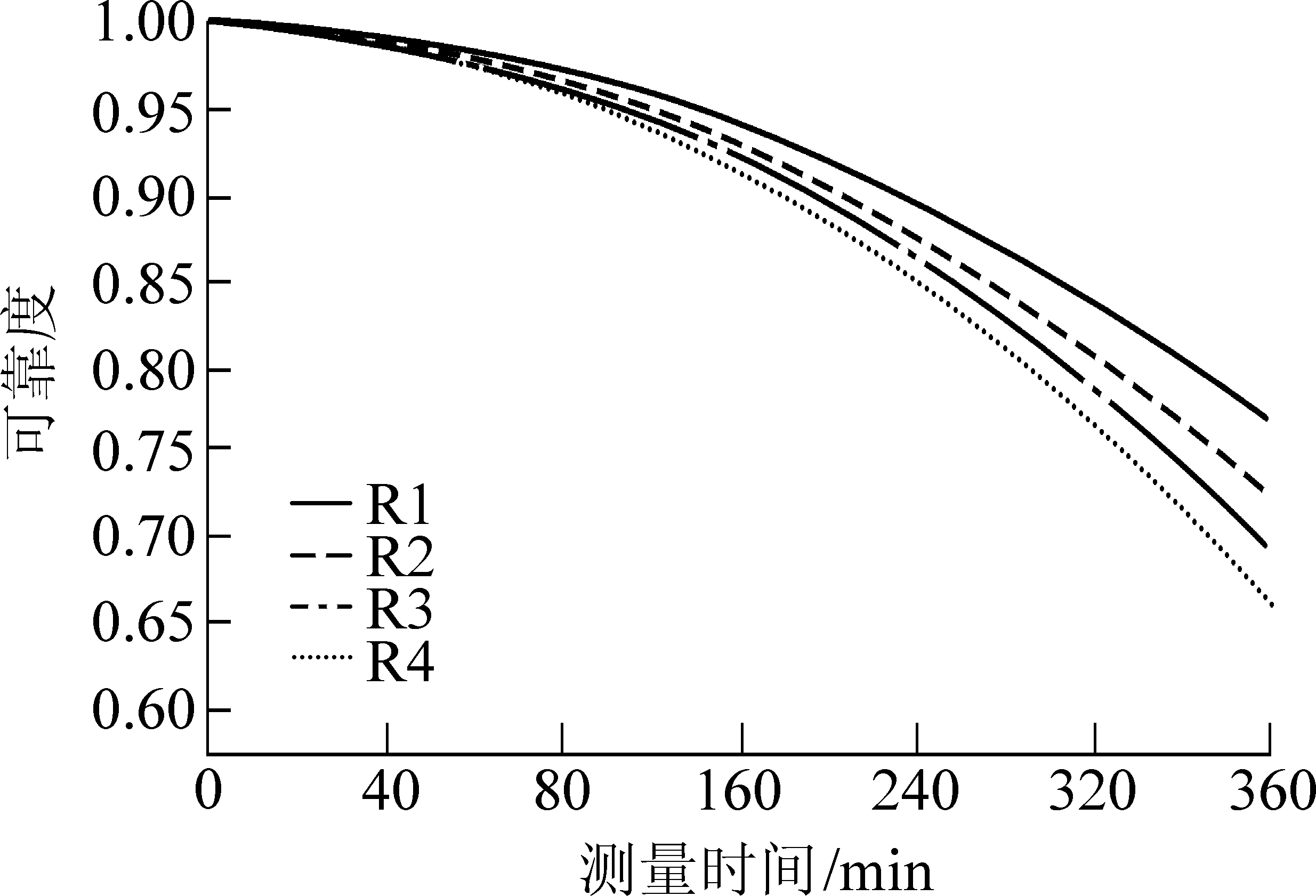
图2 不同磨损时间下的可靠度曲线
Fig.2 Reliability curves under different wear time
图2中R1—R4分别表示在80、160、240、320 min的可靠度曲线。由图2可以看出，R1—R4可靠度逐渐降低。随着磨损数据的增加，可靠度曲线越来越接近真实值。
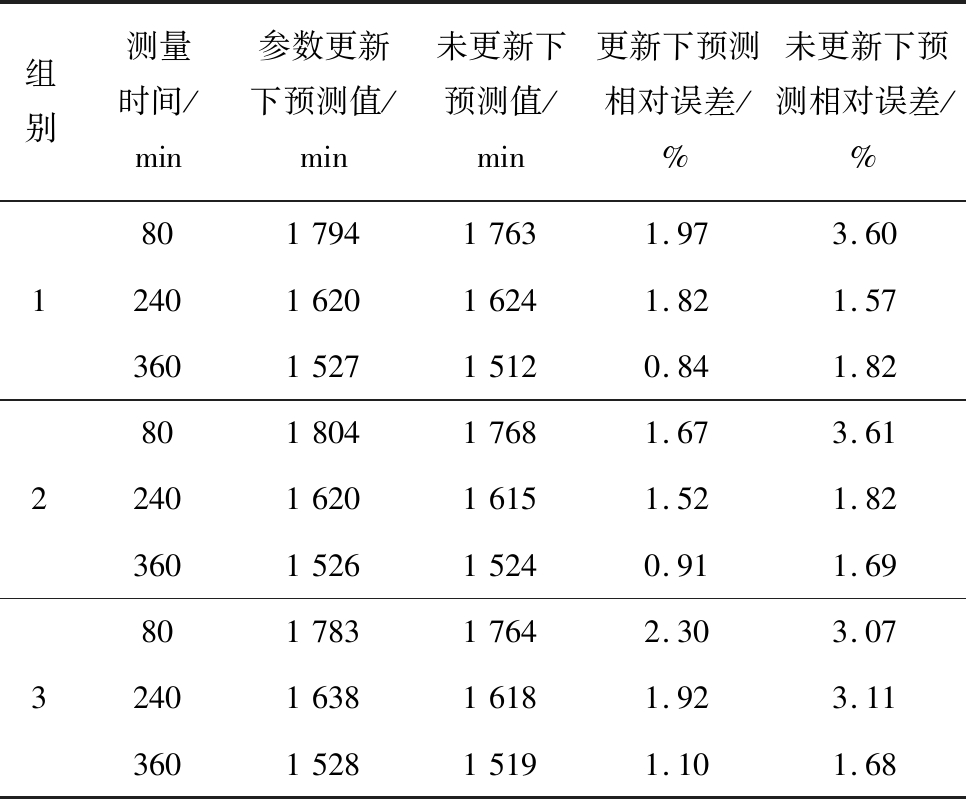
由图2可知，在给定阈值0.8的条件下，可以得到截齿在不同时间点的剩余寿命预测值。剩余寿命预测值与真实值的比较见表4，再利用贝叶斯更新方法后，得到的值误差更小。
从表4可以看出，随着监测数据的增加，未更新参数的预测精度呈上下浮动状态，无规律可循，参数更新下的预测精度逐渐提高。
表4 剩余寿命预测值与真实值的比较
Table 4 Comparison between predicted value of residual life and real value
组别测量时间/min参数更新下预测值/min未更新下预测值/min更新下预测相对误差/%未更新下预测相对误差/%180179417631.973.60240162016241.821.57360152715120.841.82280180417681.673.61240162016151.521.82360152615240.911.69380178317642.303.07240163816181.923.11360152815191.101.68
1)根据截齿磨损失效的特点，建立了基于Gamma过程的失效模型。
2)应用贝叶斯更新方法对Gamma过程的参数进行更新，从而实现截齿磨损剩余寿命的预测，提高预测准确性。
3)在给定失效阈值的前提下，应用此方法的预测精度在随着监测数据的不断增加，可以满足实际工程中对截齿剩余寿命的监测需求。
[1] 张 强，刘志恒，王海舰，等. 基于截齿振动及温度特性的煤岩识别研究[J].煤炭科学技术, 2018, 46(3): 1-9,18.
ZHANG Qiang, LIU Zhiheng, WANG Haijian,et al.Study on coal and rock identification based on vibration and temperature features of picks[J].Coal Science and Technology, 2018, 46(3):1-9,18.
[2] TIRYAKI B.In situ studies on service life and pick consumption characteristics of shearer drums[J].Journal of the South African Institute of Mining and Metallurgy，2006,31(3)：380-385.
[3] 朱 华，吴兆宏，李 刚，等.煤炭机械磨损失效研究[J].煤炭学报，2006,31(3)：380-385.
ZHU Hua，WU Zhaohong，LI Gang，et al.Study on wear failures of mining machinery[J].Journal of China Coal Society，2006,31(3)：380-385.
[4] 吴虎成，黄孝龙.采煤机截齿的失效分析及改进措施[J].煤矿机械，2013,34(5)：200-201.
WU Hucheng，HUANG Xiaolong.Failure analysis and improvement measure of cutting teeth of shearer[J].Coal Mine Machinery，2013,34(5)：200-201.
[5] 张景异，李高彩.基于图像处理的对掘进机截齿磨损率的研究[J].工业仪表与自动化装置，2009(1)：22- 24.
ZHANG Jingyi，Ll Gaocai.Research on the wear rate of the cutting teeth of the boring machine based on image processing[J].Industrial Instrumentation and Automation Device,2009(1)：22-24.
[6] DEWANGAN S,CHATTOPADHYAYA S.Characterization of wear mechanisms in distorted conical picks after coal cutting[J].Rock Mechanics & Rock Engineering,2016,49(1):225-242.
[7] 张建广.EBZ260W型掘进机截割人工岩壁的截齿磨损研究[J].矿山机械，2014,42(9):11-14.
ZHANG Jianguang.Study on pick abrasion during artificial rock cut by EBZ260W road header[J].Mining & Processing Equipment，2014，42(9):11-14.
[8] 张 强,刘志恒,王海舰,等.基于BP神经网络的截齿磨损程度在线监测[J].中国机械工程,2017,28(9):1062-1068.
ZHANG Qiang,LIU Zhiheng,WANG Haijian,et al.On-line monitoring of gear cutting wear degree based on BP neural network [J].China Mechanical Engineering,2017,28(9):1062-1068.
[9] 张 强,刘志恒,代晓丹,等.基于振动和声发射信号的截齿磨损程度识别研究[J].机械设计与研究,2018,34(1):126-132，136.
ZHANG Qiang,LIU Zhiheng,DAI Xiaodan,et al.Study on the recognition of gear cutting wear degree based on vibration and acoustic emission signal [J].Mechanical Design and Research,2018,34(1):126-132，136.
[10] 张 强,刘志恒,王海舰,等.基于多特征信息融合的截齿磨损程度识别研究[J].电子测量与仪器学报,2017,31(12):1974-1983.
ZHANG Qiang,LIU Zhiheng,WANG Haijian,et al.Study on the recognition of gear cutting wear degree based on multi-feature information fusion [J].Journal of Electronic Measurement and Instruments,2017,31(12):1974-1983.
[11] 张 强,王海舰,李立莹,等.基于自适应神经-模糊推理系统模糊信息融合的采煤机截齿磨损在线监测[J].中国机械工程,2016,27(19):2607-2614.
ZHANG Qiang,WANG Haijian,LI Liying,et al.On-line monitoring of cutting wear of shearer based on fuzzy information fusion of adaptive neural fuzzy inference system [J].China Mechanical Engineering,2016,27(19):2607-2614.
[12] 张 强,祁 秀,王海舰.基于模糊信息融合的掘进机截齿磨损监测系统[J].广西大学学报：自然科学版,2015,40(5):1177-1182.
ZHANG Qiang,QI Xiu,WANG Haijian.A roadheader tooth cutting wear monitoring system based on fuzzy information fusion [J].Journal of Guangxi University：Natural Science,2015,40(5):1177-1182.
[13] 袁一鸣.基于数据融合的掘进机截齿磨损状态监测[J].科技创新导报,2016,13(21):36-37.
YUAN Yiming.Monitoring of cutting wear status of roadheader based on data fusion [J].Science and Technology Innovation Bulletin,2016,13(21):36-37.
[14] 朱贝蓓,蔡 景,陈 康.基于Gamma过程的碳化钨涂层磨损剩余寿命[J].南京航空航天大学学报,2016,48(6):884-889.
ZHU Beibei,CAI Jing,CHEN Kang.Wear residual life of tungsten carbide coating based on gamma process [J].Journal of Nanjing University of Aeronautics and Astronautics,2016,48(6):884-889.
[15] 王浩伟,徐廷学,刘 勇.基于随机参数Gamma过程的剩余寿命预测方法[J].浙江大学学报：工学版,2015,49(4):699-704，762.
WANG Haowei,XU Tingxue,LIU Yong.Residual life prediction method based on stochastic parameter gamma process [J].Journal of Zhejiang University：Engineering Edition,2015,49(4):699-704，762.
[16] 王浩伟,徐廷学,赵建忠.融合加速退化和现场实测退化数据的剩余寿命预测方法[J].航空学报,2014,35(12):3350-3357.
WANG Haowei,XU Tingxue,ZHAO Jianzhong.Residual life prediction method for fusion of accelerated degradation and field measured degradation data [J].Journal of Aeronautical Sciences,2014,35(12):3350-3357.
[17] 王浩伟,徐廷学,周 伟.综合退化数据与寿命数据的某型电连接器寿命预测方法[J].上海交通大学学报,2014,48(5):702-706.
WANG Haowei,XU Tingxue,ZHOU Wei.A life prediction method for a certain type of electrical connector based on degraded data and life data[J].Journal of Shanghai Jiaotong University,2014,48(5):702-706.
[18] 谷玉波,贾云献,张英波.基于Gamma退化过程的剩余寿命预测及维修决策优化模型研究[J].轴承,2013(4):44-49.
GU Yubo,JIA Yunxian,ZHANG Yingbo.Research on residual life prediction and maintenance decision optimization model based on Gamma degradation process [J].Bearing,2013(4):44-49.
[19] 孙中泉,赵建印.Gamma过程退化失效可靠性分析[J].海军航空工程学院学报,2010,25(5):581-584.
SUN Zhongquan,ZHAO Jianyin.Gamma process degradation failure reliability analysis [J].Journal of the Naval Academy of Aeronautical Engineering,2010,25(5):581-584.
[20] 李常有,徐敏强,郭 耸,等.基于gamma过程及贝叶斯估计的实时可靠性评估[J].宇航学报,2009,30(4):1722-1726.
LI Changyou,XU Minqiang,GUO Song,et al.Real time reliability evaluation based on gamma process and Bayesian estimation [J].Journal of Aerospace，2009，30 (4):1722-1726.