0 引 言
岩石在受到外载荷的作用下,由于内部存在大量的微小裂隙,受外力作用后会出现裂隙的闭合、扩展及裂隙间贯通,在整个过程中伴随着部分能量以弹性波的形式释放出来,此现象称为岩石声发射(Acoustic Emission,AE)[1-2]。声发射检测技术[3]是一种评价材料或构件损伤的动态检验技术,它通过对声发射信号的处理和分析来评价声发射源的发生和发展规律,有利于岩体材料健康监测、灾害预警等工作的开展。声发射源产生的弹性波,由于会受到介质的传播特性以及传感器频率响应特性等影响,在传播过程中会发生反射、折射、衍射、频散等,同时还受到周围环境噪声的影响,故采集到的声发射信号是一种复杂的非平稳信号,容易产生模式混叠与转换现象。因此,如何选取有效的特征参数提取方法一直是声发射检测的关键难题[4-5],对岩石失稳监测、揭示岩石破裂过程具有重要意义。
目前在岩石力学领域,国内外学者展开了大量的研究,并获得了一定的成果。赵奎等[6]针对岩石声发射采用参数法确定Kaiser点存在的问题,提出了基于波形分析的确定Kaiser的小波分析研究方法;张艳博等[7]应用HHT方法研究了粉砂岩破裂声发射信号频率特性,得到了粉砂岩破裂分为4个阶段且声发射信号的有效频段为20~120 kHz;鲜晓东等[8]利用中值滤波-奇异值分解及AR模型相结合方法,得出了在避免计算模型阶次的同时实现了岩石声发射信号到达时间的自动识别;凌同华等[9]采用经验模态分解(EMD)分析冲击载荷作用下岩石声发射信号能量分布特征,得出随着岩石的密度、纵波波速、弹性模量的降低,信号的优势频率越来越集中,且有往低频发展的趋势,相比小波包分析,EMD分析更具适应性。对EMD的深入研究过程中,也发现了一些问题,典型模态、混叠现象,导致分解结果不准确。为了减轻模态混叠,在某些情况下采用了噪声辅助信号分解方法Ensemble EMD (EEMD)[10-11]。由白噪声频谱均匀分布特性,通过有限的平均处理,并不能完全抵消添加噪声对分解效果的影响,残余白噪声仍存在于重构元件中,通过增加集成试验次数,可以减少重构误差,但计算量较大。为了解决重构信号受残差噪声污染的问题,通过在目标信号中加入与相反符号成对的白噪声,提出了互补的EEMD (CEEMD)[12-13]。虽然它在消除剩余噪声影响方面优于EEMD,但仍然需要进行大量的集成试验。此外,由于信号加噪声的不同实现方式,产生的固有模态函数的数目也不同,这导致了最终平均计算难以实现的问题。白噪声幅值和集成试验次数等不合适的参数也会导致伪模的产生。
为了克服这些情况,TORRES 等[14]提出了一种改进算法,称完全自适应噪声EEMD (Complete EEMD with Adaptive Noise,称CEEMDAN法),为重构原始信号提供了一种新的方法,其误差可忽略,而且计算量小。在该方法分解的每一阶段,加入自适应白噪声,计算出唯一的残差信号,得到各阶模态、CEEMDAN法可避免模态混合现象,其分解过程是完整的。然而,有些方面,如在IMFs中存在少量的残留噪声和出现错误的模态仍然值得改进。小波阈值去噪方法是由美国学者多诺霍在1992年提出的,该方法计算简单,可在很大程度上抑制高频噪声,保留有用信息。因此,笔者将CEEMDAN法和小波阈值相结合进行去噪,以信噪比和均方根误差作为评价指标,采用凸优化模型提取重构信号的特征,实现了岩石断裂过程的实时定量监测。
1 基于CEEMDAN法的小波阈值去噪原理
1.1 CEEMDAN法原理
完整集成经验模态分解:在EMD分解的各阶段添加白噪声,通过计算唯一的余量信号获取各个模态分量,直到获取的余量信号的极值点个数至多不超过2个,即停止分解。设vi(t)为某i次试验高斯白噪声,x(t)为原始信号序列(t为时间),ε为噪声标准差,且定义算子Ek[·]为EMD分解的第k个模态分量,CEEMDAN法分解的第k个模态分量为![]() 分解步骤如下:
分解步骤如下:
1)将s(t)=x(t)+ε0vi(t)总共进行了I次试验,通过EMD分解得第1个模态分量,计算式为
(1)
2)计算第1阶段的余量信号为
(2)
3)总共进行了I次试验,每次试验对r1(t)+εE1[vi(t)]进行分解,直到得到第1个EMD分解的模态分量,第2个模态分量为
(3)
4)重复步骤3的过程,得到第k个余量信号及第k+1个模态分量分别为
(4)
(5)
5)执行步骤4,直至余量信号不能再分解,算法终止时,记所有的模态分量总个数为K,即最终的余量信号为
(6)
因此,原始信号x(t)被分解为
(7)
1.2 小波阈值去噪
小波阈值去噪步骤为①将信号变换到小波域,求取小波系数;②设置阈值,将小于该阈值的小波系数去掉;③利用处理后的小波系数进行小波重构。采用的阈值函数有硬阈值和软阈值函数。
1.3 凸优化理论
假定原始信号为x,其RMS信号可以表示为
(8)
其中,参数m、L为试验常量,L为自然数,m≥2且为整数;l为原始信号采样点序号;h为RMS信号采样点序号;n为RMS信号采样个数。L/f决定了RMS信号时域的分辨能力(f为信号采样频率),声发射事件识别目标是确定该时刻下能量大小, RMS信号可以得到x信号的包络形式,有利于减少计算时间。
RMS信号y的凸优化数学模型为[15-16]
(9)
其中,![]() 表示y的估计值;
表示y的估计值;![]() 表示L2范数下,估计信号与真实信号的接近程度;D∈R(n-1)×n是双对角矩阵,
表示L2范数下,估计信号与真实信号的接近程度;D∈R(n-1)×n是双对角矩阵,![]() 系数δ为估计信号与真实信号接近的权重。
系数δ为估计信号与真实信号接近的权重。
由式(8)可得到其解为
(10)
式中:O是单位矩阵;DT是矩阵D的转置矩阵。
2 试验采集与信号预处理
2.1 岩石单轴加载试验方案
加载系统采用中国科学院武汉岩土力学研究所研制的RMT-150C型的岩石力学试验系统,控制模式为位移加载,速率为0.002 mm/s,应变随时间呈线性变化关系;声发射采集系统主要由传感器、前置放大器、数据采集、数据存储等模块构成,传感器采用SR15型,共振频率为150 kHz,灵敏度>65 dB;前置放大器增益为40 dB;采样时间间隔为1 μs,红砂岩试件规格加工成直径为50 mm,高为100 mm的圆柱体样件。试验过程中在试件两端加垫层材料隔离噪声,且岩心的轴线应与加载的轴线重合,采用黄油作耦合剂,并用橡皮筋将探头固定在中间部位,且保持加载过程与声发射采集同步。
由应力计算公式得到的砂岩应力随时间变化曲线如图1所示,其过程清楚地可分为4个阶段。OA为压密阶段:曲线斜率由小变大,呈上凹趋势,表明微小裂隙渐渐闭合,横向膨胀较小,体积随载荷的增大而减小;AB为弹性阶段:此阶段曲线近似一条直线,说明岩样内部相对变形率保持不变;BC为失稳破坏阶段:C点为峰值应力,轴向应变增大,随着应力的进一步增大,产生的新裂纹最终汇合贯通。CD为失稳破坏后阶段:该阶段岩石仍有承载力,但声发射强度较弱。

图1 砂岩的应力随时间变化曲线
Fig.1 Curve of stress of sandstone with time variation
综上可知:砂岩破裂过程的应变和应力明显经过4个不同阶段,而且受外力作用各阶段的破裂程度不同,而声发射信号是岩体内部微裂纹断裂释放的弹性波,所以可以通过接收、检测与分析,从而判断岩石破裂过程中的应力变化,达到研究岩石破裂过程的目的[17]。
2.2 砂岩声发射信号预处理
在数据处理时,由于加载时间长、数据量大等问题,根据应力应变曲线划分的4个阶段,按时间顺序对各阶段间隔均匀地选取25组信号,每组采样长度为12 000,这样既降低了数据处理量,同时也可以准确地反映岩石破裂各阶段的信息。限于篇幅选取破裂阶段下一组声发射信号进行分析,其原始波形图及频谱分析如图2所示。

图2 原始波形图及振幅频谱
Fig.2 Original waveform and amplitude spectrum
由图2b可知:信号在频率20~50 kHz的幅值较大,且有一定的趋势;高频噪声明显。对图2a信号进行CEEMDAN法分解,其中噪声标准差ε=0.2,试验次数I=200 m,信号分解为IMF1~IMF14共14个分量和1个余量,前8个分量如图3所示。从图3中难看出各分量与原始信号的关联性,为了评价各分量与原始信号的重要性,引入相关系数和方差贡献率,真实分量与原始信号若具有较大的相关性,则相关系数和方差贡献率值也越大[18]。各IMF分量与原始信号的相关系数和方差贡献率如图4所示。

图3 原始信号分解的IMF分量(IMF1~IMF8)
Fig.3 IMF component (IMF1~IMF8) of decomposition of original signal
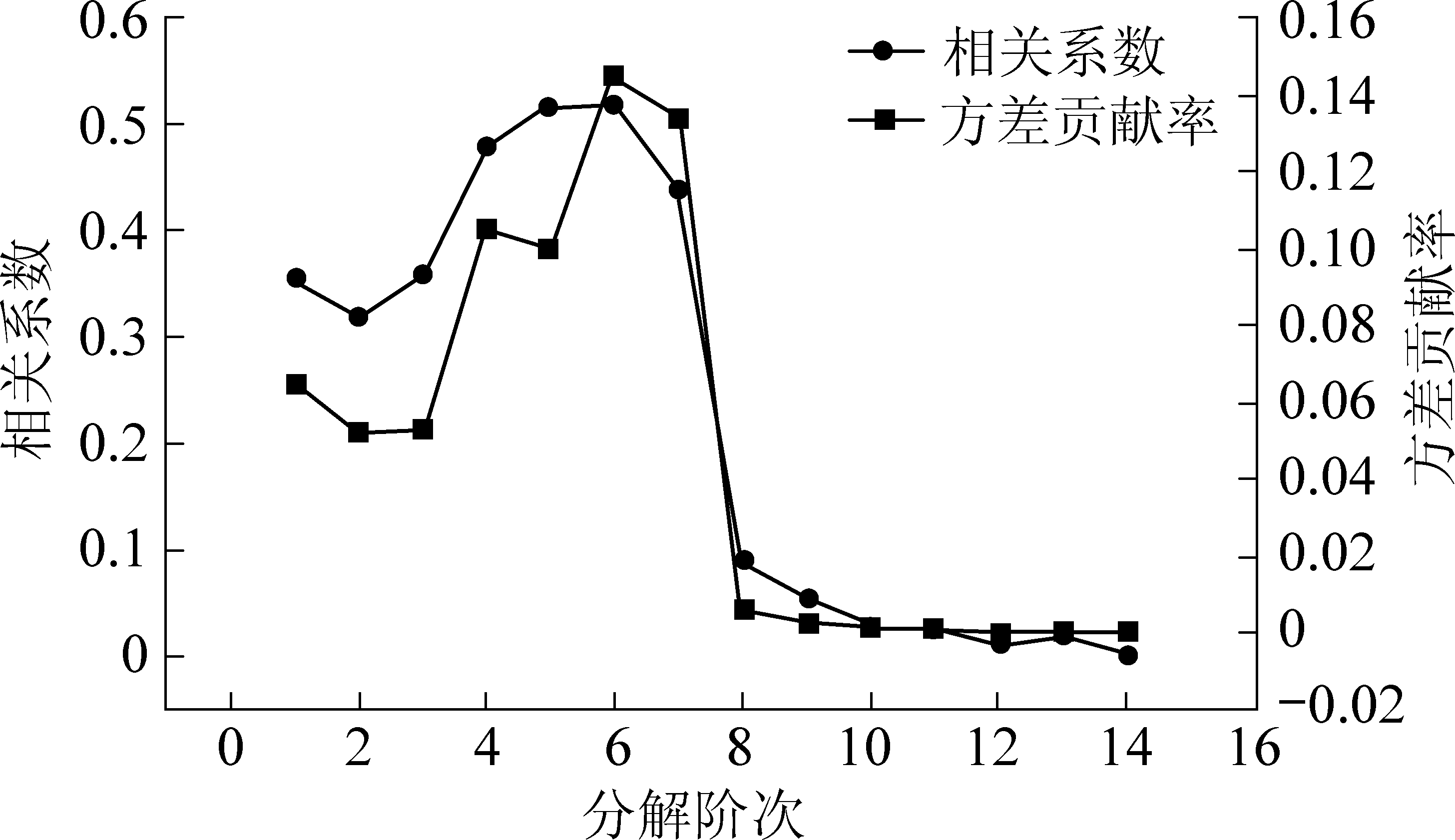
图4 各分量与原始信号的相关系数与方差贡献率
Fig.4 Correlation coefficient and variance contribution rate of each component and original signal
从图4可以看出:相关系数与方差贡献率具有很好的正相关性,且前7个分量IMF1—IMF7的相关系数和方差贡献率较大,与其他分量的差值范围分别为0.230 3~0.519 9、0.045 3~0.143 0,可认为IMF8—IMF14为真实分量,7个分量为虚假分量。
利用连续均方误差准则确定分界点,进行小波阈值去噪。其定义为[19]
(11)
(12)
式中:N为原始信号x(t)的采样点个数;xk(tj)为前k个分量tj时刻的重构信号幅值;Ck(tj)为CEEMDAN法分解后所得的第k个IMF分量,is为分界点。
由式(11)、式(12)可得:is=4,即对前4个IMF分量进行小波阈值去噪处理。根据声发射信号小波基选择经验,选择Daubechies小波族作为岩石声发射信号处理的小波基,该小波序列具有较好的紧支撑性、光滑性和近似对称性,在声发射信号处理中得到广泛应用[20]。笔者选取dB4小波,分解层次为3层,采用软阈值函数及启发式最优预测变量阈值。小波阈值处理后的图形如图5所示。

图5 去噪后的前4个分量
Fig.5 The first 4 components after de-noising
由图5可以看出,前4个IMF分量经小波阈值处理后变得更平滑,对高频噪声有很好的抑制,而且凸峰特征较为明显。将处理后的分量与其余真实分量进行重构,如图6a所示,可以看出:CEEMD-AN与小波阈值联合去噪后的重构声发射信号较平缓,且衰减特征明显,可以很好的统计原始声发射信号的事件数特征。图6b—图6e为对原始信号做CEEMDAN、小波阈值和联合去噪后的信号频谱图。
图6c为直接小波阈值去噪频谱图,从图中可知:小波阈值去噪效果较好,但由于该方法本身的特性,使得部分低频能量的有用信息损失严重;图6d和图6e分别为直接舍弃IMF1,IMF1、IMF2重构信号的频谱图,从图中可得:CEEMDAN直接舍弃IMF1分量,浅层信号的分辨率较高,压制随机噪声不完全;CEEMDAN直接舍弃IMF1和IMF2分量,虽然压制了大部分噪声,但同时也损失了某些高频成分。图6b为联合去噪的频谱图,分析可知:该方法在浅层分辨率没有太大的损失,更好的保留了低频能量,与图2b原始信号频谱比较,其对高频中的噪声进行了有效抑制,保留了部分高频有用信息,并在很大程度上克服了小波阈值和直接舍弃高频IMF分量的缺陷。
为定量评价该去噪算法的性能,引入均方根(RMSE)和信噪比(SNR)两个指标对各种算法的去噪效果进行比较,结果见表1。

图6 重构信号及各方法去噪后的频谱
Fig.6 Spectrum map after denoising reconstructed signal and service method
从表1中对比2个指标的性能可以看出,笔者方法显著降低了RMSE,且信噪比相对于直接舍弃IMF1重构提升了10.5 dB,说明噪声残留较少,有用信息也最丰富。并结合声发射仪与传统的Geiger算法对声发射事件进行定位,将偏离破裂区域外的事件作为误差,统计计算在应力为40 MPa时的定位精度见表2。
表1 4种去噪算法参数对比
Table 1 Four denoising algorithm parameters comparison
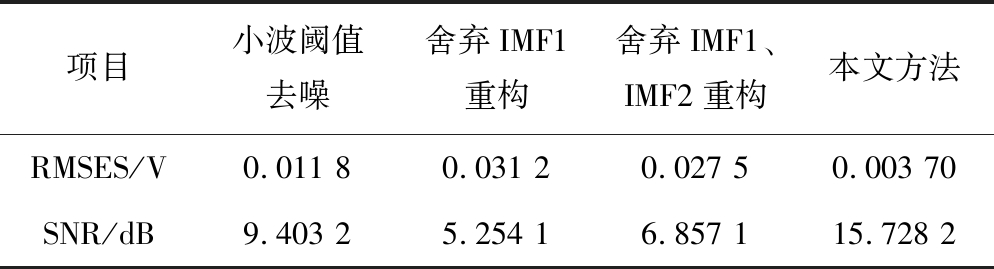
项目小波阈值去噪舍弃IMF1重构舍弃IMF1、IMF2重构本文方法RMSES/V0.011 80.031 20.027 50.003 70SNR/dB9.403 25.254 16.857 115.728 2
表2 4种去噪算法事件数定位精度对比
Table 2 Comparison of event number positioning accuracy of four denoising algorithms

项目小波阈值去噪舍弃IMF1重构舍弃IMF1、IMF2重构本文方法定位精度/%87717993
从表2可以看出,在应力为40 MPa时,用CEEMDAN和小波阈值去噪结合对声发射事件定位精度比直接小波阈值去噪后定位精度提高了6%,因此可更好地对岩石内部裂纹扩展进行监测。
3 重构信号特征提取及结果分析
3.1 声发射事件数特征提取
基于理论分析,声发射事件识别步骤如下:①将原始信号经CEEMDAN-小波阈值结合去噪;②根据式(8),得到重构信号的RMS信号y;③设定权重参数δ,由式(9)和式(10)得到信号y的平滑信号![]() ④得到
④得到![]() 的局部极大值点,设置阈值,将高于阈值的局部极大值点对应一次声发射事件。根据以上步骤对原始信号进行处理,图7为对应的声发射信号的处理过程。
的局部极大值点,设置阈值,将高于阈值的局部极大值点对应一次声发射事件。根据以上步骤对原始信号进行处理,图7为对应的声发射信号的处理过程。
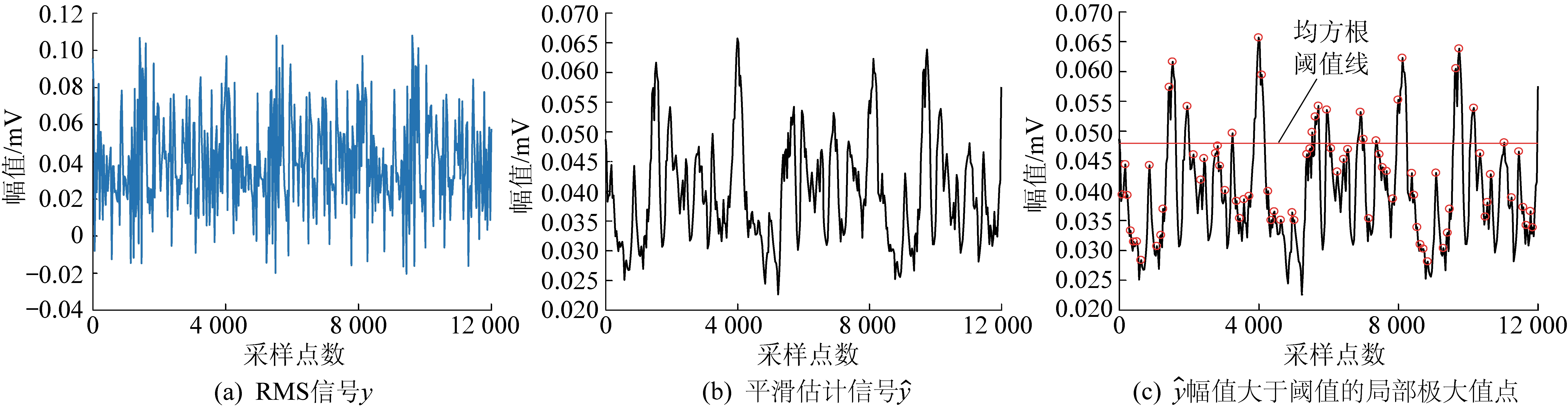
图7 声发射处理过程
Fig.7 Process of acoustic emission processing
图7中各图依次对应声发射事件特征提取过程的2、3、4三个步骤。图7c中阈值线取信号y均方根值[21],其公式为
(13)
参数L和m的值没有严格限制,可根据能够接受的RMS信号分辨率进行选择,由于突发式声发射事件在时间上有相互重叠的情况,m和L过大将有可能无法区分相邻两次的突发式事件。参数δ用于平衡相似度和光滑度两个优化目标,可根据数据波动情况不断修改参数δ的取值。实际工作中,先选取m和L,然后改变参数δ。经过多次权重、m和L参数的选取和对比,当m=10,L=30,权重δ=5时,此时信号的时域分辨率最高为2.5×10-3 s,m=10,L=30时不同权重参数取值与信号分辨率的对应图,如图8所示。
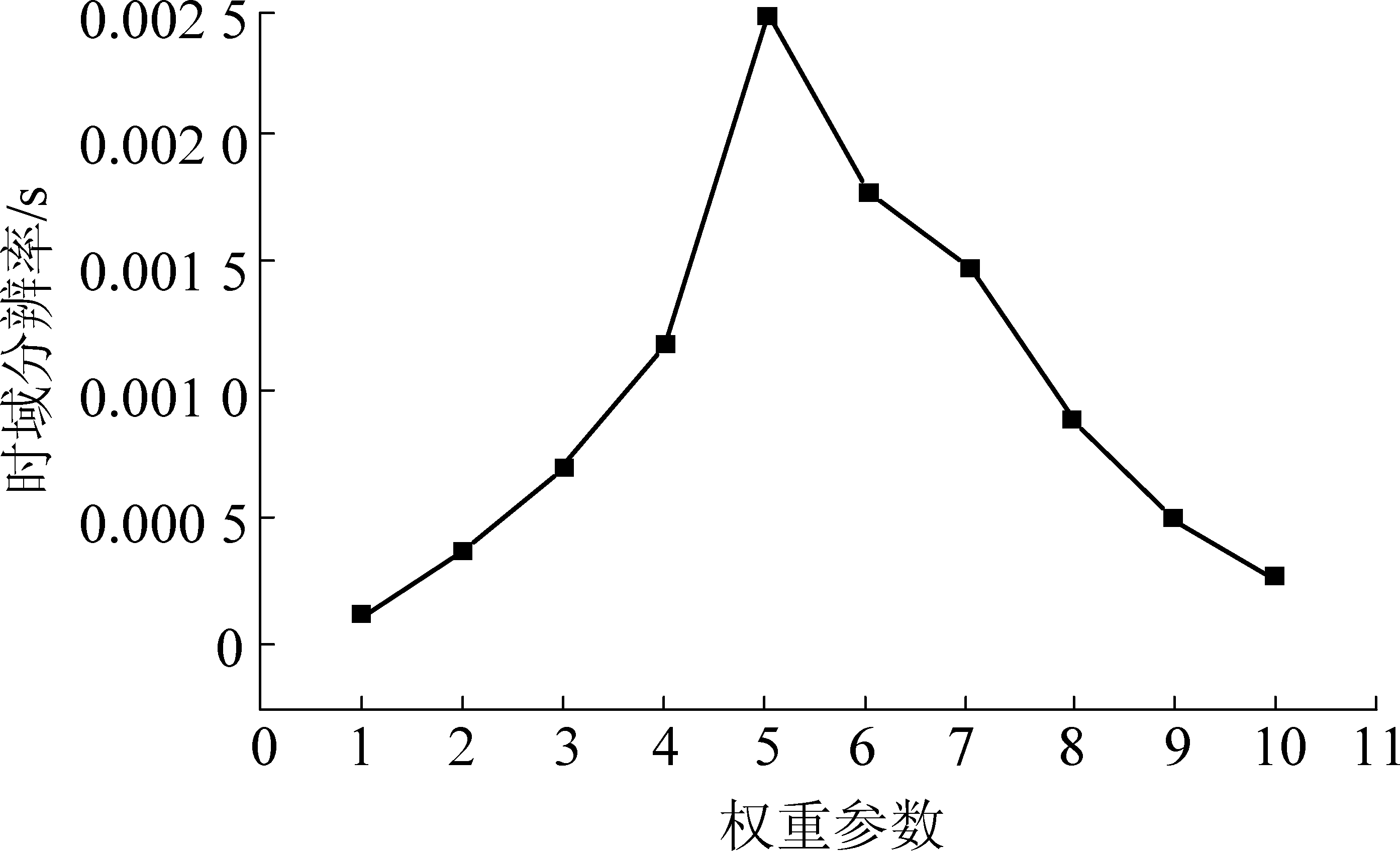
图8 不同权重参数取值对应的信号分辨率
Fig.8 Signal resolution map corresponding to different weight parameter values
如果δ的取值过大,RMS信号中微小冲击将被过分平滑而无法识别。因此δ=5时平滑的信号幅值变化小且很好的保留了微小冲击,可实现统计连续加载过程中岩石声发射事件数变化。
3.2 结果分析
将按时间间隔取得整个过程的100组信号进行去噪及凸优化理论模型事件数提取,结果如图9所示。图9为砂岩破裂整个过程声发射事件数变化图,结合图1分析可知:在砂岩单轴压缩试验中,压密阶段几乎无声发射信号,事件数很少;随着轴向应力的增加,弹性阶段破裂趋于稳定,声发射事件数少,几乎没有发生新的微裂纹;随着应力进一步增加,在临界失稳破坏阶段,大量微裂纹汇合贯通,AE事件数大量增加,在峰值应力C处达到最大值,岩样出现宏观破坏;在岩样破坏后,仍存在承载力,还会产生声发射信号,但强度很弱。对各阶段25组信号求取平均值,得到各阶段产生的平均声发射事件数所占比例:压密阶段平均事件数所占比例为7.58%,弹性阶段平均事件数所占比例为20.36%,失稳破坏阶段平均事件数所占比例为58.44%,破坏后阶段平均事件数所占比例为13.62%。因此可以看出,随着加载时间的增加,应力增大,平均声发射事件数所占比例与岩石破坏的整个过程相一致,能定量监测岩体破裂过程。
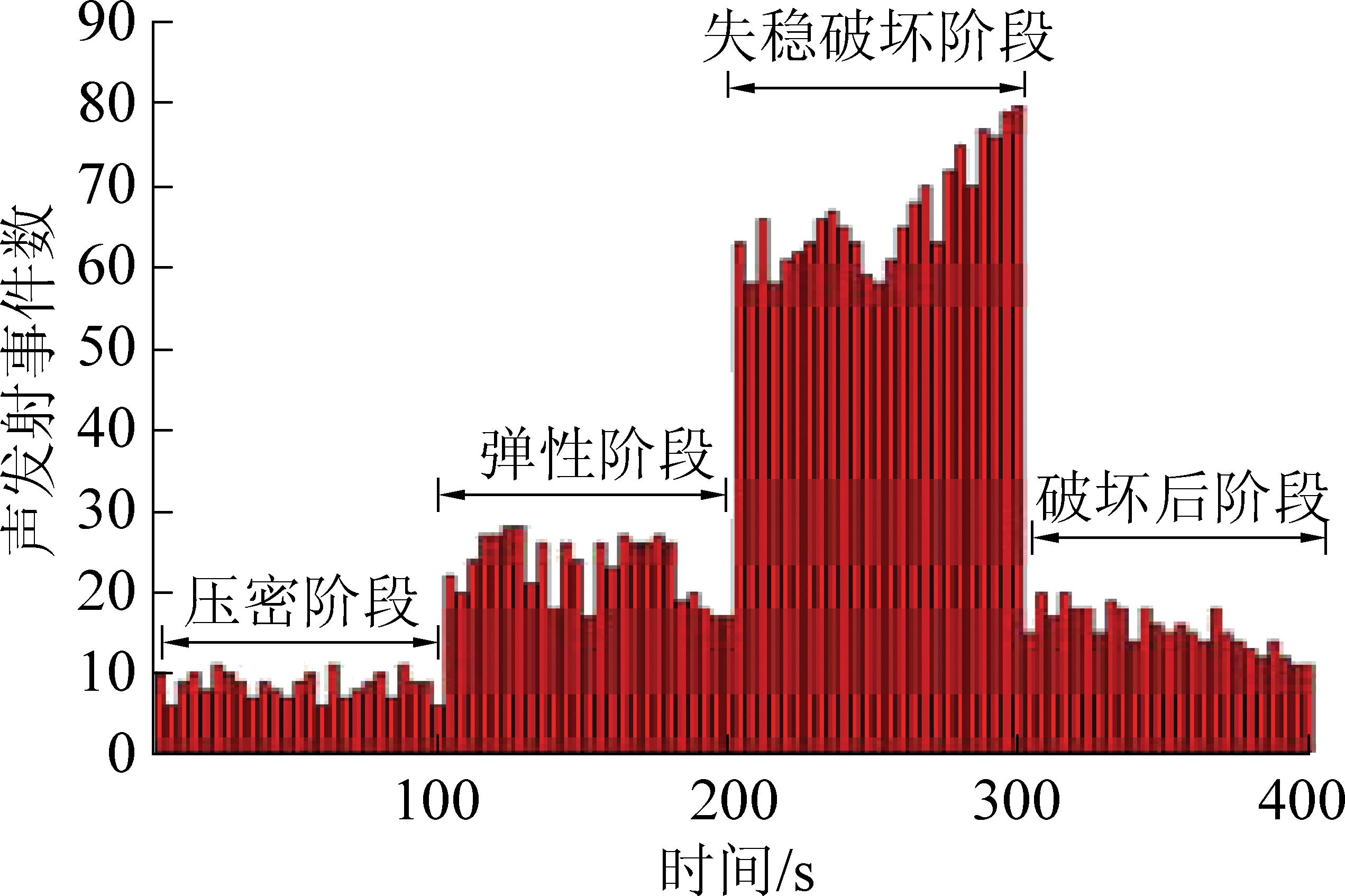
图9 整个加载过程声发射事件数变化
Fig.9 Change diagram of the number of acoustic emission events in the whole loading process
4 结 论
1) 结合CEEMDAN法与小波阈值对岩石破坏各阶段的声发射信号去噪,并利用凸优化理论模型,提取了岩石破坏各阶段的声发射事件数,并以此作为岩石破坏各阶段的定量表征。该方法为定量监测岩体失稳提供了一种新思路。
2)将CEEMDAN法与小波阈值相结合的去噪方法是一种有效的去噪方法。利用连续均方误差准则确定分界点,将该去噪方法与直接小波阈值、舍弃IMF1重构、舍弃IMF1、IMF2重构去噪方法对比,以信噪比和定位精度作为评价指标,表明该方法能达到更好的去噪效果,信噪比提升10.5 dB,且相比小波阈值去噪后声发射源定位精度提高了6%。
3)根据声发射事件数定义并利用凸优化理论模型进行特征提取,结果表明,随着加载时间的增加,应力增大,平均声发射事件数所占比例与岩石破坏的整个过程相一致,能定量监测岩体破裂过程。
[1] 付 斌,周宗红,王海泉,等.大理岩单轴循环加卸载破坏声发射先兆信息研究[J].煤炭学报,2016,41(8):1946-1953.
FU Bin,ZHOU Zonghong,WANG Haiquan,et al.Study on the precursory information of the uniaxial cycLIc loading and unloading failure point of marble[J].Journal of China Coal Society,2016,41(8):1946-1953.
[2] 魏 洋,李忠辉,孔祥国,等.砂岩单轴压缩破坏的临界慢化特征[J].煤炭学报,2018,43(2):427-432.
WEI Yang,LI Zhonghui,KONG Xiangguo,et al.Critical slowing characteristic of uniaxial compression failure of sandstone[J].Journal of China Coal Society,2018,43(2):427-432.
[3] 沈功田,戴 光,刘时风.中国声发射检测技术进展:学会成立25周年纪念[J].无损检测,2003,25(6):302-307.
SHEN Gongtian,DAI Guang,LIU Shifeng.Progress in the detection of acoustic emission in China:the 25 th anniversary of the estab lishment of the society [J].Nondestructive Testing,2003,25(6):302-307.
[4] 潘孝康,陈 结,姜德义,等.三轴卸围压条件下砂岩声发射统计特征[J].煤炭学报,2018,43(10):2750-2757.
PAN Xiaokan,CHEN Jie,JIANG Deyi,et al.Statistical characteristic of acoustic emission from sandstone under unloading confining pressure[J].Journal of China Coal Society,2018,43(10):2750-2757.
[5] 赵杨锋,张 超,刘力强,等.预制裂纹花岗岩单轴压缩全过程声发射特征试验研究[J].煤炭科学技术,2017,45(7):44-49,138.
ZHAO Yanfen,ZHANG Chao,LIU Liqiang,et al.Experimental study on full-emission characteristics of pre-cracked granite during uniaxial compression[J].Coal Science and Technology,2017,45(7):44-49,138.
[6] 赵 奎,邓 飞,金解放,等.岩石声发射Kaiser点信号的小波分析及其应用初步研究[J].岩石力学与工程学报,2006(S2):3854-3858.
ZHAO Kui,DENG Fei,JIN Jiefang,et al.A preliminary study on the wavelet analysis and its application in the acoustic emission of the rock.[J].Journal of Rock Mechanics and Engineering,2006(S2):3854-3858.
[7] 张艳博,梁 鹏,孙 林,等.基于HHT的粉砂岩破裂声发射信号频率特性研究[J].采矿与安全工程学报,2016,33(1):179-184.
ZHANG Yanbo,LIANG Peng,SUN Lin,et al.Study on the frequency characteristics of acoustic emission signals based on HHT[J].Journal of Mining and Safety Engineering,2016,33(1):179-184.
[8] 鲜晓东,袁 双,纪松林.基于消噪处理岩石声发射信号到达时间的识别方法[J].煤炭学报,2015,40(S1):100-106.
XIAN Xiaodong,YUAN Shuang,JI Songlin.Identification method for the arrival time of acoustic emission signals based on noise elimination [J].Journal of China Coal Society,2015,40(S1):100-106.
[9] 凌同华,张 胜,易志强,等.岩石声发射信号能量分布特征的EMD分析[J].振动与冲击,2012,31(11):26-31.
LING Tonghua,ZHANG Sheng,YI Zhiqiang,et al.EMD analysis of energy distribution characteristics of rock acoustic emission signals [J].Vibration and Impact,2012,31(11):26-31.
[10] LEE Y K,TANG S C,YEH J R,et al.Detecting signal quality by ensemble empirical mode decomposition and Monte Carlo verification[J].Biomedical Signal Processing & Control,2015,20:10-15.
[11] AIEDH,González A,CANTERO D.Identification of sudden stiffness changes in the acceleration response of a bridge to moving loads using ensemble empirical mode decomposition[J].Mechanical Systems & Signal Processing,2016,66:314-338.
[12] IMAOUCHEN Y,KEDADOUCHE M,ALKAMA R,et al.A frequency-weighted energy operator and complementary ensemble empirical mode decomposition for bearing fault detection[J].Mechanical Systems & Signal Processing,2016,82:103-116.
[13] NONETHELESS,SHEAR V.Gearbox fault diagnosis using complementary ensemble empirical mode decomposition and permutation entropy[J].Shock and Vibration,2016(1):1-8.
[14] TORRES M E,COLOMINAS M A,SCHLOTTHAUER G,et al.A complete ensemble empirical mode decomposition with adaptive noise[C]// IEEE International Conference on Acoustics,Speech and Signal Processing,IEEE,2011:4144-4147.
[15] BOYD S,VANDENBERGHE L.Convex optimization[M].Cambridge:Cambridge University Press,2004.
[16] ZHAO Q N,Huang T Z,ZHAO X L,et al.A convex optimization model and algorithm for Retinex[J].Mathematical Problems in Engineering,2017,doi:10.1155/2017/4012767.
[17] 陈依珂,胡淑婷,周家俊,等.单轴压缩条件下砂岩声发射特性研究[J].工程与试验,2016,56(2):19-22,64.
CHEN Yike,HU Shuting,ZHOU Jijun,et al.Study on acoustic emission characteristics of sandstone under uniaxial compression [J].Engineering and Experiment,2016,56(2):19-22,64.
[18] 尚雪义,李夕兵,彭 康,等.基于EMD-SVD的矿山微震与爆破信号特征提取及分类方法[J].岩土工程学报,2016,38(10):1849-1858.
SHANG Xueyi,LI Xibing,PENG Kang,et al.The extraction and classification methods of mine microseismic and blasting signals based on EMD-SVD [J].Journal of Geotechnical Engineering,2016,38(10):1849-1858.
[19] DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3):425-455.
[20] 苗玉杰.岩石声发射信号处理小波基选择的探讨[J].计算机光盘软件与应用,2013,16(6):15-17.
MIAO Yujie.Discussion on the selection of wavelet base for rock acoustic emission signal [J].Computer Optical Disk Software and Application,2013,16(6):15-17.
[21] CHEN P C,SU Y F,YANG S Y,et al.Determination of initial crack strength of silicon die using acoustic emission technique[J].Journal of Electronic Materials,2015,44(7):2497-2506.
