移动扫码阅读
李进朋1，张 勋2,3，黎凤岐1，黄 戈2，凡永鹏2
(1.华晋焦煤有限责任公司，山西 吕梁 033000；2.辽宁工程技术大学 矿业学院，辽宁 阜新 123000；3.山西焦煤集团有限责任公司，山西 太原 030053)
摘 要：为了对多分支水平井瓦斯抽采方案进行综合准确评价，解决以往评价标准单一和各评价因素不相容的问题，建立基于模糊结构元的多分支水平井瓦斯抽采多因素群评价模型。摆脱非此即彼的精确性，应用模糊数学的方法，构建多分支水平井的模糊产能计算公式。选取熵权法与判断矩阵法组合赋权，将专家多年累计的经验与客观数据联系起来，采用模糊评价模型对沙曲矿多分支水平井瓦斯抽采方案进行综合评价。结果表明：多分支水平井的模糊产能计算公式使得计算结果与实际检测结果更加吻合。基于模糊结构元的多因素群评价模型能有效准确排列出不同多分支水平井瓦斯抽采方案的优劣次序，为工程方案的选择提供有力指导。
关键词：多分支水平井；产能计算；瓦斯抽采；模糊产能
中图分类号：TD712
文献标志码：A
文章编号：0253-2336(2019)02-0114-06
LI Jinpeng1,ZHANG Xun2,3,LI Fengqi1,HUANG Ge2,FAN Yongpeng2
(1.Huajin Coking Coal Co.，Ltd.,Lyuliang 033000,China;2.College of Mining Engineering,Liaoning Technical University,Fuxin 123000,China;3.Shanxi Coking Coal Group Co.,Ltd.,Taiyuan 030053,China)
Abstract:In order to comprehensively and accurately evaluate the gas drainage scheme of multi-branch horizontal wells and solve the problem of the single evaluation criteria and the incompatibility of each evaluation factor,the model of multi-factor group evaluation for the gas drainage of multi-branch horizontal wells based on fuzzy structural element is established.The fuzzy production capacity formula for multi-branch horizontal wells is constructed by fuzzy mathematics method.Weight is determined by entropy weight method and judgment matrix method,the accumulated experience of experts for many years is linked to objective data,thus,the fuzzy evaluation model is used to evaluate the gas drainage scheme of multi branch horizontal wells in the Shaqu Mine.The result shows that the fuzzy production capacity formula of the multi-branch horizontal well makes the calculation result more consistent with the actual test result.The multi-factor group evaluation model based on fuzzy structure element can effectively and accurately arrange the order of gas drainage scheme for different multi-branch horizontal wells,and provide strong guidance for the selection of engineering scheme.
Key words:multi-branch horizontal well;productivity calculation;gas drainage；fuzzy production capacity
移动扫码阅读
李进朋，张 勋，黎凤岐,等.基于模糊结构元多分支水平井瓦斯抽采多因素群评价[J].煤炭科学技术,2019,47(2)：114-119.doi:10.13199/j.cnki.cst.2019.02.019
LI Jinpeng,ZHANG Xun,LI Fengqi,et al.Multi-factor group evaluation of gas drainage in mutti-branch horizontal well based on fuzzy structural element[J].Coal Science and Technology，2019，47(2)：114-119.doi:10.13199/j.cnki.cst.2019.02.019
收稿日期：2018-08-05；
责任编辑：赵 瑞
基金项目：国家科技重大专项资助项目(2016ZX05067005-003)；国家自然科学青年基金资助项目(51604144)
作者简介：李进朋(1960—),男,山西芮城人,教授级高级工程师。E-mail：ok12ok@163.com
瓦斯是制约我国煤炭生产安全的重要因素之一，随着煤矿开采深度的增加，煤层瓦斯增多，这种现象会愈加明显[1-2]。随着国内钻井技术水平的提高，采用多分支水平井对煤层瓦斯进行采前预抽也变成了我国主流的矿井瓦斯治理手段。多分支水平井不仅能够增大井筒控制面积、提高瓦斯采出率，还具有工程投入大、钻进风险大的特点[3]。因此，对多分支水平井瓦斯抽采方案进行施工前评价具有非常重要的意义。
在多分支水平井研究方面，文献[4-5]采用流体力学、渗流力学的相关理论，建立了多分支水平井产能评价通用计算公式，并依据该公式对钻井形态进行优化。李明忠等[6]建立了煤层瓦斯渗流与井筒内瓦斯变质量流耦合的数学模型，得出了多分支水平井各位置井筒瓦斯压力和单位长度瓦斯流入量。文献[7-8]根据煤体性质和多分支水平井的施工特点，总结出了多分支水平井井壁垮塌失稳机理，提出了煤层气多分支水平井安全施工策略和钻井工艺。牛杰[9]通过数值模拟的方法研究了多分支水平井瓦斯抽采时间与其有效影响半径、有效泄压面积之间的关系，为煤层中多分支水平井布置参数的确定提供了依据。
由上可知，虽然许多学者对多分支水平井做出了很多研究，但只是对钻井的一个方面进行讨论和评价，也忽略了煤岩参数具有一定模糊性。因此，笔者采用模糊数学的方法，构建多分支水平井的模糊产能计算公式，选取熵权法与判断矩阵法对钻井各评价因素组合赋权，构建了基于模糊结构元的多分支水平井瓦斯抽采多因素群评价模型，为多分支水平井瓦斯抽采方案的选取提供指导。
设E为实数论域R上的模糊子集，E(x)为其隶属函数，x∈R。若E(x)能够同时满足以下性质：
1)E(x)=0。
2)E(x)为连续函数，当x∈[-1,0)时，E(x)单调增加，当x∈[0,1)时，E(x)单调减少。
3)当x∈(-∞，-1)∪(1，+∞)时，E(x)=0。则称E(x)为R上的模糊结构元[10-11]。
当模糊集的隶属函数为式(1)，则称该模糊集为模糊三角结构元。
(1)
为简化模糊数的运算，选取模糊三角结构元对模糊数进行表示。可知，对于给定的模糊三角结构元和任意模糊数
总存在函数f(x)，使得
其中f(x)满足在区间[-1,1]上单调有界，且模糊数
的隶属函数为E[f-1(x)]，f-1(x)为f(x)关于x、y变量轮换对称函数，所以对于任意模糊数之间的运算都可以转化为f(x)之间的运算。对于常见的三角模糊数
其中，a、b、c分别为模糊数
的上界、中值和下界，所以其对应单调有界函数为
(2)
设
在[-1,1]区间内同序单调函数f(x)和g(x)满足
则模糊数
之间的自然序关系就转化为在[-1,1]区间内f(x)、g(x)的关系。令
(3)
式中：
为模糊数
间的位置关系，若
则
称
拟小于
若
则
称拟大于若
则
拟等于
设多分支水平井待评价的方案有n个，分别为P1、P2、…、Pn，其中影响各方案评价结果的因素有m个，分别为C1、C2、…、Cm，且每种因素在此多分支水平井评价方案中的重要程度为
为在Pi方案中因素Cj下对应的模糊指标值，可知，在[-1,1]一定存在同序单调函数f(x)、h(x)，使得
和hij(x)分别为模糊指标值函数和模糊权值函数。
由于在多分支水平井方案评价中，不同因素的量纲不同，所以需对模糊指标值进行规范化处理。设
为(aij,bij,cij)，其中，aij、bij、cij分别为模糊数的上界、中值、下界。基于模糊三角结构元表示的模糊数归一化方法分为2种情况：
1)效益型因素归一化方法。
(4)
式中：
、
、
分别为模糊数的最大上界、中值和下界。
2)成本型因素归一化方法。
(5)
式中：
、
、
分别为模糊数的最大上界、中值和下界。
为进行归一化处理之后的模糊指标值，其将原有的模糊指标值成比例限定在区间[0,1]内，并保持了与原有模糊指标值的一致性。
将做进一步标准化处理：
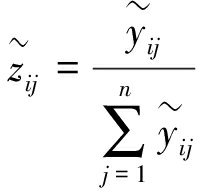
(6)
最后可得标准模糊评价值矩阵：
2.2.1 判断矩阵法主观赋权
1)要求专家对多分支水平井因素两两之间进行成对比较，并给出每对属性的权重比
尺度为1～9或其倒数。
2)根据比较结果构造权重比矩阵。
3)根据特征向量法计算权重向量，进行矩阵相容性检验。
2.2.2 熵权法客观赋权
熵作为一种系统状态的度量参量，其值越大表示系统越无序，值越小系统越有序。在评价过程中，熵权的大小也表明了因素所提供信息量的大小，信息量越大，该因素的权重应越高。
由熵的定义得评价因素Ci的模糊熵为
(7)
所以评价因素Ci所对应的权重为
(8)
2.2.3 模糊组合赋权法
采用判断矩阵法赋权主观性强，评价因素权重大小主要根据专家经验得出，而熵权法客观赋权主要是通过模糊评价矩阵计算各评价因素的模糊熵来确定其权重的大小，2种方法各有利弊，模糊组合赋权法是将专家多年累计的经验与客观数据联系起来，很大程度地发挥各自优点，弥补各自缺点，使得权值更加准确。将判断矩阵法与熵权法得出的权重进行线性组合得模糊组合权重
(9)
式中：θ为熵权法求得权重占组合权重的比例；
为判断矩阵法所得权重；
为熵权法所得权重。
由上所得的模糊指标值矩阵与模糊组合权重可以建立模糊评价模型：
[h1(E),h2(E),…,hm(E)]
(10)
式中：
为方案的模糊评价指标值；h(E)为权重的模糊结构元。
多分支水平井产能受到煤层厚度、瓦斯压力、煤体渗透性等诸多因素的影响，这些因素值在实际中通常不是一个精确的数，具有一定的模糊性。将这种未必完全确定的数值代入经典数学方法中去解决问题，一般难以取得满意的结果。采用模糊数学的方法，摆脱非此即彼的精确性，将经典的多分支水平井产能公式进行模糊化：
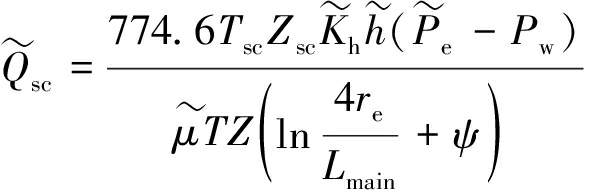
(11)
式中：
为恒压边界处煤层瓦斯压力，
为井底流压，
为煤层水平方向渗透率，
为煤层渗透率比例系数；
为瓦斯动力黏性系数，mPa·s。n为井筒分支数量；Lmain主井长度，m；Lb分支井长度，m；α为分支井和主井的夹角，
为煤层厚度，
为钻井到煤层顶板的距离，m；T为标态温度，K；Tsc为煤层温度，
为煤层中瓦斯平均动力黏性系数，mPa·s；Z为煤层中气体压缩因子；Zsc为标态气体压缩因子；rw为抽采量影响半径。
为了验证多分支水平井模糊产能公式的合理性，对沙曲矿4307工作面DS02多分支水平井产能进行计算。DS02多分支水平井主井长1 100 m，分支井数量为4个，长分别为272、272、273和797 m，与主井夹角为40°，井筒直径为0.153 m。瓦斯抽采参数与煤岩参数如下：
根据多分支水平井模糊产能公式和基于模糊结构元的模糊数运算方法可以得出多分支水平井的模糊产能集合及所对应的隶属度，这里将钻井产能简化为一个三角模糊数，可得沙曲矿4307工作面DS02多分支水平井模糊产能
井日产量的变化曲线如图1所示。
图1 多分支水平井日产量变化曲线
Fig.1 Variation curves of daily output of multi-branch horizontal well
由图1可知，在1年的瓦斯抽采过程中，只有5 d的时间钻井日产量超过20 000 m3，其余时间的日产量都在8 000 m3到18 000 m3变动，均值为13 499 m3，这和多分支井模糊产能计算结果非常吻合，可以满足工程计算的要求。
设沙曲矿计划采用多分支水平井采前抽采的方法对该矿某一工作面(引用上述沙曲矿4307工作面的工程地质条件)进行瓦斯治理，待选方案有3个，分别为：①主井长度1 100 m，分支井个数4个，长度300 m，间距200 m，与主井夹角为40°，井筒直径为0.153 m；②主井长度1 100 m，分支井数量6个，长度300 m，间距150 m，与主井夹角为40°，井筒直径为0.153 m；③主井长度1 100 m，分支井数量4个，长度400 m，间距200 m，与主井夹角为40°，井筒直径为0.153 m；采用模糊结构元多属性群评价方法对多分支水平井布置方案的优劣进行评定，为施工方案的选择提供依据。
在对多分支水平井布置方案评价过程中，主要考虑治理效果C1、抽采时间C2、钻井产量C3、施工难度C4、环境影响C5及工程费用C6这6个因素，显然这些因素都具有一定的模糊性，其中钻井产量根据以上多分支水平井模糊计算公式得出，其他因素由专家组讨论给定，见表1。
表1 各评价因素的模糊指标值
Table 1 Fuzzy index values of evaluation factors
由式(4)、式(5)归一化处理可得
指标判断矩阵及评价因素的权重分配见表2。
表2 指标判断矩阵及评价因素的权重分配
Table 2 Judgment matrix and weight distribution of evaluation factor
根据矩阵
与式(6)求得标准化的模糊指标值矩阵，以z11(E)的求解过程为例，其余元素求解过程类似，即
式中：f11(x)为模糊指标；z11(E)为对应单调有界函数；y1i为经归一化的模糊指标；
为模糊指标的结构元表示。
从以上计算过程可以看出，基于模糊三角结构元的模糊数计算，随着计算步骤的增加，模糊数的表达式越复杂，由式(7)—式(9)可以得出各评价因素组合权重，因篇幅有限，在文中不写出其基于模糊结构元的表达式。
根据式(10)，通过matlab数值运算得出
按式(3)进行模糊数的排序，计算可得：
由模糊数的排序规则
所以综合考虑到多分支水平井瓦斯治理效果、抽采时间、钻井产量、施工难度、环境影响和工程费用因素，沙曲矿宜采用方案一对该工作面进行瓦斯治理。
1)采用模糊数学的方法，建立多分支水平井的模糊产能计算公式，摆脱非此即彼的精确性，使得计算结果与实际检测结果更加吻合。
2)为了减少以往判断矩阵法主观性过强的弊端，采用熵权法与判断矩阵法组合赋权，将专家多年累计的经验与客观数据联系起来，很大程度地发挥各自优点，弥补各自缺点，使得权值更加准确、可靠。
3)构建了基于模糊结构元的多分支水平井瓦斯抽采多因素群评价模型，根据模糊结构元理论中模糊数运算与排序的方法，得出不同多分支水平井瓦斯抽采方案的优劣次序，为多分支水平井布置方式的选取提供有力指导。
参考文献:
[1] 付 华,谢 森,徐耀松,等.基于MPSO-WLS-SVM的矿井瓦斯涌出量预测模型研究[J].中国安全科学学报,2013,23(5):56-61.
FU Hua,XIE Sen,XU Yaosong,et al.Study on MPSO-WLS-SVM-based mine gas emission prediction model[J].China Safety Science Journal,2013,23(5):56-61.
[2] 肖峻峰,陈洋洋,李 平,等.深井高瓦斯工作面“一巷多用”瓦斯治理新模式[J].煤炭学报,2015,40(10):2414-2421.
XIAO Junfeng,CHEN Yangyang,LI Ping,et al.New comprehensive gas control mode based on one roadway with multi-purposes of high methane working face in deep coal mine[J].Journal of China Coal Society,2015,40(10):2414-2421.
[3] 王兆丰,田富超,赵 彬,等.羽状千米长钻孔抽采效果考察试验[J].煤炭学报,2010,35(1):76-79.
WANG Zhaofeng,TIAN Fuchao,ZHAO Bin,et al.The testing of gas drainage efficiency about feather-veined 1000m length-drill hole[J].Journal of China Coal Society,2010,35(1):76-79.
[4] 程林松,李春兰,马志远.气藏多分支水平井产能的计算方法[J].石油学报,1998,29(4):81-84.
CHENG Linsong,LI Chunlan,MA Zhiyuan.A method for calculating the productivity of multi-branch horizontal wells in gas reservoir[J].Acta Petrolei Sinica,1998,29(4):81-84.
[5] 姜振强.多分支水平井产能评价与参数优化研究[D].北京：中国地质大学(北京),2009.
[6] 李明忠,陈会娟,张贤松,等.煤层气多分支水平井井筒压力及入流量分布规律[J].中国石油大学学报,2014,38(1):92-97.
LI Mingzhong,CHEN Huijuan,ZHANG Xiansong,et al.Wellbore pressure and inflow rate distribution of multi-lateral horizontal well for coal bed methane[J].Journal of China University of Petroleum,2014,38(1):92-97.
[7] 刘大伟,王益山,虞海法,等.煤层多分支水平井安全钻井技术[J].煤炭学报,2011,36(12):2109-2114.
LIU Dawei,WANG Yishan,YU Haifa,et al.Safety drilling technology of multi-lateral horizontal wells in coal bed[J].Journal of China Coal Society,2011,36(12):2109-2114.
[8] 王永昌,苏士波,李武生,等.煤层气多分支水平井钻井工艺研究[J].天然气与石油,2013(5):58-61，8.
WANG Yongchang,SU Shibo,LI Wusheng,et al.Study on multi-branch horizontal coalbed methane well drilling technology[J].Natural Gas and Oil,2013(5):58-61，8.
[9] 牛 杰.沙曲煤矿井上下钻孔对接预抽煤层瓦斯技术效果分析与评价[D].徐州：中国矿业大学,2014.
[10] 郭嗣琮.模糊分析中的结构元方法[J].辽宁工程技术大学学报：自然科学版,2002,21(5):670-673.
GUO Sicong.Method of structuring element in fuzzy analysis[J].Journal of Liaoning Technical University：Nature and Science Edition,2002,21(5):670-673.
[11] 郭嗣琮.模糊值函数分析学的结构元方法简介(Ⅰ)：结构元与模糊数运算[J].数学的实践与认识,2008(2):87-93.
GUO Sicong.Brief introduction of fuzzy-valued function analytics base on fuzzy structured element method (Ⅰ)：structure element and fuzzy number operation [J].Mathematics in Practice and theory,2008(2):87-93.
[12] 刘海涛,郭嗣琮.基于模糊结构元表述的模糊数排序[J].模糊系统与数学,2010,24(5):61-67.
LIU Haitao,GUO Sicong.Fuzzy number sequence based on expression of fuzzy structured element[J].Fuzzy Systems and Mathematics,2010,24(5):61-67.
[13] 王胜本,赵黎明,元继学.模糊决策中常用的规范化方法[J].天津大学学报,2008,41(4):294-297.
WANG Shengben,ZHAO Liming,YUAN Jixue.Normalization methods in fuzzy decision making[J].Journal of Tianjin University,2008,41(4):294-297.