移动扫码阅读

0 引 言

带式输送机运量大，可持续运输能力强，是散料运输的首选设备，为满足日益增加的运量、运距需求，现代带式输送机不断向长距离、大功率、高带速等方向发展，这增加了带式输送机运送物料时的随机性、非线性、时变性[1]。传统的静态设计方法不能完全适用于大型带式输送机，需分析输送机的动态特性，并以此为基础改进其结构与优化运行参数，才能满足使用和安全要求。带式输送机系统的稳定性尤其重要，高稳定性能够提高运输效率、降低生产成本，而带式输送机启动、制动时产生各种形式的振动，输送带动张力不断变化，系统稳定性较差，降低了带式输送机的运输能力和工作性能。带式输送机启动时，产生的瞬态张力是稳态张力的数倍，短时间内过大的驱动力矩会造成打滑；制动时输送带内部储存的应力能将产生特殊动应力，超过启动加速时产生的动应力，可能造成物料的堆积和散料、输送带断裂，且动应力作用使张紧装置负载显著增大，导致其故障率提高。

目前，大型带式输送机启停动态特性研究主要包括输送机的动力学、数学模型[2-5]，启动制动和速度控制方式[6-8]，横向纵向振动特性分析，张紧装置设计与布置[9-10]，但缺少带式输送机系统定量分析研究。随着计算机数值模拟技术的发展，多种动态仿真软件的出现，为带式输送机的动态特性研究与结构设计提供了方便，笔者应用AMESim图形化平台建立带式输送机动态仿真模型，设计正弦速度控制曲线，分析在启动、平稳运行和制动过程中输送带纵向张力变化特性，利用分形理论，研究不同启动时间和不同张紧装置布置情况下，带式输送机系统的稳定性。

1 带式输送机模型建立

1.1 Voigt固体黏弹性模型

Voigt固体黏弹性模型是目前广泛应用的输送带黏弹性模型[11]，由一个弹簧与一个阻尼器并联组成，结构如图1所示，本构关系如下：

(1)

式中：σ(t)为动应力，Pa；E为弹性模量，Pa；η为黏性系数，Pa·s；ε(t)为动应变；t为时间,s。

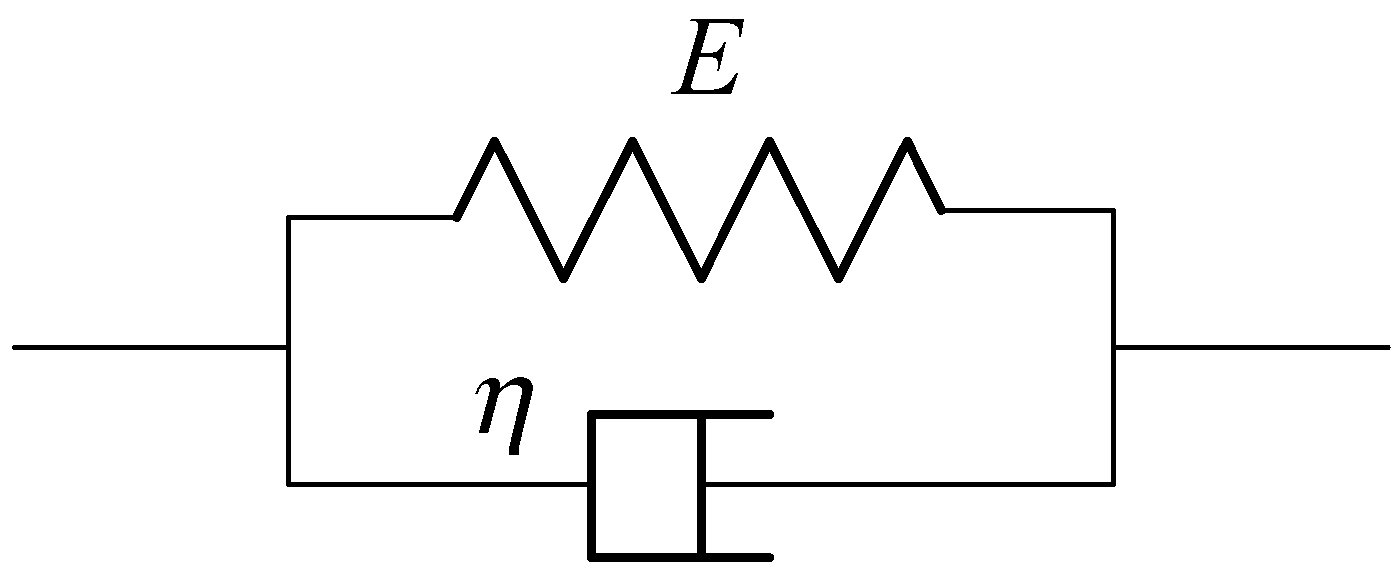
图1 Voigt固体黏弹性模型
Fig.1 Voigt solid viscoelastic model

当输送带受拉伸阶跃动应变作用时，动应变为

ε(t)=ε0H(t)

(2)

式中：ε0为初始应变；H(t)为阶跃信号。

将式(2)代入式(1)求得动应力为

(3)

对应的输送带动态力可表示为

F(t)=σ(t)S

(4)

式中，S为输送带的横截面积，m2。

输送带的蠕变柔量和松弛模量分别为

J(t)=(1-e-t/τ)/E

(5)

(6)

式中：τ为推迟时间，s。

1.2 有限元模型

带式输送机主要由驱动装置、改向滚筒、输送带、张紧装置组成，建立基于Voigt固体黏弹性模型的带式输送机离散有限元模型，如图2所示，对长运距、高带速、边界条件和初始条件复杂的带式输送机而言，应用有限元法能够得出较精确的解[12-14]。

图2 带式输送机离散有限元模型
Fig.2 Discrete finite element model of belt conveyor

模型的动力平衡方程如下：

式中：m1、m2、…、mn为1～n单元的质量，kg；k1、k2、…、kn为1～n单元的刚度系数；c1、c2、…、cn为1～n单元的阻尼系数；x1、x2、…、xn为1～n单元的位移，m；F1(t)、F2(t)、…、Fn(t)为1～n单元所受的驱动力，N。

可简化为矩阵形式如下：

(8)

式中：[M]、[C]、[K]分别为n个离散单元的质量、阻尼、刚度矩阵。

1.3 AMESim仿真模型

笔者所研究的输送带型号为ST2500，输送带单位质量为44.2 kg/m，带式输送机的主要技术参数见表1。

仅考虑输送带的纵向运动，建立内置拉紧装置的带式输送机仿真模型如图3所示，其中，承载段单元质量为27 800 kg，空载段单元质量为20 000 kg。

表1 带式输送机的主要技术参数
Table 1 Main technical parameters of belt conveyor

参数名称参数值参数名称参数值带速v/(m·s-1)7驱动滚筒直径/m2.4带宽/mm1 200改向滚筒直径/m1.3带厚/mm22弹性模量/(N·m-1)1.625×108带长/m1 200上托辊间距/m1.5输送能力/(t·h-1)2 250下托辊间距/m3运行阻尼系数0.3拉紧重锤质量/kg10 000

图3 带式输送机仿真模型
Fig.3 Simulation model of belt conveyor

2 带式输送机启动制动特性分析

带式输送机启动制动时，加速度过大或加速度突变明显，会影响带式输送机的整体稳定性。分析启动制动过程的速度、加速度变化得出带式输送机的动态特性，设计合理的速度控制方式。带式输送机系统的速度控制能够提高运输效率，降低驱动装置的能耗[7-8]，基于澳大利亚的Harrison博士提出的正弦启动曲线分析带式输送机启动、稳定运行、制动过程的动态特性，建立速度控制方式如下：

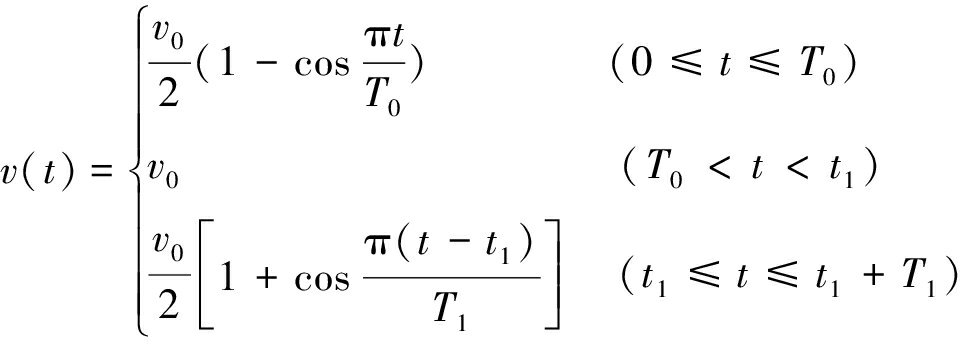
(9)

式中：v0为带式输送机稳定运行速度，m/s；T0为启动时间，s；T1为制动时间，s。

设定仿真时间为 55 s，时间间隔为0.01 s，平稳运行速度为7 m/s，如图4所示，启动时间T0=20 s，稳定运行时间为10 s，制动时间T1=20 s。启动过程中，启动加速度不断增加，当t=10 s时，加速度达到峰值，为0.63 m/s，10～20 s时，加速度逐步减小，当t=20 s时，启动过程结束，带式输送机平稳运行，加速度保持不变。制动过程中，加速度逐步增大，方向与速度方向相反，当t=40 s时，反向加速度达到峰值。

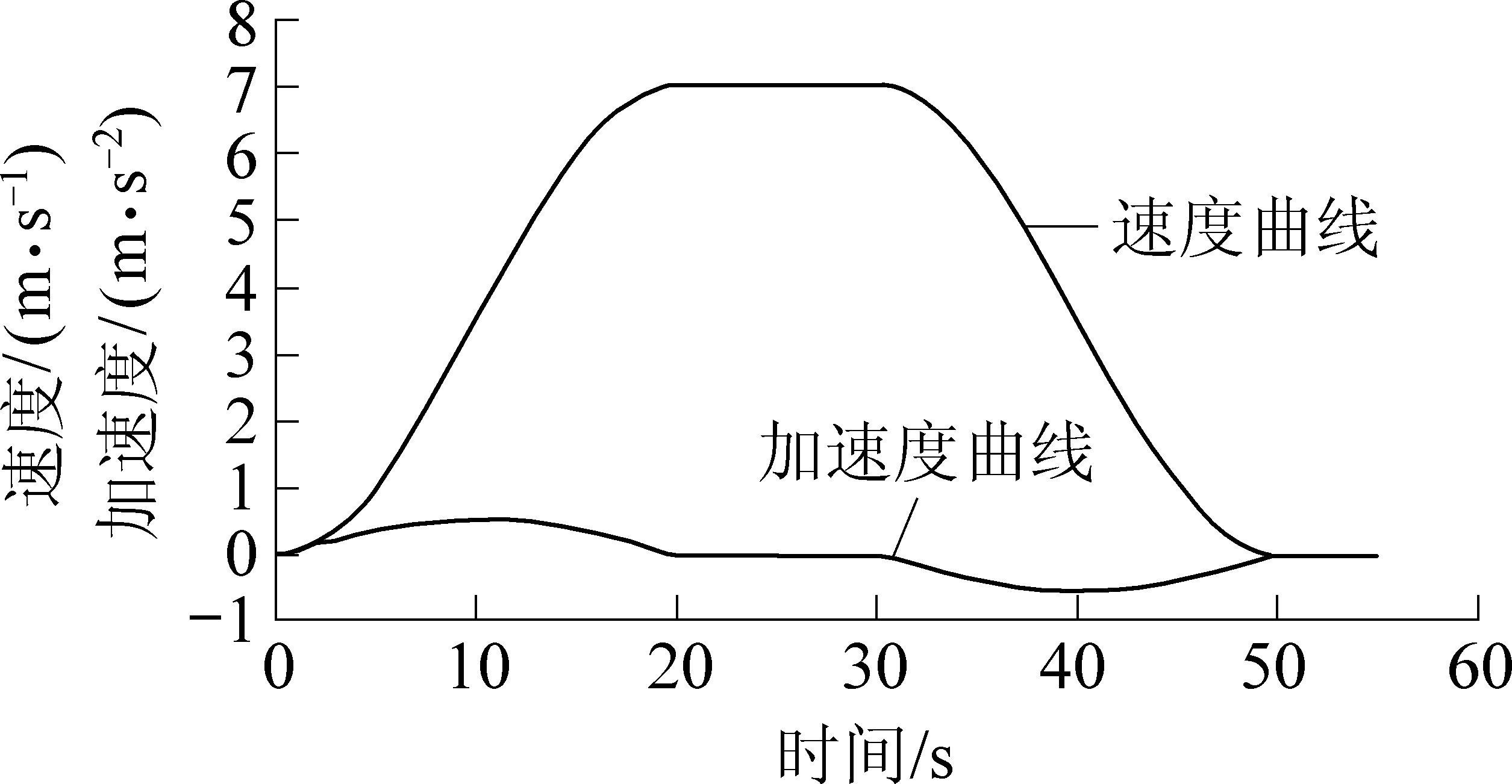
图4 启动制动速度和加速度曲线
Fig.4 Speed and acceleration curves of starting and braking

张力变化曲线如图5所示，机头部张力变化程度大于机尾部张力变化。在启动过程中，因输送带蠕变特性影响，机尾部张力变化滞后1.22 s，机头部张力峰值为2.44×105 N，机尾部张力峰值为1.82×104 N，稳定运行时机头部张力为7.93×104 N，机头部张力峰值约是机尾部张力峰值的13.4倍，启动时机头部张力峰值约是稳定运行时的3倍，故机头部故障率更高。

制动时，机尾部张力无明显滞后现象，由于加速度方向与稳定运行时的速度方向相反，制动产生的动张力与运行时的动张力相互抵消，张力明显降低，机头部张力峰值8.49×104 N，机尾部张力峰值为3.86×103 N，机头部制动时张力与稳定运行时张力差值为5.6×103 N。启动时，机头部张力峰值远大于机尾部张力峰值，故带式输送机启动时故障率更高。

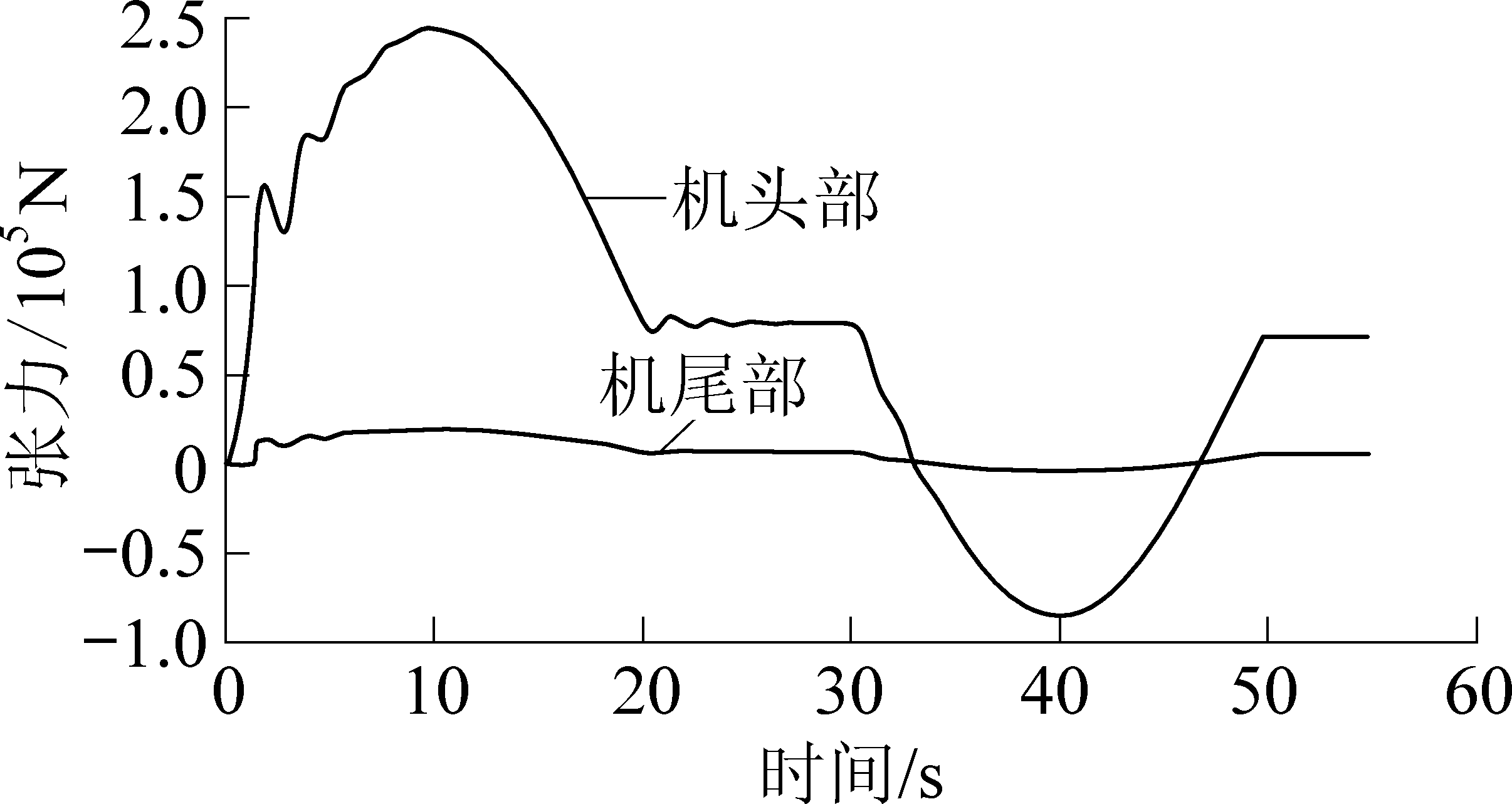
图5 张力变化曲线
Fig.5 Tension change curves

3 带式输送机启动动张力的分形特征

分形维数是分形理论的基础，是分形理论中最为重要的信号度量参数。分形维数包括自相似维数、盒维数、Hausdorff维数、关联维数等，其中，盒维数计算方便、高效，应用最为广泛。

设A是(Rn,d)空间上的任意紧子集，用Nδ(A)表示覆盖A的直径δ>0的盒子的最小数量，则A的上、下盒维数定义分别为

(10)

(11)

如果上、下盒维数相等，则其共同的值为A的盒维数[15-16]记为

(12)

当集合A是张力C(t)时，将C(t)代入式(12)，得

(13)

式中：dimBC(t)为输送带纵向张力的盒维数；C(t)为输送带随时间变化的纵向张力，N；Nδ[C(t)]为覆盖C(t)的直径为δ的盒子最小数量。

盒维数可以定量地描述非线性系统的稳定性和耗能情况，盒维数越大，则系统越不稳定，能耗越大；盒维数越小，则系统稳定性越高，能耗越低。故可通过计算张力C(t)的维数，来评价带式输送机系统，张力C(t)的维数越小，带式输送机系统的稳定性越高。利用Matlab软件中Fraclab2.2工具箱求解张力的盒维数，计算启动时间10、20、30、40、50 s时，机头部张力的盒维数，并将结果进行拟合，如图6所示。

其多项式拟合关系为

dimBC(t)=3.417e-6t3-2.311e-4t2+2.948e-3t+0.999 8

当t=37 s时，盒维数最小值为0.966，由此可知，为保证带式输送机启动的稳定，将启动时间设置在35 ～ 40 s较为合适。

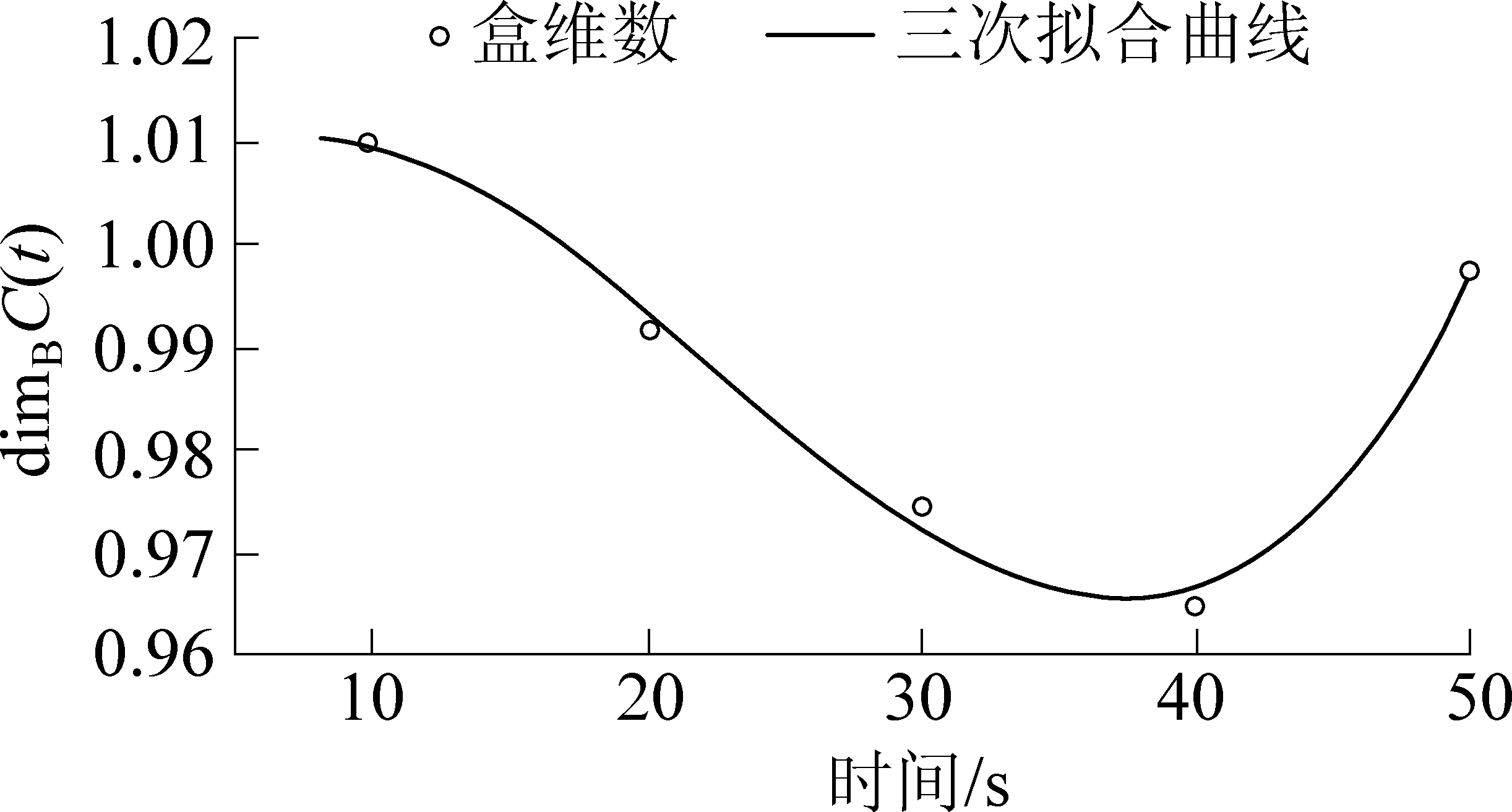
图6 启动时间与盒维数的关系
Fig.6 Relationship between start time and box dimension

4 带式输送机张紧装置布置分析

张紧装置的工作状况对带式输送机的动态特性影响较大，输送带张紧失效时，带式输送机容易打滑并造成输送带断裂和物料堆积。带式输送机启动、制动过程中，张紧装置的工作性能不仅与输送机启动、制动特性有关，还与张紧装置的安装位置有关[17-20]。笔者将布置在驱动滚筒与传动滚筒之间的张紧装置称为内置张紧装置，布置在驱动滚筒与传动滚筒外侧的张紧装置称为外置张紧装置。本次仿真研究其他工况不变时，布置在带式输送机外部和内部的重锤式张紧装置的动态特性，重锤式拉紧装置不需要其他驱动，不受输送带热胀冷缩的影响，成本较低。

设置仿真时间105 s，仿真间隔0.01 s，启动时间T0=40 s，稳定运行时间为20 s，制动时间T1=40 s。张紧装置位移如图7所示，内置张紧装置行程范围大于外置张紧装置，带式输送机启动和稳定运行时，内置张紧装置的位移量大于外置张紧装置；带式输送机制动时，外置张紧装置谷值较大。所以，带式输送机启动时，内置张紧装置更易发生故障；制动时，外置张紧装置相反方向位移量大，更易发生故障。

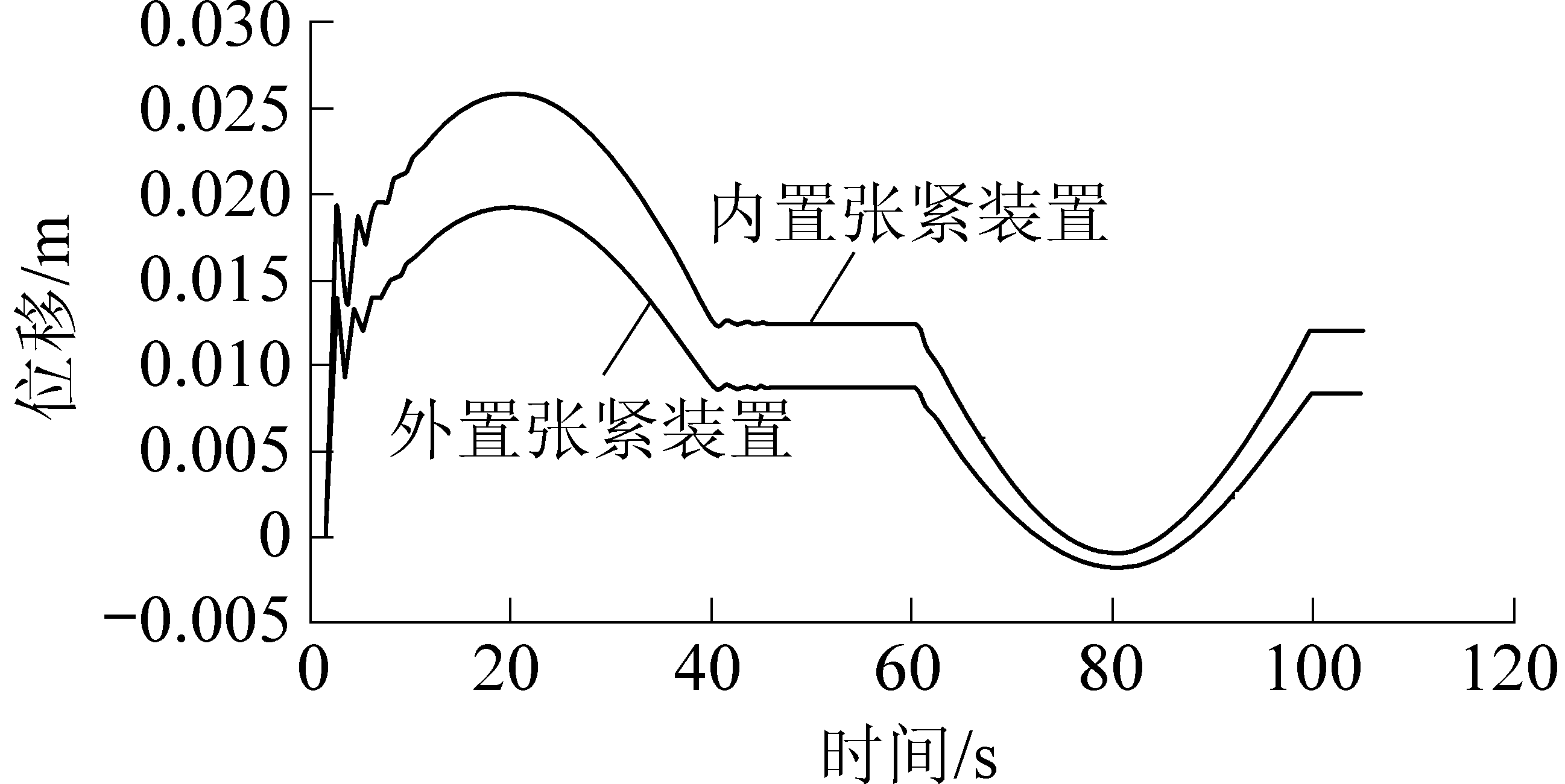
图7 张紧装置位移
Fig.7 Displacement of tensioning device

张紧装置载荷变化曲线如图8所示，启动时间40 s时，内置张紧装置在带式输送机刚启动的1～14 s内载荷变化显著，当t=1.25 s时，载荷峰值452.3 kN，启动过程结束后，受到动张力产生的惯性载荷作用，张紧装置在行程范围短暂运动。外置张紧装置在带式输送机刚启动的1.3～7.0 s内载荷变化明显，载荷峰值为518.6 kN，在启动过程结束后，受载荷变化影响时间约为5 s。

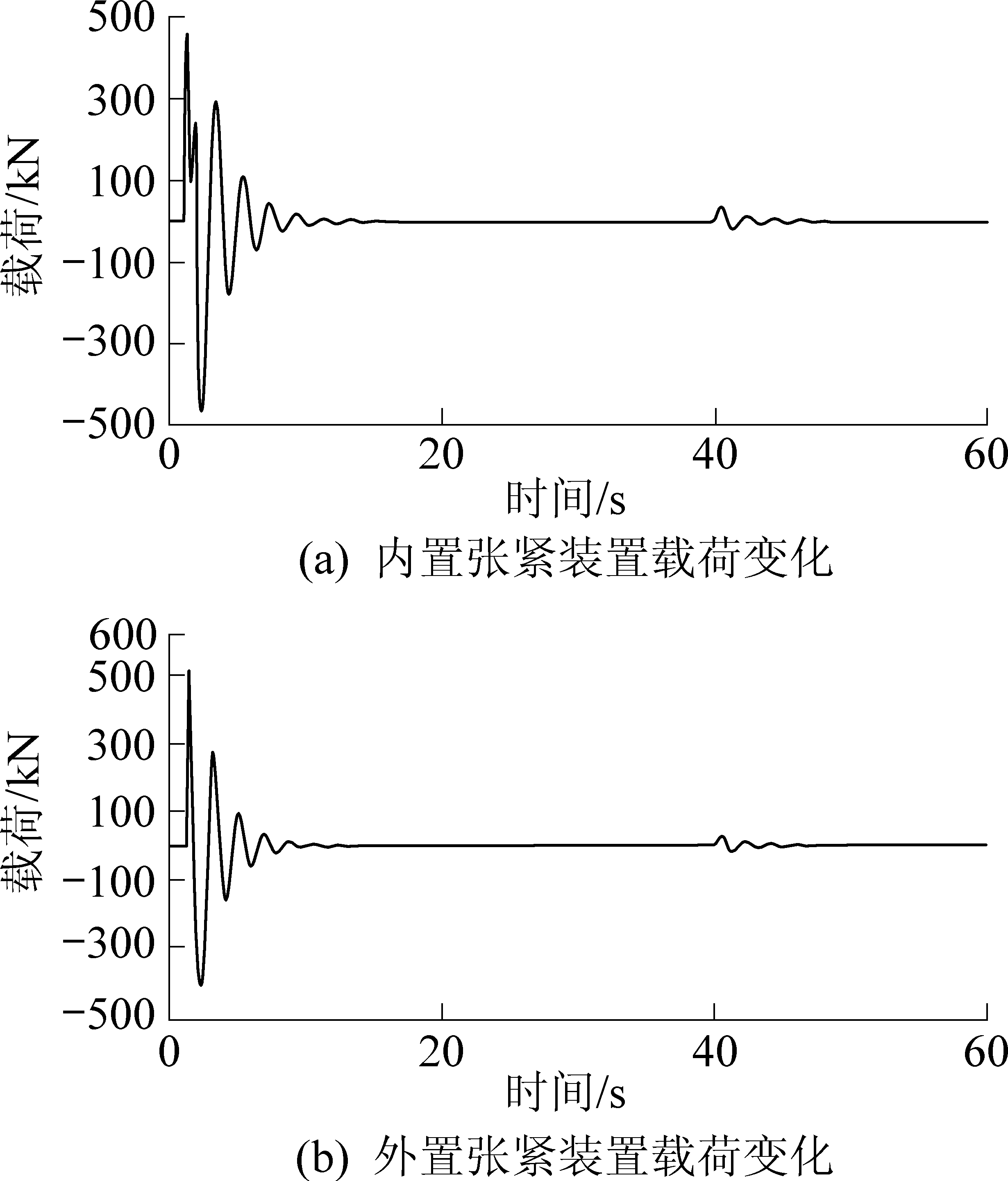
图8 张紧装置载荷变化曲线
Fig.8 Load change curves of tensioning device

将图8中的内置张紧装置和外置张紧装置，在运行过程中的载荷变化曲线导入Fraclab2.2工具箱，求解其盒维数，结果见表2。

表2 张紧装置载荷变化盒维数
Table 2 Box dimension of load change for tensioning device

项目载荷变化盒维数内置张紧装置外置张紧装置启动阶段0～40 s1.1481.133平稳运行40～60 s0.7410.772制动阶段60～100 s0.8170.835

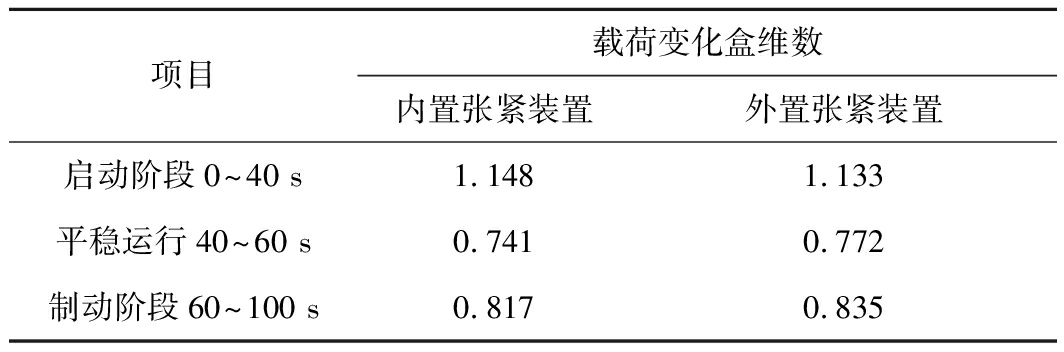
盒维数越大则张紧装置越不稳定，从表2可知，启动阶段内置张紧装置载荷盒维数比外置张紧装置载荷盒维数大0.015，在平稳运行和制动过程中外置张紧装置载荷盒维数更大，所以启动阶段内置张紧装置更易发生故障，制动阶段外置张紧装置更易发生故障。2种张紧装置启动阶段的载荷盒维数大于制动阶段的盒维数，故启动时张紧装置更易发生故障，利用分形维数评价张紧装置动态特性与通过分析张紧装置位移变化动态特性结果相同。

5 结 论

1)带式输送机启动、平稳运行和制动过程中，机头部的动张力约是平稳运行时的13.4倍，机头部的故障率大于机尾部故障率，带式输送机设计时需提高机头部的安全系数，增大机头部驱动滚筒、托辊、机架、输送带的结构强度，设计输送带撕裂保护装置。

2)带式输送机制动时，加速度与稳定运行速度方向相反，产生的张力抵消部分运行时的动张力，机头部与机尾部的张力变化程度小于启动时张力变化程度，带式输送机制动时的故障率低于启动时的故障率，但为确保紧急停机时带式输送机系统的安全，应安装飞轮等停机保护装置。

3)采用分形维数定量地评价带式输送机启动时的张力特性，张力维数越大，带式输送机系统越不稳定。拟合得出启动时间与张力维数的三次多项式，求出启动时间为37 s时，带式输送机系机头部张力维数最小。启动时间为35～40 s时带式输送机系统较为稳定，延长启动时间能够提高系统稳定性，但启动时间过长会降低带式输送机工作效率，提高耗能。

4)研究张紧装置位移和载荷变化，计算载荷维数，带式输送机启动时，载荷维数更大，内置张紧装置更易发生故障；制动时，外置张紧装置更易发生故障，验证了分形维数评价输送机系统的有效性。

参考文献:

[1] 李军霞，寇子明.下运带式输送机复合制动系统仿真及试验研究[J].煤炭学报，2015，40(S2)：553-559.

LI Junxia，KOU Ziming.The characteristic analysis and experimental research of hydraulic speeding soft brake for downward belt conveyor[J].Journal of China Coal Society，2015，40(S2)：553-559.

[2] 宋伟刚，王 丹，左 博.单点驱动带式输送机动力学分析的半解析方法[J].煤炭学报，2012，37(S1)：217-223.

SONG Weigang，WANG Dan，ZOU Bo.Semi-analytical solution to dynamic continuous model of belt conveyor with single drive[J].Journal of China Coal Society，2012，37(S1)：217-223.

[3] 王繁生.输送带柔性多体动力学建模方法研究[J].机械传动，2018，42(4)：43-46.

WANG Fansheng.Research of flexible multibody dynamics modeling of conveyor belt[J].Journal of Mechanical Transmission，2018，42(4)：43-46.

[4] GAO Yang.Dynamics analysis and modeling of rubber belt in large mine belt conveyors[J].Sensors & Transducers，2014，181(10)：210-218.

[5] 陈洪月，张 坤，李恩东，等.基于三元固体本构模型的带式输送机纵向动态特性与拉伸能耗分析[J].机械设计与研究，2017，33(6)：182-186.

CHEN Hongyue，ZHANG Kun，LI Endong，et al.Longitudinal dynamic characteristics and stretching energy consumption analysis of the belt conveyor based on the tertiary solid constitutive model[J].Machine Design & Research，2017，33(6)：182-186.

[6] 杜永强，廉自生.基于AMESim的长距离可伸缩带式输送机动态分析[J].机械工程与自动化，2017(4)：66-67.

DU Yongqiang，LIAN Zisheng.Dynamic analysis of long distance telescopic belt conveyor on AMESim[J].Mechanical Engineering & Automation，2017(4)：66-67.

[7] INDRASWARI Kusumaningtyas，ASHLEY J G Nuttall，GABRIEL Lodewijks.Dynamic of multiple-drive belt conveyors during starting[J].Applied Mechanics and Materials， 2016，842：141-146.

[8] BEBIC M Z，RISTIC L B.Speed controlled belt conveyors:drives and mechanical considerations[J].Advances in Electrical and Computer Engineering，2018，18(1)：51-60.

[9] 李冬梅，赵士明.带式输送机拉紧装置启动过程动态仿真分析[J].机械传动，2017，41(2)：100-103.

LI Dongmei，ZHAO Shiming.Dynamic simulation analysis of the start-up process of take-up device of the belt conveyor[J].Journal of Mechanical Transmission，2017，41(2)：100-103.

[10] 杨俊宇.带式输送机永磁变频自动张紧装置的研究[D].太原：太原理工大学，2017:1-86.

[11] 李纪栋,蒲绍宁,翟 超,等.基于视频识别的带式输送机煤量检测与自动调速系统[J].煤炭科学技术,2017,45(8):212-216.

LI Jidong,PU Shaoning,ZHAI Chao,et al.Coal quantity detection and automatic speed regulation system of belt conveyor based on video identification[J].Coal Science and Technology,2017,45(8):212-216.

[12] 陶伟忠.基于视频的煤矿带式输送机自动调速控制系统[J].煤炭科学技术,2017,45(5):28-33.

TAO Weizhong.Automatic speed control system of mine belt conveyor based on video[J].Coal Science and Technology,2017,45(5):28-33.

[13] BEBIC M Z，RISTIC L B.Speed controlled belt conveyors:drives and mechanical considerations[J].Advances in Electrical and Computer Engineering，2018，18(1)：51-60.

[14] HE D， PANG Y， LODEWIJKS G.Green operations of belt conveyors by means of speed control[J].Applied Energy，2017，188：330-341.

[15] 张济忠.分形[M].北京：清华大学出版社，2011：79-82.

[16] YAKOV Pesin，VAUGHN Climenhaga.分形几何与动力系统讲义[M].北京：高等教育出版社，2016：79-85.

[17] PIOTR Kulinowski.Simulation method of designing and selecting tensioning systems for mining belt conveyors[J].Archives of Mining Sciences，2014，59(1)：123-138.

[18] 董立红，赵鹏兵.带式输送机拉紧装置张力的灰色预测PID控制[J].煤炭学报，2013，38(2)：342-347.

DONG Lihong，ZHAO Pengbing.Grey predictive PID control of the tensioning device system in belt conveyor[J].Journal of China Coal Society，2013，38(2)：342-347.

[19] 周广林，李阳星，聂文明.外置拉紧装置的带式输送机动态特性[J].黑龙江科技大学学报，2017，27(2)： 133-138.

ZHOU Guanglin，LI Yangxing，NIE Wenming.Research on dynamic characteristics behind belt conveyor of external tension device[J].Journal of Heilongjiang University of Science and Technology，2017，27(2)： 133-138.

[20] 周广林，聂文明.外置张紧装置位置对带式输送机动态特性的影响研究[J].矿山机械,2017，45(7)：30-33.

ZHOU Guanglin，NIE Wenming.Research on influence of location of external tension device on dynamic characteristics of belt conveyor[J].Mining & Processing Equipment，2017，45(7)：30-33.