
移动扫码阅读
戴方尧1,胡海燕2,张爱华1
(1.中国地质大学(武汉) 构造与油气资源教育部重点实验室,湖北 武汉 430074;2.长江大学 地球科学学院,湖北 武汉 430100)
摘 要:为了深入研究分形理论模型计算不同尺度孔隙分形维数的适用性,以焦页1井龙马溪组页岩与慈页1井牛蹄塘组页岩的钻井岩心样品为研究对象,采用CO2和N2等温吸附试验,获得了2组页岩微孔与介孔的吸附数据,并分别结合微孔分形模型和FHH分形模型计算了微孔与介孔的分形维数,讨论了2种模型的有效性。研究结果表明:微孔分形模型适用于计算CO2吸附数据,可有效表征页岩微孔的分形维数;而选FHH分形模型适用于计算N2吸附的高压段数据,可有效表征页岩介孔的分形维数。微孔与介孔可具有不同的分形结构,页岩孔隙结构的评价应综合考虑两类孔隙的分形维数。
关键词:页岩;孔隙;CO2吸附;N2吸附;分形维数
中图分类号:TE122.23
文献标志码:A
文章编号:0253-2336(2019)02-0168-08
DAI Fangyao1,HU Haiyan2,ZHANG Aihua1
(1.Key Laboratory of Tectonics and Petroleum Resources of the Ministry of Education,China University of Geosciences,Wuhan 430074, China;2.School of Geosciences,Yangzte University, Wuhan 430100, China)
Abstract:In order to deeply study the adaptability of the fractal theory model to calculate the fractal dimension of the different size pores, with the drilling rock core samples of the shale in Longmaxi Formation from Jiaoye No.1 Well and the shale in Niutitang Formation from Ciye No.1 Well as the study objects, the CO2 and N2 isotherm adsorption tests were applied to get the micropore and mesopore adsorption data of the shale from the two formations. And individually to combine with the micropore fractal model and the FHH fractal model, the micropore and mesopore fractal dimensions were calculated. The efficiency of the two models was discussed. The study results showed that the micropore fractal model was suitable to calculate CO2 adsorption data and could effectively characterize the fractal dimension of micropore in shales. The FHH fractal model would be suitable to calculate the high pressure sectional data of the N2 adsorption and could effectively characterize the mesopore fractal dimension of shales. The micropore and mesopore could have different fractal structures. The evaluation of the shale pore structure should comprehensively consider the fractal dimensions of two type pores.
Key words:shale; pore; CO2 adsorption; N2 adsorption; fractal dimensions

移动扫码阅读
戴方尧,胡海燕,张爱华.有机质页岩孔隙分形模型的适用性研究[J].煤炭科学技术,2019,47(2):168-175.doi:10.13199/j.cnki.cst.2019.02.028
DAI Fangyao,HU Haiyan,ZHANG Aihua.Suitability study on fractal model of organic shale pore[J].Coal Science and Technology,2019,47(2):168-175.doi:10.13199/j.cnki.cst.2019.02.028
收稿日期:2018-11-10;
责任编辑:曾康生
基金项目:国家自然科学基金资助项目(41690134,41472122);国家科技重大专项资助项目(2016ZX05034002-003)
作者简介:戴方尧(1987—),男,重庆人,博士研究生。E-mail:dfy_cug@163.com
进入21世纪以来,北美地区在页岩气、致密气的勘探开发领域取得了长足进步[1]。受其影响,页岩气勘探前景在我国也备受关注,中国页岩气勘探开发于2005年拉开了序幕[2]。目前,涪陵焦石坝地区五峰—龙马溪组页岩储层开发已取得实质突破,我国页岩气产量预计2020年有望达到(200~300)×108 m3[3]。前人研究发现,页岩储层中的甲烷主要以吸附态、游离态和溶解态赋存于孔隙之中,其中吸附态甲烷主要富集于有机质和黏土矿物的表面[4]。
由于富有机质页岩发育大量纳米级孔隙,甚至包含大量的微孔隙(孔径<2 nm),因此,对页岩孔隙形态结构的非均质性定量化表征尤为关键,目前,国内外学者通常采用分形维数进行表征[5-8]。在多种计算模型中,Frenkel-Halsey-Hill(FHH)分形模型是页岩孔隙结构研究中所广泛使用的计算模型,该模型利用的是N2吸附数据,但N2在温度77 K条件下分子活度低,通常不能准确获得微孔范围内(尤其1 nm以下)的信息[7,9],因此,采用FHH模型所计算的分形维数并不能有效表征微孔范围的分形结构。微孔信息通常采用CO2吸附试验获取,但目前国内外文献中尚缺乏利用CO2吸附数据直接计算页岩微孔分形维数的相关模型。鉴于此,笔者将引入微孔分形模型,以焦页1井(JY1)龙马溪组(S1l)有机质页岩与慈页1井(CY1)牛蹄塘组( 1n)有机质页岩的岩心样品为依据,利用CO2吸附数据和N2吸附数据分别计算页岩微孔和介孔(2 nm<孔径<50 nm)的分形维数。通过计算出的微孔和介孔分形维数对比,系统阐述两种模型的差别与适用范围,并进一步讨论孔隙分形结构对孔隙表面吸附的意义。
1n)有机质页岩的岩心样品为依据,利用CO2吸附数据和N2吸附数据分别计算页岩微孔和介孔(2 nm<孔径<50 nm)的分形维数。通过计算出的微孔和介孔分形维数对比,系统阐述两种模型的差别与适用范围,并进一步讨论孔隙分形结构对孔隙表面吸附的意义。
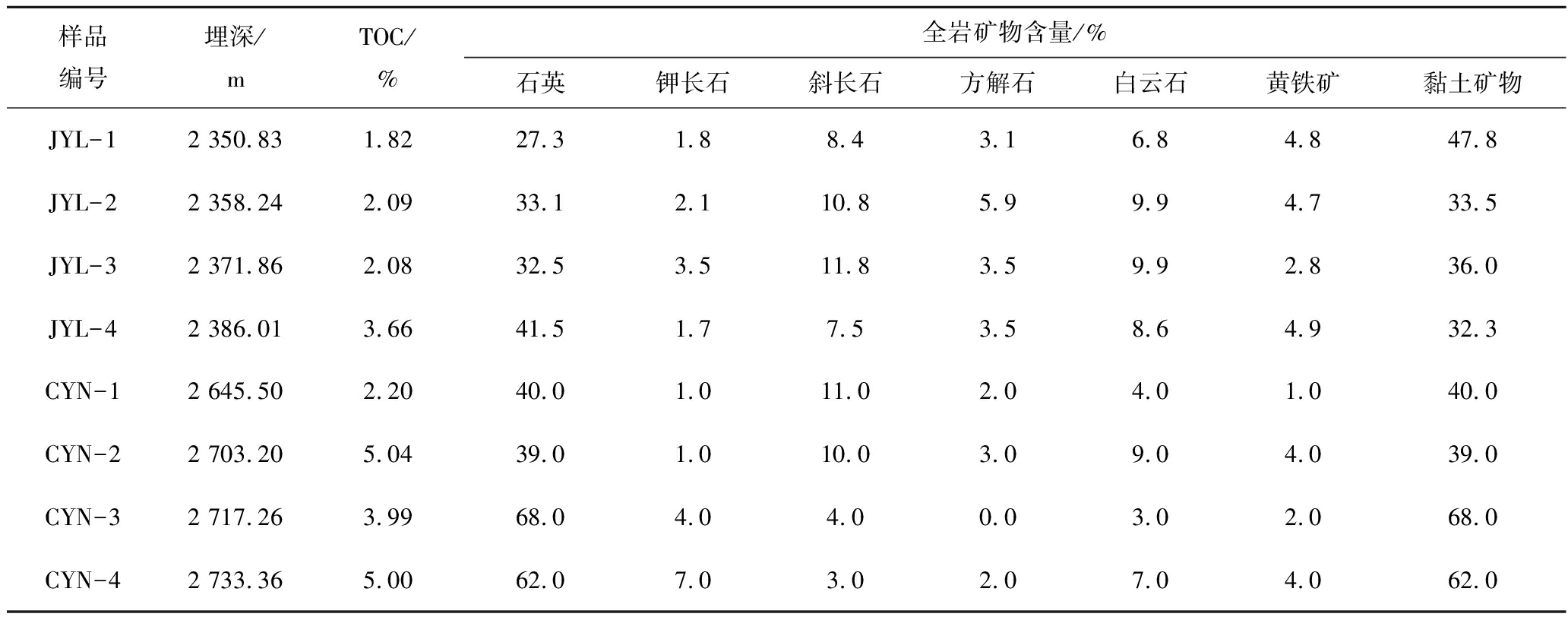
龙马溪组页岩样品取自焦页1井,该井位于焦石坝地区似箱状断背斜的东北区,从上到下钻遇三叠系、二叠系、石炭系、志留系和上奥陶统地层[10]。该井揭示了五峰—龙马溪组自下而上发育深水陆棚和浅水陆棚2组沉积:上部发育灰色泥质粉砂岩,中部发育灰黑色含碳酸盐岩粉砂质泥岩,下部发育高硅质含量的黑色炭质泥页岩[10]。牛蹄塘组页岩样品取自慈页1井,该井位于张家界市慈利地区江南雪峰推覆隆起带景龙桥向斜,从上到下依次钻遇下志留统、奥陶系、寒武系和震旦系地层。该井揭示了牛蹄塘组下部发育黑色硅质页岩夹薄层炭质页岩,向上逐渐过渡到深灰色页岩与泥灰岩的互层,上部发育灰质页岩。本次研究分别获取龙马溪组和牛蹄塘组4个井下样品,将采集的所有岩心样品进行粉碎加工,碾磨至180 μm(80目)以下的粉末样。同时筛选部分样品进行有机碳含量测试,并进行X衍射试验鉴定页岩的矿物组分,结果见表1。测试结果显示,龙马溪组样品的TOC平均含量为2.41%,牛蹄塘组样品的TOC平均含量为4.06%。两组页岩中,石英与黏土矿物均为主要的矿物组分,长石与碳酸盐矿物的含量相对较少。
表1 样品信息
Table 1 Information of samples
2组地层的页岩样品的CO2等温吸附试验送至北京理化分析测试中心进行,N2等温吸附试验送至中国地质大学(武汉)构造与油气资源教育部重点实验室进行。试验前,样品先在110 ℃的环境下进行抽真空,除去样品孔隙中的水分和挥发性物质,脱气时间持续12 h,然后进行吸附试验。CO2等温吸附试验在0 ℃(273.15 K)的环境下进行,N2吸附试验在-195.8 ℃(77.35 K)的环境下进行。
试验分析仪器为美国Quantachrome仪器公司提供的比表面和孔径分布分析仪Autosorb-iQ,该仪器可用于多种吸附测试(如CO2吸附、N2吸附、Ar吸附),测试孔径范围0.35~500 nm,比表面分析精度可低至0.000 5 m2/g。试验中,吸附阶段首先打开真空阀,将样品管中抽真空,关闭真空阀;打开分析气阀,建立一定的压力,再关闭分析气阀,待压力稳定后记录平衡压力,多次重复该步骤至吸附结束;脱附阶段先关闭样品站气阀,打开真空气阀,释放工作站中气体,再关闭真空阀,打开样品站气阀,待压力稳定后记录平衡压力,多次重复该步骤至脱附结束,获得等温吸附曲线如图1所示。
该仪器数据分析模块包括多种经典模型算法(如BJH模型、DH模型、DA模型等),以及GCMC(巨正则系综蒙特卡罗)模型、NLDFT(非定域密度函数理论)模型和QSDFT(骤冷固体密度函数理论)模型等多种统计学模型算法。

图1 样品等温吸附曲线
Fig.1 Adsorption isothermal curves of samples
通常孔径分布可利用孔隙体积V(吸附量)对孔径ø的微分(dV/dø),或孔隙比表面积S对孔径ø的微分(dS/dø)进行表征,CO2吸附数据采用NLDFT模型计算微孔孔径分布,N2吸附数据采用QSDFT计算介孔孔径分布,将微孔和介孔的孔径分布进行联合[11]。由于DFT模型计算的微孔和介孔孔径分布在1.2 nm附近存在交点,其意义表示了2种模型计算的孔径分布在该点处吻合,交点右侧N2吸附数据能较好地预测孔径分布,但进入更狭窄的微孔后,CO2吸附数据预测能力更好,据此可获得样品联合孔径分布(图2)。龙马溪组页岩和牛蹄塘组页岩各样品的联合孔径分布曲线显示,其微孔数量明显多于介孔,尤其以1 nm以下的微孔占主要部分(图3)。
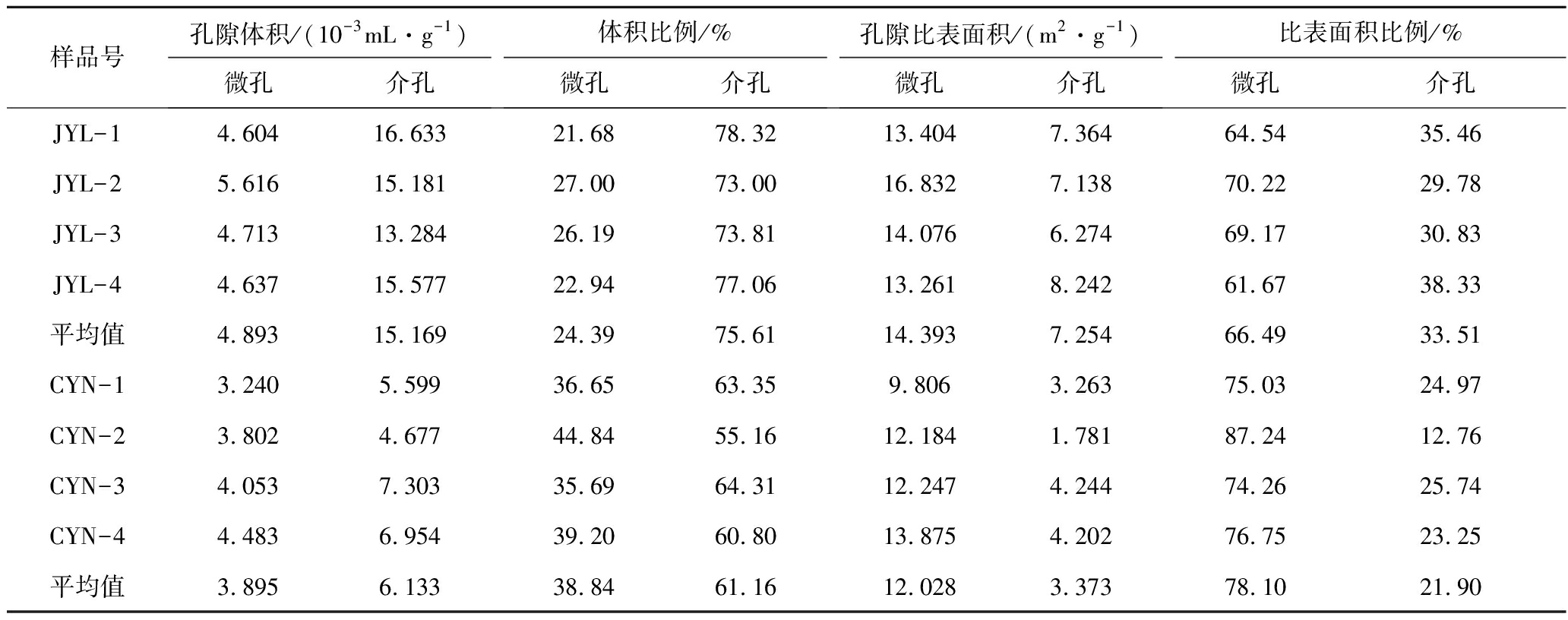
依据孔径分布曲线,可计算2组地层的页岩微孔和介孔的孔隙体积和比表面积,这里考虑到甲烷的分子直径为0.38 nm,且NLDFT模型的置信下限为0.400 nm,故选取0.4 nm以上的微孔数据为有效信息,按孔径大小分别计算出微孔和介孔的孔隙体积和比表面积,见表2。

图2 CYN-3样品孔径分布曲线
Fig.2 Pore size distribution of Sample CYN-3
由表2可知,2组页岩均呈现出介孔体积大,比表面积小,而微孔体积小,比表面积大的特征。2组页岩之间体积和表面积的差异主要来自介孔,而微孔差异不明显,可见龙马溪组页岩的介孔更为发育。有机质页岩中,微孔主要为甲烷吸附提供空间,而介孔除提供可吸附的孔隙表面空间外,还可容纳游离态的甲烷。

图3 样品孔径分布曲线
Fig.3 Pore-size distribution of samples
表2 样品微孔与介孔体积、比表面积
Table 2 Micopore and meso-pore volume,specific surface area of samples
多孔介质的分形理论早期由Pfeifer和Avnir于1983年提出[12],该理论指出孔隙分形维数D的大小可用以表征多孔材料孔隙结构的复杂度和非均质性,D值通常介于2~3,其中2指示光滑平面,3指示自由空间[13]。因此,当D值接近2,多孔介质中的孔隙结构趋于简单,表面粗糙度低,D值越接近3,则孔隙结构越复杂。
储层岩石与多孔材料类似,其孔隙结构也具有典型的分形特征[14-16]。对有机质页岩而言,岩石矿物颗粒的成岩过程和有机质的热演化过程导致页岩孔隙类型多样,结构复杂。目前,学者通常使用FHH分形模型结合N2吸附试验计算页岩孔隙的分形维数来表征孔隙结构的非均质性[9,17,18]。FHH分形模型表达式[19]为
(1)
其中,V为平衡压力下的吸附量,cm3·g-1;p为平衡压力,MPa;p0为饱和蒸汽压,MPa;f(D)为分形维数的表达式,当吸附力以范德华力为主时,f(D)与分形维数D的关系为[20]
(2)
当孔隙发生毛细孔凝聚时,表面张力为主要作用力,f(D)与分形维数D的关系[21]为
f(D)=D-3
(3)
利用式(1)中![]() 的线性关系,通过斜率可计算分形维数D。
的线性关系,通过斜率可计算分形维数D。
值得注意的是FHH分形模型考虑到多分子层吸附和毛细管凝聚作用,主要适用于介孔范围内的分形维数计算[19,21,22]。但在微孔内,吸附质分子通常发生微孔充填,该过程不同于介孔条件下的吸附行为[23],且液态N2分子在试验温度下进入微孔时存在扩散阻力[7]。因此,FHH分形模型的应用范围存在局限性,微孔分形维数的计算模型应有别于介孔[24]。
Jaroniec等[25]利用微孔活性炭作为吸附剂,通过标准吸附质苯的吸附试验,发现微孔孔径分布函数是表征其非均质性的关键,并提出了“微孔分形模型”。该模型依据孔尺度分布函数J(x)与孔尺度x之间的相关关系计算分形维数为[26]
lnJ(x)=(2-D)lnx+C
(4)
其中:x通常可以定义为孔半径,nm;Jaroniec等[27-28]依据Dubinin-Astakhov(DA)方程与Jaroniec-Choma(JC)方程[29]获得了非均质微孔固体中J(x)的表达式为
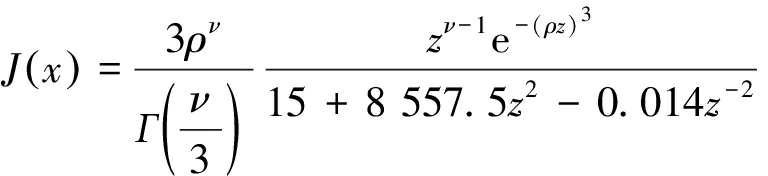
(5)
其中:Г中为伽马函数;ρ为伽玛分布的尺度参数,kJ·mol-1;ν为形状参数,无因次。ρ,ν可通过微孔全吸附方程拟合,得
(6)
其中:θ为相对吸附量;V0为最大吸附量,cm3·g-1;β为亲和系数,CO2可取0.38[23],A为吸附势,kJ·mol-1,且有
(7)
其中:R为摩尔气体常数,取8.314 J·mol-1·K-1;T为绝对温度,K。式(5)中z记为DA方![]() 中特征能E0(kJ·mol-1)的倒数(1/E0),mol·kJ-1,且对于孔径>0.45 nm的微孔,z与孔半径x之间存在经验关系式为[31]
中特征能E0(kJ·mol-1)的倒数(1/E0),mol·kJ-1,且对于孔径>0.45 nm的微孔,z与孔半径x之间存在经验关系式为[31]
x= 15z+2 852.5z3+0.014z-1-0.75
(8)
因此,利用CO2吸附数据结合DR方程可计算最大吸附量与相对吸附量[23],并拟合关键参数ρ,ν,同时利用孔径分布计算z,进而计算J(x),最后利用ln J(x)-ln x的线性关系部分,由斜率获得分形维数。本次研究将利用两种模型分别计算微孔的分形维数Dmicro和介孔的分形维数Dmeso,并讨论2种模型的适应性。
计算2组页岩样品的微孔分形维数,首先利用CO2吸附数据计算V0,然后依据式(6)非线性拟合参数ρ,ν,见表3。
表3 微孔分形模型参数拟合
Table3 Parameter fitting for micropore fractal model
将拟合参数代入式(5)计算J(x),结合式(4)获得ln J(x)-ln x的标绘图,如图4所示。利用拟合直线的斜率计算Dmicro,见表4。
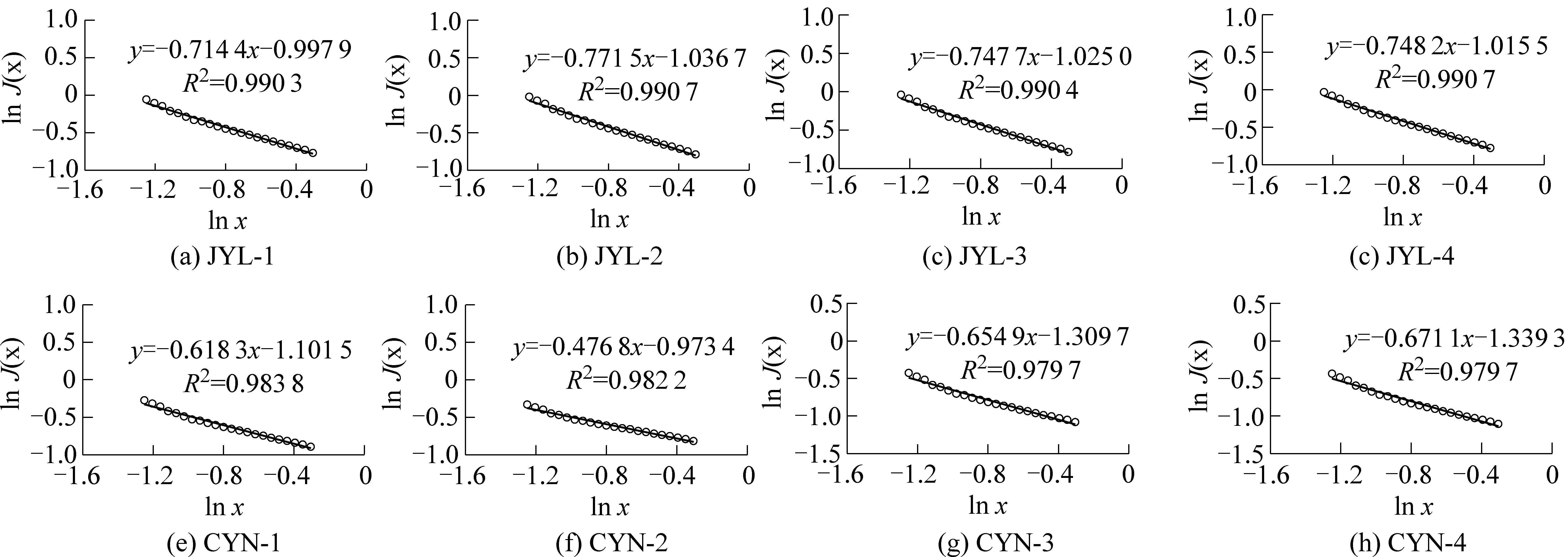
图4 ln J(x)-ln x的标绘图
Fig.4 Plotting figure of ln J(x)-ln x
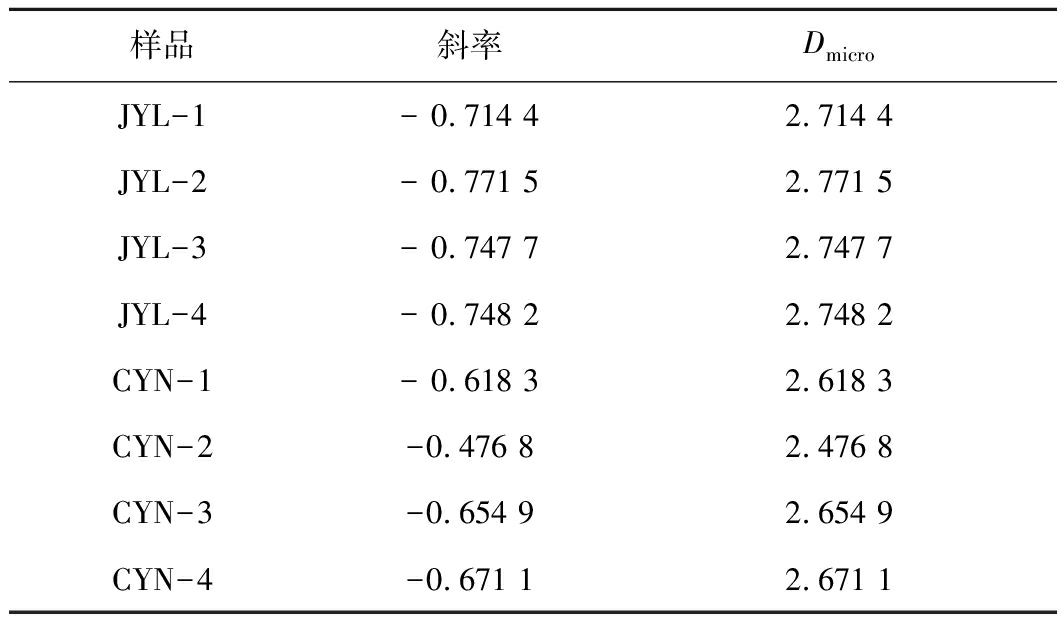
表4 样品微孔分形维数
Table 4 Fractal dimension of micropore
利用N2吸附数据采用FHH分形模型计算分形维数时,应区分范德华力为主的区域和表面张力为主的区域,通常的判别标准是N2吸附曲线中滞回环线出现的压力点作为分界点(滞回环线是毛细孔凝聚现象的重要特征[23]),依据N2在页岩上的吸附曲线特征,通常划分低压段(相对压力为0~0.45)和高压段(相对压力为0.45~1.00)。依据式(1)获得![]() 的标绘图,如图5所示。计算介孔分形维数时,低压段数据采用式(2),高压段数据采用式(3),见表5。
的标绘图,如图5所示。计算介孔分形维数时,低压段数据采用式(2),高压段数据采用式(3),见表5。

图![]() 的标绘图
的标绘图
Fig.5 Plotting figure of ln ![]()
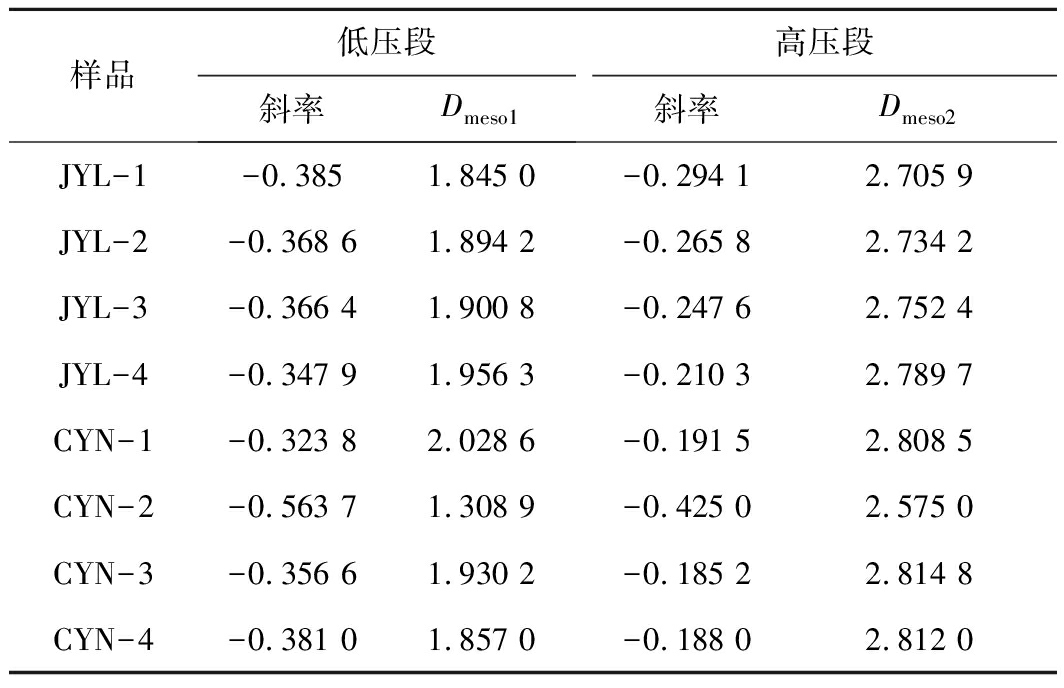
表5 样品介孔分形维数
Table 5 Fractal dimension of mesopore
从微孔分形维数的值域分布上看,Dmicro的值均介于2~3,说明微孔分形模型对两组不同页岩样品的计算结果均有效。从原理上看,该理论模型考虑了微孔充填的吸附模型(DA方程)。从数据上看,对比各样品的微孔分形维数与孔径分布,可发现在0.4 nm以上的微孔区域,龙马溪组页岩样品的孔径分布曲线中存在多个峰值,其分形维数也较高,如JYL-2具有5个峰值,分形维数具有最大值;牛蹄塘组页岩样品的孔径分布曲线峰值数相对较少,孔径分布集中,分形维数也较低。当微孔具有多个不同孔径时,其孔隙结构应更加复杂,对应的分形维数也较高,而当微孔孔径分布集中时,其孔隙结构趋于均一,对应的分形维数也较低,这说明了该计算结果的合理性。因此,微孔分形模型适用于计算CO2吸附数据,该模型的计算结果能有效表征有机质页岩中微孔的分形结构,且以1nm以下的微孔为主。微孔分形维数的差异性是微孔结构差异性的一种定量化体现。
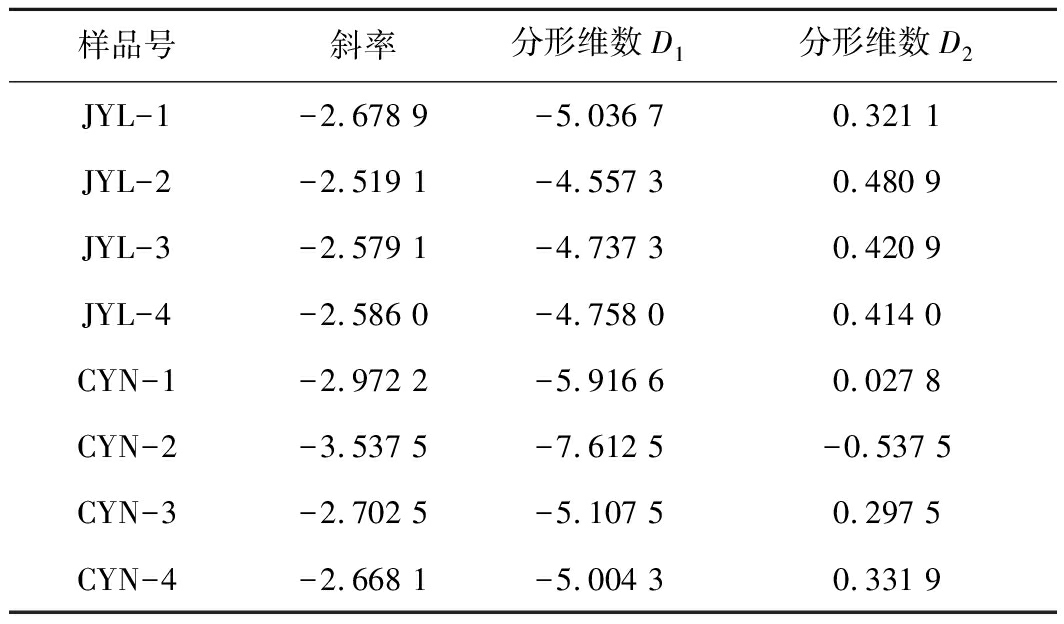
从介孔分形维数的值域分布上看,Dmeso1的值中仅存在一个有效值,其余值均低于2,Dmeso2所有值均介于2~3,说明Dmeso2更加有效。这是因为FHH分形模型中,高压段的计算模型基于毛细孔凝聚过程,考虑了表面张力的影响。对介孔而言,毛细凝聚过程为该孔径范围内的特征过程,微孔内不发生该过程,所以利用高压段的吸附数据通常可以获得有效的分形维数。而低压段的数据中包含了部分微孔吸附数据,会严重影响分形维数的计算结果。为说明微孔吸附数据对计算结果影响的严重性,笔者将CO2吸附数据采用FHH分形模型进行分形维数的计算,见表6。其中D1表示按式(2)计算的分形维数,D2表示按式(3)计算的分形维数。由表6可知,FHH分形模型计算CO2吸附数据时,无论采用何种方法,计算的分形维数均会出现系统性错误,这是由于FHH分形模型的理论基础为均匀平板状的层吸附理论,不适于微孔条件下的吸附机理(微孔充填),故该模型不宜计算微孔的吸附数据。此外,若低压段数据也采用式(3)计算分形维数,其计算结果也会介于2~3,但低压段包含微孔充填、单分子层吸附和多分子层吸附多个过程,从吸附曲线上很难严格划分各个阶段,不能严格满足“表面张力为主”的条件,相反高压段出现的毛细孔凝聚现象正是由于表面张力的作用;同时,对于一个给定的介孔空间而言,介孔的结构特征是唯一的,应具有唯一的分形维数,因此,利用高压段数据计算的分形维数更为可信。综上而言,FHH分形模型更适用于N2吸附的高压段数据,其计算结果可有效表征有机质页岩中介孔的分形维数。
表6 CO2吸附数据的FHH分形模型计算结果
Fig 6 FHH Model results of CO2adsorption data
上述分析说明对于具有跨尺度孔径分布的页岩孔隙而言,微孔孔径分布相对于介孔范围更窄,但微孔数量却更多,不同尺度的孔隙对应具有不同的分形维数,且微孔和介孔的孔隙结构信息需采用不同的试验方法才能准确获得,仅利用N2吸附数据所获得的分形维数并不能完整展示页岩孔隙的分形结构特征,应分别采用相适宜的分形模型计算孔隙的分形维数。因此,评价页岩孔隙结构的复杂度时,综合考虑微孔和介孔分形维数的差异性更为合理,更能有效表征页岩内部复杂的孔隙结构。
目前研究表明页岩中的甲烷吸附类型为物理吸附,甲烷分子受孔壁表面分子间作用力的影响[32]。介孔分形维数的差异性表明了介孔表面粗糙不均,因此吸附位的分布具有不均衡性。对于微孔而言,孔壁两侧的作用势会产生叠加,使微孔吸附能力显著强于介孔[23]。页岩微孔的分形维数指示了微孔的孔壁整体结构不规则,微孔内的势场也将随孔隙结构的变化而出现差异性叠加,因此,微孔分形维数的差异在一定程度上显示出页岩吸附能力的差异性。由此可见,甲烷在页岩孔隙表面的吸附并不能严格满足均匀单层吸附的特点,孔隙分形结构的差异性必然影响孔隙表面气体分子的吸附行为,但受限于本次试验的样品数量,页岩微孔与介孔的吸附能力与孔隙分形结构的关系仍需进一步研究。
笔者利用CO2和N2的等温吸附试验获得了JY1井龙马溪组页岩和CY1井牛蹄塘组页岩的微孔和介孔孔径分布特征,并分别结合微孔分形模型和FHH分形模型计算了微孔和介孔的分形维数,初步探索了两种分形模型的适用性:
1)两组页岩的微孔体积均小于介孔,但微孔比表面积均大于介孔;两组页岩的微孔体积和表面积的差异较小,介孔差异较大。
2)通过不同的气体吸附试验,获得不同尺度孔隙的吸附数据,亦续采用相应的分形理论模型计算孔隙的分形维数。微孔分形模型适用于计算CO2吸附数据,可有效表征页岩微孔的分形维数;FHH分形模型适用于计算N2吸附的高压段数据,可有效表征页岩介孔的分形维数。
3)页岩孔隙分形维数的差异性说明了微孔和介孔表面粗糙,孔壁结构不规则。孔隙的分形结构对孔隙表面吸附能力存在一定的影响,但二者之间的关系有待进一步研究。
参考文献:
[1] 贾承造,郑 民,张永峰.中国非常规油气资源与勘探开发前景[J].石油勘探与开发,2012,39(2):129-136.
JIA Chengzao,ZHENG Ming,ZHANG Yongfeng.Unconventional hydrocarbon resources in China and the prospect of exploration and development[J].Petroleum Exploration and Development,2012,39(2):129-136.
[2] ZOU C N,YANG Z,PAN S Q,et al.Shale gas formation and occurrence in China:an overview of the current status and future potential[J].Acta Geologica Sinica,2016,90(4):1249-1283.
[3] 邹才能,董大忠,王玉满,等.中国页岩气特征、挑战及前景(一)[J].石油勘探与开发,2015,42(6):689-701.
ZOU Caineng,DONG Dazhong,WANG Yuman,et al.Shale gas in China:characteristics,challenges and prospects (I)[J].Petroleum Exploration and Development,2015,42(6):689-701.
[4] CURTIS J B.Fractured shale-gas systems[J].AAPG Bulletin,2002,86:1921-1938.
[5] LI A,DING W L,HE J H,et al.Investigation of pore structure and fractal characteristics of organic-rich shale reservoirs:acase study of Lower Cambrian Qiongzhusi Formation in Malong Block of eastern Yunnan province,south China[J].Marine and Petroleum Geology,2016,70:46-57.
[6] YIN H,ZHOU J P,JIANG Y D,et al.Physical and structural changes in shale associated with supercritical CO2exposure[J].Fuel,2016,184:289-303.
[7] ZHOU L,KANG Z H.Fractal characterization of pores in shales using NMR:acase study from the Lower Cambrian Niutitang Formation in the Middle Yangtze Platform,southwest China[J].Journal of Natural Gas Science and Engineering,2016,35:860-872.
[8] SHAO X H,PANG X Q,LI Q W,et al.Pore structure and fractal characteristics of organic-rich shales:acase study of the Lower Silurian Longmaxi Shales in the Sichuan Basin,SW China[J].Marine and Petroleum Geology,2017,80:192-202.
[9] YANG R,HE S,YI J Z.Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi Shale from Jiaoshiba Area,Sichuan Basin:investigations using FE-SEM,gas adsorption and helium pycnometry[J].Marine and Petroleum Geology,2016,80:27-45.
[10] 郭彤楼,刘若冰.复杂构造区高演化程度海相页岩气勘探突破的启示:以四川盆地东部盆缘JY1 井为例[J].天然气地球科学,2013,24(4):643-651.
GUO Tonglou,LIU Ruobing.Implications from marine shale gas exploration breakthrough in complicated structural area at high thermal stage:taking Longmaxi Formation in Well JY1 as an example[J].Natural Gas Geoscience,2013,24(4):643-651.
[11] CLARKSON C R,SOLANO N,BUSTIN R M,et al.Pore structure characterization of north American shale gas reservoirs using USANS/SANS,gas adsorption,and mercury intrusion[J].Fuel,2013,130(1):606-616.
[12] PFEIFER P,AVNIR D.Chemistry non-integral dimensions between two and three I:fractal theory of heterogeneous surfaces[J].Journal of Chemical Physics,1983,79(7):3558-3565.
[13] MEDEK J,WEISHAUPTOVA Z.The Microporous phase of carbonaceous substances and its fractal dimension[J].Fuel,2000,79(13):1621-1626.
[14] YU B,CHENG P.A fractal permeability model for bi-dispersed porous media [J].International Journal of Heat and Mass Transfer,2002,45:2983-2993.
[15] DATHE A,EINS S,NIEMEYER J,et al.The surface fractal dimension of the soil-pore interface as measured by image analysis [J].Geoderma,2001,103:203-229.
[16] BIRD N,DIAZ M C,SAA A,et al.Fractal and multifractal analysis of pore-scale images of soil [J].Journal of Hydrology,2006,322(1-4):211-219.
[17] YANG F,NING Z F,LIU H Q.Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin,China[J].Fuel,2014,115:378-384.
[18] WANG M,XUE H T,TIAN S S,et al.Fractal characteristics of Upper Cretaceous lacustrine shale from the Songliao Basin,NE China[J].Marine and Petroleum Geology,2015,67:144-153.
[19] PFEIFER P,OBERT M,COLE M W.Fractal BET and FHH theories of adsorption:a comparative study[J].Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences,1989,423:169-188.
[20] ISMAIL M K,PFEIFER P.Fractal analysis and surface roughness of nonporous carbon fibers and carbon blacks[J].Langmuir,1994,10(5):1532-1538.
[21] AVNIR D,JARONIEC M.An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials[J].Langmuir,1989,5(6):1431-1433.
[22] QI H,MA J,WONG P Z.Adsorption isotherms of fractal surfaces[J].Colloids and Surfaces A,2002,206(1-3):401-407.
[23] 金彦任,黄振兴.吸附与孔径分布[M].北京:国防工业出版社,2015.
[24] JARONIEC M.Evaluation of the fractal dimension of microporous activated carbons[J].Fuel,1990,69(12):1573-1574.
[25] JARONIEC M,LU X C,MADEY R.Correlation between the fractal dimension and the microporous structure of a solid[J].Monatshefte Fur Chemie,1991,122(8/9):577-584.
[26] AVNIR D,PFEIFER P.Fractal dimension in chemistry,an intensive characterization of surface irregularity[J].Nouveau Journal de Chimie-new Journal of Chemistry,1983,7(2):71-72.
[27] JARONIE C M,LU X,MADEY R,et al.Evaluation of structural heterogeneities and surface irregularities of microporous solids[J].Materials Chemistry and Physics,1990,26(1):87-97.
[28] JARONIEC M,GILPIN R K,CHOMA J.Correlation between microporosity and fractal dimension of active carbons[J].Carbon,1993,31(2):325-331.
[29] CHOMA J,JARONIEC M,PIOTROWSKA J.On the mesopore correction of adsorption data used for characterizing microporous structure of activated carbons[J].Materials Chemistry and Physics,1987,18(4):409-421.
[30] DUBININ M M.Generalization of the theory of volume filling of micropores to non-homogeneous microporous structures[J].Carbon,1985,23(4):373-380.
[31] STOECKLI H F,BALLERINI L,DEBERNARDINI S.On the evolution of micropore widths and areas in the course of activation[J].Carbon,1989,27(3):501-502.
[32] 李相方,蒲云超,孙长宇,等.煤层气与页岩气吸附/解吸的理论再认识[J].石油学报,2014,35(6):1113-1129.
LI Xiangfang,PU Yunchao,SUN Changyu.Recognition of adsorption/desorption theory in coalbed methane reservoir and shale gas reservoir[J].Acta Petrolei Sinica,2014,35(6):1113-1129.