
移动扫码阅读
青年博士学术论坛
冯吉成1,石建军1,许海涛1,赵希栋1,马海燕1,2,肖 建3
(1.华北科技学院 安全工程学院,北京 东燕郊 101601;2.中国矿业大学(北京) 资源与安全工程学院,北京 100083;3.北京天地华泰矿业管理股份有限公司,北京 100013)
摘 要:针对埋深大、采掘工程和构造区附近的巷道或硐室围岩会形成蝶形塑性区的问题,采用理论计算和计算机编程的方法从极坐标下圆形孔洞围岩塑性区形成和发展的角度出发,阐述了圆形孔洞围岩塑性区形成的力学机制,分析了圆形孔洞围岩塑性区不同的几何形态和范围,重点研究了蝶形塑性区形成、发展及边界扩张的空间演化规律,并探讨了影响蝶形塑性区分布的关键因素和各因素之间的变化特征对蝶形塑性区的影响程度和工程危害。研究发现:孔洞围岩形成蝶形塑性区后,当埋深、孔半径,内摩擦角和黏聚力参数不变时,随着侧压系数从0.4减小至0.3,蝶形塑性区边界从1.43 m增加至3.22 m,随着侧压系数继续的微小变化从0.3减小至0.2,蝶形塑性区边界从3.22 m呈对角线成倍发展扩张至12.27 m,蝶叶扩张至无限大后消失,其中蝶叶扩展影响因素按程度从大到小依次划分为侧压系数、埋深、孔半径,内摩擦角和黏聚力。研究成果为矿山、水利水电、隧道、油气勘探等深部工程稳定性分析及其控制提供了理论依据。
关键词:极坐标;圆形孔洞;蝶形塑性区;影响因素;深部工程
中图分类号:TD353
文献标志码:A
文章编号:0253-2336(2019)02-0208-10
FENG Jicheng1,SHI Jianjun1,XU Haitao1,ZHAO Xidong1,MA Haiyan1,2,Xiao Jian3
(1.School of Safety Engineering,North China Institute of Science and Technology,Yanjiao 101601,China;2.School of Resource and Safety Engineering,China University of Mining and technology(Beijing),Beijing 100083,China;3.Beijing Tiandi Huatai Mining Management Co.,Ltd.,Beijing 100013,China)
Abstract:As for surrounding rock of roadway or chamber of big buried depth,near mining engineering or tectonic zone will appear butterfly plastic zone,the paper uses theoretical calculation and computer programming based on formation and development of plastic zone of circular hole surrounding rock in polar coordinates.It expounds formation mechanical mechanism of plastic zone of circular hole surrounding rock,analyzes different geometry and scope of plastic zone of circular hole surrounding rock,mainly studies formation,development and spatial evolution law of boundary expansion of butterfly plastic zone,and discusses key factors influencing distribution of butterfly plastic zone and influence extent and engineering harm of variation characteristics between the various factors on butterfly plastic zone.The research shows that after hole surrounding rock formed butterfly plastic zone,when the parameters of buried depth,hole radius,angle of internal friction and cohesion of is unchanged,the boundary of butterfly plastic zone increases from 1.43 m to 3.22 m with lateral pressure coefficient decreases from 0.4 to 0.3.With lateral pressure coefficient continue decreasing from 0.3 to 0.2,butterfly plastic zone boundary is diagonally multiplied from 3.22 to 12.27 m,butterfly leaf disappears after expansion to infinity.According to the degree,influencing factors of butterfly leaf expansion is divided into lateral pressure coefficient,buried depth,hole radius,angle of internal friction and cohesion.It provides theoretical basis for stability analysis and control of deep engineering such as mining,water conservancy and hydropower,tunnel,and oil and gas exploration.
Key words:polar coordinates; circular hole; butterfly plastic zone; influencing factors; deep engineering

移动扫码阅读
冯吉成,石建军,许海涛,等.极坐标下圆形孔硐蝶形塑性区分布特征与扩展规律[J].煤炭科学技术,2019,47(2):208-217.doi:10.13199/j.cnki.cst.2019.02.034
FENG Jicheng,SHI Jianjun,XU Haitao,et al.Distribution characteristics and expansion law of butterfly plastic zone of circular hole in polar coordinates[J].Coal Science and Technology,2019,47(2):208-217.doi:10.13199/j.cnki.cst.2019.02.034
收稿日期:2018-05-02;
责任编辑:朱恩光
基金项目:国家自然科学基金资助项目(51804118,51674119);河北省自然科学基金资助项目(E2016508003);中央高校基本科研业务费资助项目(3142018021,3142017085)
作者简介:冯吉成(1985—),男,黑龙江牡丹江人,讲师,博士。E-mail:389832929@qq.com
围岩塑性区的分布形状和几何尺寸是影响巷道围岩稳定性的重要因素,现有塑性区理论认为,围岩塑性区主要为圆形、椭圆形和冒落拱形等,这在浅部煤岩体小变形特征和断层附近条件下是普遍适用的,但近几年随着煤矿开采逐步向深部发展,发现围岩塑性区与浅部有所不同,塑性区形态呈蝶叶状[1]。
关于围岩塑性区研究,国内外学者做了大量工作,取得了丰富的研究成果。普式理论认为巷道开挖后,由于围岩内应力重新分布,次生应力造成巷道围岩破坏,这种破坏首先使巷道顶板松散岩体冒落,破碎区形态为拱形[2]。芬纳公式、卡斯特纳公式给出了无限质体中轴对称圆形隧洞塑性圈范围与材料抗剪强度、初始地应力和洞内周边均匀载荷的关系,并认为塑性区形状为圆形[3-4]。国内学者于学馥等 [5-6]提出“轴变论”理论,分析了双向不等压应力条件下巷道轴比对巷道围岩塑性区的影响,认为围岩破坏形状为椭圆形,从力学根源上验证了普式冒落拱存在。董方庭等 [7]提出了围岩松动圈概念,并以围岩松动圈的厚度为指标对围岩稳定性进行分类,该理论认为巷道支护对象主要是围岩松动圈形成过程中的碎胀力,它受多种因素的共同作用,是地应力与围岩强度的函数,是一个受多种因素作用影响的综合指标。随着矿山、水利水电、隧道,油气勘探等深部工程的逐渐增多,人们对深部工程越来越关注,何满潮[8]指出进入深部的工程岩体所属的力学系统不再是浅部工程围岩所属的线性力学系统,而是非线性力学系统。近年来,文献[1,9-10]认为对于埋深大、采动巷道和构造区附近大变形巷道岩体一般处于非均匀高偏应力环境,并建立了非等压条件下均质围岩巷道塑性区分析力学模型,理论和数值模拟均发现了巷道在非均匀应力下围岩塑性区会呈现类似椭圆形的蝶形形状,不仅验证了马念杰等[11]在20世纪80年代数值模拟得到的巷道围岩塑性区呈现“*”形、半“*”形分布,完善了Kastner的塑性区理论,更进一步将蝶形塑性区理论应用到瓦斯抽采[12]、冲击地压[13]和大变形回采巷道冒顶[14-16]等工程实践中。在此基础上,文献[17-19]又对深部动压回采巷道进行了深入研究,阐明了第I类及第II类蝶形塑性区形成的力学条件,界定了塑性区恶性扩展及其临界的定义,揭示了深部动压回采巷道的变形破坏机理。
针对蝶形塑性区理论的研究成果丰富,但在圆形孔洞围岩塑性区形成的力学机制,并完善细化极坐标下圆形孔洞围岩蝶形塑性区分布和形态特征方面的研究尚显不足。因此,笔者重点探究了孔洞围岩形成蝶形塑性区后的边界扩张空间演化规律,并探讨影响蝶形塑性区分布的关键因素和各因素之间的变化特征对蝶形塑性区的影响程度和工程危害,为矿山、水利水电、隧道、油气勘探等深部工程稳定性控制提供理论依据。
非均匀应力场条件下圆形孔洞分析如图1所示,根据弹性力学理论,在非均匀应力场条件下,在极坐标下圆形孔洞围岩某一点的应力计算公式如下:

(1)
式中:σθ为任一点的环向应力,MPa;σr为任一点的径向应力,MPa;τrθ为任一点的剪应力,MPa;γH为巷道竖向载荷,MPa;λ为侧压系数;R0为圆形巷道半径,m;r、θ为任一点的极坐标。
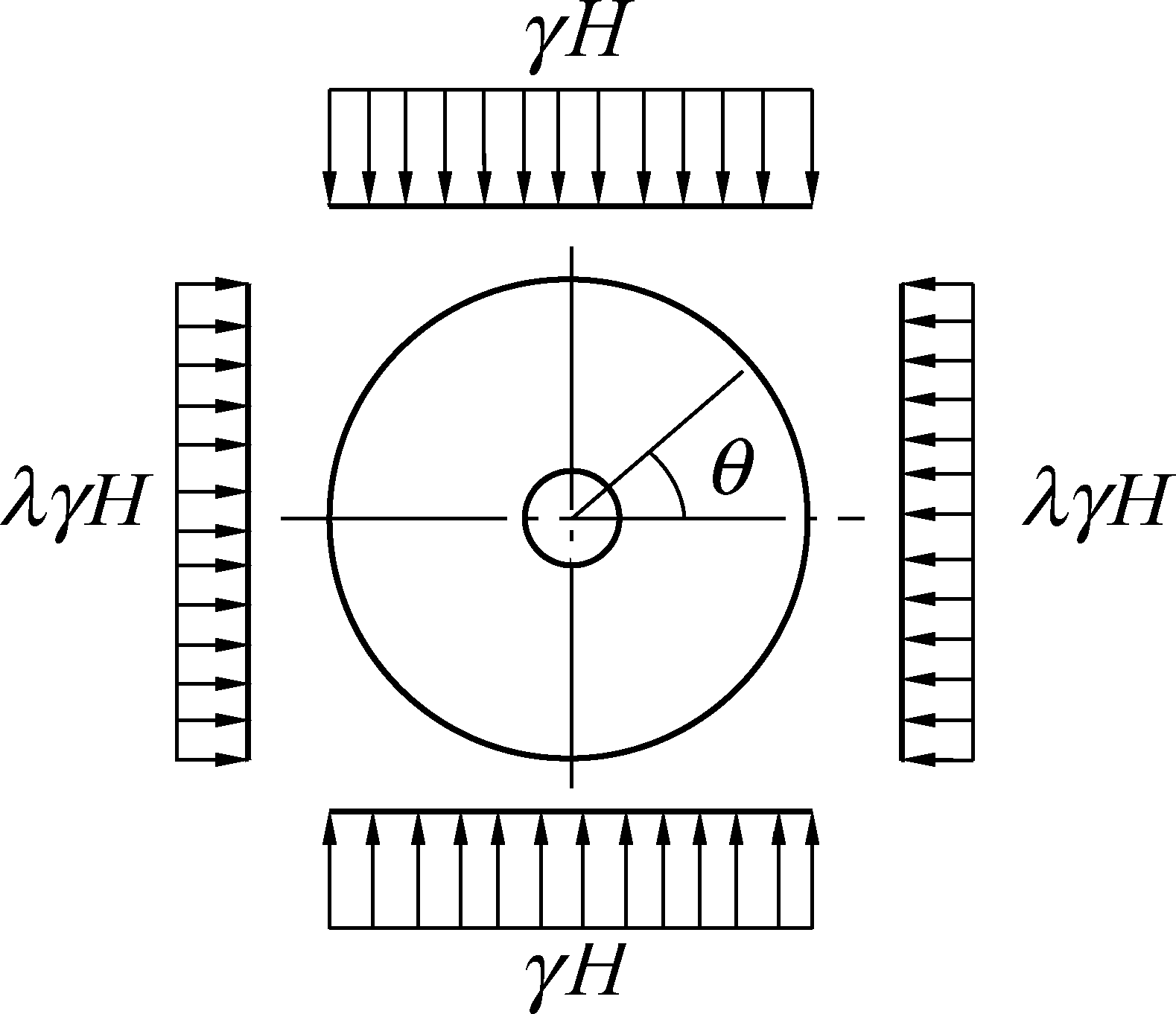
图1 非均匀应力条件下圆形孔洞受力
Fig.1 Circular hole force under nonuniform stress conditions
极坐标下非均匀应力场圆形孔洞围岩塑性边界线的近似计算将圆形孔洞一点处的弹性应力代入到塑性准则条件中,从而得到圆形孔洞围岩塑性边界线近似方程,整理得到圆形孔洞围岩塑性条件方程:

(2)
将公示(1)中极坐标下圆形孔洞一点处的弹性应力代入公式(2),整理得到极坐标下非均匀应力场圆形孔洞围岩塑性边界线近似方程[1]。
![]()
![]()
2(1-λ)2[cos22θ(5-2sin2φ)-sin22θ]+(1+λ)2+![]()
[4(1-λ)2cos 4θ+2(1-λ2)cos2θ(1-2sin2φ)-
![]() (1-λ)cos 2θsin 2φC]·
(1-λ)cos 2θsin 2φC]·![]()
(3)
极坐标下非均匀应力场圆形孔洞围岩塑性边界线近似方程受多种因素的影响,在侧压系数λ、围岩黏聚力C和内摩擦角φ、孔洞埋深H、孔洞围岩容重γ和孔半径R0都已知的情况下,可计算出圆形孔洞围岩塑性区边界线近似位置。
根据极坐标下的非均匀应力场圆形孔洞围岩塑性区边界线隐函数方程,计算分析了不同侧压系数条件下圆形孔洞围岩塑性区几何尺寸和分布形态。
以竖向载荷为15 MPa(相当于埋深600 m),直径为2.0 m的孔洞为例,围岩均质各向同性,黏聚力为2 MPa,内摩擦角为30°时,不同侧压系数条件下圆形孔洞围岩塑性区的分布特征,见表1。
表1 不同侧压系数时极坐标(0°~90°)圆形孔洞围岩塑性区最大尺寸
Table 1 Physical dimension of plastic zone of polar coordinates(0°~90°) circular hole surrounding rock under different side pressure coefficients

从表1可知,当侧压系数λ=1.0时,巷道塑性区大小都为2.55 m(0°~90°),当侧压系数λ=0.7时,孔洞塑性区最大尺寸为2.61 m(60°~90°),最小值为2.39 m(0°~5°),当侧压系数λ=0.5时,孔洞塑性区最大尺寸为2.82 m(47.5°~50°),最小值为2.12 m(0°),当侧压系数λ=0.4时,孔洞塑性区最大尺寸为3.43 m(25°),最小值为0(0°),当侧压系数λ=0.3时,孔洞塑性区最大尺寸为5.22 m(45°),最小值为0(0°~20°),当侧压系数λ=0.2时,孔洞塑性区最大尺寸为14.27 m(47.5°),最小值为2.17 m(0°~5°),当侧压系数λ=0.1时,在同一角度出现2个值,当侧压系数λ=0时,在同一角度也出现2个值,数值比当λ=0.1时小。数据可以看出,随着侧压系数的减小即水平应力与垂直应力比值减小,塑性区最大尺寸随着角度45°~90°递减而增加。
根据极坐标下的非均匀应力场孔洞围岩塑性区边界线隐函数方程,把理论计算数据转化为图形,利用MATLAB软件绘制出了不同侧压系数条件下极坐标(0°~360°)圆形孔洞围岩塑性区几何形态和破坏范围,如图2—图3所示。
由图2、图3可知,当侧压系数λ=1时,孔洞围岩塑性区为圆形,随着侧压系数的减小即水平应力与垂直应力比值减小,圆形塑性区逐渐变成椭圆形塑性区(λ=0.70),椭圆短轴为水平方向,随着侧压系数的再次减小,椭圆形短轴方向塑性区向孔洞内凹,逐渐减小至无塑性区,垂直方向塑性区基本保持不变(λ=0.50),而后随着侧压系数逐渐减少,孔洞围岩在(30°~60°、120°~150°、210°~240°、300°~330°)范围出现蝶形塑性区,并随着侧压系数的减少而蝶叶增大。

图2 极坐标下不同侧压系数时圆形孔洞围岩塑性区边界几何尺寸
Fig.2 Physical dimension of plastic zone boundary of polar coordinates circular hole surrounding rock under different side pressure coefficients

图3 极坐标下侧压系数λ=0~3时圆形孔洞围岩塑性区边界几何尺寸
Fig.3 Physical dimension of plastic zone boundary of polar coordinates circularhole surrounding rock while side pressure coefficient λ=0~3
在上述数据的基础上,当侧压系数减少为(λ=0.40)时,孔洞围岩塑性区逐渐在(30°~60°、120°~150°、210°~240°、300°~330°)对角线方向形成蝶形塑性区,塑性区最大位置在(45°、135°、225°、315°),当侧压系数再减小0.10时(λ=0.30),蝶形塑性区继续扩大,最大尺寸(45°、135°、225°、315°)约为λ=0.40时的2倍(5 m),当侧压系数再减小0.10时(λ=0.2),蝶形塑性区边界加倍扩张,最大尺寸(45°、135°、225°、315°)约为λ=0.30时的3倍(15 m),当侧压系数减小到λ=0.10时,蝶形塑性区边界扩张至无限大,蝶叶消失,在孔洞垂直方向和水平方向形成弹性核,水平方向弹性核大于垂直方向弹性核。
为了寻找从蝶形塑性区边界扩张至无限大形成弹性核的极限最小强度条件,将围岩边界范围扩大,将侧压系数继续细化,当侧压系数减小到λ=0.18时,蝶形塑性区边界扩张至约60 m,最大尺寸(45°、135°、225°、315°)约为λ=0.20时的4倍(60 m),当侧压系数减小到λ=0.17时,蝶形塑性区边界扩张至无限大,蝶叶消失,在孔洞垂直方向和水平方向形成较大弹性核,水平方向弹性核仍大于垂直方向弹性核,而后随着侧压系数的减少,垂直方向和水平方向弹性核逐渐减小,当侧压系数减小到λ=0时,在孔洞垂直方向和水平方向形成的弹性核逐渐减小,水平方向弹性核近似等于垂直方向弹性核。而当侧压系数λ=1~2时,孔洞围岩塑性区近似为椭圆形,当侧压系数λ=2~3时,孔洞围岩形成蝶形塑性区,随着侧压系数从λ=2到λ=3增大,蝶形塑性区边界在45°、135°、225°、315°方位角上扩张而增大。
综上所述,孔洞围岩塑性区随着侧压系数变化(以λ=1界逐渐减小或逐渐增大),从圆形到椭圆进而形成蝶形塑性区,当水平应力与垂直应力相差较大时(侧压系数较小或较大)形成蝶形塑性区,随着侧压系数继续的微小变化或增加很小的外力作用,蝶形塑性区边界在45°、135°、225°、315°方位角上都成倍发展扩张,扩张至无限大,蝶叶消失,在垂直方向和水平方向上形成弹性核,而后随着侧压系数的减小(增加),弹性核逐渐减小。孔洞围岩蝶形塑性区的形成、发展及边界扩张合理的解释了在水平应力与垂直应力相差较大的构造应力区、回采巷道应力系数集中区和断层等附近的孔洞围岩破坏范围大,变形大和支护体破坏严重的现象,同时也对冲击矿压、煤与瓦斯突出和岩爆等复杂动力灾害提供了一定的理论依据。
孔洞围岩蝶形塑性区的形成、发展及边界扩张受多种因素如围岩黏聚力C、内摩擦角φ、孔洞埋深H、侧压系数λ和孔洞半径R0等影响,在上述基础上继续探讨影响孔洞围岩蝶形塑性区的因素,分析各个因素对蝶形塑性区的形成、发展及边界扩张的影响规律和影响程度。
设定其它因素不变,侧压系数λ=0.3,孔洞围岩会形成蝶形塑性区,设定孔洞围岩形成了蝶形塑性区(侧压系数λ=0.3),通过改变其中一个影响因素的参数,而其它影响因素保持不变,计算分析各个影响因素对蝶形塑性区的形成、发展及边界扩张的影响规律和影响程度。
假定其它因素不变(λ=0.3,r=2.0 m,φ=30°,H=600 m,γ=2.5×104 N/m3),当黏聚力C=(0、0.5、1.0、1.5、2.0、2.5、3.0、5.0 MPa)时,孔洞围岩蝶形塑性区的发展及边界扩张随着黏聚力C的减小而增加,垂直方向上塑性区变化较小,如图4所示。
当黏聚力C=2.0 MPa时,蝶形塑性区最大尺寸为3.22 m;当黏聚力C=1.5 MPa时,蝶形塑性区最大尺寸为4.49 m,比C=2 MPa增加了2.27 m;当黏聚力C=1.0 MPa时,蝶形塑性区最大尺寸为7.09 m,比C=1.5 MPa增加了2.6 m ;当黏聚力C=0.5 MPa接近极限最小强度时,蝶形塑性区最大尺寸为24.09 m,比C=1.0 MPa增加了17.0 m;当黏聚力C=0达到极限最小强度时,蝶形塑性区扩张至无限大,蝶叶消失,在垂直方向和水平方向形成弹性核。

图4 黏聚力对孔洞围岩蝶形塑性区的影响规律
Fig.4 Effect law of cohesion on butterfly plastic zone of hole surrounding rock
由图4可知,当黏聚力C=5 MPa时,孔洞围岩无蝶形塑性区,随着黏聚力减小,在(30°~60°、120°~150°、210°~240°、300°~330°)方向上出现较小的塑性区,当黏聚力C=2 MPa时,孔洞围岩形成蝶形塑性区,随着黏聚力的依次减小,蝶形塑性区在(30°~60°、120°~150°、210°~240°、300°~330°)扩展,最大尺寸在45°、135°、225°、315°增加。当黏聚力C接近极限最小强度时,蝶形塑性区最大尺寸成倍跳跃增加,当黏聚力C达到极限最小强度时,蝶形塑性区扩张至无限大,蝶叶消失,在垂直方向和水平方向形成弹性核。
假定其它因素不变(λ=0.3,r=2.0 m,C=2 MPa,H=600 m,γ=2.5×104 N/m),当内摩擦角φ=(0°、20°、25°、30°、35°、40°、45°、50°)时,孔洞围岩蝶形塑性区的发展及边界扩张随着内摩擦角φ的减小而增加,垂直方向上塑性区变化较小,如图5所示。

图5 内摩擦角对孔洞围岩蝶形塑性区的影响规律
Fig.5 Effect law of internal friction angle on butterfly plastic zone of hole surrounding rock
计算得出当内摩擦角φ=35°时,蝶形塑性区最大尺寸为2.11 m;当内摩擦角φ=30°时,蝶形塑性区最大尺寸为3.22 m,比φ=35°增加了1.11 m ;当内摩擦角φ=25°时,蝶形塑性区最大尺寸为5.64 m,比φ=30°增加了2.42 m ;当内摩擦角φ=20°时,蝶形塑性区扩张至无限大,蝶叶消失,在垂直方向和水平方向形成弹性核;当内摩擦角φ=0°时,在垂直方向的弹性核消失,在水平方向上的弹性核减到最小。
由图5可知,当内摩擦角φ=50°时,孔洞围岩无蝶形塑性区,随内摩擦角减小,在(30°~60°、120°~150°、210°~240°、300°~330°)方向上出现较小的塑性区,当内摩擦角φ=35°时,孔洞围岩形成蝶形塑性区,随着内摩擦角的依次减小,蝶形塑性区在(30°~60°、120°~150°、210°~240°、300°~330°)扩展,最大尺寸在45°、135°、225°、315°增加。当内摩擦角φ=20°时,蝶形塑性区扩张至无限大,蝶叶消失,在垂直方向和水平方向形成弹性核,随着内摩擦角再次减小达到极限最小强度时,在垂直方向的弹性核消失,在水平方向上的弹性核减到最小。
内摩擦角φ与黏聚力C相比,当黏聚力C减小到0.5 MPa接近极限最小强度时,依然形成蝶形塑性区,而其他因素不变情况下,内摩擦角φ为20°,蝶形塑性区扩张至无限大,蝶叶消失,在垂直方向和水平方向形成弹性核;当黏聚力C减小到0,达到极限最小强度,在垂直方向和水平方向形成的弹性核逐渐减小,而当内摩擦角φ减小到0°达到极限最小强度时,在垂直方向的弹性核消失,在水平方向上的弹性核减到最小。可见,无论从孔洞围岩蝶形塑性区几何尺寸、扩张趋势,内摩擦角φ都比黏聚力C对蝶形塑性区影响程度大。
假定其它因素不变(λ=0.3,C=2 MPa,φ=30°,H=600 m,γ=2.5×104 N/m3),当孔洞半径R0=(2.0、2.5、3.0、3.5、4.0、5 m)时,孔洞围岩蝶形塑性区的发展及边界扩张随着孔洞孔洞半径R0的增加而呈增大,垂直方向上塑性区变化较小,如图6所示。
计算得出当孔洞半径R0=2.0 m时,蝶形塑性区最大尺寸为3.22 m ;当孔洞半径R0=2.5 m时,蝶形塑性区最大尺寸为4.03 m ,比R0=2 m增加了0.81 m;当孔洞半径R0=3.0 m时,蝶形塑性区最大尺寸为4.84 m ,比R0=2.5 m也增加了0.81 m ;当孔洞半径R0=3.5 m时,蝶形塑性区最大尺寸为5.64 m ,比R0=3.0 m增加了0.80 m ;当孔洞半径R0=4.0 m时,蝶形塑性区最大尺寸为6.40 m ,比R0=3.5 m增加了0.86 m ;当孔洞半径R0=5.0 m(切眼宽度)时,蝶形塑性区最大尺寸为8.10 m ,比R0=4.0 m增加了1.7 m 。

图6 孔洞半径对孔洞围岩蝶形塑性区的影响规律
Fig.6 Effect law of roadway radius on butterfly plastic zone of hole surrounding rock
由图6可知,总体规律为孔洞蝶形塑性区随着孔洞半径的增加而增大,在形成蝶形塑性区的基础上,孔洞半径每增加(减小)0.5 m,蝶形塑性区最大尺寸成等差数列增加(减小),就本节参数条件下,孔洞半径每增加(减小)0.5 m,蝶形塑性区最大尺寸成等差数列增加(减小)0.81 m。
假定其它因素不变,孔洞半径R0与孔洞埋深H对蝶形塑性区的影响规律类似,随着孔洞半径依次增加,始终不会出现蝶形塑性区扩张至无限大,蝶叶消失的情况,几何形状依然是蝶形,但从蝶形塑性区的最大尺寸对比看,当孔洞半径R0=5.0 m(切眼宽度)时,蝶形塑性区最大尺寸为8.10 m,而孔洞埋深H=1 000 m时,蝶形塑性区最大尺寸为5.76 m ;从蝶形塑性区最大尺寸变化看,孔洞半径每增加(减小)0.5 m,蝶形塑性区最大尺寸成等差数列增加(减小)0.81 m,而孔洞埋深每增加(减小)100 m,蝶形塑性区最大尺寸成等差数列增加(减小)0.635 m,这也证明了巷道宽度越大,顶板越不稳定,越易冒顶。可见,孔洞半径R0影响蝶形塑性区程度和工程危害要比内摩擦角φ和黏聚力C大。
假定其它因素不变(λ=0.3,r=2.0 m,C=2 MPa,φ=30°,γ=2.5×104 N/m3),当孔洞埋深H=(600、800、1 000、1 200、1 600、2 000 m)时,孔洞围岩蝶形塑性区的发展及边界扩张随着孔洞埋深H的增加而呈增大,垂直方向上塑性区变化较小,如图7所示。

图7 孔洞埋深对孔洞围岩蝶形塑性区的影响规律
Fig.7 Effect law of roadway burial depth on butterfly plastic zone of hole surrounding rock
计算得出孔洞埋深H=600 m时,蝶形塑性区最大尺寸为3.22 m ;孔洞埋深H=800 m时,蝶形塑性区最大尺寸为4.49 m ,比H=600 m增加了1.27 m ;当孔洞埋深H=1 000 m时,蝶形塑性区最大尺寸为5.76 m ,比H=800 m也增加了1.27 m ;当孔洞埋深H=1 200 m时,蝶形塑性区最大尺寸为7.09 m ,比H=1 000 m增加了1.33 m ;当孔洞埋深H=1 600 m时,蝶形塑性区最大尺寸为10.30 m ,比H=1 200 m增加了3.21 m ;当孔洞埋深H=2 000 m时,蝶形塑性区最大尺寸为15.00 m ,比H=1 600 m增加了4.7 m。
由图7可知,总体规律为孔洞蝶形塑性区随着孔洞埋深的增加而增大,结合数据分析可得,当其他因素不变,并已形成蝶形塑性区,孔洞埋深小于等于1 000 m情况下,孔洞埋深每增加(减小)100 m,蝶形塑性区最大尺寸成等差数列增加(减小),就本节参数条件,孔洞埋深每增加(减小)100 m,蝶形塑性区最大尺寸成等差数列增加(减小)0.635 m,而当孔洞埋深大于1 000 m范围后,孔洞埋深每增加(减小)100 m,蝶形塑性区最大尺寸成递增关系增加(减小)。
假定其它因素不变,随着孔洞埋深依次增加,孔洞蝶形塑性区边界依次发展、扩张,但不会出现蝶形塑性区扩张至无限大,蝶叶消失的情况,几何形状依然是蝶形,但随着埋深的增加,构造应力和原岩应力都会增加,相应的采掘工程应力也会增加,双向应力的比值与埋深相关性越大,尤其是采动条件下,孔洞围岩双向应力的比值随着采动的影响而发生改变,因此,孔洞埋深H影响蝶形塑性区程度要比内摩擦角φ、黏聚力C和孔洞半径R0大,但与侧压系数相比较,埋深大的区域不一定会出现蝶形塑性区,但出现蝶形塑性区的区域侧压系数即水平应力与垂直应力一定相差较大,因此,埋深对蝶形塑性区的影响程度较侧压系数小。
当侧压系数不等于1,水平应力与垂直应力相差悬殊时,侧压系数为0.3或2.5时就会出现蝶形塑性区,当侧压系数等于1时或接近1时,孔洞围岩会出现圆形和椭圆形等塑性区,在此基础上,无论上述几种因素怎样变化,都不会改变孔洞围岩塑性区几何形状,只能改变塑性区的尺寸范围,可见,侧压系数无论从改变孔洞围岩塑性区的几何形状和孔洞围岩蝶形塑性区的尺寸范围方面,都要比其它因素的影响程度大。
表2 孔洞围岩蝶形塑性区影响因素分析
Tab.2 Analysis of influence factors of the butterfly plastic zone of hole surrounding rock

综上所述,侧压系数λ、孔洞埋深H、内摩擦角φ、黏聚力C和孔洞半径R0等因素对蝶形塑性区的形成、发展和边界扩张演化都产生了重要影响,但各因素之间影响程度不同,侧压系数λ即围岩双向应力的比值相差较大时才会出现蝶形塑性区,它是影响蝶形塑性区形成的前提条件,孔洞埋深H又与构造应力、原岩应力和采掘工程应力存在必然联系,从而影响着双向应力的比值,埋深大的区域不一定会出现蝶形塑性区,但出现蝶形塑性区的区域侧压系数即水平应力与垂直应力一定相差较大,它是蝶影响形塑性区形成的基础条件,内摩擦角φ、黏聚力C和孔洞半径R0是影响蝶形塑性区发展和边界扩张即破坏范围的主要条件。因此,从对孔洞围岩蝶形塑性区影响程度和工程危害依次将各因素划分为极端不利因素、非常不利因素、中度不利因素、轻度不利因素和微弱不利因素,见表2。
1)揭示了孔洞围岩蝶形塑性区的形成、发展及边界扩张的空间演化规律,当水平应力与垂直应力相差较大(侧压系数较小或较大)时,孔洞围岩会形成蝶形塑性区,随着侧压系数继续的微小变化或增加很小的外力作用,蝶形塑性区边界在45°、135°、225°、315°方位角上都成倍发展扩张,扩张至无限大,最终蝶叶消失,在垂直方向和水平方向上形成弹性核,随后弹性核继续逐渐减小。
2)分析了各因素自身变化特性及其对孔洞围岩蝶形塑性区的影响程度和工程危害,将侧压系数λ、孔洞埋深H、孔洞半径R0、内摩擦角φ和黏聚力C因素按顺序依次划分为极端不利因素、非常不利因素、中度不利因素、轻度不利因素和微弱不利因素。
3)孔洞围岩蝶形塑性区的形成、发展及边界扩张能够合理解释在水平应力与垂直应力相差较大的构造应力区、回采巷道应力系数集中区和断层等附近围岩破坏范围大,变形大和支护体破坏严重的现象,同时也对冲击矿压、煤与瓦斯突出和岩爆等复杂动力灾害提供了一定的理论依据。
参考文献:
[1] 赵志强.大变形回采巷道围岩变形破坏机理与控制方法研究[D].北京:中国矿业大学(北京),2014.
[2] 沈明荣,陈建峰.岩体力学[M].徐州:同济大学出版社,2006.
[3] 任青文,张宏朝.关于芬纳公式的修正[J].河海大学学报,2001,29(6):109-111.
REN Qingwen,ZHANG Hongchao.Amendments to the Finner formula[J].Journal of Hehai University,2001,29(6):109-111.
[4] KASTNER H.隧道与坑道静力学[M].同济大学,译.上海:上海科学技术出版社,1980.
[5] 于学馥.轴变论与围岩变形破坏的基本规律[J].铀矿冶,1982,1(1):8-17,7.
YU Xuefu.The basic law of axial variation theory and deformation and failure of surrounding rock [J].Uranium Mining and Metallurgy,1982,1(1):9-17,7.
[6] 于学馥,乔 端.轴变论和围岩稳定轴比三规律[J].有色金属.1981,33(3):8-15.
YU Xuefu QIAO duan.Three law of axial ratio of axial variation theory and stable of surrounding rocks [J].Nonferrous.1981,33(3):8-15.
[7] 董方庭,宋宏伟,郭志宏,等.巷道围岩松动圈支护理论[J].煤炭学报,1994,19(1):22-31.
DONG Fangting,SONG Hongwei,GUO Zhihong,et al.Support theory of loose ring of roadway surrounding rock [J].Journal of China Coal Society,1994,19(1):22-31.
[8] 何满潮.深部的概念体系及工程评价指标[J].岩石力学工程学报,2005,24(16):2854-2858.
HE Manchao.Comception system and evaluation indexes for deep engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2854-2858.
[9] 马念杰,李 季,赵志强.圆形巷道围岩偏应力场及塑性区分布规律研究[J].中国矿业大学学报,2015,44(2):206-213.
MA Nianjie,LI Ji,ZHAO Zhiqiang.Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock[J].Journal of China University of Mining & Technology,2015,44(2):206-213.
[10] 郭晓菲,马念杰,赵希栋,等.圆形巷道围岩塑性区的一般形态及其判定准则[J].煤炭学报,2015,40(4):742-748.
GUO Xiaofei,MA Nianjie,ZHAO Xidong,et al.General shapes and criterion for surrounding rock mass plastic zone of round roadway[J].Journal of China Coal Society,2015,40(4):742-748.
[11] 马念杰,侯朝炯.采准巷道矿压理论及应用[M].北京:煤炭工业出版社,1992.
[12] 马念杰,李 季,赵希栋,等.深部煤与瓦斯共采中的优质瓦斯通道及其构建方法[J].煤炭学报,2015,40(4):742-748.
MA Nianjie,LI Ji,ZHAO Xidong,et al.High quality gas channel and its construction method applied to coal and gas simultaneous extraction in deep mining[J]. Journal of China Coal Society,2015,40(4):742-748.
[13] 赵志强,马念杰.煤层巷道蝶型冲击地压发生机理猜想[J].煤炭学报,2016,41(8):1871-1877.
ZHAO Zhiqiang,MA Nianjie.Mechanism conjecture of butterfly rock burst in coal seam roadway[J].Journal of China Coal Society,2016,41(8):1871-1877.
[14] 赵志强,马念杰,郭晓菲,等.大变形回采巷道蝶叶型冒顶机理与控制[J].煤炭学报,2016,41(12):2932-2939.
ZHAO Zhiqiang,MA Nianjie,GUO Xiaofei,et al.Falling principle and support design of butterfly failure roof in large deformation mining roadways[J].Journal of China Coal Society,2016,41(12):2932-2939.
[15] 李 季,马念杰,赵志强.回采巷道蝶叶形冒顶机理及其控制技术[J].煤炭科学技术,2017,45(12):46-52.
LI Ji,MA Nianjie,ZHAO Zhiqiang.Butterfly leaf type roof falling mechanism and control technology of mining gateway[J].Coal Science and Technology,2017,45(12):46-52.
[16] 贾后省,李国盛,王路瑶,等.采动巷道应力场环境特征与冒顶机理研究[J].采矿与安全工程学报,2017,34(4):708-714.
JIA Housheng,LI Guosheng,WANG Luyao,et al.Characteristics of stress-field environment and roof falling mechanism of mining influenced roadway[J].Journal of Mining & Safety Engineering,2017,34(4):708-714.
[17] 袁 越,王卫军,李树清,等.圆巷围岩塑性区形态特征指标体系构建与分析[J].矿业工程研究,2017,32(2):11-19.
YUAN Yue,WANG Weijun,LI Shuqing,et al.Establishment and analysis of the index system for morphological characteristics of plastic zone around circular roadway[J].Mineral Engineering Research,2017,32(2):11-19.
[18] 袁 越,王卫军,袁 超,等.深部矿井动压回采巷道围岩大变形破坏机理[J].煤炭学报,2016,41(12):2940-2950.
YUAN Yue,WANG Weijun,YUAN Chao,et al.Large deformation failure mechanism of surrounding rock for gateroad under dynamic pressure in deep coal mine[J].Journal of China Coal Society,2016,41(12):2940-2950.
[19] 刘 迅,王卫军,袁 超,等.深部巷道变形与塑性区几何形态特征分析[J].矿业工程研究,2017,32(2):60-67.
LIU Xun,WANG Weijun,YUAN Chao,et al.Analysis of deformation and plastic zone characteristics of deep roadway[J].Mineral Engineering Research,2017,32(2):60-67.