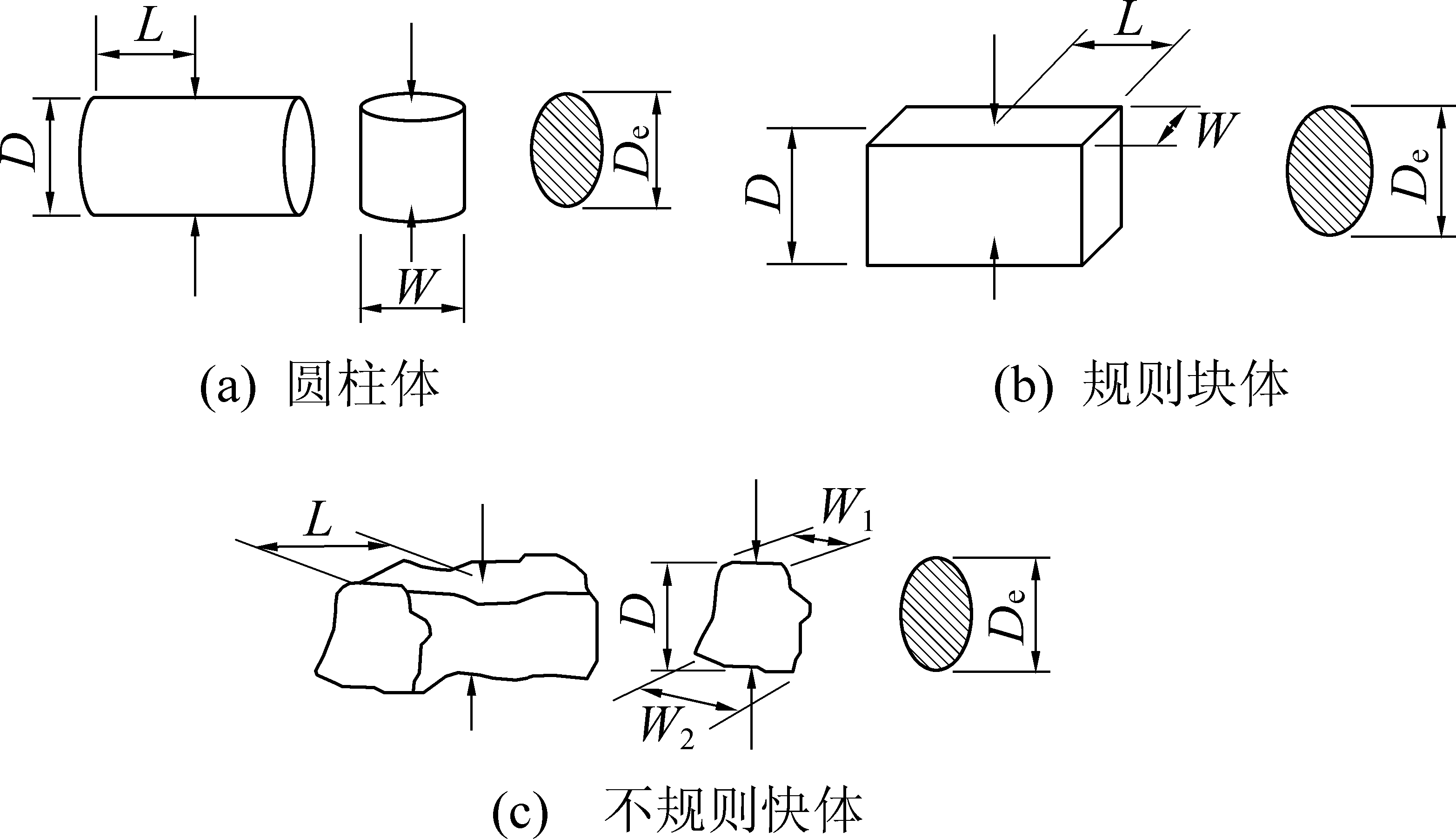
De—试样等效直径;W1—试件最小宽度;W2—试件最大宽度
图1 点载荷试样形状与尺寸要求示意
Fig.1 Diagrams of point load with different shape and size requirements
煤岩体强度是岩体力学中最基本的参数,是矿井开拓部署、巷道布置与支护、煤炭开采及冲击地压、煤与瓦斯突出等灾害防治必不可少的基础参数[1]。《工程岩体分级标准》用岩块单轴抗压强度作为岩石坚硬程度的定量指标[2]。康红普等[3]采用钻孔触探法对煤层强度测试,获得井下煤岩体强度实测数据为巷道支护提供合理性与可靠性设计,使巷道围岩稳定性与支护状况得到明显改善。王琦等[4]建立了随钻参数与岩石单轴抗压强度的定量关系模型,提出一种基于数字钻探测试完整岩石单轴抗压强度的方法。对于完整煤岩体通过实验室加工成标准试样进行测量获得单轴抗压强度值,而破碎煤层现场取样困难,获得标准试样成本高。点载荷强度试验可以针对不规则形状、圆柱体试样快速进行大量试验,是一种简易快速地测定岩石强度的试验方法[5-6]。因此,可以通过测试点载荷强度间接获得其单轴抗压强度。
在探索岩石点载荷强度与单轴抗压强度的关系方面,国内外学者做了大量研究工作,如:KAHRAMAN[7]探究了火成岩点载荷强度与单轴抗压强度的关系。RUSNAK等[8]汇总众多学者点载荷测试结果,基于转换系数确定岩性类别,为岩石分类系统提供依据。KOOHMISHI等[9]利用点载荷法对铁路基石进行强度测试,分析不同尺寸、形状与点载荷强度指数的关系。张国锋等[10]通过大量的数据归纳了泥岩点荷载强度与岩石单轴抗压强度的关系。王茹等[11]对比不规则的岩石试件和规则的石膏试件两者点荷载试验数据,总结了点荷载强度指标的应用范围。SINGH等[12]探究不同类型岩石点载荷指数与单轴压缩强度之间的关系。郭曼丽等[13]认为点荷载法测试结果与岩石的抗压强度有相关性,可作为岩体分级指标。TZIALLAS等[14]对沉积岩和变质岩等进行了单轴抗压强度和点载荷强度测试。付志亮等[15]通过对煤矿顶底板岩石进行点载荷试验和拉压强度对比试验,认为点荷载试验可为岩石强度确定提供依据。点载荷试验多用于岩石强度测试,很少用于煤体强度测试,尤其是破碎煤体点载荷测试及结果规律分析与研究较少。
为预测破碎煤体单轴抗压强度值,笔者根据点载荷强度测试特点,将现场取回的破碎煤块进行实验室点载荷试验,并对测试数据进行分析和研究。同时借鉴之前学者研究的单轴抗压强度Re与点载荷强度指数Is50关系式,结合破碎煤体点载荷强度指数特点,分析破碎煤体单轴抗压强度分布规律,为获得破碎煤体单轴抗压强度提供重要参考。
根据国际岩砂学学会点载荷测试方法[5],无论是圆柱形、规则块体和不规则块体在进行点载荷测试时要求块体高D=50±35 mm,点载荷测试位置距边缘距离L>0.5D,D<W<3.33D,其中W为垂直于加载方向的最小试件宽度。D/W的比值应该为0.3~1.0,最好接近于1。
根据试件的形状和尺寸,对于不同形状和大小的煤块进行点载荷测试,分为径向、轴向、规则块体(方块)和不规则块体4种形式如图1所示。

De—试样等效直径;W1—试件最小宽度;W2—试件最大宽度
图1 点载荷试样形状与尺寸要求示意
Fig.1 Diagrams of point load with different shape and size requirements
未经修正的点载荷强度指数为
(1)
其中:Is为点载荷强度,MPa;P为破坏载荷,N。对于圆柱体径向测试;![]() 对于圆柱体轴向、方块以及不规则块体:
对于圆柱体轴向、方块以及不规则块体:![]() 其中,A为通过上下压头接触点平面的最小横截面积,mm2。
其中,A为通过上下压头接触点平面的最小横截面积,mm2。
修正后点载荷强度指数为
Is50=FIs
(2)
其中:F为几何校正因子。且尺寸修正系数表达式:F=(De/50)0.45。
在新元煤矿31004辅助进风巷煤帮,选用直径为56 mm取心钻头进行取样,在实验室进行点载荷测试。由于煤块本身尺寸限制,本文点载荷试验涉及圆柱体轴向和不规则2种测试形式,部分试验煤块和2种形式煤块试验如图2所示。
将满足测试要求尺寸煤块进行点载荷测试,根据上述式(1)、式(2)得到修正前后煤块点载荷指数,见表1。

图2 不同形状煤块的点载荷测试
Fig.2 Placement of coal between loading platens for various shapes
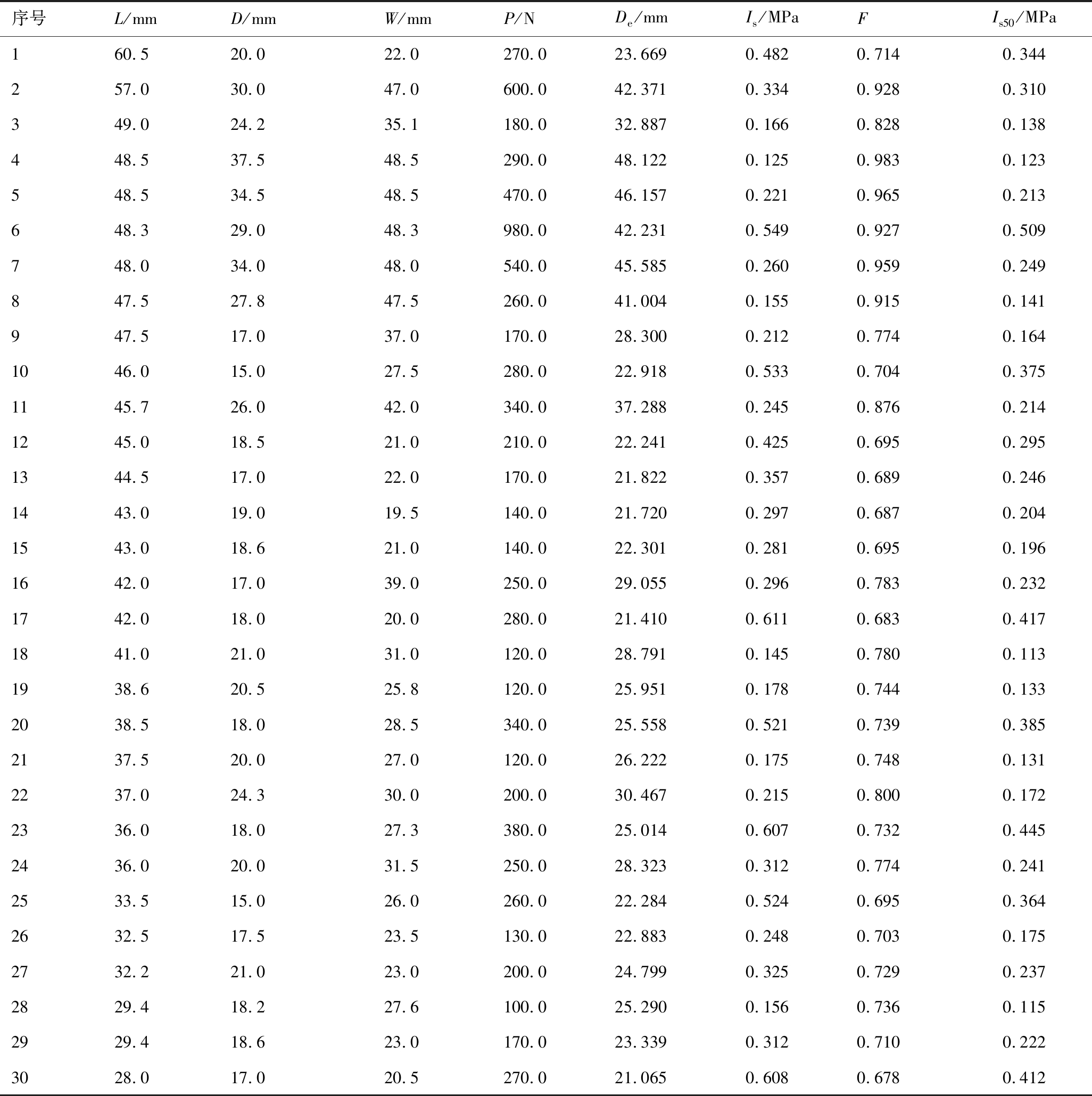
表1 不同尺寸和形状煤块点载荷试验数据汇总
Table 1 Results of point load with different shape and size samples
序号L/mmD/mmW/mmP/NDe/mmIs/MPaFIs50/MPa160.520.022.0270.023.6690.4820.7140.344257.030.047.0600.042.3710.3340.9280.310349.024.235.1180.032.8870.1660.8280.138448.537.548.5290.048.1220.1250.9830.123548.534.548.5470.046.1570.2210.9650.213648.329.048.3980.042.2310.5490.9270.509748.034.048.0540.045.5850.2600.9590.249847.527.847.5260.041.0040.1550.9150.141947.517.037.0170.028.3000.2120.7740.1641046.015.027.5280.022.9180.5330.7040.3751145.726.042.0340.037.2880.2450.8760.2141245.018.521.0210.022.2410.4250.6950.2951344.517.022.0170.021.8220.3570.6890.2461443.019.019.5140.021.7200.2970.6870.2041543.018.621.0140.022.3010.2810.6950.1961642.017.039.0250.029.0550.2960.7830.2321742.018.020.0280.021.4100.6110.6830.4171841.021.031.0120.028.7910.1450.7800.1131938.620.525.8120.025.9510.1780.7440.1332038.518.028.5340.025.5580.5210.7390.3852137.520.027.0120.026.2220.1750.7480.1312237.024.330.0200.030.4670.2150.8000.1722336.018.027.3380.025.0140.6070.7320.4452436.020.031.5250.028.3230.3120.7740.2412533.515.026.0260.022.2840.5240.6950.3642632.517.523.5130.022.8830.2480.7030.1752732.221.023.0200.024.7990.3250.7290.2372829.418.227.6100.025.2900.1560.7360.1152929.418.623.0170.023.3390.3120.7100.2223028.017.020.5270.021.0650.6080.6780.412
注:序号1—11块体长度为45.0~60.5 mm;序号12—18块体长度为40~45 mm;序号19—24块体长度为35~40 mm;序号25—30块体长度为28~35 mm。
在1951年由Weibull提出的威Weibull布,可以将试样尺寸和应力水平的影响与相同类型试样的强度变化相关联[9]。下面给出Weibull分布的累计失效概率公式为
(3)
式中:Pf(σ)为累计失效概率;σ为试样所受应力水平;σ0为试样比例参数;m为试样形状参数。
由式(4)可得出一种随机变量在压力作用下的可靠性概率为
(4)
为了推算在应力水平作用下煤块破坏时各自的可靠性概率,通常来讲,按照顺序排列点载荷测试的每一组破碎煤块,用不同的估计值来计算第i个可靠性概率[16]。常用的估计量是Pi为
(5)
式中:N为每组中煤块的数量。
通过转换式(4)得到一个应力水平为σ和煤块尺寸为d的可靠性概率,即
ln{ln[1/Ps(σ)]}=mlnσ-mlnσ0
(6)
其中:参数m和σ0分别称为威布尔参数,由上式(6)可以看出ln{-ln[Ps(σ)]}与lnσ成线性关系。根据块体长度L将表1中尺寸大小:45.0—60.5、40—45、35—40、28—35 mm测试数据分为4组。通过式(5)计算出每个点载荷指数对应的可靠性概率,得到不同尺寸煤块点载荷测试结果Weibull分布可靠性概率图,如图3所示,根据拟合公式得到其对应的Weibull分布形状参数m分别为2.11、2.28、1.63、1.93,比例参数σ0分别为3.45、3.56、3.36、3.37。

图3 不同尺寸煤块点载荷测试结果Weibull分布可靠性概率
Fig.3 Reliable probability diagram of weibull distribution based on load test results of coal blocks of different sizes
Weibull分布参数与块体大小关系曲线如图4所示,随着块体长度变化,比例参数与形状参数均为小范围波动,不同块体大小的点载荷强度指数遵循Weibull分布规律,不会随着块体大小变化而改变其分布形式。

图4 Weibull分布参数与块体长度关系曲线
Fig.4 The relation curve between Weibull distribution parameters and block size
1967年J.B.Mac Queen提出的Kmeans算法,是广泛应用于科学和工业诸多聚类算法中简单有效的算法之一[17]。Kmeans算法的工作机理是:把n个样本点分为k个簇,使得各簇内的样本点具有较高的相似性,而各簇间的样本点相似程度较低,相似度的计算是依据一个簇中样本点的平均值来进行。该算法根据聚类性能指标最小化原则,通常使用的聚类准则函数是簇内的各个样本点到该簇中心的误差平方和最小[17]。
算法具体流程如下:在样本数据集D中选择k个样本点,将k个样本点值分别赋给初始聚类中心![]() 第j次迭代时,对样本点D中的所有点pt(t=1,…,n),依次计算到各簇中心
第j次迭代时,对样本点D中的所有点pt(t=1,…,n),依次计算到各簇中心![]() 的欧氏距离d(t,i):
的欧氏距离d(t,i):
(7)
找出pt关于![]() 的最小距离,将pt归入到关于
的最小距离,将pt归入到关于![]() 距离最小的簇中,更新各簇的聚类中心:
距离最小的簇中,更新各簇的聚类中心:
(8)
计算数据集D中所有点的平方误差Ei,并与前一次误差Ei-1比较。
(9)
若|Ei+1-Ei|<δ则算法结束,否则转入式(8)进行再一次迭代。
(10)
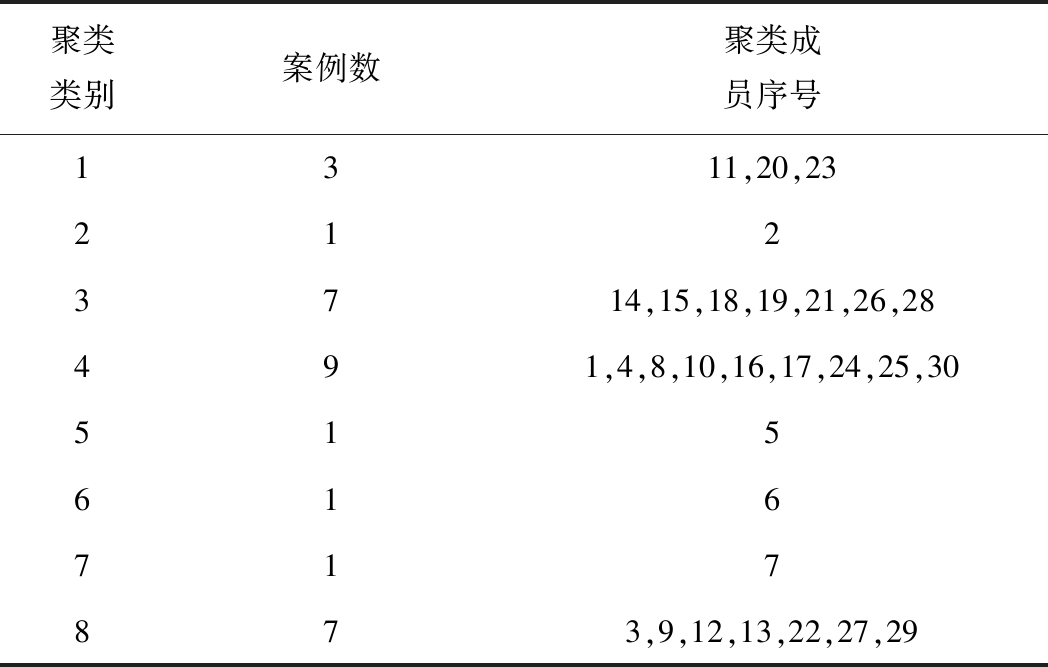
K-means算法是通过输入聚类个数8,以及包含30个数据对象的数据库,最后输出满足方差最小标准的8个聚类,具体聚类分析结果见表2。将案例个数为1的聚类视为异常点进行剔除,对剩余的聚类1,3,4,8四个类别的成员分别进行拟合,如图5所示。
表2 K-means聚类分析结果
Table 2 Cluster analysis results of K-means
聚类类别案例数聚类成员序号1311,20,232123714,15,18,19,21,26,28491,4,8,10,16,17,24,25,30515616717873,9,12,13,22,27,29
从图5可以看出,在4类拟合曲线中点载荷指数与等效直径均成反比,且聚类3、4和8斜率基本一致,随着等效直径增大,点载荷指数减小。
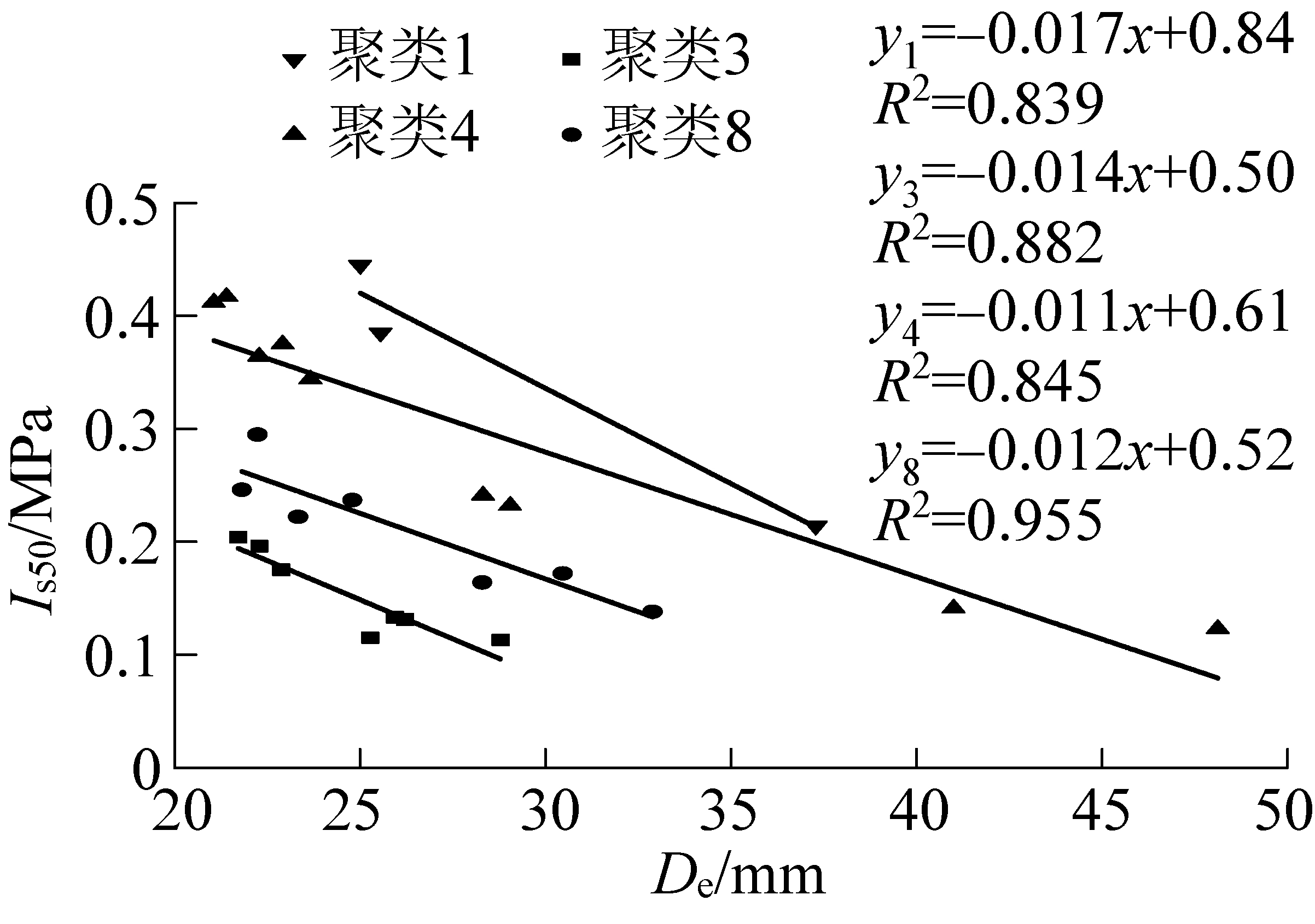
图5 点载荷强度指数与等效直径聚类结果拟合
Fig.5 The fitting diagram of point load intensity indexs and equivalent diameter clustering results
虽然对于破碎煤体无法取得标准煤样,但是考虑到之前学者对点载荷和单轴抗压强度关系研究的实践经验和数据基础。因此,通过查阅文献总结自1985年至2013年国内外学者研究点载荷强度指数与单轴抗压强度之间关系以及转换公式见表3。
结合本文研究的破碎煤体强度特点和点载荷强度指数范围,同时考虑公式的适用范围,选取6组点载荷强度指数与单轴抗压强度的关系式,分析破碎煤体单轴抗压强度规律(表中“Y”标记)。根据测试的破碎煤体点载荷强度为0.11~0.51 MPa,根据适用条件选取的点载荷强度指数与单轴抗压强度的研究关系式,结合图6可以看出,点载荷强度指数为0.11 MPa时,单轴抗压强度范围为0.7~3.1 MPa;点载荷强度指数为0.51 MPa时,单轴抗压强度范围为3.9~9.3 MPa。

图6 单轴抗压强度与点载荷强度指数关系
Fig.6 Diagram of the relationship between uniaxial compressive strength and point load strength index
将单轴抗压强度进行统计,作出分布直方图以及累计百分比曲线如图7所示,单轴抗压强度为0~5 MPa占比达到81.11%,5~8 MPa占比18.33%,大于9 MPa占比仅0.56%,根据统计可以得出笔者所测试的破碎煤体单轴抗压强度处于0.7~4.9 MPa。
表3 历年单轴抗压强度与点载荷强度指数对应公式汇总
Table 3 Formulae of uniaxial compressive strength and the corresponding point loadstrength index over the years

年份学者适用范围公式标注1985ISRM[5]各类岩石Re=(20~25)Is50—1989Vallejo等[18]页岩(煤矿)砂岩Re = 12.6Is50Re = 17.4Is50Y—1991Jermy and Bell[7]砂岩(煤矿)Re = 14.1Is50Y1996Chau and Wong[19]花岗岩、凝灰岩Re =(12.5~14.9)Is50—2001Kahraman[7]22 different rock type煤系岩石Re = 8.41Is50+ 9.51 Re = 23.62Is50-2.69—Y2003Quane and Russel[20]坚硬岩石软弱岩石Re = 24.4Is50Re = 3.86(Is50)2+ 5.65Is50—Y2004Tsiambaos and Sabatakakis[21]沉积岩Re = 7.3(Is50)1.71—2006Santi[22]页岩Re = 12.25(Is50)1.59—2007Kassim and Mohammad[23]Is<1 MPaIs> 1 MPaRe = 12.23Is50+ 1.75 Re = 14.45Is50+ 0.096Y—2008Sabatakakis等[24]Is< 2 MPaIs= 2~5 MPaIs> 5 MPaRe = 13Is50Re = 24Is50Re = 28Is50Y——2009Tziallas等[14]沉积岩Re = 14.49Is50—2010Basu[25]片状岩石Re = 11.103Is50+ 37.659—2012Singh等[12]火成岩、沉积岩和变质岩Re =(14~24)Is50—2013Li and Wong[26]变质粉砂岩变质砂岩Re = 19.83Is50Re = 21.27Is50——
注:根据测试强度值以及适用条件,表中“Y”标记作为参考公式,“—”标记不作为参考公式。
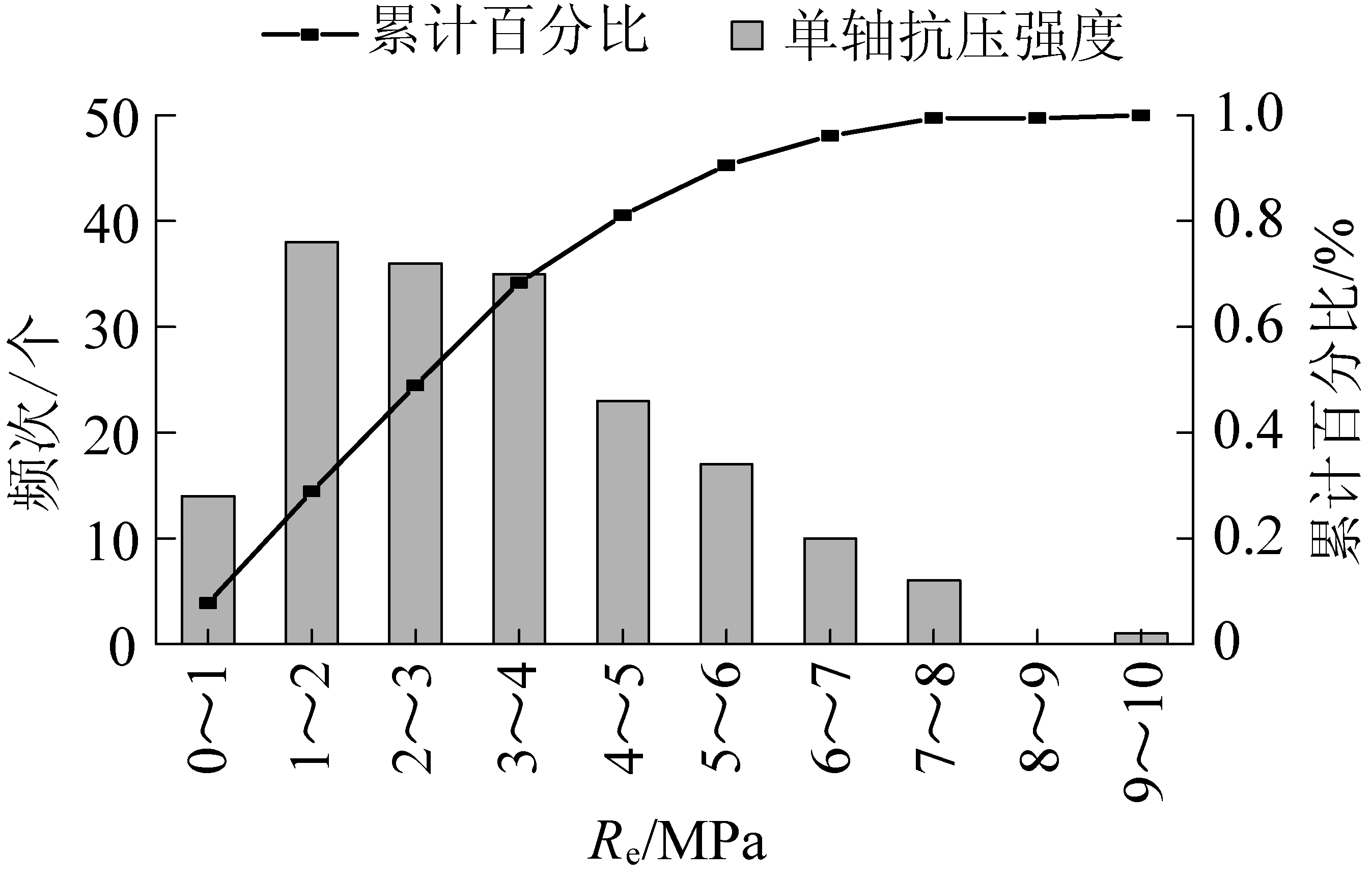
图7 破碎煤体单轴抗压强度统计分布直方图
Fig.7 Histogram of statistical distribution of uniaxial compressive strength of broken coal
1)对30组测试数据分析得出破碎煤体点载荷强度指数遵循Weibull分布且随着块体长度变化,比例参数与形状参数均为小范围波动,无显著差别,不影响其分布形式。
2)通过K-means聚类分析建立了等效直径与点载荷强度指数的关系,对聚类效果显著的4个类别成员分别进行拟合,聚类3、4和8斜率基本一致,随着等效直径的增大,点载荷强度指数减小。
3)根据历年学者研究的Re与Is50关系式,结合破碎煤体点载荷强度指数特点,分析破碎煤体单轴抗压强度分布规律,得出新元煤矿巷帮破碎区煤体单轴抗压强度处于0.7~4.9 MPa,为破碎煤体巷道围岩支护提供依据。
4)对于无法取出标准试样的情况,点载荷强度指数是研究破碎煤体强度的重要参数之一,通过选择合适的关系式建立Re与Is50联系,达到定量分析破碎煤体单轴抗压强度目的。但是由于点载荷测试随机性大,需要建立在大量测试数据基础上,而本文测试破碎煤体点载荷强度指数稳定性差,要尽量选择比较规整的块体进行试验。
[1] 康红普.煤岩体地质力学原位测试及在围岩控制中的应用[M].北京:科学出版社,2013:174-212.
[2] 中华人民共和国建设部.中华人民共和国国家标准:工程岩体分级标准[M].北京:中国计划出版社,1995.
[3] 康红普,司林坡.深部矿区煤岩体强度测试与分析[J].岩石力学与工程学报,2009,28(7):1312-1320.
KANG Hongpu,SI Linpo.Test and analysis of coal and rock mass strength in deep coal mine [J].Chinese Journal of Rock Mechanics and Engineering,2009,28(7):1312-1320.
[4] 王 琦,秦 乾,高 松,等.数字钻探随钻参数与岩石单轴抗压强度关系[J].煤炭学报,2018,43(5):1289-1295.
WANG Qi,QIN Qian,GAO Song,et al.Relationship between rock drilling parameters and rock uniaxial compressive strength based on energy analysis[J].Journal of coal science,2018,43(5):1289-1295.
[5] FRANKLIN J A.Suggested method for determining point load strength[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1985,22(2):51-60.
[6] 刘泉声,赵怡凡,张晓平,等.灰岩隧道掘进机隧道点荷载试验评价岩石强度方法的研究与探讨[J].岩土力学,2018,39(3) :977-984.
LIU Quansheng,ZHAO Yifan,ZHANG Xiaoping,et al.Study and discussion on point load test for evaluating rock strength of TBM tunnel constructed in limestone[J].Rock and Soil Mechanics,2018,39(3):977-984.
[7] KAHRAMAN S.The determination of uniaxial compressive strength from point load strength for pyroclastic rocks[J].Engineering Geology,2014,170(4):33-42.
[8] RUSNAK J,MARK C.Using the point load test to determine the uniaxial compressive strength of coal measure rock[C].Proceedings of the 19th international conference on ground control in mining.Morgantown: West Virginia University,2000: 362-371.
[9] KOOHMISHI M,PALASSI M.Evaluation of the strength of railway ballast using point load test for various size fractions and particle shapes[J].Rock Mechanics and Rock Engineering,2016,49(7):2655-2664.
[10] 张国锋,刘志双,陈显坤,等.点荷载法测试易风化泥质岩强度的可靠性分析[J].岩土力学,2014,35(S1):292-298.
ZHANG Guofeng,LIU Zhishuang,CHEN Xiankun,et al.Reliability analysis of measuring strongly weathered grey mudstone strength with point load measurement[J].Rock and Soil Mechanics,2014,35(S1):292-298.
[11] 王 茹,唐春安,王述红.岩石点荷载试验若干问题的研究[J].东北大学学报(自然科学版),2008,29(1):130-132.
WANG Ru,TANG Chunan,WANG Shuhong,Study on several problems about point load test of rock[J].Journal of Northeastern University(Natural Science) ,2008,29(1):130-132.
[12] SINGH T N,KAINTHOLA A,VENKATESH A.Correlation between point load index and uniaxial compressive strength for different rock types[J].Rock Mechanics and Rock Engineering,2012,45(2):259-264.
[13] 郭曼丽.试论岩石点荷载试验的适用性[J].岩土力学,2003,24(3):488-490.
GUO Manli.Discussion on adaptability of point load test of rocks,[J].Rock and Soil Mechanics,2003,24(3):488-490.
[14] TZIALLAS G P,TSIAMBAOS G,SAROGLOU H.Determination of rock strength and deformability of intact rocks[J].Electronic Journal of Geotechnical Engineering,2009,14(7):1-12.
[15] 付志亮,王 亮.煤层顶底板岩石点荷载强度与拉压强度对比试验研究[J].岩石力学与工程学报,2013,32(1):88-96.
FU Zhiliang,WANG liang.Comparative experimental research on point load strength,uniaxial compressive strength and tensile strength for rocks in roof and floor of coal seam[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(1):88-96.
[16] 金良琼.两参数Weibull分布的参数估计[D].昆明:云南大学,2010.
[17] 王 伟.Kmeans聚类与多波谱阈值相结合的云检测和烟检测算法研究[D].合肥:中国科学技术大学,2011.
[18] VALLEJO L E,WELSH R A,Robinson M K.Correlation between unconfined compressive and point load strengths for Appalachian rocks[C].The 30th US Symposium on Rock Mechanics (USRMS).Morgantown: Rock Mechanics Association,1989:461-468.
[19] CHAU K T,WONG R H C.Uniaxial compressive strength and point load strength of rocks[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts,1996,33(2):183-188.
[20] QUANE S L,RUSSELL J K.Rock strength as a metric of welding intensity in pyroclastic deposits[J].European Journal of Mineralogy,2003,15(5):855-864.
[21] TSIAMBAOS G,SABATAKAKIS N.Considerations on strength of intact sedimentary rocks[J].Engineering Geology,2004,72(3/4):261-273.
[22] SANTI P M.Field Methods for Characterizing Weak Rock for Engineering[J].Environmental & Engineering Geoscience,2006,12(1):1-11.
[23] KASSIM A,MOHAMMAD E T.Laboratory study of weathered rock for surface excavation works[D].Johor:Universiti Teknologi Malaysia,2007.
[24] SABATAKAKIS N,KOUKIS G,TSIAMBAOS G,et al.Index properties and strength variation controlled by microstructure for sedimentary rocks[J].Engineering Geology,2008,97(1): 80-90.
[25] BASU A,KAMRAN M.Point load test on schistose rocks and its applicability in predicting uniaxial compressive strength[J].International Journal of Rock Mechanics & Mining Sciences,2010,47(5):823-828.
[26] LI D,WONG L N Y.Reply to Comment by Saffet Yagiz on “Point Load Test on Meta-Sedimentary Rocks and Correlations to UCS and BTS”[J].Rock Mechanics and Rock Engineering,2013,46(4):913-915.

移动扫码阅读