近年来，随着煤炭行业科技水平的持续提升，我国煤矿安全形势趋于好转，重特大事故、百万吨死亡率等指标均实现了显著降低。但是，与美国、澳大利亚等发达国家相比仍存在较大差距，安全形势依然严峻，瓦斯事故依旧突出[1]。为保障煤矿安全生产，防止瓦斯事故发生，迫切需要引入新技术、新方法，深度挖掘瓦斯监测历史样本数据，通过可靠的实时预测跟踪算法研究，实现对瓦斯在线监测的精准预测，大幅提升煤矿瓦斯灾害预警及应急响应能力[2]，减少瓦斯事故的经济损失，保障矿工生命安全。
目前，国内外主要有2种预测煤矿瓦斯的方法：一是基于物理参数的计算与估计方法；二是基于监测数据的统计分析方法[3]。第1类方法是基于物理参数来间接预测瓦斯量，如钻屑法[4]、微震监测方法[5]、氡气法[6]、声发射技术[7]等。基于物理参数方法在一定条件下能实现瓦斯量的预测，但其存在操作过程繁琐、干扰性大、预见性不足等特点，且随着井下监测系统的普及，已逐步被第2类方法替代。第2类方法主要是利用大量的煤矿井下监测数据，应用机器学习方法对数据的变化特征进行建模，实现对瓦斯量的预测，例如：基于指数平滑法、神经网络建模法[8-9]、支持向量机建模法[10-11]、灰色系统建模法[12-13]、组合预测法[14-16]等方法，这些方法对矿井瓦斯预测模型的构建及优化产生了积极影响。然而，上述大多数预测方法都采用常规静态学习方式对瓦斯监测数据进行训练，模型一经训练即用于预测，在预测过程中不会自主进行参数的在线学习或动态校正。
大量现场监测数据表明，瓦斯浓度的变化受采掘速度、煤层瓦斯含量、矿井风流量等多种因素影响，瓦斯浓度时间序列随着时间的推移不断累积，新的瓦斯浓度样本值刻画出矿井当前最新作业环境状态。由此可见，预测的时效性和准确性是衡量所建立瓦斯浓度预测模型是否有效可靠的关键，其根本点需要实现瓦斯浓度预测模型参数实时更新。此外，煤矿监测数据含有大量的干扰噪声，严重影响了预测的准确度，这些都对矿井瓦斯浓度在线预测提出了挑战。
为此，笔者提出了一种可实现瓦斯浓度实时预测的Lagrange-ARIMA学习算法。首先对煤矿安全监测数据进行预处理，即依据拉伊达准则处理异常值为缺失值，并应用滑动Lagrange插值对缺失值进行插值；其次基于ARIMA模型，融入序贯学习思想，提出了适用于煤矿瓦斯浓度时变系统的ARIMA序贯学习模型；最后应用某煤矿工作面瓦斯监测数据进行试验，通过对数据进行预处理、滑动Lagrange插值、数据平稳性检验、白噪声检测、最优窗口尺度确定等分析，实现瓦斯数据实时预测，取得良好实际应用效果。
由于矿井生产环境复杂多变，监测系统随时可能发生线路松动或脱落、通信故障、硬件失效、电磁干扰等状况，造成监测数据缺失或异常，一定程度上对监测数据的有效预测分析增加了困难。现有针对瓦斯浓度监测缺失值或异常值最常用的在线处理方法是删除记录、平均值修正或最近临插补。这些方法在大多数情况下有效，有一定的适用性，但其破坏了监测数据的完整性，有可能丢弃大量隐藏在数据中的关键信息，对灾变前预测分析尤为不适用。
为有效解决上述瓦斯浓度监测数据中的缺失值或异常值问题，采用滑动Lagrange插值法进行处理。研究发现，Lagrange插值法在插值端点易出现龙格现象，使得插值误差较大，不能满足数据处理要求[17]。为此，使用滑动Lagrange插值法对待查数据进行预测，以确保待插点始终处于待插区域的中间，实现缺失值或异常值的重建。
构造一具有n个瓦斯浓度时间序列数据集合：
s={xi,yi}i=1,2,…,n
式中：xi为时序点；yi为瓦斯浓度监测数据。
依据相关数学知识可知，对于平面上无两点在一条直线上的n+1个点可以构造一个n次多项式Ln(x)使其过这n+1个点。构造n+1次插值多项式为
(1)
其中，li(x)为Lagrange基函数，均是n次多项式,并使其在各节点xj(j=0,1,…,n)上满足
(2)
于是，
(3)
其中，αi为待定系数，联合式(2)和式(3)得
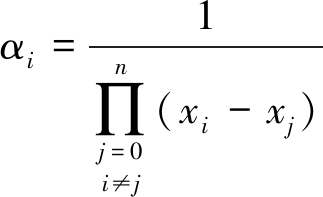
(4)
从而
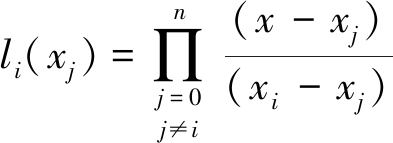
(5)
代入式(1)得
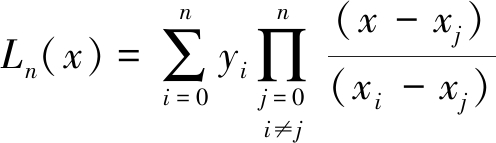
(6)
式(6)即Lagrange插值多项式。
自回归差分移动平均模型(Autoregressive Integrated Moving Average Model，ARIMA)是较常用的时间序列预测方法之一[18]。ARIMA(p,d,q)中AR为自回归模型、MA为移动平均模型。其中，p为自回归项的数量;d时间序列成为平稳序列所需的差分次数；q为移动平均项的数量。设t时刻监测的矿井瓦斯浓度为yt，分别构建瓦斯浓度预测AR模型及MA模型。
建立AR模型：
yt=φ0+φ1yt-1+φ2yt-2+…+φpyt-p+εt
(7)
其中：φ0为常数；φ1、φ2、…、φp为模型参数，即在时刻t处的瓦斯浓度yt的取值是前p个时段监测值形成的时间序列yt-1、yt-2、…,yt-p的多元线性回归，可视为过去p个时段序列值对yt产生主要影响。当前随机干扰项εt构成误差项，为零均值白噪声序列。
建立MA模型：
yt=μ+εt-θ1εt-1-θ2εt-2-…-θqεt-q
(8)
即在时刻t处的瓦斯浓度yt的值为前q个时段的随机扰动序列εt-1、εt-2、…、εt-q的多元线性函数，可视为过去q个时段序列值对yt产生主要影响。μ是瓦斯浓度序列{Yt}的均值;θ1、θ2、…、θq为模型参数。
构建瓦斯浓度预测的ARMA模型：
(9)
即在时刻t处的瓦斯浓度yt的取值是前p个时段yt-1、yt-2、…、yt-p序列值和前q个时段的随机扰动εt-1、εt-2、…、εt-q序列值的多元线性函数。可以看出，过去p期的序列值和过去q期的误差项共同对yt产生影响。
如果瓦斯浓度时间序列为非平稳序列，则需对序列先进行d阶差分运算，使其成为一个平稳序列，然后再进行ARMA模型预测，即ARIMA模型。
前述ARIMA模型并不具备在线学习的能力，对于瓦斯浓度预测这类时变要求较高的时间序列预测效果有限。因此，对ARIMA模型进行如下改进：
定义1 ：设在1个时间监测周期t内的瓦斯浓度时间序列为y1、y2、…、yt，ft+1为t+1即下一时刻的预测值，有
ft+1 =ARIMA(p,d,q)
(10)
ARIMA模型参数估计由yt-1、yt-2、…、yt-N+1确定，其中N为学习窗口尺度，其值由L1范数最小化(L1-min)方法确定。
对瓦斯浓度集{Yt}，设
为t时刻瓦斯浓度预测值，则测试误差ε(t)为
(11)
在
条件下，即求得学习窗口尺度N值，并利用尺度为N的滑动窗口实现实时数据与历史数据的动态增减。
1)利用拉伊达准则，查找瓦斯监测数据库中的各类异常值，将异常值视为缺失值。具体为：如果统计的瓦斯监测数据残差绝对值大于其3倍的标准偏差σ时，即若式(12)、式(13)联合成立，则认为该误差为疏失误差，瓦斯监测值为异常值，并将其视为缺失值。
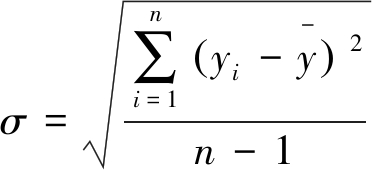
(12)
(13)
式中：
为瓦斯浓度序列均值。
2)使用滑动Lagrange插值法对认定的和已识别的瓦斯监测缺失值进行插值。
3)使用单位根检验(Augment Dickey Fullerton test，ADF)法，进行插值后的瓦斯浓度时间序列平稳性检验。ADF检验模型如下：
模型
模型
模型
其中：Δ代表一阶差分算子；δ为系数；βt为趋势项；α为截距；
为v个分布滞后项;v为确定εt满足白噪声的最大滞后阶数。实际检验时按模型3、模型2、模型1顺序进行。如果检验拒绝零假设H0:δ=0，表明原序列为平稳序列，即可停止检验。否则就继续检验，直到检验完模型1为止。
4)确定ARMA模型的p、q值。ARMA的阶数p、q值可以根据绘制自相关图和偏自相关图的拖尾和截尾来确定。但由于在线学习窗口尺度变化不定，使得ARMA模型的阶数也不断变化。因此基于贝叶斯信息准则(Bayesian information criterion，BIC)，采用相对最优模型自动识别p、q的值。首先设定多个(p,q)组合，并输入时间序列数据建立相对应的ARMA(p,q)模型，然后计算每个模型的BIC值，如式(14)所示。
(14)
其中：
为模型取阶数为p、q时的误差方差估计。
通过选择p、q使BIC值达到最小的一组(p,q)，即为拟合效果最佳的ARMA阶数，并由式(15)计算模型拟合数据均方根误差(Root Mean Square Error，RMSE)。
(15)
以某煤矿综采工作面1 095个瓦斯(CH4)体积分数作为试验数据，采样间隔为5 min。将数据按照4∶1划分为训练集和测试集，即训练集876条数据，测试集219条数据。计算得到试验数据均值为0.189%，标准差为0.072%，最小值为0.079%，最大值0.576%，原始数据无缺失。为验证Lagrange插值法的有效性，将第i×100个(i=1，2，…，10)共10个数据点的数据进行剔除，默认为缺失值，构造生成一个预处理数据序列，如图1所示。
图1 瓦斯样本数据集及缺失值构建
Fig.1 Data set of gas samples and construction of missing values
1)应用拉伊达准则对数据中的异常值进行处理，视为缺失值。
2)确定滑动Lagrange插值窗口的尺度，并应用Lagrange插值对含有缺失值的数据进行预处理。
3)对训练集应用ADF方法进行数据序列平稳性检验，确定序列差分必要性。
4)采用LB(Ljung-Box，LB)统计量的方法对训练集(或者差分后的训练集)进行白噪声检测。
5)确定在线序贯学习的最优窗口尺度，采用BIC方法确定在线学习时p、q的取值。
6)在测试集上进行预测。
7)用评价指标对预测结果进行评价。
1)滑动Lagrange插值结果。在上述构造的带有缺失值的序列上，应用滑动Lagrange插值，得到预测总偏差最小的Lagrange插值窗口尺度为2，插值结果见表1。
表1 缺失序列Lagrange插值结果
Table 1 Result for missing sequences ofLagrange interpolation
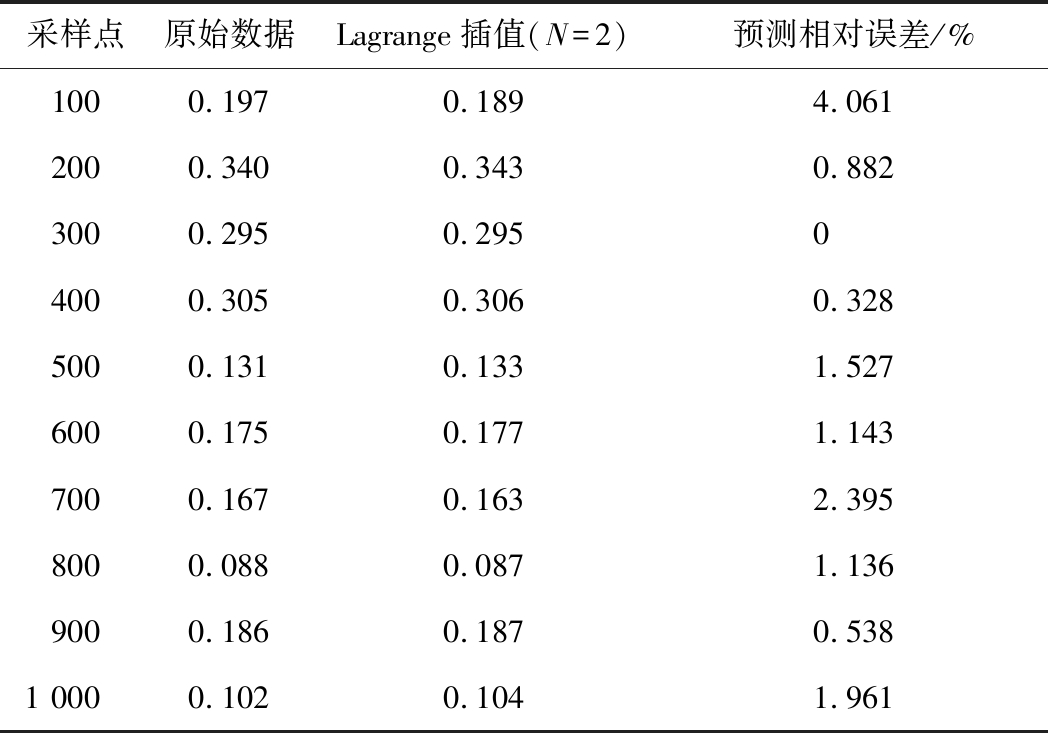
采样点原始数据Lagrange插值(N=2)预测相对误差/%1000.1970.1894.0612000.3400.3430.8823000.2950.29504000.3050.3060.3285000.1310.1331.5276000.1750.1771.1437000.1670.1632.3958000.0880.0871.1369000.1860.1870.5381 0000.1020.1041.961
从表1可以看出，针对构造的10个剔除缺失点，运用滑动Lagrange插值均取得了较好的插值结果，平均相对误差仅为1.397%，表明Lagrange插值适用于监测瓦斯数据的预处理。
2)数据平稳性检验。利用ADF方法对原始训练集序列进行数据序列平稳性检验，求得p值为0.000 46，小于0.05，可认为试验数据序列为平稳序列，不需对其进行差分运算，即ARIMA模型中d值为0。
3)白噪声检测。采用LB统计量的方法对原始序列进行白噪声检验，计算p值为4.917×10-191，小于0.05，可以看出原始序列为非白噪声序列，具有预测价值。
4)确定模型中p、q的值。绘制训练集的自相关图和偏自相关图，如图2、图3所示。
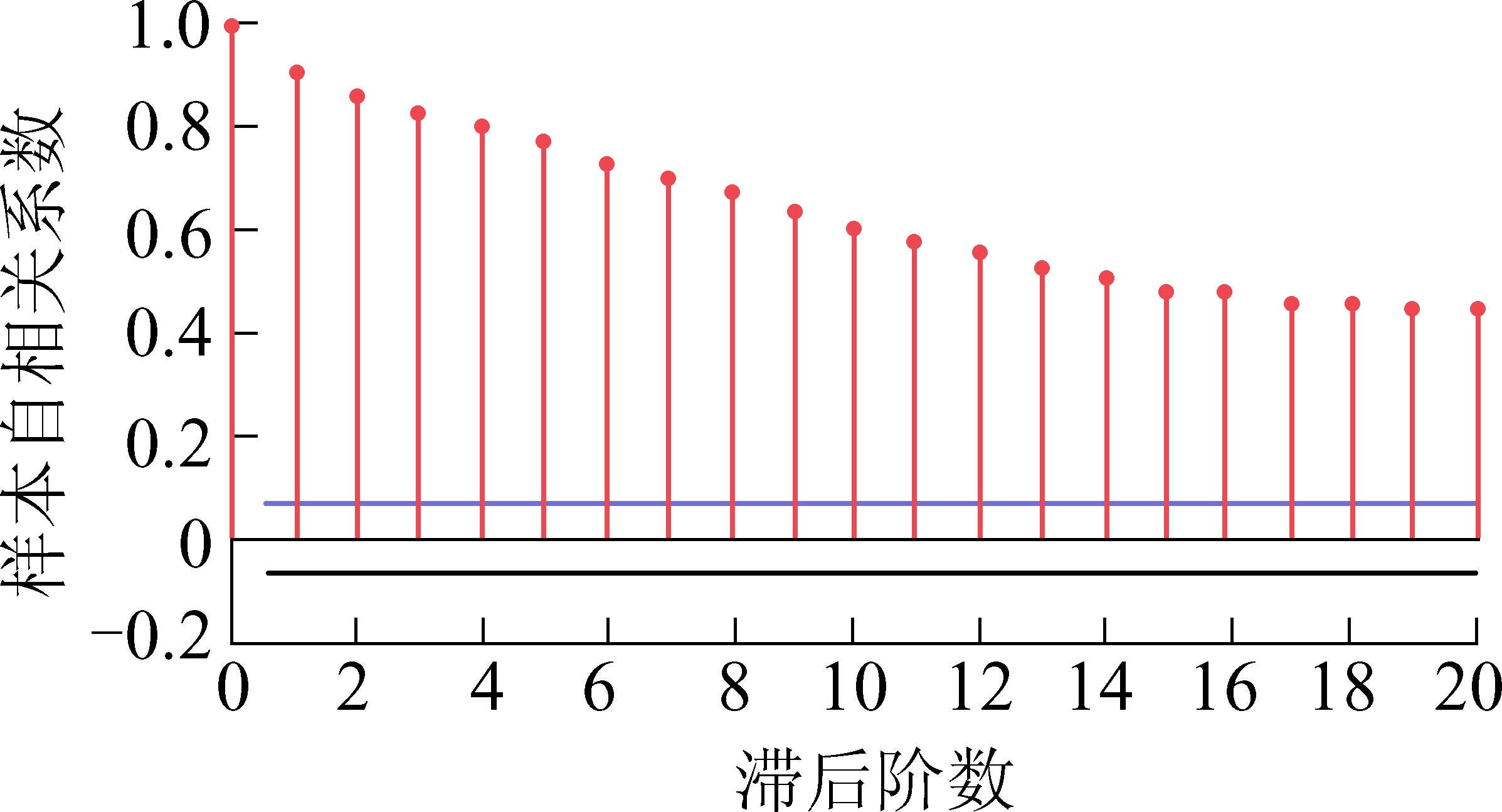
图2 训练集自相关系数
Fig.2 Auto correlation function of training set
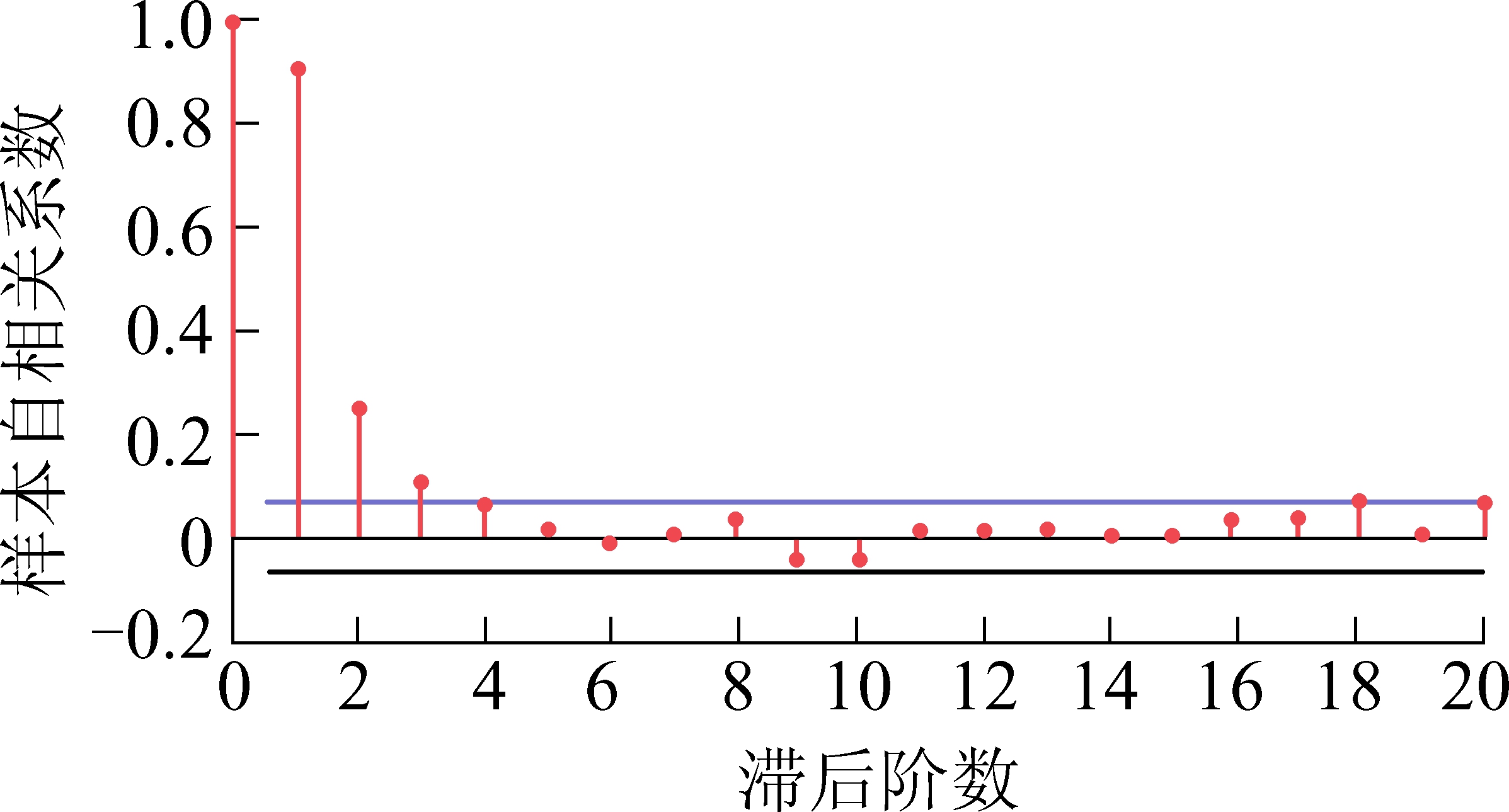
图3 训练集偏自相关系数
Fig.3 Partial auto correlation function of training set
从图2、图3可以看出，训练集的自相关系数拖尾，偏自相关系数3阶截尾，因此对训练集静态学习来说适用于ARIMA(3,0,0)模型，也就是p取值为3，q取值为0。
5)静态预测。运用训练集上静态学习的模型在测试集上进行逐点预测，结果显示预测模型所得平均绝对误差(Mean Absolute Error，MAE)为0.014 1，如图4所示。
图4 ARIMA模型静态学习预测结果
Fig.4 Prediction results by ARIMA model with static learning
6)序贯学习窗口尺度的确定。为实现在线学习，确定在线序贯学习窗口尺度N。设定学习窗口的下界为10，上界为200。将窗口尺度从10增至200，创建相应的ARIMA模型，并在测试集上进行逐点预测，求出每个模型在测试集上的L1范数，得出L1范数在不同学习窗口尺度下的变化情况，如图5所示。
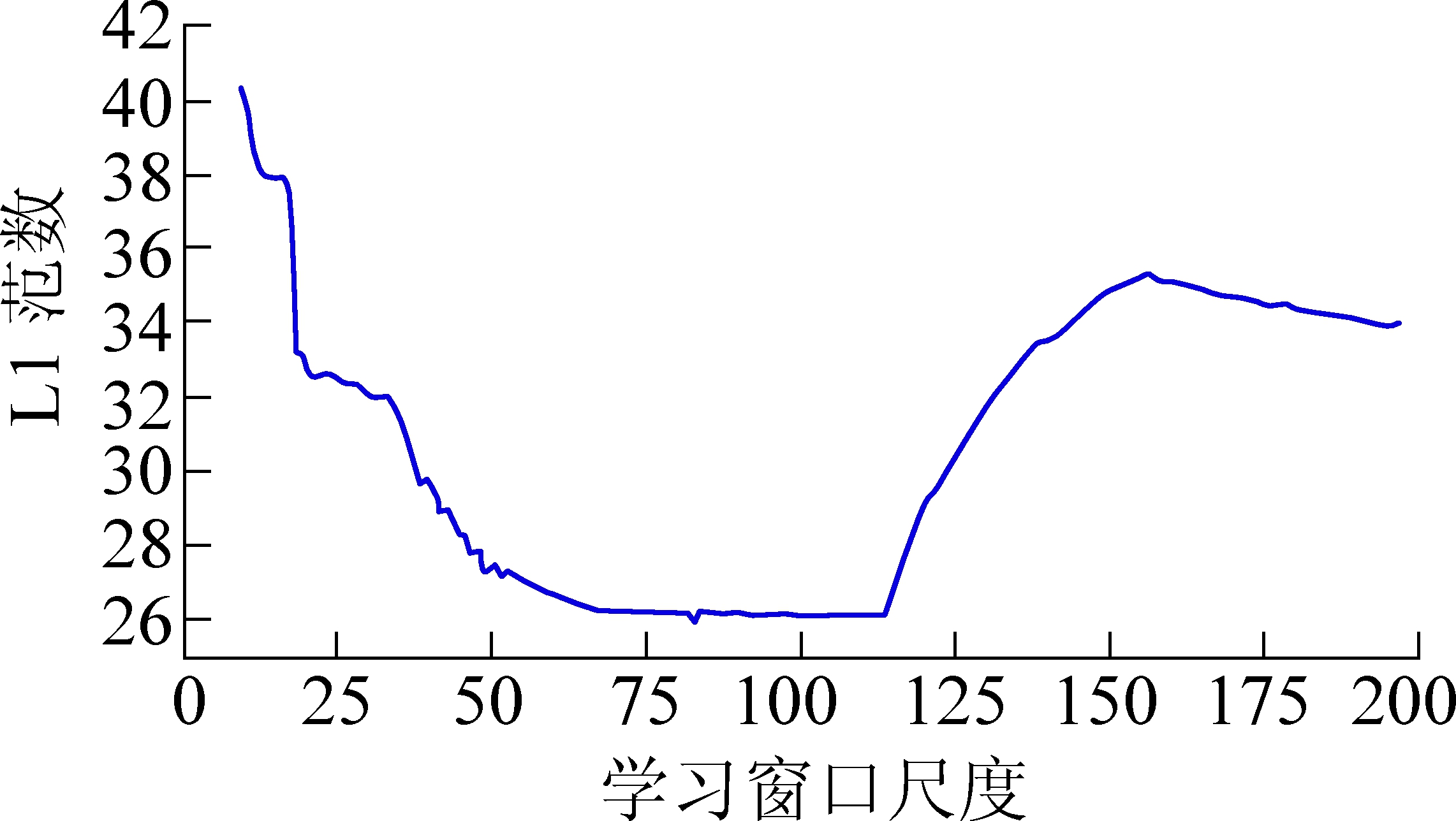
图5 学习窗口尺度与L1范数关系
Fig.5 The relationship with the width of learning window and L1-norm
从图5可知，学习窗口尺度与L1范数表现如下特征：学习窗口尺度在70之前，L1范数呈下降趋势；70～117趋于平稳；在85时，L1范数取得最小值；学习窗口尺度超过117之后，L1范数又呈上升趋势。选择在线序贯学习窗口尺度85，L1范数为2.58，MAE为0.011 8，比静态全训练集上学习取得的MAE误差值0.014 1降低了16.3%，相比窗口尺度876降低90.3%，建模复杂度显著降低，因此更适合在线预测。
7)实时在线预测。在确定了在线学习窗口尺度为85后，应用该模型在线逐点预测50个数据点，结果显示预测模型所得MAE为0.015 86，效果良好，如图6所示。
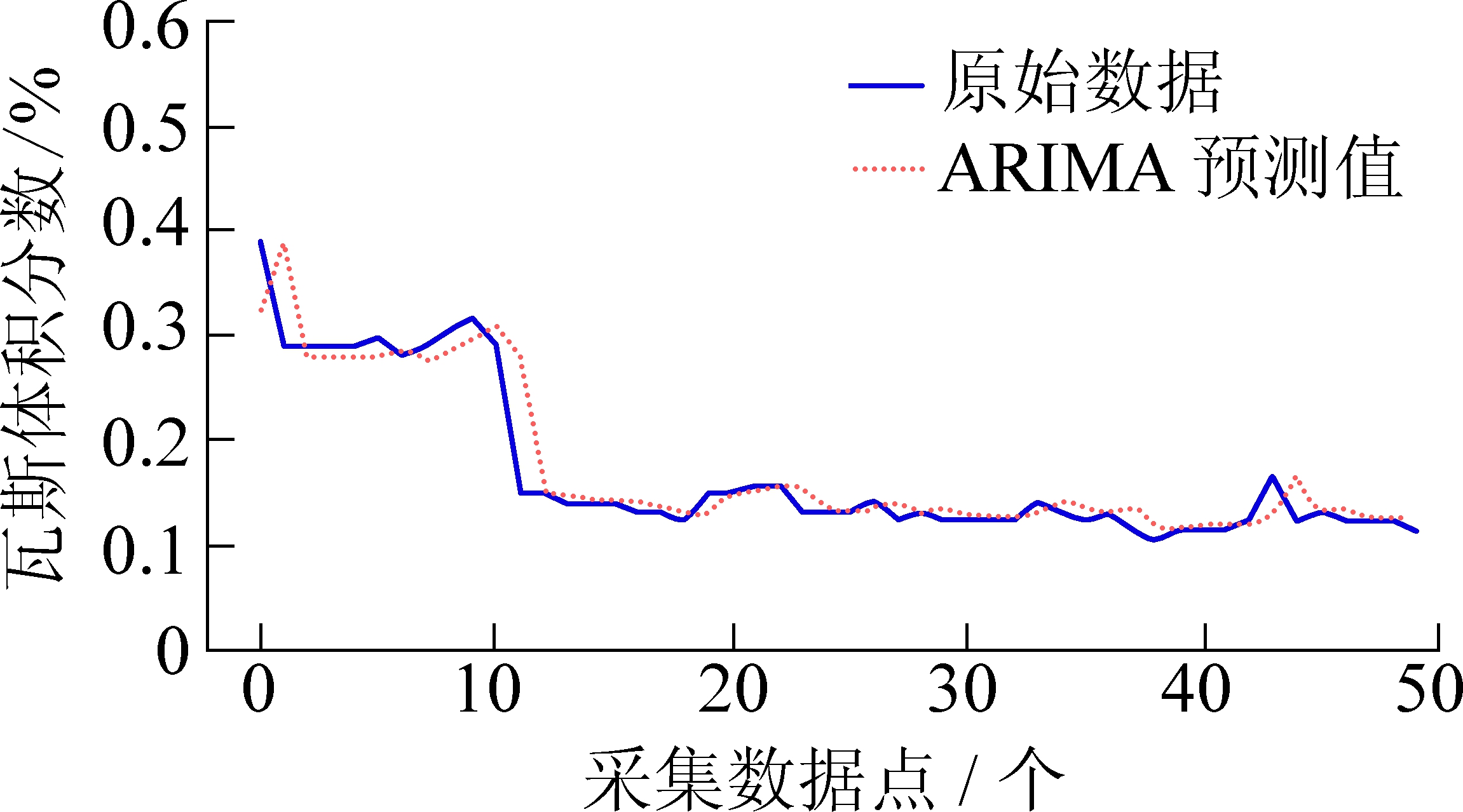
图6 ARIMA模型在线学习预测结果
Fig.6 Prediction results by ARIMA model with online learning
1)提出了一种矿井瓦斯浓度Lagrange-ARIMA实时预测模型，实现对瓦斯浓度时间序列在线实时预测。
2)构建的滑动Lagrange插值法消除了待插区间端点的龙格现象，平均相对误差为1.397%。利用L1范数确定的学习窗口尺度能实现实时数据与历史数据的动态增减，满足矿井瓦斯浓度预测的数据前处理要求。
3)相比ARIMA静态学习模型，Lagrange-ARIMA实时预测模型预测效果更好，学习窗口尺度显著降低。实例显示，当学习窗口尺度为85时，在线逐点预测50个点，预测瓦斯浓度序列MAE为0.015 86，适合矿井瓦斯浓度实时预测需求。
[1] 刘业娇,袁 亮,薛俊华,等.2007—2016年全国煤矿瓦斯灾害事故发生规律分析[J].矿业安全与环保,2018,45(3):124-128.
LIU Yejiao,YUAN Liang,XUE Junhua,et al.Analysis of the occurrence regularity of coal mine gas disasters in China from 2007 to 2016 [J].Mining Safety and Environmental Protection,2018,45(3):124-128.
[2] 袁 亮.我国煤炭工业安全科学技术创新与发展[J].煤矿安全,2015,46(S1):5-11.
YUAN Liang.Innovation and development of safety science and technology in coal industry of China[J].Safety in Coal Mines,2015,46(S1):5-11.
[3] 龚尚福,李岩松.基于数据融合的井下瓦斯浓度状态预测[J].西安科技大学学报,2018,38(3):506-514.
GONG Shangfu,LI Yansong.Prediction of underground gas concentration state based on data fusion [J].Journal of Xi'an University of Science and Technology,2018,38(3): 506-514.
[4] 张庆华,蒲 阳.高产高效矿井煤与瓦斯突出动态预测技术研究[J].煤炭科学技术,2018,46(10):65-72.
ZHANG Qinghua,PU Yang.Research on dynamic prediction technology of coal and gas outburst in high-yield and high-efficiency mines [J].Coal Science and Technology,2018,46(10): 65-72.
[5] 朱南南,张 浪,舒龙勇,等.煤与瓦斯突出的微震前兆特性试验研究与预警案例分析[J].岩石力学与工程学报,2018,37(6):1419-1429.
ZHU Nannan,ZHANG Lang,SHU Longyong,et al.Experimental study on microseismic precursor characteristics of coal and gas outbursts and case analysis of early warning [J].Journal of Rock Mechanics and Engineering,2018,37(6): 1419-1429.
[6] 魏建平,李恩福,姚邦华,等.煤岩动力灾害的氡监测技术初探[J].安全与环境学报,2015,15(6):58-62.
WEI Jianping,LI Enfu,YAO Banghua,et al.Preliminary study on radon monitoring technology for coal-rock dynamic disasters [J].Journal of Safety and Environment,2015,15 (6): 58-62.
[7] 陈玉涛,覃 俊,李建功.声发射技术在煤与瓦斯突出预测中的应用研究[J].矿业安全与环保,2017,44(6):11-16.
CHEN Yutao,QIN Jun,LI Jiangong.Application of AE technique in coal and gas outburst prediction [J].Mining Safety and Environmental Protection,2017,44(6):11-16.
[8] 李伟山,王 琳,卫 晨.LSTM在煤矿瓦斯预测预警系统中的应用与设计[J].西安科技大学学报,2018,38(6):1027-1035.
LI Weishan,WANG Lin,WEI Chen.Application and design of LSTM in coal mine gas prediction and early warning system[J].Journal of Xi’an University of Science and Technology,2018,38(6):1027-1035.
[9] 姚青华,邱本花.基于改进BP神经网络的矿井瓦斯浓度预测算法[J].煤炭技术,2017,36(5):182-184.
YAO Qinghua,QIU Benhua.Mine gas concentration prediction algorithm based on improved BP neural network [J].Coal Technology,2017,36 (5): 182-184.
[10] 李 欢,贾 佳,杨秀宇,等.煤矿综采工作面瓦斯浓度预测模型[J].工矿自动化,2018,44(12):48-53.
LI Huan,JIA Jia,YANG Xiuyu,et al.Gas concentration prediction model for fully mechanized coal mining face [J].Industry and Mine Automation,2018,44 (12):48-53.
[11] 董晓雷,贾进章,白 洋,等.基于SVM耦合遗传算法的回采工作面瓦斯涌出量预测[J].安全与环境学报,2016,16(2):114-118.
DONG Xiaolei,JIA Jinzhang,BAI Yang,et al.Prediction of gas emission in mining face based on SVM coupled genetic algorithm[J].Journal of Safety and Environment,2016,16(2):114-118.
[12] 周鑫隆,章 光,吕 辰,等.深部煤层瓦斯含量的差值GM-RBF预测模型及其应用[J].安全与环境学报,2017,17(6):2050-2055.
ZHOU Xinlong,ZHANG Guang,LYU Chen,et al.The GM-RBF prediction model for the difference of gas content in deep coal seams and its application[J].Journal of Safety and Environment,2017,17(6):2050-2055.
[13] 温廷新,于凤娥,邵良杉.基于灰色关联熵的煤与瓦斯突出概率神经网络预测模型[J].计算机应用研究,2018,35(11):3326-3329.
WEN Tingxin,YU Feng’e,SHAO Liangshan.Probabilistic neural network prediction model for coal and gas outburst based on grey relational entropy[J].Application Research of Computers,2018,35(11):3326-3329.
[14] 贾澎涛,邓 军.基于泛平均运算的矿井瓦斯浓度组合预测模型[J].中国安全科学学报,2012,22(6):41-46.
JIA Pengtao,DENG Jun.Combination prediction model of mine gas concentration based on pan-average operation [J].China Safety Science Journal,2012,22 (6): 41-46.
[15] 高荣翔,曹庆贵,马英琪,等.基于GM(1,N)_GRNN组合模型的瓦斯涌出量预测研究[J].中国矿业,2018,27(3):116-120.
GAO Rongxiang,CAO Qinggui,MA Yingqi,et al.Study on the prediction of gas emission based on GM(1,N)_GRNN combination model[J].China Mining Magazine,2018,27(3):116-120.
[16] 温廷新,孙 雪,孔祥博,等.基于PSOBP-AdaBoost模型的瓦斯涌出量分源预测研究[J].中国安全科学学报,2016,26(5):94-98.
WEN Tingxin,SUN Xue,KONG Xiangbo,et al.Study on gas emission prediction based on PSOBP-AdaBoost model [J].China Safety Science Journal,2016,26 (5): 94-98.
[17] 张雨浓,李名鸣,陈锦浩,等.龙格现象难题破解之系数与阶次双确定方法[J].计算机工程与应用,2013,49(3):44-49.
ZHANG Yunong,LI Mingming,CHEN Jinhao,et al.Solving the problem of Runge phenomenon by coefficients and order determination method[J].Computer Engineering and Applications,2013,49(3):44-49.
[18] XU Dongwei,WANG Yongdong,JIA Limin,et al.Realtimeroad traffic state prediction based on ARIMA and Kalman filter[J].Frontiers of Information Technology & Electronic Engineering, 2017, 18(2): 287-302.
移动扫码阅读