移动扫码阅读
地质与测量
移动扫码阅读
21世纪初，钱鸣高等[1]提出了绿色开采的概念和技术体系。近年来，随着煤炭科学技术的发展以及我国煤炭开发面临的新形势，一些学者[2-3]又提出了煤炭科学精准开采的概念体系，绿色和科学开采最核心的理念是减小煤炭开发对地表环境的扰动和损害[4-5]。因此，开采沉陷的预测和防治一直是绿色开采研究的重点[6-7]。由于煤层上覆岩层的复杂性及不确定性，建立精确的上覆岩层移动和变形的应力-应变本构模型难度较大[8-9]，因此现场观测一直是研究开采沉陷最重要手段[10-11]。地表下沉量是最容易观测的指标之一，对观测数据进行曲线拟合是最常用的数据分析处理方法。曲线拟合是指选择适当的数学函数逼近离散数据，进而确定观测数据与观测间隔(观测时间或频次)之间的关系，最常用的方法是最小二乘法回归分析。用拟合函数表达下沉量与时间的关系及变化趋势，在拟合精度较高的情况下，可用于预测未来时间内发生的下沉变形量，也可进行相似条件下的类比分析。这种函数中的时间变量并不是发生沉陷的原因，也并不能控制沉陷过程，函数中的常量参数只能决定函数本身的形态特征，因而拟合函数的选取尤为重要。
大量实测研究[10-11]发现，先加速后减速的变速下沉是长壁开采法工作面地表下沉过程最显著的特征，下沉量随观测时间的增加大致呈现前小后大的"S"型有限增长曲线。基于这种特征，一些数学函数被用于下沉量观测数据曲线拟合，刘玉成等[12-14]对一些常用于拟合岩土体变形曲线的数学函数进行了分析，认为负指数(Weibull)形式的时间函数可较好地拟合开采沉陷引起的地表下沉的时间序列曲线，并用FLAC3D软件进行了模拟开采验证。后来，王正帅等[15]又采用了命名为Richards的时间函数对煤层开采引起的地表下沉曲线进行了拟合研究，认为其能较好地拟合下沉量时间序列，也能描述地表下沉先加速后减速的过程。但笔者分析认为，Richards函数实质为负指数有限增长函数，除多增加1个参数使得数学形式更复杂外，其实质与Weibull函数无多大区别，从曲线拟合角度认为，多增加参数使得数学形式复杂反而使得参数的拟合结果因参数之间的相互影响而离散性增大，参数的增加使得各参数所体现的功能变得更加模糊。张兵等[16]在文献[17]分段Knothe时间函数模型基础上,对分段建模进行了技术上的改进。但笔者分析认为，拟合函数本身为唯象模型，事先确定最大下沉速度及对应的时间点本就困难，即便可根据全过程观测数据获得的最大下沉速度进行分段建模，但这样的模型无法通过前段的观测数据通过曲线拟合而预测未来的发展趋势，便失去应用价值。
尤明庆[18]通过例证研究认为，对于曲线拟合选择复杂的公式和过多的待定参数以追求过高的拟合精度，可能使拟合公式所表示的参数变化规律完全失真，对此必须要有清醒的认识。因此，笔者认为对1组长壁开采法工作面引起的地表下沉量观测数据进行曲线拟合，有2点必须认真考虑：①选择的拟合函数本身能表达曲线的特征；②函数形式简单、参数数量适中，便于求取参数和实际应用。基于这种考虑，在分析了文献[15-17]中的时间函数模型的基础上，提出了一种数学公式简单、参数适中的其图像为双曲线的拟合函数，经分析论证、实例验证认为该函数不但拟合精度高，而且能描述地表先加速后减速的变速下沉过程。可用多元非线性曲线拟合软件1stOpt1.5较容易的获取拟合参数。
一般情况下，长壁法布置工作面开采煤层的采空区上覆岩层的移动整体上呈现为“三带”分布，地表的移动和下沉主要受控于弯曲下沉带[10-11]。地表移动的整个过程，其实质为弯曲下沉带岩层的原岩应力与其下部岩层支撑反力之间相互作用的自组织自平衡过程。作为抽象描述，将弯曲带中的原岩应力用P0表示，下部岩层的反力用Pk表示，则从宏观角度，将地表移动的动态过程用牛顿第二定律表示为
P0-Pk=ma
式中：m为弯曲带岩层的总质量，a弯曲带下沉加速度。
作为抽象描述，在上式中，当P0>Pk则a>0整个弯曲带加速下沉；当P0<Pk则a<0整个弯曲带减速下沉。从牛顿力学运动学可知，变速运动体现为运动时间上的非线性，以时间为自变量的幂指函数是最常见的非线性函数。开采沉陷的Knothe[12]时间函数形式上是负指数函数，但公式中的时间变量为常变量，这就是Knothe模型与下沉速度不符的内在原因。
为对比分析，列出了Knothe及Weibull函数[12-13]。Knothe时间下沉量w(t)函数为
w(t)=wm(1-e-ct)
(1)
式中：wm为最大下沉量；t为时间变量；c为拟合参数。
速度和加速度分别为
v(t)=wmce-ct
(2)
a(t)=-wmc2e-ct
(3)
虽然，由(1)式可知，当t=0时，w(t)=0；当t→
时，w(t)→wm，该函数的曲线符合地表下沉过程的有限增长特征。但是，由式(2)和式(3)可知，Knothe函数求出的速度和加速度函数均为单调递减函数，在t=0时，速度和加速度最大，表示地表开始就从最大速度wmc和最大加速度-wmc2减速下沉，这显然不符合实际。
刘玉成等[12]将Knothe函数中时间变量由常变量t变为非线性变量tb，其公式为
w(t)=wm(1-e-ctb)
(4)
式中：b为拟合参数。
速度和加速度分别为
v(t)=wmbctb-1e-ctb
(5)
a(t)=wmbc[(b-1)t(b-2)-bct2(b-1)]e-ctb
(6)
由式(6)求出下沉速度最大的时间t0为
(7)
可以将t0值代入式(6)得：当t从0到
时，a(t)>0；当t从到时，a(t)<0。由微分法求函数极值原理可知，当t为时下沉速度达到峰值vm为
(8)
速度峰值时刻的下沉量为
(9)
可知，Weibull函数的曲线不仅符合地表下沉过程的有限增长特征，而且符合先加速后减速的变速下沉过程。
图像为双曲线的复合函数[19]在岩土工程领域常用于拟合及预测建筑物的沉降[20]，最简单的双曲线型函数为
(10)
速度和加速度分别为
(11)
(12)
虽然，由式(10)可知，当t=0时，w(t)=0；当t→时，w(t)→wm，该函数的曲线符合有限增长的特征。但是，由式(11)和式(12)可知，双曲线函数式(10)求出的速度和加速度函数均为单调递减函数，当t=0时，速度和加速度最大，表示地表开始就从最大速度1/c和最大加速度-2/(wmb2)减速下沉，这显然不符合实际。究其原因，在式(10)中时间变量t为常变量。
将式(10)中的时间常变量t改为幂指数形式的复合函数tb，则式(10)变为如下的形式为
(13)
求得速度为
(14)
求得加速度为
(15)
令a(t)=0时，解式(15)得3个方程解，即
(16)
将式(16)中的3个t值代入式(15)，得到：当t从
时，a(t)>0；当t从
时，a(t)<0。由微分法求函数极值原理可知，当
下沉速度达到最大，即速度达到峰值，此时的速度为
(17)
速度峰值时刻的下沉量为
w=wm(b-1)/2b
(18)
又可知式(13)表示的函数求出的速度具有确定的峰值，可描述开采沉陷地表下沉先加速后减速的变速运动过程，而且能求出速度峰值时间点和此时刻的最大下沉速度和下沉量。
由第1节的分析可知，式(13)表示的函数形式简单、参数数量适中，式中的常数共3个，其中wm为可作为最大下沉量，b和c可称作曲线形态的影响系数。为进一步分析参数对曲线形态特征的影响规律，试取1组数据作图分析，取wm=10 mm、b=3，可作出c=0.5、5.0、10.0对应的下沉量速度曲线如图1a、图2a所示；取wm=10 mm、c=5.0，可作出b=2、3、4相应下沉曲线和速度曲线如图1b、图2b所示；作出wm=10 mm、c=10时的最大下沉速度与参数b的关系曲线如图3a所示，作出wm=10 mm、b=3时的最大下沉速度与参数c的关系曲线如图3b所示。
仅从参数变化后的曲线特征分析，当t→时，w→wm，参数wm可作为最大下沉量；参数b、c影响下沉速度的大小、速度衰减的快慢、下沉趋于稳定的时间。在相同条件下，下沉速度的大小、速度衰减的快慢、下沉趋于稳定的时间与参数c为负相关性，而与参数b为正相关性。从参数b、c所表达的物理意义来看，两个参数都与开采条件有关，上覆岩层越软弱、结构面越多，完整性越差则b越大，反之上覆岩层越坚硬、结构面越少，完整性越好则c越大。由于开采过程及受采动影响的上覆岩层的复杂性，两个参数的具体影响因素还需进一步研究。
图1 不同参数对应的下沉曲线
Fig.1 Subsidence curves corresponding to different parameters
图2 不同参数对应的下沉速度曲线
Fig.2 Subsidence velocity curves corresponding to different parameters
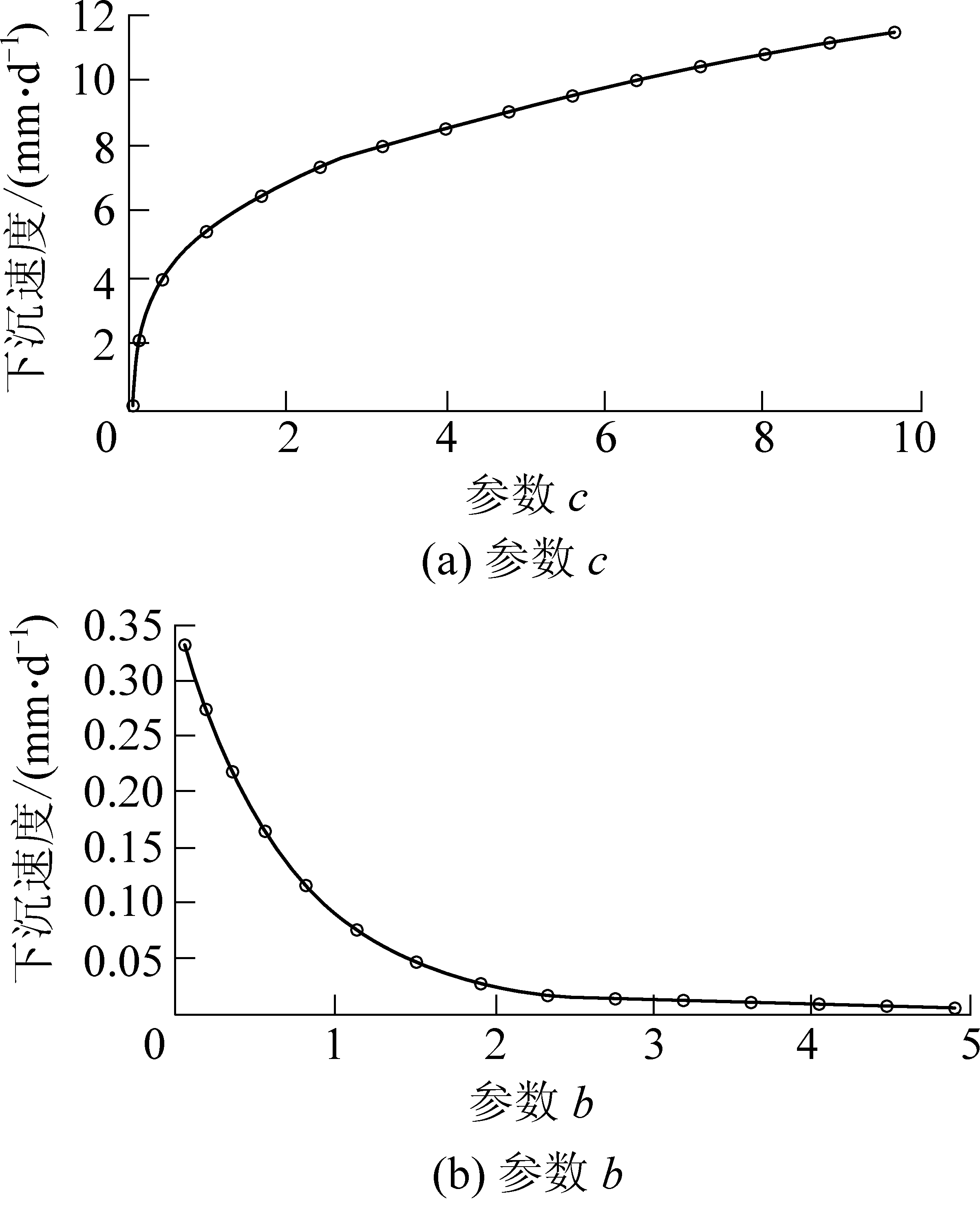
图3 最大下沉速度与参数的关系曲线
Fig.3 Relation of the maximum subsidence speed and parameters
上节用假想数据作出图形只是为了说明函数中的参数对曲线的特征的影响。为了对比分析，对一组真实的观测数据[12]分别用Knothe函数(式(1))、Weibull函数(式(4))、双曲线函数(式(10))和本文提出的双曲线函数(式(13))用多元非线性曲线拟合软件1stOpt 1.5编制运算程序进行了曲线拟合。各函数的拟合结果见表1，各函数对下沉量的计算值及实测值的对比见表2，Weihull函数和双曲线型函数预测结果如图4所示。
图4 预测的下沉曲线与下沉速度曲线
Fig.4 Prediction curves of subsidenceand subsidence velocity
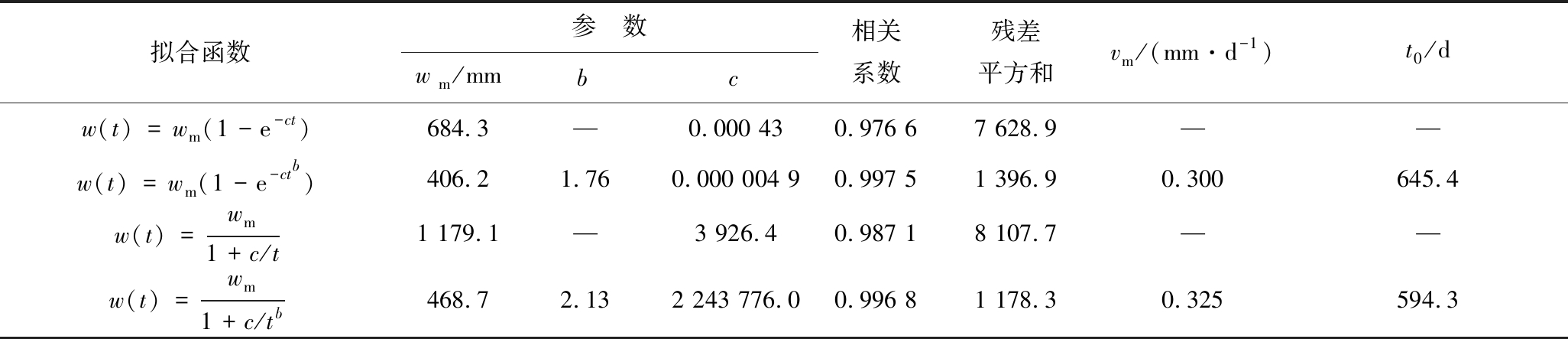
表1 各函数的拟合结果
Table 1 Fitting results of each function
拟合函数参 数wm/mmbc相关系数残差平方和vm/(mm·d-1)t0/dw(t)=wm(1-e-ct)684.3—0.000 430.976 67 628.9——w(t)=wm(1-e-ctb)406.21.760.000 004 90.997 51 396.90.300645.4w(t)=wm1+c/t1 179.1—3 926.40.987 18 107.7——w(t)=wm1+c/tb468.72.132 243 776.00.996 81 178.30.325594.3
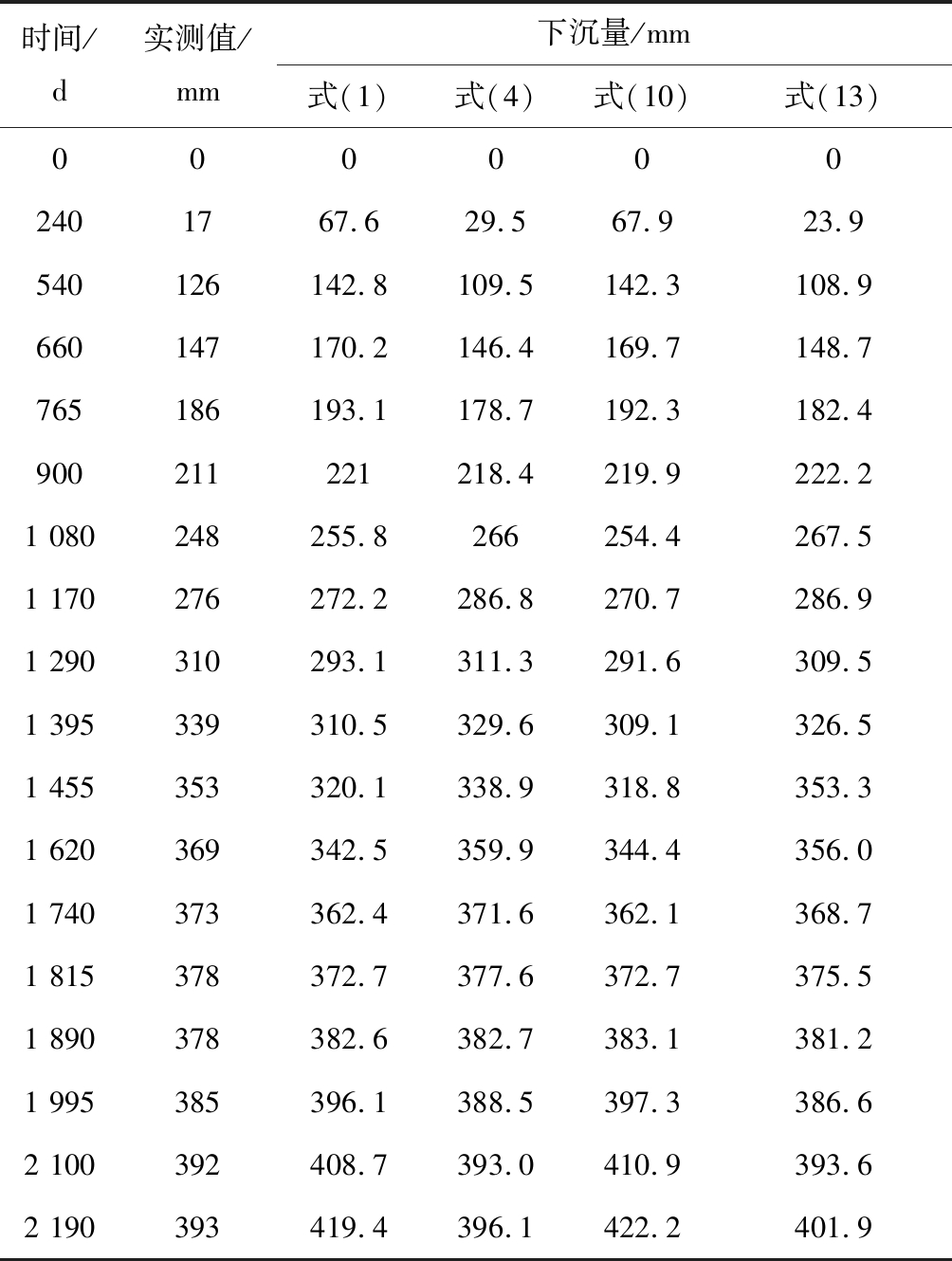
表2 各函数的计算下沉量与实测下沉量
Table 2 Calculated and measured subsidence of each function
时间/d实测值/mm下沉量/mm式(1)式(4)式(10)式(13)0000002401767.629.567.923.9540126142.8109.5142.3108.9660147170.2146.4169.7148.7765186193.1178.7192.3182.4900211221218.4219.9222.21 080248255.8266254.4267.51 170276272.2286.8270.7286.91 290310293.1311.3291.6309.51 395339310.5329.6309.1326.51 455353320.1338.9318.8353.31 620369342.5359.9344.4356.01 740373362.4371.6362.1368.71 815378372.7377.6372.7375.51 890378382.6382.7383.1381.21 995385396.1388.5397.3386.62 100392408.7393.0410.9393.62 190393419.4396.1422.2401.9
由表1、表2和图4可知，用4种函数拟合同1组观测数据，虽然均可取得较高的拟合精度，都能对观测点的最大下沉量wm作出预测，但函数式(4)和式(13)预测的最大下沉量接近于实测达到的最大下沉量(393 mm)，而函数式(1)和式(10)预测的最大下沉量分别高出3倍和2倍的实测达到的最大下沉量(393 mm)，出现这种结果的原因是函数式(1)和式(10)不能表达开采沉陷先加速后减速的变速下沉过程。由式(4)计算出的最大下沉速度为0.30 mm/d和对应的时间645.4 d；由式(13)计算出的最大下沉速度为0.325 mm/d和对应的时间594.3 d，从表2看出，这2个计算结果均可能接近实测值(假如在连续观测条件下)。由以上分析可知，函数式(4)和函数式(13)均可用作开采沉陷地表下沉观测量时间序列的拟合函数。
1)提出了一种适合长壁开采法工作面引起的地表下沉时间序列曲线的拟合函数。经分析论证，得出此函数从下沉曲线形态，下沉速度和下沉加速3个方面均符合下沉时间序列曲线的特征。
2)与其他3种时间函数相比较，得出笔者提出的拟合函数公式简单、参数数量适中，可用1stOpt1.5软件编制计算程序，容易求取拟合参数。
3)用笔者提出的时间函数拟合了一条实测的地表下沉时间序列曲线，得出拟合精度高，拟合的相关系数为0.996 8。此函数预测的最大下沉量为468.7 mm，计算出的最大下沉速度为0.325 mm/d，对应的时间594.3 d，均与实测值接近。
[1] 钱鸣高，许家林，缪协兴.煤矿绿色开采技术[J].中国矿业大学学报,2003,32(4):343-347.
QIAN Minggao,XU Jialin,MIAO Xiexing.Green technique in coal mining[J].Journal of China University of Mining & Technology,2003,32(4):343-347.
[2] 袁 亮.煤炭精准开采科学构想[J].煤炭学报,2017,42(1):1-7.
Yuan Liang.Scientific conception of precision coal mining[J].Journal of China Coal Society,2017,42(1):1-7
[3] 钱鸣高，许家林，王家臣.再论煤炭的科学开采[J].煤炭学报,2018,43(1):1-13.
QIAN Minggao,XU Jialin,WANG Jiachen.Further on the sustainable mining of coal[J].Journal of China Coal Society,2018,43(1):1-13
[4] 刘见中，申宝宏，姜鹏飞，等.提高我国煤炭科学产能的技术对策[J].煤炭科学技术,2013,41(1):21-55.
LIU Jianzhong,SHEN Baohong,JIANG Pengfei,et al.Technical countermeasures of improving china coal production capacity[J].Coal Science and Technology，2013,41(1):21-55.
[5] 李绪国.我国煤炭资源安全高效绿色开发现状与思路[J].煤炭科学技术,2013,41(8):53-57.
LI Xuguo.Status and idea on safety and high efficient and green development of china coal resources[J].Coal Science and Technology，2013,41(8):53-57
[6] 崔希民，邓喀中．煤矿开采沉陷预计理论与方法研究评述[J]．煤炭科学技术，2017,45(1):160-169.
CUI Ximin,DENG Kazhong．Research review of predicting theory and method for coal mining subsidence[J].Coal Science and Technology，2017,45(1):160-169.
[7] 左建平，孙运江，文金浩，等.岩层移动理论与力学模型及其展望[J].煤炭科学技术，2018，46(1) :1-11，87.
ZUO Jianping，SUN Yunjiang，WEN Jinhao，et al.Theoretical and mechanical models of rock strata movement and their prospects[J].Coal Science and Technology，2018，46(1) :1-11，87.
[8] 李德海,许国胜,余华中.厚松散层煤层开采地表动态移动变形特征研究[J].煤炭科学技术，2014,42(7):103-106.
LI Dehai,XU Guosheng,YU Huazhong.Study on features of surface dynamic movement and deformation caused by coal mining under thick alluvium[J].Coal Science and Technology，2014，42(7) :103-106.
[9] 侯得峰，李德海，许国胜，等．厚松散层下采高对地表动态沉降特征的影响[J]．煤炭科学技术，2016，44(12) :191-196.
HOU Defeng,LI Dehai,XU Guosheng,，et al.Impact of mining thickness on dynamic subsidence characteristics in condition of mining under thick unconsolidated layers[J].Coal Science and Technology，2016，44(12) :191-196
[10] 何国清,杨 伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[11] 沈光寒,李白英,吴 戈,等.矿井特殊开采的理论与实践[M].北京:煤炭工业出版社,1992.
[12] 刘玉成,曹树刚,刘延保.可描述地表沉陷动态过程的时间函数模型探讨[J].岩土力学,2010,31(3):925-930.
LIU Yucheng,CAO Shugang,LIU Yanbao.Discussion on some time functions for describing dynamic course of surface subsidence due to mining[J].Rock and Soil Mechanics,2010,31(3):925-930.
[13] 刘玉成.基于Weibull时间序列的动态沉陷曲线模型[J].岩土力学,2013,34 (8):2409-2413.
LIU Yucheng.Dynamic surface subsidence curve model based on Weibull time function[J].Rock and Soil Mechanics,2013,34(8):2409-2413.
[14] 刘玉成.煤层开采地表移动过程的FLAC3D 模拟研究[J].煤炭科学技术,2012,40 (5):93-95.
LIU Yucheng.Study on FLAC3D simulation of surface ground movement process for underground seam mining [J].Coal Science and Technology,2012,40 (5):93-95.
[15] 王正帅,邓喀中.采动区地表动态沉降预测的 Richards 模型[J].岩土力学,2011,32(6):1664-1668.
WANG Zhengshuai,DENG Kazhong.Richards Model of surface dynamic subsidence prediction in mining area[J].Rock and Soil Mechanics,2011,32(6):1664-1668.
[16] 张 兵,崔希民.开采沉陷动态预计的分段 Knothe时间函数模型优化[J].岩土力学,2017,38(2):541-548.
ZHANG Bing,CUI Ximin.Optimization of segmented Knothe Time Function model for dynamic prediction of mining subsidence[J].Rock and Soil Mechanics,2017,38(2):541-548.
[17] 常占强,王金庄.关于地表点下沉时间函数的研究：改进的克诺特时间函数[J].岩石力学与工程学报,2003,22(9):1496-1499.
CHANG Zhanqiang,WANG Jinzhuang.Study on time function of subsidence：the improved Knothe Time Function[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(9):1496-1499.
[18] 尤明庆.试验结果的数学拟合与力学模型[J].岩石力学与工程学报，2008，27(2)：251-256
YOU Mingqing.Discussion on mathematical fitness and mechanical model of experimental results [J].Chinese Journal of Rock Mechanics and Engineering,2008,27(2)：251-256
[19] 朱珉仁.Morgan-Mercer-Flodin 模型和 Weibull 模型的拟合[J].数学的实践与认识,2003,33(1):1-4.
Zhu Minren.Fitting on Morgan-Mercer-Flodin Model and Weibull Model[J].Mathematics in Practice and Theory,2003,33 (1):1-4
[20] 殷宗泽.土工原理[M].北京：中国水利水电出版社，2007.