
移动扫码阅读
青年博士学术论坛
煤矿井下采空区是由遗煤和垮落岩石构成的非均质多孔介质,采空区中的气体、液体分布于煤岩体的孔隙空间,在连通的孔隙之间相互流通。其中,采空区中下部覆岩垮落破碎与遗煤混合的区域为遗煤自燃、瓦斯积聚提供了有利条件,是发生煤矿灾害的重要部位。受采空区特殊地理位置条件限制,采场气体运移规律主要采用数值模拟方法,将采空区假设成某种孔隙结构下的多孔介质,根据工作面实际地质和开采条件,采用砌体梁理论和“O”型圈理论计算采空区孔隙率、内部阻力等参数,结合Darcy定律建立采空区流体分布计算模型,利用有限元网格化处理方法,计算采空区流场分布[1-2]。
孔隙率和渗透率是影响风流场模拟结果的重要参数,目前对于孔隙率的研究通常基于采动垮落分布特征[3],Szlazak J[4]得出了采空区孔隙率与风流渗入采空区距离之间呈线性关系;邓军[5]根据采空区矿压分布和顶板岩性,得出了采空区孔隙率沿走向的分布近似为负指数变化关系;周西华[6]采用图像处理方法对采空区冒落矸石堆积状态进行分析,得出了孔隙总面积与视场面积的比值即孔隙率;李宗翔等[7]基于“O”型圈模型得到孔隙率二维分布模型及三维采空区冒落非均质多孔介质数学模型;Wolf K H[8]根据孔隙率的差异将采空区近似分区,得到了不连续的孔隙率和渗透率分布规律;梁运涛等[9]引用顶板岩层沉降理论,发展了垮落带介质孔隙率和渗透率的非均匀连续分布模型;有学者将采空区的孔隙率按区域设定为不同常数,或者根据岩梁裂隙发育规律,将采空区孔隙率设置为分段函数[10];王伟等[11]利用sigmoid函数建立了采空区的渗透率模型;郑斌等[12]利用分形理论建立了渗透率的分布模型;高莎莎等[13]研究了煤中矿物质与CO2反应引起煤层渗透率随时间的变化特征;孟艳军等[14]对煤岩气水相对渗透率进行了分析。
工作面正常回采期间,受开采压力、时间等因素影响,采空区的孔隙率动态变化。由于采空区为非均质多孔介质,采空区孔隙率的变化影响流场的分布规律,在采空区风流场模拟过程中,使用传统二维模型的计算结果与实际偏差较大。笔者通过分析采空区孔隙率分布规律,构建采空区孔隙率和渗透率三维分布模型,以期为采空区风流场的研究提供基础参数依据。
姚桥煤矿位于大屯矿区东部,主采煤层为7、8号煤层,煤层赋存稳定、厚度较大、倾角平缓,开采条件较好,年产量为4.45 Mt。姚桥煤矿为瓦斯矿井,相对瓦斯涌出量为0.016 9 m3/t,煤尘爆炸指数为36.07%~46.13%,具有爆炸危险性,煤层自然发火期为1~3个月,为Ⅱ类自燃矿井。
该矿7271工作面位于西九采区,走向长度358 m,倾向长度260 m,煤层倾角平均6°,煤层平均厚度4.9 m,设计采高4.6 m,煤密度为1.38 g/cm3;采煤方法为走向长壁放顶煤一次采全高、顶板全部垮落,割煤高度为2.5 m,沿回风巷方向俯采段约109 m,沿轨道巷俯采段约139 m,回风巷最大俯采角度13°,轨道巷最大俯采角度8°。
随着工作面的推进,采场上覆岩层破断垮落,在垂直方向上形成垮落带、裂隙带和弯曲下沉带,水平方向形成了自然堆积区、载荷影响区、压实稳定区,如图1所示。
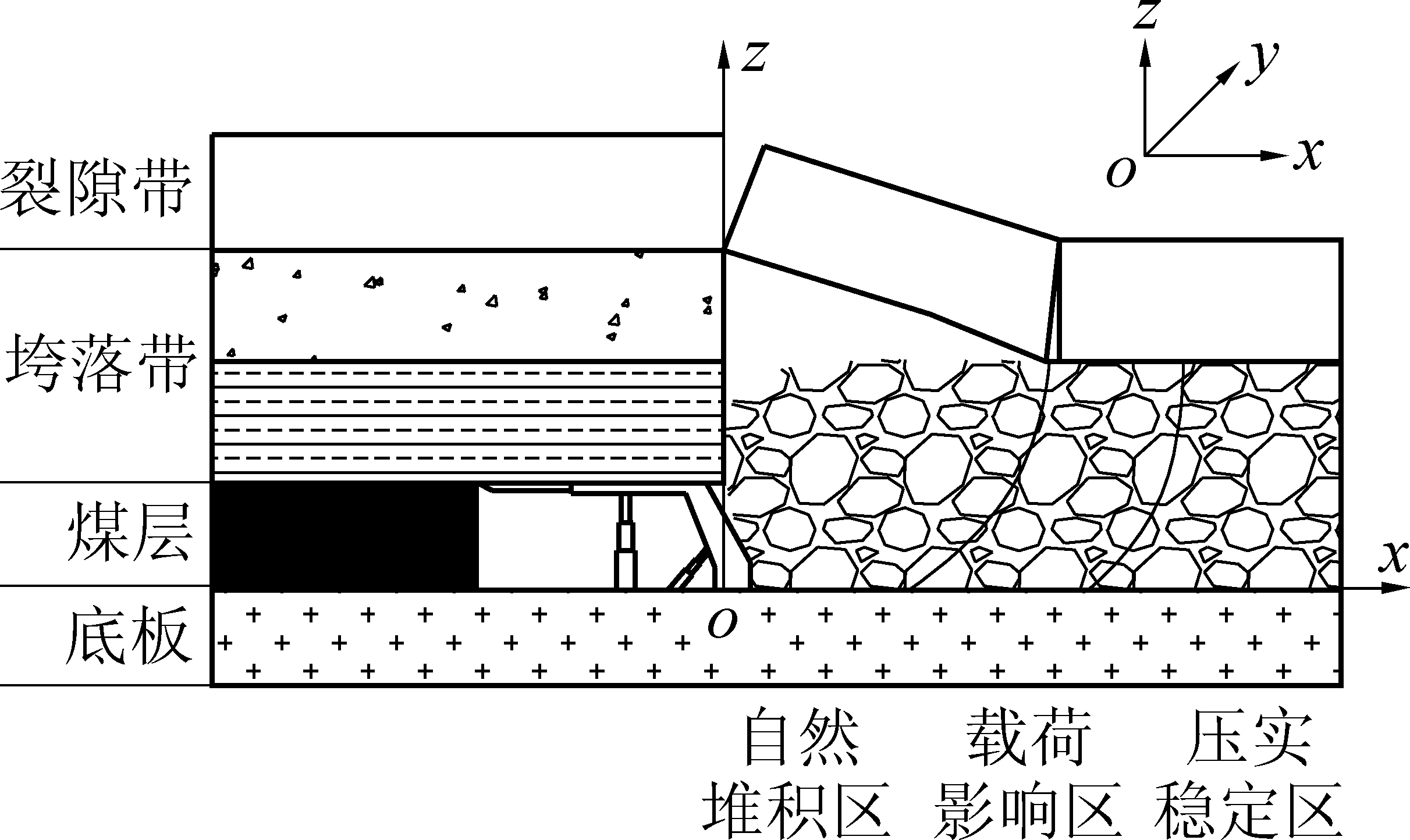
图1 采场分区分带示意
Fig.1 Schematic map of stope zoning regions
采空区内煤岩孔隙率越大,风流通过能力越强。沿采空区深度方向,采空区的孔隙率在靠近工作面侧较大,距工作面越远,采空区的孔隙率越小,在压实稳定区内采空区孔隙率基本稳定。沿工作面倾向,受悬臂梁结构的影响,采空区内靠近煤柱侧孔隙率较大,中部的孔隙率较小。
采空区的渗透率与采空区孔隙率分布密切相关,通过建立孔隙率的三维分布模型,根据Ergun方程推导得出采空区的渗透率三维分布函数。
数学模型的坐标如图1所示。x为工作面走向,坐标原点位于支架后部,沿采空区深度方向逐渐增大,设工作面回采长度为Lx,则x≤Lx;y为工作面倾向,工作面长度为Ly,由于U型通风采空区的对称特性,将坐标零点设置于工作面中部,沿着风流方向为正,且y≤Ly/2;z为工作面空间高度方向,坐标原点位于工作面底板,方向与高度方向一致。
采用砌体梁理论得出采空区上覆岩层随着工作面推进的岩层下沉量近似公式为
(1)
式中:W为上覆岩层下沉量,m;Wmax为关键层最大下沉量,m;l为关键层岩块断裂长度,m。
(2)
式中:σT为关键层的拉伸强度,MPa;h是关键层的厚度,m;q为岩块自身质量及其上部岩层质量,kg。
Wmax=m-∑h(Kp-1)
(3)
式中:m为煤层厚度,m;∑h为直接顶总厚度,m;Kp为岩块碎胀系数。
煤层开采后,在关键层到煤层底板的范围内,孔隙率为采高与关键层下沉量之和与该区域总高度之比,化简后可得
ε(x)=(m-W)/H
(4)
式中:ε(x)为距煤壁x处采空区的孔隙率;H为采空区岩块垮落后的高度,m。
在y方向上,孔隙率的分布函数ε(y)可看作是以y坐标对称的2条指数曲线,将x方向上的孔隙率分布扩展到xy平面上,构建与x方向相似的孔隙率分布函数,即
ε(x,y)=ε(x)eay+b
(5)
式中:a、b为待定系数。
边界条件为![]() =ε(x)|x=0,求解可得
=ε(x)|x=0,求解可得![]()
在高度方向上,以关键层为分界线,在关键层下部,受上覆岩层的重力影响,孔隙率沿z方向呈现逐渐增大的分布特征;在关键层上部,孔隙率沿z方向逐渐减小。采空区的数值模型主要集中在底部煤岩混合区域,关键层上部对于灾害的影响很小,因此,重点关注z≤H的区域。设该区域内孔隙率在z轴方向上服从线性规律,由实测经验公式得出xyz空间孔隙率分布函数为
ε(x,y,z)=ε(x,y)cz+d
(6)
式中:c、d为待定系数。
边界条件ε(x,y,z)|z=0=ε(x,y),ε(x,y,z)|z=H=1,求解可得![]()
整理可得
(7)
根据Ergun方程,采空区渗透率α与孔隙率关系,即
(8)
式中:Dm为采空区破碎煤岩平均粒径,m。
将式(1)—式(7)代入式(8)即可得到采空区渗透率的分布。
姚桥煤矿7271综放工作面的主要参数:m=4.6 m,Kp=1.29,∑h=6.28 m,计算得出Wmax=2.74 m,Dm=0.4 m,σT=1.3 MPa,q=2.36×109 kg,H =10.59 m,Ly=260 m,整理可得
(9)
代入式(8)后,做出z=0平面上的采空区渗透率分布如图2所示。
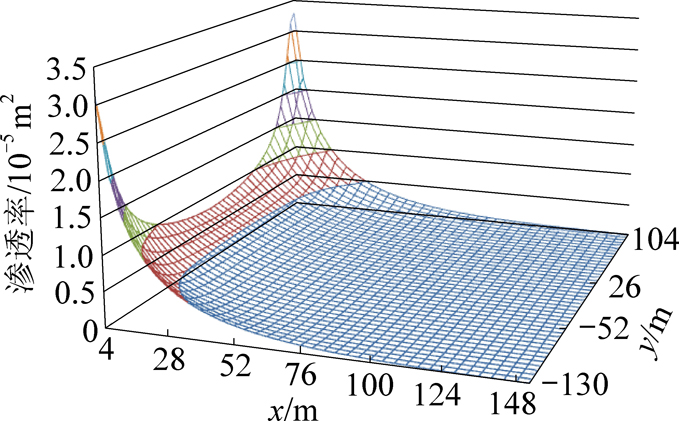
图2 采空区渗透率分布(z=0)
Fig.2 Permeability distribution in goaf (z=0)
以姚桥煤矿7271综放工作面注CO2防灭火技术为研究背景,采用FLUENT流场数值模拟的方法,在其他参数均相同的前提下,模拟不同渗透率影响采空区气体运移规律。
1)物理模型。物理模型分为3个区域:工作面与巷道、采空区、注CO2管道区域,具体物理参数如下:
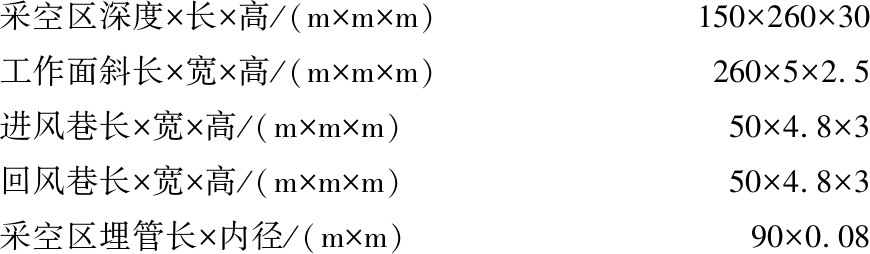
采空区深度×长×高/(m×m×m)150×260×30工作面斜长×宽×高/(m×m×m)260×5×2.5进风巷长×宽×高/(m×m×m)50×4.8×3回风巷长×宽×高/(m×m×m)50×4.8×3采空区埋管长×内径/(m×m)90×0.08
工作面3个区域全部设为流体类型(Fluid Type),设置为Porous Zone。为了减少采空区上部模型的网格数量,采用不规则网格划分方法,在采空区下部加密网格,在采空区上部使用尺寸较大的网格,使用Tet/Hybrid,TGrid类型网格对采场进行网格划分。
2)边界条件设置。进风巷进口设为VELOCITY INLET,7271综放工作面风量为1 300 m3/min,换算成风速为1.44 m/s,进风口气体的体积分数:O2为20%,N2为80%。
注CO2管道出口设置成VELOCITY INLET进口边界,注气量为540 m3/h,换算成风速为0.19 m/s,气体的体积分数:CO2为95%,N2为5%。
回风巷出口设置为OUTFLOW出口边界;采空区与工作面的交界面均设置为interior。
3)控制参数设置。求解器选择分离式求解器;湍流模型选用realizable k-ε两方程模型;设置收敛残差为10-6,通过迭代残差动态监视计算结果的收敛性。
利用UDF编写并加载渗透率三维分布模型,进行了数值模拟计算。为了清楚描述采空区的气体分布情况,选择距离底板为1 m的剖面作为研究对象,采用渗透率三维分布函数模拟得出采空区CO2及O2体积分数分布云图如图3a和3b所示。
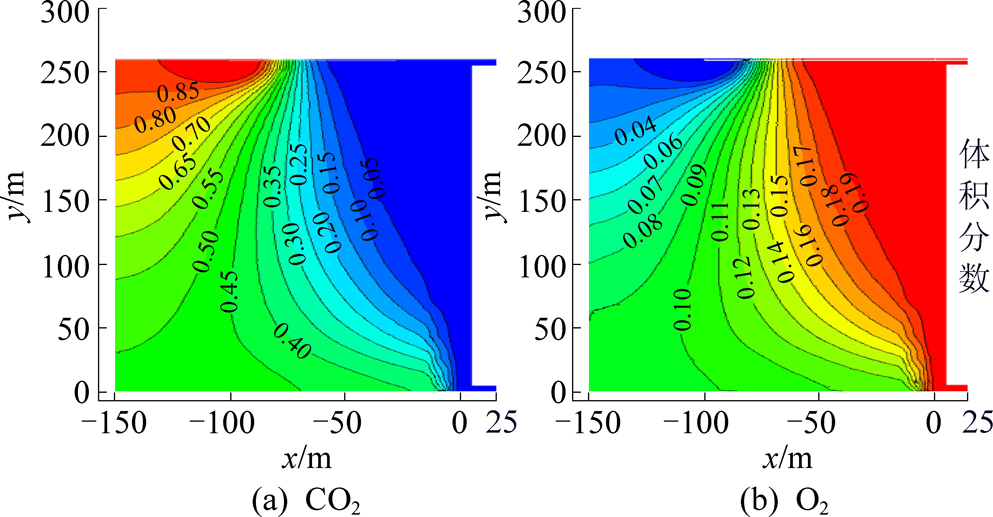
图3 渗透率三维分布模型中采空区z=1 m平面气体浓度分布云图
Fig.3 Cloud map of gas concentration distribution with 3D permeability model in goaf where z=1 m
为了研究不同渗透率分布对数值模拟结果的影响,分别模拟采空区渗透率α=10-5、10-6、10-7、10-8 m2时采空区的气体流场分布,得出采空区O2体积分数分布如图4所示。

图4 常数渗透率采空区z=1 m平面O2浓度分布云图
Fig.4 Cloud map of O2 concentration distribution with constant permeability in goaf where z=1 m
由图4可知,随着渗透率的增大,工作面漏入采空区的漏风量变大,散热带和氧化带宽度变大,大量O2随着漏风向低压能区运移,使得CO2不易在采空区中部聚集,因此,采空区中的O2体积分数较高,CO2体积分数较低;当渗透率减小时,CO2体积分数由回风巷侧逐渐向进风巷侧升高。对比图3和图4可知,图3b中靠近工作面侧的渗透率逐渐增大,因此,在采空区中部不会出现如图4所示的弧形运移分布规律。
2017年10月17日7271综放工作面推进至距离开切眼约90 m处,压注二氧化碳流量为540 m3/h,压注时间为24 h,为了检验惰化效果,在回风巷侧采空区深度60 m处(A点)监测O2体积分数,在上隅角(B点)处监测CO2体积分数,压注二氧化碳的管线布置及气体监测位置如图5所示。

图5 压注管线布置及气体监测位置示意
Fig.5 Layout of the pipelines and monitoring locations
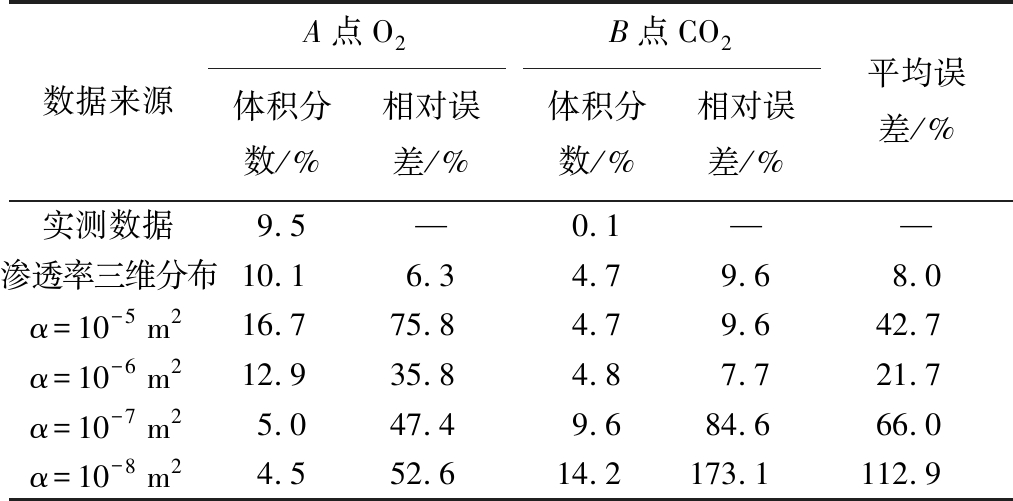
提取模拟结果与实测结果进行对比分析见表1。由表1可知,采用各向同性常数渗透率时,随着渗透率的减小,A点处O2体积分数减小,B点处CO2体积分数增大;数值模拟采用渗透率三维函数得出A、B点气体体积分数与实测数据的平均误差为8.0%,远小于使用常数渗透率模拟出的结果。因此,采用渗透率三维分布函数得出的结果更符合实际。
表1 不同渗透率下采空区气体体积分数对比
Table 1 Comparison of gas concentration with differentpermeability distribution in goaf
数据来源A点O2体积分数/%相对误差/%B点CO2体积分数/%相对误差/%平均误差/%实测数据9.5—0.1——渗透率三维分布10.16.34.79.68.0α=10-5 m216.775.84.79.642.7α=10-6 m212.935.84.87.721.7α=10-7 m25.047.49.684.666.0α=10-8 m24.552.614.2173.1112.9
1)分析了采空区非均质多孔介质孔隙分布特征规律,沿采空区深度方向,采空区的孔隙率在靠近工作面侧较大,深部的孔隙率较小,且变化幅度较小;沿工作面倾向,采空区内靠近煤柱侧孔隙率变化较大,中部的孔隙率基本稳定。
2)建立了采空区孔隙率三维分布数学模型,根据Ergun方程,推导出采空区渗透率三维分布模型,绘制了姚桥矿7271综放工作面底板(z=0 m)上的渗透率分布函数。
3)研究了不同渗透率影响采空区CO2流场分布的规律,随着渗透率的增大,工作面漏入采空区的漏风量变大,CO2不易在采空区中聚集;当渗透率减小时,CO2体积分数由回风巷侧逐渐向进风巷侧升高。
4)对比分析了姚桥煤矿7271综放工作面采空区注CO2时使用渗透率分布函数及固定常数时CO2的运移规律,数值模拟采用渗透率三维函数得出的结果与实测数据的平均误差为8.0%,优于固定常数渗透率。
[1] 余明高,鲁来祥,常绪华,等.煤巷高冒区遗煤自燃数值模拟分析[J].防灾减灾工程学报,2009,29(6):658-662.
YU Minggao,LU Laixiang,CHANG Xuhua,et al.Numerical simulation analysis on spontaneous combustion of residual coal in top-coal falling region of coal drift[J].Journal of Disaster Prevention and Mitigation Engineering,2009,29(6):658-662.
[2] YUAN L M,SMITH A C.Numerical study on effects of coal properties on spontaneous heating in longwall gob areas[J].Fuel,2008,87(15):3409-3419.
[3] 余明高,晁江坤,褚廷湘,等.承压破碎煤体渗透特性参数演化实验研究[J].煤炭学报,2017,42(4):916-922.
YU Minggao,CHAO Jiangkun,CHU Tingxiang,et al.Experimental study on permeability parameter evolution of pressure-bear broken coal[J].Journal of China Coal Society,2017,42(4):916-922.
[4] SZLAZAL J.The determination of a coefficient of long wall gob permeability[J].Archives of Mining Sciences,2001,46(4):451-468.
[5] 邓 军,徐精彩,文 虎.采空区自然发火动态数学模型研究[J].湘潭矿业学院学报,1998,13(1):11-16.
DENG Jun,XU Jingcai,WEN Hu.Study of dynamic mathematical model of coalspontaneous combustion in mined-out areas[J].Journal of Xiangtan Mining Institute,1998,13(1):11-16.
[6] 周西华,王继仁,卢国斌,等.回采工作面温度场分布规律的数值模拟[J].煤炭学报,2002,27(1):59-63.
ZHOU Xihua,WANG Jiren,LU Guobin,et al.The numerical simulation of distribution law of temperature field in coal face[J].Journal of China Coal Society,2002,27(1):59-63.
[7] 高光超,李宗翔,张 春,等.基于三维“O”型圈的采空区多场分布特征数值模拟[J].安全与环境学报,2017,17(3):931-936.
GAO Guangchao,LI Zongxiang,ZHANG Chun,et al.Numerical simulation for multi-fielddistribution characteristic features ofthegoaf based on 3D “O”type circle[J].Journal of Safety and Environment,2017,17(3):931-936.
[8] WOLF H K,BRUINING H.Modelling the interaction between underground coal fires and their roof rocks[J].Fuel,2007,86:2761-2777.
[9] 梁运涛,张腾飞,王树刚,等.采空区孔隙率非均质模型及其流场分布模拟[J].煤炭学报,2009,34(9):1203-1207.
LIANG Yuntao,ZHANG Tengfei,WANG Shugang,et al.Heterogeneousmodel of porosity in gobs and its airflow field distribution[J].Journal of China Coal Society,2009,34(9):1203-1207.
[10] 高建良,王海生.采空区渗透率分布对流场的影响[J].中国安全科学学报,2010,20(3):81-85.
GAO Jianliang,WANG Haisheng.Influence of permeability distribution on airflow field of leakage in gob[J].China Safety Science Journal,2010,20(3):81-85.
[11] 王 伟,程远平,刘洪永,等.基于sigmoid函数的采空区渗透率模型及瓦斯流场模拟应用[J].采矿与安全工程学报,2017,34(6):1232-1239.
WANG Wei,CHENG Yuanping,LIU Hongyong,et al.Permeability model of gob based on sigmoid functionand application in the airflow field simulation[J].Journal of Mining & Safety Engineering,2017,34(6):1232-1239.
[12] 郑 斌,李菊花.基于Kozeny-Carman方程的渗透率分形模型[J].天然气地球科学,2015,26(1):193-198.
ZHENG Bin,LI Juhua.A new fractal permeability model for porous media based on kozeny-carman equation[J].Natural Gas Geoscience,2015,26(1):193-198.
[13] 高莎莎,王延斌,倪小明,等.CO2注入煤层中煤储层渗透率变化规律研究[J].煤炭科学技术,2014,42(2):54-57,62.
GAO Shasha,WANG Yanbin,NI Xiaoming,et al.Study on laws of coal seam permeability change in CO2-ECBM[J].Coal Science and Technology,2014,42(2):54-57,62.
[14] 孟艳军,汤达祯,许 浩,等.煤岩气水相对渗透率研究进展与展望[J].煤炭科学技术,2014,42(8):51-55.
MENG Yanjun,TANG Dazhen,XU Hao,et al.Progress and prospect of gas-water relative permeability of coal and rock[J].Coal Science and Technology,2014,42(8):51-55.