0 引 言
目前,我国煤与瓦斯突出防治依然存在着防御战线过长、防突措施盲目、针对性较差的问题,其主要原因是不能准确地划分突出危险带。大量实际观测资料和研究成果表明,煤与瓦斯突出的分布具有分区分带性的特点,地质构造尤其是断层构造是控制煤与瓦斯突出分区分带的主导性地质因素[1-2],因此地质构造是突出区域预测研究的重点内容,对断层构造网络复杂程度及其与瓦斯突出关系的认识,仍然停留在定性分析和经验描述的阶段,缺乏系统的规律性分析和定量化描述[3]。因此,定量描述突出带的地质构造特征,确定区域构造特征与突出的关系,准确预测突出危险带,是一项亟待解决的技术难题,对实现突出矿井的分类指导和分级管理具有重要意义。
由Mandelbrot创立并发展的分形几何学理论,为定量描述不规则事物及其变化规律提供了有力的工具,断层作为自然界中的一种非常普遍的地质现象,其分布和几何形态具有明显的分形特征[4-5],日本学者HIRATA[6]证明:无论是微破裂、节理系、断层系,不同尺度的断层,其几何图像都具有特定的分形维数。因此分形理论在油气田、金属矿床、煤岩孔隙结构等方面得到了广泛的应用,并取得了许多有意义的成果[7-11]。
一些学者探讨了煤田断层分形特征与突出之间的关系[4-5],即通过计算井田不同单元的分维值将断层复杂程度定量化,进而将分维值大小与突出危险性进行对比分析,所用理论均为单分形理论,指标多为容量维。研究表明,断层体系不属于均匀的线性分形,而是复杂分形[12],近年来一些学者认为,断层构造等许多地质现象具有多重分形结构特征[13-14],多重分形分析比单分形分析更能真实地反映断层构造的复杂性和本质特征,多重分形理论已经大量应用于大尺度地球科学研究中,如矿床及油气田分布[15-16]、地震[17-18]等,在小尺度及微观尺度的破裂系研究中也经常用到多重分形理论,如岩石节理(破裂)[19-20]等,在煤矿区断层构造研究中还未见有多重分形应用的相关文献,更无文献涉及到断层多重分形特征与突出危险性关系方面的研究。因此,有必要将多重分形理论应用于煤矿区断层研究中,并进行单分形和多重分形特征的对比分析,探讨并揭示断层分形和多重分形的瓦斯地质意义,为煤与瓦斯突出区域预测提供更加丰富的研究手段。
1 焦作矿区概况
焦作矿区地处太行山背斜南端东翼,构造面貌以断裂为主(图1),兼有缓波状褶皱起伏。矿区主要断裂构造按其展布方向大略分为3组,即北北东—北东向、近东西向及少量北西向。

图1 焦作矿区构造纲要
Fig.1 Structural outline of Jiaozuo Mining Area
焦作矿区共发生煤与瓦斯突出338次(截至2017年),从已发生突出点的分布看,具有明显的不均衡性,受区域构造、矿区构造演化的控制,焦作矿区存在2条大的控制性断层,分别是近东西向的凤凰岭断层和北西向展布的峪河口断层,凤凰岭断层以南有朱村、焦南等矿,历史上曾发生过突出事故,但突出次数不多;凤凰岭断层以北、峪河口断层以西区域,分布有演马庄、古汉山等9对矿井,全部为突出矿井,历史上曾多次发生突出事故,其中九里山矿和演马庄矿均发生过1 000 t以上煤量的特大型突出事故;峪河口断层以东主要为低瓦斯矿井,如赵固一矿、赵固二矿等。
2 断层构造单分形特征
根据焦作矿区断层分布状态,对断层的单分形特征进行研究,以得到断层分布的基本规律。测量断层分维的一种简便而又客观的方法是盒维数法。根据盒维数的定义,对于给定的研究区域,用不同尺度的网格进行覆盖并统计包含有断层的网格数目[21]。笔者选用1∶25 000焦作矿区断裂构造图为底图,计算矿区的断层分形维数。将矿区分为35个单元格,每个单元格边长为6.4 km,网格尺度ε分别取6.4、3.2、1.6、0.8 km,可得到一系列ε-N(ε)对应值,最后由下式求出分维值:
(1)
实际计算时,在双对数坐标下以N(ε)为纵坐标,以ε为横坐标,拟合直线斜率的相反数即容量维D。从计算过程可知,拟合曲线的线性相关系数均大于0.95,说明各单元格断层分布均具有自相似的特征,服从分形分布规律。利用Surfer绘图软件绘制分维等值线图,数据采用Kriging法进行内插加密,可得到断层分形维数等值线图(图2),其中色谱柱代表分形维数值。

图2 焦作矿区断层分形维数等值线
Fig.2 Fractal dimension contour of faults in Jiaozuo Mining Area
从图2可以看出,焦作矿区断层分维值呈现分区特征,其中3个1.6分维值等值线圈闭的3个区域尤为明显,它们分别对应着3个分维高值区,与断层的实际展布形态相吻合,说明分维值较好地反映了断层构造的复杂程度,是构造复杂程度的较好度量指标。用Ⅰ、Ⅱ两条线将3个区分开,从下至上分别命名为A、B、C区,可见3个区内断层分形维数最大值基本一致。
3 断层构造多重分形特征
表征多重分形的主要方法是使用多重分形谱f(α)或广义维数Dq,本文采用了第1种方法。多重分形谱f(α)在对多重分形进行精确的数学刻画的同时,通过f(α)- α曲线为多重分形提供了自然而形象的直观描述,是描述多重分形的一套参量。
按照多重分形的算法理论,基于Matlab平台,编制质量指数τ(q)、奇异指数α(q)以及多重分形谱f(α)的计算程序。网格尺度ε分别取15、12、9.6、6.4 km,q取值-5~5,为使拟合曲线光滑,步长取0.2,以B区断层多重分形计算为例,对于给定的q值,当ε趋于0时,求出其对应的![]() 极限值,并用最小二乘法作一元线性拟合,拟合出直线斜率作为τ(q)、α值,根据f(α)的表达式作f(α)-α曲线。其中ε≥0,i≥0(取整数),q为任意实数。多重分形计算流程如图3所示。
极限值,并用最小二乘法作一元线性拟合,拟合出直线斜率作为τ(q)、α值,根据f(α)的表达式作f(α)-α曲线。其中ε≥0,i≥0(取整数),q为任意实数。多重分形计算流程如图3所示。
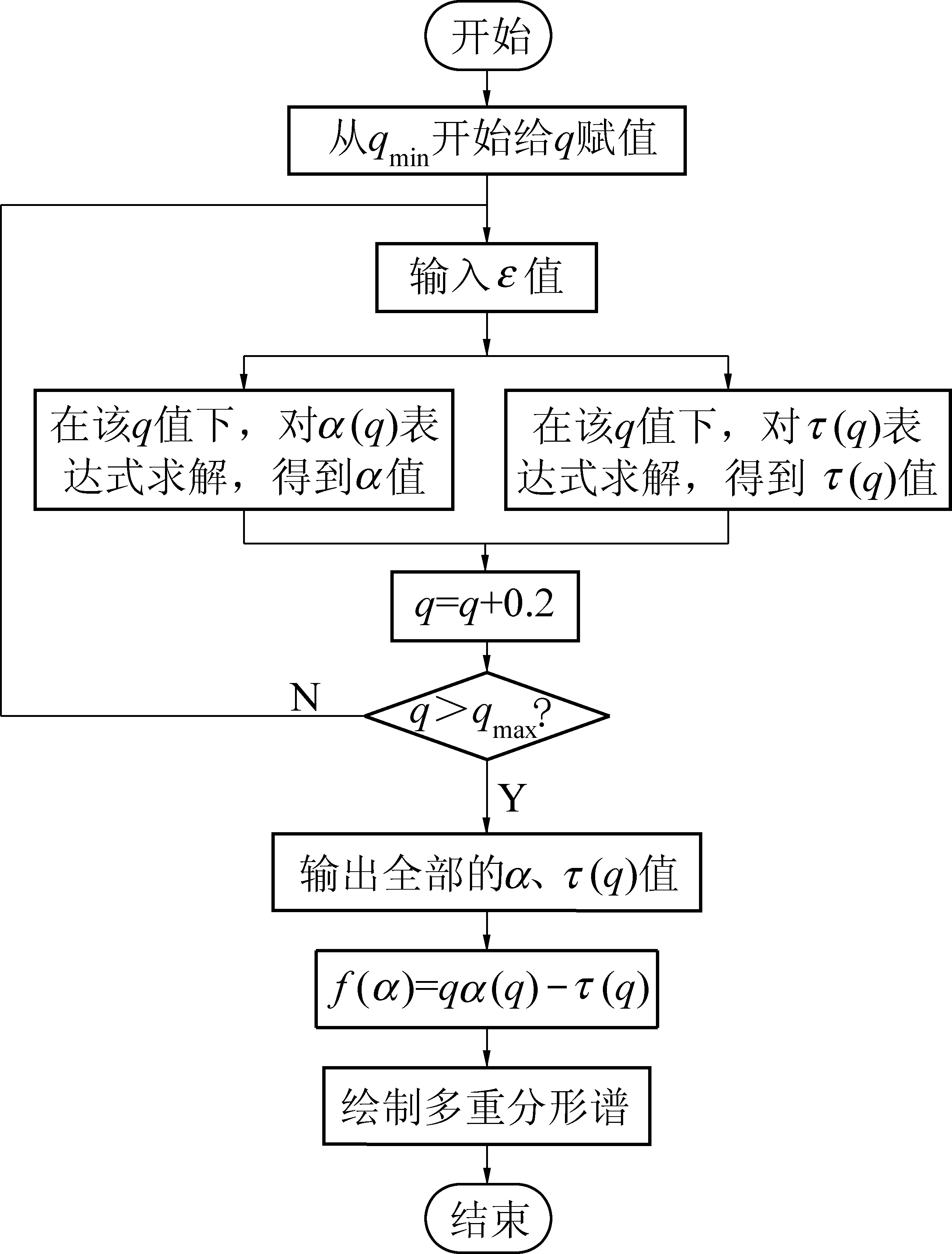
图3 多重分形谱计算流程
Fig.3 Flow chart of multifractal spectrum calculation
根据多重分形谱的计算流程,计算其多重分形谱。定义一个配分函数χq(ε)为概率测度pi(ε)的q阶距,ln χq(ε)与ln ε之间显现了较好的线性关系,因此ln χq(ε)与ln ε满足幂律关系,即说明在规定的尺度变化范围内断层分布具有无标度性,也就是断层具有分形的特征;τ(q)是一个上凸的函数,即τ(q)与q之间存在着非线性关系,这表明了研究区域的断层分布的确具有多重分形的特征。根据以上理论模型可得出焦作矿区3个区域断层的多重分形谱(图4)。
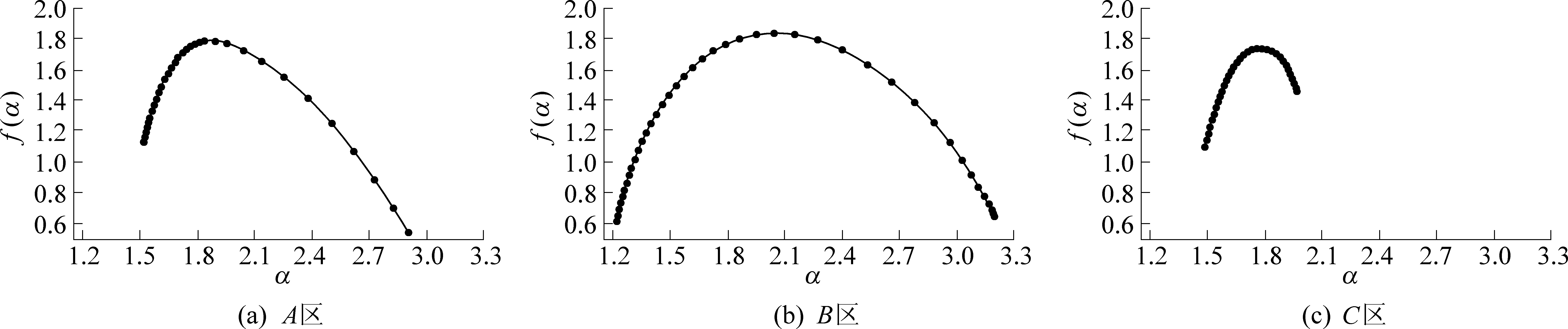
图4 A、B、C区断层多重分形谱
Fig.4 Multifractal spectrum of faults in area A,B and C
4 单分形与多重分形特征对比分析
在图2中,Ⅰ、Ⅱ线对应着凤凰岭断层和峪河口断层,由此划分为3个研究区域,根据单分形方法计算可得,3个区域均具有较高的分维值,说明断层构造情况比较复杂,文献[5]指出,构造分维值是煤田内地质构造复杂程度的一项综合性反映指标,分维值较大,反映煤田内地质构造展布方向不规则,次级构造发育,煤层被切割和扭曲严重。根据研究,这些地区往往地应力较大,应力集中点较多,煤体结构破坏严重,构造煤发育,煤中蕴含大量瓦斯,瓦斯应力较高,根据突出的综合假说[22],这些块段往往是煤与瓦斯突出危险性较大的块段。断层分维和褶曲分维与突出危险性之间存在着密切的关系,可以应用断层分维和褶曲分维进行煤与瓦斯突出区域的划分。文献[4]指出,突出与非突出井田的断层分布均服从分形规律,断层构造越复杂,构造分维数就越大,井田中断层分布的分维值与瓦斯突出之间存在着正相关关系,突出井田的断层构造分维值大于非突出井田,突出越严重,分维数越大,断层系统的分维值可以作为瓦斯突出带预测的一项指标。
从突出实际发生的规律来看,焦作矿区突出点的分布具有明显的不均衡性,存在较明显的区域性分布特征。受区域构造、矿区构造演化的控制,凤凰岭断层以南历史上曾发生过突出事故,但突出次数不多,凤凰岭断层以北、峪河口断层以西区域全部为突出矿井,历史上曾多次发生突出事故;峪河口断层以东主要为低瓦斯矿井。虽然3个区域突出严重情况有很大差别,但是从单分形的研究结果来看却未能体现这一区别,因此用单分形分析方法无法解释这种差异现象。
多重分形方法可以更加深入揭示出更多断层分布的信息,进而与突出的分布规律进行关联研究。多重分形谱更能真实反映断裂体系空间分布的复杂程度和结构特征,通过对比发现,各区多重分形谱形状有很大差异,对这种差异性可以提取特征参数进行分析:
1)对称性:是描述多重分形谱特征的一个参量,一般情况下[23],多重分形谱是钩状曲线,当多重分形谱呈左钩状时,大概率子集的数目大于小概率子集的数目,说明小断层较发育,多重分形谱呈右钩状时,大概率子集的数目小于小概率子集的数目,说明大断层较发育且数量较少。对称性可以用Δf=f(αmin)- f(αmax)表示,当|Δf|→0时,曲线对称性最好。
2)多重分形谱宽:谱宽的大小定量表征了分形体内部的差异性、非均匀性和各子集分布的两极化特征,反映了在整个分形结构上概率分布不均匀的程度[24],表示了研究区域内部断层分布密度、长度和空间分布非均匀性等性质的差异程度和变化范围。Δα=αmax-αmin,Δα越大,断层概率分布越不均匀,数据的波动越剧烈,反之断层分布越集中、均匀。
多重分形谱参数Δf和Δα均与构造演化过程相关,不同区域的多重分形谱有很大差异,存在着必然的瓦斯地质原因,下面分区论述:
1)A区Δα小于B区,断层概率分布均匀性略好,多重分形谱呈左钩状,说明中小规模断层较密集,瓦斯含量普遍在30 m3/t以上,发生过突出事故,但是由于构造煤不发育,厚度最大的地方仅占煤厚的1/10,因此突出次数不多。
2)B区Δα最大,说明断层概率分布最不均匀,多重分形谱对称性较好,且αmax值较大,其地质意义是大断层伴生的次级小断层发育,构造演化过程比较复杂,造成断层概率分布极不均匀,这种构造演化背景导致该区瓦斯压力和瓦斯含量较高,其中九里山矿最大瓦斯含量达33 m3/t,古汉山矿最大瓦斯压力达2.42 MPa,故该区发生瓦斯突出的次数较多、规模较大。
3)C区多重分形谱呈右钩状,且Δα最小,说明大断层伴生次级小断层较少,复杂程度不高,断层均匀程度较好。C区下边界峪河口断层是正断层,瓦斯逸散作用显著,瓦斯含量基本在8 m3/t以下,远小于峪河口断层以南区域,C区内未发生过突出现象。
根据以上分析可以看出,Δα越大,断层概率分布越不均匀,数据的波动越剧烈;反之断层分布越集中、均匀。从图4可计算得,Δα从大到小依次为B区、A区、C区,与各区域突出次数进行比较发现,2条曲线变化规律具有一致性(图5)。
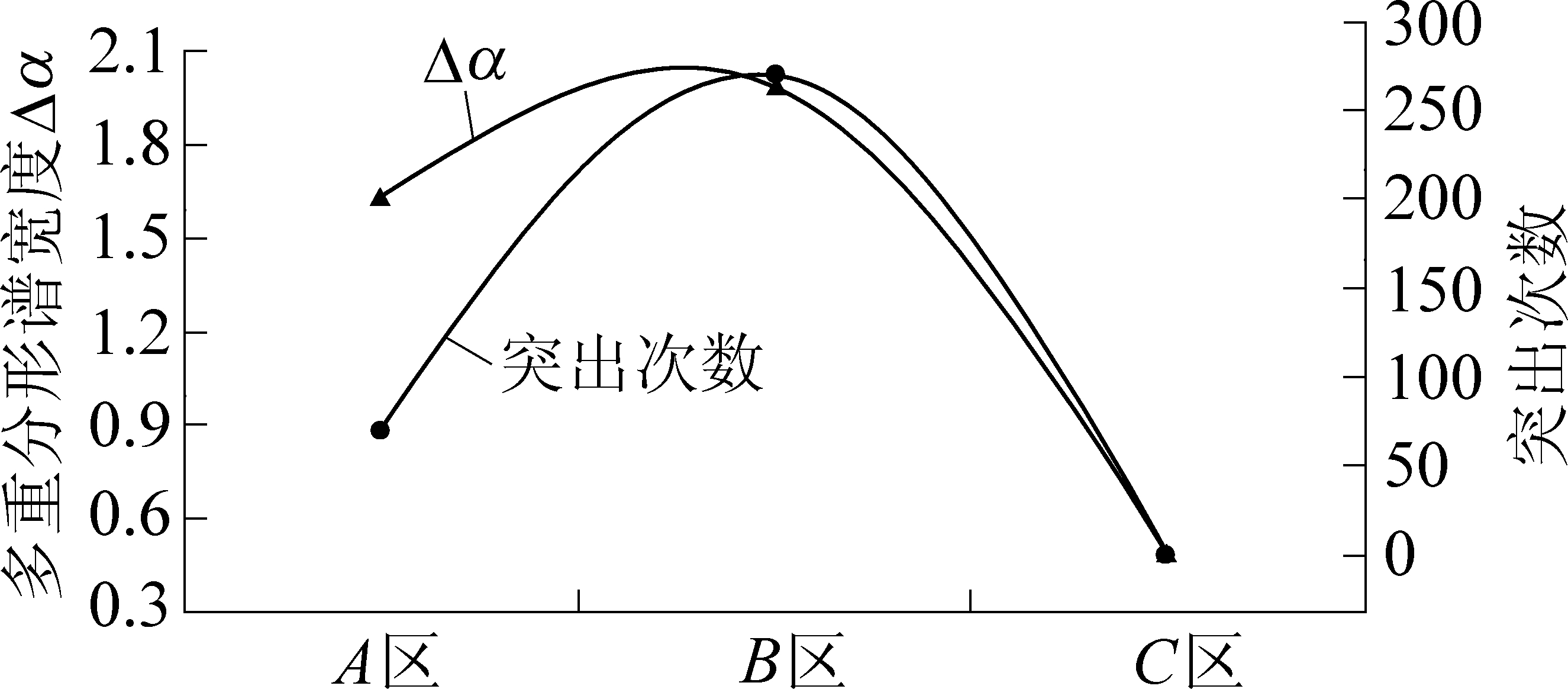
图5 A、B、C三区域谱宽与突出次数对比
Fig.5 Comparison of spectral width and outburst in Area A,B and C
断层多重分形特点与构造演化过程关系密切,经过对比分析不同区域断层多重分形特征,结合瓦斯地质分析,可以对矿区突出危险性进行区域性划分,突出危险严重程度从大到小依次为B区、A区、C区,这种划分也与实际突出情况相吻合。
5 结 论
1)断层的单分形特征代表了区域断层分布的复杂程度,焦作矿区3个区域的单分形维数呈现较大数值,说明焦作矿区断层构造较复杂,由断层控制的这些区域往往构造煤发育,地应力和瓦斯压力较高,各区域均发生过煤与瓦斯突出事故。
2)对焦作矿区断层进行了多重分形分析,提取多重分形谱对称性Δf、多重分形谱宽度Δα等特征参数进行分析,对称性Δf反映了大、小断层发育的均衡程度,谱宽Δα反映了断层概率分布的不均匀程度,二者均与构造演化过程密切相关,反映了构造背景、断层组合和运动方式的差异,决定了瓦斯突出的区域分布特征。
3)焦作矿区3个研究区域多重分形谱特征参数与突出严重程度呈现很好的对应关系,多重分形分析与单分形分析相比,能够挖掘更多的断层信息,从多重分形特征参数的数学意义可推演其地质意义,进而能够反映断层的演化背景和演化过程,这对于分析断层对突出的控制作用提供了定量或半定量化的分析手段。
[1] LI H Y.Major and minor structural features of a bedding shear zone along a coal seam and related gas outburst,Pingdingshan coalfield,northern China[J].International Journal of Coal Geology 2001,47,101-113.
[2] 徐志斌,王继尧,张大顺,等.煤矿断层网络复杂程度的分维描述[J].煤炭学报,1996,21(4): 358-363.
XU Zhibin,WANG Jiyao,ZHANG Dashun, et al.Fractal dimension description of complexity of fault network in coal mines[J].Journal of China Coal Society,1996,21(4): 358-363.
[3] SHEPHERD J,RIXON L K,GRIFFITH L.Outbursts and geological structures in coal mines: a review[J].Int J Rock Mech Sci,1981,18: 267-283.
[4] 刘明举,刘希亮,何 俊.煤与瓦斯突出分形预测研究[J].煤炭学报,1998,23(6): 616-619.
LIU Mingju,LIU Xiliang,HE Jun.Fractal prediction research of coal and gas outburst[J].Journal of China Coal Society,1998,23(6): 616-619.
[5] 何 俊,刘明举,颜爱华.煤田地质构造与瓦斯突出关系分形研究[J].煤炭学报,2002,27(6): 623-626.
HE Jun,LIU Mingju,YAN Aihua.Fractal research of relation between geological tectonic coalfields and gas outburst[J].Journal of China Coal Society,2002,27 (6): 623-626.
[6] HIRATA T,SATOH T,ITO K.Fractal structure of spatial distribution of micro fracturing in rock[J].Geophys J Roy Astron Soc,1987,90,369-374.
[7] YAO Y B,LIU D M,TANG D Z,et al.Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals[J].International Journal of Coal Geology,2008,73:27-42.
[8] LI T,CAI M F,CAI M.Earthquake-induced unusual gas emission in coalmines - A km-scale in-situ experimental investigation at Laohutai mine[J].International Journal of Coal Geology,2007,71: 209-224.
[9] 余恩晓,马立涛,周福双,等.煤岩孔隙结构分形特征表征方法研究[J].煤炭科学技术,2018,46(11): 8-12.
YU Enxiao,MA Litao,ZHOU Fushuang,et al.Study on method to characterize fractal features of pore structures in coal and rock mass [J].Coal Science and Technology,2018,46(11): 8-12.
[10] 高 尚,王 亮,高 杰,等.基于分形理论的不同变质程度硬煤孔隙结构试验研究[J].煤炭科学技术,2018,46(8): 93-100.
GAO Shang,WANG Liang,GAO Jie,et al.Experimental study on pore structures of hard coal with different metamorphic grade based on fractal theory [J].Coal Science and Technology,2018,46(8):93-100.
[11] 汤 政,姜 波,宋 昱,等.宿县矿区构造煤压缩特性及孔隙结构分形特征研究[J].煤炭科学技术,2017,45(12):174-181.
TANG Zheng,JIANG Bo,SONG Yu,et al.Study on compression characteristics and pore structural fractalfeature of structure coal in Suxian Mining Area[J].Coal Science and Technology,2017,45(12): 174-181.
[12] 刘晓冬,徐景祯,王新峰.断裂体系多重分形谱特征及其应用.石油地球物理勘探[J].1999,34(3): 285-289,301.
LIU Xiaodong,XU Jingzhen,WANG Xinfeng.Multi-fractals spectrumbehavior of fault system and its application[J].Oil Geophysical Prospecting,1999,34(3): 285-289,301.
[13] 胡修权, 施泽进, 田亚铭, 等. 川东南地区茅口组断裂多重分形特征及意义[J]. 成都理工大学学报:自然科学版, 2014, 41(4): 476-482.
HU Xiuquan, SHI Zejin, TIAN Yaming,et al. Muitifractal feature and significance of Maokou formation faults in the southeast of Sichuan[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2014, 41(4): 476-482.
[14] PANAHI A,CHENG Q M.Multifractality as a measure of spatial distribution of geochemical patterns[J].Mathematical Geology,36,827-846.
[15] ZHAO J N,CHEN S Y,ZUO R G, et al.Mapping complexity of spatial distribution of faults using fractal and multifractal models: vectoring towards exploration targets [J].Computers & Geosciences ,2011,37: 1958-1966.
[16] XIE S Y,CHENG Q M,CHEN G.Application of local singularity in prospecting potential oil/gas targets[J].Nonlinear Processes in Geophysics,2007,14:285-292.
[17] HIRABAYASHI T,ITO K,YOSHII T.Multifractal analysis of earthquakes[J].Pure and Applied Geophysics,1992,138:591-610.
[18] KIYASHCHENKO D,SMIMOVA N,TROYAN V,et al.Seismic hazard precursory evolution: fractal and multifractal aspects[J].Physics and Chemistry of The Earth,2004,29:4-9.
[19] 谢和平,王金安.岩石节理(断裂)表面的多重分形性质[J].力学学报,1998,30(3):314-320.
XIE Heping,WANG Jinan.Multifractal behaviors of fracture surfaces in rocks [J].Acta Mechanica Sinica,1998,30(3): 314-320.
[20] SHIVAKUMAR K,RAO M V M S,SRINIVASAN C K,et al.Multifractal Analysis of the Spatial Distribution of Area Rockbursts at Kolar Gold Mines[J].International Journal of Rock Mechanics and Mining Sciences,1996,33: 167-172.
[21] 陈雪梅,张 晞,徐莉莉,等.煤与矸石分形维数的差异研究[J].煤炭科学技术,2017,45(7):196-199.
CHEN Xuemei,ZHANG Xi,XU Lili,et al.Study on fractal dimension differences of coal and rock[J].Coal Science and Technology,2017,45(7):196-199.
[22] 焦作工学院瓦斯地质研究所.瓦斯地质概论[M].北京: 煤炭工业出版社,1990.
[23] 孙 霞,吴自勤,黄 畇.分形原理及其应用[M].合肥: 中国科技大学出版社,2003.
[24] 李 彤,商朋见.多重分形在掌纹识别中的研究[J].物理学报,2007,56(8): 4393-4400.
LI Tong,SHANG Pengjian.A multifractal approach to palmprint recognition[J] .Acta Physica Sinica,2007,56(8):4393-4400.
