 1,刘延婷2,徐玉芸2,袁 昊2,李德根3
1,刘延婷2,徐玉芸2,袁 昊2,李德根3煤岩破碎特性是研制破碎机构及机械重要的理论基础,而煤岩是非均质且为各向异性的物质,在煤岩内部随机分布各种裂隙。通过刀具截割煤岩载荷谱分析煤岩破碎的内在特性和力学机理,其对刀具破碎煤岩理论与新型刀具的研制具有重要意义[1]。GOKTAN等[2]采用全尺寸直线截割试验台,测得镐型截齿沿直线截割煤岩的截割阻力,通过半经验法给出修正的镐型截齿非对称截割半经验公式。刘芮葭等[3]根据刨煤机单刨刀截割试验建立其截割阻力模型。EVANS[4]假定截割孔大小相对截深可忽略不计,建立了截齿峰值截割力计算公式。ROXBOXBOROUGH等[5-7]在EVANS模型基础上改进了峰值截割力的计算公式。牛东民[8]从断裂力学角度分析了刀具切削力的变化规律,建立了理论模型。TIRYAK等[9]研究截齿截割比能耗与煤岩截割关联特性,指出截割比能耗与煤岩的抗压强度呈线性关系。刘春生等[10-14]通过截齿平面截割和旋转截割试验,给出截齿截割阻力的试验理论模型及其载荷谱特征。张艳林等[15-18]利用有限元软件分析了截割刀具截割煤岩时截割力曲线以及截割过程中煤岩的应力云图。目前,国内外学者对传统刀具破碎煤岩载荷特性与工作机构相关研究较多,笔者借鉴已有刀具的研究成果,为解决煤岩高效破碎的问题,研制了碟盘截割硬岩刀具,与传统截割头相比,碟盘刀齿数量明显增多,单个刀齿所承受的载荷明显减小,同时其具有齿尖和碟盘楔面2个部分作用使煤岩破碎。为研究碟盘破碎煤岩的载荷特性,选取碟盘刀齿中间一个齿为研究对象,由于碟盘中间齿的载荷最大,其大小和方向与其他刀齿存在位置角的转换关系,笔者运用数值模拟、理论和试验的方法研究其载荷特性,为构建整个碟盘载荷提供一定的基础。
碟盘刀具如图1a所示,其是一种新型破碎煤岩刀具,刀具整体呈碟盘形状,在碟盘下边缘端圆周上均匀分布着刀齿。文中碟盘刀齿数为100个,取碟盘刀具中间的一个齿(与径向速度方向相同的刀齿)为分析单元,分析刀齿载荷及随楔面角的变化规律。
采用ABAQUS有限元软件模拟等效碟盘刀齿破碎煤岩的过程,分析刀齿由齿尖到楔面接触煤岩过程中的载荷特性,以及径向载荷Fj与轴向载荷Fs随刀齿楔面角度的变化规律。煤岩采用Drucker-Prager模型,弹性模量为1 400 MPa、泊松比为0.3,忽略煤岩材料中裂隙等因素,假设刀齿在径向运动过程中速度vj的方向大小恒定不变。
刀齿与煤岩模型可以在Pro/E中建立后导入ABAQUS软件中,材料模块赋予属性参数,约束刀齿与煤岩的接触条件和刀齿的运动状态,同时,根据刀齿与煤岩的形状,以及接触区域进行分区网格划分,刀齿径向速度vj切削煤岩的有限元模型如图1b所示。
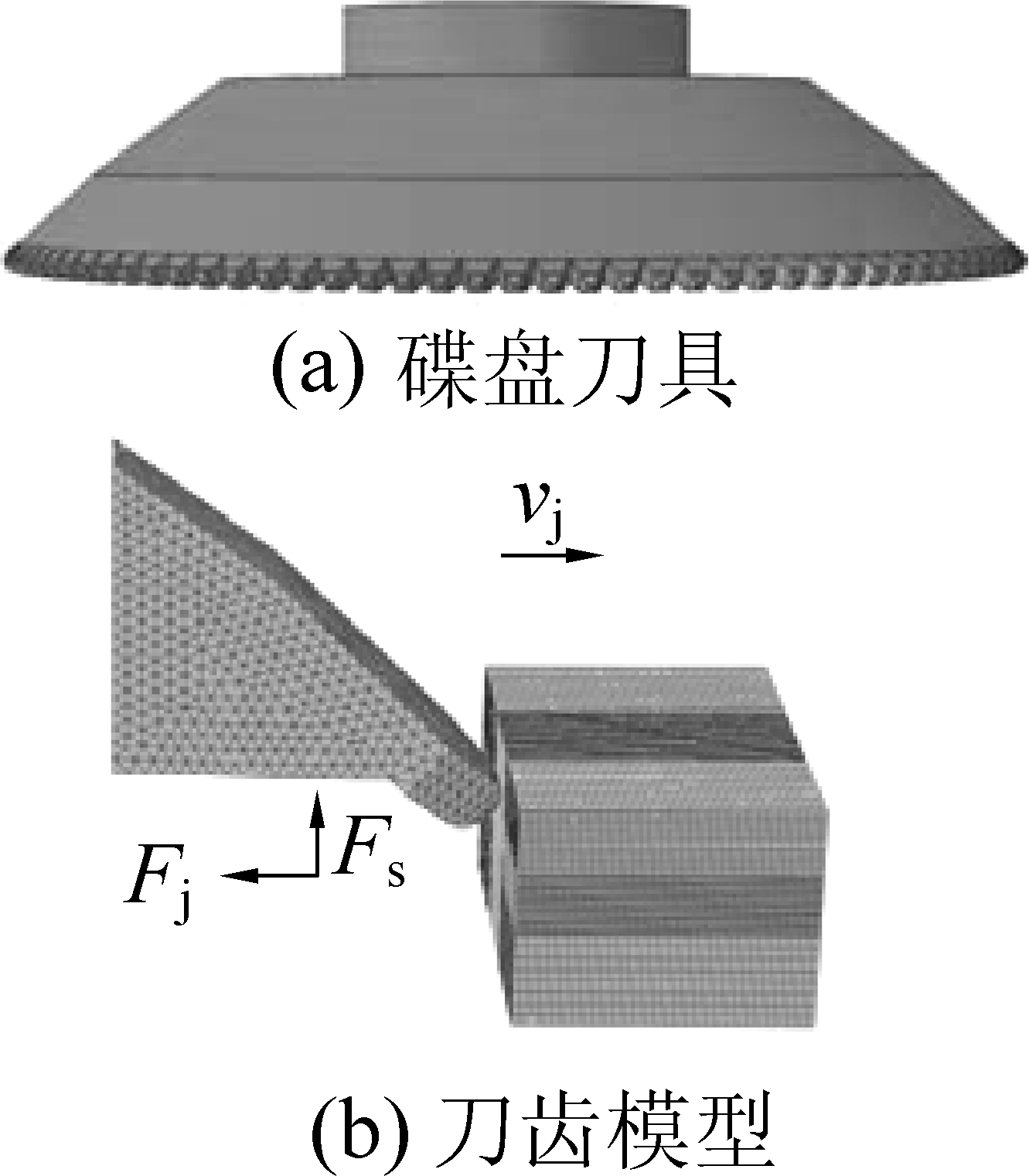
图1 碟盘刀具与刀齿模型
Fig.1 Disc cutter and cutter tooth model
分析刀齿径向速度vj切削煤岩时,楔面角对破碎煤岩载荷的影响,数值模拟时楔面角α分别为35°、40°、45°、50°、55°,间隔5°,vj=400 mm/s,切削厚度h=14 mm。不同楔面角下刀齿径向切削煤岩的径向载荷Fj与轴向载荷Fs如图2和图3所示。
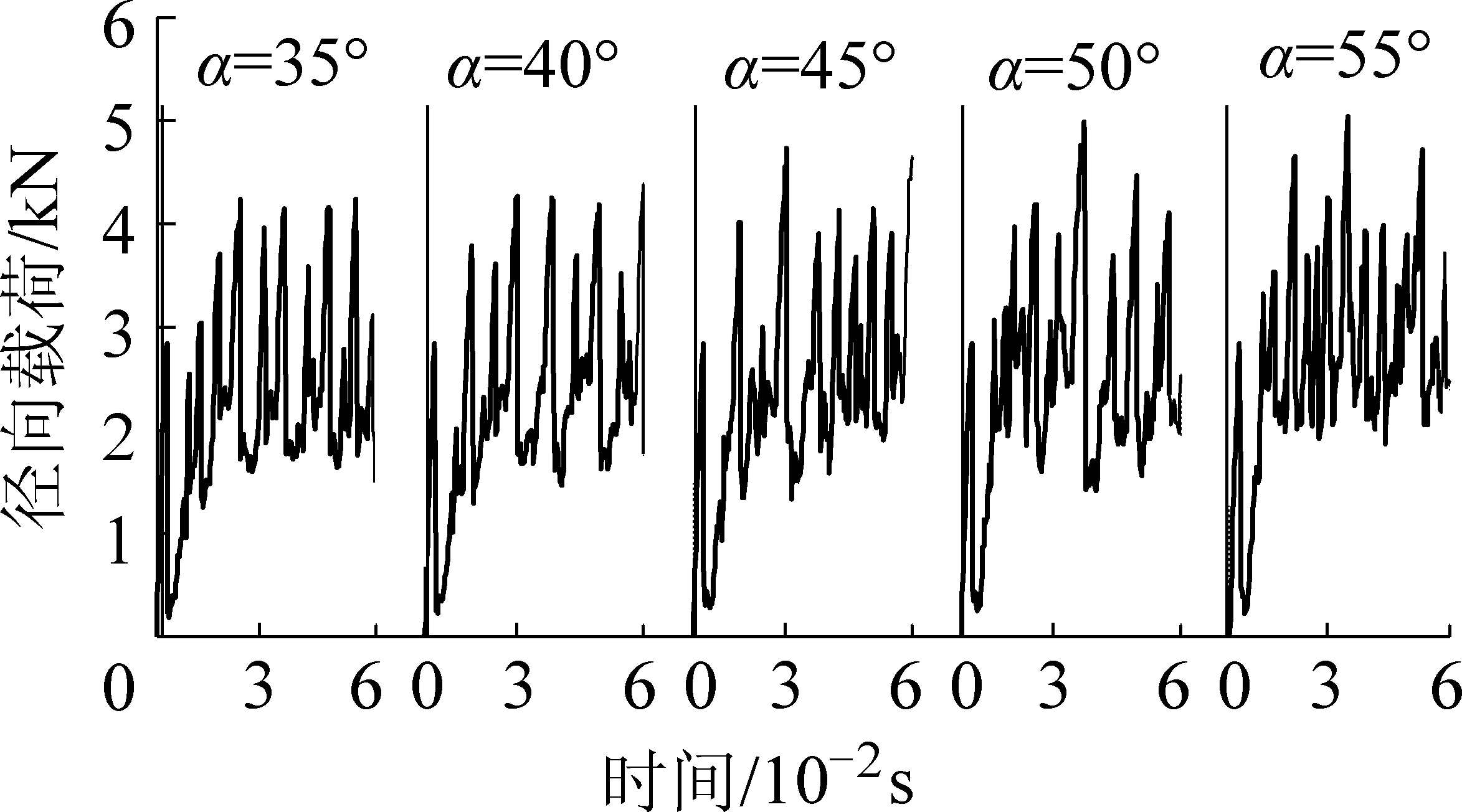
图2 径向切削径向载荷数值模拟
Fig.2 Numerical simulation of radial cutting radial load
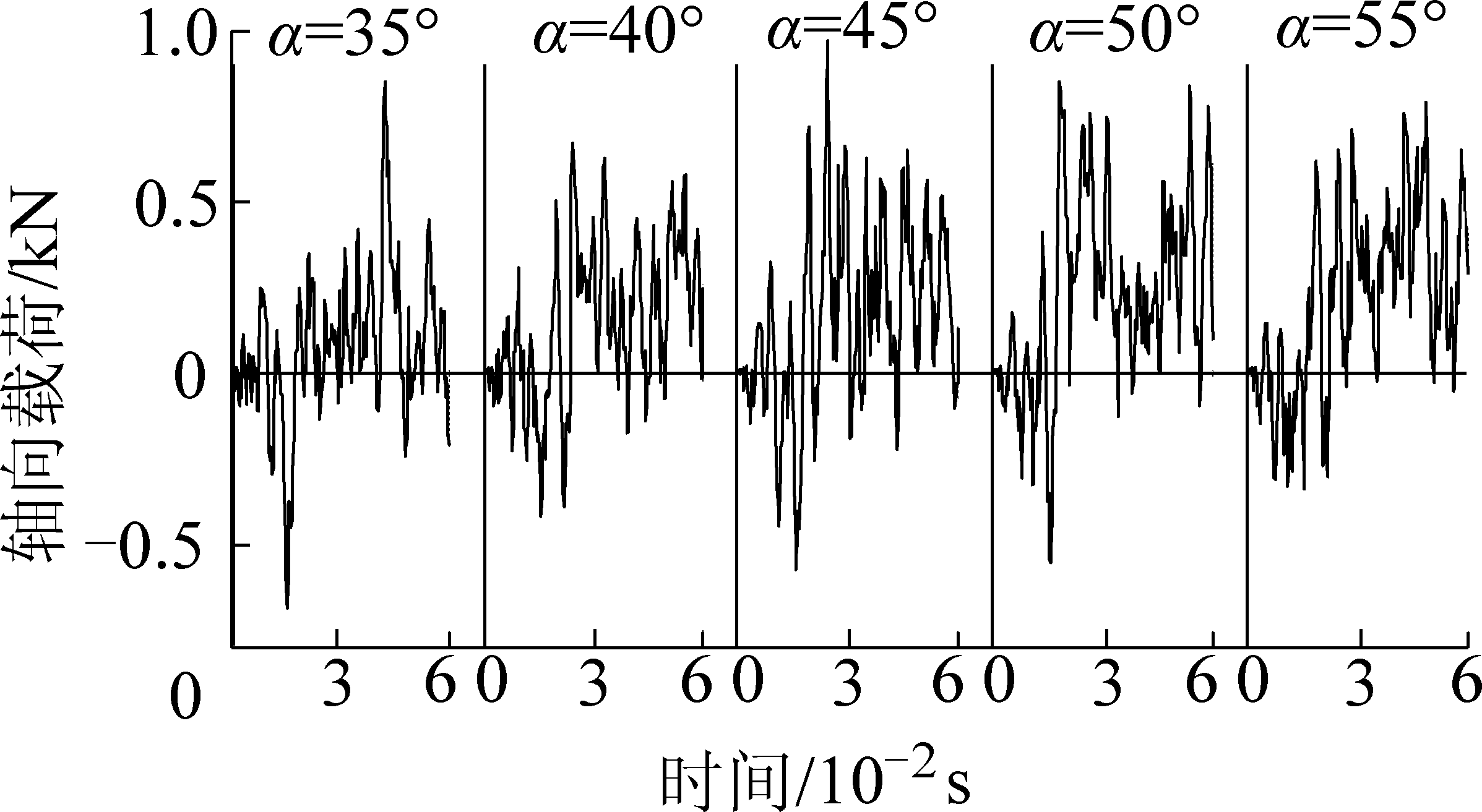
图3 径向切削轴向载荷数值模拟
Fig.3 Numerical simulation of radial cutting axial load
由图2和图3可见,刀齿开始由齿尖接触煤岩的过程中,随着楔入深度增加,刀齿径向载荷逐渐增加,轴向载荷的方向呈现正负交替变化(初期总体方向向下)。当继续楔入刀齿楔面作用面积随之增大,刀齿径向载荷增加。当刀齿完全楔入煤岩中,径向载荷随煤岩局部破碎而波动变化,呈跃进式破碎的特点。刀齿齿尖处于煤岩内封闭区域,在煤岩未破碎时,载荷逐渐增加,且随楔面载荷的增加,煤岩中裂隙迅速扩张,楔面上方煤岩强度降低,刀齿齿尖处载荷便大于楔面载荷,刀齿轴向载荷方向由向下变成向上(为正值)。
在同一煤质和切削厚度下,刀齿破碎煤岩过程中的载荷大小是评价刀齿截割效率的重要依据,对不同楔面角下切削载荷进行统计分析,刀齿载荷峰值均值见表1。
表1 不同楔面角下数值模拟载荷
Table 1 Numerical simulation loads at different wedge angles
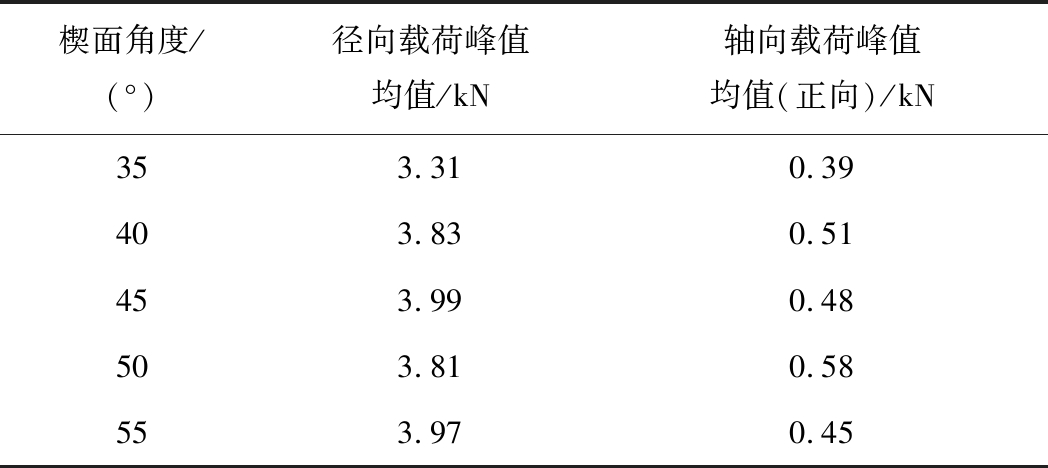
楔面角度/(°)径向载荷峰值均值/kN轴向载荷峰值均值(正向)/kN353.310.39403.830.51453.990.48503.810.58553.970.45
由图1、图2和表1可知,随刀齿楔面角的增加,径向载荷峰值均值明显增加;径向载荷远大于轴向载荷,而轴向载荷总体变化特征基本不变,载荷方向存在正负的改变,其方向总体趋势先向下后向上,反映刀齿齿尖和楔面的不同作用效应。
利用煤岩截割试验台进行刀齿径向切削煤岩试验,试验台如图4所示。试验采用碟盘刀具等效刀齿,α分别为35°、40°、45°、50°和55°,h=14 mm,煤岩截割阻抗200~220 kN/m,单轴抗压强度17~19 MPa。

1—传感器;2—齿座;3—刀齿;4—煤壁
图 4 煤岩切削试验台
Fig.4 Coal rock cutting test bed
由试验装置的特定结构,其等效刀齿载荷检测与传感器设置存在一定的几何关系,如图5所示。

l1—支点到传感器距离;l2—支点到齿尖径向距离;H1—刀齿齿尖到传感器心轴的轴向距离;H2—传感器测试心轴半径;f—传感器心轴与齿座之间的摩擦因数,一般取0.1~0.12;N—支撑点处的正压力;F′s—传感器测得的轴向载荷,kN;F′j—传感器测得的径向载荷
图5 刀齿切削煤岩测试力学模型
Fig.5 Test mechanical model of cutter tooth cutting coal rock
刀齿切削煤岩等效在齿尖处,轴向载荷Fs、径向载荷Fj与传感器的数值关系为
Fj=F′j+f(Fs+F′j)
由于试验装置和条件,试验过程明显呈现出3个阶段:第Ⅰ阶段为初始阶段,刀齿由齿尖逐渐楔入到煤岩中,在煤岩厚度D一定时,不同刀齿楔面楔入到煤岩中的距离不同,当刀齿楔面楔入厚度与切削厚度相同时初始阶段结束。第Ⅱ阶段为正常切削阶段,刀齿完全楔入煤岩中开始等切削厚度切削煤岩。第Ⅲ阶段为终止阶段,刀齿进入封闭煤岩区域,煤岩切削厚度增大,径向切削速度vj迅速减小至零。3个阶段刀齿与煤岩作用如图6所示。
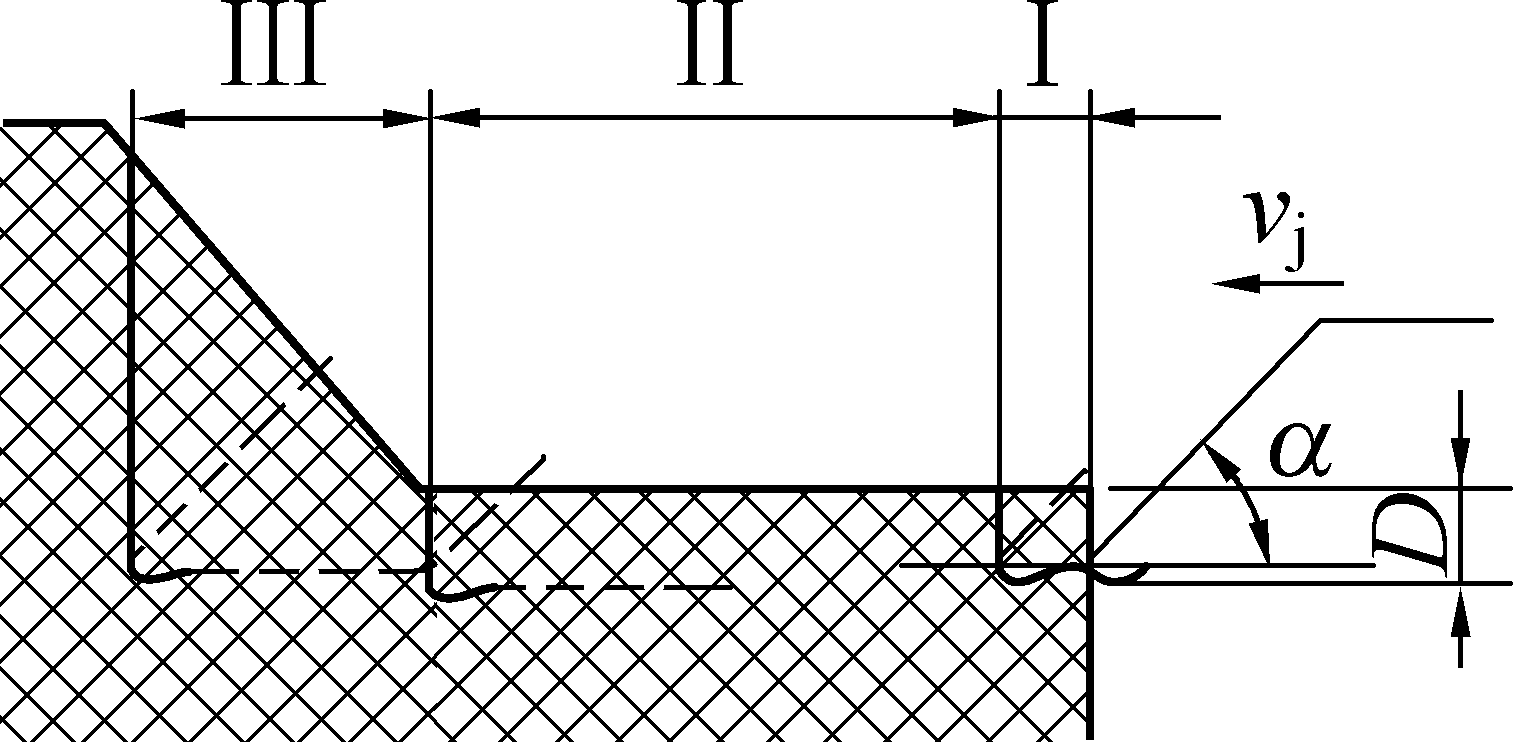
图6 刀齿与煤岩作用示意
Fig.6 Schematic of action of blade and coal & rock
不同楔面角刀齿径向切削煤岩的径向载荷与轴向载荷如图7和图8所示,由此可以看出,其试验载荷谱与图6所示的3个阶段一致。
在第Ⅰ阶段,刀齿开始接触破碎煤岩段,由于冲击作用,刀齿载荷出现较大的波动峰值,同时,在开始与煤岩接触,刀齿齿尖起主要作用,齿尖接触煤岩时,齿尖的上半部先起作用,呈现出载荷方向向下,随刀齿逐渐楔入煤岩,齿尖的下半部挤压煤岩,同时,刀齿楔面上方煤煤岩被损伤,煤岩中出现裂隙,煤岩强度降低,刀齿楔面上方载荷减小,而刀齿齿尖下方起主要作用,则齿尖轴向载荷大于楔面,轴向载荷改变方向向上,第Ⅰ阶段过渡到第Ⅱ阶段。在第Ⅱ阶段,刀齿稳定切削厚度破碎煤岩,刀齿径向载荷波动增加,轴向楔面载荷变化较小,而齿尖轴向载荷增大,轴向载荷方向向上。第Ⅲ阶段,终止阶段,因切削厚度突变和切削减速造成刀齿径向与轴向载荷产生突变(先增大后减小)。在第Ⅱ阶段中刀齿径向载荷和轴向载荷曲线最大值与均值统计结果见表2。

图7 径向切削试验径向载荷
Fig.7 Radial cutting test radial load
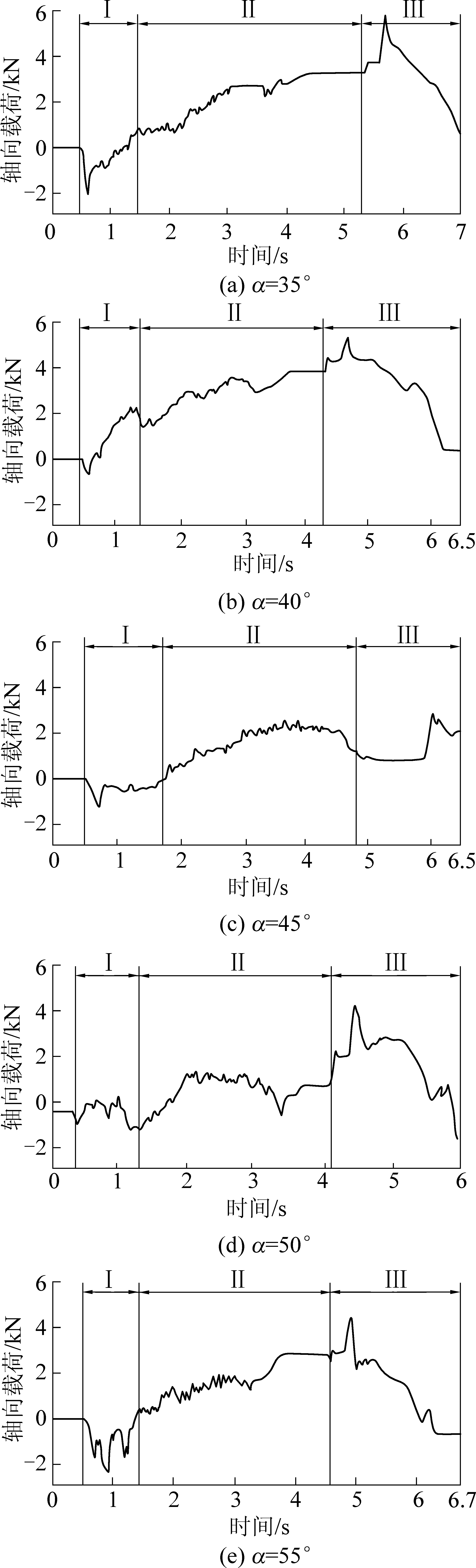
图8 径向切削试验轴向载荷
Fig.8 Radial cutting test axial load
表2 第Ⅱ阶段试验载荷统计值
Table 2 Test load statistics of the Second stage
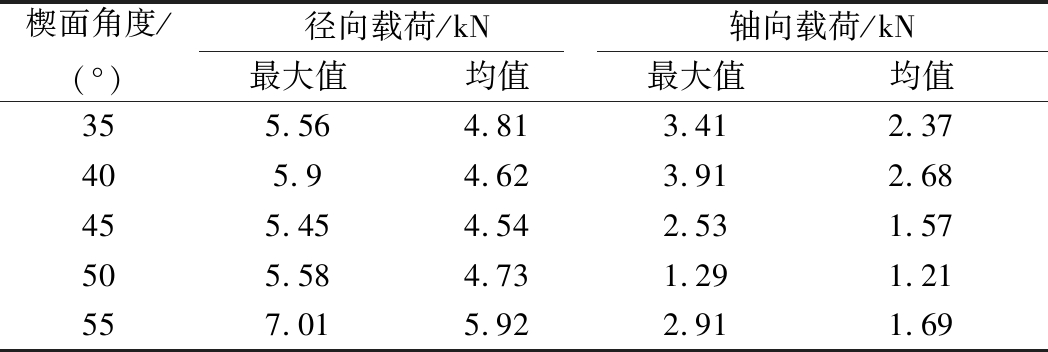
楔面角度/(°)径向载荷/kN轴向载荷/kN最大值 均值最大值均值355.564.813.412.37405.94.623.912.68455.454.542.531.57505.584.731.291.21557.015.922.911.69
由表2可知,刀齿在第Ⅱ阶段,刀齿径向载荷最大值与均值随楔面角的增加而增加。在第Ⅰ阶段径向载荷的试验值与模拟值变化规律相符合,试验轴向载荷与模拟轴向载荷具有相同的方向交替波动特性,且随楔面角的增加轴向载荷减小。
当等效刀齿径向切削时,即刀齿轴向振动速度vs=0,径向切削速度vj>0时,轴向载荷和径向载荷的理论模型见文献[20],而当刀齿速度vs>0、vj>0时,即刀齿轴向向上振动与径向复合切削煤岩时,复合运动的速度大小和方向的改变,导致其等效切削厚度有所变化,刀齿瞬时速度方向切削厚度计算模型如图9所示,其等效切削厚度为h′0。崩落面在速度方向上的投影高度h′为
式中:vs为平均轴向振动速度,mm/s;ψ为煤岩崩落面倾角,(°);l为崩落面长度,h=lsin ψ,mm;βv为刀齿瞬时合速度的水平夹角,βv=arctan(vs![]() ),(°)。
),(°)。
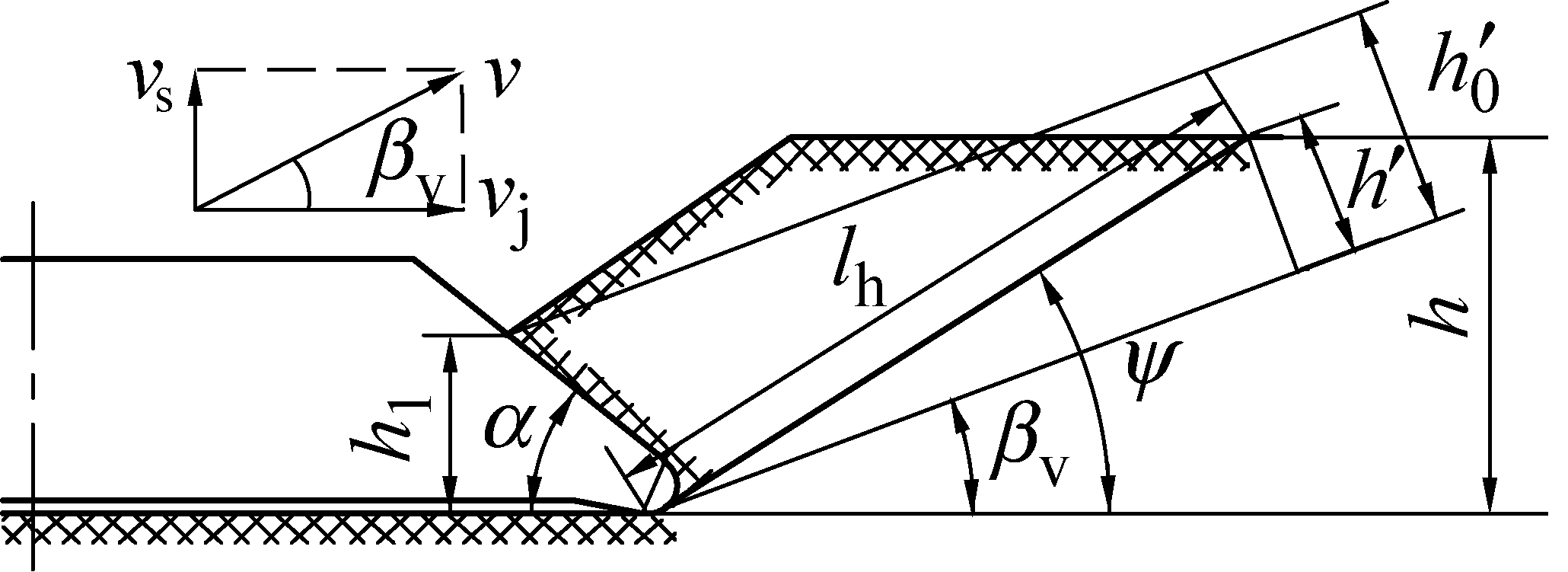
图9 等效切削厚度模型
Fig.9 Model of equivalent cutting thickness
由于刀齿轴向振动速度周期变化与煤岩破碎的随机性等效切削厚度存在周期性的变化,其复合破碎煤岩的等效切削厚度![]() 为
为
式中:Kv为轴向振动速度的影响系数,当βv(vs=0)时,Kv=1;当βv=ψ时,Kv=0.5。
在破碎阶段,刀齿齿尖压力锥体半锥角为![]() 在此时破碎,轴向振动引起的齿尖轴向载荷Psi为
在此时破碎,轴向振动引起的齿尖轴向载荷Psi为
![]()
其中:当i=1,Ps1为刀齿轴向向上振动引起的齿尖轴向载荷;当i=2,Ps2为刀齿轴向向下振动引起的齿尖轴向载荷;SOsi为刀齿齿尖煤岩压力锥体面积,mm2;r0i为在压裂阶段,压力体作用面的半径,mm;α0为煤岩在压裂阶段压力等效锥体半锥角,(°);α′0为在破碎阶段,压力等效锥体破裂面之间的等效夹角,(°)。
由刀齿的结构形式与运动特点,从刀齿切削煤岩机理出发,分析刀齿在不同的运动状态下,刀齿各个部位的受力关系,同时,利用复合效应的叠加原理,对刀齿齿尖与楔面处的力矢量叠加,得出刀齿径向切削时径向载荷Fj和轴向载荷Fs的数学模型式(1),同时,刀齿径向与轴向向上振动复合切削煤岩时的径向载荷Fj1和轴向载荷Fs1的数学模型见式(2)[20]。
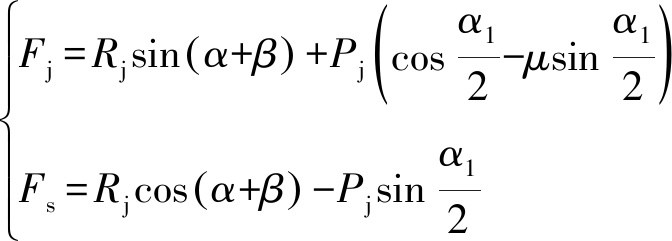
(1)
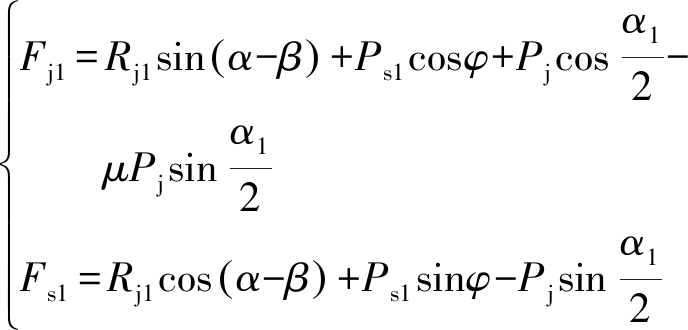
(2)
式中:Rj为刀齿径向切削煤岩时楔面合力,kN;Rj1为刀齿复合轴向向上作用破碎煤岩时楔面合力,kN;Pj为刀齿径向切削时齿尖合力,kN;Ps1为刀齿轴向向上运动时齿尖向上分力,kN;β为刀齿楔面正压力与合力之间夹角,(°);α1/2为刀齿齿尖合力的水平夹角,(°);φ为刀齿轴向向上运动齿尖合力的水平夹角,(°);μ为刀齿与煤岩之间的摩擦因数。
根据煤岩实际与工况条件,对刀齿径向切削和轴向向上振动径向复合运动2种状态下的理论模型进行分析,刀齿理论模型参数见表3。
表3 刀齿理论模型模拟参数
Table 3 Simulation parameters of cutter theoretical model
α/(°)α0/(°)α1/(°)ψ/(°)β/(°)μ1μb/mmh/mmr/mmσj/MPaσy/MPa35~5530.23048160.580.29121441.919
当α分别为35°、40°、45°、50°和55°时,由表2对刀齿径向切削煤岩第Ⅱ阶段试验均值与最大值载荷进行拟合关系,以及刀齿径向切削煤岩时理论模型载荷随楔面角的关系如图10所示。
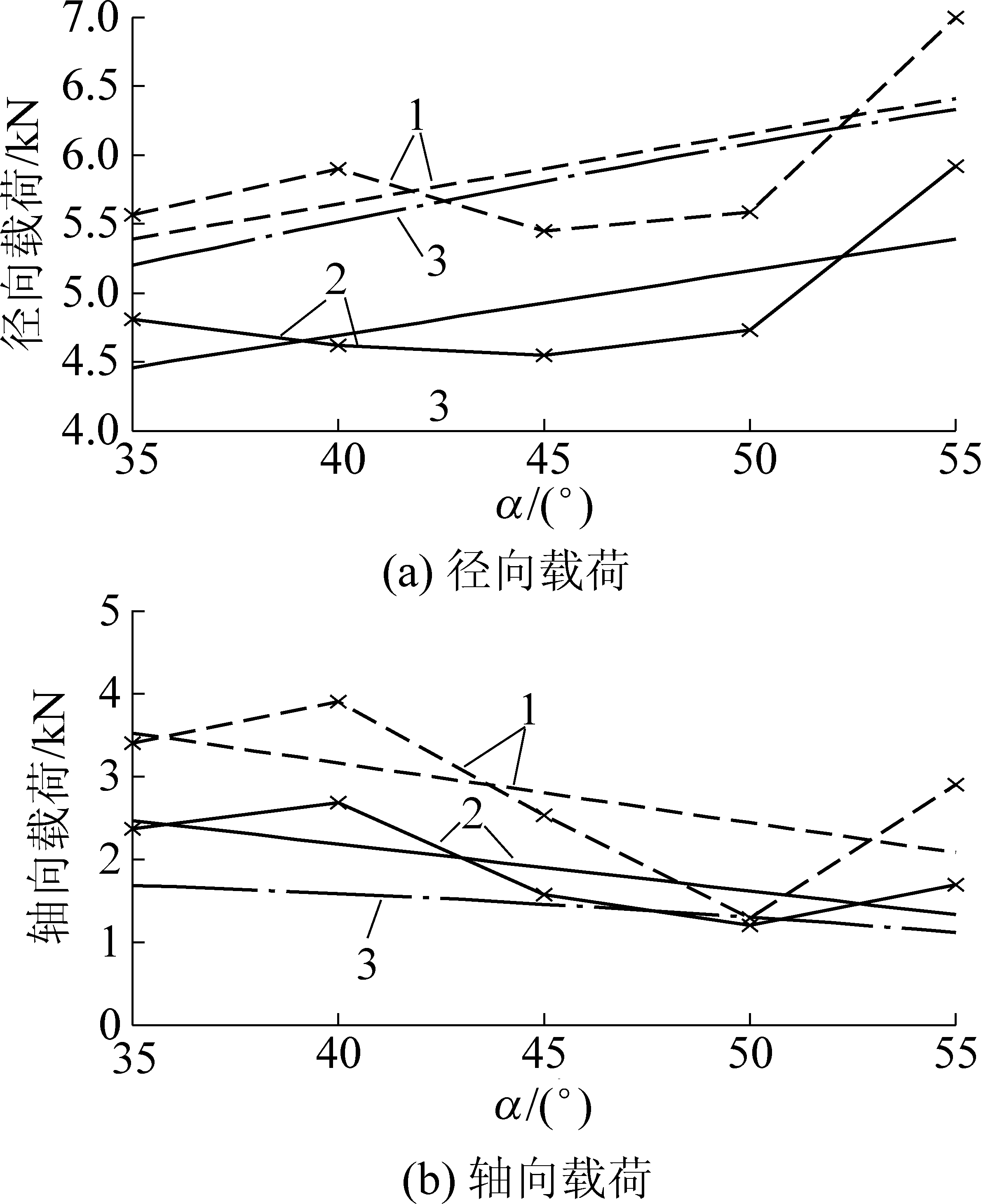
1—试验最大载荷点和拟合曲线;2—试验均值载荷点和拟合曲线;3—理论模型值
图10 刀齿径向切削理论与试验载荷
Fig.10 Radial cutting theory and test load
当α=35°、40°、45°、50°和55°时,由表2对刀齿径向切削煤岩第Ⅱ阶段试验均值与最大值载荷进行拟合关系,以及刀齿轴向向上振动径向复合切削煤岩时理论模型载荷随楔面角度的关系如图11所示。

1—试验最大载荷点和拟合曲线;2—试验均值载荷点和拟合曲线;3—理论模型值(轴向向上振动)
图11 刀齿复合切削理论与径向切削试验载荷
Fig.11 Combined cutting theory and radial cutting test load
由图10可见,刀齿径向切削煤岩试验最大值载荷、均值载荷的拟合关系与理论模型结果是吻合的,刀齿径向载荷随楔面角的增加而增加,而轴向载荷反之。刀齿的理论径向载荷和试验最大值与均值分别小5%和大14%,轴向载荷理论值与试验均值小19.5%。由图11可见,刀齿轴向向上振动径向复合切削煤岩时,刀齿理论载荷与刀齿径向切削破碎煤岩试验载荷变化规律相一致。刀齿轴向向上振动径向复合切削载荷理论值小于径向切削试验载荷均值,减少了约32%,而刀齿轴向载荷方向与径向切削时方向确相反,向下,其刀齿轴向振动径向复合切削轴向载荷与径向切削试验轴向载荷均值减少了约27%。由上述分析可以得出,刀齿径向切削载荷的理论值与试验值有较好的吻合度,而刀齿轴向振动径向复合切削载荷与刀齿径向切削的理论值和试验值相比显著减少,碟盘中其他刀齿可以采用同样的分析方法,其与径向切削速度方向存在方向位置角的转换关系。研究表明刀齿轴向振动径向复合切削具有更强的煤岩破碎能力。
1)刀齿数值模拟与试验径向载荷均随楔面角的增加而增加,且大于轴向载荷。刀齿齿尖与楔面的不同作用效应,轴向载荷方向呈现正负(下上)的变化,当完全楔入煤岩中,轴向载荷方向呈现由向下变为向上的变化规律。
2)刀齿轴向向上振动径向复合切削煤岩瞬时速度大小方向存在周期性的变化,煤岩的等效切削厚度与之正相关,给出了刀齿等效切削厚度算法,刀齿理论载荷与径向切削试验载荷随楔面角的变化规律相同。
3)刀齿切削煤岩试验,验证了刀齿径向切削煤岩力学模型的准确性,其刀齿理论径向载荷与试验最大值和平均值分别减小5%和增大14%,轴向载荷均理论与试验均值减小19.5%;刀齿轴向向上振动径向载荷理论值比径向切削试验载荷均值减少了约32%,而轴向载荷与试验轴向载荷均值减少了约27%。表明刀齿轴向振动径向复合切削方法具有更强的煤岩破碎能力。
4)从数值模拟、理论和试验3个角度研究了刀齿的力学特性,建立了其力学模型,为研制高效的硬岩破碎刀具提供了参考,同时为智能快速掘进装备提供了新型刀具的研制方法。
[1] 刘春生,李德根.截齿截割煤岩的力学模型与性能评价[M].哈尔滨:哈尔滨工业大学出版社,2017.
[2] GOKTAN R M,GUNES N.A semi-empirical approach to cuttingforce prediction for point-attack picks[J].The Journal of the South African Institute of Mining and Metallurgy,2005,105:257-264.
[3] 张 强,石抗抗,王海舰,等. 基于压电俘能装置的刨刀受力检测系统[J]. 煤炭科学技术, 2017, 45(2): 136-140.
ZHANG Qiang,SHI Kangkang,WANG Haijian,et al. Stress detecting system of plough based on piezoelectric energy harvester[J]. Coal Science and Technology, 2017, 45(2):136-140.
[4] EVANS I.A theory of the cutting force for point attack picks[J].International Journal of Mining Engineering,1984,2(1) : 63-71.
[5] ROXBOXBOROUGH F F,LIU Z C.Theoretical considerations on pick shape in rock and coal cutting[C]// Proceedings of the 6th Underground Operator’s Conference.Kalgoorlie,Australia,1995: 189 -193.
[6] GOKTAN R M.A suggested improvement on Evans’cutting theory for conical bit[Z].Brisbane,Queensland,1997:A4 -A57.
[7] 王立平,蒋斌松,张 翼,等.基于Evans 截割模型的镐型截齿峰值截割力的计算[J].煤炭学报,2016,41(9):2367-2372.
WANG Liping,JIANG Binsong,ZHANG Yi,et al.Calculation of peak cutting force of conical picks based on Evans’cutting model[J].Journal of China Coal Society,2016,41(9):2367-2372.
[8] 牛东民.煤炭切削力学模型的研究[J].煤炭学报,1994,19(5):526-529.
NIU Dongmin.Mechanical model of coal cutting[J].Journal of China Coal Society,1994,19(5):526-529.
[9] TIRYAKI B,CAGATAY Dikmen A.Effects of rock properties on specific cutting energy in linear cutting of sandstones by picks[J].Rock Mechanics and Rock Engineering,2006,39(2):89-120.
[10] 刘春生,靳立红.基于截槽非对称条件镐形截齿的截割理论模型[J].煤炭学报,2009,34(7):983-987.
LIU Chunsheng,JIN Lihong.The cut mechanical model of pickshaped cutter under conditions of dissymmetricals lotting[J].Journal of China Coal Society,2009,34(7):983-987.
[11] 刘春生,于信伟,任昌玉.滚筒式采煤机工作机构[M].哈尔滨:哈尔滨工程大学出版社,2010.
[12] 刘春生,任春平,李德根.修正离散正则化算法的截割煤岩载荷谱的重构与推演[J].煤炭学报,2014,39(5):981-986.
LIU Chunsheng,REN Chunping,LI Degen.Reconstruction and deduction of cutting coal and rock load spectrum on modified discrete regularization algorithm[J].Journal of China Coal Society,2014,39(5):981-986.
[13] 刘春生.采煤机截齿截割阻力曲线分形特征研究[J].煤炭学报,2004,29(1):115-118.
LIU Chunsheng.Fractal characteristic study of shearer cutter cutting resistance curves[J].Journal of China Coal Society,2004,29( 1) :115-118.
[14] 刘春生,王庆华,李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(11):2623-2628.
LIU Chunsheng,WANG Qinghua,LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J].Journal of China Coal Society,2015,40(11):2623-2628.
[15] 毛 君,刘歆妍,陈洪月,等.不同截齿安装角对采煤机截割性能的影响[J].煤炭科学技术,2017,45(10):144-149.
MAO Jun,LIU Xinyan,CHEN Hongyue,et al.Different installation angle of cutting picks affected to cutting performances of coal shearer[J].Coal Science and Technology,2017,45(10):144-149.
[16] 张艳林,闫炳雷,陈 锷,等.基于ANSYS/LS-DYNA的掘进机截齿截割煤岩动力学分析[J],机械设计,2013,30(2):74-76.
ZHANG Yanlin,YAN Binglei,CHEN E,et al.Dynamic analysis on conical pick cutting based on ANSYS/ LS_DYNA[J].Journal of Machine Design,2013,30(2):74-76.
[17] 刘春生,宋 杨.不同楔入角的镐齿破岩截割力模型与仿真[J].黑龙江科技大学学报,2012,22(3):277-281.
LIU Chunsheng,SONG Yang.Development and simulation of cutting force model on conical pick cutting rock at different wedge angles[J].Journal of Heilongjiang Institute of Science and Technology,2012,22(3):277-281.
[18] 郭辰光,李 源,胡 迪,等.刨刀刨削煤岩特性数值模拟研究[J].煤炭科学技术,2017,45(2):141-145.
GUO Chenguang,LI Yuan,HU Di,et al.Numerical simulation study on coal and rock ploughing and planing features of plough cutters[J].Coal Science and Technology,2017,45(2):141-145.
[19] 徐玉芸.复合运动碟盘刀齿破碎煤岩的力学模型与载荷特性[D].哈尔滨:黑龙江科技大学,2018.
[20] 刘春生,徐玉芸,李德根,等.边缘牙齿形碟盘破碎煤岩的力学机理及其模型[J].煤炭学报,2018,43(1):272-279.
LIU Chunsheng,XU Yuyun,LI Degen,et al.Mechanical mechanism and model of rock breaking by edge tooth disk[J].Journal of China Coal Society,2018,43(1):272-279.