0 引 言
随着浅层煤炭资源的枯竭以及深部开采技术的发展,地质异常给煤矿生产和安全都带来隐患,针对煤矿地质异常问题,必须做到预测预报、有掘必探[1]。目前煤矿地质异常探测方法主要有物探和钻探2种方法,相比于物探方法,钻探方法能够更准确、直接地解决岩性划分以及前方异常地质体位置判别。煤矿钻探方法岩性划分主要有2种方法,一是靠取心技术;二是靠岩屑录井,存在一定程度的误差[2]。通过在钻头后方安装三分量加速度传感器,利用在钻头后方采集到的振动信号,识别钻机的工作状态,获取钻头前方地质情况的技术,称之为钻柱振动录井[3]。20世纪60年代,FINNIC等[4]第一次提出钻柱振动录井技术,并对钻柱的纵向和扭转振动在试验和理论上进行初步研究,分析了钻柱的固有频率;文献[5-6]利用在钻柱不同位置的应变传感器记录钻头与地层的相互作用,得到钻柱振动时相关规律;20世纪70年代,LUTZ等[7]提出了瞬态录井的系统,将钻柱轴向振动的瞬时峰值曲线与声波、伽马、中子等测井曲线进行对比研究,在对岩石硬度等判断上取得一定效果。文献[8]首次使用有限元法对底部钻具组合的动态行为进行分析,并论述遥测技术在钻具振动分析中的应用。20世纪80年代,BESAISOW等[9]对钻具振动的原理进行研究,论证了钻具振动信号可以在钻具顶部获得,并且能够如实反映井下钻具的振动状态。文献[10-11]在钻具振动监测中硬件和数据储存上进行一定研究。21世纪初,MACPHERSON对钻具钻进时同时在井下和地面采集纵向加速度信号,并对比了2种信号的谱图,证明钻柱顶端获得的信号能够真实反映井下的工况[12-13]。2010年崔士波等[14]通过分析在钻柱顶端采集的钻头振动信号能够获得钻头、钻具的工作状态,以及所钻地层甚至钻头前方地层的岩性、地层压力等信息,进行井下诊断和钻前预测。随着钻柱振动理论的不断发展,钻柱振动录井技术也趋于成熟,但石油领域的钻井较深,对数据的储存以及硬件的支持都是挑战,而将该方法应用在井下工程钻探的地质异常监测预判,尚未见到报道。
在钻进过程中,钻头破岩分别会产生轴向、横向和扭转方向的振动[15],不同方向的振动具有不同的时频信息,而切割方向的时频信息对岩性识别具有指导意义[16]。其中低频段(0~25 Hz)主要反映了钻头与前方接触引起的谐波,中频段(25~200 Hz)主要反映钻头牙齿与地层作用时产生的振动频率成分,高频段(200 Hz以上)主要为不同地层与钻柱作用时产生的声波噪声,它能反映出地层的变化,从而为地层分层提供参考信息[17-18]。钻柱振动信号是一种非平稳非线性的信号,时频分析技术是解决此问题最常用的分析方法,常用的时频分析方法主要有傅里叶变换、小波变换、Hilbert变换等[19],不同的时频分析方法有各自优势,确定最优的分析方法来处理钻柱振动信号。
鉴于此,笔者通过对数字模拟信号采用不同的时频分析方法进行对比处理与分析,确定适合的矿井钻柱振动信号处理方法,对贵州实采数据进行时频分析实际钻进时煤岩分界位置和钻机工作状态的变化,进而指导实际矿井钻探工作的开展。
1 钻柱横向振动原理
钻机在井下工作时,钻头前方钻进接触岩石,同时受到多种荷载作用会引起钻柱振动,如图1所示,振动形态一般分为钻柱的扭转振动、纵向振动以及横向振动。通过在钻头后的第1根钻杆内部安装三分量加速度传感器,来测量钻头钻进时破岩的信号,以识别钻机工作状态和获取前方的地质情况。如图2所示,模拟井下钻探中地质模型,钻进破岩时三分量中X和Z分量相互垂直,同时测量横向振动(切割方向)信号,Y分量测量纵向(钻进方向)信号。
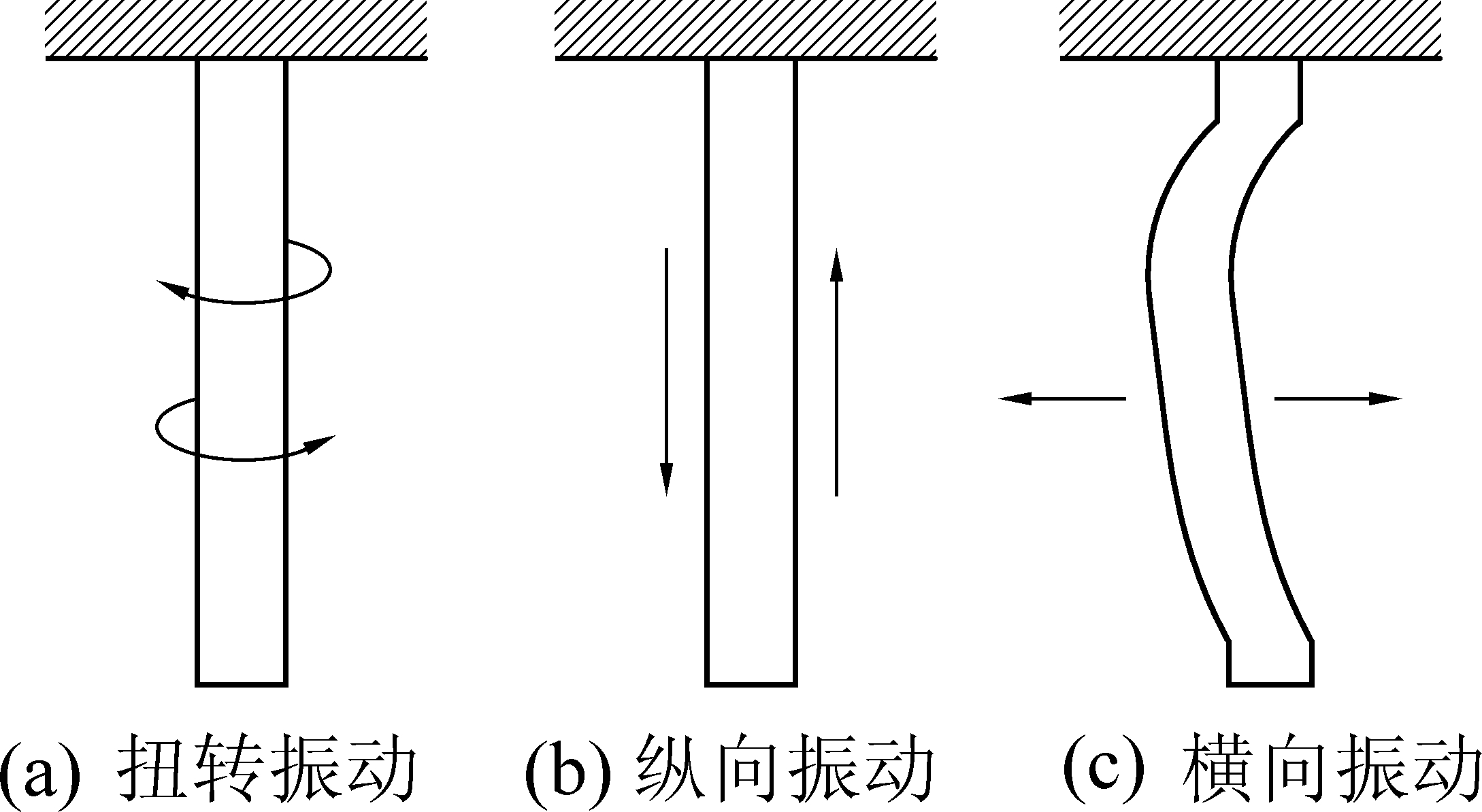
图1 钻柱振动的3种形态示意
Fig.1 Schematic of three forms for drill vibration
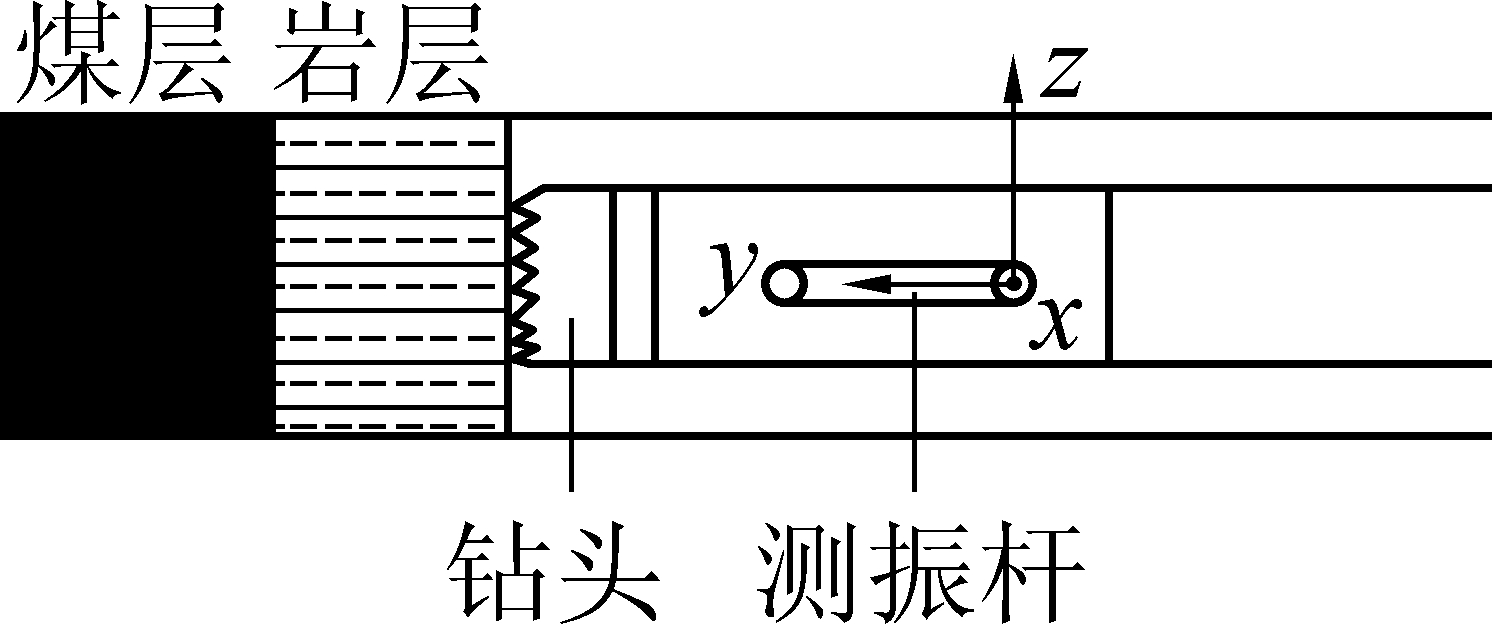
图2 三分量检波器示意
Fig.2 Schematic of three component geophone
横向振动作为切割方向,可作为识别岩性的指导信息,其钻具的横向振动力学模型如图3所示,其中,L为钻柱在横向振动状态下的长度,钻柱上产生动态载荷轴向力S1=S0sin(θt),其中S0、θ分别为周期性轴向力的最大值和角频率。动态载荷S1和静态载荷S共同作用为钻柱振动时全部荷载,钻柱的轴向载荷钻柱可以看作两端支点的一段杆件,钻杆轴向为y轴,横向振动方向取x轴,截取微元dx;图中横向振动规律可表示为[20]
(1)
式中:t为时间;ρ为钻柱密度;I为钻柱截面积相对中性轴的惯性矩;A为钻柱横截面积;E为弹性模量。
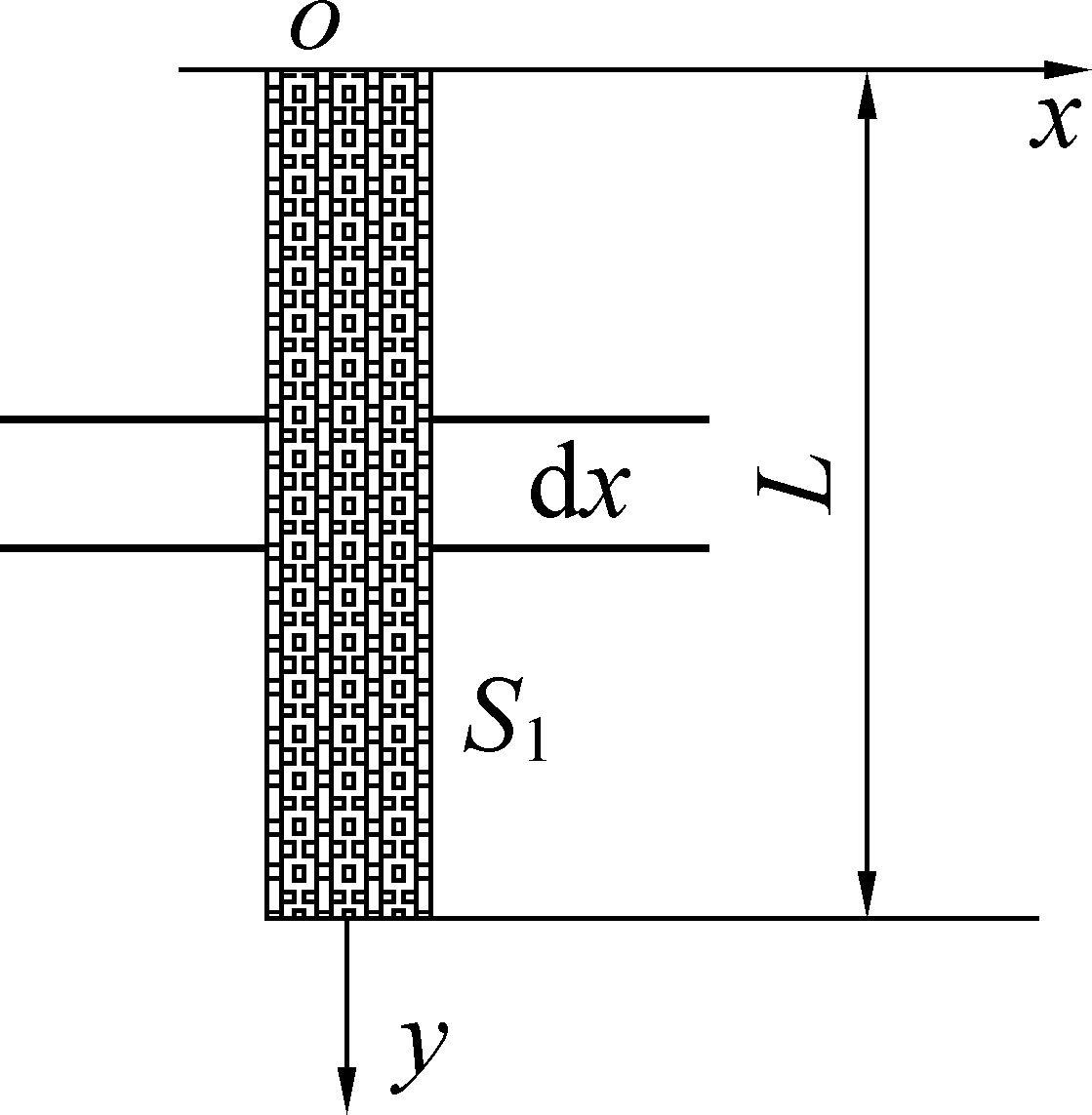
图3 钻具横向振动力学模型
Fig.3 Lateral vibration mechanics model of drilling tool
设![]()
(2)
将式(2)代入式(1),得:
(3)
(4)

(5)
式中:ω为钻柱固有横向频率;ζ为钻头激发力因子;m为阶数。
2 钻进数值模拟信号分析
钻头旋转破岩时,切割方向在重力的作用下为正弦运动曲线,钻进到不同的岩性时频率和振幅都有明显的区别,且在实际工作中一直会有固定的低频噪声。钻进模拟信号各分量参数见表1。
表1 钻进模拟信号各分量参数
Table 1 Each component parameters of drilling simulation signal

信号分量123时间/s0~55~100~10频率/Hz50205振幅10g5g2g
采样频率为200 Hz,在0~5 s采用模拟信号分量1,振幅A1=10g(g为重力加速度),频率f1=50高频高能量信号,模拟钻进遇到坚硬岩层;在5~10 s采用模拟信号分量2,A2=5g,f2=20低频低能量信号,模拟钻进时遇到较软岩层;在全程0~10 s都伴随模拟信号分量3,A3=2g,f3=5的超低频信号,来模拟钻进时钻机旋转频率等固有噪声,合成模拟信号如图4所示。

图4 钻进数值模拟信号
Fig.4 Drilling numerical simulation signal
2.1 钻进信号短时傅里叶变换
DENNIS Gabor[21]于1946年首次引入窗口的概念,提出短时傅里叶变换(STFT),其基本原理是通过确定窗函数来截取信号,对窗函数截取的信号采用傅里叶变换,窗函数以外的信号恒等于零或趋近于零。设任意信号x(t),其短时傅里叶变换表达式为
STFT(τ,f)=![]() x(t)Q(t-τ)e2πifdt
x(t)Q(t-τ)e2πifdt
(6)
式中:x(t)为被分析的信号;Q(t)为窗函数;τ为时窗时刻。
短时傅里叶变换处理数值模拟信号,通过不断滑动时窗来计算频谱,故时频分辨率会受到Heisenberg测不准原理的影响,短时窗有较高的时间分辨率,但频率分辨率较低,反之亦然。如图5a、图5b所示,分别采用短时窗50点和长时窗200点对模拟信号进行短时傅里叶变换,采用短时窗进行变换时,在时间轴上可以清楚地分辨出在5 s时频率变化,时间分辨率高;频率轴2个频率点变宽,主频位置不变。在采用长时窗变换时,时间轴相对模糊,而频率轴2个主频点变窄,频率分辨率提高。

图5 50点和200点短时傅里叶变换图
Fig.5 50 and 200 point short time Fourier transform
2.2 钻进信号小波变换
法国地球物理学家MORLET[22]于1984年首次提出小波分析方法来分析地震波的局部性,小波分析时窗口面积大小是固定的,可以通过改变窗口的形状来克服短时傅里叶变换过程中高频信号时间分辨率低的问题,同时满足时间和频率高分辨率的要求,当然小波分析过程中也存在一定的问题,例如:小波变换分析非平稳信号是在所谓的时间-尺度平面上,而不是在真正的时频平面上,无法准确描述出频率随时间的变换,小波基的选择等问题。任意的f(t),其连续小波变换的表达式为
(7)
式中:![]() 为w的复共轭,w为满足容许条件的母小波函数;a为伸缩因子;b为平移因子。
为w的复共轭,w为满足容许条件的母小波函数;a为伸缩因子;b为平移因子。
数值模拟信号小波包变换如图6、图7所示,小波包树共3层,采样频率为200 Hz。
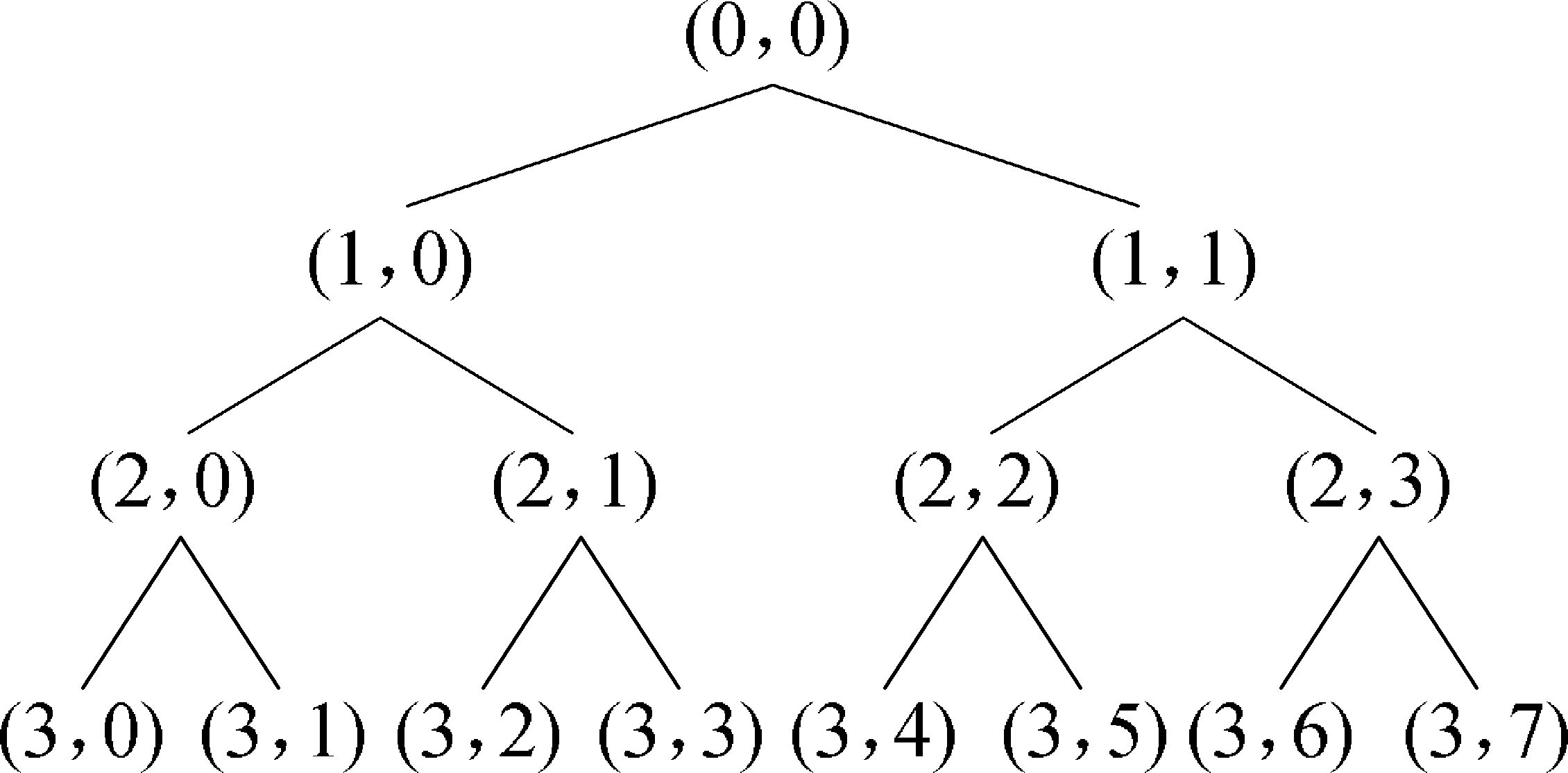
图6 小波包树分解示意
Fig.6 Wavelet packet tree decomposition schematic
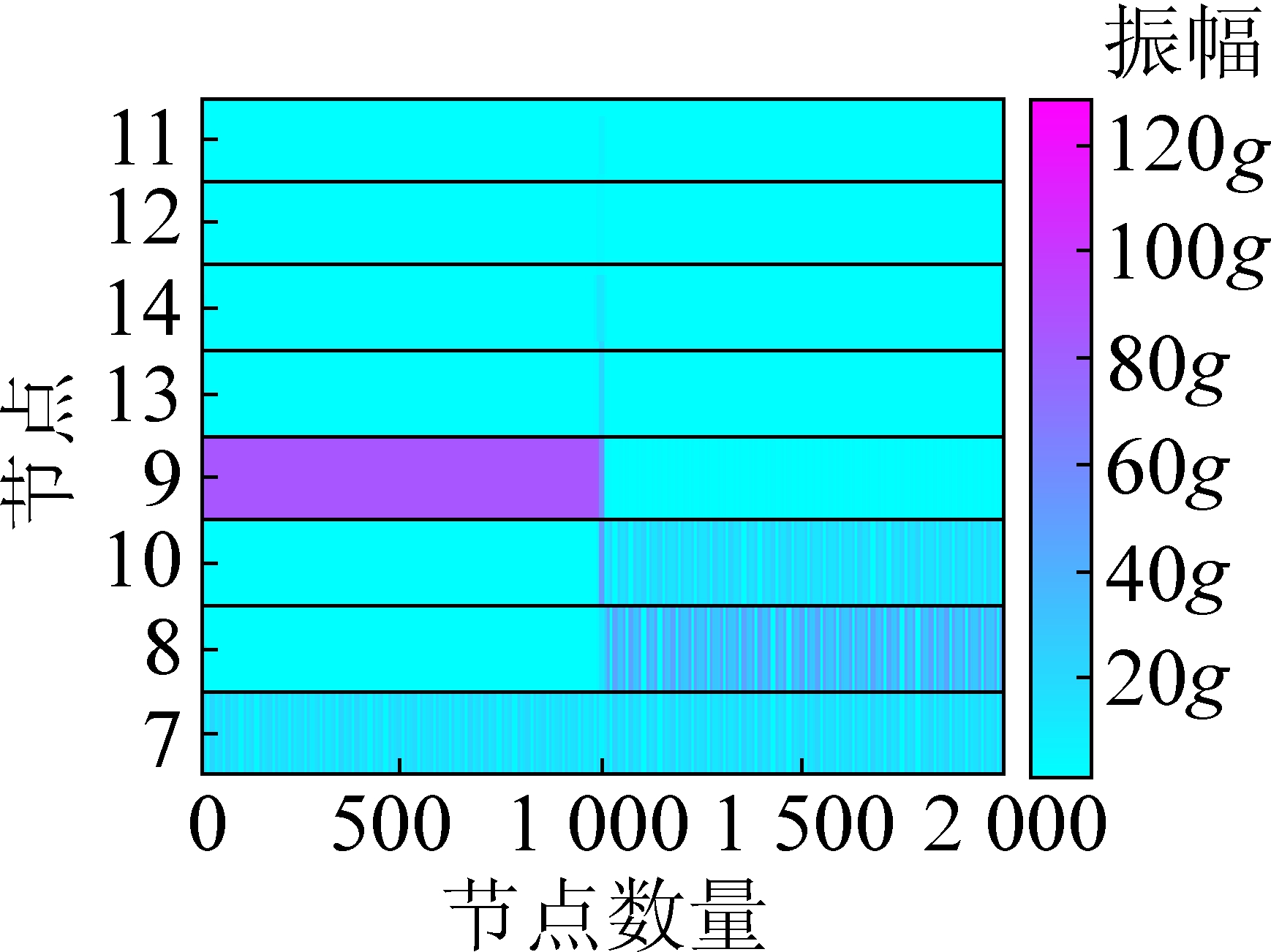
图7 小波包分解频率段示意
Fig.7 Schematic diagram of frequency section of wavelet packet decomposition
根据采样定理,奈奎斯特采样频率为100 Hz,分解了3层,最后1层为8个频率段,每个频率段的频率区间为0~12.5 Hz,从下到上分别对应(0~12.5、12.5~25.0 Hz等),在0~5 s时对应的频率为50 Hz,且振幅较大,在小波包变换后第4频段,且颜色对应较深;5~10 s时对应的20 Hz,振幅一般,对应频段为第2频段,但在第3频段位置也出现一定的低能量;0~10 s含有低振幅低频率噪声信号,在第一频段可以清楚看到一直存在的低振幅信号。虽然小波包分解上可以清楚确定各时间段频率和能量的分布,但小波包无法根据时间变换找出对应具体频率值的变换,且在小波包变换时,在相邻频段会出现一定的频段假象,影响试验结果的分析。
2.3 钻进信号Hilbert-Huang变换
美国华裔科学家Huang于1998年首次提出经验模态分解(EMD)来解决Hilbert变换中瞬时频率只适用于单频信号分量的问题[23-25]。实际信号为s(t),其Hilbert变换为
(8)
瞬时频率fi定义式为
(9)
数值模拟信号Hilbert-Huang变换如图8所示,根据每个时刻固有模态函数,确定出每一时刻的多个瞬时频率所对应的不同能量,变换后结果与设计的数值模拟信号基本相符,只是在边界位置边界效应和模态混叠的现象非常明显,在5 s处分界位置发生了模态的变化,出现了一些假频的信号。
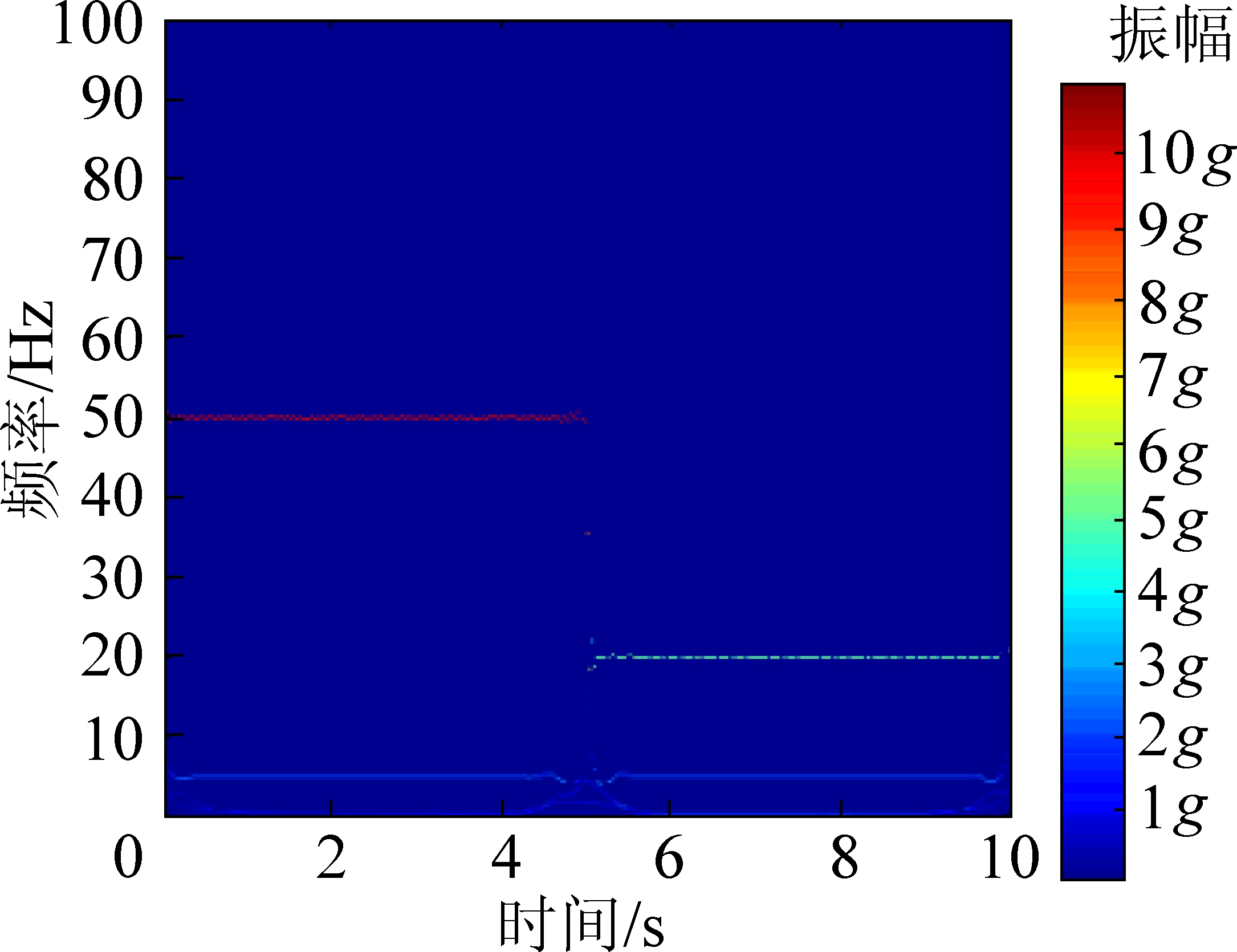
图8 数值模拟信号Hilbert-Huang变换图
Fig.8 Hilbert-Huang transform diagram of numerical simulation signal
通过比较不同时频分析方法对数值模拟信号的处理效果,小波包变换和Hilbert-Huang变换可以基本确定信号的时频特征,但是边界效应和假频现象的出现会一定程度上影响对数值信号的分析,给解释带来困难;短时傅里叶变换通过调整合适的时窗,可以同时满足对时间分辨率和频率分辨率的要求,不会出现假频和边界效应的现象,故可应用在数据处理中主频和主频变化位置时间的确定等问题上。
3 应用实例
现场数据采集位于贵州某矿11104运输石门,主要岩性为粉砂质泥岩,煤岩分界面位于石门前方约26 m位置,如图9所示。本次试验仪器的采样频率为3 300 Hz,根据钻柱录井技术采集的三分量时域信号,选取38 s具有明显特征信息一段时域信号进行分析研究,从采集到的时域信号可以清楚地确定钻机工作时各个工作状态以及钻进过程中岩性变化的位置,基于第2节不同的时频分析方法对数值模拟信号的分析比较,决定采用短时傅里叶变换来对工作状态和岩性划分做频域分析。

图9 三分量时域信号分析
Fig.9 Three component time domain signal analysis
如图10所示,抽取切割Z方向信号,对其做短时傅里叶变换,时窗长度为8 000点,滑动长度为4 000点,信号长度16 000点,结果如图11a所示,低频信号(10 Hz以下)能量很强,反映钻机在工作时所固有的频率,低频所具有的强能量已经压制住钻柱振动录井中具有实际信息的高频信号,故采用高通滤波对10 Hz以下的频率进行过滤,结果如图11b所示,通过滤波后的频域信号具有明显的主频区分和能量区分,直观上可以从能量的强弱和频带的宽度来区分破岩和破煤的信号以及工作状态的划分。截取0~10 s和25~35 s位置分别来进行煤岩识别钻机工作状态确定的详细分析。
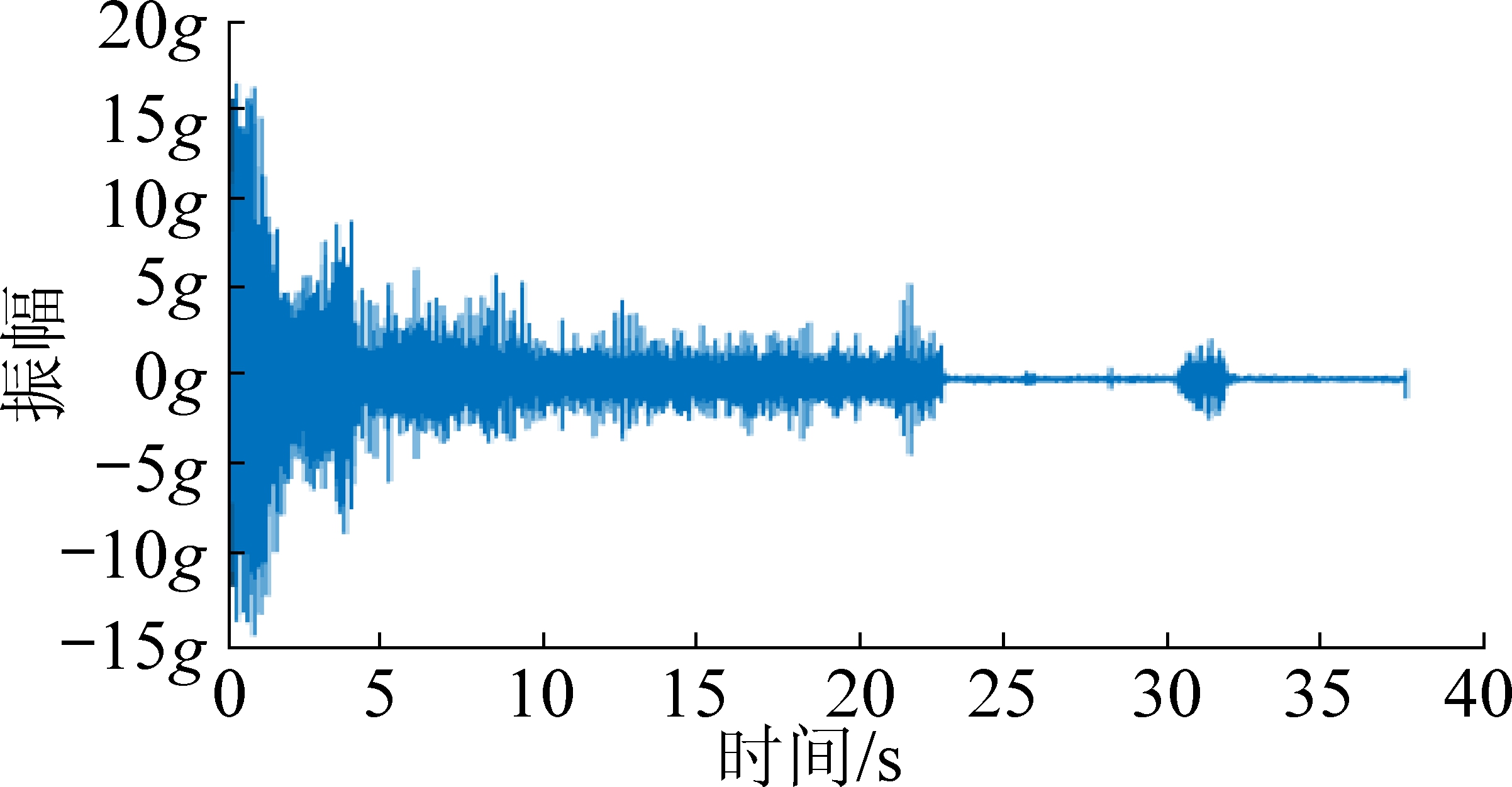
图10 Z方向时域信号
Fig.10 Z direction time domain signal
Z分量信号0~10 s和25~35 s信号经过短时傅里叶变换并滤波后如图12所示,时窗长度为8 000点,滑动点数为4 000点。钻头破岩较破煤时,低频信号(200 Hz以下)可通过能量的强弱对钻进不同的岩性进行很好的区分,破岩的能量比破煤的能量强5倍以上,在400 Hz和800 Hz位置破岩时能量较破煤时更明显,破煤只能在对应位置看到少量能量,在800 Hz以上就无明显能量。由图12b可以看出在对钻机工作状态划分时,钻机旋转未破岩在200 Hz和400 Hz都有很少能量,不足破岩和破煤时的1%,这些细微能量可作为对钻机旋转未破岩的工作状态的确定;钻机去水龙头和水平进退钻由于钻机没有进行旋转,只存在原有钻机工作的固有低频,可根据这种只具很低频率的信号作为钻机此种工作状态的确定。

图11 短时傅里叶变换滤波前后对比
Fig.11 Short time Fourier transform diagram in condition of unfiltered and filtered

图12 0~10 s和 25~35 s短时傅里叶变换
Fig.12 Short time Fourier transform in 0~10 s and 25~35 s
利用短时傅里叶变换的时频分析方法,可以综合判断出在破岩和破煤时频域信号的差异,以及钻机在不同工作状态时频域的差异,结合这些差异可以更好地指导在实际工作中对钻孔岩性的划分。
通过本次贵州实采钻柱振动录井数据的分析,也证明了本技术在煤矿生产当中应用的可行性。
4 结 论
1)采用不同幅频特征的正弦信号来模拟钻进过程中的不同破岩信号,选择不同长度窗口分别对其进行短时傅里叶变换。选择50个点的短时窗分析时,在时间上有较高的分辨率,频率的变化在第5 s时可准确判断,但频率分辨率较低,无法准确地确定频率的变化;在选择200个点的长时窗分析时,可清楚判断频率由50 Hz变化为20 Hz,但无法准确地确定在何时发生变化,故时窗长度的选择同时决定时间和频率上分辨效果。
2)分别对比短时傅里叶变换、小波包分解和Hilbert-Huang变化对钻进模拟信号处理效果。小波包分解和Hilbert-Huang变化在模拟信号5 s处分别出现了假频和模态混叠现象,干扰了对钻进模拟信号的分析,给解释带来困难。
3)采用短时傅里叶变换对实际钻柱振动录井过程中进行岩性划分和钻机工作状态识别。钻头破岩较破煤时,200 Hz以下能量比破煤的能量强5倍以上,400 Hz和800 Hz位置破岩时能量较破煤时更明显,破煤只能在对应位置看到少量能量,破岩仍具有很强能量,在800 Hz以上破煤就无能量。钻机旋转未破岩在200 Hz和400 Hz都有很少能量,能量值不足破岩和破煤时的1%,钻机去水龙头和水平进退钻由于钻机没有进行旋转,只存在10 Hz以下原有钻机工作的固有低频。
[1] 国家安全生产监督管理总局信息研究院.煤矿防治水规定[M].北京:煤炭工业出版社, 2009.
[2] ZHANG K,HOU R,ZHANG G,et al.Rock drillability assessment and lithology classification based on the operating parameters of a drifter: case study in a coal mine in China[J].Rock Mechanics & Rock Engineering,2016,49(1):329-334.
[3] 宿 雪,葛洪魁,杨 微,等.钻柱振动录井的研究现状及发展趋势[J].石油钻探技术,2009,37(5):15-19.
SU Xue,GE Hongkui,YANG Wei,et al.Research status and development trend of drill string vibration logging [J].Petroleum Drilling Technology,2009,37 (5): 15-19.
[4] FINNIE I,BAILEY J J.An experimental study of drill-string vibration[J].Journal of Engineering for Industry,1960,82(2):503-510.
[5] DAREING D W,LIVESAY B J.Longitudinal and angular drill-string vibrations with damping[J].Journal of Engineering for Industry,1968,90(4):671-681.
[6] DEILY F H,DAREING D W,PAFF G H,et al.Downhole measurements of drill string forces and motions[J].Journal of Manufacturing Science & Engineering,1968,90(2):200-211.
[7] LUTZ J.Instantaneous logging based on a dynamic theory of drilling[J].Journal of Petroleum Technology,1972,24(6):750-758.
[8] DENISON E B.High data-rate drilling telemetry system[J].Journal of Petroleum Technology,1979,31(2):155-163.
[9] BESAISOW A A,JAN Y M,SCHUH F J.Development of a surface drillstring vibration measurement system[C].Las Vegas:SPE Technical Conference and Exhibition,1985.
[10] WOLF S F.Field measurements of downhole drillstring vibrations[C]Las Vegas:SPE Technical Conference and Exhibition,1985.
[11] CLOSE D A,OWENS S C,MACPHERSON J D.Measurement of bha vibration using MWD[C].Dallas:SPE/IADC Drilling Conference,1988.
[12] MACPHERSON J D,JOGI P N,KINGMAN J E E.Application and analysis of simultaneous near bit and surface dynamics measurements[J].Spe Drilling & Completion,1998,16(4):230-238.
[13] SCHEN A E,SNELL A D,STANES B H.Optimization of bit drilling performance using a new small vibration logging tool l[R].SPE/IADC,2005.
[14] 崔士波,葛洪魁,陆 斌,等.钻柱振动信号特征及多次波成像[J].地球物理学进展,2010(2):714-720.
CUI Shibo.GE Hongkui,LU Bing,et al.Characteristics of drill string vibration signals and progress of multiple wave imaging [J].Progress in Geophysics,2010(2):714-720.
[15] 李子丰,张永贵,侯绪田,等.钻柱纵向和扭转振动分析[J].工程力学,2004,21(6):203-210.
LI Zifeng,ZHANG Yonggui,HOU Xutian,et al.Longitudinal and torsional vibration analysis of drill string [J].Engineering Mechanics,2004,21 (6):203-210.
[16] 韩 韧.矿井钻机随钻测振方法及其应用[D].徐州:中国矿业大学,2016.
[17] 高 岩,陈亚西,郭学增.钻柱振动信号采集系统及谱分析[J].录井工程,1998(3):44-51.
GAO Yan,CHEN Yanxi,GUO Xuezeng.Drill string vibration signal acquisition system and spectrum analysis [J].Logging Engineering,1998 (3): 44-51.
[18] 高 岩.三牙轮钻头钻进时钻柱轴向振动的特征[J].石油学报,2000,21(6):93-96.
GAO Yan.Characteristics of axial vibration of drill string during drilling of tri-cone bit [J].Journal of Petroleum,2000,21 (6): 93-96.
[19] 胡明顺,潘冬明,徐红利,等.几种时频分析方法对比及在煤田地震勘探中的应用[J].物探与化探,2009,33(6):691-695.
HU Mingshun,PAN Dongming,XU Hongli,et al.Comparison of several time-frequency analysis methods and their application in coalfield seismic exploration[J].Geophysical and Geochemical Exploration,2009,33(6): 691-695.
[20] HEISIG G,NEUBERT M.Lateral Drillstring Vibrations in Extended-Reach Wells[C].New orleans:IADC/SPE Drilling Conference,2000.
[21] GABOR D.Theory of communication[J].Iee Proc London,1946,93(73):58.
[22] GROSSMANN A,MORLET J.Decomposition of hardy functions into square integrable wavelets of constant shape[J].Siam J Math Anal 1984,15(4):723-736.
[23] RAHMAN M S, ZHENG K,GUPTA H. FSO-VR: steerable free space optics link for virtual reality headsets[C].Proceedings of the 4th ACM Workshop on Wearable Systems and Applications,2018.
[24] ZHENG K, Longtin J P, Gupta H. Vibration control analysis on energy saving for data centers using Optical Wireless Communication (OWC)[C].ASTFE Digital Library. Begel House Inc,2017.
[25] 郝 欢,王华力,魏 勤.经验模态分解理论及其应用[J].高技术通讯,2016,26(1):67-80.
HAO Huan ,WANG Huali,WEI Qin.Empirical mode decomposition theory and its application [J].High Technology News,2016,26(1): 67-80.
