0 引 言
在充分和超充分采动条件下,地表点的移动随着工作面的推进经历着一个由开始移动到剧烈移动,最后到停止移动的全过程[1-3]。地表下沉盆地将出现一静态的平底区域,在此区域内地表下沉量相同,地表仅有微小变形(各变形值等于或接近零)。若建筑位于该平底区域,其要经受动态变形的影响,建筑所受变形为全动态变形,虽然这种动态变形是临时性的,但是,它同样可以使建筑物在工作面推进过程中遭受破坏。开采沉陷是一个典型的时空力学过程[4],仅根据稳定(或静态)的沉陷规律并不能很好地解决地表建构筑物保护问题。
在进行动态移动沉陷研究中,实现动态预计可以较好地评价采动过程中地表建构筑物的变形过程和破坏程度[4]。地表动态移动沉陷受覆岩性质[5-6]、松散层厚度[7]、沉陷阶段[8]等诸多因素影响。其中,为了探究工作面推进速度对地表动态移动变形的影响,文献[9-10]以现场实测、相似材料模拟、数值模拟等手段,对不同推进速度下综放面围岩应力、位移、破坏情况等进行研究,获得了工作面推进速度对综放开采安全生产的影响;邵明明等[11]探讨了不同推进速度下逆断层上切应力和滑移量变化特征;文献[12-13]分析回采工作面的推进速度变化、停采对地面建筑物保护的影响;文献[14-16]分别给出了推进工作面推进速度与其地表动态移动变形的动态关系方程;F·朔贝尔等[17]认为,在特定的地质采矿条件下,存在一个对建筑物不利的推进速度危险区域,避开这一推进速度区域推进,能够有效地减小采动建筑物破坏应力;余学义[18]认为提高开采速度有利于减小地表采动损害;廉旭刚等[19]在对同一地质采矿条件下不同推进速度时的地表移动变形研究后认为,推进速度与地表移动曲线的动态峰值成反比,提高推进速度能够降低开采对地表的破坏,但无法降低开采对工作面开切眼与终采线上方地表的破坏。
为了实现对工作面地表建构筑物的有效保护,应深入研究沉陷移动变形的动态规律,从静态盆地与地表非稳定盆地间的演变过程与关系入手,切实考虑沉陷移动过程中动态变形值的大小与工作面推进速度的关系,满足地表建筑工程对沉陷变形的要求。笔者以东胜煤田10多个观测站实测数据为基础,分析工作面开采速度对地表动态倾斜和动态水平变形等的影响规律,并以高压线塔为保护对象,将研究结果成功地应用到地表建构筑物的保护中。
1 观测站概况
东胜矿区总体构造形态为一向南西倾斜的单斜构造,地层产状平缓,倾角一般1°~5°,地质构造简单。该矿生地层划分属于华北地层区鄂尔多斯分区,位于高头窑小区、乌审旗小区和准格尔旗-临县小区的交界地带。煤田上覆地层有侏罗系中统直罗组(J2z)、安定组(J2a)、白垩系下统志丹群(K1zh)、古匠系上新统(N2)、第四系(Q3-4)。主要含煤地层为侏罗系中下统延安组(J1-2y),含煤6组,23个可采煤层,其中2-1下、2-2中、3-1、4-1、4-2中、5-1、6-1中、6-2中为主要可采煤层,其他有5层为次要可采煤层,10层局部可采煤层,可采煤层总厚1.63~28.60 m,平均15.64 m,可采含煤系数1.04%~12.95%,平均7.57%。
从20世纪90年代至今,东胜矿区在柳塔矿、布尔台矿、寸草塔二矿、杨家村矿、察哈素矿、大柳塔矿、乌兰木伦矿、韩家湾矿、补连塔矿等10多个煤矿建立了地表移动观测站(表1)。
表1 东胜矿区煤层开采地表动态移动特征参数
Table 1 Surface dynamic movement parameter of coal seam mining in Dongsheng Miningfield

测站采深H/m采高m/m煤层倾角α/(°)推进速度C/(m·d-1)最大下沉量Wmax/mm超前影响角ω/(°)最大下沉速度角ø/(°)最大下沉速度Vmax/(mm·d-1)柳塔矿121061506.91~35.05 41770.464.8231.2布尔台矿22103-12953.41~48.32 13070.659.612.9寸草塔矿221112502.81~39.71 67263.957.342.2寸草塔二矿221113102.91~37.21 86564.458.428.3杨家村矿2222011335.01~45.13 50061.060.0240.0察哈素矿31014184.51~38.93 60076.057.8158.0大柳塔矿1203614.01~32.42 37864.062.3131.3乌兰木伦矿22071022.20~12.81 71682.071.798.2韩家湾矿23041304.12~48.02 29685.850.0185.3补连塔323012606.11~39.24 75870.076.8490.0
2 地表动态移动实测规律
2.1 地表移动持续时间特性分析
根据实测资料回归得到东胜煤田浅埋深快速开采条件下地表移动时间T0、Th与采深H、工作面推进速度C关系式为
T0=7.6H/C-12 (R2=0.91)
(1)
Th=3.2H/C (R2=0.94)
(2)
式中:T0、Th 分别为地表总移动时间和活跃阶段时间,d;H为采深,m;C为工作面推进速度,m/d。
由式(1)和式(2)可以看出,采深越大,地表移动持续时间越长;工作面推进速度越快,地表移动持续时间越短。
2.2 地表动态移动特征
超前影响角ω、最大下沉速度角ø和地表最大下沉速度Vmax与采深H、工作面推进速度C和采高m,经回归分析得到如下关系式为
ω=60.27+0.003 4HC (R2=0.79)
(3)
ø=62.91-0.006 4(H-h)C/m (R2=0.86)
(4)
Vmax=0.014 7![]() (R2=0.89)
(R2=0.89)
(5)
式中:Wmax为充分开采条件下,工作面地表最大下沉量,m,Wmax=mqcos α;q为下沉系数;α为煤层倾角;h为松散层厚度,m/d。
式(3)表明,采深与推进速度越大,超前影响角越大。式(4)表明,基岩厚度与工作面推进速度越大,最大下沉速度滞后角越小;采高越大,最大下沉速度滞后角越大。
地表最大下沉速度反映了地表移动的剧烈程度,主要和采深、工作面推进速度、采高和覆岩岩性有关。东胜矿区地表动态移动特征参数见表1 。式(5)表明,采深越大,地表最大下沉速度越小;采高与工作面推进速度越大,最大下沉速度越大。
3 地表动态沉陷数值模拟分析
3.1 矿区概况
FLAC3D软件适用于岩土工程中几何和物理高度非线性问题的稳定性分析,如地下开采的采动影响规律、地下巷道的大变形问题及围岩应力场问题、煤层开采后的覆岩破坏、移动及地表沉陷等问题。数值模型以东胜煤田典型地质采矿条件为原型,工作面平均采深150 m,煤层采高3 m,水平煤层,松散层厚度10 m。从地表往下各岩层岩样力学参数见表2。煤、岩层及松散层材料破坏准则采用摩尔-库仑(Mohr-Coulomb)准则。
表2 岩体物理力学参数
Table 2 physical and mechanical parameters of rock mass
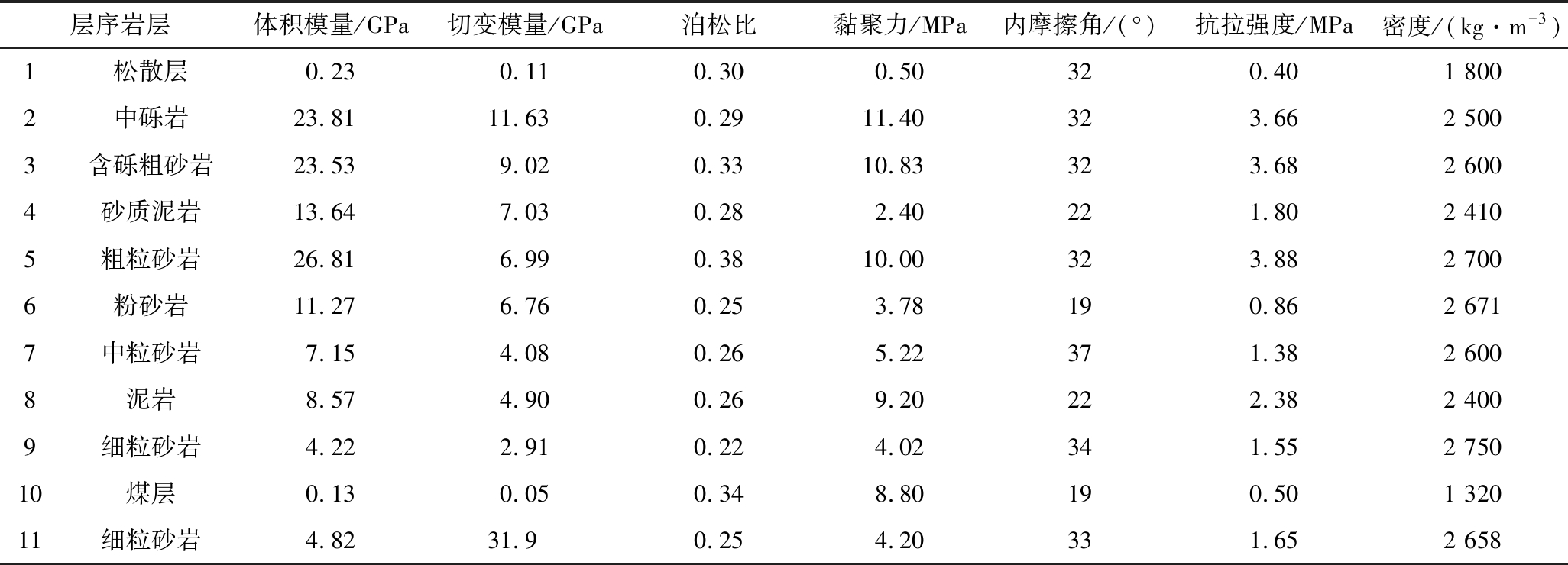
层序岩层体积模量/GPa切变模量/GPa泊松比黏聚力/MPa内摩擦角/(°)抗拉强度/MPa密度/(kg·m-3)1松散层0.230.110.300.50320.401 8002中砾岩23.8111.630.2911.40323.662 5003含砾粗砂岩23.539.020.3310.83323.682 6004砂质泥岩13.647.030.282.40221.802 4105粗粒砂岩26.816.990.3810.00323.882 7006粉砂岩11.276.760.253.78190.862 6717中粒砂岩7.154.080.265.22371.382 6008泥岩8.574.900.269.20222.382 4009细粒砂岩4.222.910.224.02341.552 75010煤层0.130.050.348.80190.501 32011细粒砂岩4.8231.90.254.20331.652 658
3.2 边界条件的确定
模型的左侧和右侧:采用简化位移边界条件,在水平X方向上可以运动、在垂直Y方向上固定的铰支,即u=0;模型底部:边界固定,边界水平、垂直位移均为零,即u=V=0;模型顶部:采用自由边界。
3.3 模拟方案设计
为了探究工作面不同推进速度影响下,煤层开采过程中地表动态移动变形特征,以上述东胜矿区某矿某工作面的地质采矿条件为原型,设计了6个模拟方案。各方案工作面推进速度分别为2.5、5.0、7.5、10.0、15.0、20.0 m/d。模拟开采工作面走向方向开采长度360 m,倾斜方向开采宽度240 m,采深150 m,采高3 m,基岩厚度取140 m,松散层厚度取10 m。基岩层与松散层层位与物理力学参数按照表2取值。计算模型尺寸:长×宽×高=800 m×640 m×200 m。
为便于分析地表动态移动变形规律,获取地表沉陷移动及变形数据,在计算模型上设置了2条监测线:A线沿工作面开采方向布置了133个测点,测线点间距5 m;B线垂直于工作面开采方向布置了109个测点,测线点间距5 m。图1显示了计算模型地表测点设置情况。

图1 工作面与地表测点设置相对位置关系
Fig.1 Relative position between working face of model and surface survey points.
3.4 工作面推进速度对地表变形影响分析
为了更有效地保护受采动影响的地表建构筑物,不仅需要掌握地表静态盆地的移动与变形的分布规律,而且还需要掌握地表动态移动变形规律。图2—图4分别为工作面推进速度5.0 和10.0 m/d时A测线在采动过程中地表下沉、倾斜和水平变形曲线。

图2 A测线在采动过程中地表下沉曲线
Fig.2 Surface dynamic subsidence curves of Line A

图3 A测线在采动过程中地表倾斜曲线
Fig.3 Surface dynamic inclination deformation curves of Line A

图4 A测线在采动过程中地表水平变形曲线
Fig.4 Surface dynamic horizontal deformation curves of Line A
分析工作面推进速度为5.0、10.0 m/d的地表移动变化曲线,可得到不同开采速度条件下地表移动变形量的动态变化特征:
1)相同的地质采矿条件下,不同的开采速度造成的地表移动变形过程有较大的不同。工作面开采过程中,快速推进较慢速推进在地表产生的下沉量大,而当工作面停采一定时间后,下沉曲线最终形态(静态盆地曲线)与开采速度大小无关。
2)地表移动初期,地表倾斜曲线上具有2个最大值:开切眼一侧的最大值指向工作面推进方向,其位置逐渐向前移动,且该最大值随着工作面的推进逐渐增大,直至地表移动稳定;工作面一侧最大值指向工作面推进的反方向,其位置随着工作面向前推进逐渐向前移动,数值亦逐渐增大。当工作面推进到(1.4~1.5)H后,达到全动态最大倾斜值,这时倾斜曲线的形状将保持不变,并随着工作面推进向前移动。工作面停采后,最大倾斜值继续增加,直至稳定时止。同时,随着工作面向前推进,动态倾斜曲线的零点亦逐渐向前移动。当出现全动态最大倾斜值后,零点变为零值区。零值区随工作面推进逐渐向前扩展,直至地表移动稳定时为止。从图3动态曲线变化中还可看出,在动态倾斜影响下,工作面中部地表将经历一定峰值(全动态最大倾斜)的破坏,此峰值的大小与推进速度成负相关。移动盆地中部地表在移动过程中,不仅变形数值随时间变化,而且符号(倾斜方向)也与时间有关。
3)地表在开采过程中经过一定峰值正水平拉伸破坏后,转变为压缩变形破坏,当工作面推进距离大于1.5H时,工作面中部压缩变形接近零,出现零值区域,即重新恢复到无拉压状态。
4)快速开采条件下,能够有效降低地表动态移动变形值,但快速开采并不能降低地表最终的移动变形量。
5)在静态下沉盆地中,最大地表变形值一般出现在盆地边缘附近,即开切眼和终采线上方地表;在下沉盆地中央部分,下沉达到最大值,下沉基本均匀分布。但是,在工作面开采过程中,静态盆地中心区地表处于动态最大变形状态,此时地表下沉和变形分布对临时盆地中心明显呈非对称状态。
3.5 工作面推进速度对地表动态变形峰值的影响
从图2—图4可以看出,当工作面距开切眼(0.7~0.9)H时,在至开切眼约0.4H处,地表的压缩变形量比地表移动稳定后的最终值还大。但在一般情况下,工作面开采过程中的最大变形值都小于地表稳定后的最终值。当工作面推进距离大于1.5H时,出现全动态下沉盆地。当建筑物处于全动态下沉盆地上时,建筑物处地表沿工作面推进方向的全动态最大变形量与全静态最大变形量之比,应根据本矿区实测资料估计。
由一些实测资料[1-3]得出:全动态最大倾斜位于推进工作面后方(0.1~0.25)H处,为全静态最大倾斜的0.6~0.8倍。全动态最大拉伸或最大正曲率位于推进工作面前方(0~0.1)H处,全静态最大压缩或最大负曲率位于推进工作面后方(0.3~0.5)H处。全静态盆地最大变形值估算出来后,按照此关系即可估算建筑物遭受的最大动态变形量。
表3给出了工作面推进速度C分别为2.5、5.0、7.5、10.0、15.0、20.0 m/d的各数值模拟计算的地表动态变形峰值。
表3 地表静态盆地最大变形值与动态变形峰值统计
Table 3 Maximum deformation value of static basins and peak value of dynamic deformation on surface

项目C=2.5 m/dC=5.0 m/dC=10.0 m/dC=12.5 m/dC=15.0 m/dC=20.0 m/dC/r比值0.030.070.130.170.200.27最大水平变形ε0/(mm·m-1)14.8014.8014.8014.8014.8014.80动态水平变形峰值ε′0/(mm·m-1)6.205.103.202.902.101.60ε′0/ε0比值0.420.340.220.200.140.11最大倾斜i0/(mm·m-1)28.8028.8028.8028.8028.8028.80动态倾斜峰值i′0/(mm·m-1)17.8015.40 12.60 10.80 9.20 6.10 i′0/i0比值0.62 0.53 0.44 0.38 0.32 0.21
根据表3数据,回归得到![]() 与工作面推进速度C及主要影响半径r比值(C/r)符合指数函数关系(图5、图6)。其关系式为
与工作面推进速度C及主要影响半径r比值(C/r)符合指数函数关系(图5、图6)。其关系式为
(6)
(7)
式中:![]() 分别为地表移动过程中倾斜峰值、水平变形峰值;i0、ε0分别为地表最终最大倾斜值、最大水平变形值;r为主要影响半径,m,r=H/tan β, tan β为主要影响角正切。
分别为地表移动过程中倾斜峰值、水平变形峰值;i0、ε0分别为地表最终最大倾斜值、最大水平变形值;r为主要影响半径,m,r=H/tan β, tan β为主要影响角正切。
综合以上分析,工作面推进速度对移动中的地表变形有很大的影响。工作面推进到一定距离后,至工作面停采前,地表各动态移动变形的峰值与推进速度成反比;工作面推进速度愈大,动态变形峰值就愈小。
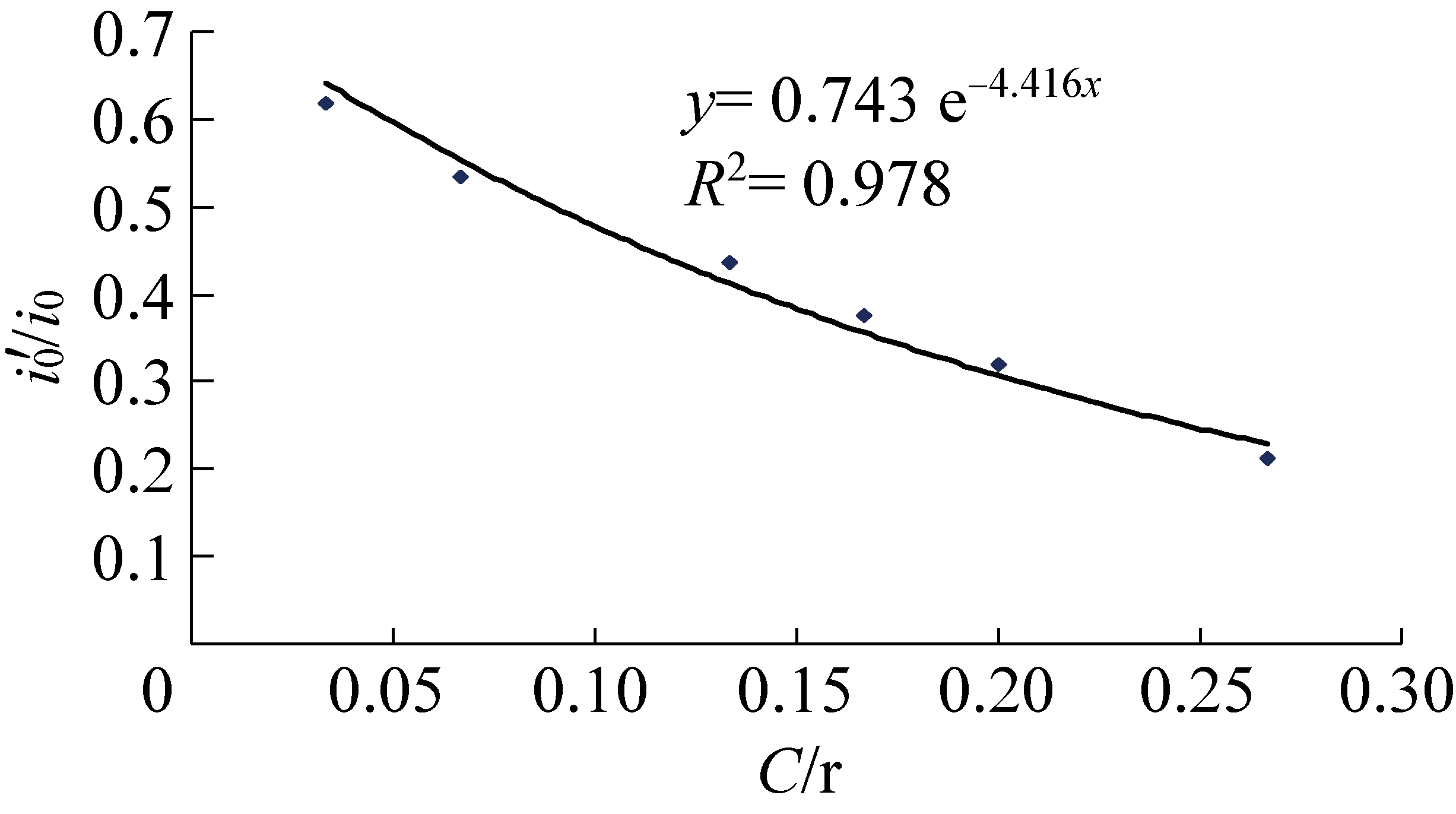
图![]() 与C/r间相关关系
与C/r间相关关系
Fig.5 Curve of correlation of ![]() and C/r
and C/r

图![]() 与C/r间相关关系
与C/r间相关关系
Fig.6 Curve of correlation of ![]() and C/r
and C/r
4 工作面安全推进速度的确定
布尔台煤矿22103-1工作面长4 249.9 m,宽360.0 m,开采2-1煤层,采高2.9 m,倾角1°~4°;上覆基岩厚224~357 m,松散层厚3.2~34.8 m;地表标高+1 260—+1 370 m,煤层底板标高+1 103—+1 046 m。工作面地表大部分为风积沙所覆盖,沟谷部分有基岩出露。对应工作面地表有布兰线220 kV铁塔3座;北乌线220 kV铁塔3座,青布线110 kV双杆4对,无名线110 kV双杆3趟17对。
通过开采沉陷预计表明,该工作面回采后,地表静态最大倾斜值将达到20.5 mm/m,静态最大水平变形将达到9.4 mm/m,这将超过杆塔能承受的倾斜极限值7 mm/m。为了保障输电线路的安全运行和22103-1工作面顺利回采,拟通过提高工作面推进速度,来降低工作面动态变形峰值至高压线塔临界变形值之下。
式(6)和式(7)表明:地表动态变形峰值与工作面开采速度之间基本符合指数函数的关系。设建筑物地表临界变形量为[ε]、倾斜为[i],由式(6)和式(7)得
(8)
式中:[C]为工作面安全推进速度,m/d。
对于东胜矿区,式(8)变化为
(9)
取r=H/tan β=224/2.2=102 m,i0=20.5 mm/m,取[i]=7.0 mm/m,[ε]=6.0 mm/m,代入式(9)可得[C]=6.6 m/d。结果表明,应使22103-1工作面推进速度达到6.6 m/d以上(实际回采中,平均推进速度达到8.3 m/d)。地表岩移实测表明,地表动态倾斜仅在局部区域达到了7 mm/m,在工作面回采过程中对受较大影响的杆塔基础实施调斜、抬高和加固措施,实现了22103-1工作面高压线路下压煤的安全回采。
5 结 论
1)据实测资料回归得到东胜矿区浅埋深快速开采条件下地表移动时间T0、Th与工作面采深H和工作面推进速度C存在如下关系为T0=7.6H/C-12,Th=3.2H/C。
2)东胜矿区地表最大下沉速度Vmax与工作面地表最大下沉量Wmax,工作面采深H和工作面推进速度C存在如下关系为Vmax=0.0147![]() 。
。
3)地表动态变形峰值、地表最终最大变形值与工作面推进速度C及主要影响半径r比值(C/r)符合指数函数的关系。
4)工作面安全推进速度[C]与地表临界变形值[ε]、[i]可由式(8)做定量表述,研究结果在高压线塔下压煤安全开采方案制定中的应用,验证了研究结果的有效性。
[1] 何国清,杨 伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[2] 刘国琛,廖国华.煤矿地表移动的基本规律[M].北京:中国工业出版社,1965.
[3] 煤炭科学研究院北京开采研究所.煤矿地表移动与覆岩破坏规律及其应用[M].北京:煤炭工业出版社,1981.
[4] 崔希民,邓喀中.煤矿开采沉陷预计理论与方法研究评述[J].煤炭科学技术,2017,45(1):160-169.
CUI Ximin,DENG Kazhong.Research review of predicting theory and method for coal mining subsidence[J].Coal Science and Technology,2017,45 (1):160-169.
[5] 钱鸣高,缪协兴,许家林.资源与环境协调(绿色)开采[J].煤炭学报,2007,32(1):1-7.
QIAN Minggao,MIAO Xiexing,XU Jialin.Green mining of coal resources harmonizing with environment[J].Journal of China Coal Society,2007,32(1):1-7.
[6] A G Hoffman,D M Clark,Bechtel T D.Abandoned deep mine subsidence investigation and remedisl design[R].Interstate 70,Guermsey County,Ohio,in 46th Highway Symposium:Charleston,West Virginia,1995.
[7] 李德海,许国胜,余华中.厚松散层煤层开采地表动态移动变形特征研究[J].煤炭科学技术,2014,42(7):103-106.
LI Dehai,XU Guosheng,YU Huazhong.Study on features of surface dynamic movement and deformation caused by coal mining under thick alluvium [J].Coal Science and Technology,2014,42 (7):103-106.
[8] 黄乐亭,王金庄.地表动态沉陷变形的3个阶段与变形速度的研究[J].煤炭学报,2006,31(4):420-424.
HUANG Leting,WANG Jinzhuang.Study on the three stages and deformation velocity of dynamic surface subsidence deformation [J].Journal of China Coal Society,2006,31 (4):420-424.
[9] 姜玉龙,张东峰,张小强,等.推进速度对回采巷道稳定性的影响[J].煤矿安全,2015,46(9):228-231.
JIANG Yulong,ZHANG Dongfeng,ZHANG Xiaoqiang,et al.Effect of advance speed on stability of mining gateways in fully mechanized face[J].Safety in Coal Mines,2015,46 (9):228-231.
[10] 谢广祥,常聚才,华心祝.开采速度对综放面围岩力学特征影响研究[J].岩土工程学报,2007,29(7):963-967.
XIE Guangxiang,CHANG Ju Cai,HUA Xin Zhu.Influence of mining velocity on mechanical characteristics of surrounding rock of fully mechanized top-coal caving face [J].Chinese Journal of Geotechnical Engineering,2007,29 (7):963-967.
[11] 邵明明,江 灿,王宏伟.不同开采速度下断层活化规律的数值分析[C]//北京力学会.北京力学会第二十四届学术年会会议论文集.北京:北京力学会,2018.
[12] 李德海,王长江,崔洪瑞,等.地表和岩层变形与工作面推进速度的关系[J].矿山压力与顶板管理,1995,12(S1):39-43.
LI Dehai,WANG Changjiang,CUI Hongrui,et al.Relationship between surface and rock deformation and advancing speed of working face [J].Ground Pressure and Strata Control,1995,12 (S1):39-43.
[13] 宁永香,焦希颖.回采速度对地表动态移动变形值的影响[J].煤炭科学技术,2004,32(11):74-76.
NING Yong Xiang,JIAO Xiying.Ming speed influenced to surface ground dynamic displacement and deformation[J].Coal Science and Technology,2004,32 (11):74-76.
[14] 彭小沾,崔希民,臧永强,等,时间函数与地表动态移动变形规律研究[J].北京科技大学学报,2004,26(4):341-344.
PENG Xiao ZHAN,CUI Ximin,ZANG Yongqiang,et al.Study on time function and dynamic movement and deformation of the earth surface [J].Journal of University of Science and Technology Beijing,2004,26 (4):341-344
[15] 朱广轶,徐征慧,解 陈,等.老采空区地表残余移动变形影响函数研究[J].岩石力学与工程学报,2014,33(10):1962-1970.
ZHU Guangyi,XU Zhenghui ,XIE Chen,et al.Study of influence functions of surface residual movement and deformation above old goaf[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(10):1962-1970.
[16] 崔希民,缪协兴,赵英利,等.论地表移动过程的时间函数[J].煤炭学报,1999,24(5):453-456.
CUI Ximin,MIAO Xiexing,ZHAO Yingli,et al.Discussion on the time function of time dependent surface movement[J].Journal of China Coal Society,1999,24(5):453-456.
[17] 朔贝尔F,冯克浦.减小开采损害的最佳回采速度[J].矿山测量,1989(2):80-84.
F Hebell,FENG Kepu.Reducing the optimal speed of mining damage [J].Mine Survey,1989 (2):80-84.
[18] 余学义.开采速度对地表建筑物损害影响分析[J].西安科技学院学报,2001,21(2):97-101.
YU Xueyi.Analysis of damage effect of mining velocity on surface buildings[J].Journal of Xi′an University of Science and Technology,2001,21(2):97-101.
[19] 廉旭刚,郭博婷,胡海峰.工作面推进速度对地表移动变形的影响研究[J].煤炭工程,2016,48(4):74-77.
LIAN Xugang,GUO Boting,HU Haifeng.Influences of working face advancing rate on surface movement and deformation [J].Coal Engineering,2016,48 (4):74-77.
