0 引 言
随着计算机技术的发展，数值模拟正成为研究岩石力学工程的有效手段，但数值模拟参数如何选择更加符合现场实际情况是广大岩石力学工作者一直关注的问题。在参数选择上部分学者认为模拟只是对比结果的相对性，对于参数选择并不十分严格，部分学者则根据经验取岩石物理力学参数的1/4～1/2，实际上这涉及到岩石力学行为的尺度律问题。因此，针对岩石尺寸效应的研究对于矿井数值模拟参数的选取十分重要。就多尺寸或者跨尺寸问题来说，是一个非常宽泛而又难以解决的问题，笔者仅针对煤岩体强度尺寸效应方面进行初步研究。
白以龙[1]指出细观尺寸是不变的材料常数，当把室内小型试验与工程原型比较时，该尺度比将随宏观尺寸的变化而变化，从而破坏了几何相似。关于岩体强度方面的尺寸效应是研究最多且最重要的内容。岩石强度尺寸效应并不是指具体2个大小不同岩样强度的差异，也不能简单地解释为，岩样尺度越小，所含的缺陷就越少，因而强度增大，实际上，尺寸效应是综合的平均效应，即大量形状和大小完全相同的岩样，其强度平均值随直径或边长的增大而减小的规律。刘宝琛等[2]基于国内外大量单轴压缩的试验结果，总结出尺寸效应的3条共性规律，提出了尺寸效应的指数函数表达式；尤明庆等[3]认为岩样强度的离散性可能掩盖尺寸效应，要获得较为准确的表达式不仅要有足够的试验数据，还要有足够多的大尺寸岩样的试验结果；周国林等[4]在考虑岩石变形和破坏局部化的基础上，提出了一个新的强度准则，并利用该准则定量描述了岩石强度的尺寸效应；杨友卿[5]将损伤力学与分形几何理论相结合起来，定量分析了岩石强度的尺寸效应；何满潮等[6]通过建立工程岩体的连续性模型，对工程岩体力学参数的尺寸效应开展研究。
研究岩体尺寸效应必须运用统计观点，针对这方面研究，学者们通过理论分析[7-9]、数值模拟[10-12]、实验室试验建立了部分数学模型，形成了相关理论[13-14]，目前主要包含2类认识：一是认为岩石材料强度尺寸效应是由于岩样端部摩擦效应所致；二是认为岩石材料强度尺寸效应源于材料的非均质性。可见，岩石尺度律的问题还需要大量的理论试验研究，以获得更深层次的理解认识。同时查阅相关文献发现关于岩石尺寸效应的研究大多是基于缺陷较少的大理石、花岗岩、灰岩等展开的，对于断层、裂缝、裂隙、孔洞、孔隙多且分布不均匀的煤，尤其是强度值接近于岩的强冲击倾向性煤研究较少。因此笔者针对强冲击倾向性煤体为研究对象，通过实验室试验和数值模拟探讨煤体尺寸效应的外在表象和内在本质。
1 煤体强度尺寸效应的实验室试验
以某矿强冲击倾向性煤体作为研究对象，具体指标如下：冲击倾向性鉴定中的动态破坏时间、弹性能量指数、冲击能量指数、单轴抗压强度分别为118 ms、15.062、25.702、28.243 MPa，分别被鉴定为弱、强、强、强，综合判定为强冲击倾向性。
在实验室制取不同尺寸试样，进行单轴加载试验。通过试验发现不同尺寸试样其单轴抗压强度差别较大，具有明显的尺寸效应，见表1。从表1可得表面有宏观或微小裂隙的试样与同尺寸试样相比其强度明显偏小，这也是造成煤岩物理力学参数测试中数据离散性的主要原因。
表1 不同尺寸试样单轴抗压强度试验值
Table 1 Uniaxial compressive strength test values ofspecimens with different sizes
尺寸(长×宽×高)/mm×mm×mm试样编号Rc/MPa表面裂隙情况Rc平均值/MPa50×50×10050-133.247无裂隙50-224.652微小竖向裂隙50-331.092无裂隙50-426.948微小横向裂隙50-523.412微小竖向裂隙50-629.852无裂隙28.20175×75×15075-125.406无裂隙75-221.339微小竖向裂隙75-323.042无裂隙75-423.507无裂隙75-519.933横向层理裂隙75-619.324微小竖向裂隙22.109100×100×200100-111.417明显宏观竖向、横向裂隙,小范围交叉100-219.527横向微小裂隙100-320.124无裂隙100-421.579无裂隙100-517.775微小竖向裂隙100-617.722明显宏观竖向裂隙17.745
结合刘宝琛等[2]提出的尺寸效应的经验公式：Rc=r+αexp(-βD)(r为岩体强度,MPa；α为岩石强度与岩体强度之差；β为衰减系数；D为试样尺寸)，对实验室3种尺寸下单轴抗压强度进行指数曲线拟合，结果如图1所示。
图1 试样强度尺寸效应数据拟合曲线
Fig.1 Fitting curve of specimen strength size effect data
通过曲线拟合发现，强冲击倾向性煤样单轴强度表现出明显的尺寸效应，通过拟合得出该类煤体的强度为9.125 MPa，细观微元平均强度为49.962 MPa，衰减系数为0.015。
由于所取煤块本身缺陷分布的不均匀性以及试样在制备过程中的机械损伤，导致试样强度值存在离散性，离散性出现的主要原因是样本空间小，实验样本数少，而大缺陷试样的存在使数据偏离度增大。拟合曲线获得的经验公式能够说明试样本身存在尺寸效应，但确切表达式的获取需要大量的样本空间，同时该算式没有把尺寸效应的内在本质表达出来。
2 煤体强度尺寸效应理论分析
准脆性材料的2个重要特征是强度的离散性和强度的体积效应，这与脆性材料内部存在大量不同尺寸随机分布的孔洞、裂隙等细观缺陷有关。材料强度的这种不确定性可用概率统计理论来分析[9]。Weibull分布最早采用最弱链概念分析和描述强度的尺寸效应现象，该理论认为材料的强度决定于其最弱链的强度，即当某点的应力超过该点的缺陷强度时，破坏就会发生。
首先假定材料是各向同性且统计平均的，其次最危险裂纹的失稳扩展将导致整个构件断裂。煤岩失稳破坏的强度分布可由三参数Weibull分布近似表示，其概率密度函数f(σ)为
(1)
其中，〈·〉为McCauley括号；σu为σ的下限值；σ0为尺度参数，σ0>0；m为均质度，且m>0，m越大，材料越均匀；σ为强度统称。由一条裂纹引发煤岩失稳破坏的概率为
(2)
由最弱链原理可知，含有N条裂纹引发煤岩失稳破坏的概率为
(3)
煤岩试样内部裂纹、缺陷数量随试件体积的增大而增加，即N∝V，V为裂隙扩展区(σ≥σu)体积。对于一般情况，式(3)可推广为
(4)
其中，γ为裂纹体密度。对于脆性材料，取σu=0得：
(5)
其中，
，显然，Vc∝V，则由式(5)可以得到强度的均值为：
(6)
其中，Γ为伽马函数。当m趋于无穷大时，
即在材料为无限均匀时不存在着尺寸效应。
设2种尺寸的试件在均匀受力下，对应的平均强度和体积分别为
和
则
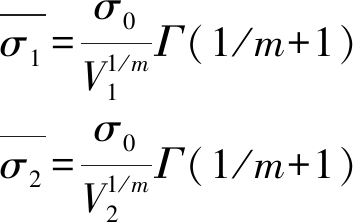
(7)
由式(7)得到尺寸效应的关系为
(8)
对式(8)两边取对数可得到m值，此时
故已知2组试验数据就可以通过计算得到m。把某试样体积V0当作参照体(一般把实验室标准试样当做参照体)，令Vc=V/V0，进而求解出σ0，而此时Weibull强度尺寸效应可简化为
(9)
3 煤体强度尺寸效应影响因素分析
3.1 影响因素分析
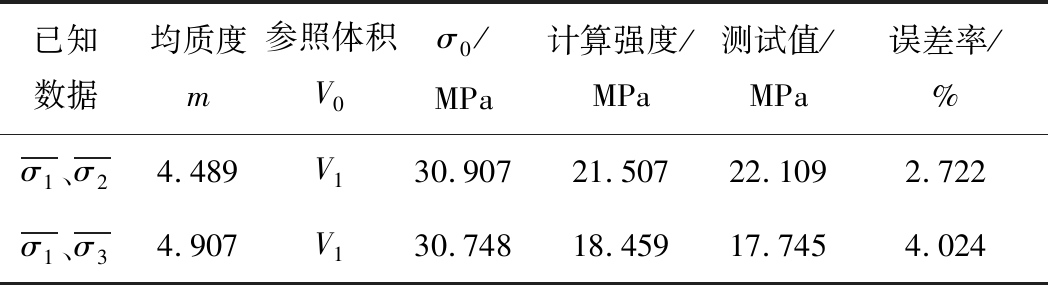
以不同尺寸试验数据为基础，同时结合式(7)、(8)，获得试验样本的m值、σ0值，详见表2，表2中
分别表示50 mm×50 mm×100 mm试样的平均强度和体积，
分别为75 mm×75 mm×100 mm，100 mm×100 mm×100 mm试样的平均强度。
表2 不同条件下Weibull分布各参数计算值
Table 2 Calculated values of Weibull distributionparameters under different conditions
已知数据均质度m参照体积V0σ0/MPa计算强度/MPa测试值/MPa误差率/%σ1、σ24.489V130.90721.50722.1092.722σ1、σ34.907V130.74818.45917.7454.024
从表2中可以看出，采用式(9)计算出的平均强度与试验结果相差不大，误差小于5%，可见，基于Weibull分布推导的尺寸效应表达式能够反映出煤岩体的强度尺寸效应。而不同条件下计算的m值存在差异，表明m值改变将直接影响尺寸效应结果的准确性。
基于Γ(x)的性质可知，Γ(1/m+1)在区间[2.2，+∞)内为增函数且Γ(1/m+1)>0。结合Weibull强度尺寸效应的表达式(9)，当V/V0>1、m∈[2.2，+∞)时，平均应力
为m的增函数。可见均质度m对强度尺寸效应影响明显。
3.2 均质度影响效应分析
RFPA2D模拟软件是基于有限元理论和统计损伤理论，考虑材料性质的非均性及缺陷分布的随机性，并把这种材料性质的统计分布假设结合到数值计算方法(有限元法)中，对满足给定强度准则的单元进行破坏处理，从而实现非均匀性材料破坏过程的数值模拟。
模拟仅考虑尺寸和均质度2个参量的变化，采用正交实验，分析均质度和尺寸改变对单轴抗压强度的影响。模型尺寸依次取：15 mm×15 mm×30 mm、25 mm×25 mm×50 mm、50 mm×50 mm×100 mm、75 mm×75 mm×150 mm、100 mm×100 mm×200 mm、150 mm×150 mm×300 mm；模型均质度m分别取0.5、1、1.5、2、3、4、6、8、10、15、20。划分单元尺寸为1 mm×1 mm×1 mm，加载速度为0.002 mm/步，采用步中步加载方式。提取不同加载步下的应力值，绘制同尺寸不同均质度试样的应力应变曲线(以50 mm×50 mm×100 mm尺寸试样为例)及单轴抗压强度随均质度m的变化曲线，如图2所示。
图2 均质度对试样单轴抗压强度的影响
Fig. 2 Effect of homogeneity on uniaxial compressive strength of specimens
从图2a可得随着均质度增大，单轴抗压强度增大，试样应力应变曲线在破坏时呈现直线下降现象，趋于脆性破坏。这说明均质度大的无缺陷材料，其承受破坏能力增加，一旦破坏将是致命的、突然的脆性破坏。从图2c可得随着均质度增大，单轴抗压强度增长曲线呈上凸型，均质度变化敏感区域为m∈[0.5～3.0]，可以将曲线大致划分为3个阶段：波动上升阶段(m<2)，随着m增大，曲线呈波动变化，整体上升；快速增长阶段(2≤m≤6)，随着m增大，单轴抗压强度增加非常显著；渐缓增长阶段(m>6)、此阶段随着m增大曲线趋势渐缓，曲线斜率明显减小，当m大到一定数值时，强度值应当逐渐收敛到某一定值。
从图2d可得，无论均质度m如何变化，在均质度固定时，随着尺寸增大，峰值强度降低，单轴抗压强度均表现出明显的尺寸效应；随着均质度增大，尺寸变化对强度的影响程度降低。在m=0.5时，15 mm×15 mm×30 mm试样强度为与150 mm×150 mm×300 mm试样强度差为9.90 MPa，当m=20时，15 mm×15 mm×30 mm试样强度为与150 mm×150 mm×300 mm试样强度差为4.01 MPa，呈现递减趋势，可见随着均质度m增大，煤岩试样内部缺陷、裂隙减少，趋于各向同性体，尺寸效应减弱。
通过以上数值模拟可知，均质度m对煤岩体强度尺寸效应影响较大。具体来讲缺陷级别和缺陷层次对强度尺寸效应影响显著，煤岩体的构造层次越小，在本层次上强度越高，不同层次缺陷并存时，高层次缺陷对岩体的变形、稳定、破坏起着主导控制作用。煤岩体内部缺陷的分布状态可以通过均质度大小来衡量，因此可认为均质度是煤岩体轻度尺寸效应的主要影响因素，是导致强度尺寸效应的根本原因。当缺陷层次相对于煤岩层体积较大时，煤岩层均质度m下降，强度明显降低，煤体在较低应力状态下就发生破坏，这也解释了工作面回采过程中遇到隐蔽断层时，通常会发生较大动力灾害。
4 结 论
1)强冲击倾向性煤体强度具有明显的尺寸效应，随着尺寸增大，强度降低，符合指数函数关系，但曲线的准确表达参数需要大量的样本空间。
2)利用最弱链理论的Weibull分布推导获得尺寸效应的数学表达式，结合实验室数据验证公式的合理性，得出均质度m对煤岩体强度影响较大。
3)在尺寸一定时，随着均质度增大，煤岩强度表现为上凸的增长曲线，可划分为3个阶段：波动上升阶段、快速增长阶段、渐缓增长阶段，当均质度增大到一定值时，强度值逐渐收敛到某一定值，即为煤岩体细观尺寸强度。
4)随着均质度增大，煤岩试样内部缺陷、裂隙减少，趋于各向同性体，尺寸效应减弱。
[1] 白以龙.工程结构损伤的两个重要科学问题:分布式损伤和尺寸效应[J].华南理工大学学报:自然科学版,2002,30(11):11-14.
BAI Yilong.Two important scientific problems in engineering structures:distributed damages and scale effect[J].Journal of South China University of Technology:Natural Science Edition, 2002, 30 (11) :11-14.
[2] 刘宝琛,张寄生,杜奇中,等.岩石抗压强度的尺寸效应[J].岩石力学与工程学报, 1998, 17(6): 611-614.
LIU Baochen，ZHANG Jisheng，DU Qizhong，et al. A study of size effect for compression strength of rock[J]. Chinese Journal of Rock Mechanics and Engineering,1998,17(6): 611-614.
[3] 尤明庆,华安增. 岩样单轴压缩下的尺寸效应和矿柱支承性能[J].煤炭学报,1997,22(1)：37-41.
YOU Mingqing,HUA Anzeng. The size effect of uniaxial compression of rock specimen and support capacity of ore pillar[J]. Journal of China Coal Society,1997,22(1):37-41.
[4] 周国林,谭国柱,李启光,等.剪切破坏模式下岩石的强度准则[J].岩石力学与工程学报,2001, 20(6):753-762.
ZHOU Guolin,TAN Guozhu,LI Qiguang,et al. New strength criterion for rock with shear failure mode[J]. Chinese Journal of Rock Mechanics and Engineering,2001,20(6):753-762.
[5] 杨友卿.岩石强度的损伤力学分析[J].岩石力学与工程学报,1999,18(1):23-27.
YANG Youqing. Continuum damage mechanics analysis of rock strength[J]. Chinese Journal of Rock Mechanics and Engineering，1999，18(1):23-27.
[6] 何满潮,薛廷河,彭延飞. 工程岩体力学参数确定方法的研究[J].岩石力学与工程学报,2001,20(2):225-229.
HE Manchao,XUE Tinghe, PENG Yanfei. A new way of determining mechanical parameters of engineering rock masses[J]. Chinese Journal of Rock Mechanics and Engineering,2001,20(2): 225-229.
[7] 李 宏,朱浮声,王泳嘉，等.岩石统计细观损伤与局部弱化失稳的尺寸效应[J].岩石力学与工程学报,1999,18(1):28-32.
LI Hong,ZHU Fusheng,WANG Yongjia,et al. Size effects of statistical meso-damage and local softening instability of rock[J]. Chinese Journal of Rock Mechanics and Engineering,1999,18(1): 28-32.
[8] 戚承志,钱七虎.岩体构造层次及其力学行为[J].世界地震工程, 2004, 20(2): 35-38.
QI Chengzhi,QIAN Qihu. Hierarchy of rock masses and their mechanical behavior[J].World Earthquake Engineering,2004, 20(2):35-38.
[9] 张 明,卢裕杰,杨 强.准脆性材料的破坏概率与强度尺寸效应[J].岩石力学与工程学报,2010,29(9): 1782-1789.
ZHANG Ming, LU Yujie, YANG Qiang. Failure probability and strength size effect of quasi-brittle materials [J].Chinese Journal of Rock and Engineering, 2010,29(9): 1782-1789.
[10] 张 明,卢裕杰,介玉新，等.不同加载条件下岩石强度尺寸效应的数值模拟[J].水力发电学报,2011,30(4):147-154.
ZHANG Ming, LU Yujie, JIE Yuxin,et al.Numerical simulation of strength size effect of rock under different loading [J]. Journal of Hydroelectric Engineering,2011, 30(4):147-154.
[11] 吕兆兴,冯增朝,赵阳升.岩石的非均质性对其材料强度尺寸效应的影响[J]. 煤炭学报, 2007, 32(9): 917-920.
LYU Zhaoxing,FENG Zengchao, ZHAO Yangsheng. Influence of rock in-homogeneity on strength-size effect of rock materials [J]. Journal of China Coal Society,2007,32(9) : 917-920.
[12] 林 鹏,唐春安,黄凯珠,等.脆性介质中裂纹与孔洞缺陷的分类与尺寸效应[J].岩石力学与工程学报,2002, 21 (S2):2296-2300.
LIN Peng,TANG Chun’an,WONG Kaizhu,et al. Classification and size effect of flaw and pore in brittle medium[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21 (S2):2296-2300.
[13] 赵 瑜,李晓红,卢义玉,等.瓦斯压力对非均质煤岩抗压强度尺寸效应的影响[J].煤炭学报,2009,34(8):1081-1085.
ZHAO Yu,LI Xiaohong,LU Yiyu,et al.Influence of gas pressure on compressive strength size effect of inhomogeneous coal[J].Journal of China Coal Society,2009,34(8):1081-1085.
[14] 冯增朝,赵阳升. 岩体裂隙尺度对其变形与破坏的控制作用[J]. 岩石力学与工程学报,2008, 27(1):78-83.
FENG Zengchao,ZHAO Yangsheng. Control effect of fissure scale on deformation andfailure of rock mass[J]. Chinese Journal of Rock Mechanics and Engineering,2008, 27(1): 78-83.
