0 引 言
陷落柱是煤层开采过程中经常遇到的一种特殊地质构造,陷落柱的存在对综采工作面的布置和推进产生巨大的影响[1,2]。在陷落柱比较发育的区域,回采工作面很难实现常规化布置,导致综采工作面的开采效率大幅度降低,同时增加了发生圧架、压巷或突水事故的可能性[3-6],掌握陷落柱周围塑性扩展区域和应力分布特征有助于工作面安全顺利通过陷落柱。
由于陷落柱在煤田地质中分布的特殊性以及对煤层开采的巨大影响,许多学者研究分析了陷落柱对煤层开采的影响。左建平等[7]针对陷落柱附近的辅助运输巷底鼓严重的问题,建立了陷落柱周围塑性破坏区的力学模型,确定了巷道加固段长度;黄友金等[8]运用数值模拟软件研究了工作面推进过程中陷落柱变形以及煤层应力变化情况;许进鹏等[9-11]运用弹塑性理论,分析了陷落柱周边的应力分布状态,并运用模拟软件进行验证;屠世浩等[12]根据陷落柱围岩破坏特征,建立了陷落柱围岩的应力厚筒壁四区模型,并依据四区模型提出了工作面过陷落柱的安全防护措施。以上学者的研究成果确定了陷落柱周边的应力分布状态以及对工作面推进的影响,极大丰富了对陷落柱的认识。然而,多数学者对陷落柱的研究是基于工作面或巷道过单一陷落柱的类型,而对于近距离陷落柱对工作面推进的影响以及陷落柱之间的相互影响鲜有研究。
笔者以某矿63310工作面的陷落柱为研究对象,采用理论分析、数值模拟和现场监测相结合的方法,研究分析近距离陷落柱周围的塑性扩展区域、应力分布特征和陷落柱之间的应力分布状态,为多陷落柱分布的工作面顺利推进提供依据。
1 工程概况
某矿63310工作面埋深388~473 m、平均415 m,工作面走向长1 000 m、倾向长256 m,主采的3号煤层厚2.0~3.5 m、平均2.5 m,煤层倾角为3°~13°、平均6°。工作面直接顶为厚4.8 m的细粒砂岩和砂质泥岩,基本顶为厚6.99 m的中粒砂岩,直接底为厚9.98 m的砂质泥岩,基本底为厚3.5 m的粉砂岩。工作面内陷落柱长轴为15~75 m,短轴为10~28 m,主要分布在工作面偏回风巷侧,具体分布和参数如图1和表1所示。

图1 63310工作面陷落柱分布
Fig.1 Distribution of collapse columns in No.63310 working face
表1 工作面内陷落柱的具体参数
Table 1 Specific parameters of the collapsingcolumn in working face
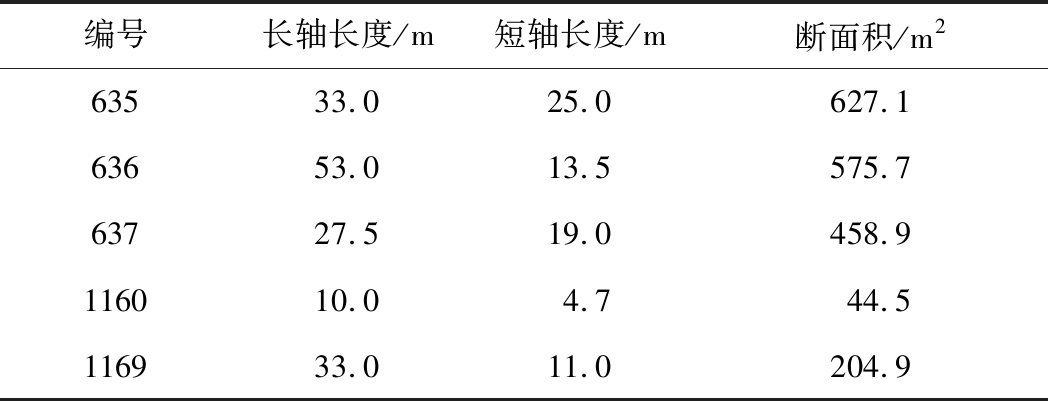
编号长轴长度/m短轴长度/m断面积/m263533.025.0627.163653.013.5575.763727.519.0458.9116010.04.744.5116933.011.0204.9
由图1可知635号和637号陷落柱在工作面走向相距26.83 m,倾向方向相距5.27 m,柱体边缘间的距离为27.34 m,分布距离较近,开采期间陷落柱附近未出现涌水情况。工作面在推过近距离陷落柱过程中,陷落柱有可能在采动应力的影响下导致塑性扩展区域贯通,造成陷落柱之间围岩破碎,威胁工作面的安全开采。因此,有必要研究近距离陷落柱对工作面推进的影响规律。
2 近距离陷落柱的塑性发育特征
工作面揭露陷落柱的现场观测表明陷落柱柱体内部岩体呈现松散、弱胶结堆积状态,柱体周边一定范围内围岩节理裂隙比较发育。假设围岩为均质,各向同性介质,陷落柱断面为圆形,则单一陷落柱周边的塑型扩展区域如图2所示,其中:λH为原岩应力;R为陷落柱周边塑性扩展区域的半径;R0为陷落柱的半径;P0为平均水平应力;P为陷落柱内部柱体对内壁的水平支撑力;陷落柱在上覆岩层和侧向围岩作用下,周边产生塑性扩展区域。

图2 单一陷落柱周边的塑性扩展区域
Fig.2 Plastic expansion area around a single collapse column
文献[10]应用弹塑性力学理论,确定了圆形陷落柱周边塑性区的径向应力分布见式(1)。
(1)
文献[13]依据弹性区和塑性区交界点应力分布的特点,确定了弹性区和塑性区交界处的径向应力为
σr2=P0(1-sin φ)-Ccos φ
(2)
根据应力分布的连续性特征,联立式(1)和式(2),可以确定塑性扩展区域的半径为
(3)
式中:φ为内摩擦角,(°);C为黏聚力,MPa。
对于近距离陷落柱,由于单个陷落柱周边形成一定范围的塑性扩展区域,导致近距离陷落柱的塑性扩展区域有可能出现交叉重叠,其周边的塑性扩展区域如图3所示。

图3 近距离陷落柱周边的塑性扩展区域
Fig.3 Plastic expansion area around the close-range collapse column
由图3可知近距离陷落柱之间的距离与单个陷落柱的塑性扩展区域的大小存在一定的关系,即:
ΔL=L-R1-R2
(4)
式中:ΔL为近距离陷落柱相邻边缘之间的距离,m;L为近距离陷落柱柱体中心之间的距离,m;R1和R2分别为2个陷落柱的塑性扩展区域的半径,m。
根据弹塑性力学和公式(4)可知:ΔL的大小决定了近距离陷落柱之间的应力分布状态。当ΔL<0时,陷落柱的塑性扩展区域存在交叉重叠,此时陷落柱之间处于塑性应力降低状态;当ΔL=0时,陷落柱塑性扩展区域的边界刚好接触,陷落柱之间处于由塑性应力降低向弹性应力升高过渡的临界状态;当ΔL>0时,陷落柱之间处于弹性应力升高状态或原岩应力状态,而且由于相互之间的叠加作用,导致应力集中程度大于单个陷落柱的应力集中程度。ΔL值的大小可用于判断工作面推进多陷落柱条件时陷落柱之间的应力状态。陷落柱之间不同距离的应力分布如图4所示,KA、KB、KD分别表示不同位置的应力集中系数。

图4 陷落柱之间不同距离的应力分布
Fig.4 Stress distribution at different distances between collapse columns
由图4可知,陷落柱相距不同距离时,应力集中系数均满足KA>1和KB>1。其中,图4a中两陷落柱相距较远,塑性扩展区域未贯通,应力未叠加,此时KD=1;图4b中两陷落柱塑性扩展区域贯通,应力叠加,即KD>KA和KD>KB;图4c中两陷落柱塑性扩展区域边界相切,应力相互影响,此时KD=1;图4d中两陷落柱塑性扩展区域贯通,应力相互影响,即KD<1。由式(3)可知:陷落柱周围塑性扩展区域的半径与陷落柱半径成正比。根据635号和637号陷落柱条件,取R01=12 m、R02=16 m、φ=25°、C=1.82 MPa;由于柱体内部为松散弱胶结岩体,对陷落柱内壁的支撑力较小,可忽略不计,故P取0。
对于平均水平应力P0,霍克和布朗[14]在总结大量有关地应力资料后,提出平均水平应力和垂直应力比值K的表达式,即:
100/H+0.3≤K≤1 500/H+0.5
(5)
式中:K为平均水平应力和垂直应力的比值,即K=P0/σz;H为煤层的埋深,取415 m。
康红普等[15-16]通过大量现场地应力实测,总结归纳后提出了山西煤矿井下平均水平应力与垂直应力的比值K同埋深H的关系,用如下公式表示:
K=129.6/H+0.559 5
(6)
由式(5)和式(6)可知:当63310工作面埋深388~473 m时,依据式(5)求得K值介于0.54~4.11;依据式(6)求得K值介于0.83~0.89。结合式(5)和式(6)求得的应力比值,最终确定平均水平应力和垂直应力的比值介于0.83~0.89,由σz=λH=10.375 MPa,求得平均水平应力P0=Kσz=8.61~9.23 MPa;代入式(3)求得637号和635号陷落柱的塑性扩展半径分别为:R1=18.26~18.88 m和R2=24.35~25.17 m。
采用上文提出的判断方法ΔL进行验证,确定近距离陷落柱之间的应力状态。结合图1中两陷落柱柱体边缘之间的距离,取635号和637号陷落柱塑性扩展区域的半径分别为25.17 m和18.88 m,则ΔL=11.29 m>0,即陷落柱之间处于弹性应力升高状态。
3 近距离陷落柱对工作面推进影响数值模拟分析
3.1 数值模型
为进一步研究近距离陷落柱对工作面推进的影响,采用Flac3D数值软件模拟工作面的推进过程,建立如图5所示的数值模型。

图5 工作面推进陷落柱的模型
Fig.5 Model of the working surface advancing collapse column
模型尺寸为280 m×160 m×67 m(长×宽×高),采用摩尔-库仑本构模型。因63310工作面实际长度为256 m,为简化模型的计算量,根据对称性原则,选取工作面的1/2建立模型。模型中工作面沿着y方向布置,长度为128 m,留设32 m保护煤柱,以消除边界效应对结果的影响;工作面沿x方向推进,开切眼位置距离左边界30 m。模型底部固定垂直方向位移,四周限制水平方向位移。根据煤层埋深和建模高度,在模型上方施加9.5 MPa的均布载荷,用以模拟上覆岩层的质量;左右及前后边界按水平应力和垂直应力之间的关系施加沿z方向的渐变载荷。模型分13次开挖,前5次每次推进距离为20 m;揭露陷落柱后,每次开挖距离变为10 m,直至推过陷落柱。工作面后方的采空区充填体和垮落带岩层采用完全弾性模型[12,17-19],其中垮落带高度采用式(7)[18-19]进行计算:
(7)
式中:Hk为垮落带高度,m;h为采高,m;c1和c2为与顶板岩性有关的参数,具体参数选择见表2。
表2 垮落带高度系数[11]
Table 2 Height coefficient of the collapse zone

直接顶类型单轴抗压强度/MPa与顶板岩性有关的参数c1c2坚硬岩层>402.116较硬岩层20~404.719软弱岩层<206.232
63310工作面直接顶以砂质泥岩和泥岩为主,属于较硬岩层;煤层开采高度为2.5 m,结合表2中的数据,求得垮落带高度Hk=8.13 m。模型中各岩层的物理力学参数见表3。
表3 各岩层的物理力学参数
Table 3 Physical and mechanicalparameters of each rock layer

岩性B/GPaG/GPaf/(°)C/MPaT/MPaρ/(kg·m-3)ZS19.613.8369.845.982 580NY9.977.35322.862.482 600XS16.112403.494.562 800SY5.563.57363.522.342 640MC1.730.82252.680.871 450SN10.85.70357.353.012 450FS10.88.13388.425.462 300XLZ1.751.59170.90.061 800
注:B为体积模量;G为剪切模量;f为内摩擦角;C为黏聚力;T为抗拉强度;ρ为密度;ZS为中粒砂岩;SN为砂质泥岩;NY为泥岩;XS为细粒砂岩;SY为砂质页岩;MC为煤层;FS为粉砂岩;XLZ为陷落柱。
由于陷落柱柱体内部为松散、胶结程度较差的岩体,结合文献[8,20]对陷落柱的处理方法,采用弱化柱体内部岩体参数的方法模拟陷落柱;为方便建模,结合工作面推进方向2个陷落柱的曲率,将陷落柱的断面设置为圆形,半径取长短轴的均值。635号和637号陷落柱在模型中分布如图6—图7所示,陷落柱半径分别为12、16 m。

图6 模型中Z=38 m水平剖面图
Fig.6 Horizontal section of Z=38 m in the model
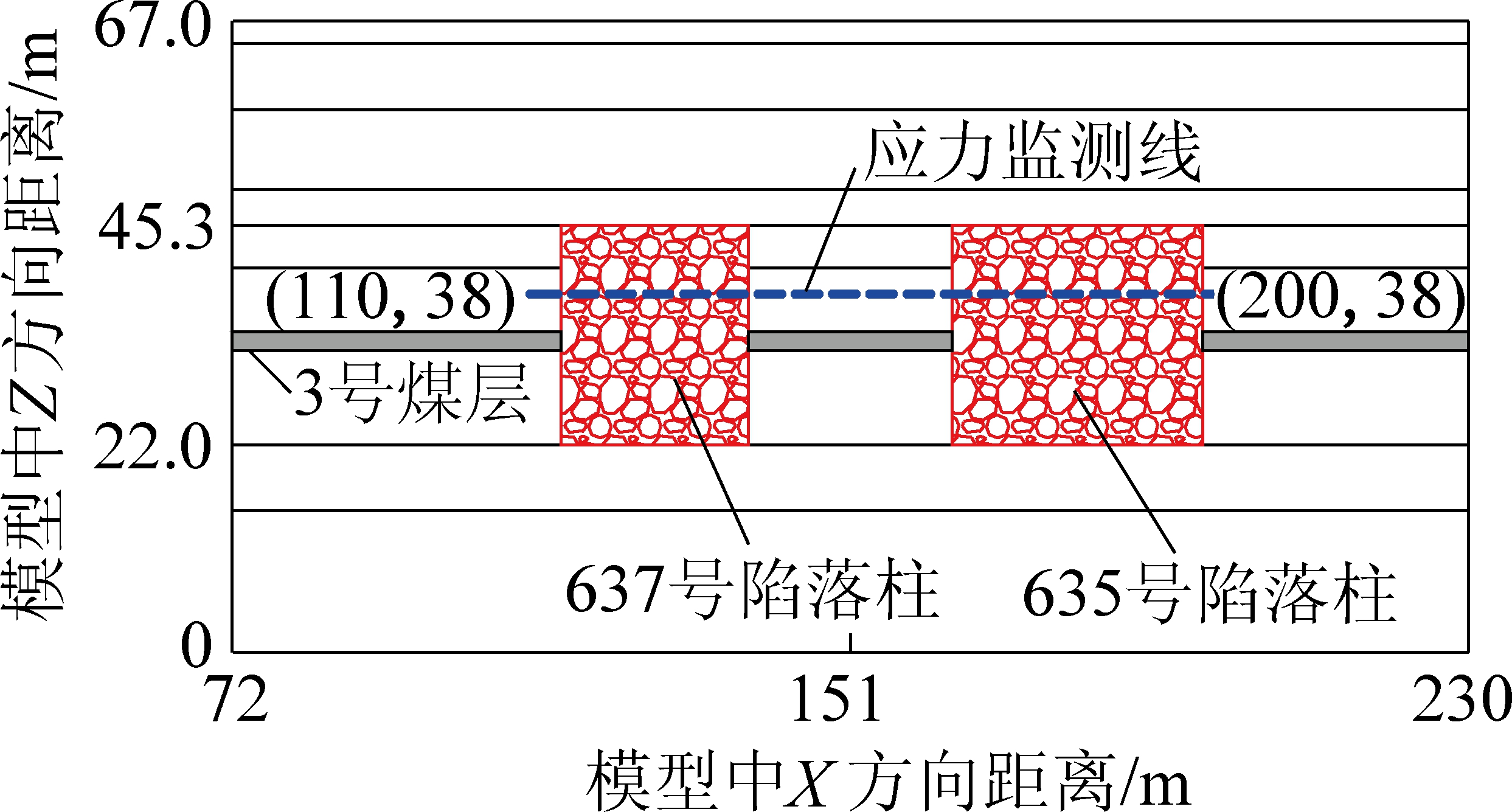
图7 1号截面剖面图
Fig.7 No.1 section profile
3.2 陷落柱对工作面推进的影响程度
为便于研究近距离陷落柱对工作面推进的影响程度,选取应力集中系数为指标,分析工作面推进过程中陷落柱的应力分布规律。设置2号和3号测线,如图6所示,提取2号和3号测线上工作面前方应力集中系数最大值,建立工作面距陷落柱不同位置时的应力集中系数变化图和集中系数增长率变化图,如图8所示。

图8 工作面前方最大应力集中系数变化情况
Fig.8 Change of maximum stress concentration factor ahead of working face
由图8可知随着工作面逐渐向陷落柱推进,工作面前方应力集中系数最大值发生变化;总体变化趋势是:距离陷落柱一定范围内,集中系数先增大到最大值,之后随工作面推进集中系数逐渐减小。图中2号集中系数显示工作面距离637号陷落柱24 m时,工作面前方集中系数达到最大值;之后随工作面推进,前方最大集中系数逐渐减小。结合2号增长率变化曲线可知:工作面前方最大集中系数增长率随工作面推进逐渐减小,在工作面距离637号陷落柱30 m左右的距离时,增长率降低幅度达到最大值,即工作面距离637号陷落柱的安全距离为30 m左右。3号测线与2号测线监测结果基本相似,结合上述分析可知:工作面距635号陷落柱的安全距离为50 m左右。
3.3 陷落柱周边的塑性扩展特征
为研究陷落柱周边的塑性扩展区域与工作面推进之间的关系,选取模型中Z=35 m水平上的塑性区发育特征进行分析。其中近距离陷落柱的塑性扩展区域的分布特征如图9—图10所示。
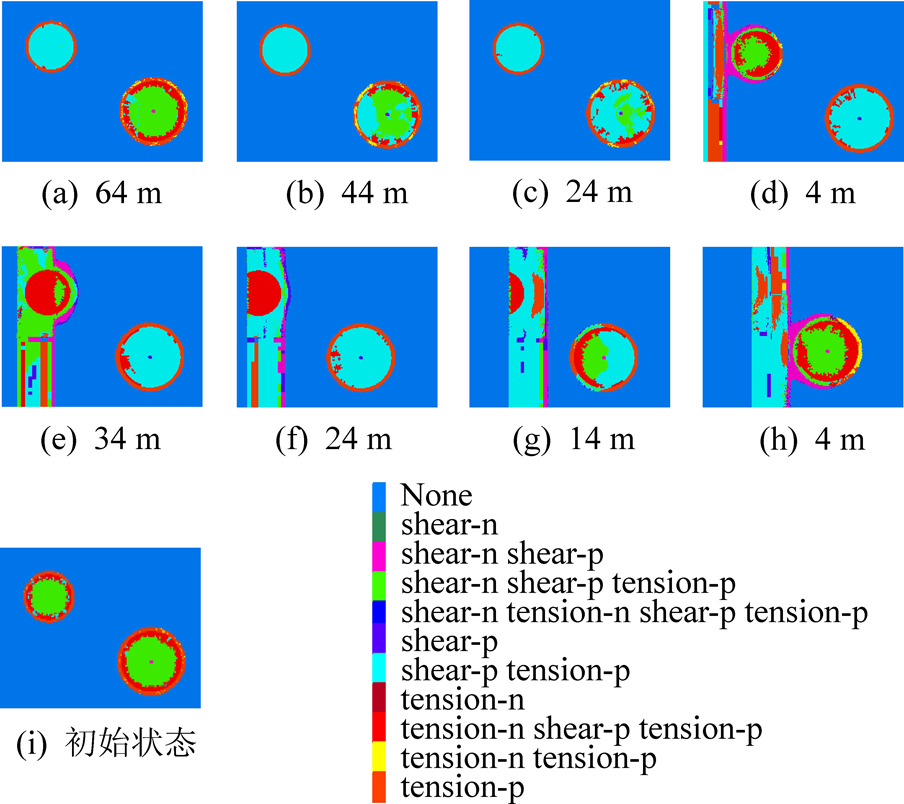
图9 工作面距陷落柱不同距离的塑性扩展
Fig.9 Plasticity extension of working face at different distances from collapse column
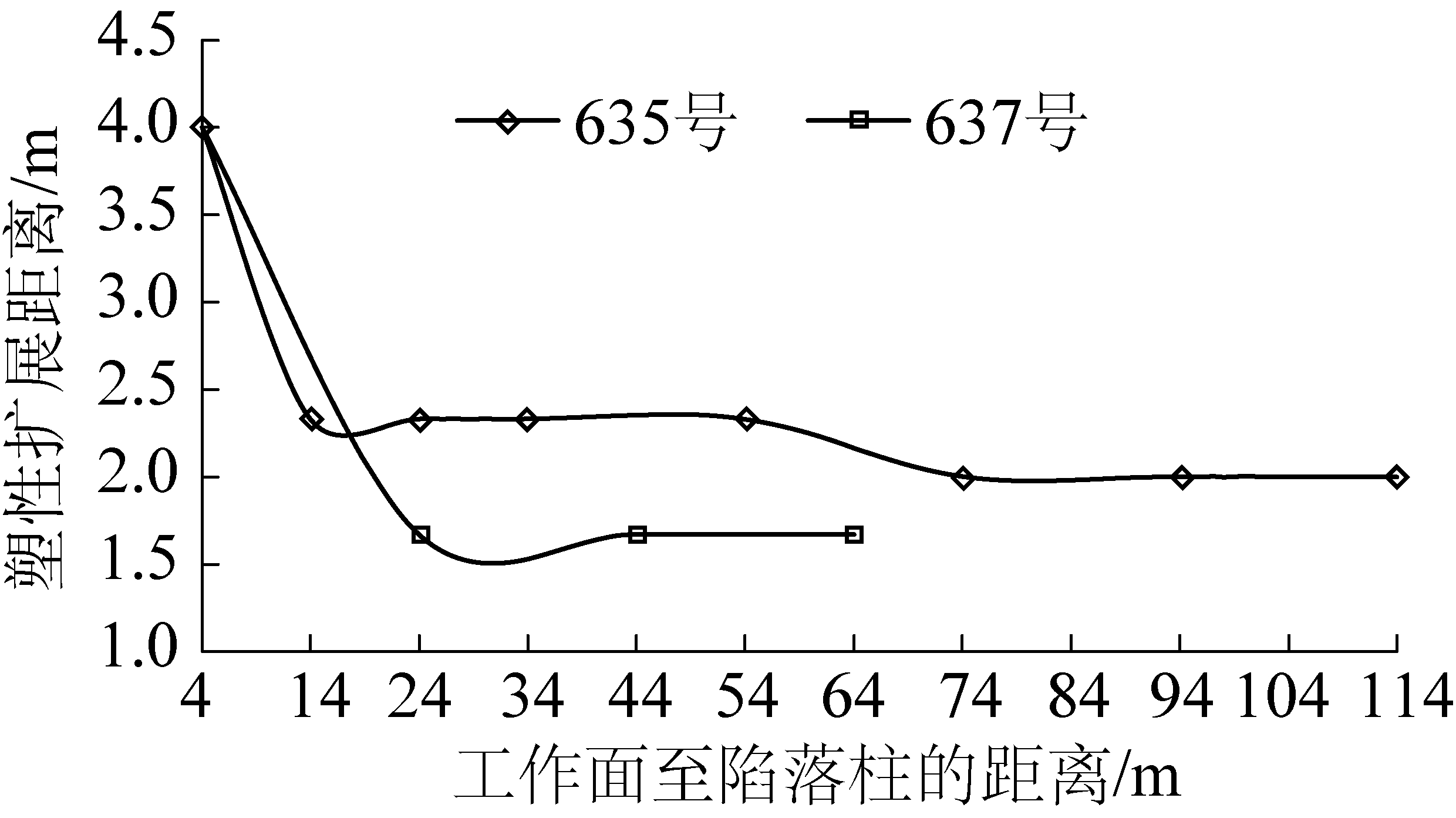
图10 陷落柱周边的塑性扩展变化情况
Fig.10 Changes in plasticity around the collapse column
由图9—图10可知:工作面逐渐向陷落柱推进,陷落柱周边塑性扩展区域随之发生变化。图9i显示初始化平衡后陷落柱内处于塑性状态,周边塑性扩展距离为1.8 m左右。
1)图9a—图9d为工作面距离637号陷落柱不同距离时的塑性扩展情况。由图10可知工作面距637号陷落柱24 m时,陷落柱周边的塑性扩展范围快速增大;而图9b和图9c显示:工作面距离637号陷落柱44 m到24 m的过程中,陷落柱靠近工作面侧的塑性发育特征发生变化,出现拉伸破坏和剪切破坏,即637号陷落柱距工作面约30 m左右时对工作面推进产生影响。图9e—图9h为工作面距离635号陷落柱不同距离时的塑性扩展情况,其中图9d中距635号陷落柱的距离为54 m;结合图9d—图9h可知:635号陷落柱位于工作面前方约50 m左右的范围时将对工作面推进产生影响。
2)由图9a—图9g可知:工作面在揭露陷落柱前,陷落柱之间的塑性扩展区域未出现贯通;当工作面推进至635号和637号陷落柱之间时(图9h),陷落柱之间的塑性扩展区域相互贯通。根据弹塑性力学知识可知,塑性区内处于应力降低状态,塑性区的贯通与否决定了近距离陷落柱之间的应力分布状态。在工作面未揭露陷落柱之前,陷落柱之间塑性区未贯通,即处于应力升高状态;当工作面大范围揭露637号陷落柱,或处于两陷落柱的中间位置,此时塑性区相互贯通,柱体之间处于应力降低状态。塑性区的发育特征间接证明了提出的判断方法ΔL。
3.4 陷落柱柱体之间的应力分布特征
为研究近距离陷落柱之间的应力分布状态,监测1号截面在Z=38 m水平上竖直方向的应力,如图6所示。1号截面和应力监测位置如图7所示。提取每次开挖之后的竖直方向应力,计算开采前后应力集中系数,建立集中系数变化如图11所示。其中637号陷落柱位于图7中115~136 m范围内,635号陷落柱位于166~194 m范围内。

图11 陷落柱柱体之间的应力集中系数分布
Fig.11 Distribution of stress concentration factors between columns of collapsing columns
由图11可知随着工作面的推进,测线处的集中系数随之发生变化。
1)工作面推进20 m时,测线上集中系数分布与基准线基本重合,即635号和637号陷落柱对工作面未产生影响;推进40 m时,637号陷落柱距工作面较近,陷落柱柱体范围内应力集中系数小于1,但变化较小,而635号陷落柱距工作面较远,柱体内部应力集中系数依然维持在1左右;推进60 m和80 m后,635号和637号柱体范围内的集中系数均小于1,即此时陷落柱对工作面推进产生影响。
2)前4次开挖过程中,柱体中间位置(136~166 m)的应力集中程度不明显,分析原因可知此时工作面距陷落柱较远,加之建立模型为实际模型的一半,导致开挖后陷落柱对工作面影响较小。图11b中显示推进110 m后,两陷落柱范围内均处于应力降低区域,且637号陷落柱内应力降低程度更剧烈,分析原因可知,工作面距637号陷落柱更近,此时柱体中间位置处于弹性应力升高状态,集中系数最大可达到3.0左右。推进120 m后已对637号陷落柱范围内的采空区和垮落带岩层二次赋值,故此时637号陷落柱柱体一定范围内处于弹性应力升高状态。推进130 m较推进120 m滞后10 m,故应力分布规律也滞后10 m,应力分布趋势基本一致。
3)图11c显示随后的推进过程中,应力分布趋势基本一致,选取推进140 m的应力分布进行分析可知:推进140 m后揭露了部分635号陷落柱,揭露部分的范围处于应力降低区域;柱体中间位置处的应力随着工作面的继续向前推进,其应力也越来越大。在110~140 m范围内,由于距工作面较远,加之对采空区和垮落带的充填作用,在上覆岩层的弯曲下沉过程中逐渐被压实,故此范围内应力变化较小。综上所述:随着工作面推进,635号和637号陷落柱对工作面推进产生影响,柱体中间位置(136~166 m)在工作面未揭露637号之前处于弹性应力升高状态,应力集中系数最高达到3.0~3.5(图11b的推进110、120、130 m)。
3.5 现场监测与试验结果对比
现场实际开采过程中,工作面在距637号陷落柱35 m左右的距离时,陷落柱附近的支架来压出现异常,压力变化频繁。工作面揭露637号陷落柱后,陷落柱周边围岩比较破碎,支架出现接顶不充分等现象。现场监测与数值模拟相互吻合。
4 结 论
1)采用理论计算求解了单个陷落柱周围的塑性扩展区域的范围,确定了635号和637号陷落柱周边的塑性扩展半径分别介于24.35~25.17 m和18.26~18.88 m。
2)提出了近距离陷落柱柱体之间应力分布状态的判断方法ΔL。当ΔL<0时,陷落柱之间处于塑性应力降低状态;当ΔL=0时,陷落柱之间处于由塑性应力降低向弹性应力升高过渡的临界状态;当ΔL>0时,相邻陷落柱之间处于弹性应力升高状态或应力状态。
3)数值模拟方法研究了陷落柱周边的塑性扩展范围和应力分布状态。确定了工作面距637号陷落柱的安全距离为大于30 m;距635号陷落柱的安全距离为大于50 m。验证了635号和637号陷落柱间的应力分布状态及提出的判断方法ΔL。
[1] 郝兵元,张玉江,戚庭野,等.综采面过陷落柱采动应力与柱体应力相互影响模拟研究[J].采矿与安全工程学报,2015,32(2):192-198.
HAO Bingyuan,ZHANG Yujiang,QI Tingye,et al.Simulation of interaction between mine-induced stress and stress of collapse column with fully-mechanized working face advancing[J].Journal of Mining & Safety Engineering,2015,32(2):192-198.
[2] 田 多,师皓宇,梁兴旺,等.综放工作面过陷落柱阶段划分及其顶板结构分析[J].采矿与安全工程学报,2015,32(1):49-53.
TIAN Duo,SHI Haoyu,LIANG Xingwang,et al.Stage division and roof structure analysis during fully mechanized caving face passing a collapse column[J].Journal of Mining & Safety Engineering,2015,32(1):49-53.
[3] 李振华,谢 晖,李见波,等.采动影响陷落柱活化导水规律试验研究[J].中南大学学报:自然科学版,2014,45(12):4377-4383.
LI Zhenhua,XIE Hui,LI Jianbo,et al.Experimental study of mining effect on collapse column activated water conducting mechanism[J].Journal of Central South University:Science and Technology,2014,45(12):4377-4383.
[4] 李振华,李见波,贺志宏.双柳煤矿陷落柱发育特征及突水危险性分析[J].采矿与安全工程学报,2014,31(1):84-89.
LI Zhenhua,LI Jianbo,HE Zhihong.Analysis on development characteristics of Karst collapse column and water inrush risk in Shuangliu coal mine[J].Journal of Mining & Safety Engineering,2014,31(1):84-89.
[5] 宋彦琦,王兴雨,程 鹏,等.椭圆形陷落柱厚壁筒突水模式力学判据及数值模拟[J].煤炭学报,2011,36(3):452-455.
SONG Yanqi,WANG Xingyu,CHENG Peng,et al.The mechanical criterion and numerical simulation of thick-walled elliptical cylinder collapse column model under water inrush[J].Journal of China Coal Society,2011,36(3):452-455.
[6] 尹尚先,王尚旭.陷落柱影响采场围岩破坏和底板突水的数值模拟分析[J].煤炭学报,2003,28(3):264-269.
YIN Shangxian,WANG Shangxu.A numerical simulation analysis of influence of karstic collapse columns on rock mass yield and water inrush from coal floor[J].Journal of China Coal Society,2003,28(3):264-269.
[7] 左建平,孙运江,李 楷,等.陷落柱影响区软岩巷道加固段长度及其底鼓控制研究[J].中国矿业大学学报,2017,46(1):18-26.
ZUO Jianping,SUN Yunjiang,LI Kai,et al.Study of the reinforced supporting length and floor heave control technology of soft rock roadway influenced by collapse column[J].Journal of China University of mining & Technology,2017,46(1):18-26.
[8] 黄友金,朱川曲,周 泽,等.漳村煤矿2502工作面过陷落柱方案的探究[J].湖南科技大学学报:自然科学版,2017,32(1):1-6.
Huang Youjin,ZHU Chuanqu,ZHOU Ze,et al.Study on scheme—the collapse column of working face of Zhangcun Coal Mine 2502[J].Journal of Hunan University of Science & Technology:Natural Science Edition,2017,32(1):1-6.
[9] 许进鹏.陷落柱活化导水机理研究[D].青岛:山东科技大学,2006.
[10] 许进鹏,宋 扬,成云海,等.陷落柱及其周边地应力分布研究[J].矿山压力与顶板管理,2005,22(4):118-120.
XU Jinpeng,SONG Yang,CHENG Yunhai,et al.Distributing of ground stress in and around Karst collapse column[J].Ground Pressure and Strata Control,2005,22(4):118-120.
[11] 许进鹏,梁开武,徐新启.陷落柱形成的力学机理及数值模拟研究[J].采矿与安全工程学报,2008,25(1):82-86.
XU Jinpeng,LIANG Kaiwu,XU Xinqi.Mechanics Mechanism of Forming Karst Collapse Columns and Numerical Simulation[J].Journal of Mining & Safety Engineering,2008,25(1):82-86.
[12] 张 村,屠世浩,白庆升,等.陷落柱周边应力变化及推采控制研究[J].中国矿业大学学报,2014,43(6):974-980.
ZHANG Cun,TU Shihao,BAI Qingsheng,et al.Stress changes around collapse column and the control technology by directly passing operation in longwall working face[J].Journal of China University of mining & Technology,2014,43(6):974-980.
[13] 黄 磊,卢义玉,夏彬伟,等.深埋软弱岩层钻孔围岩应变软化弹塑性分析[J].岩土力学,2013,34(S1):179-186.
HUANG Lei,LU Yiyu,XIA Binwei,et al.Elastoplastic analysis of surrounding rock of drilling with strain softening model in deep soft rock[J].Rock and Soil Mechanics,2013,34(S1):179-186.
[14] 赵德安,陈志敏,蔡小林,等.中国地应力场分布规律统计分析[J].岩石力学与工程学报,2007,26(6):1265-1271.
ZHAO Dean,CHEN Zhimin,CAI Xiaolin,et al.Analysis of Distribution Rule of Geostress in China[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1265-1271.
[15] 康红普,司林坡,张 晓.浅部煤矿井下地应力分布特征研究及应用[J].煤炭学报,2016,41(6):1332-1340.
KANG Hongpu,SI Linpo,ZHANG Xiao.Characteristics of underground in-situ stress distribution in shallow coal mines and its applications[J].Journal of China Coal Society,2016,41(6):1332-1340.
[16] 康红普,林 健,颜立新,等.山西煤矿矿区井下地应力场分布特征研究[J].地球物理学报,2009,52(7):1782-1792.
KANG Hongpu,LIN Jian,YAN Lixin,et al.Study on characteristics of underground in-situ stress distribution in Shanxi coal mining fields[J].Chinese Journal of Geophysics,2009,52(7):1782-1792.
[17] 谢和平,周宏伟,王金安,等. M.FLAC在煤矿开采沉陷预测中的应用及对比分析[J].岩石力学与工程学报,1999,18(4):29-33.
XIE Heping,ZHOU Hongwei,WANG Jinan,et al.Application of FLAC to predict gound surface[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(4):29-33.
[18] 蒋力帅,武泉森,李小裕,等.采动应力与采空区压实承载耦合分析方法研究[J].煤炭学报,2017,42(8):1951-1959.
JIANG Lishuai,WU Quansen,LI Xiaoyu,et al.Numerical simulation on coupling method between mining-induced stress and goaf compression[J].Journal of China Coal Society,2017,42(8):1951-1959.
[19] 白庆升,屠世浩,袁 永,等.基于采空区压实理论的采动响应反演[J].中国矿业大学学报,2013,42(3):355-361.
BAI Qingsheng,TU Shihao,YUAN Yong,et al.Back analysis of mining induced responses on the basis of goaf compaction theory[J].Journal of China University of Mining & Technology,2013,42(3):355-361.
[20] 王家臣,杨胜利.采动影响对陷落柱活化导水机理数值模拟研究[J].采矿与安全工程学报,2009,47(2):140-144.
WANG Jiachen,YANG Shengli.Numerical simulation of mining effect on collapse column activated water conducting mechanism[J].Journal of Mining & Safety Engineering,2009,47(2):140-144.
