0 引 言
煤层气主要以吸附态赋存于煤储层中。其中,甲烷是煤层气的主要气体成分,煤对甲烷的吸附属于物理吸附,多数情况下可根据Langmuir理论模型计算预测煤储层的含气量[1]。然而,Langmuir方程是基于温度不变的前提,仅考虑了压力变化对吸附量的影响。对于埋藏深度较大的深部煤层气,由于处于较高的压力场和温度场中,煤储层的吸附含气性不仅取决于储层压力,还在很大程度上受储层温度影响[2-3]。同时,由于甲烷的临界压力为4.59 MPa,临界温度为-82.6 ℃[4],而煤储层压力通常介于4~10 MPa,储层温度通常介于15~40 ℃,因此地层条件下,煤层气多以既非气(汽)态又非液态的超临界态存在[5-7]。而Langmuir吸附理论属亚临界模型,难以准确研究超临界态甲烷的吸附行为[8]。本质上,甲烷在煤表面的吸附是一个能量自发降低的趋势,吸附过程伴随着能量变化[9-10]。前人研究多是关于煤岩自身各种因素对甲烷吸附的影响,如煤阶、煤体结构、煤岩类型等,并采用吸附热、吸附势、表面自由能等参数解释了能量变化规律[11-13],但关于超临界条件下外部因素如温度和压力对煤吸附甲烷过程中的能量变化的控制作用研究较少,并且没有对吸附体系中吸附剂和吸附质的能量属性进行区分,易引起各类能量参数的混淆理解。
笔者基于不同温度条件下的无烟煤等温吸附试验数据,通过Gibbs方程分析超临界与亚临界吸附差异性,依据吸附势理论探讨超临界条件下吸附势与吸附空间随温度和压力变化的规律及原因,以及温度和压力对吸附体系表面自由能和吸附活化能的控制机理,以揭示能量参数与吸附体系的归属关系和内在关联,以深化煤层气吸附理论,并对煤储层含气性评价提供理论指导。
1 样品与试验
试验所用煤样采自沁水盆地南部晋城矿区,煤岩类型属半亮煤,煤体结构属糜棱煤,镜质体反射率含量2.74%,镜质组含量80.1%,惰质组含量17.8%,空气干燥基下的水分1.02%,灰分9.83%,挥发分5.42%。室内将煤样研磨并筛分至0.18~0.25 mm,制备成含平衡水分样。
等温吸附测试在IS-100等温吸附试验仪上开展,参考实际煤储层温度和压力范围,设置25、35、45 ℃三个温度条件,平衡压力从0逐渐增加到11.2 MPa,每个温度压力组合点的平衡时间持续12 h以上。试验结果如图1所示。

图1 不同温度下的等温吸附曲线
Fig.1 Isothermal adsorption curves under different temperatures
由图1可知,随着平衡压力的增大,甲烷吸附量逐渐增加。在压力相对较低时,煤岩吸附甲烷量随压力增大的增加速率较快,但各温度下的等温吸附曲线彼此相互靠拢,温度对煤岩吸附甲烷的影响作用并不明显;在压力相对较高时,煤岩吸附甲烷量随压力增大的增加速率变缓,但随温度升高呈现明显降低的趋势,温度对煤岩吸附的影响效应开始显现。
2 甲烷超临界吸附问题讨论
2.1 超临界与亚临界吸附差异
等温吸附过程中,根据实际气体状态方程PVf=ZnfRT,某一平衡压力下的游离相甲烷密度为
(1)
式中:ρf为游离相甲烷密度,g/cm3;mf为游离相甲烷质量,g;nf为游离相甲烷物质的量,mol;M为甲烷的摩尔分子量,g/mol;Vf为自由空间体积,cm3;P为平衡气体压力,MPa;T为热力学温度,K;Z为甲烷气体的压缩因子,取值见表1;R为通用气体常数,取8.314 J/(mol·K)。
超临界状态下的吸附相甲烷密度是一个近似值,并且与压力无关,无法直接测量,因此许多学者提出了不同计算吸附相密度的方法,OZAWA等[14]提出的吸附相密度经验公式为
ρad=ρbexp[-0.002 5(T-Tb)]
(2)
式中:ρad为吸附相甲烷密度,g/cm3;ρb为甲烷的沸点密度,取0.422 4 g/cm3;T为绝对温度,K;Tb为一个大气压下甲烷的沸点温度,取111.7 K。
表1 不同温压条件下的甲烷压缩因子
Table 1 Methane compressibility factors under
different pressure and temperature
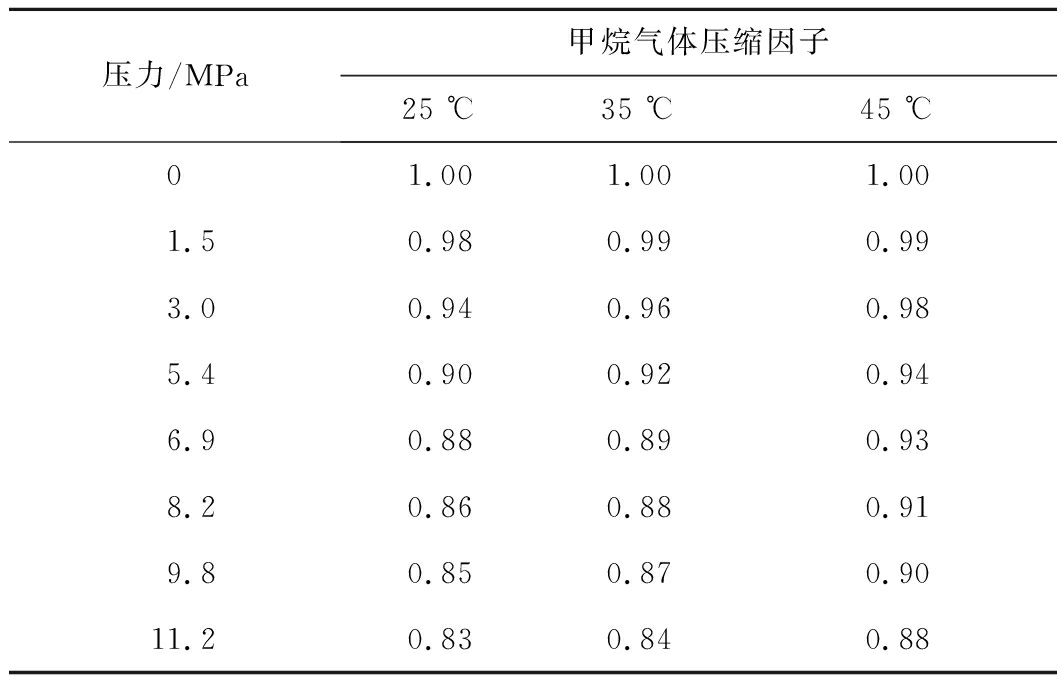
压力/MPa甲烷气体压缩因子25 ℃35 ℃45 ℃01.001.001.001.50.980.990.993.00.940.960.985.40.900.920.946.90.880.890.938.20.860.880.919.80.850.870.9011.20.830.840.88
Dubinin和Astakhov则提出了另一种计算吸附相密度的经验公式[15]:
(3)
其中:Pc为甲烷临界压力,MPa,取4.599 2 MPa;Tc为甲烷临界温度,K,取190.56 K;由于式(3)与甲烷临界参数密切相关,因此采用式(3)估算吸附相密度。
等温吸附试验得到的气体吸附量指的是Gibbs过剩吸附量,而理论吸附模型中的气体吸附量指的是绝对吸附量[8]。当体系温度低于气体的临界温度时,过剩吸附量与绝对吸附量近似相等,而当体系温度高于气体的临界温度时,过剩吸附量小于绝对吸附量,且二者之差随着体系平衡压力的增大而逐渐增大[16]。因此,在研究超临界条件下的煤岩-甲烷体系吸附机理时,需要首先将过剩吸附量转化成绝对吸附量。根据Gibbs定义,二者关系为
(4)
式中:Va为甲烷的绝对吸附量,cm3/g;Ve为甲烷的过剩吸附量,cm3/g。
不同温度下的绝对吸附量始终大于过剩吸附量(图2),随温度升高,二者差异呈减小趋势变化。当平衡压力小于3 MPa时,绝对吸附量曲线几乎与过剩吸附量曲线重合,而当平衡压力超过3 MPa时,二者开始出现偏离,且平衡压力越高,绝对吸附量与过剩吸附量的差值越大。分析认为:在高温、低压条件下,游离相气体密度非常小,因此式(4)中ρf/ρad密度比可以忽略不计,这就使得过剩吸附量与绝对吸附量几乎相同;在低温、高压条件下,密度比将成为主控项,不可忽略不计,过剩吸附量也不再与绝对吸附量相等,在假设的理想情形下,当游离相气体密度与吸附相密度接近时,过剩吸附量将成为0,即此时的吸附相和游离相将不再能够区分开来。
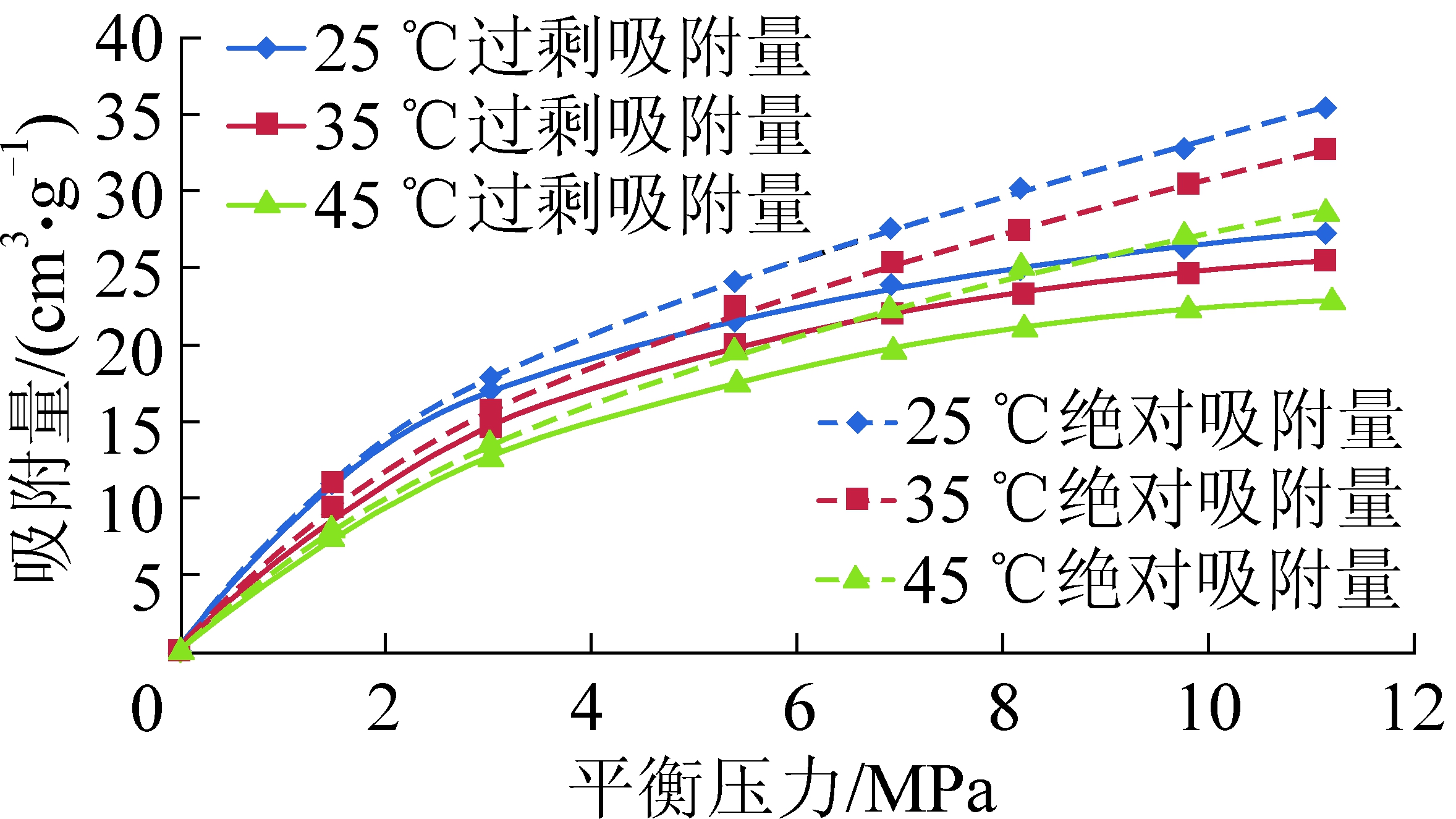
图2 过剩吸附量和绝对吸附量随温度和压力的变化趋势
Fig.2 Variations of excess and absolute adsorption volume
with pressure and temperature
2.2 吸附势与吸附空间
1914年,Polanyi提出吸附势理论,其实质反映了吸附剂在吸附1 g/mol吸附质时的吉布斯自由能变化。该理论认为固体表面存在势能场,周围的吸附质分子在引力作用下被吸附到固体表面。不同于Langmuir理论的单分子层吸附,Polanyi吸附势理论不需要建立吸附层的指定物理模型,气体分子依据吸附势大小依次充填孔容积。
吸附势与吸附空间构成了Polanyi吸附势理论的基本物理参数,依据热力学定律,吸附势是把单位质量的吸附质从非吸附相转移到吸附相所做的功[9,17],即
(5)
式中:ε为吸附势,J/mol;P0为气体饱和蒸汽压力,MPa。
在超临界情形下,甲烷的饱和蒸汽压力将失去其物理含义,可以用虚拟饱和蒸汽压力替代。用来计算虚拟饱和蒸汽压的经验公式很多,其中以Dubinin-Astakhov经验公式的应用最为广泛[6,15,18],即
(6)
式中:n为与吸附系统有关的常数,对于Dubinin-Radushkevich公式取值2。Dubinin-Radushkevich公式是Dubinin-Astakhov公式中n=2的特例,此种情况是假定微孔呈Gaussin分布状态,比较适用于孔隙尺寸分布较窄的均匀微孔系统。
将式(6)代入式(5),可得到超临界条件下的吸附势计算公式:
(7)
吸附空间是用来表征吸附剂微孔结构的特征参数,代表了吸附质占据吸附剂的空间体积大小,即:
(8)
式中:ω为吸附空间容积,cm3/g;V0为标准状况下的气体摩尔体积,取22.4 L/mol。
将式(3)、式(4)代入式(8),可以得到超临界条件下的吸附空间计算公式:
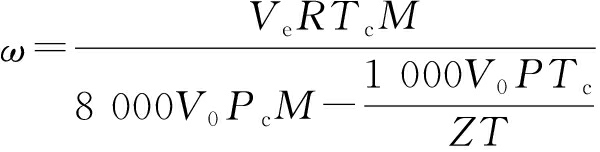
(9)
温度一定时,随着平衡压力的升高,吸附势减小,吸附空间增大(图3)。由于煤岩表面不同吸附位具有不同的吸附势能,平衡压力越高,煤岩越容易吸附甲烷分子,所需的吸附势减小,此时势能较低的吸附位也具备吸附甲烷分子的能力,故甲烷分子所占据的吸附空间体积增加。
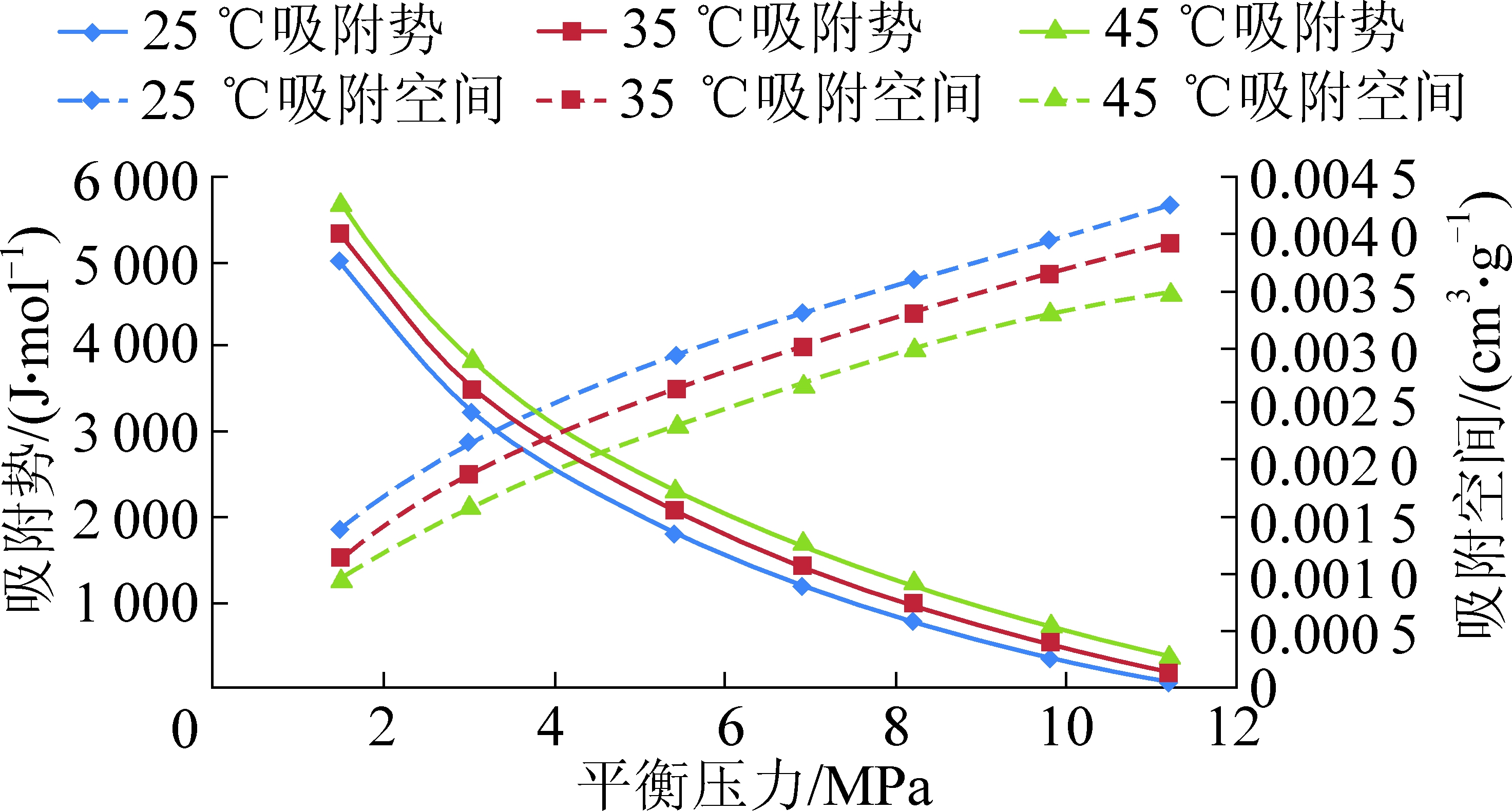
图3 吸附势和吸附空间随温度和压力的变化趋势
Fig.3 Variations of adsorption potential and adsorption
space with pressure and temperature
平衡压力一定时,随着温度的升高,吸附势增大,吸附空间减小。这是因为温度越高,气体分子热运动越剧烈,越容易摆脱范德华力的束缚,煤岩吸附甲烷分子越困难,所需的吸附势能增大,此时势能较低的吸附位丧失吸附甲烷分子的能力,只有势能较高的吸附位满足吸附条件,故甲烷分子所占据的吸附空间体积减小。
此外,还可进一步得到吸附势与吸附空间的数量关系(图4),即吸附特性曲线[13,19]。由图4可以看出,对于特定吸附体系(甲烷-煤岩体系),任意温度及压力下吸附空间与吸附势的关系可用单一的吸附特征曲线来表示,该曲线不随外部温度及压力条件的改变而变化。在煤-甲烷超临界吸附体系中,吸附势和吸附空间呈负对数型数量关系,即
ε=-aln ω+b
(10)
式中,a和b为吸附特征曲线的拟合系数。

图4 甲烷-煤岩吸附体系的吸附特性曲线
Fig.4 Adsorption characteristic curve of
methane-coal adsorption system
2.3 表面自由能
煤岩表面的碳原子受力不平衡,在内部碳原子的引力作用下所获得的能量即表面自由能[20]。能量最低原理指明任何界面都有自发降低其界面能量的趋势。由于固体表面的原子难以移动或收缩,因此只能通过吸附气体分子来降低其表面能,这也是吸附发生的根本动力。物理吸附使得甲烷气体由三维气相转变成二维吸附表面相,自由度损失,熵和焓减小。
根据表面化学理论,由吸附引起的表面张力降低值可表示为[9]
-dσ=RTΓd[ln(mP)]
(11)
式中:σ为表面张力,J/m2;Γ为表面超量,mol/m2;m为用以消去压力单位的系数,取1 MPa-1。
表面超量是指甲烷气体在煤表面区域的浓度与煤结构内浓度的差值,可表示为
(12)
式中,S为煤比表面积,m2/g。
因此,煤吸附甲烷的累计表面自由能降低值可表示为
(13)
式中:Δγ为累计表面自由能降低值,J/m2,表示未吸附气体状态下煤的表面自由能与吸附气体之后煤的表面自由能之间差值。
对式(13)中P进行微分,可得:
(14)
式中:ΔγP为各压力点处的表面自由能变化值,J/m2,表示某一压力下的累计表面自由能降低值与相邻压力下的累计表面自由能降低值之差。
随平衡压力的增大,累计表面自由能降低值呈现增加的趋势(图5),随温度的升高,累计表面自由能降低值呈现减小的趋势。能量最低原理指明,体系的能量越低,其稳定性越强,煤表面通过吸附甲烷分子来降低其表面自由能。平衡压力增大对煤吸附甲烷具有促进作用,故累计表面自由能降低的越多;而温度升高增加了甲烷分子热运动动能,对煤吸附甲烷具有抑制作用,故累计表面自由能降低得越少。
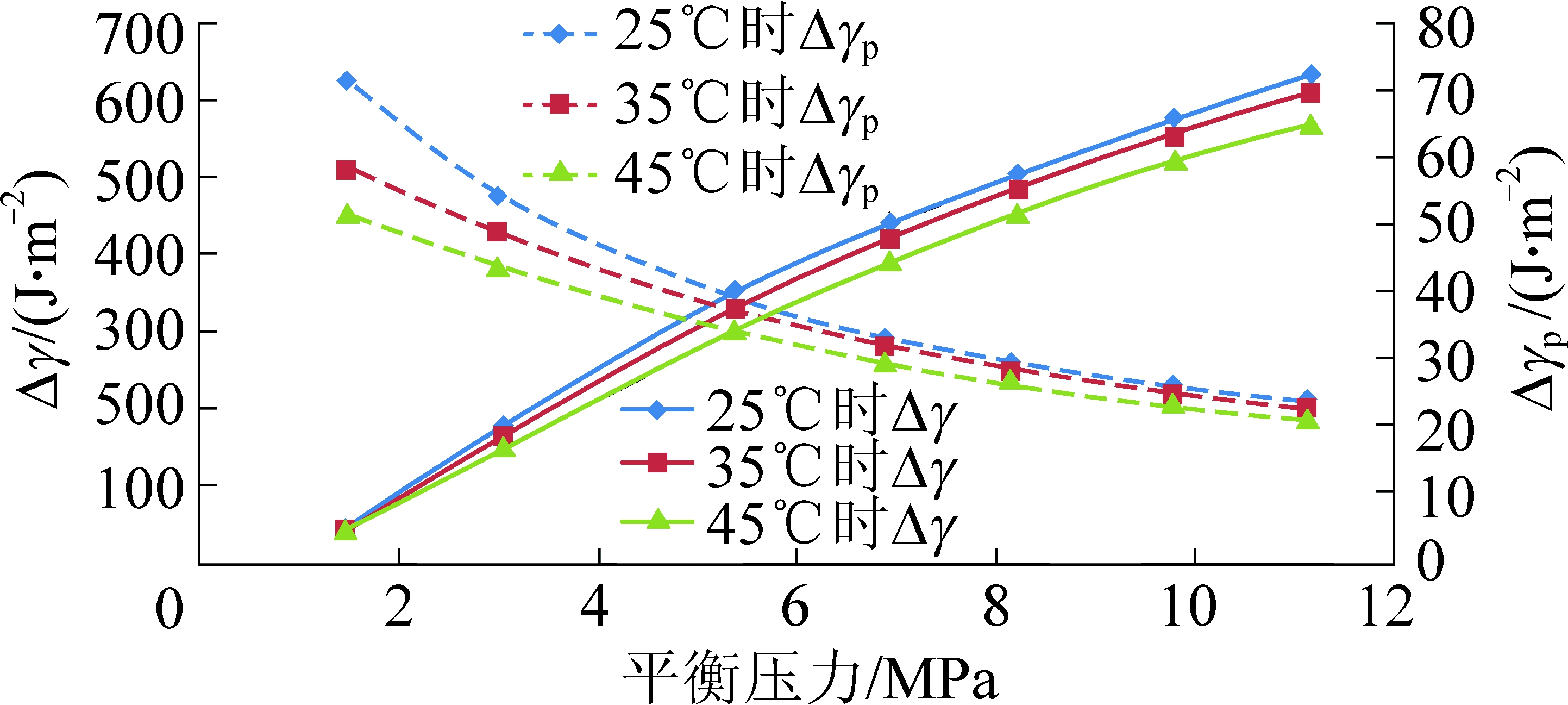
图5 表面自由能随温度和压力的变化趋势
Fig.5 Variations of surface free energy
with pressure and temperature
随平衡压力的增大,各压力点处的表面自由能变化值呈减小趋势变化,反映了累计表面自由能降低值随压力升高的增长速率减慢。吸附过程中,甲烷分子优先占据煤中的高能吸附位,随压力的增大,煤中的低能吸附位也开始被甲烷占据,而低能吸附位吸附甲烷所释放的能量要小于高能吸附位,因此累计表面自由能降低值的增长速率减慢。随温度升高,各压力点处的表面自由能变化值呈减小趋势,体现了高温对吸附的抑制作用。
2.4 扩散系数与吸附活化能
甲烷在煤储层中的传质过程由扩散和表面吸附2个部分组成,由于表面吸附几乎是瞬间完成,因此吸附速率的快慢主要取决于扩散速率。基于多孔介质孔径尺寸与气体分子平均自由程的相对大小,扩散模式可划分为菲克型、克努森型和过渡型[21-22]。当孔隙直径大于10倍分子平均自由程时,气体分子平均自由程较孔径要小得多,分子之间的碰撞占主导,此时为菲克型扩散;当分子平均自由程大于10倍孔径时,气体分子平均自由程较孔径要大得多,分子与孔隙壁之间的碰撞占主导,此时为克努森型扩散;当气体分子平均自由程与孔径相当时,2种碰撞同时占主导,此时为过渡型扩散。
气体分子平均自由程定义如下:
(15)
式中:kB为玻尔兹曼常数,J/K,取1.38×10-23 J/K;dm为气体有效分子直径,nm。
以孔径与分子平均自由程比值等于10为界限,当温度为25~90 ℃时,对于10 nm孔径,气体压力高于8 MPa后,孔径与自由程比值均大于10;对于50 nm孔径,气体压力高于1.5 MPa后,孔径与自由程比值均大于10;对于100 nm孔径,气体压力高于0.7 MPa后,孔径与自由程比值均大于10;对于500 nm孔径,气体压力高于0.2 MPa后,孔径与自由程比值均大于10(图6)。由于煤储层平均孔隙直径范围从几十到几百纳米不等,流体压力大致为4~10 MPa,储层温度范围大致为15~40 ℃,因此绝大多数情况下,煤层气在煤储层中扩散时的孔径与自由程比值大于10,属于菲克型扩散,遵循菲克扩散定律。
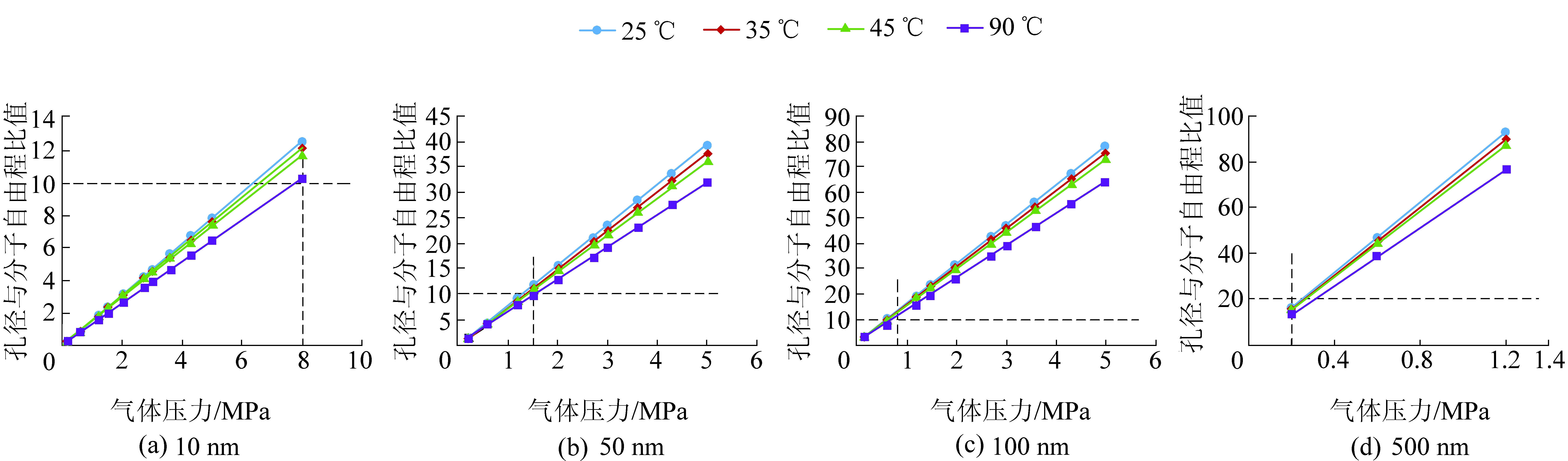
图6 孔径与分子平均自由程比值随温度和压力变化趋势
Fig.6 Variations of the ratio of pore diameter to molecule average free path with pressure and temperature
当气体扩散模式属菲克型时,气体分子的扩散系数可表示为[23]
(16)
式中:D为扩散系数,m2/s;mA、mB分别为组分A、B的气体分子摩尔质量,g/mol;dA、dB分别为气体A、B的分子直径,m。当组分A和B为同种气体时,D为气体分子的自扩散系数。
相同温度下,甲烷在煤中的扩散系数随气体压力增加而减小,这是由于气体分子的平均自由程与压力成反比(式(15)),气体压力越大,分子平均自由程越小,气体分子在单位时间内的碰撞次数增多,扩散阻力增大,扩散系数减小;而相同气体压力下,温度越高,气体分子热运动越剧烈,平均自由程越大(式(15)),单位时间内的碰撞次数减少,扩散系数呈增大趋势变化(图7)。
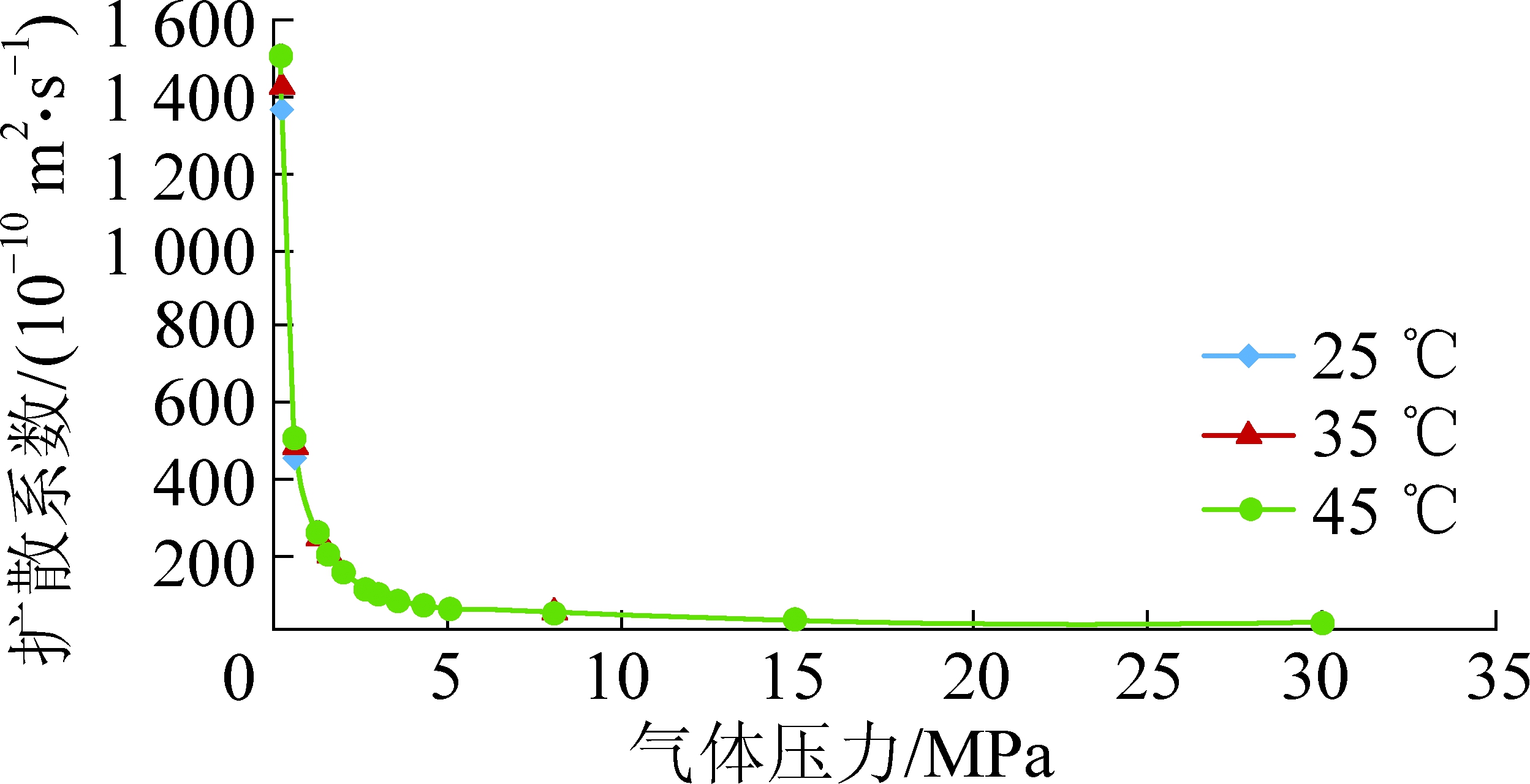
图7 扩散系数随温度和压力的变化趋势
Fig.7 Variations of gas diffusion coefficient
with pressure and temperature
碰撞理论指出,气体分子与固体表面之间通过碰撞发生吸附,然而并不是所有的分子碰撞都会发生吸附,一定温度下,只有当气体分子的能量超过活化能时方可有效吸附。求取活化能可基于经典Arrhenius定律[24],即:
(17)
式中:De为气体分子的有效扩散率,s-1;Ea为吸附活化能,J;Af为指前因子。
有效扩散率与扩散系数具有如下关系:
(18)
式中,r0为扩散路径长度,这里用多孔介质的平均孔隙半径代替,m。
联立式(17)和式(18),并对等号两侧取对数,可得:
(19)
在直角坐标系中以![]() 为纵坐标,以1/T横坐标,将不同温度下的扩散系数代入式(19)可得到一条直线,通过直线斜率即可求得活化能Ea。
为纵坐标,以1/T横坐标,将不同温度下的扩散系数代入式(19)可得到一条直线,通过直线斜率即可求得活化能Ea。
当温度区间一定时,随气体压力的增加,直线斜率的绝对值不发生改变,即吸附活化能为定值,不受气体压力影响。而当气体压力一定时,随温度区间的升高,直线斜率的绝对值呈增大趋势变化(图8)。可见气体分子吸附活化能的大小受温度影响,温度越高,由于气体分子热运动越剧烈,发生吸附时所需获得的吸附活化能越大。
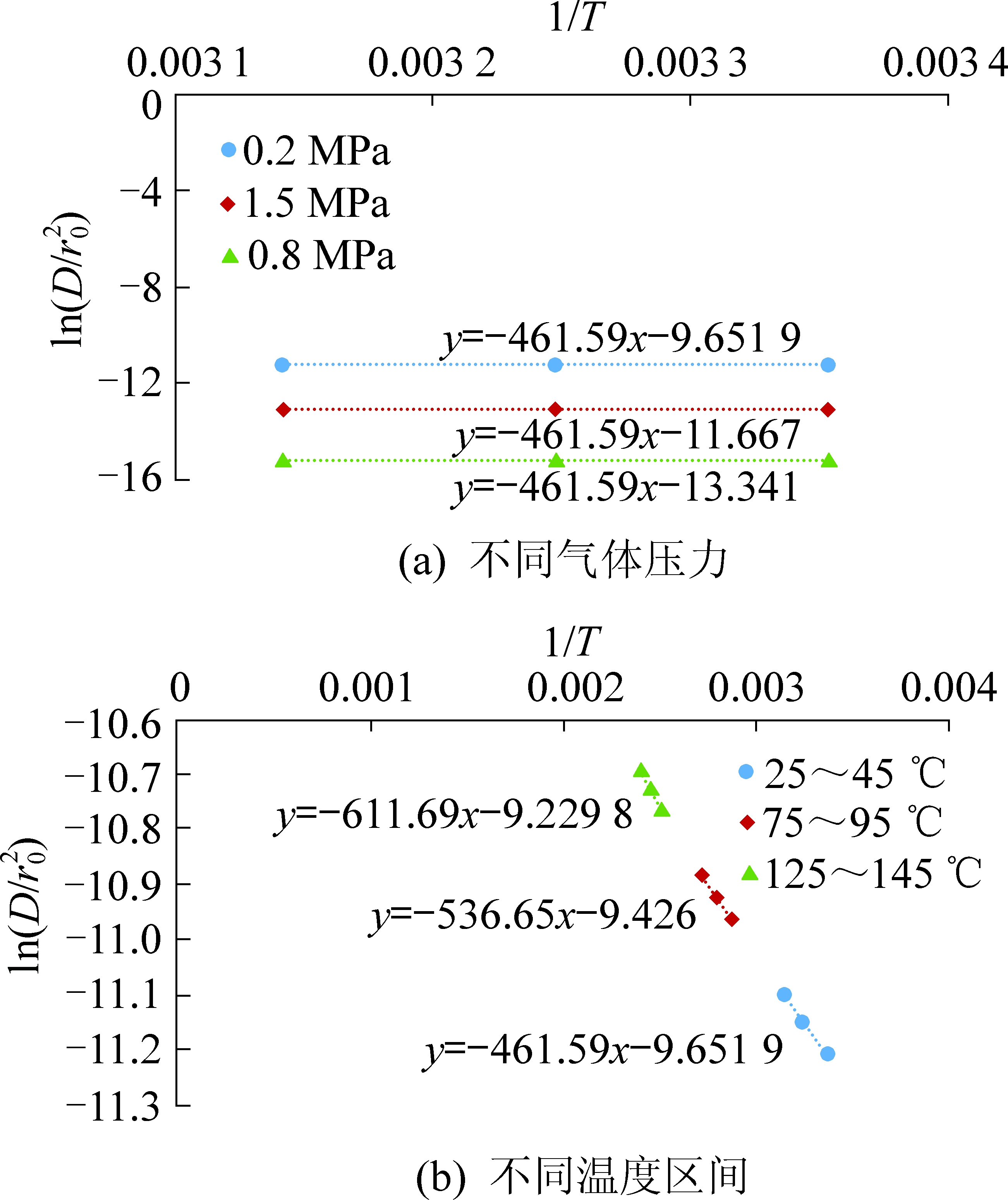
图8 气体压力和温度影响下的吸附活化能变化
Fig.8 Variations of adsorption activation energy
affected by gas pressure and temperature
2.5 吸附体系的能量参数隶属关系
通过以上分析可知,吸附势、吸附活化能和表面自由能都是表征吸附体系能量特征的参数,但三者反映了不同主体之间的能量属性关系。一个吸附体系包括吸附剂和吸附质,对于煤-甲烷吸附体系,煤岩表面为吸附剂,甲烷气体为吸附质。吸附势反映的是吸附剂(煤岩)表面上吸附位的势能高低,是吸附剂对吸附质的引力作用,属于吸附剂的能量属性参数,受到温度和压力的共同影响。吸附活化能反映的是吸附质(甲烷气体)分子自身的动能大小,属于吸附质的能量属性参数,由动能方程可知,当分子质量一定时,动能由速度决定,而压力增大不会改变分子热运动速度,温度升高会引起分子热运动加速,因此吸附活化能不受压力影响,而受温度影响。表面自由能在吸附发生前为吸附剂表面分子间作用力的体现,在吸附发生后为吸附剂表面分子与吸附质分子间作用力的体现,其变化量揭示了吸附作用的本质;压力增加促使吸附,表面自由能的减少量增大,表面自由能降低;温度升高促使解吸,表面自由能的减少量降低,表面自由能增大。
3 结 论
1)基于甲烷在深部高温高压条件下的超临界状态,依据Gibbs公式将等温吸附中的过剩吸附量转换为绝对吸附量;不同温度下的绝对吸附量始终大于过剩吸附量,受吸附体系中游离相与吸附相密度比值影响,二者差异随平衡压力的增大而增加,随温度的升高而减小。
2)将吸附势理论与甲烷超临界状态参数相结合,得出随平衡压力的升高,吸附势减小,吸附空间增大;随温度的升高,吸附势增大,吸附空间减小;对于特定的煤-甲烷吸附体系,任意温度和压力下吸附空间与吸附势的关系可被表达为单一的吸附特征曲线。
3)吸附发生的根本动力是降低表面自由能,满足能量最低原理。累计表面自由能降低值随平衡压力的增大而增大,随温度的升高而减小;各压力点处的表面自由能变化值随平衡压力和温度升高均呈减小趋势变化。
4)煤储层条件下,甲烷在煤层中的扩散模式以菲克型为主,扩散系数受温度和压力的共同影响,随压力增大而减小,随温度升高而增大。气体分子吸附活化能本质为分子动能的体现,不受体系压力影响,但受体系温度控制,温度越高,气体分子的热运动越剧烈,发生吸附时所需获得的吸附活化能越大。
[1] 汤达祯,刘大锰,唐书恒,等. 煤层气开发过程储层动态地质效应[M]. 北京:科学出版社,2014.
[2] 李 松,汤达祯,许 浩,等. 深部煤层气储层地质研究进展[J]. 地学前缘,2016,22(3):10-16.
LI Song, TANG Dazhen, XU Hao,et al. Progress in geological researches on the deep coalbed methane reservoirs [J].Earth Science Frontiers, 2016, 22(3): 10-16.
[3] 赵丽娟,秦 勇,WANG Geoff,等. 高温高压条件下深部煤层气吸附行为[J]. 高校地质学报,2013,19(4):648-654.
ZHAO Lijuan, QIN Yong,WANG Geoff,et al. Adsorption behavior of deep coalbed methane under high temperatures and pressures [J]. Geological Journal of China Universities, 2013, 19(4): 648-654.
[4] 尹 帅,单钰铭,郑莲慧,等. 页岩气等温吸附量及等量吸附热研究[J]. 科学技术与工程,2013,13(29):8572-8578.
YIN Shuai, SHAN Yuming, ZHENG Lianhui, et al. Research of shale gas isothemal adsorption quantity and equal amount adsorption heat [J]. Science Technology and Engineering, 2013, 13(29): 8572-8578.
[5] GASPARIK M, BERTIER P, GENSTERBLUM Y, et al. Geological controls on the methane storage capacity in organic-rich shales [J]. International Journal of Coal Geology, 2014, 123: 34-51.
[6] 盛 茂,李根生,陈立强,等. 页岩气超临界吸附机理分析及等温吸附模型的建立[J]. 煤炭学报,2014,39(S1):179-183.
SHENG Mao, LI Gensheng, CHEN Liqiang, et al. Mechanisms analysis of shale-gas supercritical adsorption and modeling of isorption adsorption [J]. Journal of China Coal Society, 2014, 39(S1): 179-183.
[7] CHAREONSUPPANIMIT P, MOHAMMAD S A, ROBINSON Jr R L, et al. Modeling the temperature dependence of supercritical gas adsorption on activated carbons, coals and shales [J]. International Journal of Coal Geology, 2015, 138:113-126.
[8] 熊 健,刘向君,梁利喜,等. 页岩气超临界吸附的Dubibin-Astakhov改进模型[J]. 石油学报,2015,36(7):849-857.
XIONG Jian, LIU Xiangjun, LIANG Lixi, et al. Improved Dubibin-Astakhov model for shale-gas supercritical adsorption [J]. Acta Petrolei Sinica, 2015, 36(7): 849-857.
[9] 刘珊珊,孟召平. 等温吸附过程中不同煤体结构煤能量变化规律[J]. 煤炭学报,2015,40(6):1422-1427.
LIU Shanshan, MENG Zhaoping. Study on energy variation of different coal-body structure coals in the process of isothermal adsorption [J]. Journal of China Coal Society, 2015, 40(6):1422-1427.
[10] 李希建,尹 鑫,李维维,等. 页岩对甲烷高温高压等温吸附的热力学特性[J]. 煤炭学报,2018,43(S1):229-235.
LI Xijian, YIN Xin, LI Weiwei, et al. Thermodynamic characteristics of isothermal adsorption of methane at high temperature and pressure in shale [J]. Journal of China Coal Society, 2018, 43(S1): 229-235.
[11] 简 阔,张玉贵,赫少攀,等. 构造煤甲烷吸附表面能研究[J]. 煤田地质与勘探,2014,42(1):31-34.
JIAN Kuo, ZHANG Yugui, HE Shaopan, et al. The surface energy of methane adsorption of tectonic coal [J]. Coal Geology & Exploration, 2014, 42(1): 31-34.
[12] 崔永君,张庆玲,杨锡禄. 不同煤的吸附性能及等量吸附热的变化规律[J]. 天然气工业,2003,23(4):130-131.
[13] 苏现波,陈 润,林晓英,等. 吸附势理论在煤层气吸附/解吸中的应用[J]. 地质学报,2008,82(10):1382-1389.
SU Xianbo, CHEN Run, LIN Xiaoying, et al. Application of adsorption potential theory in the fractionation of coalbed gas during the process of adsorption/desorption[J]. Acta Geologica Sinica, 2008, 82(10): 1382-1389.
[14] OZAWA W, KUSUMI S, OGINO Y J. Physical adsorption of gases at high pressure.Ⅳ. An improvement of the Dubinin-Astakhov adsorption equation [J]. Journal of Colloid and Interface Science, 1976, 56(1): 83-91.
[15] DUBININ M M, ASTAKHOV V A. Development of the concepts of volume filling of micropores in the adsorption of gases and vapors by micro-porous adsorbents [J]. Bulletin of Academy of Science of the USSR, Division of Chemical Science,1971, 20(1): 3-7.
[16] 周 理. 超临界吸附研究疑惑、问题与分析[C]//第四届全国氢能学术会议论文集.沈阳:第四届全国氢能学术会议,2002:154-162.
[17] 姜 伟,吴财芳,姜 玮,等. 吸附势理论在煤层气吸附解吸研究中的应用[J]. 煤炭科学技术,2011,39(5):102-104.
JIANG Wei, WU Caifang, JIANG Wei,et al. Application of adsorption potential theory to study on adsorption-desorption of coalbed methane [J]. Coal Science and Technology, 2011, 39(5): 102-104.
[18] 熊 健,刘向君,梁利喜. 基于吸附势理论的页岩吸附甲烷模型及其应用[J]. 成都理工大学学报:自然科学版,2014,41(5):604-611.
XIONG Jian, LIU Xiangjun, LIANG Lixi. Adsorption model of shale to CH4 based on adsorption potential theory and its application [J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2014, 41(5): 604-611.
[19] 王 庆,宁正福,张 睿,等. 基于吸附势理论的页岩气藏吸附平衡预测[J]. 新疆石油地质,2015,36(3):308-312.
WANG Qing, NING Zhengfu, ZHANG Rui, et al. Adsorption equilibrium prediction of shale gas pool based on adsorption potential theory [J]. Xinjiang Petroleum Geology,2015, 36(3): 308-312.
[20] 戴广龙. 煤低温氧化过程中微晶结构变化规律研究[J]. 煤炭学报,2011,36(2):322-325.
DAI Guanglong. Research on microcrystalline structure change regularity in the coal low temperature oxidation process [J]. Journal of China Coal Society, 2011, 36(2): 322-325.
[21] 聂百胜,张 力,马文芳. 煤层甲烷在煤孔隙中扩散的微观机理[J]. 煤田地质与勘探,2000,28(6):20-22.
NIE Baisheng, ZHANG Li, MA Wenfang. Diffusion micro-mechanism of coal bed methane in coal pores [J]. Coal Geology & Exploration, 2000, 28(6): 20-22.
[22] 张小东,刘炎昊,桑树勋,等.高煤级煤储层条件下的气体扩散机制[J]. 中国矿业大学学报,2011,40(1):43-48.
ZHANG Xiaodong, LIU Yanhao, SANG Shuxun, et al. Study of the gas diffusion mechanism in high-rank coal reservoirs [J]. Journal of China University of Mining & Technology, 2011, 40(1):43-48.
[23] 李国庆,孟召平,王保玉. 高煤阶煤层气扩散-渗流机理及初期排采强度数值模拟[J]. 煤炭学报,2014,39(9):1919-1926.
LI Guoqing, MENG Zhaoping, WANG Baoyu. Diffusion and seepage mechanisms of high rank coal-bed methane reservoir and its numerical simulation at early drainage rate [J]. Journal of China Coal Society, 2014, 39(9): 1919-1926.
[24] DELPHINE C, ZBIGNIEW P, PHILIPPE B. Effect of pressure and temperature on diffusion of CO2 and CH4 into coal from the Lorraine basin (France) [J]. International Journal of Coal Geology, 2010, 81: 373-380.
