0 引 言
准确定量评价煤层气排采井的井间干扰程度是合理井网布置的前提。关于井间干扰程度评价,国内外研究者进行了大量的研究。采用的测试方法主要有注入/压降试井、不稳定试井、干扰试井等。这3种方法均是通过测试压力随时间的变化,采用半对数曲线或图版法对测试结果进行分析。注入/压降法主要是通过注入一定量的液体,测试时要求在单一水相状态下进行,这一测试要求与现场实际排采存在多种相态的情况不太相符[1-4],而且注入/压降试井测试时间一般比较短,仅能对近井地带的影响距离、渗透率等进行测试,此方法评价井间干扰具有一定的局限性。不稳定试井要求排量稳定,这一要求与实际存在一定的出入[5-6]。干扰试井是通过激动井中压力激动,监测井中监测压力随时间的变化,采用该方法时,因测试的是激励井压力与观测井间的压差,与实际排采的压差存在一定差异,可以大致判断是否能形成井间干扰,但无法量化井间干扰程度[7-8]。数值模拟的方法主要有Eclipse、Comet、CMG、Matlab等,这些软件都是黑箱模型,参数取值往往基于经验,预测结果具有较多的主观性[9-11]。数学模型方法主要有基于地下水动力学的降深法、库萨金公式法、裘布依公式法、试井与达西定律相结合的方法等[12-15]。采用地下水动力学的降深法,对于降深边界及排采时渗透率的确定准确与否对结果影响较大。库萨金公式适合无越流补给的情况,裘布依适合于有越流补给情况。采用这3种模型进行计算时,若不考虑排采过程中由于相态等变化引起的渗透率的变化,其计算结果与实际存在较大出入。目前,我国煤层气井的排采是在储层改造后进行的,储层改造后不同方向上渗透率的差异性,排采过程中相态的变化等都会对水压传播距离计算产生影响。为了更加客观、准确地对煤层气井在无越流补给时的井间干扰程度进行定量评价,笔者充分考虑煤层气井排采时由于水/气相态、比例等变化引起的水相渗透率的变化,结合不同改造方向渗透率的差异,分别对不同排采阶段水相渗透率进行求解,代入经典的库萨金公式,得出更适合实际的无越流补给的水压传播距离的数学模型,在此基础上建立水压传播距离图版,以期为准确评价煤层气井间干扰提供一种理论方法。
1 煤层气井井间干扰数学模型的构建
1.1 井间干扰建模的基本思路
煤层气直井的排采是在三维空间进行的,煤储层渗透率对压力传播方向具有重要影响。我国煤储层原始渗透率较低,采用煤层气直井开发时均需经过储层改造,因此进行数学建模时,首先需要得出储层改造后的渗透率。煤层气井排采时,围岩对煤层是否有补给,以及补给量的多少都会对排采过程中压力传播路径和距离产生重要影响。笔者不考虑围岩对煤层的补给,仅研究无越流补给下排采过程水压传播距离。煤层气井排采时不同的相态、不同的水/气比例,都将导致水相渗透率的变化,引起传播距离公式的变化。计算思路为:
1)基于试井原理,结合水力压裂时的压降曲线,构建水力压裂后渗透率预测模型。
2)根据煤层气井排采时的相态、水/气比例的明显变化,求解得出气/水两相流低产阶段、稳产阶段等不同排采阶段水相渗透率。
3)把不同阶段的渗透率数学模型代入经典的库萨金公式,最终得出煤层气井整个排采过程水压传播距离的数学模型。
1.2 不同排采阶段水压传播数学模型的构建
1.2.1 水力压裂后渗透率数学模型的构建
假设水平等厚无限大双重介质煤层气井以恒定产量q生产,基质和裂缝之间的窜流为拟稳态,流动服从达西定律,忽略重力和毛管力的影响,则基于沃伦-茹特模型的渗流数学模型为
(1)
Pf(r,0)=Pm(r,0)=Pi
(2)
(3)
Pf(∞,t)=Pm(∞,t)=Pi
(4)
式中:φm为基质孔隙度;r为径向距离;Cmt为基岩系统的综合压缩系数,MPa-1;Pm为基质中的压力,MPa;t为生产时间;α为变形因子;Km为基质渗透率,μm2;μ为水的黏度系数,mPa·s;B为水的体积系数;Pf为裂缝中的压力,MPa;Kf为压裂后煤储层裂缝渗透率,μm2;Pi为原始地层压力,MPa;h为开采层厚度,m;rw为井半径,m。
Warren和Root对上述数学模型给出储层裂缝中压力的近似解析解为
![]()
[ln(θt)+Ei(-σt)-Ei(-σωt)+0.809]
(5)
且有:![]()
式中:φf为裂缝孔隙度;Ei(-x)为幂积分函数;Pwf为井底流动压力,MPa;Cm为流体在基质岩块中的综合压缩系数,MPa-1;Cf为流体在裂缝中的综合压缩系数,MPa-1。
当生产时间较长,即t较大时,式(5)中的2个Ei函数均趋于0,则式(5)可简化为
(6)
式中:θ为裂缝的方位,取值为[0°,90°];S为表皮因子。
由式(6)可知,井底压差与生产时间的对数呈直线关系,则压后渗透率为
(7)
式中:m为斜率。
1.2.2 单相水流阶段水压传播距离数学模型的构建
当煤层气井几乎无越流补给时,根据库萨金公式可知,排采时影响半径可表示为
(8)
式中:Re为排采水压影响半径,m;ρ为水的密度,m3/kg;g为重力加速度;Δh为动液面下降值,m。
水力压裂时裂缝受到主应力方向、优势裂隙方向的影响,导致压裂时裂缝为椭圆形,存在长轴与短轴,本次压裂时长轴与短轴的计算公式由参考文献[16]得出。忽略长轴与短轴方向的渗透率随长度的变化,即认为其渗透率为一定值。长轴方向压裂影响半径为L1,短轴方向压裂影响半径为L2。
设单相水流阶段动液面降低值为Δh1,若水压影响半径未突破长轴压裂影响半径时,将Δh1代入公式(8),替换Δh即可求出单相水流阶段水压在长轴方向上的传播影响半径Rc1。
当水压影响半径突破长轴压裂影响半径时,先计算出长轴压裂影响半径内的动液面下降值Δhc1,即

(9)
(10)
式中:Δh0为原始状态下动液面高度值,m;Kcy为煤储层原始渗透率,m2。
在短轴方向上,若水压影响半径未突破短轴方向压裂影响半径时,与长轴方向计算方法一致,即把动液面下降值Δh1代入式(8),得出单相水流阶段短轴方向水压传播影响半径Rd1。
当水压影响半径突破短轴压裂影响半径时,则首先需要计算出短轴压裂影响半径内的动液面下降值Δhd1,即

(11)
然后得出单相水流阶段短轴方向水压传播影响半径Rd1为
(12)
1.2.3 气/水两相流低产阶段水压传播距离数学模型的构建
当煤层气井开始产气时,由于供气体积相对较小,此时一般采取低产气方式,把这一阶段称为低产气阶段。假设低产气阶段日产气量是相等的。这一阶段由于气体的产出,导致水相相对渗透率发生变化。根据煤层气井的实际产水量和产气量,计算出煤层裂隙中的含水率Wc,即:
(13)
式中:Qw为日产水量,m3/d;Qg为日产气量,m3/d。
根据Corey公式可知,含水率与含水饱和度之间[16]可表示为
(14)
式中:Sw为含水饱和度;![]() 为Corey系数。
为Corey系数。
根据生产数据数值模拟拟合得出水相相对渗透率与含水饱和度关系为
Krw=aebSw
(15)
若低产气时未达到长轴压裂影响边界,设低产气阶段动液面降低值为Δh2,此时水相渗透率可表示为
Kw1=KfaebSw
(16)
式中:a、b为生产数据拟合系数,分别取0.002 7、6.214 4;Kw1为低产气阶段水相相对渗透率,m2。
则长轴方向低产气阶段水压影响距离为
(17)
若低产气阶段已经达到了长轴压裂影响范围,则首先需要根据长轴压裂影响范围,计算出动液面的降低值,即
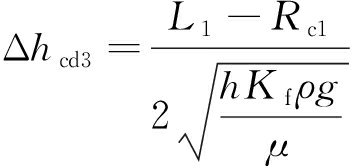
(18)
(19)
式中:Δhcd3为长轴影响半径内低产气阶段动液面的下降值,m。
则排采至低产气阶段长轴方向影响距离Rdg1可表示为
Rdg1=Rc1+Rcd2
(20)
同理,短轴方向低产气阶段计算思路与长轴方向相同,在此不再赘述。
1.2.4 气/水两相流稳定产气阶段水压传播距离数学模型的构建
当煤层气井低产气一段时间后,随着供气体积的增加,进入了稳定产气阶段。这时,产气量的增加进一步阻碍了水的流动,水相相对渗透率进一步下降。采用与低产气阶段相同的方法,计算出此时煤层裂隙中的含水率,进而计算出含水饱和度,然后根据含水饱和度与水相相对渗透率关系得出此阶段水相相对渗透率,在此不再赘述。
1.2.5 定压阶段水压传播距离数学模型的构建
井底压力不能无限下降,当下降到一定程度时,煤层气井的排采进入定压生产阶段。此时进行排采时,水压开始向纵向发展,横向上随着排采的进行,边界外的水在压差作用下向边界内补给,因此求解出边界处压力降低变化是得出定压排采水压影响半径的关键步骤。
某一时刻储层压力分布可表示为[17]
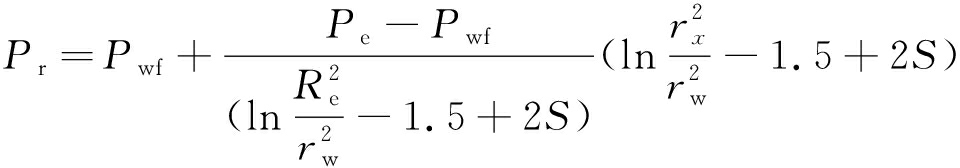
(21)
式中:rx为距离井筒中心x处的距离,m;Pr为rx处的压力,MPa;Pe为储层压力,MPa。
当煤层气井几乎为无越流补给时,设定压排采时长轴方向上影响半径为Rcg,短轴方向上影响半径为Rdg。因稳定产气阶段压力下降值较小,此时分别以距Rcg较近处的影响半径Rrcg和Rdg较近处的影响半径Rrdg为研究对象,根据稳定产气阶段的井底压力下降情况、排采时间、稳定产气阶段的产水量、定压排采时的产水量,结合公式(21),分别得出不同排采时间下Rrcg和Rrdg处的压力变化Prcg、Prdg,即:
Prcg=Pe-(a1ln trcg+b1)
(22)
Prdg=Pe-(a2ln trdg+b2)
(23)
远端的水向边界流动时,其长轴方向上Rrcg处的动液面降低值为
Srcg=98(a1ln trcg+b1)
(24)
短轴方向上Rrdg处的动液面降低值可表示为
Srdg=98(a2ln trdg+b2)
(25)
式中:a1、a2、b1、b2为均拟合系数。
根据式(13)—式(15)得出水相相对渗透率Krw。
由此可得出在定压生产阶段长轴方向随着排采时间变化的影响半径:
(26)
同理,可得出定压生产阶段短轴方向随着排采时间变化的影响半径:
(27)
式中:Rrcg为定压生产阶段长轴上的影响半径,m;trcg为定压开始排采时到某一天的排采时间,d;Rrdg为定压生产阶段短轴上的影响半径,m;trdg为定压开始排采时到某一天的排采时间,d;Krwc、Krwd分别为长轴、短轴方向的水相相对渗透率。
2 实例应用与分析
2.1 煤层气排采在不同方向上的干扰评价
笔者选择沁水盆地柿庄南区块进行过干扰试井的TS-2井组进行计算。井组分布如图1所示。井间干扰试井是通过改变一口井的排采工作制度,邻近的另外几口井下入高精度的压力计,前者称为“激动井”,后者称为“观测井”。本次TS-2井为激动井,激动注入压力为3.1 MPa,储层渗透率定为2×10-3 μm2。各观测井与TS-2井的距离及干扰试井基本参数见表2。排采不同阶段长轴和短轴方向水压传播距离计算模型所需的基本参数见表1。
根据表1中数据,分别对单相水流阶段、低产气阶段、稳定产气阶段、定压阶段的长轴和短轴方向的水压传播距离进行计算,最终得出整个排采阶段长轴和短轴方向上水压影响距离,具体计算结果及干扰试井判断井间干扰情况见表2。
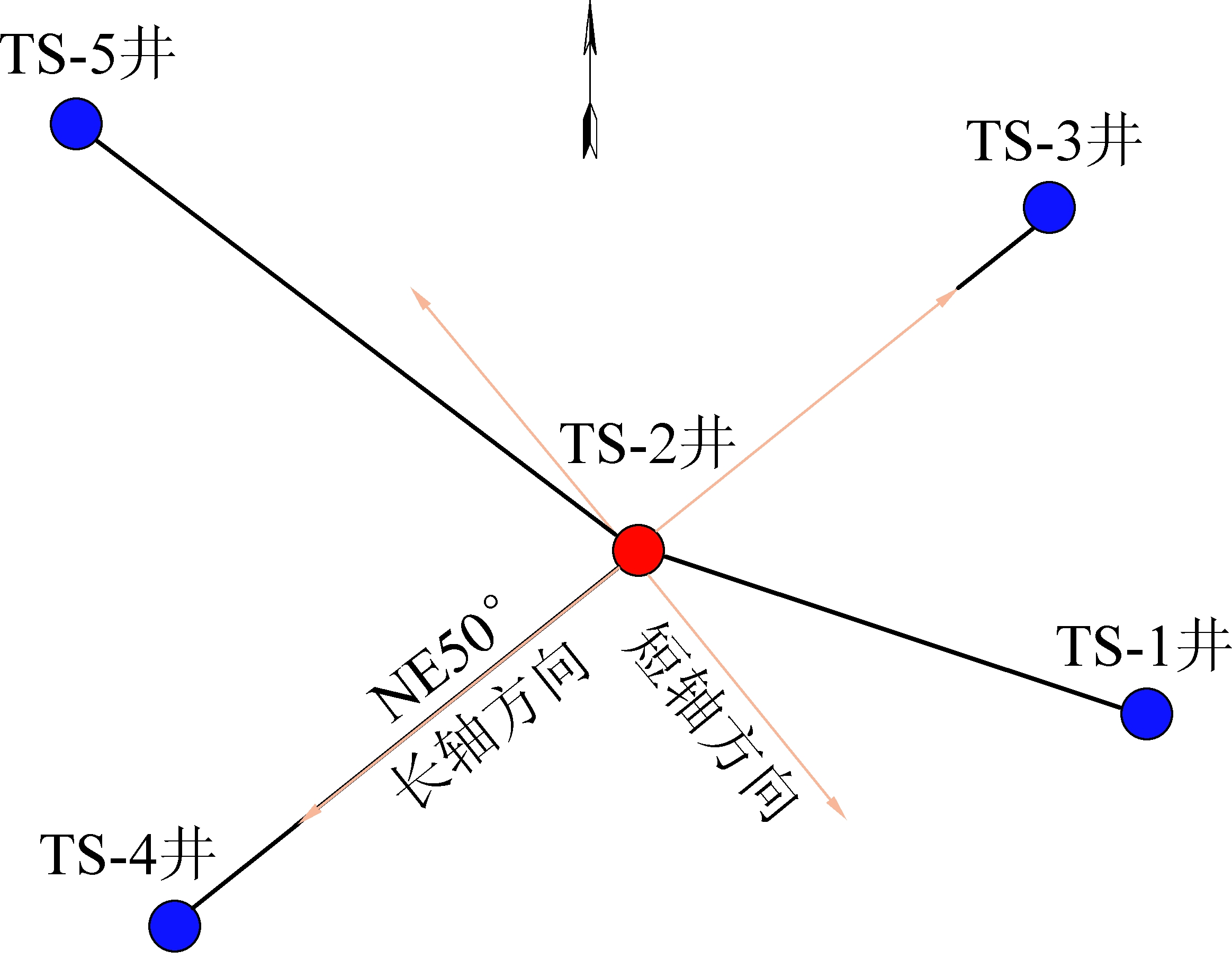
图1 干扰试井井组分布
Fig.1 Schematic of well group distribution
表1 模型计算所需基本参数
Table1 Required basic parameters of model

井号储层压力/MPa临界解吸压力/MPa单相流排采时间/d含水层厚度/m单相流阶段低产气阶段动液面降低值/m渗透系数/(m·d-1)动液面降低值/m渗透系数/(m·d-1)TS-1井2.61.9195.877.30.010 399.50.006 2TS-2井2.41.317817.2105.40.004 566.70.002 7TS-3井3.11.63796.0142.70.003 672.50.002 1TS-4井2.81.3936.0144.70.005 188.00.003 1TS-5井2.71.641917.73.30.002 2122.00.001 3井号稳产阶段定压阶段井底压力/MPa动液面降低值/m渗透系数/(m·d-1)动液面降低值/ma1b1a2b2TS-1井0.717.60.004 5238.10.297 80.712 80.355 40.850 7TS-2井0.418.60.001 9115.70.056 00.857 60.064 10.981 7TS-3井0.540.20.001 2119.00.024 91.096 40.027 81.225 9TS-4井0.44.90.001 7107.20.070 00.671 50.086 50.755 2TS-5井0.514.70.000 755.80.004 90.540 20.005 50.604 8
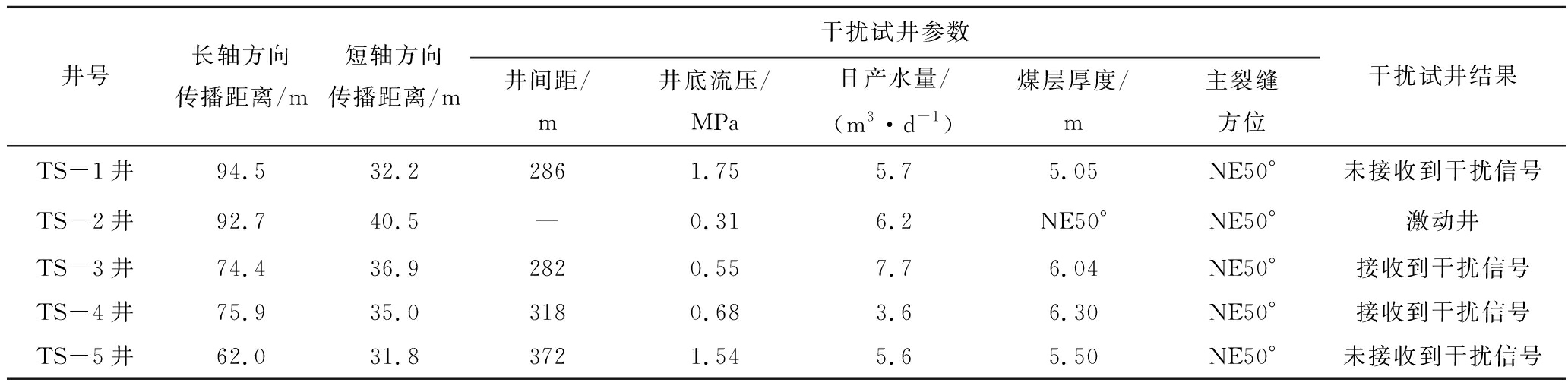
表2 整个排采阶段水压传播距离计算结果及干扰试井测试结果
Table 2 Calculation results of water pressure propagation distance in the whole drainage stage and the results of interference well test
井号长轴方向传播距离/m短轴方向传播距离/m干扰试井参数井间距/m井底流压/MPa日产水量/(m3·d-1)煤层厚度/m主裂缝方位干扰试井结果TS-1井94.532.22861.755.75.05NE50°未接收到干扰信号TS-2井92.740.5—0.316.2NE50°NE50°激动井TS-3井74.436.92820.557.76.04NE50°接收到干扰信号TS-4井75.935.03180.683.66.30NE50°接收到干扰信号TS-5井62.031.83721.545.65.50NE50°未接收到干扰信号
由于压裂改造长度的差异,导致排采时水压传播距离在不同方向上差别比较明显。干扰试井结果表明,在NE50°方向上能接收到信号。干扰试井的激动井的注入压力设置为3.1 MPa,与实际储层压力2.4 MPa不同,导致干扰试井的解释只具有参考意义。同时干扰试井通过是否接收到干扰信号来判别是否形成干扰,是一种定性的判断。
为了验证计算结果的可靠性,采用Eclipse数值模拟软件,结合这几口井实际参数,进行数值模拟,所选用的参数如下:

煤层厚度/m6煤层埋深/m600煤层原始压力/MPa2.4兰氏压力/MPa2.78兰氏体积/(m3·t-1)32.3吸附时间/d8含气量/(m3·t-1)14.6煤层孔隙度0.04渗透率/(10-3 μm2)0.4
井距200 m煤层气井干扰如图2所示。从图2可知,该井长轴压力传播影响距离90 m左右,短轴压力传播影响距离40 m左右。这与计算结果差别不大,一定程度上验证了计算结果较可靠。

图2 井距200 m煤层气井干扰示意
Fig.2 Interference of CBM Wells with a spacing of 200 m
2.2 不同储层参数下水压传播距离图版及研究区井网部署建议
2.2.1 不同储层参数下水压传播距离图版
根据柿庄南区块煤储层压力梯度、煤层埋深、压裂后渗透率情况,以埋深700 m为例,分别进行了储层压力梯度0.4、0.5、0.6、0.7、0.8 MPa/hm,压裂后渗透率分别为0.5×10-3、1×10-3、1.5×10-3、2×10-3、4×10-3、8×10-3、16×10-3 μm2 下煤层气井整个排采阶段水压传播长轴距离、短轴距离与渗透率关系,如图3所示。
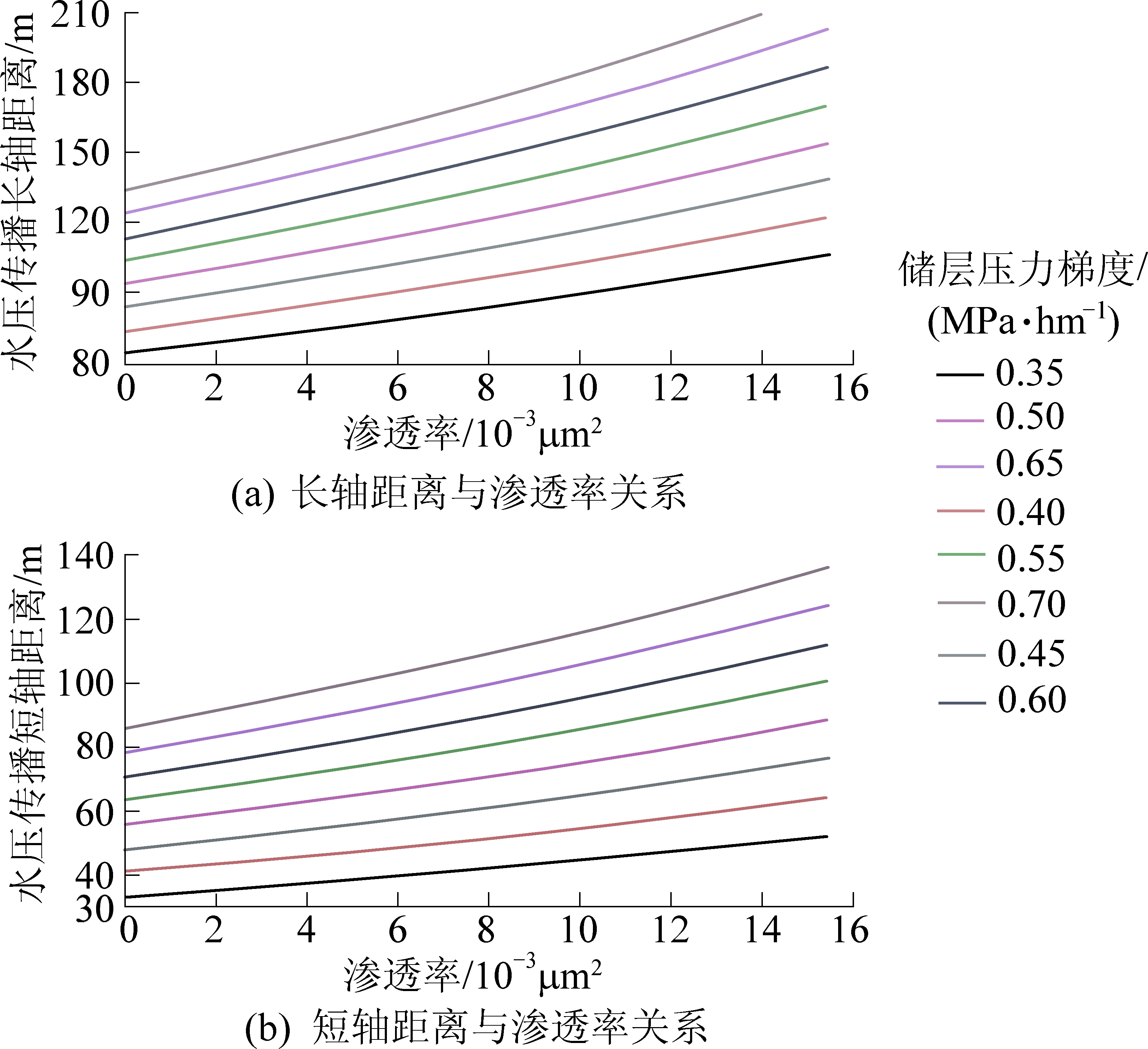
图3 水压传播长轴距离、短轴距离与渗透率关系
Fig.3 Relationships between distance in long axis
direction、short axis and permeability
从图3可看出,在储层压力梯度不变的情况下,随着渗透率的增加,影响距离呈指数型增加;在渗透率不变的情况下,随着储层压力的增加,影响距离呈线性增加。当储层压力梯度为0.5 MPa/hm,压裂后渗透率一般为(0.5~8.0)×10-3μm2,长轴影响距离一般为95~120 m,短轴影响距离一般为56~75 m,该储层条件下井网应小于240 m×150 m。
2.2.2 研究区井网部署建议
根据水压传播距离数学模型可知,水力压裂后渗透率和储层压力梯度的大小对水压传播距离具有重要影响。裂缝监测结果表明,该区水力压裂后主裂缝的优势方向为NE40°—60°,煤体结构不同,导致压裂后渗透率差异较大。该区储层压力梯度一般为0.4~0.7 MPa/hm。通过对研究区已有的不同煤体结构水力压裂后渗透率的计算,提出了不同储层参数下井网部署建议,见表4。
表4 柿庄南区块不同储层参数下井网部署建议
Table 4 Suggestions on well pattern deployment for different
reservoir parameters in South Shizhuang Block
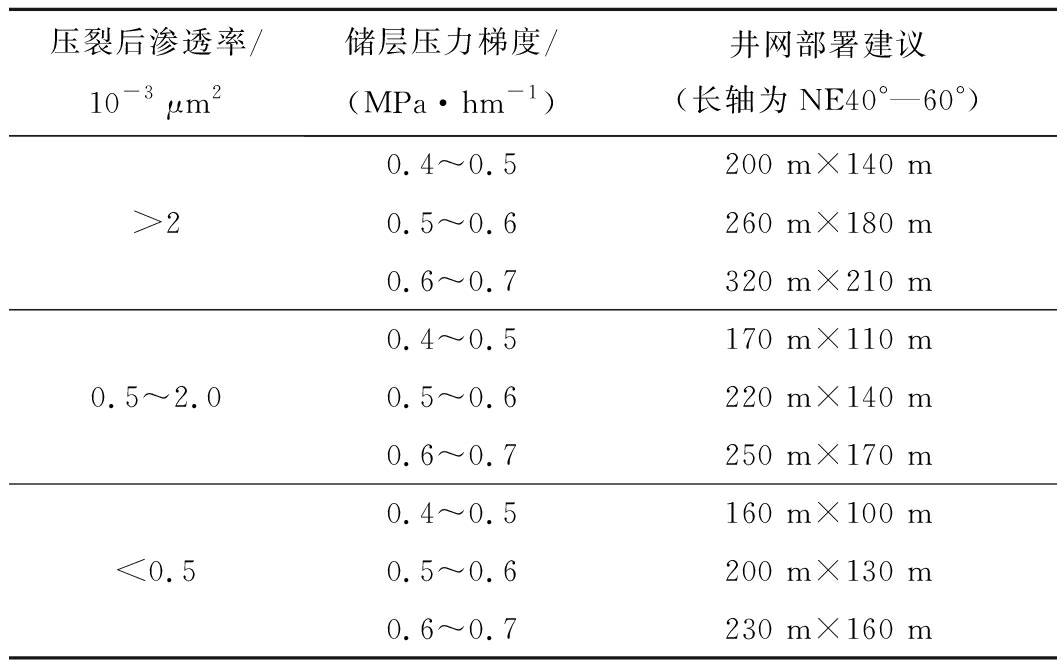
压裂后渗透率/10-3 μm2储层压力梯度/(MPa·hm-1)井网部署建议(长轴为NE40°—60°)>20.4~0.5200 m×140 m0.5~0.6260 m×180 m0.6~0.7320 m×210 m0.5~2.00.4~0.5170 m×110 m0.5~0.6220 m×140 m0.6~0.7250 m×170 m<0.50.4~0.5160 m×100 m0.5~0.6200 m×130 m0.6~0.7230 m×160 m
2.3 提出的数学模型与方法的应用条件
数学模型的计算结果主要受不同煤体结构压裂后渗透率预测结果和围岩含水层补给情况的影响。
水力压裂后的渗透率预测模型是基于达西定律的。当煤层段碎粒煤或糜棱煤所占比例较高时,压裂后的渗透率相对较小,流体流动时所需阻力相对较大,其流动有时候不再符合达西定律,导致渗透率的预测结果与实际存在一定的出入,这将影响最终水压传播的计算结果。另外,所用的基本公式为库萨金公式,该公式适用于无越流补给条件。但在排采时,围岩或多或少都会对煤层补给,含水层厚度的取值是否与实际更符合,对结果也会造成一定的影响。在实际应用时,需根据现场实际情况,对含水层厚度进行修正,使计算结果与实际更符合。
3 结 论
1)根据沃伦-茹特渗流模型,结合压裂时的压降曲线、排采过程中气/水所占比例的变化,分别构建了单相水流阶段、气/水两相流低产阶段、气/水两相流稳产阶段水相渗透率预测模型,把这些模型嵌入到经典的无越流补给的库萨金水压影响距离模型中,能分别对煤层气井整个排采阶段水压传播半径进行定量评价。
2)干扰试井和Eclipse数值模拟软件验证了计算结果的准确性。根据建立的水压数学模型,建立了储层压力-渗透率-水压传播距离图版。结果表明:当储层压力梯度为0.5 MPa/hm,压裂后渗透率一般为(0.5~8)×10-3μm2,长轴影响距离一般为95~120 m,短轴影响距离一般为56~75 m,该储层条件下井网应小于240 m×150 m。在渗透率不变的情况下,随着储层压力梯度的增加,井网间距近似呈线性增加。
3)水力压裂后渗透率预测结果的准确与否对水压传播距离计算具有重要影响。目前建立的数学模型对碎粒煤和糜棱煤所占比例较高时,适用性较差,需在今后进一步进行研究。
[1] 方世跃,许 哲,何建琴,等.煤层气井注入/压降试井研究进展[J].煤炭科学技术,2018,46(9):227-232.
FANG Shiyue,XU Zhe,HE Jianqin,et al.Study progress of injection / pressure drop test well for coalbed methane well [J].Coal Science and Technology,2018,46(9):227-232.
[2] 安 杰,杨振东,柳光伟,等.低压煤储层注入/压降试井存在的问题及方法研究[J].油气井测试,2014,23(2):15-17.
AN Jie,YANG Zhendong,LIU Guangwei,et al.Problem in injection/fall well test to low pressure coal reservoir and its method[J].Well Testing,2014,23(2):15-17.
[3] 王庆红,王常岭,吕万一,等.注入/压降工艺在低渗透油藏中的应用[J].油气井测试,2000,9(3):67-69.
WANG Qinghong,WANG Changling,LYU Wanyi,et al.Application of injection/pressure drop process in low permeability reservoirs[J].Well Testing,2000,9(3):67-69.
[4] 董斯良,张晓鹏,李孝利.煤层气井注入/压降法试井工艺[J].油气井测试,1997(3):64-66.
DONG Siliang,ZHANG Xiaopeng,LI Xiaoli.CBM well injection/pressure drop test process[J].Well Testing,1997(3):64-66.
[5] 廖红伟,王 琛,左代荣.应用不稳定试井判断井间连通性[J].石油勘探与开发,2002,29(4):87-89.
LIAO Hongwei,WANG Chen,ZUO Dairong.Applying transient testing to the judgement of inter-well connectivity[J].Petroleum Exploration and Development,2002,29(4):87-89.
[6] 周 蓉.复杂渗流条件下的不稳定试井分析及应用[D].北京:中国科学院力学研究所,2002.
[7] 安 杰,刘大为,张 平.煤层气已排采井井间干扰试井解释方法及应用[J].煤炭学报,2017,42(5):1236-1242.
AN Jie,LIU Dawei,ZHANG Ping.Research on the interpretation method and its application of interference well test analysis for CBM drainage wells [J].Journal of China Coal Sciety,2017,42(5):1236-1242.
[8] 杨春阳.干扰试井资料在气井中的应用[J].化工管理,2015(30):71-71.
YANG Chunyang.Application of interference test data in gas well[J].Chemical Enterprise Management,2015(30):71-71.
[9] 徐兵祥,李相方,任维娜,等.基于均衡降压理念的煤层气井网井距优化模型[J].中国矿业大学学报,2014,43(1):88-93.
XU Binxiang,LI Xiangfang,REN Weina,et al.Optimization model of well pattern and spacing in CBM reservoirs using the concept of balanced depressurization [J].Journal of China University of Mining & Technology,2014,43(1):88-93.
[10] 刘世奇,桑树勋,李梦溪,等.沁水盆地南部煤层气井网排采压降漏斗的控制因素[J].中国矿业大学学报,2012,41(6):943-950.
LIU Shiqi,SANG Shuxun,LI Mengxi,et al.Control factors of coalbed methane well depressurization cone under drainage well network in southern qinshui basin[J].Journal of China University of Mining & Technology,2012,41(6):943-950.
[11] 杜严飞,吴财芳,邹明俊,等.煤层气排采过程中煤储层压力传播规律研究[J].煤炭工程,2011,43(7):87-89.
DU Yanfei,WU Caifang,ZOU Mingjun,et al.Study on reservoir pressure transmission law during gas mining and drainage process of coal bed methane well [J].Coal Engineering,2011,43(7):87-89.
[12] 许小凯.煤层气直井排采过程中煤储层应力敏感性及其压降传播规律[D].北京:中国矿业大学(北京),2016.
[13] 田永东.沁水盆地南部煤储层参数及其对煤层气井产能的控制[D].北京:中国矿业大学(北京),2009.
[14] 胡海洋.不同储层类型煤层气直井排采控制研究[D].焦作:河南理工大学,2015.
[15] 葛家理.现代油藏渗流力学原理[M].北京:石油工业出版社,2003,85-93.
[16] 左胜杰,马 丽,单学军.利用煤层气田生产数据计算相渗的新方法[C]//2013年煤层气学术研讨会论文集,206-214.
[17] 李 瑞.煤层气排采中储层压降传递特征及其对煤层气产出的影响:以沁水盆地为例[D].武汉:中国地质大学(武汉),2017.
