0 引 言
断层在采动影响下发生活化时,常引发塌方、冒顶、突水、矿震、冲击地压等事故[1]。对于有天然气、页岩气、石油等气(液)态资源赋存的断层,断层的活化又为资源的喷涌提供通道[2]。因此,国内外众多学者对断层活化的机理产生了浓厚兴趣并为此开展了大量的研究工作,取得了丰硕的成果。
文献[3-5]应用关键层结构模型分析了断层突水机理;师本强等[6]对采场覆岩中断层因工作面推进而活化突水进行了力学分析,导出了断层的活化准则;刘志军等[7]编制了有限元程序分析了各断层要素影响下采场的应力分布规律及突水机理,并建立了正、逆断层的突水判据;潘一山等[8]将断层冲击地压看成是断层带与上下盘围岩系统的变形失稳,建立了扰动响应的稳定性判别准则;蒋金泉等[9]采用三维数值计算方法模拟了上盘、下盘工作面向逆断层推进过程中的采动应力演化特征、煤层顶板运动特征及断层活化规律;徐晓惠等[10]建立逆断层简化模型分析了采动影响下逆断层特征参数对断层活化的作用;宋义敏等[11]通过搭建高速数据采集系统对断层冲击地压失稳瞬态过程进行研究,发现断层冲击地压发生与侧向压力的量值有关;卜万奎等[12]针对含断层缺陷底板的受力特征建立了力学模型,研究发现断层倾角越大越易活化;齐庆新等[13]采用相似模拟和数值模拟相结合的手段分析了冲击地压的诱发机制;夏永学等[14]采用Anderson断层模型并通过相关实测数据分析,研究了断层冲击地压与地应力类型、采深和应力累积水平值的关系;姜福兴等[15]将数值模拟和现场微震数据进行耦合分析,揭示了开采致断层活化和灾变机制;林远东等[16]基于梯度塑性理论建立了断层活化判据,得到了断层活化的影响因素;吕进国等[17-18]通过模拟工作面从断层上下盘向断层方向的回采过程,发现断层上法向应力和切应力对采动影响具有不同的敏感性;BRACE等[19-20]将断层诱发地震的现象和岩石摩擦滑动的特征进行对比,提出用粘滑解释浅源地震发生过程的观点,奠定了断层粘滑失稳理论的基础;文献[21-24]指出断层活动及断裂过程与断层带内的流体有关。
众多学者常采用相似模拟、数值模拟及现场实测的方法进行研究,具有成本高、耗时长的特点,且三种方法所获结论的吻合度往往不高。而选择合理的力学模型及应用数理方法进行研究,并将所获结论与相关实践相印证的方法具有明显优势。笔者采用Anderson断层模型[25]和M-C强度准则,以断层带、上盘和下盘为系统,经严密的数理推导建立了断层自锁与断层活化的判别准则,研究了系统参量对断层稳定性的影响规律,并在此基础上提出了有效控制断层稳定性的措施;研究成果对发育有断层的地下资源开采、地下结构及防震减灾等工程具有重要参考价值。
1 断层自锁与活化的判别准则
1.1 Anderson断层模型和断层面上点的应力状态
文献[26-27]的研究结果表明,断层受采动的影响与工作面的位置有关。断层面附近岩层高位点先于低位点受到采动影响,且随断层与工作面距离的减少,断层面活化失稳危险先升高后降低;随工作面过断层前后,危险区由高层位向低层位岩层转移。采动对断层面应力场及断层稳定性的影响主要表现有2点。
1)工作面由断层下盘向断层推进过程中,当工作面距断层较远时,断层面上的应力状态基本保持不变;当工作面距断层30 m时,断层面上的正应力下降而剪应力上升;当工作面距断层20 m时,断层面上的正应力迅速下降而剪应力迅速上升;当工作面距断层10 m时,断层面上的正应力和剪应力都迅速减小,但正应力减小的幅度远大于剪应力减小的幅度,断层面剪应力与正应力的比值急剧增加。因此,在采动作用下断层面上剪应力的增加或正应力的减小,都会诱发断层滑移失稳。
2)当工作面由断层上盘向断层推进时,断层面上的正应力逐渐增加,而剪应力先增加后减小;当工作面距离断层大于30 m时,断层剪应力和正应力均增加,但断层剪应力与正应力的比值基本不变;当工作面继续向断层推进时,正应力继续上升,而剪应力下降,断层围岩系统处于稳定状态。
由此可见,断层受扰动后断层面上应力状态的变化情况决定了断层的稳定性。断层面上应力状态的变化是断层围岩受扰动后地应力重新分布作用的结果。Anderson断层模型[25]能较好地反映系统受扰动后地应力与断层稳定性的关系,如图1所示。
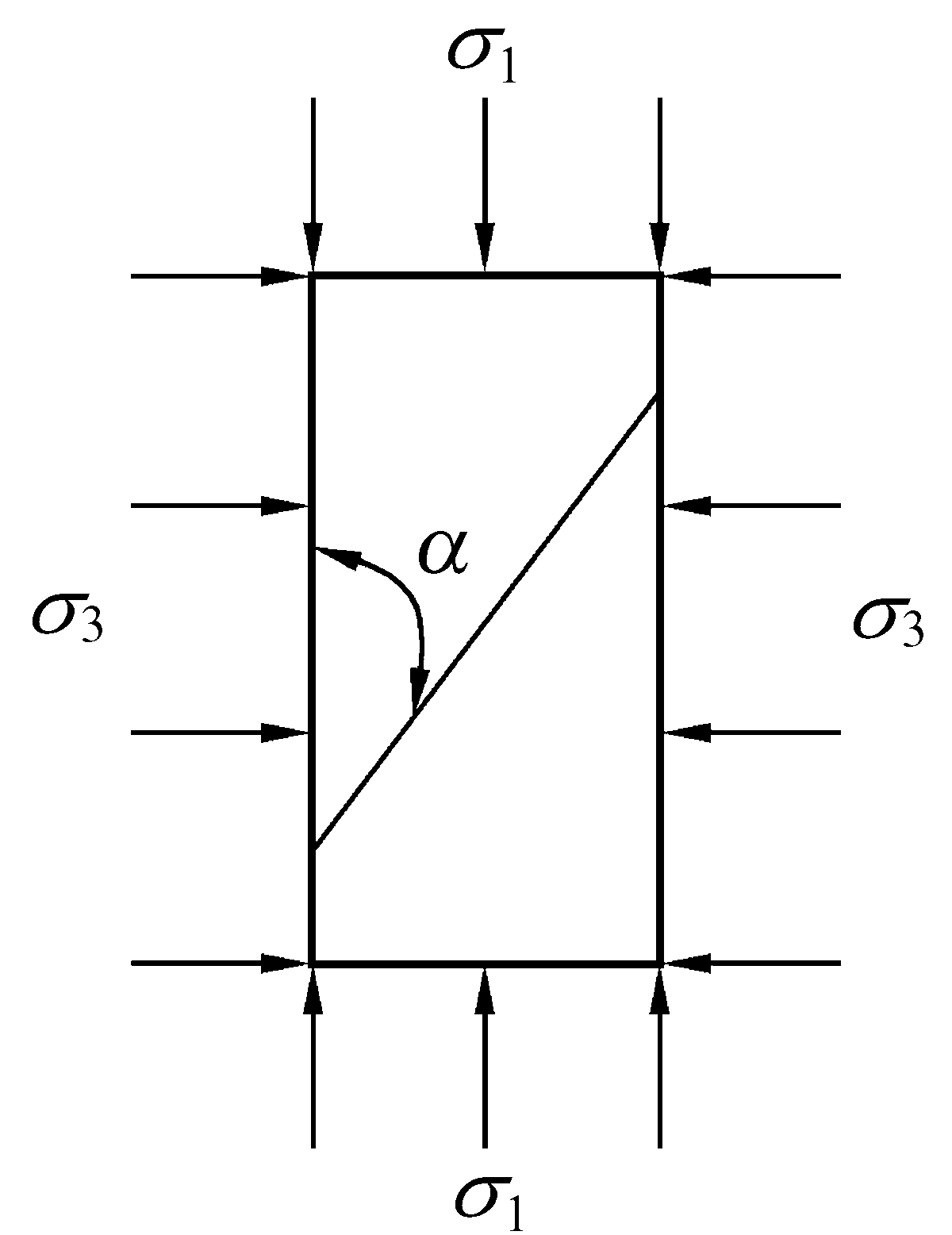
图1 Anderson断层模型[25]
Fig.1 Anderson model of fault
图1中σ1和σ3分别为系统在采动影响下所受垂直应力和垂直于断层走向的侧向水平应力,且σ1>σ3;若垂直应力小于水平应力时,需将图中σ1和σ3的下标互换。α为σ1与断层面的夹角,称之为断层倾角,取值范围为α∈(0,π)。然而,对于α为钝角的情况,可通过坐标变换转化为锐角的情形。因此,在后续的分析过程中,将α限定在(0,π/2)范围内。
由点的应力状态分析[28]得断层面上的应力为
(1)
(2)
式中:σ为断层面上正应力,MPa;τ为断层面上切应力,MPa;pi为断层裂隙流体压力,MPa。
由式(1)、式(2)得
(3)
式(3)表示的Mohr应力圆如图2所示。该应力圆的圆心O1的坐标为((σ1+σ3-2pi)/2,0),应力圆的半径为R=(σ1-σ3)/2,断层面上的应力情况对应于应力圆上B点的横坐标和纵坐标,其随α在(0,π/2)内变化。
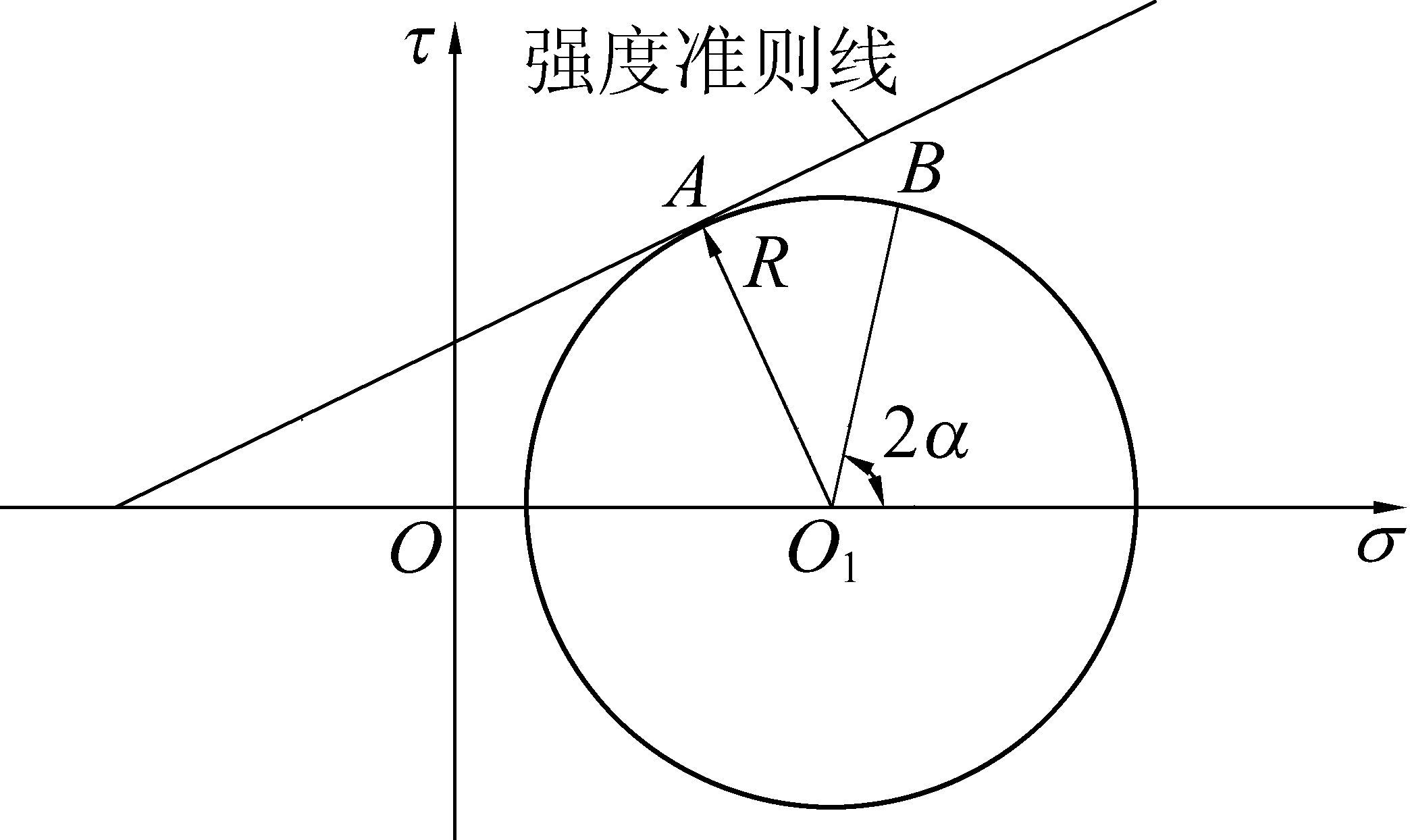
图2 断层面上点的应力圆
Fig.2 Stress circle of the point of fault plane
1.2 极限平衡状态断层强度准则和视摩擦因数
断层处于极限平衡状态下,断层面上的正应力σ和切应力τ满足Mohr-Coulomb强度准则[29],即
τ=c+kσ
(4)
式中:c为断层面黏聚力,MPa;k为断层摩擦因数。
由式(4)可知,断层摩擦因数k的值越大,结构面的抗剪强度越高。而断层摩擦因数k是由断层的内摩擦角φ所确定的量,其与φ的关系[29]为
k=tan φ
(5)
式中:φ为断层的内摩擦角,rad。
断层内摩擦角φ与断层带岩土的岩性有关,其取值范围为φ∈(0,π/2)。断层内摩擦角φ的大小是由断层带岩土的材料及结构面之间的粗糙度所确定的量,在岩土材料不变的条件下,结构面越粗糙断层的内摩擦角φ越大。
由式(4)和式(5)可知,断层内摩擦角φ越大,断层的摩擦因数k越大,结构面的抗剪强度便越高。再由三角函数关系sin2 φ+cos2 φ=1及式(5)得
(6)
(7)
断层在极限平衡状态下,断层面上点的应力圆与式(4)表示的直线相切于点A,如图2所示。若此时B点移至A点,α对应角度α1,则由图可知
α1=π/4+φ/2
(8)
将α1称为断层极限平衡的特征角,简称为断层特征角,其大小由断层的内摩擦角φ确定。
由式(1)、式(2)、式(4)、式(6)和式(7)得断层处于极限平衡状态时,断层摩擦因数与地应力(包括σ1和σ3)、断层面黏聚力c和断层裂隙流体压力pi的关系为
(9)
且有![]()
由式(5)及断层内摩擦角φ的取值范围可知,k为正值,则式(9)的分子中相减项无实际意义,略去。从而,断层在极限平衡状态下各参量间的量值关系为
(10)
极限平衡为非稳态平衡,受微小干扰后该状态易被打破。因此,断层的极限平衡状态被认为是断层活化的起点。由式(10)可见,断层的活化启动与断层内摩擦角φ、地应力(包括σ1和σ3)、断层面黏聚力c及断层裂隙流体压力pi相关。则令
(11)
将k1称为断层视摩擦因数。由式(11)可见,断层视摩擦因数k1与采动影响下的地应力(包括σ1和σ3)、断层面黏聚力c及断层裂隙流体压力pi有关。
1.3 断层自锁与活化的判别准则
经纬等[30]的研究结果表明,岩石发生强度破坏后内摩擦角φ的变化不大,而黏聚力c却大幅降低。因此,在断层内摩擦角φ变化不大的情况下,由式(5)知,断层面的Mohr-Coulomb强度准则所示的直线斜率可认为不变,但因受采动影响下断层面黏聚力c的降低而使得直线整体下移。另外,在采动影响下地应力将重新分布,虽然此时断层面上点的应力圆圆心O1及半径R与图2中对于应力圆的描述并无差别,即应力圆的圆心坐标仍为![]() 半径
半径![]() 且
且![]() 空间关系如图3所示,但此时σ1、σ3及pi已然在采动影响下发生了变化。
空间关系如图3所示,但此时σ1、σ3及pi已然在采动影响下发生了变化。
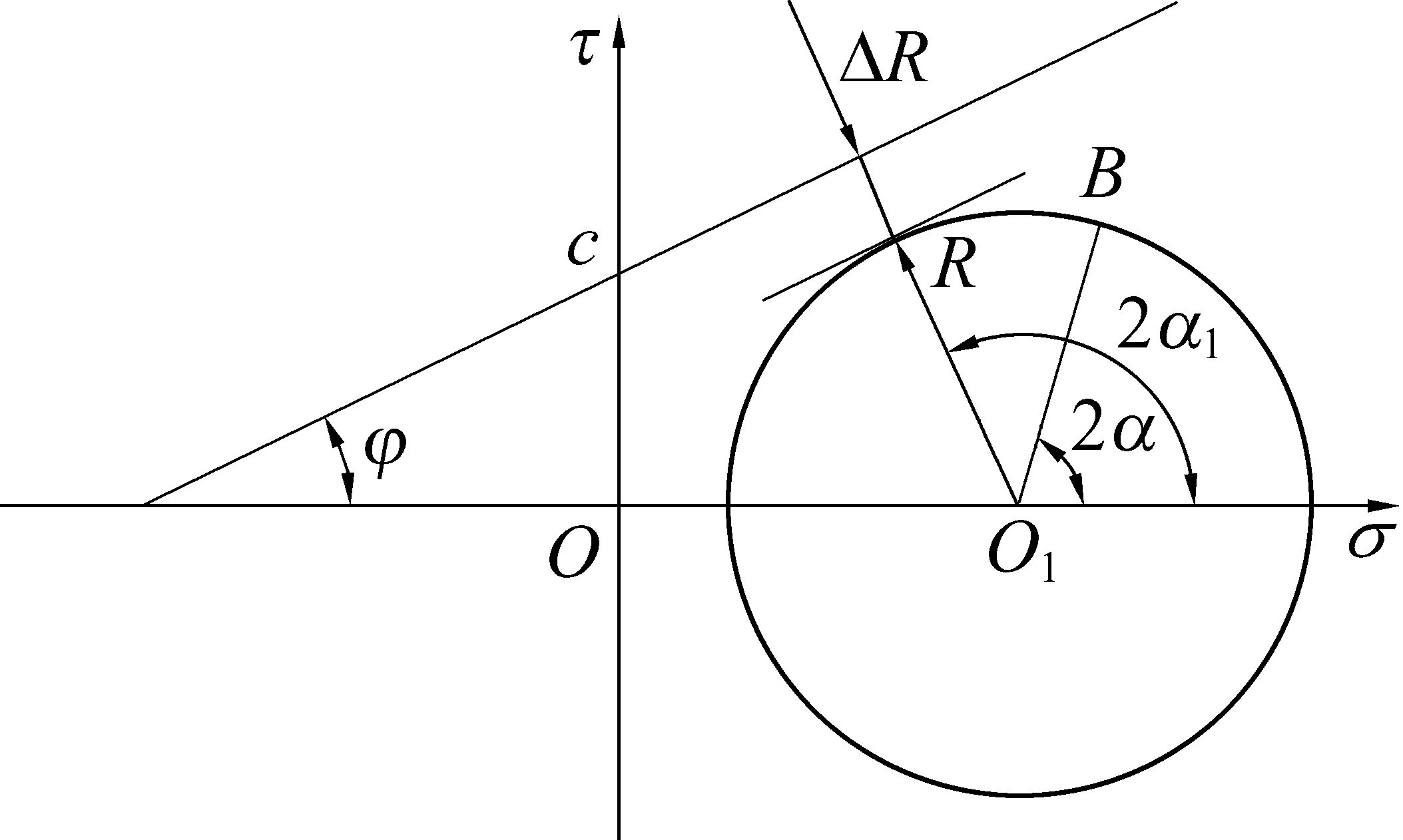
图3 判别断层状态示意
Fig.3 Schematic diagram of discriminating fault’s state
设采动影响下断层面上点的Mohr应力圆与断层面的Mohr-Coulomb强度准则表示的直线之间的最小间距为ΔR,由图3所示几何关系得
(12)
将![]() 及R的表达式代入并展开得
及R的表达式代入并展开得
(13)
因受采动的影响,表示Mohr-Coulomb强度准则的直线整体下移,且断层面上点的Mohr应力圆的圆心和半径都在动态变化着,则Mohr-Coulomb强度准则表示的直线与断层面上点的Mohr应力圆可能存在3种几何关系,对应着断层不同的3种状态。
1)当ΔR>0时,表示Mohr-Coulomb强度准则所确定的直线与断层面上点的Mohr应力圆为相离关系,此时断层处于稳定的平衡状态。将断层处于稳定的平衡状态称为断层自锁。
2)当ΔR=0时,表示Mohr-Coulomb强度准则所确定的直线与断层面上点的Mohr应力圆为相切关系,此时断层处于极限平衡状态。极限平衡状态下的断层,受微小干扰后该平衡即被打破,故可认为此时断层处于活化启动状态。
3)当ΔR<0时,表示Mohr-Coulomb强度准则所确定的直线与断层面上点的Mohr应力圆为相割关系,此时断层处于活化状态。
1.3.1 断层自锁判别准则
由上述分析可知,断层自锁的几何条件为
ΔR>0
(14)
由式(6)、式(7)、式(13)和式(14)得
(15)
或
(16)
由式(5)及断层内摩擦角φ取值范围知,断层摩擦因数k为正值,则式(16)无实际意义,略去。从而,由式(5)和式(15)得断层自锁判别准则为
(17)
结合式(5)、式(11)和式(17),可将断层自锁的判别准则简记为
k1<k
(18)
式(18)表明,断层视摩擦因数k1小于断层摩擦因数k时断层处于自锁状态。
1.3.2 断层活化判别准则
同理,断层活化的几何条件为
ΔR≤0
(19)
由式(6)、式(7)、式(13)和式(19)解得
(20)
式(20)中所示的下限为负值,无实际意义,略去。从而,断层活化的判别准则为
(21)
式(21)取等号时,表示断层处于活化启动阶段。结合式(5)、式(11)和式(21),可将断层活化的判别准则简记为
k1≥k
(22)
式(22)表明,当断层视摩擦因数k1大于或等于断层摩擦因数k时断层处于活化状态。
2 系统参量对断层稳定性的影响
由断层自锁与活化的判别准则可知,断层的稳定性由断层视摩擦因数k1与断层摩擦因数k之间的量值关系决定。由式(5)可知,k是由断层内摩擦角φ所确定的量。由式(11)可知,k1是断层所受地应力(σ1和σ3)、裂隙流体压力pi及断层面黏聚力c等参量的函数,其随着各参量的变化而变化。断层面为弱面结构,黏聚力c受采动的影响将会变小甚至降低为零;地应力(σ1和σ3)受采动的影响将重新分布;裂隙流体压力pi在采动影响下,当断层处于应力增高区内时,因裂隙压密使pi变大,反之pi则降低。
可应用函数的单调性及增减性判别准则来研究系统参量(包括α、φ、σ1、σ3、c及pi等)在采动作用下对断层稳定性的影响,为有效控制断层的稳定性奠定理论基础。
2.1 断层倾角对断层稳定性的影响
由图2及式(8)可知,断层特征角α1是由断层内摩擦角确定的量;而断层面上点的正应力和切应力是断层倾角α的函数。由图3可知,断层倾角α对断层稳定性的影响,取决于α和α1之间的量值关系。
1)若α>α1,即当α>π/4+φ/2时,随着断层倾角α的减小,断层面上的应力值在应力圆上所对应的点到式(4)所示直线的距离ΔR越小,断层发生活化的倾向性越大。
2)若α<α1,即当α<π/4+φ/2时,随着断层倾角α的增大,断层面上的应力值在应力圆上所对应的点到式(4)所示直线的距离ΔR越小,断层发生活化的倾向性越大。
3)若α=α1,即当α=π/4+φ/2时,断层面上的应力值在应力圆上所对应的点到式(4)所示直线的距离ΔR达到最小,断层发生活化的倾向性最大。
因此,断层倾角α越接近于断层特征角α1,断层发生活化的倾向性越大。
2.2 断层内摩擦角对断层稳定性的影响
由式(5)可知,tan φ在φ的取值区间内是单调递增的,则断层内摩擦角φ越大,断层摩擦因数k越大。而k越大,式(18)所示的断层自锁条件越易获得满足。因此,断层内摩擦角φ越大断层的稳定性越好。
2.3 地应力对断层稳定性的影响
2.3.1 垂直方向应力对断层的影响
将视摩擦因数k1对垂直应力σ1求一阶导数得
(23)
式(23)的分子、分母均为正值,从而有dk1/dσ1>0。由函数增减性判别准则可知,k1随着σ1的增大而增大。由式(22)可知,当垂直应力增大时,断层活化的条件易获得满足,即垂直应力越大断层越易发生活化。
2.3.2 水平应力对断层的影响
将视摩擦因数k1对水平应力σ3求一阶导数得
(24)
由有效应力的概念[1]及主应力的符号规定[28]知:σ1>σ3>pi。则式(24)中分子,必有c-B<-(σ3-pi),即式(24)的分子-(c-B)2+(σ3-pi)2<0。式(24)中分母显然为正值,则dk1/dσ3<0。由函数增减性判别准则可知,断层视摩擦因数k1随着σ3的增大而减小。由式(18)知,主应力σ3越大,断层自锁条件越易获得满足,即断层的稳定性随着σ3的增大而增强。
综合上述2种情况可知,在采动影响下,系统的垂直应力σ1越大而水平应力σ3越小,断层稳定性越差。
2.4 断层面黏聚力对断层的影响
将视摩擦因数k1对黏聚力c求一阶导数得
(25)
因σ1>σ3>pi,有B>c,则式(25)的分子为负值,而分母为正值,故dk1/dc<0。由函数增减性判别准则知,断层视摩擦因数随着断层面黏聚力c的增大而减小。由式(18)可见,当断层面黏聚力c越大时,断层自锁条件越易获得满足,即断层面黏聚力c越大断层的稳定性越好。
2.5 裂隙流体压力对断层的影响
将断层视摩擦因数k1对断层裂隙流体压力pi求一阶导数得
(26)
因σ1>σ3>pi,从而上式分子中各项满足:(σ1-pi)2(c+B)2>(σ1-pi)2(σ3-pi)2,而(σ3-pi)2(c+B)2<(σ1-pi)2(σ3-pi)2,即式(26)的分子为正值。而分母显然为正,故dk1/dpi>0。由函数增减性判别准则可知,断层视摩擦因数k1随裂隙流体压力pi的增大而增大。由式(22)可知,随着pi的增大,断层活化条件容易获得满足,即断层裂隙流体压力pi越大断层越易发生活化。
3 讨 论
3.1 视摩擦因数与应力积累水平值的关系
断层活化启动后,断层面黏聚力c迅速降低,当黏聚力c降至零且断层裂隙流体为零时,对应的视摩擦因数记为k11。由式(11)可得
(27)
该结果与文献[14]中分析断层面黏聚力c为零且断层中没有裂隙流体时的应力积累水平值完全对应。因此,本文所定义的断层视摩擦因数k1更具有代表性,能更好地反映断层在采动影响下的应力积累水平。
文献[14]所导出的应力积累水平的表达式中并没有体现裂隙流体压力对应力积累水平的影响。为了对比分析,令式(11)中的黏聚力c为零,对应的视摩擦因数记为k12,从而得
(28)
对比式(27)和式(28),显然有k12>k11,即断层裂隙中有裂隙流体压力pi作用时,系统的应力积累水平比裂隙中没有流体的情况更高,断层发生活化的力学响应将更剧烈。
因此,本文定义的断层视摩擦因数可认为是对文献[14]提出的应力积累水平值的修正。断层视摩擦因数能更好地反映断层在采动影响下地应力、黏聚力和裂隙流体压力等因素共同作用的应力积累水平。
3.2 断层稳定性的控制方法
由系统参量对系统稳定性的影响规律可知,当地应力的σ1越大而σ3越小、断层面黏聚力c越小、裂隙流体压力pi越大,断层的视摩擦因数k1越大。由断层自锁与活化准则可知,断层视摩擦因数k1越大断层越易活化;而断层面内摩擦角φ越大,断层摩擦因数k越大,断层的稳定性随之增强。基于此,可采取相应措施对断层的稳定性进行有效控制。
1)实现断层自锁的措施。在地下资源开采、地下结构、隧道等工程施工中遇断层时,断层处于自锁方能确保施工安全。据地应力对系统稳定性的影响规律,可设计、选择合理的施工方案(如厚煤层采用分层开采)以降低采动对系统稳定性的影响;据断层面黏聚力对系统稳定性的影响规律,可采用超前预注浆方式使黏聚力增大;若断层中有裂隙流体赋存时,据裂隙流体压力对系统稳定性的影响规律,可采用钻孔疏排的方式降低流体压力。
2)实现断层活化的措施。断层的活化为断层中流体的喷涌提供了通道。对于开采石油、天然气、页岩气等工程,断层处于活化状态更有利于提高产能。据断层面黏聚力对系统稳定性的影响规律,可采用局部多点微爆破的方式使断层面黏聚力减小;据裂隙流体压力对系统稳定性的影响规律,可采用钻孔注高压水使裂隙流体压力增大的方式使断层活化。
工程实践表明[31-35],上述方法能有效控制断层的稳定性。由此可见,本文采用数理分析导出的断层自锁与活化判别准则及系统参量对断层稳定性的影响规律,对发育有断层的地下资源开采及防震减灾、隧道、地下结构等工程具有重要参考价值。
4 结 论
采用Anderson断层模型和Mohr-Coulomb强度准则和应用数理分析的方法研究了断层的稳定性及系统参量对断层稳定性的影响规律,并以此为基础提出了有效控制断层稳定性的措施,获得了如下结论:
1)断层视摩擦因数k1与地应力(σ1和σ3)、断层面黏聚力c及断层裂隙流体压力pi有关,反映了断层在采动影响下地应力(σ1和σ3)、裂隙流体压力pi及断层黏聚力c等因素共同作用的应力积累水平,其值越大,断层活化的倾向性越高。
2)断层摩擦因数k是由断层内摩擦角φ确定的参量,反映了断层带与断层上盘和下盘在接触面上的粗糙度。接触面越粗糙则内摩擦角φ越大,导致断层摩擦因数k越大。断层摩擦因数k越大,断层的稳定性越好。
3)断层是处于自锁还是活化状态,取决于断层视摩擦因数k1与断层摩擦因数k之间的量值关系。当断层视摩擦因数k1小于断层摩擦因数k时,断层处于自锁状态;当断层视摩擦因数k1大于或等于断层摩擦因数k时,断层处于活化状态。
4)断层倾角α、内摩擦角φ、断层面黏聚力c、裂隙流体压力pi、地应力(σ1和σ3)等系统参量对断层稳定性的影响为:断层倾角α越接近于断层特征角,断层活化的倾向性越大;断层内摩擦角φ越小断层越易活化;断层面黏聚力c越小断层越易活化;断层裂隙流体压力pi越大断层越易活化;垂直应力σ1越大,水平应力σ3越小,断层越易活化。
5)根据系统参量对断层稳定性的影响规律,可选择、设计合理的施工方案(如厚煤层采用分层开采)以降低采动的影响、采用超前预注浆增大断层面黏聚力、钻孔疏放裂隙流体以降低裂隙流体压力等措施增强断层的稳定性;可采用局部多点微爆破降低断层面黏聚力、钻孔注高压水使裂隙流体压力增大等措施以增大断层活化的倾向性。
[1] 蔡美峰,刘相寿,黄先彬.岩石力学与工程[M].北京:科学出版社,2002.
[2] 施龙青,韩 进.底板突水机理及预测预报[M].徐州:中国矿业大学出版社,2004.
[3] 黎良杰,钱鸣高,闻 全,等.底板岩体结构稳定性与底板突水关系的研究[J].中国矿业大学学报,1995,24(4):18-23.
LI Liangjie,QIAN Minggao,WEN Quan,et al.Relationship between the stability of floor structure and water-inrush from floor[J].Journal of China University of Mining & Technology,1995,24(4):18-23.
[4] 黎良杰,钱鸣高,李树刚.断层突水机理分析[J].煤炭学报,1996,21(2):119-123.
LI Liangjie,QIAN Minggao,LI Shugang.Mechanism of water-inrush though fault[J].Journal of China Coal Society,1996,21(2):119-123.
[5] 李青锋,王卫军,朱川曲,等.基于隔水关键层原理的断层突水机理分析[J].采矿与安全工程学报,2009,26(1):87-90.
LI Qingfeng,WANG Weijun,ZHU Chuanqu,et al.Analysis of fault water-inrush mechanism based on the principle of water resistant key strata[J].Journal of Mining and Safety Engineering,2009,26(1):87-90.
[6] 师本强,侯忠杰.覆岩中断层活化突水的力学分析及其应用[J].岩土力学,2011,32(10):3053-3057.
SHI Benqiang,HOU Zhongjie.Mechanical analysis of fault activation water inrush in over burden rock and its application[J].Rock and Soil Mechanics,2011,32(10):3053-3057.
[7] 刘志军,胡耀青.承压水上采煤断层突水的固流耦合研究[J].煤炭学报,2007,32(10):119-123.
LIU Zhijun,HU Yaoqing.Solid-liquid coupling study on water inrush through faults in coal mining above confined aquifer[J].Journal of China Coal Society,2007,32(10):119-123.
[8] 潘一山,王来贵,章梦涛,等.断层冲击矿压发生的理论与试验研究[J].岩石力学与工程学报,1998,17(6):642-649.
PAN Yishan,WANG Laigui,ZHANG Mengtao,et al.The theoretical and testing study of fault rock burst[J].Chinese Journal of Rock Mechanics and Engineering,1998,17(6):642-649.
[9] 蒋金泉,武泉林,曲 华.硬厚岩层下逆断层采动应力演化与断层活化特征[J].煤炭学报.2015,40(2):267-277.
JIANG Jinquan,WU Quanlin,QU Hua.Characteristic of mining stress evolution and activation of the reverse fault below the hard-thick strata[J].Journal of China Coal Society,2015,40(2):267-277.
[10] 徐晓惠,吕进国,刘 闯,等.采动影响下逆断层特征参数对断层活化的作用规律[J].重庆大学学报,2015,38(3):107-115.
XU Xiaohui,LYV Jinguo,LIU Chuang,et al.Influence law of fault activation induced by coal extraction based on characteristic parameters of thrust fault[J].Journal of Chongqing University,2015,38(3):107-115.
[11] 宋义敏,马少鹏,杨小彬,等.断层冲击地压失稳瞬态过程的试验研究[J].岩石力学与工程学报,2011,30(4):812-817.
SONG Yimin,MA Shaopeng,YANG Xiaobin,et al.Experimental investigation on instability transient process of fault rock burst[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(4):812-817.
[12] 卜万奎,徐 慧.某矿区带压开采逆断层活化及突水性分析[J].煤炭学报,2011,36(7):1177-1183.
BU Wankui,XU Hui.Analysis on reverse fault activation and water inrush possibility for coal mining above confined aquifer in a mining area[J].Journal of China Coal Society,2011,36(7):1177-1183.
[13] 齐庆新,李晓璐,赵善坤.煤矿冲击地压应力控制理论与实践[J].煤炭科学技术,2013,41(6):1-5.
QI Qingxin,LI Xiaolu,ZHAO Shankun.Theory and practices on stress control of mine pressure bumping[J].Coal Science and Technology,2013,41(6):1-5.
[14] 夏永学,王金华,毛德兵.断层活化的地应力判别准则及诱发冲击地压的典型微震特征[J].煤炭学报,2016,41(12):3008-3015.
XIA Yongxue,WANG Jinhua,MAO Debing.Analysis of fault activation induced rock burst risk based on in-situ stress measurements[J].Journal of China Coal Society,2016,41(12):3008-3015.
[15] 姜福兴,刘伟建,叶根喜,等.构造活化的微震监测与数值模拟耦合研究[J].岩石力学与工程学报,2010,29(S2):3590-3597.
JIANG Fuxing,LIU Weijian,YE Genxi,et al.Coupling study of micro-seismic monitoring and numerical simulation for tectonic activation[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S2):3590-3597.
[16] 林远东,涂 敏,刘文震,等.基于梯度塑性理论的断层活化机理[J].煤炭学报,2012,37(12):2060-2064.
LIN Yuandong,TU Min,LIU Wenzhen,et al.Faults activation mechanism based on gradient-dependent plasticity[J].Journal of China Coal Society,2012,37(12):2060-2064.
[17] 吕进国,姜耀东,李守国,等.巨厚坚硬顶板条件下断层诱冲特征及机制[J].煤炭学报,2014,39(10):1961-1969.
LYu Jinguo,JIANG Yaodong,LI Shouguo,et al.Characteristics and mechanism research of coal bumps induced by faults based on extra thick and hard roof[J].Journal of China Coal Society,2014,39(10):1961-1969.
[18] 吕进国.巨厚坚硬顶板条件下逆断层对冲击地压作用机制研究[D].北京:中国矿业大学(北京),2013.
[19] BRACE W F.Laboratory studies of stick-slip and their application to earthquakes[J].Tectonophysics,1972,14(3/4):189-200.
[20] BRACE W F,BYERLEE J D.Stick-slip as a mechanism for earthquakes[J].Science,1966,153 :990-992.
[21] HICKMAN S,SIBSON R,BRUHN R.Introduction to special section:mechanical involvement of fluids in faulting[J].Journal of Geophysical Research:Solid Earth,1995,100(B7):12831-12840.
[22] WIBBERLEY C A,SHIMAMOTO T.Earthquake slip weakening and asperities explained by thermal pressurization[J].Nature:UK Edition,2005,436 689-692.
[23] POLAK A,ELSWORTH D,YASUHARA H,et al.Permeability reduction of a natural fracture under net dissolution by hydrothermal fluids[J].Geophysical Research Letters,2003,30(20):2020.
[24] RICE J R.Heating and weakening of faults during earthquake slip[J].Journal of Geophysical Research:Solid Earth.2006,111(B5):1-29.
[25] ANDERSON E M.The dynamics of faulting and dyke formation with application to Britain[M].London:Oliver and Boyd,1951.
[26] 赵毅鑫,王 浩,卢志国,等.开采扰动下断层面库仑应力及诱发矿震时空演化特征[J].煤炭学报,2018,43(2):340-347.
ZHAO Yixin,WANG Hao,LU Zhiguo,et al.Characteristics of tremor time-space evolution and Coulomb stress distribution along the fault during workface excavation[J].Journal of China Coal Society,2018,43(2):340-347.
[27] 李志华,窦林名,陆振裕,等.采动诱发断层滑移失稳的研究[J].采矿与安全工程学报,2010,27(4):499-504.
LI Zhihua,DOU Linming,LU Zhenyu,et al.Study of the fault slide destabilization induced by coal mining[J].Journal o f Mining & Safety Engineering,2010,27(4):499-504.
[28] 吴家龙.弹性力学[M].北京:高等教育出版社,2016.
[29] BYERLEE J D.Friction of rocks[J].Pure and Applied Geophysics,1978,116(4/5):615-626.
[30] 经 纬,薛维培,姚直书.巷道围岩塑性软化区岩石内摩擦角与黏聚力变化规律[J].煤炭学报,2018,43(8):2203-2210.
JING Wei,XUE Weipei,YAO Zhishu.Variation of the internal friction angle and cohesion of the plastic softening zone rock in roadway surrounding rock[J].Journal of China Coal Society,2018,43(8):2203-2210.
[31] 刘招伟,张顶立,张民庆.圆梁山隧道毛坝向斜高水压富水区注浆施工技术[J].岩石力学与工程学报,2005,24(10):1728-1734.
LIU Zhaowei,ZHANG Dingli,ZHANG Minqing.Grouting technique for high-pressure and water-rich area in Maoba syncline at Yuanliangshan Tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(10):1728-1734.
[32] 李海燕,王 琦,江 贝,等.深立井大水工作面注浆堵水技术[J].煤炭学报,2011,36(S2):444-448.
LI Haiyan,WANG Qi,JIANG Bei,et al.Technology of grouting and blocking water on working face with massive water in deep vertical shaft[J].Journal of China Coal Society,2011,36(S2):444-448.
[33] 郭小红,陈飞飞,褚以惇,等.富水软弱带公路隧道支护技术研究[J].岩土力学,2011,32(S2):449-454.
GUO Xiaohong,CHEN Feifei,CHU Yidun,et al.Research on support techniques for tunnel in watery and weak stratum[J].Rock and Soil Mechanics,2011,32(S2):449-454.
[34] 杨晓华,谢永利.公路隧道坍方综合处治技术[J].长安大学学报:自然科学版,2004,24(1):61-64.
YANG Xiaohua,XIE Yongli.Synthetical treatment technique for highway tunnel collapse[J].Journal of Chang-an University :Natural Science,2004,24(1):61-64.
[35] 李海燕,胥洪彬,李召峰,等.深部巷道断层涌水治理研究[J] 采矿与安全工程学报,2018,35(3):635-641,648.
LI Haiyan,XU Hongbin,LI Zhaofeng,et al.Study on treatment of fault water gushing in deep roadway[J].Journal of Mining & Safety Engineering,2018,35(3):635-641,648.
