0 引 言
排土工程是露天开采的重要组成部分,受煤层赋存条件和剥、采、排时空关系的约束,开采初期必然有剥离物排弃至采场外部,这就要求在境界之外的适当地段设置排土场以容纳这些外排剥离物[1-3]。排土场的建设过程就是在地表重构大型人工土石堆积体的过程,其涉及安全、环保和经济等诸多方面。关于露天矿排土工程的优化问题,多年来各国学者从多角度进行了研究。在排土场边坡稳定控制技术方面,ZHANG等[4]研究了倾斜基底高段排土的边坡稳定性分析及控制技术;李伟[5]研究了排土场边坡变形破坏机理;王瑞等[6]针对排土场容量不足的难题,研究了增高扩容及边坡稳定性控制技术;关锌[7]研究了露天矿软弱基底引起排土场滑坡的机理,得出排土场滑坡机理主要为单台阶圆弧滑移和整体“坐落-滑移式”破坏2种形式;RASSAM等[8]研究了凹形边坡的稳定性问题,得出在水平面上呈凹形的高废石堆边坡的极限稳定角至少要比直线形边坡大2°。在排土工程规划方面,王忠鑫等[9-10]提出了露天矿排土场综合优化需要解决的若干关键技术,研究了相邻露天矿的排土运输系统优化问题,建立了相邻露天矿压帮排土高度及排土参数优化的数学模型;李三川等[11]以排土场剥离运输功最小为基本原则,建立了排土场运输费用现值模型及排土场征地费用现值模型。在生态环境恢复和评价方面,SMOLI等[12]建立了露天矿排土场微量元素和有机物含量试验分析模型,进行了矿区的生态和健康风险评价;吕刚等[13]建立了排土场土壤水文效应评价指标体系和评价模型;任志胜等[14]研究了排土场不同复配方式人工新构土体水分时空变化规律;JORDANOVA等[15]进行了磁法在排土场土壤修复评价中的应用研究。相关的研究成果还有很多,但研究的核心问题基本可归为以上3大类,本文不再一一赘述。
总体来说,已有研究主要针对容量保障、边坡安全以及生态恢复等方面,但对于确定的外排总量需求,排土场的形态可以有无限多种,不同形态参数所产生的排土工程费用也不尽相同。因此,研究排土场形态参数的整体优化方法对于解决露天开采的实际问题具有重要意义,目前尚无该方面的研究。
1 排土场形态参数L-P优化模型
排土场是剥离物按一定的顺序和参数堆置而成的大型堆积体[16-18],其形态一般呈阶梯状,排土场的一般形态如图1所示。

图1 排土场形态
Fig.1 Dump form
排土场的设计过程主要是其形态参数的确定过程,对于露天矿而言,当首采区、初始拉沟位置以及开采程序确定后,开采期间所发生的外排量即已确定。而对于确定的外排量,在安全和环境等约束下,其形态有无限多种几何表达形式,如何寻找最优的几何形态是需要解决的关键问题。
该问题可以进一步抽象为:任务量一定,如何统筹安排,以最低的成本完成这项任务,即最低成本问题,属于典型的线性规划问题,因此建立L-P(Linear Programming)数学模型是该问题的最佳解决途径。
1.1 线性规划问题标准型
线性规划的概念产生于1947年的军事行动计划有关实践,而相关问题早在1823年Fourier和1911年Poussin就已经被正式提出[19]。线性规划就是在满足线性约束条件下,求目标函数的极值。线性规划的目标函数可以是求最大值,也可以是求最小值,约束条件可以是不等式也可以是等式,变量可以有非负要求也可以没有非负要求。
设xj(j=1,2,…,n)是待确定的非负的决策变量;cj(j=1,2,…,n)是与决策变量相对应的价值系数;aij(i=1,2,…,m,j=1,2,…,n)是技术系数;bi(i=1,2,…,m)是右端项,则规定线性规划问题的标准型为[20-21]:
(1)
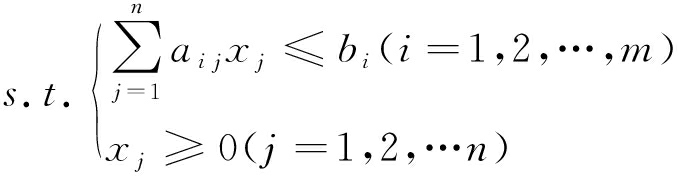
(2)
线性规划的标准型要求目标函数求最小值,约束条件均为等式方程,右端项bi≥0,且所有决策变量xj均为非负。不符合这几个条件的线性模型要首先转化为标准型。
1.2 目标函数
排土场形态参数优化的目的是实现排土总费用最低[20-21]。从排土费用构成看,主要包括卡车的运输费用、推土机辅助作业费用和排土场占地费用3大部分。其中,推土机辅助作业费用是推土量的函数,其与排土场的形态参数无关,因此优化模型中可以不予考虑。卡车的运输费用可以分为重车上运费用和空车下运费用。一般来说,排土场的排弃高度越高,卡车重载爬坡运输距离越长,重载平段运输距离越短,重车上运费用越高,但排土场占地面积越小,占地费用越低。反之,若排土场排弃高度越低,卡车重载爬坡运输距离越短,重载平段运输距离越长,重车上运费用越低,但排土场占地面积越大,占地费用越高。即运输费用和占地费用均是排弃高度的函数。当排土场基底为(近)水平、不考虑物料排弃顺序对台阶高度的影响时,排弃高度是由排土场占地面积和台阶个数共同决定的。
从理论上分析,当排土台阶周界形状为圆形时,排土场占地的利用率最高,但实际生产中受到征地等外部条件的限制,往往并非如此。为了模型计算的便利性,本文假设排土台阶周界形状为圆形。
既定排土量全周期内的累计排土费用现值定义为排土总费用A,它是总排弃量T、排土台阶个数n、最下排土台阶底面半径r、单台阶高度h、最终平盘宽度b、坡道坡度g、卡车坡段小时运行成本c、卡车平段小时运行成本c1、卡车上坡行车速度s以及平段行车速度s1的函数。当排土量和设备型号确定时,使排土总费用A(T,n,r,h,b,g,c,c1,s,s1)达到最小时的参数即为最优形态参数P={n,r,h,b,g}。
目标函数为
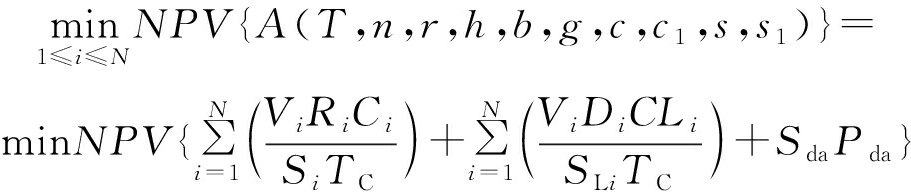
(3)
式中:Vi为第i个台阶的排弃量,m3;Ri为第1~i个台阶坡顶的坡道长度,km;Ci为卡车坡段小时运行成本,元/h;CLi为卡车平段小时运行成本,元/h;Si和SLi分别为卡车在坡道和平段上的平均行车速度,km/h;TC为卡车标准载重,m3;Sda为排土场占地面积,km2;Pda为购地单价,元/km2;i为台阶顺序号(自下而上);N为台阶总数量,个。
1.3 约束条件
1)排土范围约束。任意排土台阶的底部周界半径ri满足如下约束:
∀i≤N,∃ri≥0
(4)
2)坡道长度。卡车自采掘场工作面至排土场工作面的运输距离由3个部分组成:①第1部分为采掘场工作面至采掘场地表出入沟口的距离L1;②第2部分为采掘场地表出入沟口至排土场第1个台阶坡道入口的距离L2;③第3部分为排土场第1个台阶坡道入口至排土工作面的距离L3。其中L1和L2与排土场的形态参数无关,对于本L-P模型而言属于常数,因此模型中可以不予考虑,仅研究L3的计算原理即可。L3可分为坡道长度Ri和平段运距Di两部分。
第i个排土台阶的坡道长度Ri满足如下几何约束:
(5)
式中:hj为第j个台阶的高度,m;gj为第j个台阶坡底至坡顶的坡道坡度。
3)平段运距。卡车自第i个台阶坡道出口至本台阶排土重心G(xi,yi,zi)的运距Di是排土台阶高度hi和台阶坡面角α的函数。Di满足如下约束:

(6)
4)单台阶容量。任意台阶的排土容量都是有上限的,第i个台阶的排土容量Vi是排土台阶高度hi、台阶底部周界半径ri和台阶坡面角α的函数。Vi满足如下约束:
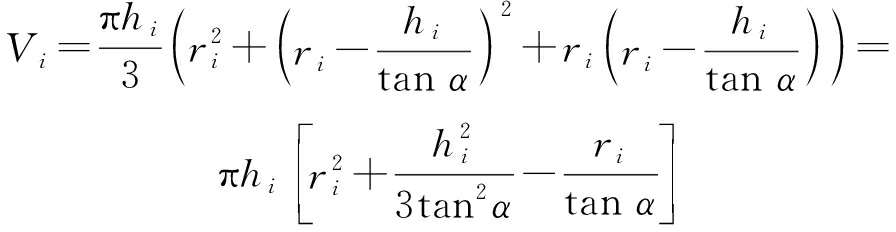
(7)
5)总容量约束。排土场的总容量应满足总外排量的需求,即:
(8)
式中:TT为需求的总外排量(实方,且已考虑备用系数),m3。
6)排土场占地面积。排土场占地面积Sda仅与第1个台阶的底部周界有关,是底部周界半径r1的函数。
(9)
7)非负约束。模型中所有变量取值均为非负数,即:
Ri,Vi,Ti,Si,SLi,TC,Sda,Pda≥0
(10)
2 模型求解算法
模型求解的总体思路如下:在外排总需求量TT的约束下,根据露天矿设备配置情况,确定模型中的设备参数变量TC、Ci、CLi的取值。排土场各形态参数分别在设定的取值范围内按固定步长取值的情景下,进行迭代运算,求解不同参数匹配时的排土总费用A,最终在所有计算结果中优选得出最优方案。
以单台阶高度h为变量进行迭代运算的过程为例,计算步骤如下:
1)步骤1:输入已知的露天矿排土总需求量TT;输入露天矿卡车规格参数,包括卡车标准载重TC、卡车坡段小时运行成本Ci和卡车平段小时运行成本CLi;输入排土台阶个数N、台阶坡面角α、最终平盘宽度b和坡道坡度g;输入购地单价Pda。
2)步骤2:令h=1,根据露天矿排土总需求量TT确定排土场第1个台阶的底部周界半径rh1,满足:
(11)
其中,Vi(hi)为当台阶高度为h时,第i个台阶的排土容量。ri取值从1 m开始,直到出现满足式(11)的ri取值,即排土台阶高度为h时的排土场第1个台阶的底部周界半径rh1。计算h=1时的排土总费用Ah1。
3)步骤3:令h=2,首先根据露天矿排土总需求量TT确定所需排土场第1个台阶的底部周界半径rh2,满足:
(12)
其中:Vi(hi)为当台阶高度为h时,第i个台阶的排土容量。ri取值从1 m开始,直到出现满足式(12)的ri取值,即为排土台阶高度为h时的排土场第1个台阶的底部周界半径rh2。
计算h=2时的排土总费用Ah2。
4)步骤4:令h=h+1,计算排土场第1个台阶的底部周界半径rh,h+1和排土总费用Ah,h+1。
若Ah,h+1<Ah,h,则重复执行步骤4,否则转入步骤5。
5)步骤5:算法结束,输出不同台阶高度时各排弃方案的排土场形态参数及总排土费用计算结果。
其他形态参数的算法类似,不再详述。
3 工程应用
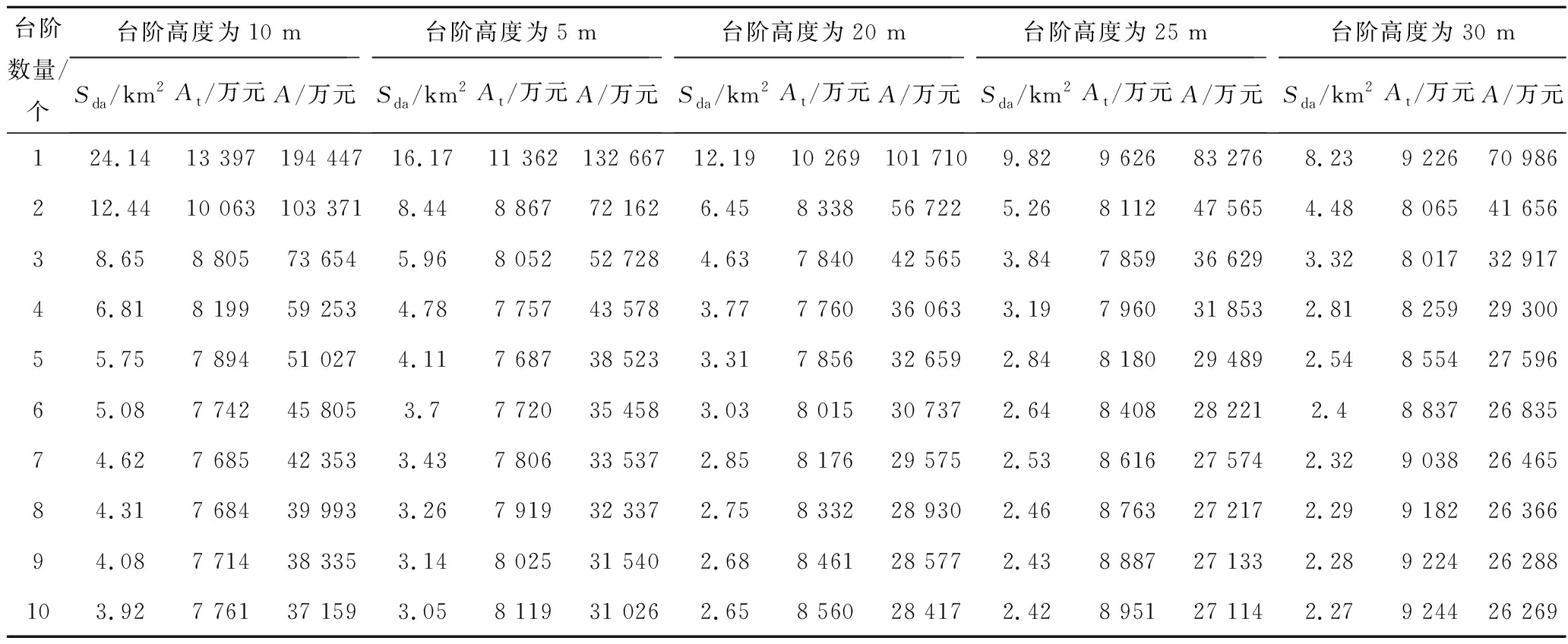
以某露天矿外排土场形态参数优化为例,该矿总外排量为24 000 万m3,选择设置1个沿帮外排土场,剥离物运输卡车载重220 t,排土场压占土地类型为草地,购地单价为75元/m3。应用本文构建的L-P模型及算法对排土场形态参数进行了整体优化。经过对台阶坡面角α、最终平盘宽度b、台阶数N、台阶高度h和坡道坡度g等参数逐一设置为函数变量,运用模型算法遍历参数集,经逐层筛选,最终得到了最优的排土场形态参数。
根据设定的本矿已知参数,应用模型求解算法在MATLAB2017a环境下进行仿真运算。因模型运算输出结果较多,文章篇幅所限,文中仅列出当α=33°,b=40 m,g=8%时,L-P优化模型的部分输出结果,见表1。
表1 模型优化结果
Table 1 Results of model optimization
台阶数量/个台阶高度为10 m台阶高度为5 m台阶高度为20 m台阶高度为25 m台阶高度为30 mSda/km2At/万元A/万元Sda/km2At/万元A/万元Sda/km2At/万元A/万元Sda/km2At/万元A/万元Sda/km2At/万元A/万元124.1413 397194 44716.1711 362132 66712.1910 269101 7109.829 62683 2768.239 22670 986212.4410 063103 3718.448 86772 1626.458 33856 7225.268 11247 5654.488 06541 65638.658 80573 6545.968 05252 7284.637 84042 5653.847 85936 6293.328 01732 91746.818 19959 2534.787 75743 5783.777 76036 0633.197 96031 8532.818 25929 30055.757 89451 0274.117 68738 5233.317 85632 6592.848 18029 4892.548 55427 59665.087 74245 8053.77 72035 4583.038 01530 7372.648 40828 2212.48 83726 83574.627 68542 3533.437 80633 5372.858 17629 5752.538 61627 5742.329 03826 46584.317 68439 9933.267 91932 3372.758 33228 9302.468 76327 2172.299 18226 36694.087 71438 3353.148 02531 5402.688 46128 5772.438 88727 1332.289 22426 288103.927 76137 1593.058 11931 0262.658 56028 4172.428 95127 1142.279 24426 269
注:At为运输费用;A为排土总费用。
在外排总量、边坡稳定、运输安全等的约束下,不同台阶高度h时外排总费用A计算结果如图2所示。
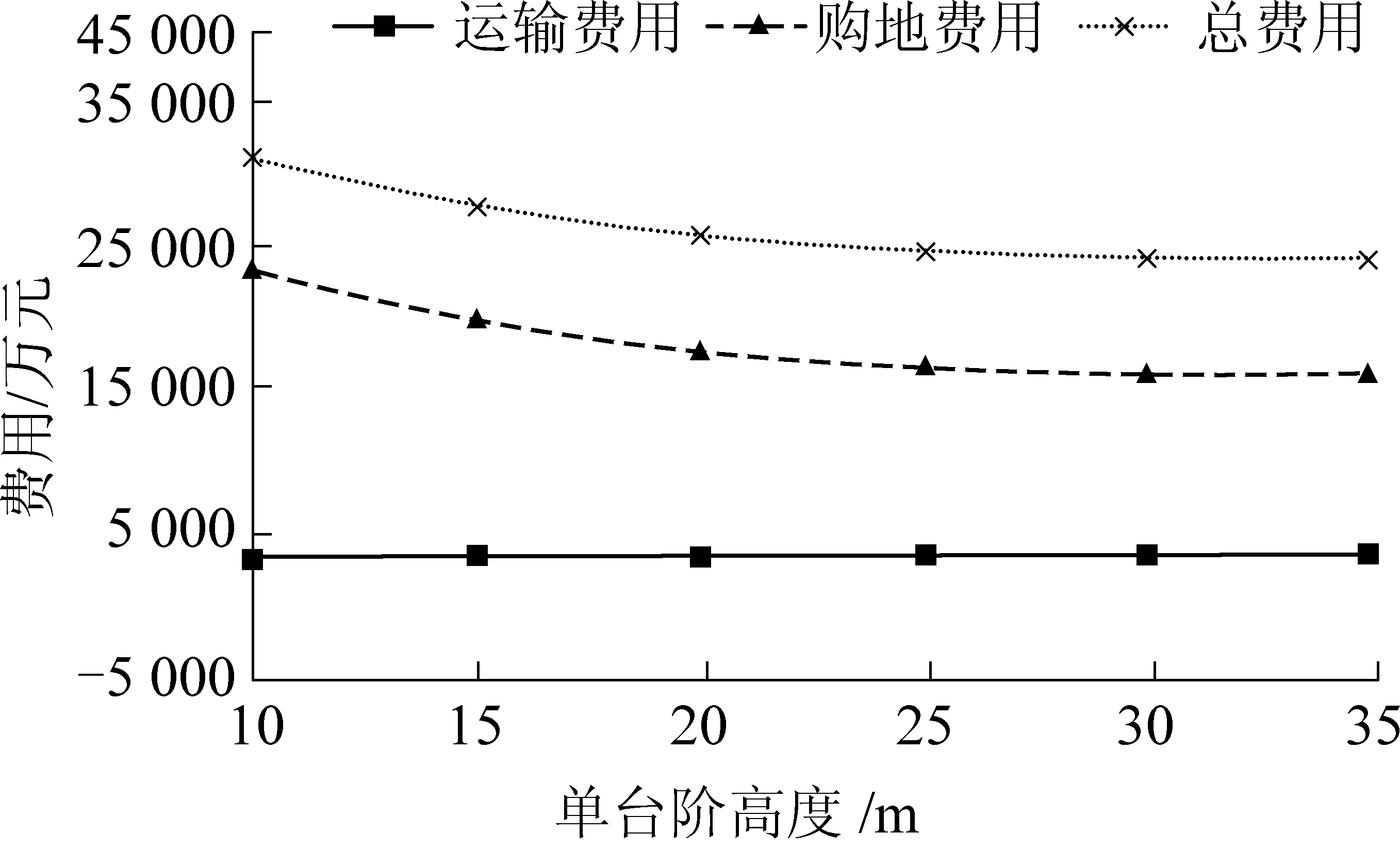
图2 模型优化结果曲线
Fig.2 Results curves of model optimization
从图2可以看出,随着单台阶排土高度h的增大,排土工程的运输费用At略有增加,增幅不大。但在终了排弃标高相同的情况下,随着h的增大,排土场的占地面积Sda显著减小,购地费用明显降低。该露天矿排土总费用中的购地费用占比较大,达72%~78%,平均占比74%,是影响外排土场形态参数的关键因素,主要是因为其占用的土地类型为草地,购地价格较高的原因。
不同台阶高度h时外排总费用A变化率如图3所示。
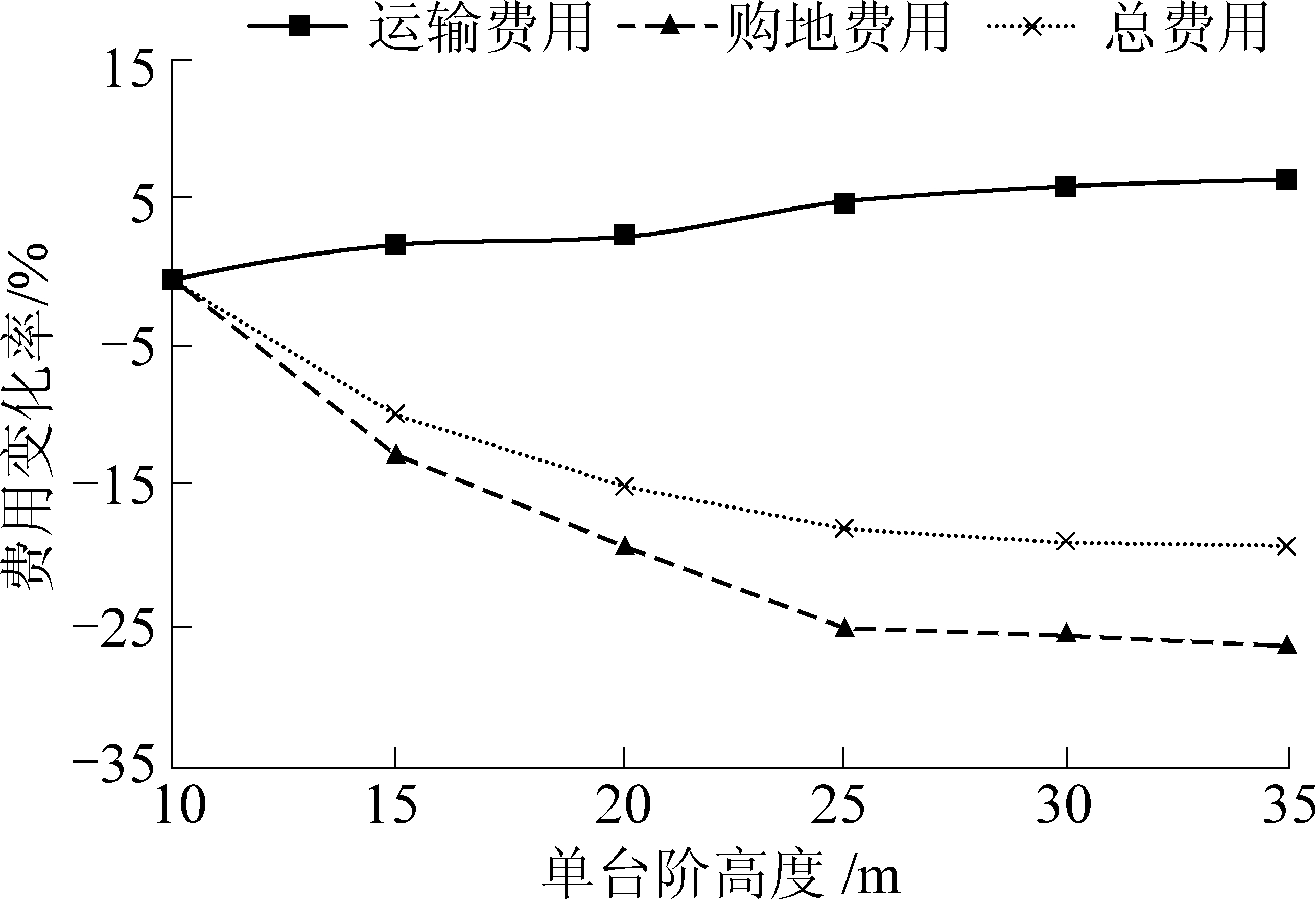
图3 台阶高度与排土费用变化率关系
Fig.3 Relationship between the bench
height and the change rate of haulage
从图3可知,随着单台阶高度h的增大,运输费用At呈现逐渐增加的趋势,变化率区间为1.50%~6.61%;购地费用呈现逐渐减小的趋势,变化率区间为-13.41%~-25.80%;总费用呈现逐渐减小的趋势,变化率区间为-10.18%~-18.78%。当台阶高度由30 m增大到35 m时,运输费用和购地费用分别变化了0.75%和-0.41%,总费用A增加了0.72%,变化很小。
不同台阶高度h时外排总费用A变化速率如图4所示。从图4可知,随着单台阶高度的增大,运输费用和购地费用的变化速率均逐渐减小。运输费用的变化速率区间为2.01%~0.71%,购地费用的变化速率区间为15.49%~0.56%,总费用的变化速率区间为-11.33%~-0.20%。可见当台阶高度为35 m时,总费用的变化速率已经趋近为“0”,可以认为总费用已经基本保持不变。

图4 台阶高度与排土费用变化速率关系
Fig.4 Relationship between the bench
height and the change velocity of haulage
当用地范围不受限时,如地处荒漠戈壁的狭长型露天煤矿,研究排土台阶数量对运输费用的影响就显得十分必要。本矿外排运输费用随台阶数量的变化规律如图5所示。
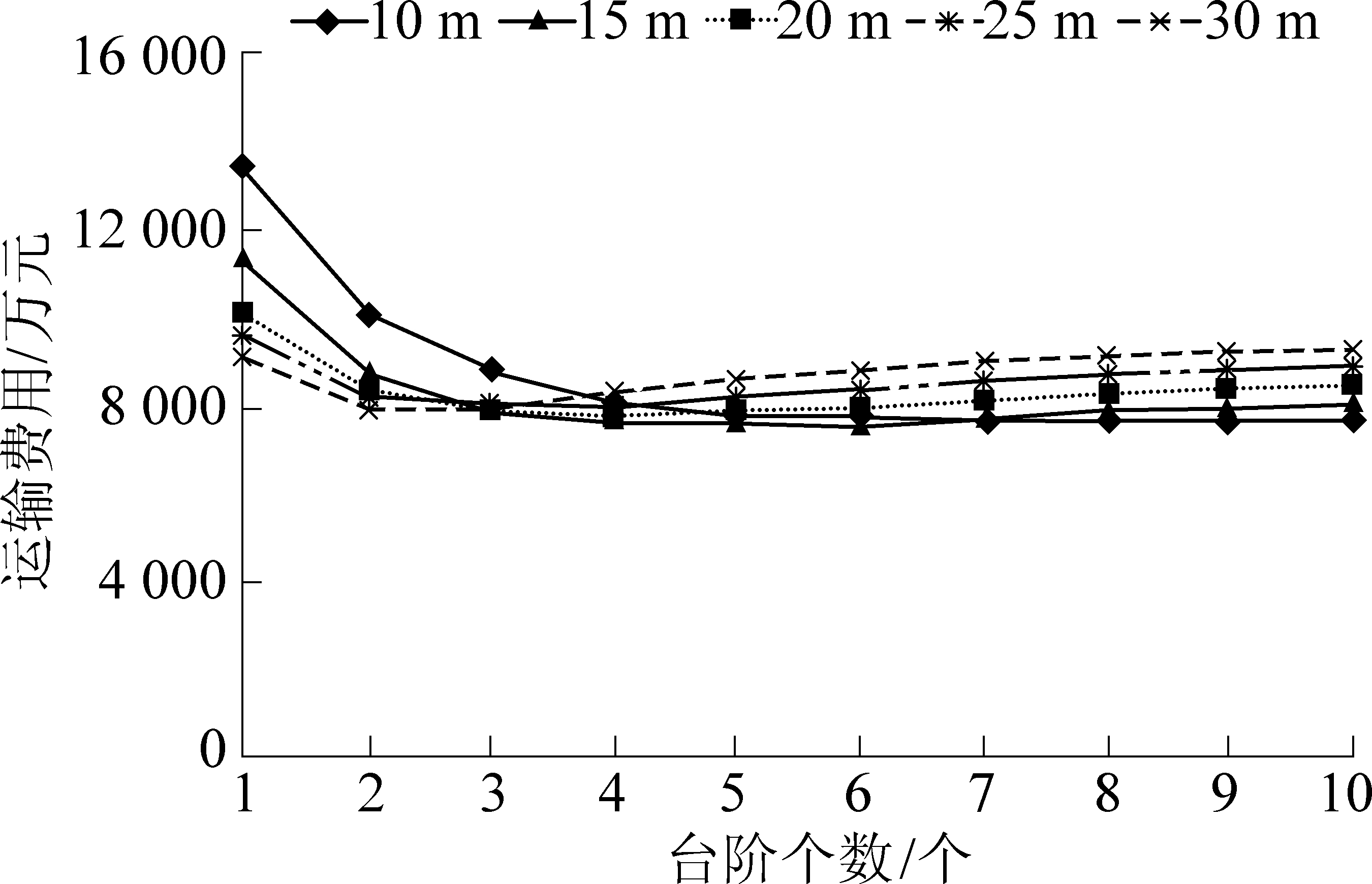
图5 运输费用随台阶数量演化规律
Fig.5 Evolution law of transportation
cost with the number of benches
从图5可知,运输费用随台阶数量的增多呈现先降后增的“U”型变化趋势,从经济性角度分析,露天矿外排土场存在最优的排弃高度。不同单台阶高度时的最优排弃高度略有差异。最终排弃高度的确定还需根据排土场压占土地的类型和价值来综合确定,应在经济效益和环境效益之间寻求平衡[22]。
本次所研究的露天矿当排弃高度为90~120 m时的运输费用最低。但若考虑购地费用及边坡稳定性等因素,根据表1可知,最佳排弃高度为120 m左右。运输费用受露天矿运输设备的性能参数影响较大,不同的设备配置也会影响优化的结果。
综上所述,该露天矿外排土场的形态参数优化结果,底部周界半径945 m,台阶高度30 m,平盘宽度40 m,台阶坡面角33°,台阶数量4个,坡道坡度8%。
4 结 论
1)外排土场的形态参数对排土工程的经济性有着重要影响,是典型的线性规划问题,可通过构建L-P数学模型来解决。
2)模型优化的结果揭示了排土费用随形态参数的变化规律,确定的排土场形态参数满足工程实践的要求,结果是可用的。
3)模型优化结果证明了运输费用随台阶数量的增多呈现先降后增的U型变化趋势,即露天矿外排土场存在最优的排弃高度,设计中不应盲目追求增高扩容,过度加高将导致排土工程的不经济。
4)在终了排弃标高一致的前提下,运输费用随单台阶高度的增大而有所增加。因此,在购地价格低廉的地区,露天矿排土台阶高度应根据排土设备作业参数适当降低,而在购地价格较高的地区,台阶高度应适当提高,以节省运输工程费用。
[1] CHOUDHURY S,CHATTERJEE S.Pit optimisation and life of mine scheduling for a tenement in the Central African Copper belt [J].International Journal of Surface Mining Reclamation & Environment,2014,28(3):200-213.
[2] HEKMAT A,OSANLOO M,SHIRAZI A M.New approach for selection of waste dump sites in open pit mines [J].Mining Technology,2008,117(1):24-31.
[3] SHARIATI S,YAZDANI-CHAMZINI A,SALSANI A,et al.Proposing a new model for waste dump site selection: case study of ayerma phosphate mine[J].Engineering Economics,2014,25(4):410-419.
[4] ZHANG D,INOUE N,SASAOKA T,et al.Study on formation mechanism of dumping piles on dumping area stability.Open Journal of Geology,2014,4,161-175.
[5] 李 伟.露天煤矿排土场边坡稳定性分析与治理技术[J].煤炭科学技术,2014,42(10):37-40.
LI Wei.Treatment technology and stability analysis of dump slope in open mine [J].Coal Science and Technology,2014,42(10):37-40.
[6] 王 瑞,王永增,陆占国.齐大山排土场边坡参数优化及稳定性分析[J].金属矿山,2013,42(2):41-43.
WANG Rui,WANG Yongzeng,LU Zhanguo.The slope parameters optimization and stability analysis of Qidashan waste dump [J].Metal Mine,2013,42(2):41-43.
[7] 关 锌.露天矿软弱基底内部排土场稳定性研究[J].煤炭科学技术,2013,42(1):63-65.
GUAN Xin.Study on stability of in pit dump with soft and weak base floor in open pit mine [J].Coal Science and Technology,2013,42(1):63-65.
[8] RASSAM D,WILLIAMS D.3-Dimensional effects on slope stability of high waste rock dumps [J].International Journal of Surface Mining Reclamation & Environment,1999,13(1):19-24.
[9] 王忠鑫,王烨欣.排土场综合优化若干关键问题及技术方向[J].露天采矿技术,2013(2):46-48.
WANG Zhongxin,WANG Yexin.Key problems and technical directions of dump comprehensive optimization [J].Opencast Mining Technology,2013(2):46-48.
[10] 王忠鑫,苏迁军,刘 玲,等.相邻露天矿无煤柱联合开采技术及其协同效应分析[J].煤炭工程,2017,49(9):31-35.
WANG Zhongxin,SU Qianjun,LIU ling,et al.Non - coal pillar combined mining technology and synergistic effect of adjacent open pit mines [J].Coal Engineering,2017,49(9):31-35.
[11] 李三川,白润才,刘光伟,等.露天煤矿排土场建设发展程序优化研究[J].煤炭科学技术,2017,45(3):49-55.
LI Sanchuan,BAI Runcai,LIU Guangwei,et al.Optimized study on construction and development program of dumping site in surface mine[J].Coal Science and Technology,2017,45(3):49-55.
[12] SMOLI SKI A,DROBEK L,DOMBEK V,et al.Modeling of experimental data on trace elements and organic compounds content in industrial waste dumps [J].Chemosphere,2016,162:189-198.
SKI A,DROBEK L,DOMBEK V,et al.Modeling of experimental data on trace elements and organic compounds content in industrial waste dumps [J].Chemosphere,2016,162:189-198.
[13] 吕 刚,刘雅卓,李叶鑫,等.海州露天煤矿排土场植被恢复的土壤水文效应评价[J].生态环境学报,2017,26(1):67-72.
LV Gang,LIU Yazhuo,LI Yexin,et al.Evaluation of soil hydrology effects of the vegetation restoration in Haizhou open-pit coal mine dump [J].Ecology and Environmental Sciences,2017,26(1): 67-72.
[14] 任志胜,申卫博,解 倩,等.砒砂岩区排土场新构土体保水效应研究[J].土壤学报,2016,53(5):1148-1159.
REN Zhisheng,SHEN Weibo,XIE Qian,et al.Study on the Water Retention Effect of Earth Disposal Site’s Soil Reconstruction in Soft Sandstone Region[J].Acta Pedologica sinica,2016,53(5):1148-1159.
[15] JORDANOVA N,PETROVSKE,KAPICKA A,et al.Application of magnetic methods for assessment of soil restoration in the vicinity of metallurgical copper-processing plant in Bulgaria.[J].Environmental Monitoring & Assessment,2017,189(4):158-171.
[16] IRAJI A,FARZANEH O,HOSSEININIA E S.A modification to densesand dynamic simulation capability of Pastor-Zienkiewicz-
Chan model [J].Acta Geotechnica,2014,9:343-353.
[17] KARMARKAR N.A new polynomial-time algorithm for linear programming[C]// Springer-Verlag,1984:302-311.
[18] 郭志军.线性规划模型的建立及Mathematica求解[J].长沙大学学报,2010,24(5):17-19.
GUO Zhijun.Linear Programming Model and Mathematical Solution [J].Journal of Changsha University,2010,(9):17-18.
[19] LUSTIG I J,MARSTEN R E,SHANNO D F.Computational experience with a primal-dual interior point method for linear programming [J].Linear Algebra & Its Applications,1991,152(91):191-222.
[20] HO I H.Parametric studies of slope stability analyses using three-dimensional finite element technique: Geometric effect [J].Journal of Geoengineering,2014,9(1):33-43.
[21] LU N,GODT J.Infinite slope stability under steady unsaturated seepage conditions [J].Water Resources Research,2008,44(11):2276-2283.
[22] 王家臣,王忠鑫,王卫卫,等.露天矿开采扰动效应:概念、特征与评价指标体系框架[J].煤炭学报,2017,42(S2):295-301.
WANG Jiachen,WANG Zhongxin,Wang Weiwei,et al.Disturbance effect of open-pit mine: concept,characteristics and evaluation index system framework [J].Journal of China Coal Society,2017,42(S2):295-301.
