0 引 言
自然界应力场的变化将引起岩石或多或少的损伤破坏，通过建立的损伤本构关系来反映该损伤破坏过程，是岩石力学研究发展的途径之一。目前，对于岩石变形破坏过程的本构关系的研究已有很多并取得了一定的成果。文献[1-3]基于岩石损伤力学基本理论，采用岩石统一能量屈服准则作为损伤阈值的判定准则，建立了岩石损伤统计本构模型，更好地反映了岩石的应变软化现象；CHEN Xin等[4]对岩石进行单轴压缩试验，研究了节理岩体变形行为的模型参数，对脆性岩石工程计算有一定的借鉴意义；文献[5-6]利用连续损伤理论和统计强度理论，建立了完整模拟岩石破裂全过程的损伤统计本构模型；ZHOU Hongwei等[7]提出了一种基于时间分数阶导数的蠕变本构模型，并确定了模型参数；文献[8-9]通过引进岩石微元强度，根据Lemaitre应变等价原理，得到了红砂岩的冻融劣化模式，并得到了冻融循环和围压对岩石物理力学性质的影响规律；谢祥妙[10]对模型进行有效的改进，建立了可反映后期残余强度特征的损伤本构模型；文献[11-12]考虑岩石峰后残余强度对损伤变量进行修正，建立了能够反映岩石峰后软化特征的三维损伤统计本构模型；李博等[13]通过引入损伤变量的修正系数，建立不同围压下的损伤软化本构模型；王苏生等[14]基于岩石微元强度服从Weibull随机分布的假定，通过有效应力原理引入孔隙水压力，提出了一种新的岩石微元强度计算方法；文献[15-16]为了反映岩石应变软化现象，基于weibull随机分布，假定岩石微元强度服从Drucker-Prager准则，结合连续损伤理论，建立岩石统计损伤软化模型；熊良宵等[17]通过对三种Mohr强度准则的对比分析，得出双曲线型Mohr强度准则更适合用于描述高应力条件下岩石的强度变形特征；ZHOU Shuwei等[18]基于统计损伤理论，提出了岩石在循环应力-温度作用下的本构模型；文献[19-20]通过引进岩石冻融损伤变量，利用其服从随机分布并根据Lemaitre应变等价原理，建立了能反映岩石应变软化过程的损伤统计本构模型。但是众多研究中也存有一定缺陷。首先，由于试验设备与测试方法存在的问题，大多数研究并没有考虑侧向应力的作用，在单轴作用下大多岩石呈脆性破坏，并不能体现实际工程岩石在地应力作用下峰后的变形特征。因此，在建立本构模型时仅考虑了峰前阶段的变形特征；再者，通过引入修正因子对损伤变量进行修正，但在某一特定围压下，虽然能够反映残余强度变化，但增长较快，后期并不适合反映残余强度；再者，基于岩石损伤为0的状况下进行研究，而岩石原始存有微元破坏，因此所建模型由于岩石划分笼统，具有其本身的局限性。基于此笔者建立能反映岩石各变形阶段特征的损伤模型，最后通过试验验证其合理性，并分析各参数对其影响程度。
1 基于修正系数的岩石本构模型
1.1 损伤本构模型的建立
在建立岩石损伤本构模型时既要充分考虑岩石在上述各个阶段的变形特征，同时还需要对岩石的原始损伤程度进行考虑。首先作如下假设： ① 将岩石抽象为原始破坏、未损伤和损伤3部分，初始破坏部分不承受任何荷载，未损伤、损伤部分分别承受有效应力
残余应力σr。对应的作用面积分别为:原始破坏部分A0、未损伤部分A1和损伤部分A2。② 岩石损伤只在σi主应力方向发生，另外2个主应力方向不发生损伤，即岩石在σi所受荷载由损伤和未损伤部分材料共同承担，而岩石在侧向方向名义应力σj、σk与有效应力
相等。③ 未损伤部分材料服从广义胡克定律，并依据岩石物理参数泊松比的意义以及岩石各部分的变形协调关系，可得到
σi=Eεi+μ(σ′j+σ′k)
(1)
式中：E、εi、μ分别为岩石弹性模量、应变及泊松比；i、j、k=1、2、3。
基于上述假定，可得
σiA=σ′iA1+σrA2
(2)
式中：A为岩石总面积。
岩石在受荷之前就存有一定的损伤，由于现有条件并不能很好地测出该损伤的大小，但该损伤与岩石整体存有相应的定量关系，因此可通过引入修正系数来描述该损伤部分与岩石整体部分的关系，即
A0=γA
(3)
式中：γ为修正系数。
定义受荷损伤变量Dt为
Dt=A2/(A-A2)
(4)
岩石开始就存在微元破坏，使得损伤变量初始值不为0，因此对岩石损伤变量D定义为
(5)
由式(2)-(5)可得
(6)
式中：D为损伤变量。
在条件②、③假设的基础上，可得常规三轴应力状态下最大主应力和主应变的损伤本构模型为
σ1=(Eε1+2μσ3)(1-D)+σr(D-γ)
(7)
式中：σ1、ε1、σ3分别为轴向名义应力、轴向应变和侧向应力。
假定岩石材料微元体强度F服从Weibull分布，则其概率密度函数可表示为
(8)
式中：F0、m分别为模型参数。
对式(8)积分，可得到损伤变量表达式为
D=1-(1-γ)exp[-(F/F0)m]
(9)
将式(9)代入式(6)可得
(10)
假定岩石的破坏服从摩尔-库仑准则，其判据的基本形式如下
式中： σ′1、σ′3分别为轴向有效应力、侧向有效应力；c、φ分别为岩石黏聚力和内摩擦角。
由此微元体强度F可表示为
F=σ′1-βσ′3
(11)
式中：β=(1-sin φ)/(1+sin φ)。
由②、③假定联立式(11)可得
F=Eε1+(2μ-β)σ3
(12)
1.2 模型参数的确定
在岩石应力应变关系曲线中，峰值应力σsc与所对应的应变值εsc满足以下几何条件：① ε1=εsc，σ1=σsc； ②
将条件①代入式(10)，得到关于参数F0和m的关系式
(13)
式中:Fsc为曲线极值点对应的F，即Fsc为式(12)中当ε1=εsc时F的值。
由式(10)求取偏微分得
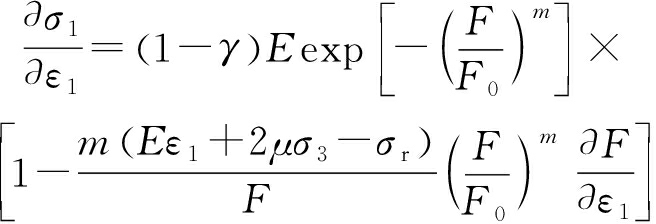
(14)
利用条件②并化简得到F0和m的如下系式
(15)
通过式(12)求取偏微分
=E
(16)
将式(13)、式(15)及式(16)联立可得模型参数表达式
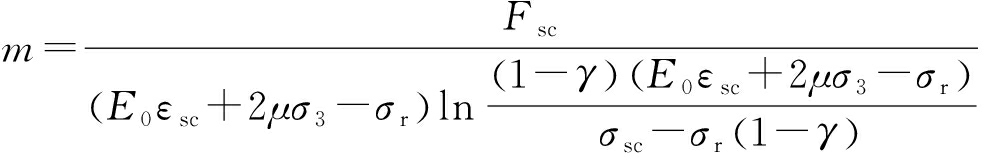
(17)
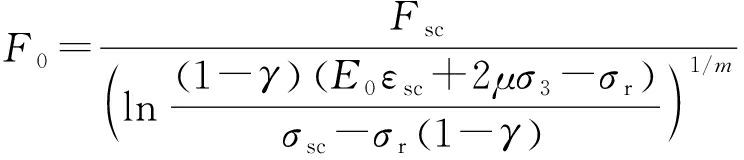
(18)
2 模型验证及损伤特性分析
2.1 模型验证与损伤特性分析
为了对推导的本构模型进行验证，进行了红砂岩常规三轴压缩力学特性试验。试验将红岩石加工成直径50 mm、高100 mm的圆柱体试样，首先测出试件的纵波波速，选取波速接近的试件3个，分别在2、4、6 MPa的3种围压环境下进行三轴压缩试验。试验所采用的仪器为MTS815岩石力学试验系统。由于试验机自身的原因，控制试验仪器，先将围压加载至预先设定值，再进行轴向加载。试验得到单个岩石试件在不同围压下的力学参数见表1。
表1 红砂岩的力学参数
Table 1 Mechanical parameters of red sandstone
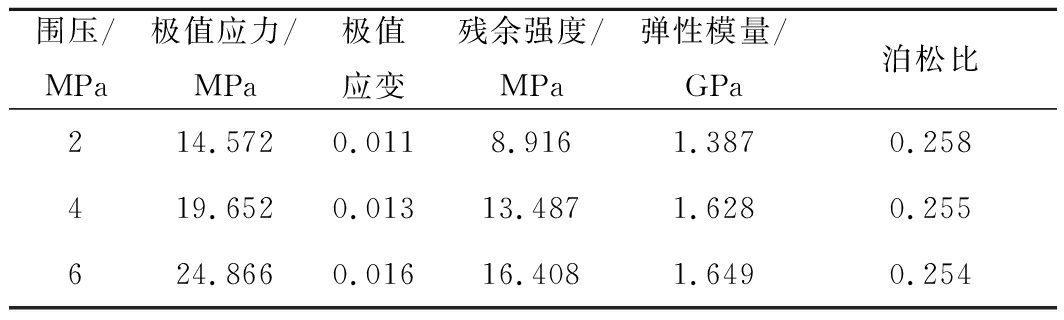
围压/MPa极值应力/MPa极值应变残余强度/MPa弹性模量/GPa泊松比214.5720.0118.9161.3870.258419.6520.01313.4871.6280.255624.8660.01616.4081.6490.254
式(10)中的参数m和F0由式(17)、式(18)替换，将表1试验数据代入并选取合适的γ值，计算得到本构模型的理论曲线，并与试验曲线对比，如图1所示，以此来证明推导的模型合理性。由此可知，建立模型的理论曲线和试验曲线吻合较好，能够较好的反映岩石变形阶段特征。
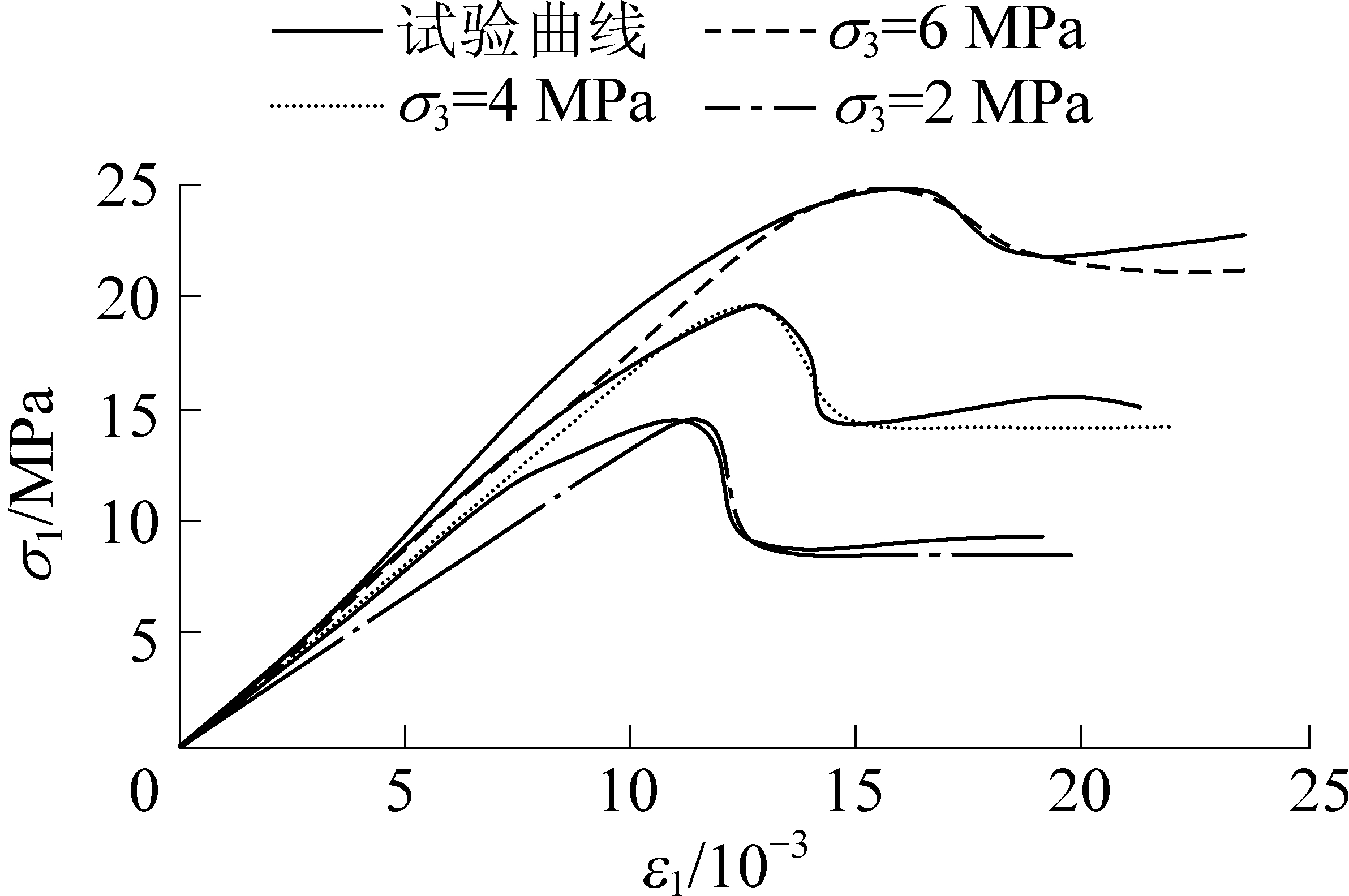
图1 理论与试验应力-应变曲线对比
Fig.1 Comparison of stress-strain
curves in theory and experiment
式(9)中的参数m和F0由式(17)、式(18)替换，将表1试验数据及选取的γ值代入计算得到损伤演化曲线，如图2所示。
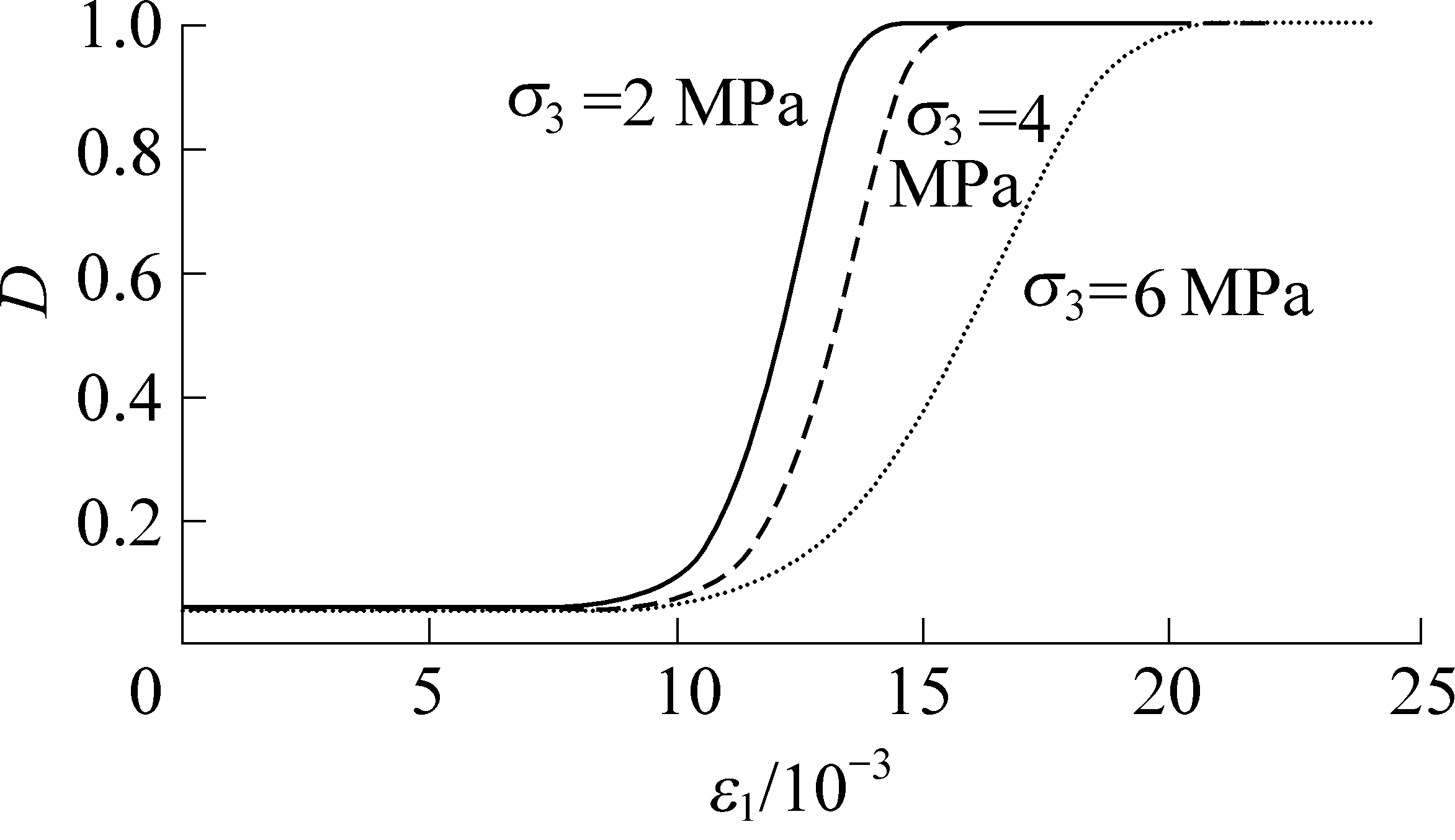
图2 不同围压下红砂岩损伤演化
Fig.2 Damage evolution of red sandstone
under different confining pressures
由图2可得，围压作用下，砂岩的损伤变量始终在区间[γ,1]内变动，这是由于考虑了砂岩初始损伤，更加符合实际工程中砂岩的损伤特性。当应变达到了一定值时，砂岩的总损伤增加到1，表明砂岩完全破坏；岩石在加载损伤前只是孔隙压密、裂缝出现，砂岩并没有破坏，因此总损伤变量在以上阶段并没有变化。随着围压的增大，砂岩的损伤劣化程度降低。这是由于围压具有抑制砂岩内部破坏的作用，导致了砂岩抵抗破坏的能力增强。
在岩石微元强度服从Weibull分布的本构模型中，包含影响应力-应变曲线的尺度和形态分布参数m和F0。随着参数m和F0的改变，将影响该本构模型的形态。将其单独进行分析，确定其物理意义以及它们对岩石本构模型的影响。以围压4 MPa为例对模型参数进行分析，如图3—图4所示。
由图3—图4可得：参数m和F0的改变并不影响图形曲线的整体变化趋势；Weibull参数的变化对岩石损伤之前的应力应变曲线并没有影响，同时也没有改变岩石完全破坏后残余强度的大小；但参数m和F0的变化均对岩石损伤阶段的影响较大。随着F0增大，弹性阶段延长，峰值应力增大且对应的应变增加，峰后损伤逐渐变缓，最终刚达到完全破坏时的应变增大，说明了岩石的延性增强；随着m的增加，弹性阶段延长、峰值点右移，但不太明显，峰值应力增加，峰后损伤加剧，达到完全破坏提前。因此，Weibull参数的选取对反映真实岩石损伤有很大的影响。
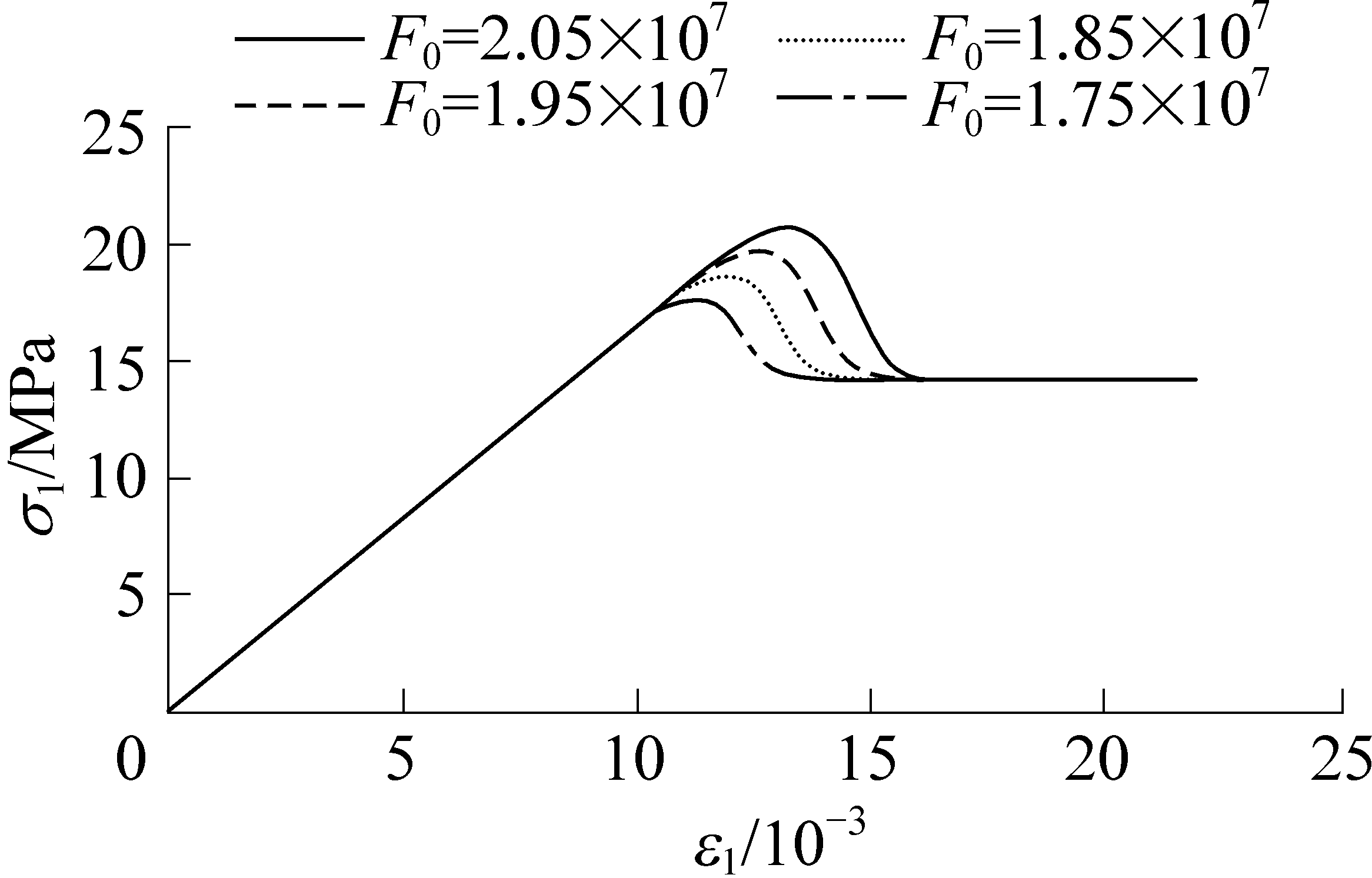
图3 σ3 =4 MPa时F0对模型应力-应变曲线的影响
Fig.3 Effect of F0 on stress-strain model curves when σ3 =4 MPa
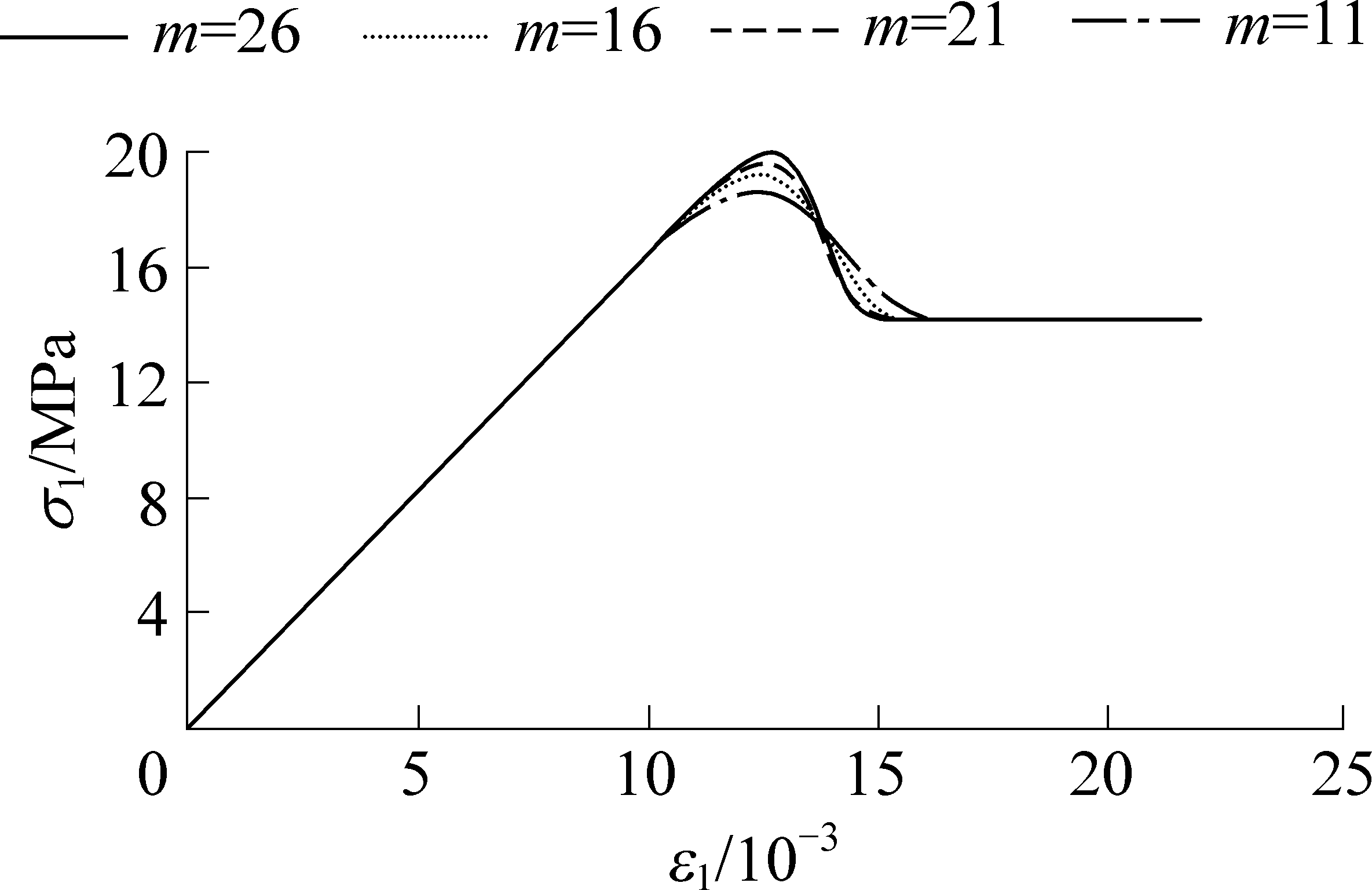
图4 σ3 =4 MPa时m对模型应力-应变曲线的影响
Fig.4 Effect of m on stress-strain model curves when σ3 =4 MPa
3 模型中修正系数分析
γ与岩体本身性质有着密切的关系，代表岩石破坏程度的实际意义。γ量纲为1，取值范围[0，1]。理想岩石，γ=0，对于工程中的岩石，γ>0。由于选取的岩石试件性质相近，γ的大小在不同围压下的取值一致或变化不大，在围压为2、4、6 MPa时，γ分别取0.065、0.060、0.050，符合条件。为了分析参数γ对本构模型是否存在影响，以围压2、4 MPa为例选取不同的γ值分析其对本构模型的影响，如图5所示。
图5 不同γ值对应力-应变曲线的影响
Fig.5 Effect of different γ value on stress-strain curves
由图5可知，γ的取值既不会影响理论曲线的发展趋势，也没有改变峰值点的大小和位置。随着γ减小，峰前峰后同一应变对应的应力都在降低。这是由于γ反映了岩石原始损伤程度，对于原始破坏程度越大，岩石初始被压密时的变形越大，导致弹性模量减小；随着载荷的增加，岩石出现损伤，在此期间达到最大抗压强度，由于岩石颗粒间的黏聚力随着初始损伤程度的增加而减小，因此峰后同一应变下，随着γ的增加岩石损伤加剧。表现在γ越大，岩石最终先达到完全破坏，且达到完全破坏后的残余强度降低。
4 结 论
1)将应力作用下的岩石抽象为破坏、未损伤和损伤3部分。从岩石变形全过程入手，推导了岩石损伤模型。通过试验验证了建立的模型合理性。该模型能较好的反映岩石各变形阶段的特征。
2)Weibull参数的变化并不改变图形曲线的整体变化趋势，对岩石损伤之前的应力应变曲线并没有影响，同时也没有改变岩石完全破坏后残余强度的大小；而对其损伤阶段的影响较大。
3)引入的修正系数γ的取值既不会影响本构模型理论曲线的发展趋势，也不会改变峰值的位置和大小；随着γ减小，峰前峰后同一应变时对应的应力都有所降低，尤其是峰后损伤段降低较大。
[1] LI Xiang,CAO Wengui,SU Yonghua.A statistical damage constitutive model for softening behavior of rocks[J].Engineering Geology,2012,143-144:1-17.
[2] 张 德，刘恩龙，刘星炎，等. 基于修正Mohr-Coulomb屈服准则的冻结砂土损伤本构模型[J]. 岩石力学与工程学报，2018，37(4)：978-986.
ZHANG De，LIU Enlong，LIU Xingyan，et al.A damage constitutive model for frozen sandy soils based on modified Mohr-Coulomb yield criterion[J].Chinese Journal of Rock Mechanics and Engineering，2018，37(4)：978-986.
[3] 周 辉,李 震,朱国金,等.基于岩石统一能量屈服准则的硬岩损伤模型[J].岩土力学,2016,37(3): 609-624.
ZHOU hui,LI zhen,ZHU Guojin,et al.A damage model for hard rock based on unified energy yield criterion of rock[J].Rock and Soil Mechanics,2016，37(3): 609-624.
[4] CHEN Xin,LIAO Zhihong,PENG Xi.Deformability characteristics of jointed rock masses under uniaxial compression[J].International Journal of Mining Sciences and Technology,2012,22(2):213-221.
[5] LI Shuchun,XU Jiang,TAO Yunqi,et al.Study on damage constitutive model of rocks based on lognormal distribution[J].Journal of Coal Science & Engineering,2007,13(4): 430-433.
[6] 李树春，许 江，王 鸿，等.岩石损伤统计本构模型及其参数确定的研究[J].矿业研究与开发,2007,27(2): 6-8.
LI Shuchun，XU Jiang，WANG Hong，et al.Research on statistical damage constitutive model of rock and determination of its parameters[J].Mining Research and Development,2007,27(2): 6-8.
[7] ZHOU Hongwei,WANG Chunping,HAN B B,et al.A creep constitutive model for salt rock based on fractional derivatives [J].International Journal of Rock Mechanics & Mining Sciences,2011,48(1): 116-121.
[8] WANG Zhiliang,LI Yongchi,WANG Jianguo.A damage-softening statistical constitutive model considering rock residual strength[J].Computers & Geosciences,2007,33(1): 1-9.
[9] 张慧梅,夏浩峻,杨更社,等.冻融循环和围压对岩石物理力学性质影响的试验研究[J].煤炭学报,2018,43(2): 441-448.
ZHANG Huimei,XIA Haojun,YANG Gengshe,et al.Experimental research of influences of freeze-thaw cycles and confining pressure on physical-mechanical characteristics of rocks[J].Journal of China Coal Society，2018,43(2): 441-448.
[10] 谢祥妙.冻融荷载作用下砂岩损伤特性分析 [D].西安，西安科技大学，2015.
[11] LI Hangzhou,LIAO Hongjian,XIONG Guangdong,et al.A three-dimensional statistical damage constitutive model for geomaterials[J].Journal of Mechanical Science and Technology,2015,29(1): 71-77.
[12] 曹瑞琅,贺少辉,韦 京,等.基于残余强度修正的岩石损伤软化统计本构模型研究[J].岩土力学，2013，34(6)：1652-1660.
CAO Ruilang,HE Shaohui,WEI Jing,et al.Study of modified statistical damage softening constitutive model for rock considering residual strength[J].Rock and Soil Mechanics,2013,34(6): 1652-1660.
[13] 李 博，吴润江，高为超.岩石损伤软化的修正本构模型[J].地震工程学报,2016,38(5): 783-786.
LI Bo,WU Runjiang,GAO Weichao.A modified damage softening constitutive model for rock[J].China Earthquake Engineering Journal,2016,38(5): 783-786.
[14] 王苏生,徐卫亚,王 伟,等.岩石统计损伤本构模型与试验[J].河海大学学报：自然科学版,2017,45(5): 464-470.
WANG Susheng,XU Weiya,WANG Wei,et al.The statistical damage constitutive model of rocks and its experiment[J].Journal of Hohai University：Natural Sciences,2017,45(5): 464-470.
[15] 黄海峰,巨能攀,蓝康文,等.岩石统计损伤软化模型及其参数反演[J].长江科学院报,2018,35(6):102-106.
HUANG Haifeng,JU Nengpan,LAN Kangwen,et al.Statistical damage softening model for rock and back analysis of its parameters[J].Journal of Yangtze River Scientific Research Institute,2018,35(6): 102-106.
[16] 房智恒.基于Mohr-Coulomb准则的岩石损伤本构模型研究[J].矿业工程研究,2017,32(1): 7-13.
FANG Zhiheng.Rock damage constitutive model based on mohr-coulomb criterion[J].Mineral Engineering Research,2017,32(1): 7-13.
[17] 熊良宵,虞利军.三种Mohr强度准则的对比分析[J].长江科学院院报,2016,33(4): 81-85.
XIONG Liangxiao,YU Lijun.Comparative study of three mohr strength criteria[J].Journal of Yangtze River Scientific Research Institute,2016,33(4): 81-85.
[18] ZHOU Shuwei,XIA Cachu,ZHAO Haibin,et al.Statistical damage constitutive model for rocks subjected to cyclic stress and cyclic temperature[J].Acta Geophysica,2017,65(5): 893-906.
[19] 张慧梅,孟祥振,彭 川,等.岩石变形全过程冻融损伤模型及其参数[J].西安科技大学学报,2018,38(2):260-265.
ZHANG Huimei,MENG Xiangzhen,PENG Chuan,et al.freeze-thaw damage model and parameters rock deformation in whole process[J].Journal of Xian University of Science and Technology,2018,38(2): 260-265.
[20] HUANG Shibing,LIU Quansheng,CHENG Aiping,et al.A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application[J].Cold Regions Science and Technology,2018,145: 142-150.
