0 引 言
铁路、公路隧道及煤矿井下巷道施工过程中突水、突泥等地质灾害严重威胁施工及人员安全[1-2]，同时会对环境产生不利影响。为了解决上述灾害问题，需要找到一种能有效探测含水异常体的勘探方法。在隧道及巷道复杂的施工环境及水文地质条件下，对水害的精确探测是十分困难的。工程上对水害探测主要应用电磁类勘探方法，地层含水体在电性上表现为低阻，矿井瞬变电磁法作为一种应用广泛的电磁感应勘探方法，对低阻体非常敏感，能够对隧道及巷道顶底板含水层进行探测[3-4]。
矿井瞬变电磁法的探测基础是不同物质的导电性和导磁性存在差异，该方法通过发射线圈在周围空间建立一次磁场，然后由计算机控制在某时刻突然关闭发射电流，一次磁场随之消失，根据法拉第电磁感应定律，在周围介质中会产生感应电流，进而激发出感应二次磁场，二次磁场大小及方向与介质的电导率等特征有关，利用接收装置记录二次磁场，通过对二次磁场进行计算反演便可以得到介质的电性特征[5]。由于接收装置记录的二次磁场是叠加场，直接处理的方法难以区分异常是位于发射线圈的哪一侧。电磁感应中各物理量之间的数学关系是非常复杂的，想要得到准确的结果，正反演计算过程就需要选用合适的算法。对于正演过程而言，传统的做法是直接代入半空间瞬变电磁响应计算公式，这样最终得到的解释模型实际上是发射线框两侧模型的叠加，为了使目标模型与实际相符，就需要选用全空间正演算法[6-8]。
对于反演算法而言，粒子群优化(Particle Swarm Optimization，简称PSO)算法是一种群体智能非线性全局最优化算法，近几年一些地球物理学家将其应用于反演领域，取得了不同的反演效果[9-12]。MONTEIRO等[13]利用粒子群算法对潜埋异常体的自然电位数据进行反演，取得很好的反演效果，指出粒子群算法具有速度快和不需要初始模型的特点；XIONG等[14]应用粒子群算法实现了磁法数据的反演计算；程久龙[15]利用粒子群算法实现了瞬变电磁和直流电法的联合反演，并将其应用于隧道及巷道超前探测中；PALLERO等[16]利用粒子群算法进行重力反演，证明该算法对计算资源要求不高，适合工程应用；程久龙[17]利用粒子群算法对矿井瞬变电磁数据进行反演，证明该算法早期适应性强，反演求解过程不需要给定初始模型,但在算法寻优后期存在拟合速度变慢，误差曲线下降不明显的问题。虽然当前全局最优化算法是研究的热点，但研究相对成熟的局部最优化算法依然应用广泛。最小二乘法作为经典的局部最优化算法，从提出到现在已历经近两百年时间，得益于人们在实践中不停地对算法进行优化改进，该算法仍然在最优化问题求解中广泛应用，其中比较著名的是LEVENBERG[18]提出并由MARQUARDT[19]改进的阻尼最小二乘法(DLS)。SAIN等[20]运用阻尼最小二乘法进行广角地震反射时间反演，PUJOL[21]以埋藏球体的重力反演问题为例,对阻尼最小二乘算法的反演效果进行了分析。王乐洋等[22]利用最小二乘算法进行地壳形变分析，发现初值为观测值中位数时最小二乘方法效果较好。最小二乘算法晚期寻优速度快，但初值选择合适与否直接关系到最终寻优效果，依靠个人经验指定初值的方法过于随意往往难以取得较好效果。
笔者对粒子群算法进行了改进，综合利用粒子群和阻尼最小二乘算法的优点，设计新的反演组合算法。基于新设计的组合算法和单一算法分别对数值模拟数据进行反演计算，通过对反演结果对比分析，认为组合反演算法反演效率高，且不需要人为给定初始模型。最后利用组合算法对实测数据进行反演处理，结果与实际地质资料及现场揭露情况相符，证明组合算法能够对巷道及隧道瞬变电磁探测数据进行精确快速处理。
1 正演理论及反演算法
1.1 正演理论
进行隧道或巷道探测时，探测点四周大多被围岩包围，在探测范围内可以近似为全空间，因此正演所建模型也应该是全空间的，根据回线源辐射电磁场的传播理论，KRIVOCHIEVA等[23]推导了有限大小回线源电磁场理论公式，给出了全空间介质中任意位置点感应电磁场磁场和电场分量的计算公式，对于第i层，深度为z的点P(i,z)处对应的电场分量E和磁场分量H可用下式表示为
(1)
(2)
式中：f为频率；μ为磁导率；J1为第一类一阶贝塞尔函数；λ为汉克尔变换积分变量；r为收发距；
和
为输入函数。
1.2 反演算法
1.2.1 粒子群优化算法
EBERHART等[24]提出了PSO算法，其算法中，首先初始化一定数目的粒子，最优化问题的解用寻优粒子位置表示，计算过程中，所有粒子在算法支配下向着最优解的可能位置转移。寻优粒子数为m，搜索范围为n维空间，粒子速度为V ki，粒子空间位置分别为：X ki，单个粒子最优个体位置为
所有粒子最优群体位置gbestXk，i=1,2,…,m为粒子个数序号，k=1,2,…；itermax为代表迭代次数；itermax为最大迭代次数。粒子速度及位置更新式为
(3)
(4)
式(3)、式(4)即为粒子群算法基本公式，其中，j指代搜索维度，c1和c2定义为学习因子，一般可取c1=c2=2，r1，r2为(0,1)之间的随机数。
SHI等[25]对式(3)进行优化，提出惯性因子ω的概念，改进后的公式为
(5)
惯性因子计算式如下：
(6)
式中：ωmax取0.9；ωmin为0.4。
师学明等[10]提出了惯性因子非线性振荡递减策略为
ω=0.99kr/2+α
(7)
式中：r为(0,1)随机数；α为[0,0.5]的常数。
1.2.2 DLS算法
在15—17世纪，科学家提出了最小二乘法。MARQUARDT等[26]改进为阻尼最小二乘法(Damped Least Squares,DLS)，提高了对非线性问题的求解效果。针对方程组问题为
Aδ=c
式中：A为方程组系数；δ为待求未知数；c为常数。对应的阻尼最小二乘求解为
(ATA+λI)δ=ATc
式中：AT为系数矩阵A的转置矩阵；λ为阻尼因子，一般取值大于0；I为单位矩阵。
1.2.3 PSO-DLS组合算法
为了便于与DLS算法组合，在前人研究结果基础上，提出一种粒子群算法惯性因子改进策略，其计算式为
ω=1/[2(1+e(k-10))]+0.9kr/2
(8)
将上述方法与前人方法进行比较，其中式(3)记为B.PSO,式(5)记为M1.PSO,式(7)记为M2.PSO，本研究提出的改进方法式(8)记为MN.PSO。利用Griewank数学测试函数进行测试比较如图1所示。
图1 不同改进策略测试函数适应度变化曲线
Fig.1 Fitting curves tested by different optimized strategies
PSO-DLS组合反演方法，反演初期PSO算法首先介入计算，根据需要设定合理的粒子个数及迭代次数等参数，迭代次数超过10次后，PSO算法终止计算，启动DLS算法寻优，将PSO算法迭代输出模型作为DLS算法初始模型，继续迭代，直到反演结果满足要求为止。
2 模拟数据反演
为了验证算法的反演效果建立数学地电模型。
2.1 改进的PSO算法反演
PSO算法中粒子取50个，最大反演迭代次数限定为20次。反演拟合误差下降曲线如图2所示，从图2中，粒子群算法反演早期误差下降较快，晚期下降速度变缓。
图2 PSO反演拟合误差随迭代变化曲线
Fig.2 The fitting error changing with iteration of PSO algorithms
2.2 DLS算法反演
DLS反演采用同样的装置，最大迭代次数也为20次，2次反演结果如图3所示。
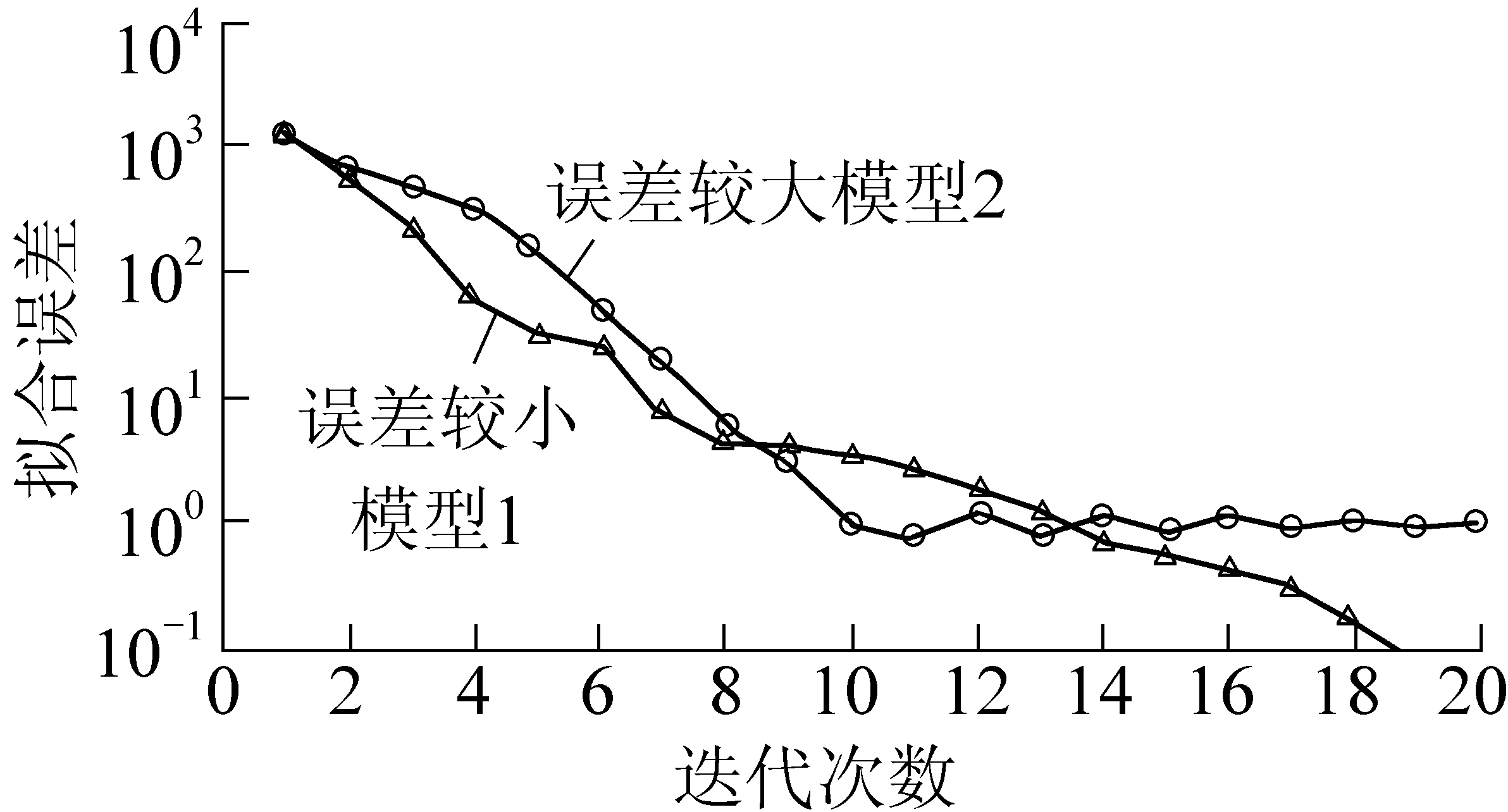
图3 2种不同初始模型条件下DLS
反演拟合误差随迭代变化曲线
Fig.3 DLS inversion fitting error curve changing with
iteration under two different initial model conditions
阻尼最小二乘法需要人为给定初始模型，图3中就是不同初始模型条件下的反演效果，图3中模型1曲线反演拟合误差曲线总体是下降趋势，说明初始模型较为准确，整个反演过程，拟合曲线下降速率基本一致；图3中模型2曲线初始模型给的不恰当，迭代晚期拟合误差曲线在拟合误差为1上下震荡，拟合误差趋近于1，反演陷入局部极小陷阱。对比2次反演，虽然反演初始拟合误差相近，但反演结果却大相径庭。反演问题是复杂的非线性问题，其目标函数曲线可能存在多个局部极小值。
2.3 改进的PSO-DLS组合反演
与前面一致，组合反演结果如图4所示，图中为PSO-DLS组合反演拟合误差曲线，从中可看出，组合反演方法成功的解决了单一算法反演中初始模型给定困难和晚期拟合误差下降变缓的问题。
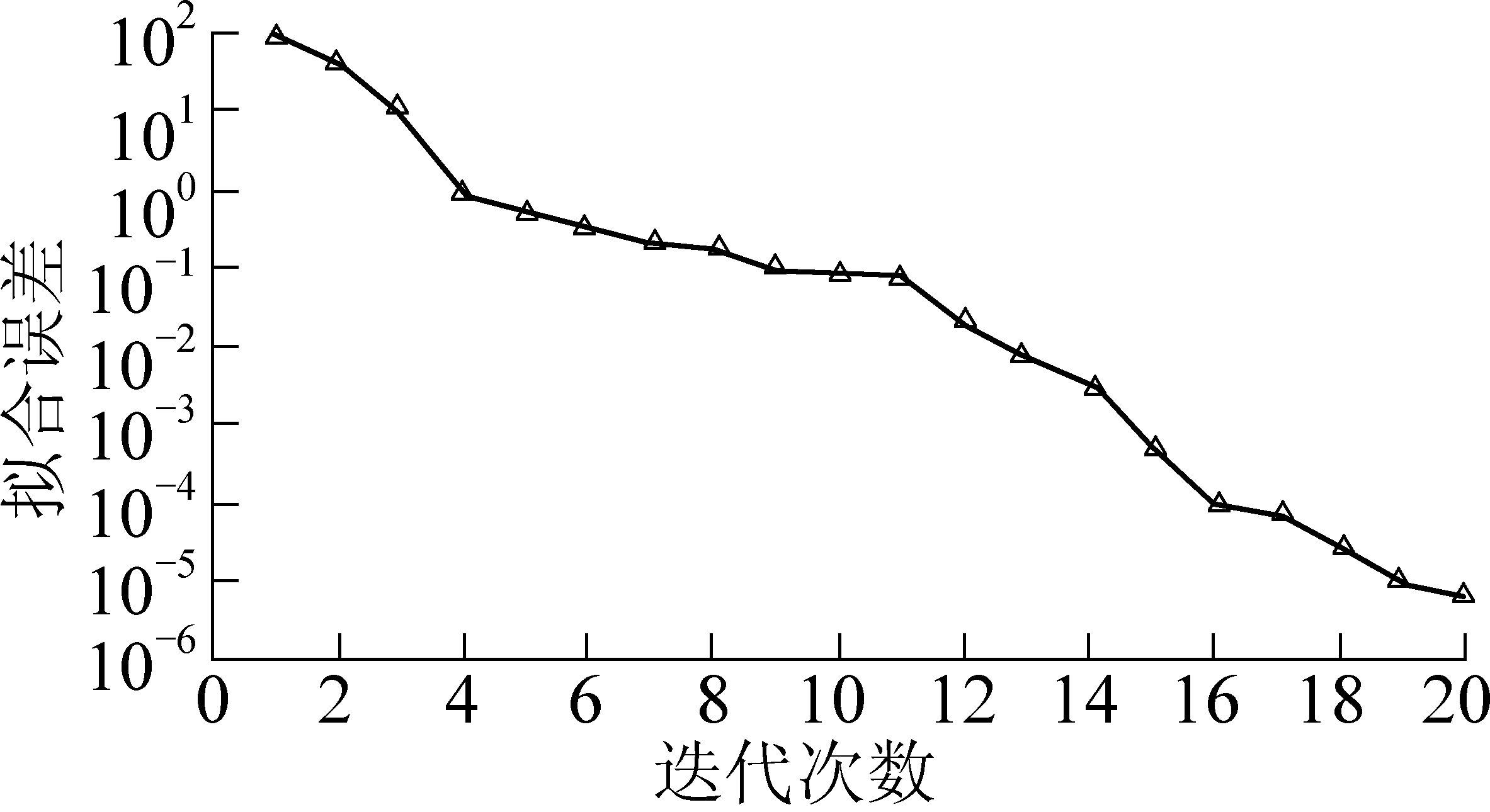
图4 改进PSO-DLS算法反演拟合误差
Fig.4 Inversion fitting error of improved PSO-DLS algorithm
3 现场实测数据反演
根据某煤矿已知水文地质资料，工作面顶底板存在砂岩含水层，工作面内褶曲和断层构造发育。由于构造原因，裂隙发育，加之存在含水层，造成工作面水文地质条件较差，对安全生产造成不利影响。采用矿井瞬变电磁法在巷道内施工，对顶底板含水低阻异常体进行探测。数据采集完成后，采用提出的改进PSO-DLS组合反演算法进行反演处理，根据收集的地质资料，探测区域附近存在钻孔305，综合测区附近钻孔测井资料，处理结果如图5所示。
图5 反演电阻率断面与测井数据对比
Fig.5 Comparison of inversion resistivity section and log data
实测数据组合反演处理后得到的电阻率剖面如图5所示。电阻率剖面中，蓝绿色代表低电阻率，砖红色代表高电阻率。探测距离范围内，反演结果实现了顶底板异常分离。顶板方向探测高度0～70 m范围内为中-高阻电阻率区域，在巷道距离850 m和950 m附近高阻层不连续，其中950 m附近高阻层被上方的低阻区切断。顶板探测距离70 m及以上区域存在一低阻条带。底板方向探测深度0到 70 m范围整体呈现中-低阻电阻率分布，其中在巷道距离970～1 100 m电阻率值较低，分析该低阻区形态及分布，发现其与顶板方向切断高阻层的低阻区可能具有一定的水力联系，探测深度-70 m以下范围整体为一高阻区。
从图5中知，反演电阻率断面与钻孔305电阻率总体分层规律基本一致，中间0位置附近为高阻，为煤层和巷道的反映，从0 m往正方向电阻率总体变化趋势为低阻-高阻-低阻，从0往负方向电阻率总体变化趋势为低阻-高阻，两图中高阻和低阻层位对应较好。
根据地质资料在该区域内有构造发育，其中探测区域内有F144正断层通过。巷道实际揭露970 m位置附近顶板及底板破碎，顶板有淋水情况。巷道距离950 m位置附近，顶板及底板与巷道走向近似平行方向的高阻及低阻区域均有明显错断，顶板上低阻区下侵并将高阻层切断，底板低阻及高阻区域也有明显的错动迹象，且底板断层下盘附近有较强低阻反应，推断可能是断层形成导水通道，将顶板含水层中的水导入底板岩层裂隙汇集所致，电阻率界面错断特征与断层吻合。
4 结 论
1)提出了一种适用于巷道或隧道瞬变电磁探测的PSO-DLS组合反演方法，解决了PSO算法后期寻优速度下降和DLS算法初始模型的给定问题。证明组合反演方法比2种算法单独反演寻优效率更高。
2)利用组合算法对煤矿巷道中采集的实际探测数据进行反演，迭代过程中正演基于全空间正演理论，实现了顶底板异常分离显示，反演结果与实际地质资料及巷道揭露情况吻合。
3)考虑到二维或三维模型更加符合实际地质情况，将来可以将此组合算法扩展到高维反演中，另外本研究中假设模型是各项同性的，但地层实际上是各项异性的，将来可以对算法进一步优化，以便能适应于各向异性地层反演。
[1] 李术才,孙怀凤,李 貅,等.隧道瞬变电磁超前预报平行磁场响应探测方法[J].岩石力学与工程学报,2014,33(7):1309-1318.
LI Shucai,SUN Huaifeng,LI Xiu,et al.Advanced geology prediction with parallel transient electromagnetic detection in tunnelling[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1309-1318.
[2] LI Shucai,TIAN Hao,XUE Yiguo,et al.Study on major construction disasters and controlling technology at the Qingdao Kiaochow Bay Subsea Tunnel[J].Journal of Coastal Research,2015,73:403-409.
[3] 薛国强,于景邨.瞬变电磁法在煤炭领域的研究与应用新进展[J].地球物理学进展,2017,32(1):0319-0326.
XUE Guoqiang,YU Jingcun.New development of TEM research and application in coal mine exploration[J].Progress in Geophysics,2017,32(1):0319-0326.
[4] YANG Haiyan,LI Fengping,YUE Jianhua,et al.Cone-shaped source characteristics and inductance effect of transient electromagnetic method[J].Applied Geophysics,2017,14(1):165-174.
[5] ZHOU Nannan,XUE Guoqiang,HOU Dongyang,et al.Short-offset grounded-wire TEM method for efficient detection of mined-out areas in vegetation-covered mountainous coalfields[J].Exploration Geophysics,2016,48(4):374-382.
[6] SMITH R.Electromagnetic induction methods in mining geophysics from 2008 to 2012[J].Surveys in Geophysics,2013,35(1):123-156.
[7] VIGNOLI G,FIANDACA G,CHRISTIANSEN A V,et al.Sharp spatially constrained inversion with applications to transient electromagnetic data[J].Geophysical Prospecting,2015,63(1):243-255.
[8] YU J,MALEKIAN R,CHANG J,et al.Modeling of whole-space transient electromagnetic responses based on FDTD and its application in the mining industry[J].IEEE Transactions on Industrial Informatics,2017,13(6):2974-2982.
[9] SHAW R,SRIVASTAVA S.Particle swarm optimization:a new tool to invert geophysical data[J].Geophysics,2007,72(2):F75-F83.
[10] 师学明,肖 敏,范建柯,等.大地电磁阻尼粒子群优化反演法研究[J].地球物理学报,2009,52(4):1114-1120.
SHI Xueming,XIAO Min,FAN Jianke,et al.The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J].Chinese Journal of Geophysics,2009,52(4):1114-1120.
[11] YUAN S,WANG S,TIAN N.Swarm intelligence optimization and its application in geophysical data inversion[J].Applied Geophysics,2009,6(2):166-174.
[12] FERNáNDEZ M J L,GARCíA G E,FERNáNDEZ J P,et al.PSO:A powerful algorithm to solve geophysical inverse problems:application to a 1D-DC resistivity case[J].Journal of Applied Geophysics,2010,71(1):13-25.
[13] MONTEIRO S F A.Inversion of self-potential of idealized bodies’ anomalies using particle swarm optimization[J].Computers & Geosciences,2010,36(9):1185-1190.
[14] XIONG Jie,ZHANG Tao.Multiobjective particle swarm inversion algorithm for two-dimensional magnetic data[J].Applied Geophysics,2015,12(2):127-136.
[15] CHENG Jiulong,LI Fei,PENG Suping,et al.Joint inversion of TEM and DC in roadway advanced detection based on particle swarm optimization[J].Journal of Applied Geophysics,2015,123:30-35.
[16] PALLERO J L G,FERN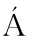
NDEZ-MART
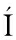NEZ J L,BONVALOT S,et al.Gravity inversion and uncertainty assessment of basement relief via particle swarm optimization[J].Journal of Applied Geophysics,2015,116:180-191.
[17] 程久龙,李明星,肖艳丽,等.全空间条件下矿井瞬变电磁法粒子群优化反演研究[J].地球物理学报,2014,57(10):3478-3484.
CHENG Jiulong,LI Mingxing,XIAO Yanli,et al.Study on particle swarm optimization inversion of mine transient electromagnetic method in whole-space[J].Chinese Journal of Geophysics,2014,57(10):3478-3484.
[18] LEVENBERG K.A method for the solution of certain non-linear problems in least squares[J].Quarterly of Applied Mathematics,1944,2(2):164-168.
[19] MARQUARDT D W.An algorithm for least squares estimation of nonlinear parameters[J].Journal of the Society for Industrial and Applied Mathematics,1963,11(2):431-441.
[20] SAIN K,KAILA K L.Inversion of wide-angle seismic reflection times with damped least squares[J].Geophysics,1994,59(11):1735-1744.
[21] PUJOL J.The solution of nonlinear inverse problems and the Levenberg-Marquardt method[J].Geophysics,2007,72(4):W1-W16.
[22] 王乐洋,陈汉青.地壳形变分析的抗差最小二乘配置迭代解法[J].地球物理学报,2017,60(8):3062-3071.
WANG Leyang,CHEN Hanqing.Analysis of crustal deformation based on iterative solutions of Robust Least Squares Collocation[J].Chinese Journal of Geophysics,2017,60(8):3062-3071.
[23] KRIVOCHIEVA S,CHOUTEAU M.Whole-space modeling of a layered earth in time-domain electromagnetic measurements[J].Journal of Applied Geophysics,2002,50(4):375-391.
[24] EBERHART R,KENNEDY J.A New Optimizer Using Particle Swarm Theory.MHS'95.Proceedings of the sixth international Symposium on Micro Machine and Human Science,39-43.
[25] SHI Y,EBERHART R.A Modified Particle Swarm Optimizer.IEEE International Conference on Evolutionary Computation Proceedings[C]//IEEE World Congress on Computational Intelligence1998,2:69-73.
[26] MARQUARDTDW.An algorithm for least squares estimation of nonlinear parameters.journal of the Society for Industrial and Applied Mathematics,1963,11:431-441.
