0 引 言
带式输送机是煤矿开采不可替代的运输装备之一,具有适应性强、运输物料范围广、效率高、营运费用低等优点[1-2]。带式输送机的启动是变加速非稳态过程,启动时往往会产生动张力,使输送带产生强烈振动,导致物料洒落。启动时张力过大会对带式输送机各部件造成损害,甚至会出现断带现象[3-4],而启动时张力过小,可能会出现打滑现象,严重时会引起井下火灾,造成事故[5],为带式输送机选择合理的驱动方式,控制启动时产生的动张力,能有效地避免上述存在的问题。双盘式磁力耦合器是一种纯机械的非电子装置,通过电磁感应原理实现电动机和负载之间转矩无接触传递,具有结构简单、空载启动、过载保护、隔振、无谐波和电磁干扰等优点[6],非常适合矿用长距离带式输送机的复杂作业环境。
近年来,国内外专家学者对带式输送机的启动特性进行了大量研究,李亚辉等[7]对液力耦合器和液黏性调速装置的各方面参数进行对比分析,为不同工况的带式输送机选择合适的驱动装置。王光炳[8]分析了液黏调速装置对带式输送机运行特性的影响,并对其传递转矩、效率及调速特性进行分析,降低了输送带动张力,使启动更平稳。TIAN Z等[9]基于磁路设计理论,设计磁流变软试验台,研究了输出转速与时间的关系和调节速度响应的快慢,分析是否符合带式输送机的启动要求。基于此,笔者将双盘式磁力耦合器作为带式输送机的驱动装置,建立磁力耦合器的动态数学模型,采用PID闭环控制系统,运用AMEsim软件建立带式输送机满载启动工况的仿真模型[10],并对不同启动时间的启动特性进行动态仿真分析。
1 带式输送机磁力传动系统
1.1 系统结构
带式输送机传动系统包括三相异步电动机、联轴器、双盘式磁力耦合器、减速器、带式输送机等[11],结构如图1所示。
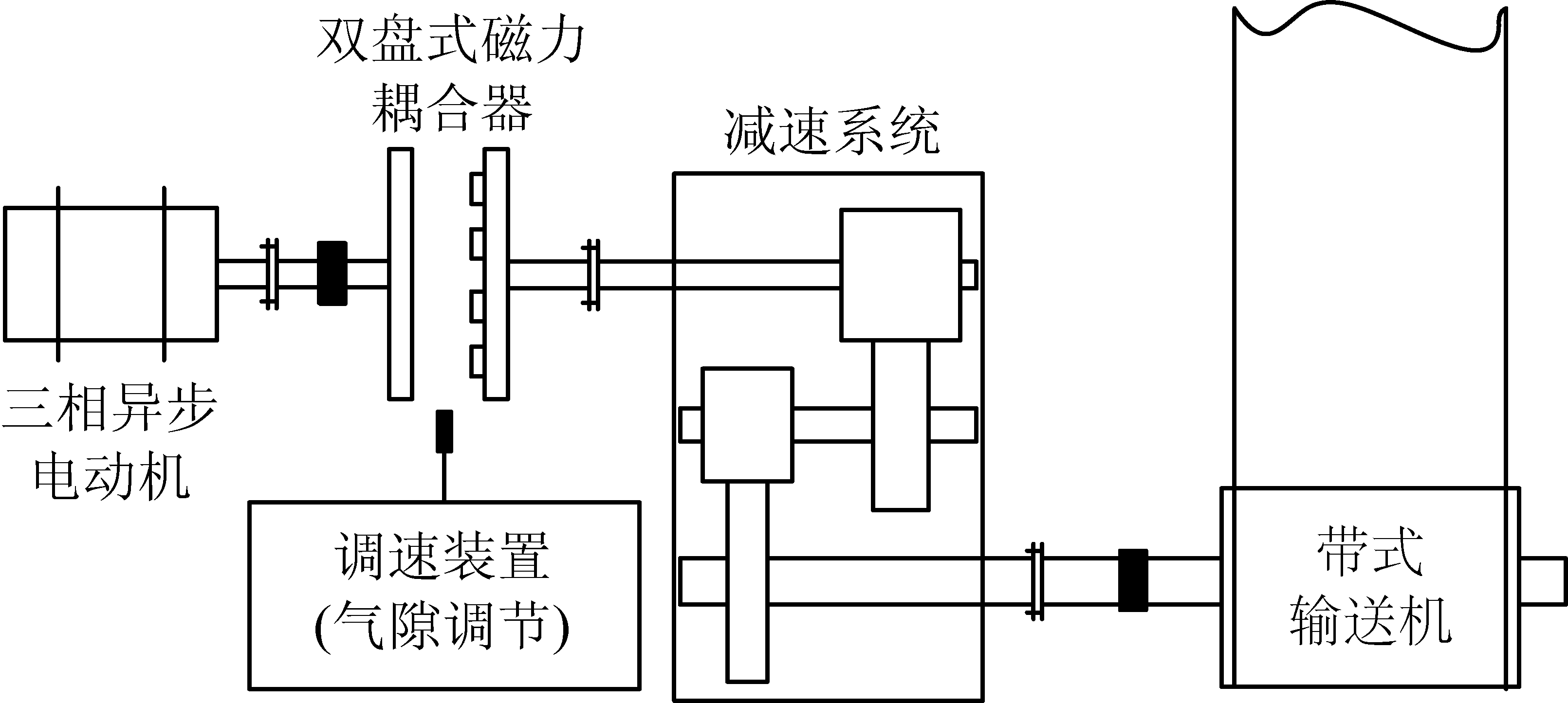
图1 带式输送机磁力传动系统结构
Fig.1 Structure of magnetic drive system for belt conveyor
1.2 双盘式磁力耦合器动态模型
1.2.1 双盘式磁力耦合器结构
双盘式磁力耦合器是由双“铜盘-永磁体盘”和调隙装置组成[12],结构如图2所示,与相同尺寸的单盘式或圆筒式磁力耦合器相比,双盘式结构能传递更大的转矩。

1—输入轴;2—铜盘;3—永磁体盘;4—调隙装置; 5—磁体轭铁; 6—导体轭铁;7—输出轴
图2 双盘式磁力耦合器
Fig.2 Double disc magnetic couplers
1.2.2 双盘式磁力耦合器动态数学模型
在不考虑磁力耦合器运行时各种阻力的情况下,根据能量守恒定律,双盘式磁力耦合器的输入功率为
(1)
式中:Pin为磁力耦合器输入功率,W;Pout为磁力耦合器输出功率,W;Ploss为磁力耦合器铜盘涡流损耗功率,W;Wm为气隙中磁场能量,W;t为时间,s。
调速过程气隙中磁场能量为
(2)
式中:V为气隙体积,m3;u0为真空磁导率,u0≈1;B为气隙其感应强度,T。
磁力耦合器调速时,磁力耦合器输入功率为
(3)
式中:T1(t)为磁力耦合器的输入转矩,N·m;θ1(t)为磁力耦合器输入角位移,rad。
输出功率为
(4)
式中:T2(t)为磁力耦合器的输出转矩,N·m;θ2(t)为磁力耦合器输出角位移,rad。
磁力耦合器在传动过程中,转矩损失很小,可忽略不计,则近似认为:
T1(t)=T2(t)
(5)
假设永磁体产生的磁场在气隙中均匀分布,随着气隙改变,穿过铜盘涡流环的磁通量变化规律近似为
(6)
式中:φ(t)为穿过涡流环的磁通量,Wb;Am为永磁体横截面积,m2;p为一个永磁体盘上永磁体磁极对数。
基于法拉第电磁感应定律,由等效磁路法[13]计算出调速过程气隙磁阻为
(7)
式中:Rδ为气隙磁阻,1/m2;δ(t)为调速时气隙随时间的变化关系,mm。
调速过程气隙磁感应强度为

(8)
式中:Hc为永磁体的矫顽力,A/m;h为永磁体极化方向长度,m;ρ′为铜盘电阻率,Ω·m;Rm(t)为铜盘、气隙和永磁体内部总磁阻,1/m2;Δh为集肤深度,m; ke为等效折算系数,取2.5[14]。
在磁力耦合器稳态时涡流损耗的基础上[15],进一步推导出双盘式磁力耦合器调速过程铜盘涡流损耗总功率为
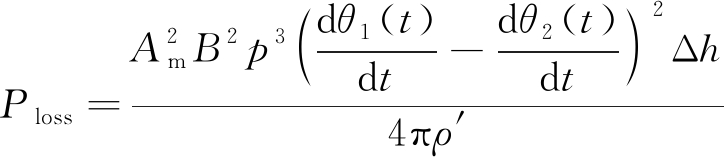
(9)
联立上述公式可得,调速时磁力耦合器传递转矩随时间的变化关系为
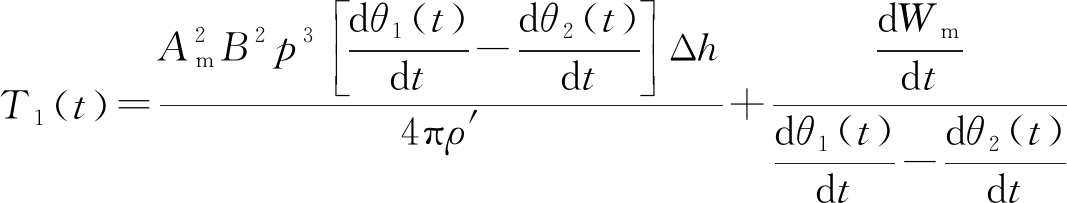
(10)
边界条件为
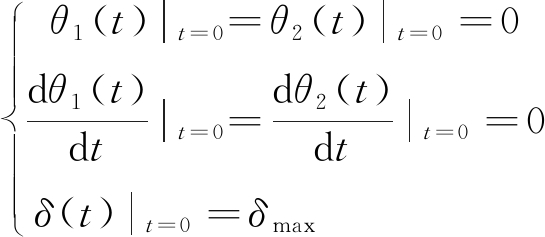
(11)
式中:δmax为磁力耦合器最大气隙,并且当气隙为δmax时,磁力耦合器能恰好带动负载转动。
1.3 带式输送机工作特性
带式输送机输送带为柔性体,其启动过程动力传递为
(12)
式中:Tf为带式输送机负载力矩,N·m;η为减速器传递效率;i为减速比;J为带式输送机转动惯量,kg·m2;C为带式输送机黏性阻尼系数,N·m·s/rad;θ3(t)为带式输送机驱动滚筒角位移,rad。
2 带式输送机磁力软启动仿真模型
2.1 双盘式磁力耦合器控制系统
采用PID闭环控制系统实现带式输送机磁力软启动,计算带式输送机满足Harrison启动速度时磁力耦合器的理论输出转速,并通过测量得到负载转矩,代入磁力耦合器的数学模型,得到磁力耦合器的工作时的理论气隙。利用转矩转速传感器,检测带式输送机工作时驱动滚筒的转矩和转速,用反馈元件计算出磁力耦合器工作时的实际气隙,PID控制系统通过电动执行器,调节磁力耦合器的气隙,达到启动调速的目的。双盘式磁力耦合器控制系统框图如图3所示。

图3 双盘式磁力耦合器控制系统框图
Fig.3 Block diagram of double disc magnetic coupler control system
2.2 双盘式磁力耦合器仿真模型
根据上述的磁力耦合器数学模型,运用AMEsim软件,建立磁力耦合器仿真模型。为使系统仿真模型简洁,利用元件集成技术创建超级元件[16-17],双盘式磁力耦合器仿真模型如图4所示。
2.3 带式输送机磁力软启动仿真模型
以Kelvin-Voigt模型[18]为输送带黏弹性模型,选择重锤拉紧方式,三相异步电机为驱动装置,双盘式磁力耦合器为调速装置,并采用PID闭环控制系统进行调速,运用质量块模拟带式输送机满载启动工况,建立带式输送机磁力软启动仿真模型,如图5所示。
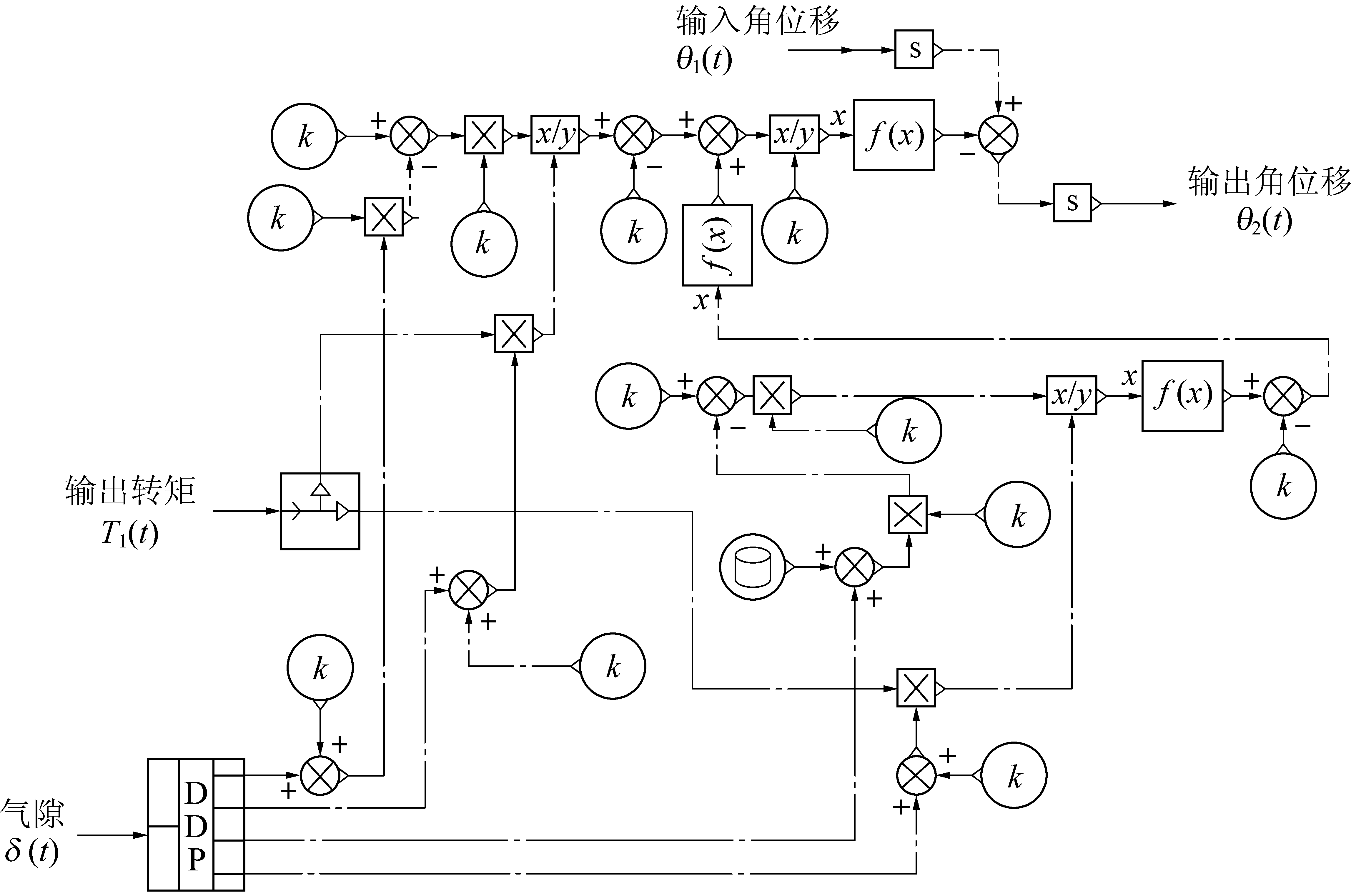
图4 双盘式磁力耦合器仿真模型
Fig.4 Simulation model of double disc magnetic coupler

图5 带式输送机磁力软启动仿真模型
Fig.5 Simulation model of magnetic soft start of belt conveyor
3 带式输送机满载启动动态仿真分析
3.1 带式输送机仿真模型参数
以长距离带式输送机为分析对象,输送带型号为ST2000的钢丝绳输送带,运量为1 400 t/h,运输倾角为2°,重锤拉紧力为4 kN,承载段输送带按每100 m划分为1个单元,回程段按每160 m划分为1个单元,建立带式输送机模型,具体参数如下:

运输距离/m1 600带宽/m1.4带速/(m·s-1)2.5输送带单位长度质量/(kg·m-1)40.4物料线质量/(kg·m-1)155.56上分支托辊单位长度等效质量/(kg·m-1)43.7下分支托辊单位长度等效质量/(kg·m-1)15输送带弹性模量/(N·m-1)1.3×108输送带和滚筒之间摩擦因数0.3模拟摩擦阻力因数0.025滚筒直径/m1黏弹性流变系数0.8减速比0.031 9
3.2 仿真结果分析
根据上述仿真模型和带式输送机的运行参数,对长距离带式输送机满载启动工况进行动态仿真,带式输送机以常用的Harrison加速控制曲线启动[19],启动时间分别为60、80和100 s,仿真时间设置为110 s。
带式输送机磁力软启动过程机头、机尾部输送带速度变化曲线如图6所示,从图6可以看出:随着启动时间的增加,带式输送机启动过程越来越平稳,速度波动越来越小;当启动时间为60 s时,启动加速度过大,机尾部输送带速度波动较大,可能出现输送带抖动现象,导致物料洒落;带式输送机尾在机头启动后13 s左右开始启动,当启动时间为80 s和100 s时,机头、机尾部输送带速度波动较小,启动比较平缓,由于输送带的黏弹性,启动初期出现浪涌现象[20],但磁力耦合器调速装置使其变得十分不明显。
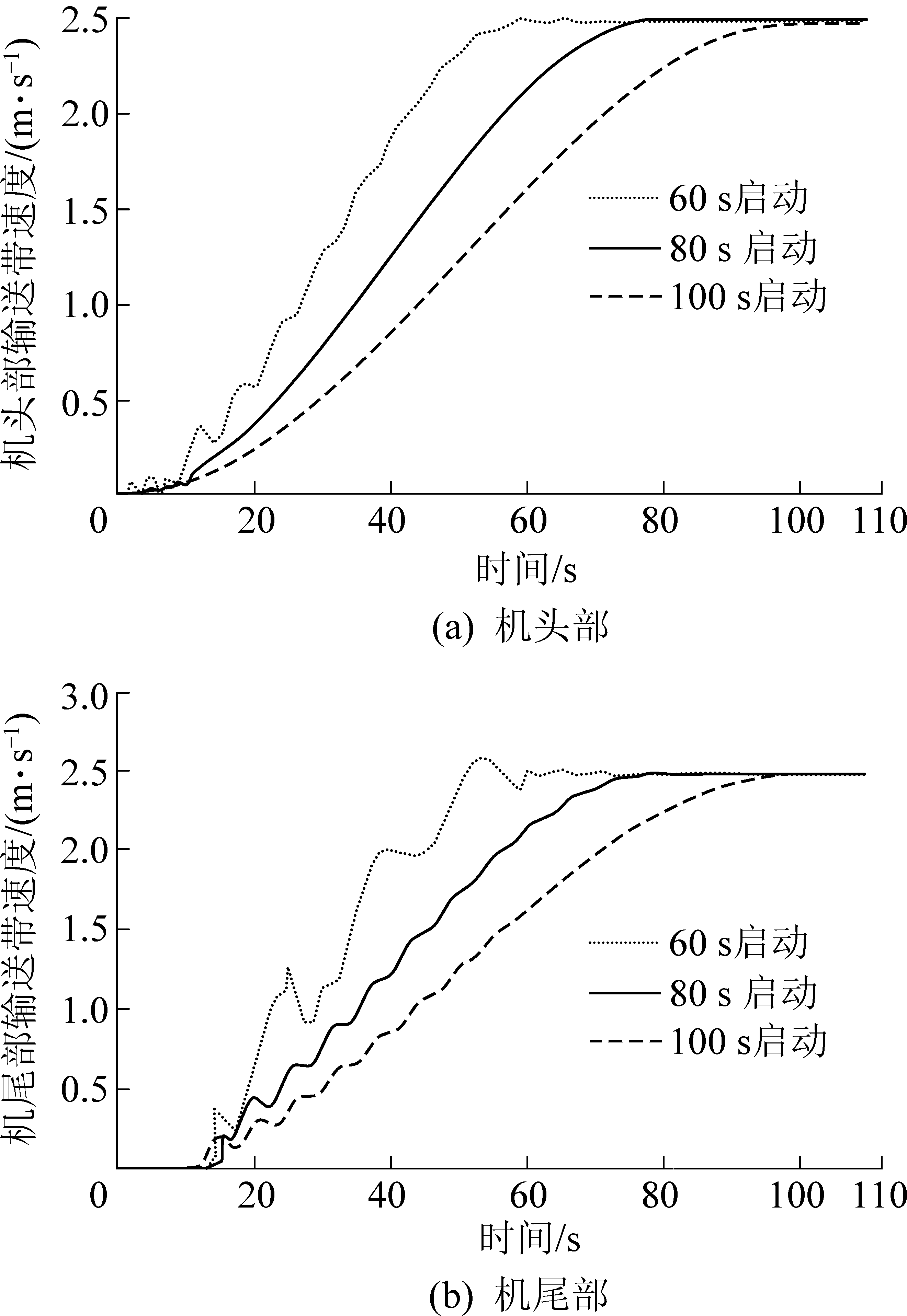
图6 输送带速度变化曲线
Fig.6 Speed change curves of conveyor belt
带式输送机启动过程磁力耦合器铜盘和永磁体盘之间气隙随时间的变化曲线如图7所示,从图7可以看出:为达到Harrison曲线启动,气隙从最大值22 mm减小到4 mm,并在不同启动时间,磁力耦合器的气隙变化与带式输送机启动时速度变化趋势相反;启动过程气隙逐渐减小,根据磁力耦合器的数学模型,当负载转矩不变时,磁力耦合器通过减小铜盘和永磁体盘之间的气隙来提高输出转速。

图7 双盘式磁力耦合器气隙变化曲线
Fig.7 Air gap change curves of double disc magnetic coupler

图8 输送带张力曲线
Fig.8 Tension curves of conveyor belt
带式输送机磁力软启动机头、机尾部输送带张力变化曲线如图8所示,从图8可以看出:带式输送机启动初期,机头、机尾部输送带张力迅速达到最大张力值,随着启动进行,张力逐渐减小并趋于稳定;随着启动时间的增加,输送带张力变化逐渐稳定,波动幅度越来越小,启动结束后,机头输送带张力都稳定于30.5 kN左右,机尾张力都稳定于15 kN左右;当以60 s启动时,机头输送带张力波动较为平缓,但机尾输送带张力波动大且无规则,张力波动幅值达到14 kN,由于双盘式磁力耦合器的调速装置为电动执行器,其机械执行需要的时间较长,当启动时间较短时,气隙调节速度过快,导致张力波动较大;当以80 s和100 s启动时,机头输送带张力变化相接近,机尾输送带张力差别很小,幅值分别为5 kN和3 kN,双盘式磁力耦合器传动装置控制带式输送机启动张紧力连续平稳的变化,且张力变化值在5 kN以内,改善了带式输送机的动力学性能。
带式输送机拉紧装置位移变化曲线如图9所示,从图9可以看出:当以不同启动时间进行启动时,拉紧装置的最大位移分别为1.65、1.45和1.42 m,变化趋势相接近,在距离初始位置1.05 m处上下小幅波动。由于拉紧装置布置在输送带回程段中间位置,表明带式输送机磁力软启动过程,输送带回程段动张力受启动时间变化的影响很小。
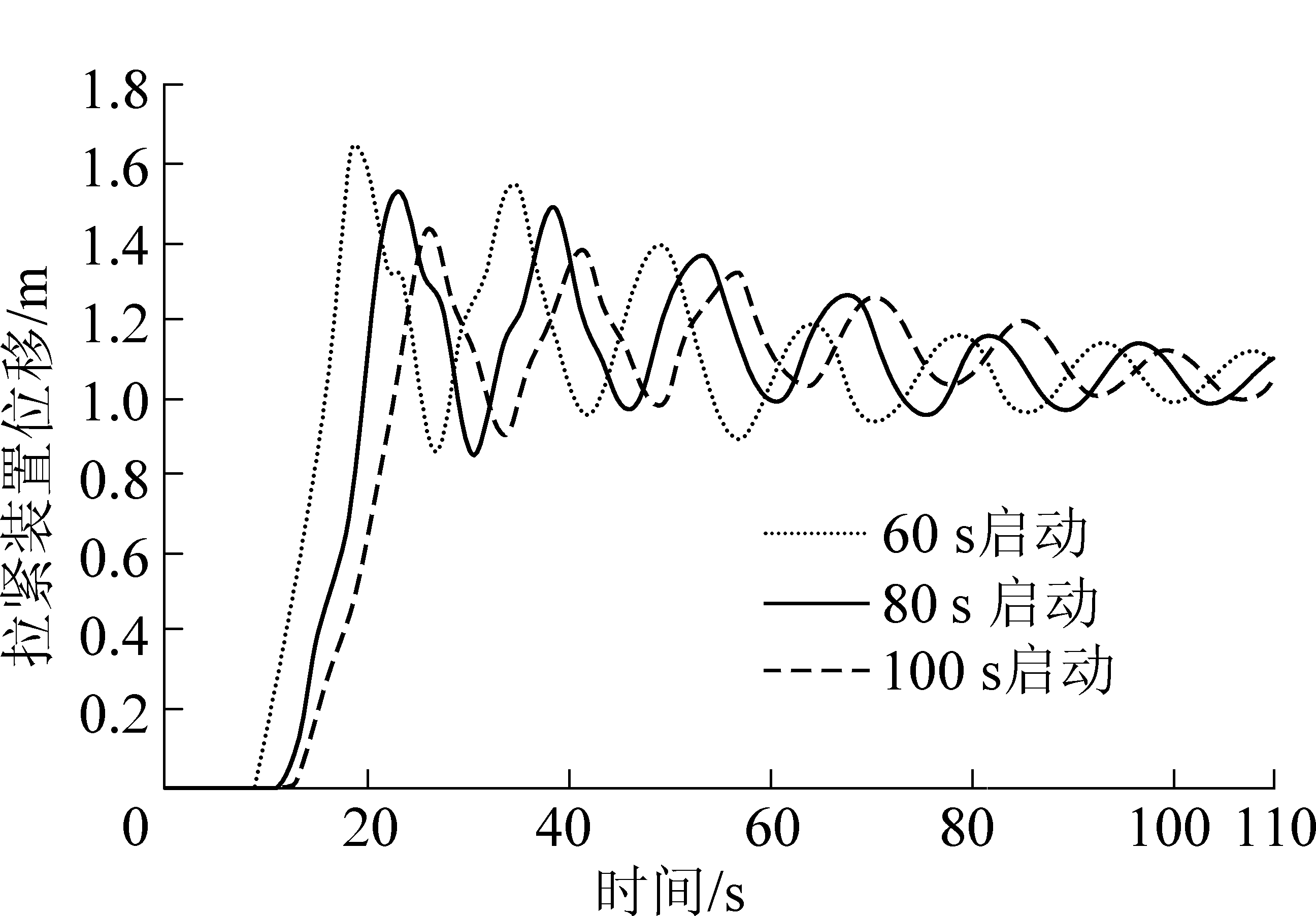
图9 拉紧装置位移曲线
Fig.9 Displacement curves of tension device
4 结 论
基于永磁涡流传动,将双盘式磁力耦合器作为带式输送机启动装置,实现了带式输送机启动可控,减少了带式输送机的启动冲击,具有良好的启动性能。
1)在磁力耦合器稳态模型的基础上建立双盘式磁力耦合器动态数学模型,启动调速时,气隙变化趋势与输送带速度变化趋势相反,当以不同的时间启动时,气隙都从最大22 mm减小到4 mm,随着启动时间的增加,气隙变化速度逐渐变慢。
2)带式输送机以60 s启动时,磁力耦合器气隙调节速度过快,使输送带速度波动大,机尾输送带张力波动幅度大且无规则,最大张力达到29 kN,张紧装置最大位移为1.65 m,此时启动过程不平稳,易出现输送带断裂,物料散落事故。
3)带式输送机以80 s和100 s启动时,输送带速度相对较平稳,机头、机尾输送带启动时张力波动小,机尾输送带张力波动幅值约为5 kN和3 kN,启动过程平稳,当对带式输送机启动精度要求不高时,为节约时间,80 s启动就能满足要求。
[1] 武林海.带式输送机常见故障检测及防治系统研究[J].煤矿机械,2019,40(2):145-147.
WU Linhai.Research on common fault detection and prevention system of belt conveyor[J].Coal Mine Machinery,2019,40(2):145-147.
[2] 刘 菲,曾文浩,杨永泰,等.基于ADAMS的滚筒式输送机构的传动速率优化[J].机床与液压,2019,47(2):135-138.
LIU Fei,ZENG Wenhao,YANG Yongtai,et al.Optimization of transmission rate for roller conveyor based on ADAMS[J].Machine Tool & Hydraulics,2019,47(2):135-138.
[3] ZHOU G L,HAN R F.Dynamic analysis of belt conveyor based on ADAMS and PRO/E[J].Advanced Materials Research,2013,764:119-123.
[4] 吴 波,廉自生,张 鑫.长距离带式输送机输送带的动态特性仿真[J].煤炭科学技术,2014,42(2):82-84.
WU Bo,LIAN Zisheng,ZHANG Xin.Dynamic characteristic simulation for belt of long distance belt conveyor[J].Coal Science and Technology,2014,42(2):82-84.
[5] 李显荣,董长双,李军霞,等.带式输送机打滑动力学模型及有限元仿真研究[J].煤炭技术,2015(2):205-208.
LI Xianrong,DONG Changshuang,LI Junxia,et al.Study on belt conveyor’s skidding dynamic model and finite element simulation[J].Coal Technology,2015(2):205-208.
[6] 牛耀宏,孟国营.矿用永磁耦合联轴器过载保护实验研究[J].煤炭工程,2014,46(2):106-107.
NIU Yaohong,MENG Guoying.Study on overload protection experiment of mine permanent magnetic coupling clutch[J].Coal Engineering,2014,46(2):106-107.
[7] 李亚辉,付 转,刘媛荣,等.福伊特液力耦合器与液黏软启动装置的分析比较[J].煤矿机械,2012,33(3):146-148.
LI Yahui,FU Zhuan,LIU Yuanrong,et al.Analysis and comparison of voith fluid coupling and hydro-viscous soft start device[J].Coal Mine Machinery,2012,33(3):146-148.
[8] 王光炳.带式输送机可控软起动装置的研究[J].煤炭学报,2003,28(3):316-321.
WANG Guangbing.Study on belt conveyor controlled start transmission equipment[J].Journal of China Coal Society,2003,28(3):316-321.
[9] TIAN Z,HOU Y.Modeling a magneto-rheological soft starter for use with belt conveyors[J].International Journal of Mining Science & Technology,2012,22(3):385-389.
[10] 周广林,韩忠惠,张继通.基于分形维数的大型带式输送机动态特性研究[J].煤炭科学技术,2019,47(2):125-130.
ZHOU Guangling,HAN Zhonghui,ZHANG Jitong.Research on dynamic characteristics of large belt conveyor based on fractal dimension[J].Coal Science and Technology,2019,47(2):125-130.
[11] 贾砚成.基于“永磁直驱+芳纶胶带”节能高效高可靠性胶带运输系统[J].煤矿现代化,2018(1):75-77.
JIA Yancheng.The reliable energy-saving and efficient belt conveyor transportation system basedon permanent magnetic direct drive and aramid fiber belt[J].Coal Mine Modernization,2018(1):75-77.
[12] 杨超君,管春松,丁 磊,等.盘式异步磁力联轴器传动特性[J].机械工程学报,2014,50(1):76-84.
YANG Chaojun,GUAN Chunsong,DING Lei,et al.Transmission characteristics of axial asynchronous permanent magnet couplings[J].Journal of Mechanical Engineering,2014,50(1):76-84.
[13] 司纪凯,何 松,封海潮,等.表面-内置式永磁转子同步电机等效磁路法特性分析[J].煤炭学报,2015,40(5):1199-1205.
SI Jikai,HE Song,FENG Haichao,et al.Characteristic analysis of surface-mounted and interior hybrid permanent magnet synchronous motor based on equivalent magnetic circuit method[J].Journal of China Coal Society,2015,40(5):1199-1205.
[14] 王 爽,郭永存,王鹏彧,等.复合式磁力耦合器的设计与试验研究[J].西安交通大学学报,2017,51(7):115-123.
WANG Shuang,GUO Yongcun,WANG Pengyu,et al.Design and experimental research on hybrid magnetic coupler[J].Journal of Xi’an Jiaotong University,2017,51(7):115-123.
[15] 郭永存,方 成,王鹏彧,等.可调速型盘式磁力耦合器永磁体温度场研究[J].工矿自动化,2017,43(8):61-66.
GUO Yongcun,FANG Cheng,WANG Pengyu,et al.Research on temperature field of permanent magnet in disc-type speed-regulation magnetic coupler[J].Industry and Mine Automation,2017,43(8):61-66.
[16] LI G B,YE R Y,LI R Q.Study on conveyor AMESim model and motor starting interval[J].Key Engineering Materials,2010,450:43-46.
[17] 赵东升.基于AMEsim的带式输送机仿真建模方法研究[J].中国矿业,2013(2):114-116.
ZHAO Dongsheng.Research on belt conveyor simulation modeling methods base on AMEsim[J].China Mining Magazine,2013(2):114-116.
[18] KAROLEWSKI B,LIGOCKI P.Modelling of long belt conveyors[J].Eksploatacja I Niezawodnosc-Maintenance and Reliability,2014,16(2):179-187.
[19] 李玉瑾.带式输送机的动态特性分析与软起动设计[J].煤炭学报,2002,27(3):294-299.
LI Yujin.Dynamic analysis and soft starting design of belt conveyor[J].Journal of China Coal Society,2002,27(3):294-299.
[20] 胡 坤.带式输送机绿色设计关键技术与应用研究[D].淮南:安徽理工大学,2012:41-43.
