0 引 言
矿井防尘供水管网的正常有效运行是矿井安全生产、粉尘防治、矿工健康以及事故应急避险的重要保障[1-4]。由于生产的发展,管路变化、用水量变化、局部泵站运行参数变化、管段漏损事故等因素都会导致管网水力条件发生变化,甚至对管网的运行状态造成不良影响。研究矿井防尘供水管网的运行情况、掌握其水力、水质运行规律,对于满足井下生产用水需求、降低供水成本、提高管网可靠性以及进行矿井防尘供水管网优化改造具有重要意义[5]。然而矿井防尘供水管网往往位于地面以下,水平或者垂直跨度大,井下生产环境复杂,安全风险类型较多,不易进行检测;而且考虑到矿井供水安全及生产的需求,也不宜直接在实际管网上进行大量试验。因此,建立与实际管网相似的水力试验模型,将在实际管网中难以开展的研究工作在试验模型中进行,是研究矿井实际供水管网运行问题的一种重要手段。
现有水力模型的研究主要围绕水工、河工等模型展开。在对市政供水管网水力模型的研究上,通常可分为2个方面:一方面是研究利用计算机技术将水力建模、地理信息系统与数据监测采集系统相结合,建立信息化、智能化的运行管理仿真平台[6-7];另一方面是在实际管网上工程试验不易实施或持续试验时,基于水力相似原理搭建缩小的物理模型来进行管网的水力模拟试验[8-10]。在市政供水管网的物理模型设计中,管网水流流动的动力来源为泵站供给的压力,管段垂直高差较小,重力对水力变化的影响较小;而矿井防尘供水管网一般是以重力主导静压供水系统,主要呈现枝状拓扑结构,分水平分采区供水,管网内水压随着采深的增加而增大,有的能高达4 MPa以上。因此,矿井防尘供水管网相似物理模型的构建,不能照搬市政供水管网压力相似准则,而应该采用更切合矿井防尘供水管网实际的相似物理模型构建方法。
笔者从流体力学基本方程出发,使用量纲分析法对相似理论进行分析推导,以重力相似准则为主导构建矿井防尘供水管网的相似物理模型,推导出原型管网与模型管网各物理量间的变态相似比尺表达式;并进一步使用EPANET水力仿真模拟软件对原型管网和模型管网水力工况进行解算,验证相似模型构建的合理可行。同时,基于信息理论和相关系数构建测点优化数学模型,对压力监测点进行优化布置。通过实验室相似物理模型的构建,以期为矿井防尘供水管网的水力、水质及运行安全等问题提供一种便捷有效的研究手段。
1 基于量纲分析的相似模型理论推导
1.1 水力相似准则的推导
水力相似理论是水力模型试验的理论依据,也是对液流现象进行理论分析的一个重要手段。当水力原型由于各种原因不能直接进行量测时,可以通过设计制作专门的相似模型进行试验,即在模型中重演与原型相似的水流现象,以观测分析研究水流的运动规律。而若要这2个水力体系可以比拟,就必须使两者相应点上的物理量都维持各自的固定比例关系,即满足几何相似、运动相似以及动力相似。除此之外,还应有边界条件相似,对非恒定过程,还要求初始条件相似。
矿井防尘供水管网原型和模型中的水流流动都是水体在重力和黏滞力作用下在一定的边界里运动,可以看作是一个不可压缩连续均匀黏性流体的不恒定运动过程,遵循连续性方程和纳维-斯托克斯(N-S)方程式:
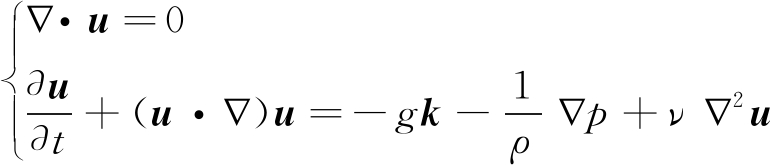
(1)
式中:
![]() 为哈密顿算子;u为流速;g为重力加速度;i、j、k为直角坐标系三个坐标轴的单位矢量;ρ为流体密度;p为压力;t为时间;ν为运动黏度,ν=μ/ρ,μ为动力黏度。
为哈密顿算子;u为流速;g为重力加速度;i、j、k为直角坐标系三个坐标轴的单位矢量;ρ为流体密度;p为压力;t为时间;ν为运动黏度,ν=μ/ρ,μ为动力黏度。
若要保证原型管网和模型管网中的流动是相似的,则要求两者的无量纲解相等,也就是说控制流动的无量纲方程、无量纲边界条件和初始条件都应该相同。因此,使用流动的时间T、长度L、流速U和压强P这些特征量,将上述方程中的自变量和因变量无量纲化(式(2)),可以得到无量纲方程式(式(3))。
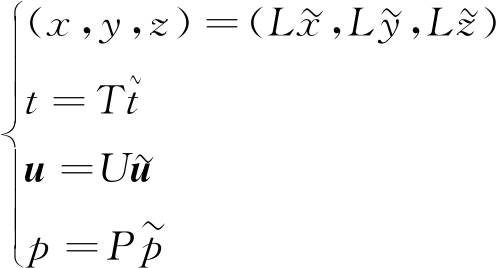
(2)

(3)
式中:![]() 和
和![]() 为各变量的量纲。
为各变量的量纲。
将上述方程中无量纲N-S方程对流项前的系数归一,得到:
(4)
因为对于相似流动,要求两者上述方程的无量纲解相等,所以对应的特征无量纲数![]() 必须相等。这4个特征无量纲量分别称为4个相似准数,并对应非恒定惯性力相似准则、重力相似准则、压力相似准则和黏性力相似准则(式(5))。
必须相等。这4个特征无量纲量分别称为4个相似准数,并对应非恒定惯性力相似准则、重力相似准则、压力相似准则和黏性力相似准则(式(5))。

(5)
严格的相似模型构建要求遵循上述多个相似准则,但在实际中通常难以实现,普遍的对策是根据水流特性、研究目的和试验条件而选定最主要的准则,从而能够实现主要方面的相似,并使次要方面的影响限制在可容许的范围之内[11]。针对矿井防尘供水管网中重力对水流的影响很大,由较大的垂直高差产生的静水压力是整个管网最主要动力源的实际情况,笔者基于重力相似准则,辅以压力相似准则来设计矿井防尘供水管网相似模型。
1.2 变态相似比尺的推导
矿井防尘供水管网垂直高差一般在数百米以上,单线管长能长达数千米,管道直径范围为50~200 mm。考虑试验场地、制作条件以及供水能力等多方面的限制,基于变态相似理论来构建管网的相似试验模型,即相似模型至少在一个方向上的长度比尺与其他方向不一样。根据重力相似准则,首先保证原型与模型的弗劳德准数相等,即:
Frprototype=Frmodel
(6)
从而可以推得:
(7)
式中:δu和δl分别为流速相似比尺和管段长度相似比尺。
由管段流量![]() 可得:
可得:
(8)
式中:A为管段截面积;d为管径;u为流速;δQ和δd分别为流量和管径相似比尺。
将式(7)代入式(8),可得流量相似比尺为:
(9)
在优先满足重力相似准则后,根据压力相似准则,原型和模型的欧拉相似准数相等,即
Euprototype=Eumodel
(10)
可得管段中2点的压力差相似比尺为
(11)
对于均匀流流动达到充分发展状态的水平管段中2点之间的压力差来自沿程压力损失,则根据达西公式有
(12)
式中:Δp为压力差;hf为沿程压力损失;λ为沿程阻力系数;l为管的长度。
结合式(11)可以得到
(13)
式中:δλ为沿程阻力系数相似比。
从而可得充分发展的水平均匀管流的沿程阻力系数相似比尺为
δλ=δd/δl
(14)
2 矿井防尘供水管网变态相似模型构建
原型管网为开滦集团某煤矿的井下防尘供水管网,矿区设有地面静压水池与矿井供水管网相连,为井下提供消防、防尘等生产用水。水源主要来自地下水和大气降水,井下设有蓄水仓,作为消防储备用水。该供水管网是以枝状拓扑结构为主的集中静压供水方式。通过筛选原型管网中关键管段与关键节点,对原型管网进行简化后的布置如图1所示,简化后的管段和节点总数分别为27和28。该井下供水系统中主要采用直径159、108、89 mm的供水管,其内径分别为150、100、80 mm。原型管网的拓扑结构及节点标高、管长信息如图2所示。各类型用水点的日防尘用水需求和日总防尘用水需求如图3所示。基于前文推导的变态相似比尺表达式,结合国内给排水管规格的标准,选取长度比尺δl=100,管径平均比尺δd=3.85。相应地,可以推导出其他物理量相似比尺如下:

δl100δd3.85δQ=δ2dδl148.225δu=δl10δΔp=δl100δλ=δd/δl0.038 5

①— 为节点编号
为节点编号
图1 矿井防尘供水管网原型布置简化示意
Fig.1 Simplified layout of underground mine water supply network

①— 为节点编号
为节点编号
图2 原型管网节点和管段信息
Fig.2 Nodes and pipes parameters of the prototype pipe network

图3 原型管网日防尘用水需求变化情况
Fig.3 Daily water demands for dust control of the prototype pipe network
3 基于水力模拟的变态相似模型模拟验证
为验证上文中推导的变态相似模型理论的合理性,使用美国国家环境保护局(Environmental Protection Agency,EPA)开发的EPANET软件,运用混合节点-环方法[12]对原型管网和模型管网进行水力仿真模拟,比较2种水力条件下的流量、流速以及压差的相对误差。
据此在EPANET中绘制管网水力模型如图4所示。除了设置水力模型中各关键节点标高、管段长度、管径大小、粗糙系数外,还设置各用水点的需水量。管段材质主要为无缝钢管,取海曾-威廉粗糙系数C=140。需水量取值根据矿井供水管网各工作面的日最大防尘用水量确定。同样,基于上文确定的变态相似比尺,在EPANET中建立变态相似管网的水力模型,各管段内径设为原型管网管段内径以及管径相似比尺的乘积,用水点需水量为原型管网用水点需水量与前文推导的流量相似比尺的乘积。

图4 原型管网和模型管网的水力模型
Fig.4 Hydraulic model diagram of the prototype pipe network and the model pipe network
对所构建的水力模型进行解算后,原型管网与模型管网节点和管段的流量、流速及相似比尺误差分析见表1。根据求解结果,计算2号节点与各水平用水点的压差及其相似比尺误差见表2。
由表1和表2可知,使用EPANAT软件对原型管网与相似模型管网进行水力模拟得到的管段流量相似比尺、流速相似比尺与理论设定值误差很小,最大相对误差分别为-0.83%和-1.52%以内,其平均相对误差分别为0.20%和0.46%。压差相似比尺的误差比流量相似比尺、流速相似比尺的误差稍大一些,这可能是因为在水平或者倾斜管段的重力变化较小,造成节点压差比的误差增大,但压差相似比尺的最大相对误差为-7.74%,不超过10%,平均相对误差为-4.20%。该相似模型的构建优先满足重力相似准则,因而由压力相似准则推导出的压差相似比尺的精度可以适当放宽一点。综合来看,模型管网与原型管网具有较好的相似度。
表1 原型管网和模型管网水力求解管段流量及流速对比
Table 1 Comparison of volume flow rate and velocity based on hydraulic simulations of prototype and model pipe networks

管段编号原型管网长度/m直径/m流量/(m3·h-1)流速/(m·s-1)模型管网长度/m直径/m流量/(m3·h-1)流速/(m·s-1)流量相似比尺计算值理论值相对误差/%流速相似比尺计算值理论值相对误差/%1260150153.202.4082.638.961.0340.241148.162 148.225 -0.049.9910-0.08 250010032.441.1475.025.970.2190.115148.128148.225-0.079.9710-0.26340010026.560.9394.025.970.1790.094148.380148.2250.109.9910-0.1141008026.561.4681.020.780.1790.147148.380148.2250.109.9910-0.1452001005.880.2082.025.970.0400.021147.000148.225-0.839.9010-0.956100805.880.3251.020.780.0400.033147.000148.225-0.839.8510-1.5276501005.880.2086.525.970.0400.021147.000148.225-0.839.9010-0.95850805.880.3250.520.780.0400.033147.000148.225-0.839.8510-1.529200150114.881.8062.038.960.7750.181148.232148.2250.009.9810-0.221060010044.161.5626.025.970.2980.156148.188148.225-0.0310.01100.131120010011.720.4152.025.970.0790.042148.354148.2250.099.8810-1.1912808011.720.6480.820.780.0790.065148.354148.2250.099.9710-0.311311010032.441.1471.125.970.2190.115148.128148.225-0.079.9710-0.261450805.880.3250.520.780.0400.033147.000148.225-0.839.8510-1.521520010026.560.9392.025.970.1790.094148.380148.2250.109.9910-0.1116708026.561.4680.720.780.1790.147148.380 148.225 0.109.9910-0.14 1750010070.722.5015.025.970.4770.250148.260148.2250.0210.00100.04181008026.561.4681.020.780.1790.147148.380148.2250.109.9910-0.14
续表

管段编号原型管网长度/m直径/m流量/(m3·h-1)流速(m·s-1)模型管网长度/m直径/m流量/(m3·h-1)流速/(m·s-1)流量相似比尺计算值理论值相对误差/%流速相似比尺计算值理论值相对误差/%1930010044.161.5623.025.970.2980.156148.188148.225-0.0310.01100.132020010026.560.9392.025.970.1790.094148.380148.2250.109.9910-0.1121508026.561.4680.520.780.1790.147148.380148.2250.109.9910-0.142278010017.600.6237.825.970.1190.062147.899148.225-0.2210.05100.482320010017.600.6232.025.970.1190.062147.899148.225-0.2210.05100.482420010011.720.4152.025.970.0790.042148.354148.2250.099.8810-1.1925508011.720.6480.520.780.0790.065148.354148.2250.099.9710-0.31262001005.880.2082.025.970.0400.021147.000148.225-0.839.9010-0.952770805.880.3250.720.780.0400.033147.000148.225-0.839.8510-1.52
表2 原型管网和模型管网水力求解压差对比
Table 2 Comparison of water head difference based on hydraulic simulations of prototype and model pipe networks

节点-节点压差/m原型管网模型管网压差相似比尺计算值理论值相对误差/%2-7103.721.1094.29100-5.712-949.590.5099.18100-0.822-10187.571.9098.85100-1.152-15323.363.3995.39100-4.612-17350.053.6994.86100-5.142-28421.634.5792.26100-7.74
4 矿井防尘供水管网相似模型测点优化
在前文对矿井防尘供水管网相似模型合理性验证的基础上,搭建实际相似物理模型进行水力工况研究时,需要在管网中布置压力监测点。所布置的监测点既要能最大程度地反映管网的运行状态,又能减少设备成本投入,同时也为实现对实际管网实时监测测点布置提供参考。如图3所示,原型管网所在矿井每日采用三班制作业模式,包括1个检修班(0—8点)和2个作业班(8—16点和16—24点),在检修班期间,井下工作面产尘量较小,用水量也相对较小,各工作面用水量在0~4 m3/h。在作业班期间,工作面的用水量基本达到高峰值,其中综采工作面、综掘工作面、开拓工作面的最大防尘用水量分别能达到26.56、11.72、5.88 m3/h,全天中最大总防尘用水量约为151.82 m3/h。在各班次交接期间,用水量会存在短时段的下降,比如在14—16点期间。可见,井下防尘用水量变化是一个动态、周期性的过程,根据各工作面的日防尘用水需求,基于EPANET水力模拟24 h内的管网运行工况,利用信息理论构建数学模型,以求解各节点水压的相关系数,针对压力数据高度相关节点进行优化。
设矿井防尘供水管网关键拓扑结构中节点总数为n,对任一节点Ni,(i=1,2,3,…,n)。根据防尘需水量水力模拟得到节点Ni在24个时刻的压力数据为Pit=[pi1,pi2,pi3,…,pit],(t=1,2,3,…,24)。则根据信息理论,节点压力信息量Ii的优化数学模型为:
Ii=maxf(Pit)
(15)
其中,
(16)
则对于任意2个压力监测点Ni和Nj,分别可以得到节点压力信息量Ii和Ij,其相关系数可以通过下式计算得到:
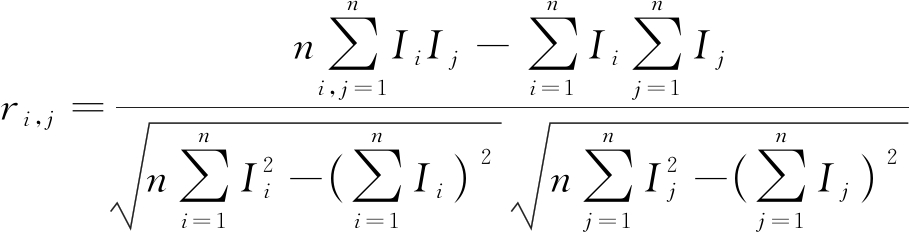
(17)
根据上述模型计算得到相关系数大于0.9的高度相关组合为:[N4,N5],[N6,N7],[N8,N9],[N12,N13],[N16,N17],[N21,N22],[N25,N26],[N27,N28],说明上述组合中的节点压力信息具有高度相关性,因而可以通过选取其中部分节点同其他非高度相关节点作为压力监测点,并根据这些监测点的压力信息,推导出其他节点的压力信息,节点压力信息的拟合关系可以在相似物理模型试验中进一步验证。
5 结 论
1)从流体力学基本方程出发,基于管流变态相似理论,推导出矿井防尘供水管网原型与相似模型管长、管径、流量、流速、压差等各物理量之间的相似比尺表达式,为原型管网和模型管网各物理量之间的换算以及实验室等效物理模型的设计提供了理论依据与方法。
2)根据矿井防尘供水管网原型,选取长度相似比尺100,管径平均相似比尺3.85,根据相似理论推导确定了其他物理量相似比尺,建立了矿井防尘供水管网相似试验模型。并进一步采用EPANET水力模拟软件对原型管网与模型管网的水力工况进行解算,得到管段流量、流速、压差的平均相对误差分别为0.20%、0.46%和-4.20%,表明试验模型和原型能够较好地满足相似关系,该建模方法合理可行。
3)基于信息理论和相关系数构建测点优化数学模型,计算得到[N4,N5],[N6,N7]等高度相关节点组合,为防尘供水管网实时水力监测提供监测点布置参考。
[1] 何绪文,张晓航,李福勤,等.煤矿矿井水资源化综合利用体系与技术创新[J].煤炭科学技术,2018,46(9):4-11.
HE Xuwen,ZHANG Xiaohang,LI Fuqin,et al.Comprehensive utilization system and technical innovation of coal mine water resources[J].Coal Science and Technology,2018,46(9):4-11.
[2] 彭 亚,蒋仲安,付恩琦,等.综采工作面煤层注水防尘优化及效果研究[J].煤炭科学技术,2018,46(1):224-230.
PENG Ya,JIANG Zhongan,FU Enqi,et al.Study on seam water injection and dust control optimization and effect of fully-mechanized coal mining face[J].Coal Science and Technology,2018,46(1):224-230.
[3] 王晓珍.煤巷掘进过程中粉尘浓度影响因素分析[J].中国安全生产科学技术,2011,7(4):75-79.
WANG Xiaozhen.Anlysis of dust concentration influence factor in coal roadway driving[J].Journal of Safety Science and Technology,2011,7(4):75-79.
[4] 韩 硕,蒋仲安,彭 亚.基于免疫算法的矿井防尘供水管网优化[J].煤炭技术,2017,36(11):183-186.
HAN Shuo,JIANG Zhongan,PENG Ya.Mine water supply pipe network optimization based on immune algorithm[J].Coal Technology,2017,36(11):183-186.
[5] 郭建伟,陈 晶,刘小满,等.基于生产用水途径的矿井水井下处理系统配置[J].煤炭科学技术,2018,46(S1):239-243.
GUO Jianwei,CHEN Jing,LIU Xiaoman,et al.Mine water treatment system configuration based on production water use way[J].Coal Science and Technology,2018,46(S1):239-243.
[6] 高金良,姚 芳,叶 健.考虑漏失和用户用水的供水管网PDD模型构建及应用[J].哈尔滨工业大学学报,2017,49(2):49-53.
GAO Jinliang,YAO Fang,YE Jian.Construction and application of PDD model considering leakage and water-users in water supply network[J].Journal of Harbin Institute of Technology,2017,49(2):49-53.
[7] 班福忱,黑月明,吴 丹.基于EPANET和ArcObjects的在线水力模型系统开发[J].中国给水排水,2018,34(3):57-60.
BAN Fuchen,HEI Yueming,WU Dan.Online hydraulic model system based on EPANET and ArcObjects[J].China Water & Wastewater,2018,34(3):57-60.
[8] 徐先伯,白 丹,党志良,等.城市给水管网物理仿真模型研究[J].给水排水,2017,53(S1):291-294.
XU Xianbo,BAI Dan,DANG Zhiliang,et al.Study on physical simulation model of urban water supply network[J].Water & Wastewater Engineering,2017,53(S1):291-294.
[9] 张新波,贾 辉,王 捷,等.基于城市供水管网变态物理模型的管网试验研究[J].天津工业大学学报,2013,32(3):61-65.
ZHANG Xinbo,JIA Hui,WANG Jie,et al.Simulation tests of municipal water distribution system based on distorted physical model[J].Journal of Tianjin Polytechnic University,2013,32(3):61-65.
[10] 何忠华,袁一星.城市供水管网的试验模型研究[J].中国给水排水,2013,29(15):154-158.
HE Zhonghua,YUAN Yixing.Research on experimental model of water distribution system[J].China Water & Wastewater,2013,29(15):154-158.
[11] 郭维东,韩会玲,裴国霞.水力学[M].北京:中国水利水电出版社,2005.
[12] VENKATA RAMANA G,SUDHEER CHEKKA VSS.Validation and examination of existing water distribution network for continuous supply of water using EPANET[J].Water Resources Management,2018,32(6):1993-2011.
