0 引 言
目前对于全岩巷道的掘进大多还是以钻爆的方式进行,并且我国含有夹矸的较硬煤岩保有量较大,因此提高截割刀具破碎煤岩的效率及性能尤为重要,国内外专家学者对破碎煤岩进行了大量研究,并取得了一定的研究成果。HURT等 [1]通过研究给出了截齿破碎较硬煤岩时的主要失效问题。OKAN等[2]通过对截齿破碎煤岩的数值模拟并分析得出的截割载荷特性,结果表明,离散单元法能较好地用于煤岩截割仿真分析。MOSTAFAVI等[3]通过研究截齿截割煤岩3种不同作用位置的截割效率和规律,得出截齿正面与煤岩成零度角时效果最好。李勇等[4-5]基于高应力研究了镐型截齿的破碎煤岩规律,发现了提高破碎效率和降低磨损量的方法。刘春生等[6-11]利用分形、熵等理论对单齿及多齿载荷谱进行分析,给出了截齿各项参数对煤岩的破碎影响规律,并基于ABAQUS对碟盘刀具进行了大量数值模拟,为破碎机构及刀具的发展奠定了理论依据及数值基础。柴博等[12]利用有限元进行了截割头截割煤岩的模拟,结果表明:有限元能可靠精确地计算截割载荷,提供为不同地质的煤岩选择合适的截割头提供了依据。关立坤等[13]采用ABAQUS有限元动态仿真端盘截齿截割煤岩,得出截割阻力随着轴向倾斜角和二次旋转角的增大而增加,牵引阻力和侧向阻力变化平稳。李晨等[14]应用有限元分析方法模拟了锚杆的受力特性与试验有较好的吻合度。孙荣军等[15]利用数值模拟的方法对PDC破碎煤岩的比能进行研究,得出最佳表面形状。梁运培等[16]在不同煤岩厚度和变截线距的工况下进行了镐齿破碎煤岩的试验,并采用回归分析的方法得到了力学参数与截割厚度和截线距之间的关系。祝效华等[17]利用ABAQUS建立了钻齿破岩动力学有限元模型,得出有利于提高破岩效率的最佳载荷比。以上学者在煤岩破碎方面的数值模拟及试验做了大量研究,笔者借鉴众学者的研究经验和对破碎煤岩的研究结果,基于ABAQUS有限元软件进行碟盘刀具破碎煤岩的数值模拟,以煤岩的切削厚度为变量,分析碟盘刀具在有无轴向振动条件下破碎煤岩的载荷变化趋势,并利用分形特征参数间接描述煤岩的粉碎量特征,相对反映煤岩的破碎块度,为实际工程的应用及采掘机械的设计研发奠定基础。
1 碟盘刀具破碎煤岩数值模型及参数
为分析碟盘刀具切削煤岩的破碎效果,利用ABAQUS有限元软件建立碟盘刀具及切削煤岩有限元模型(图1),碟盘边缘均布100个头部近似球形的齿形刀如图1a所示。碟盘结构尺寸为:直径R=150 mm,刀头齿尖圆弧r=3 mm,碟盘楔面角度α=45°,设置碟盘属性为刚体;煤岩体三维模型尺寸为:长420 mm、宽280 mm、高120 mm,煤岩体设置为Drucker-Prager塑性本构模型,设置煤岩体材料属性为:强快模量E=1 400 MPa,泊松比μ=0.3[7]。在ABAQUS仿真中碟盘的运动形式主要由2个部分组成,分别是:在图中X轴方向设置径向速度vj,沿Y轴方向设置振动频率f和幅值A。
对刀具和煤岩体都采用六面体C3D8R的单元网格类型,为提高计算精度和减少仿真计算时间,把煤岩与刀具接触的部分进行区域加密划分,其他部分疏松化,使得煤岩体单元节点数达到358 488个,而被切削部分网格数达到30万个左右,如图1b所示。

图1 碟盘刀具破碎煤岩数值模型
Fig.1 Numerical model of broken coal and rock with disc cutter
2 碟盘刀具破碎煤岩数值模拟
为分析碟盘刀具对破碎煤岩载荷的影响,将从无振动和有振动2个方面进行碟盘刀具破碎煤岩的数值模拟,使刀具的径向速度恒等于300 mm/s及相同煤岩参数条件下,在切削厚度h=14~30 mm、间隔4 mm进行碟盘刀具破碎煤岩仿真。
2.1 碟盘刀具径向破碎煤岩数值模拟
2.1.1 径向切削煤岩载荷
在给定仿真条件下,碟盘楔面角度为45°,设置碟盘频率、幅值及轴向速度为0,因此碟盘刀具仅有径向切削运动,得出的仿真载荷谱如图2所示。

图2 切削作用载荷谱
Fig.2 Cutting action load spectrum
从图2可看出,在仿真过程中不施加轴向振动的条件下,碟盘刀具仅有径向单作用破碎煤岩时,径向、轴向及径向与轴向的矢量叠加的载荷呈现出大小交替变化的锯齿状波动,并且载荷变化呈先剧烈上升随后趋于稳定的变化形式。从图2可看出,随着切削厚度的增加,径向、轴向及径向与轴向矢量叠加载荷呈现出逐渐增大的趋势,在没有施加轴向振动的情况下,轴向载荷只在刚开始接触煤岩时有负值,此时刀具切削煤岩所受合力向上,因此为负值,当随着刀具径向位移的增大,碟盘楔面与煤岩的接触面积逐渐增大,导致刀具承受轴向向下的力逐渐增大,而刀具齿尖所受的力基本保持不变,因此所受合力方向向下,此时轴向载荷变为正值。随着切削厚度的增加三向载荷都具有逐渐增加的趋势,与切削厚度成正相关,并且切削厚度越大刀具切削载荷所达到稳定值的时间越长。
2.1.2 径向切削煤岩的应力云图
楔面角度45°的碟盘刀具在不同切削厚度,单作用径向切削煤岩时在XY平面内的应力分布云图如图3所示。从图3可看出,煤岩体在XY平面内Mises应力主要集中在刀具的楔面部分和齿尖处,当切削厚度较小时刀具齿尖的应力作用范围与刀具楔面应力作用范围相近,随着切削厚度的增加刀具齿尖对煤岩的应力影响范围缓慢增加,而刀具楔面的应力影响范围增加趋势明显,由此看出刀具齿尖主要作用是帮助使刀具更加有利于楔入煤岩,而刀具的楔面对煤岩起主要破坏作用,刀具破碎煤岩的应力变化趋势与刀具破碎煤岩的载荷变化趋势相互对应。

图3 径向切削Mises应力分布
Fig.3 Radial cutting Mises stress distribution
2.2 碟盘刀具振动与切削复合破碎煤岩
2.2.1 振动切削煤岩载荷
在给定的仿真条件下,进行碟盘刀具破碎煤岩的仿真试验时施加轴向振动,频率为50 Hz,振动幅值为1 mm,所得的刀具在复合作用下破碎煤岩的载荷谱如图4所示。

图4 振动切削复合破碎煤岩载荷谱
Fig.4 Vibration cutting composite broken coal and rock load spectrum
从图4可看出,当对碟盘刀具施加正弦函数周期性振动时,其径向、轴向及径向与轴向的叠加载荷谱也呈现出周期性波动变化。
从图4a可看出,在同一楔面角度下,随碟盘刀具切削煤岩厚度的增加,径向载荷有逐渐变大的趋势,而刀具齿尖对煤岩的作用力不随切削厚度改变而变化,对不同切削厚度的径向载荷谱与刀具的运动轨迹对应分析可知,当切削厚度为14、18 mm时,径向载荷谱的波峰极值出现在刀具轴向振动位移的最低点与0点之间,当切削厚度大于18 mm时,径向载荷的波峰极值出现在刀具轴向位移的最高点附近。从图4b可看出,轴向载荷随切削厚度的增大呈逐渐增加趋势,并且在0.02 s时刀具轴向载荷的下峰值不随切削厚度的改变而变化,因为此时刀具齿尖最先与煤岩接触,当刀具运动时间逐渐增加,刀具楔面逐渐起主导作用时,轴向载荷下峰值逐渐由负值转为正值。从图4c可看出,径向与轴向的矢量叠加载荷随切削厚度的增加呈逐渐增加的趋势,结合图中运动轨迹可知,当刀具运动至轴向位移曲线最高点附近时载荷达到上波峰极值。
2.2.2 振动切削煤岩应力云图
碟盘刀具在不同切削厚度下,轴向振动与径向复合破碎煤岩时在XY平面内的应力分布云图如图5所示,此时刻的云图选自与刀具单作用切削煤岩时同一时刻的云图。从图中可看出随着切削厚度的增加刀具齿尖与刀具楔面对煤岩的作用力都呈增加的趋势,与刀具单作用切削煤岩的应力分布具有相同的规律,但刀具在轴向振动与径向切削煤岩时,刀具的楔面对煤岩的应力影响范围比单作用径向切削煤岩应力影响范围要大。

图5 振动切削Mises应力分布
Fig.5 Vibration cutting Mises stress distribution
3 试验结果分析
3.1 载荷特征值
将碟盘刀具在切削厚度为14~30 mm,进行有无振动破碎煤岩的数值模拟结果进行分析,对得出的载荷峰值进行统计时,由于切削不同厚度的煤岩,碟盘刀具所起作用的时间是不同的,所以统计轴向载荷上峰值时,按所达到刀具起作用的时间后的载荷值进行统计。有无振动条件下仿真载荷见表1,其中Fb、Fd分别表示碟盘刀具无振动与有振动条件下破碎煤岩的载荷下标j、z和H分别表示径向、轴向及径向与轴向的矢量叠加方向,下标M、p分别表示载荷的极大值及上峰值的均值。
表1 不同切削厚度仿真载荷极值及上峰值均值
Table 1 Simulation load extremum and upper peak value of different cutting thickness

h/mm径向/kNFbjMFbjpFdjMFdjp轴向/kNFbzMFbzpFdzMFdzp径向与轴向的矢量叠加/kNFbHMFbHpFdHMFdHp1432.130.629.727.615.414.420.719.535.434.333.532.41840.838.034.834.126.424.232.229.848.544.245.943.82245.044.044.542.136.032.946.244.257.155.062.858.72654.953.252.449.546.445.555.955.371.769.675.369.83063.661.364.256.956.555.071.671.584.981.696.082.2
由表1可知,无振动条件下碟盘刀具破碎煤岩的径向载荷的峰值极大值与上峰值均值比有振动条件下的分别大6.2%和8.4%,而其轴向载荷的峰值极大值与上峰值均值比有振动条件下的分别小17.1%和22.3%,当切削厚度为14和18 mm时,无振动条件下所得的径向与轴向的矢量叠加载荷的峰值极大值与其均值比有振动条件下的大,当切削厚度为22~30 mm时无振动条件下所得的径向与轴向的矢量叠加载荷的峰值极大值与其均值比有振动条件下的小。
根据表1绘制出不同切削厚度下无振动与有振动载荷的峰值极大值与上峰值均值拟合曲线,如图6所示。
从图6可看出,碟盘刀具在有无振动的条件下破碎煤岩的径向、轴向及径向与轴向的矢量叠加载荷的上峰值极大值与其均值,随切削厚度的增加具有线性增加的趋势。从图6a可看出,无振动条件下径向载荷的峰值极大值与有振动的随切削厚度的增加逐渐接近,而2种条件下峰值的均值差基本保持不变。从图6b可看出,随切削厚度的增加,2种条件下轴向载荷的上峰值极大值及其均值的差有变大趋势。从图6c可看出,在14~18 mm之间无振动条件下所统计的径向与轴向的矢量叠加载荷上峰值极大值与其均值比有振动的大,当切削厚度大于18 mm时,无振动条件下所统计的径向与轴向的矢量叠加载荷上峰值极大值与其均值比有振动的小。
3.2 载荷曲线粉碎量分形特征
载荷谱不仅反映煤岩破碎过程中产生载荷的大小,而且结合分形理论对载荷曲线进行分析,也能反映煤岩破碎过程中粉尘量的多少,其与横坐标时间轴所围成的面积代表着刀具破碎煤岩过程中所消耗的能量[17-19],分形面积可用式(1)计算:

图6 数值模拟载荷峰值极大值及均值拟合曲线
Fig.6 Numerical simulation of load peak maximum value and mean fitting curves
S(ε)=![]() NLε2dt
NLε2dt
(1)
式中:NL为分形盒子数;ε为盒子边长
为有效描述轴向振动对碟盘刀具破碎煤岩时粉碎程度特征的影响,利用分形特征参数间接描述煤岩粉碎量,给出煤岩块度的相对特征,利用MANDELBROT B[20]提出的闭合曲线周长与其围成面积的关系式进行描述,见式(2)。
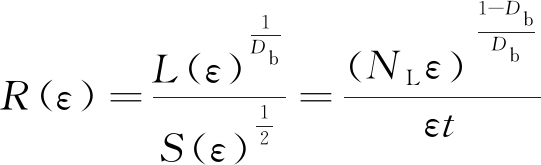
(2)
式中:R(ε)为比例系数;L(ε)为曲线分形长度,L(ε)=NLε;Db为盒维数。
文献[18]中指出,比例系数R(ε)可作为评价载荷谱轮廓特征以及截割煤岩过程产生小块分离和煤岩粉碎量等的指标,当R(ε)越大时,在煤岩破碎过程中粉碎量越大,当R(ε)越小时,在煤岩破碎过程中粉碎量越小。对文中碟盘刀具载荷曲线进行封闭处理,则式(2)可写成:
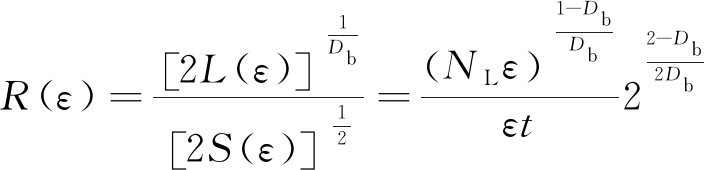
(3)
根据式(3)对有无轴向振动条件下碟盘刀具在楔面角度为45°、切削厚度14~30 mm下的载荷曲线进行比例系数R(ε)计算及大小对比。其2种条件下的结果见表2。
表2 不同切削厚度径向载荷分形比例系数
Table 2 Fractal proportional coefficient of radial load with different cutting thickness

切削厚度/mm振动切削比例系数切削比例系数1418222630513.5306.2157.4110.880.1630.3512.9132.0148.496.5
从表2可看出,随着切削厚度的增加碟盘刀具在有无轴向振动的条件下,径向载荷谱的比例系数均呈现出减小的趋势,说明适当地增加刀具破碎煤岩厚度,有利于减少其粉碎量,增加煤岩的破碎块度,并且从表2数据可知,改变刀具破碎煤岩的厚度时,不施加轴向振动的径向载荷比例系数比有振动的大20.5%~67.5%,由此可知,在同一楔面角度下,碟盘刀具有轴向振动的破碎方式相比无振动,更有利于大块煤岩的剥落,且产生较少的煤岩粉碎量,减少无用功。
4 结 论
1)碟盘刀具在有无振动条件下的数值模拟可知,随切削厚度的增加,径向、轴向及径向与轴向的矢量叠加载荷都具有逐渐增加的趋势,且刀具破碎煤岩的Mises应力云图的影响范围也呈现出逐渐增加的趋势。
2)切削厚度改变时,无振动条件下碟盘刀具切削煤岩的径向载荷的峰值极大值与上峰值均值比有振动条件下的分别大6.2%和8.4%。
3)对有无轴向振动条件下刀具破碎煤岩得出的径向载荷谱计算分形比例系数可知,碟盘刀具在径向切削煤岩时比例系数比振动切削破碎煤岩的分别大20.5%~67.5%,由此可知有轴向振动破碎煤岩时有利于大块崩落,比无轴向振动的情况所产生的煤岩粉碎量少,减少无用功。
4)通过以上对碟盘刀具振动对切削厚度的影响可知,振动切削的工作方式更加有利于煤岩的破碎以及增加煤岩的块度,减少切削过程中产生的粉尘,本研究可为实际工程应用,解决实际问题提供参考。
[1] HURT K G, MACANDREW K M.Cutting efficiency and life of rock-cutting picks[J].Mining Science and Technology,1985(2):139-151.
[2] OKAN S U, NUR Iali Akcin.Numerical simulation of rock cutting using the discrete element method[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(3):434-442.
[3] MOSTAFAVI,SEYED SALEH,YAO Qingyu, et al.The effect of pick orientation on rock fragmentation[C].12th International Congress on Rock Mechanics of the International Society for Rock Mechanics.Beijing,2012:1753-1756.
[4] 李 勇.高应力硬岩镐形截齿截割破岩研究[D].长沙:中南大学,2012.
[5] 李 勇,李夕兵.镐形截齿硬岩截割磨损研究[J].矿业研究与开发,2012,32(6):85-88.
LI Yong,LI Xibing.Wear analysis on pick-shaped cutter in cutting hard rock[J].Mining Research and Development,2012,32(6):85-88.
[6] 刘春生,王庆华,李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(11):2623-2628.
LIU Chunsheng,WANG Qinghua,LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spec-trum[J].Journal of China Coal Society,2015,40(11):2623-2628.
[7] 刘春生,徐玉芸,李德根,等.碟盘刀齿冲击与切削复合破碎煤岩的载荷特性[J].黑龙江科技大学学报,2017,27(2):97-103.
LIU Chunsheng,XU Yuyun,LI Degen,et al.Numerical simulation of mechanical properties of disc cutter tooth vibration and coal-rock compound cutting[J].Heilongjiang University of Science & Technology,2017,27(2):97-103.
[8] 刘春生,袁 昊,李德根,等.载荷谱细观特征量与截割性能评价的熵模型[J].煤炭学报,2017,42(9):2468-2474.
LIU Chunsheng,YUAN Hao,LI Degen,et al.Meso-feature of load spectrum and entropy model for cutting performance evaluation[J].Journal of China Coal Society,2017,42(9):2468-2474.
[9] 刘春生,袁 昊,张艳军,等.不同楔面角度碟盘刀具切削煤岩的载荷与小波能量熵[J].黑龙江科技大学学报,2018,28 (5):543-551.
LIU Chunsheng,YUAN Hao,ZHAG Yanjun,et al.Cutting load of coal-rock and wavelet energy entropy of disc cutters with different wedge angles[J].Journal of Heilongjiang University of Science and Technology,2018,28(5):543-551.
[10] 刘春生,徐玉芸,袁 昊,等.碟盘刀具振动与切削破碎煤岩力学特性的数值模拟[J].黑龙江科技大学学报,2018,28(1):36-42.
LIU Chunsheng,XU Yuyun,YUAN Hao,et al.Numerical simulation of mechanical properties of disk cutter vibration and cutting and crushing coal[J].Journal of Heilongjiang University of Science and Technology,2018,28(1):36-42.
[11] 刘春生,徐玉芸,李德根,等.边缘牙齿形碟盘破碎煤岩的力学机理及其模型[J].煤炭学报,2018,43(1):272-279.
LIU Chunsheng,XU Yuyun,LI Degen,et al.Mechanical mechanism and model of fractured coal rock in edge-shaped disc-shaped disc[J].Journal of China Coal Society,2018,43(1):272-279.
[12] 柴 博,李建辉.不同性质煤岩下掘进机截割载荷研究[J].辽宁工程技术大学学报:自然科学版,2017,36(2):170-175.
CHAI Bo,LI Jianhui.Study on roadheader cutting load at different properties of coal and rock [J].Journal of Liaoning Technical University:Natural Science Edition,2017,36(2):170-175.
[13] 关立坤,杨 涛,任学平.采煤机滚筒端盘截齿角对截割载荷特性的影响[J].煤矿开采,2018,23(2):15-17.
GUAN Likun,YANG Tao,REN Xueping.Influence of shearer drum crown wheel cutting pick angle to cutting loading characteristic[J].Coal Mining Technology,2018,23 (2):15-17.
[14] 李 晨,何满潮,宫伟力.不同冲击速率下恒阻大变形锚杆动力学特性分析[J].煤炭科学技术,2015,43(9):53-58.
LI Chen,HE Manchao,GONG Weili.Analysis on kinetic features of constant resistance high deformed bolt under different impact velocity[J].Coal Science and Technology,2015,43 (9):53-58.
[15] 孙荣军,谷拴成,石智军,等.硬岩钻进用仿生PDC切削齿优化与破岩机理研究[J].煤炭科学技术,2018,46(5):143-148,165.
SUN Rongjun,GU Shuancheng,SHI Zhijun,et al.Study on optimized bionic PDC cutter applied to hard rock drilling and rock cutting mechanism[J].Coal Science and Technology, 2018,46(5):143-148,165.
[16] 梁运培,王 想,王清峰.截割厚度与截线距对镐型截齿破岩力学参数的影响[J].振动与冲击,2018,37(3):27-33.
LIANG Yunpei,WANG Xiang,WANG Qingfeng.Effects of cut depth and cut spacing on tool forces acting on a conical pick in rock cutting[J].Journal of Vibration and Shock,2018,37 (3):27-33.
[17] 祝效华,郭光亮.动静载荷比对钻齿破岩效率的影响研究[J].振动与冲击,2019,38(1):22-28.
ZHU Xiaohua,GUO Guangliang.Study on the influence of dynamic and static load ratio on rock breaking efficiency of drilling teeth[J].Journal of Vibration and Shock,2019,38(1):22-28
[18] 刘春生.采煤机截齿截割阻力曲线分形特征研究[J].煤炭学报,2004,29(1):115-118.
LIU Chunsheng.Fractal characteristic study of shearer cutter cutting resistance curves[J].Journal of China Coal Society, 2004,29 (1):115-118.
[19] FALCONER K.分形几何—数学基础及其应用[M].曾文曲,刘世耀,译.沈阳:东北大学出版社,1996.
[20] MANDELBROT B.分形对象:形、机遇和维数[M].文志英,译.北京:世界图书出版社,1999.
