0 引 言
超宽带(UWB)信号具有较强的穿透能力、分辨率、目标识别力、多径分辨能力以及探测盲区较小等独特优点，因此非常适合应用于矿井下的探测成像系统[1-2]。王艳芬等[3]对超宽带(UWB)在矿井下通信进行研究，提出选取一阶高斯脉冲波形作为井下的UWB通信的发射信号。煤矿井下较地面来说，环境条件往往受到众多因素的影响，巷道内介质的组分复杂特性多变，在井下形成一个相对限定的封闭空间。因此，入射信号的传播受到岩壁的限制，多径衰落严重，传输衰减较大。然而已有的地面上的成像系统性能研究成果对这些特点的考虑有限，许多成熟的成像算法并不能有效地对矿井下的超宽带(UWB)探测成像系统性能进行研究分析。因此，深入研究超宽带(UWB)信号在矿井下的穿透特性，构建实用的成像算法，对设计出适合于煤矿井下的救援系统具有重要意义。
2002年美国联邦通信委员会(The Federal Communications Commission，FCC)针对超宽带作如下定义[4]：分数带宽(Fractional Bandwidth，FBW)大于20%或者在-10 dB处的带宽大于500 MHz的信号均为UWB信号。文献[5]指出在信号采集准则即奈奎斯特采样定理前提下，由于UWB雷达存在带宽过大和频率过高的特性，且受到雷达测不准原理的限制，前端采样系统和后端图像存储系统面临较大压力。为了解决此技术性问题，相关领域专家开始对压缩感知理论[6]进行研究。
压缩感(Compressed Sampling，CS)[7-9]理论最早是在1977年由国外专家Kashin提出。压缩感知理论主要是在数据信息获取技术上的一种理论，通过信号区域的某个稀疏性条件，可以实现打破传统Nyquist信号采样原则，通过采集较少的数据信息就可以实现对原始信号的重构[10]。同时，该理论在软件方面也容易实现，编程简单，只需通过计算较少数据信号的非相干投影，就可以重构得到原始较大回波信号[11]。由于只需要通过后台处理采集较少的数据信号，因此可以大幅降低成像采集系统前端传感器的压力[12]。基于CS理论的信号处理技术对于宽带、超宽带信号而言，是增强成像系统分辨力的一种有效技术。因此，笔者提出将压缩感知理论与井下超宽带雷达探测成像系统相结合，建立适用于煤矿井下的UWB雷达成像算法。
1 井下超宽带成像与压缩感知应用
1.1 井下超宽带超宽带成像工作原理
超宽带雷达在矿井下探测成像的原理如图1所示，与传统地面上雷达成像系统相似，发射机发射UWB信号穿透塌方体，入射信号在进入塌方体内部后遇到各种不同参数的障碍物(如沙土、岩石、空气等)，而这些介质将会对超宽带信号的正常传播产生干扰，导致入射信号的电磁阻抗发生变化，进而引起入射电磁波发生反射、散射等物理效应，超宽带回波信号经历塌方体的阻碍后将电磁波再次反射到雷达系统的接收机部分，接收天线将按照某个设定好的间隔数进行方位向移动，采集回波信号信息，最后对天线采样的总回波信号进行相关数据处理：目标信号与杂波信号的分离以及目标的成像算法选取等。在井下探测过程中，产生采样时间长，处理数据量大的问题。
图1 矿井下超宽带雷达探测成像原理
Fig.1 Imaging principle of UWB radar detection under mine
由雷达成像原理可知，要实现二维平面上的目标定位成像，天线阵列数最低不能少于2个组。井下多采用图2所示的共享式多发多收天线MIMO结构，其中ε0为天线所在空间的介质参数，εrε0为塌方体介质混合参数，收发天线携带UWB信号穿透塌方体障碍物进入到目标体所在空间内，对其进行信息采集，由于其增强信号的收发能力，可更好地实现塌方体下目标的三维成像。
图2 UWB井下三维成像天线阵列
Fig.2 3D Imaging antenna array of UWB underground mine
集中式MIMO雷达由于采用较为紧凑的阵元空间分布，导致目标的多通道空间采样之间呈现部分相关性，从而限制了系统空间分辨率准确度，影响成像结果。矿井下目标探测成像[14]属于半空间的电磁散射问题，因此需要采用FDTD理论进行全波电磁仿真，天线阵列采样平面位于吸收边界、总场以及散射场边界之中，直接对目标的散射场进行采样。
1.2 压缩感知成像
井下UWB雷达二维成像模型[15]如图3所示。
图3 井下UWB雷达二维成像模型
Fig.3 2D Imaging model of UWB radar underground
在该模型中，分别形成了天线阵列和成像区域2个不同的区域，从图3可以看出，成像区域在网格化后被划分为K×L个均匀的小的网格，在稀疏性标准下，要求每个成像目标回波的网格对应一个像素点。假设成像过程中的采样数量为M，f0～fN-1为采样周期内的频率变换范围，成像区域的目标点数量为p，发射天线的扫描频点合计为N个，因此，对UWB回波信号在m=1、2、…、M不同位置处进行连续采样，接收天线得到的回波信号Sm见式(1)。
(1)
式中：ρp为第p个点目标的反射系数；fn为采样频率；τp，m为UWB信号与第p个点目标在第m个天线采样处的双程传输时延。
假设井下成像区域的二维反射率分布为r(K, L)，为了利用压缩感知理论求解出该分布值，需要构建成像背景稀疏化的参数模型，因此通过列堆叠将r(K, L)转换成一个KL×1维的向量，记为wx。如图4所示。
图4 网格划分示意
Fig.4 Sketch of mesh generation
第m个采样点接收的回波信号可以表示为一个基矩阵Bm和反射系数向量wx相乘的形式，如下：
Sm=Bmwx
(2)
其中：Sm为回波信号的频域值，且Sm=[s0(f0),…,sm(fN-1)]T ， 因此，当天线阵元的工作频率为fn 时，采样位置m处的回波信号可由Sm(fn)表示。N×KL基矩阵Bm的第j列向量为
[Bm]f=[ej2πf0τm,j,…,ej2πfN-1τm,j]T
(3)
其中：τm,j为第j个网格目标在第m个收发天线采样处产生的双程时延。假设井下UWB成像系统分别对M个不同位置回波信号进行采集，则用一个NM×1维的列向量可以代表总采样的回波数据，即
同时，总回波矩阵对应的基矩阵可表示为
因此，通过总回波信号的基矩阵Bx与目标反射系数向量wx相乘，即得到接收天线采样的总回波数据Sx为
Sx=Bxwx
(4)
对于井下环境来说，其回波信号的反射系数向量wx满足CS理论对信号的稀疏性要求。在此前提下，为构建一个合适的测量矩阵，其实现方式首先是从总回波信号数据M中任意选取Q1个回波数据，再从Q1个回波数据中任意选取Q2个回波数据，经过2轮对回波数据的随机挑选，形成了Q1Q2×NM的测量矩阵Ψc，且Q1Q2≪NM，最后将该测量矩阵Ψc与回波总数据Sx进行投影运算，即式(5)：
tx=ΨcSx=ΨcBxwx=Φxwx
(5)
式中:tx为稀疏回波数据的投影运算值；Φx=ΨcBx为一个大小为Q1Q2×KL的投影矩阵。
2 压缩感知相位补偿算法
2.1 目标二维像重构
为了满足井下安全生产的要求，采用脉冲超宽带信号作为井下雷达成像的发射信号，表示如下：
(6)
式中：
为脉冲宽度；γ为调频斜率；fc为载波中心频率；t为回波时延。
对于散射点P(x,y)，经CS技术对脉冲回波信号进行压缩处理后，其第m个脉冲的回波数据由下式计算可得：
(7)
其中：βmn为第m个脉冲采集的回波数据经过压缩处理后的值；ex(j2πmn/M)为由散射点在巷道壁反射产生的回波分量；exp[jφt(m)]为由目标体平动产生的平动多普勒分量，exp(jφe)为由观测误差导致的相位误差。通常exp[jφt(m)]和exp(jφe)都是未知的，是影响方位向聚焦的主要原因，需要对这部分相位分量进行补偿。因此，UWB雷达目标成像可以表述为求解优化如下联合代价函数的过程。
T(P,Θ)=λ‖Y-ΦΘψP‖2+β‖P‖1+ηE(P)
(8)
其中：P为目标成像结果的二维矩阵，λ、 β为正则化参数，分别用来指定在重构代价函数中重构误差‖Y-ΦΘΨP‖2与二维像l0范数的贡献值，作用于回波矩阵中的每一列；Y为稀疏回波矩阵；Φ为随机观测矩阵，由随机序列回拨决定；对角矩阵Θ为每个回波的相位误差；‖P‖1为重构目标的稀疏性分量；E(P)为对图像质量的评估，如图像熵和图像对比度的倒数，采用图像熵[17]作为评估办法，则稀疏成像的重构过程可以改写为如下优化问题：
P=arg minP{T(P,Θ)} s.t. Y=ΦΘΨP
(9)
基于当前相位误差的估计值对稀疏回波进行相位补偿后，重构方位向图像的公式为
(10)
式中，测量矩阵 M1=ΦΘIΨ。
2.2 相位误差估计
针对基于CS的原始回波数据重构算法中，存在的方位向误差问题，提出将此相位误差问题等价为图像最优化问题，即相位补偿的过程是通过图像熵算法进行优化的过程，由相关文献可以推导出图像熵[18]的计算式为
(11)
式中，D(m, n) 为目标成像散射点的散射密度，即
(12)
式中，
为图像的总能量。
为了提高成像时的聚焦效果，则必须降低回波信号能量集中的图像熵值。在这里用Y(m)表示第m次回波信号中矩阵大小，θ(m)为该回波信号的初相误差，则对回波的相位补偿转换为图像熵最小化计算，由下式可得：
Y′(m)=Y(m)exp[-jθ(m)]
(13)
基于式(13)，参考最小熵相位补偿方法的推导过程，可以通过下式的计算，得到最小化目标信号图像熵的相位误差为
(14)
其中，ω*(m)为ω(m)的伴随矩阵。由：
(15)
其中：k、q为图像熵算法中的选代参数。P*(n,q)为P(n,q)重构相位回波分量的伴随矩阵。上述计算过程完成了算法中对当前相位误差的估计，再将计算所得的当前误差估计结果代入下一次迭代运算，将此迭代过程反复更新计算，直到计算所得误差结果符合迭代终止条件，迭代过程即可终止，进而实现补偿作用。因此，基于相位补偿的压缩感知相位自聚焦算法流程如下，已知稀疏回波矩阵Y，稀疏字典矩阵Ψ。
1)设置初始迭代次数l=1，初始相位误差向量θ1，根据随机回波序列构造随机观测矩阵Φ，设定迭代终止门限δT。
2)利用当前相位误差补偿更新测量矩阵M1=ΦΘΨ，其中Θ1=diag[exp(-jθ1)]，θ1为初始相位误差向量，取0，并利用压缩感知方法求解，见式(16)，重构得到目标的二维像Pl+1。
(16)
式中：‖*‖2为重构目标回波的误差分量，‖*‖1为重构目标回波的稀疏性分量。
3)如果l>1，计算与上一次迭代得到二维像结果的相对误差为
δ=‖Pl+1-Pl
/‖Pl
(17)
如果小于迭代终止门限，即满足δ≤δT，则迭代停止，否则继续。
4)求
更新相位误差向量。
5)令l=l+1，并返回第2步。
通过表1的算法流程可知，基于CS算法的回波数据补偿是将相位误差和目标信号重构过程结合在一起，在反复的迭代计算中，基于当前相位误差对重构图像进行更新，直至满足成像回波数据的要求。
3 仿真试验与分析
3.1 算法性能分析
在以下仿真场景中，假定收发天线为一对平行于x轴的理想线源天线，二者均距地面0.02 m,采用GprMax软件进行仿真合成井下成像模型散射数据，再利用Matlab处理散射数据获取成像图形，雷达仿真参数如下：载频14 GHz，脉宽50 μs，采样频率600 MHz，幅度1.0 A，脉冲重复频率700 Hz。
1)场景一：试验场景一如图5a所示，井下成像区域为{x,y}=(2.5 m，5.0 m)，假设成像区域中有一圆柱体目标，其圆心坐标为(1.25 m,2.25 m)，半径为0.55 m。图5b为原始成像图，图5c、图5d为经过算法处理后的成像效果图，对比2个成像结果可以看出，未经处理的原始算法成像中出现了严重的散焦，同时由于复杂背景介质的影响带来了虚假像；而经过相位补偿的数据处理后，算法基本抑制了多成分介质的影响，定位准确且目标像聚焦程度高，因此本文算法成像性能要优于原始算法。
图5 场景一及其仿真结果
Fig.5 Scenario 1 and simulation results
2)场景二：试验场景二如图6a所示，成像区域参数同场景一。图中长方体目标左下角坐标为(0.55 m，1.05 m)，右上角坐标为(1.06 m，3.65 m)，圆柱形目标体的中心位置位于(1.75 m，2.5 m)，半径0.05 m。图6b为原始成像图，图6c、图6d为组合目标体在2种不同成像算法下的结果。从图可知，原始成像算法下目标2与目标1真实像被其他背景介质的虚像掩盖且二者的多径虚像发生重叠。而在本文算法处理后的成像中，抑制了多径现象带来的虚像，很好地重构了2个目标体的真实像。
图6 场景二及其仿真结果
Fig.6 Scenario 2 and simulation results
3.2 噪声分析
基于场景2的模型参数，对加入不同程度的高斯白噪声成像效果进行数值模拟。经过本文所构架的算法处理结果如图7所示。图7a为没有噪声的情况下，经相位补偿CS重构的探测区域灰度图像和回波信号数据恢复情况。图7b、图7c对应分别为加入10%、50%高斯白噪声后的探测区域灰度图像及数据恢复情况。成像结果表明：在无噪声的成像背景下，测量误差很小，本文算法基本能准确重建目标的物理信息；在加入10%、50%噪声干扰后，算法的有效性仍然存在，只不过加大了计算的复杂度及时长，且无法保证实时性，导致最后的成像性能变差。
在实际应用中，由于在矿井下发生塌方事故后，所有电气设备均处于停电状态，井下噪声干扰基本不存在，因此本文算法在井下实际救援应用中具有可行性。
3.3 数值分析
为定量评价重建图像质量，将本文算法与现有的压缩感知重构算法[19]，如OMP、平滑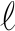
0范数(Smooth 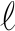0, SL0) 和贝叶斯压缩感知算法进行比较。笔者采用图像相对误差RE和相关系数CC作为成像质量的评价指标[22]，其表达式为
(18)
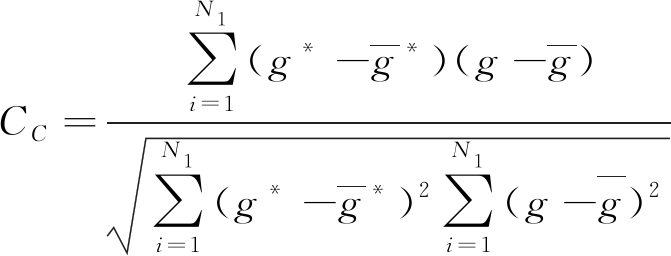
(19)
其中：g、g*分别为重建介电常数分布及真实介电常数分布；
分别为g、g*的均值；N1为图像像素数量，取812个。
分别选取天线阵列数为15、45个，采用第3.1节及第3.2节3个不同场景进行预测，获取采样数为115个，从表3—表6可以看出，基于相位补偿CS算法的图像重建质量并没有因为天线阵列数的增加而显著提高，相反，对于较为复杂目标场景，如场景2、3，重建图像的相对误差有所增大、相关系数有所减小，即出现了重建图像质量下降的现象。同时也可以看出，本文所提算法成像的相对误差小于前面3种成像算法，而相关系数大于其他3种成像算法，说明经过相位补偿处理的CS算法成像图与真实状态更加接近，因此成像性能更具优势。
左图为采用算法后的数据恢复变化图；右图为加入白噪声后的探测区域成像图
图7 不同噪声干扰下的成像以及数据恢复情况
Fig. 7 Imaging and data recovery under different noise interference
表3 MIMO为15时成像相对误差
Table 3 Imaging relative error when MIMO is 15
算法OMP重构算法l0重构算法贝叶斯CS算法相位补偿CS算法场景11.132 30.709 50.765 90.527 6场景21.135 21.089 90.728 90.540 1场景31.127 71.122 20.653 50.620 8
表4 MIMO为15时成像相关系数
Table 4 Imaging correlation coefficients when MIMO is 15
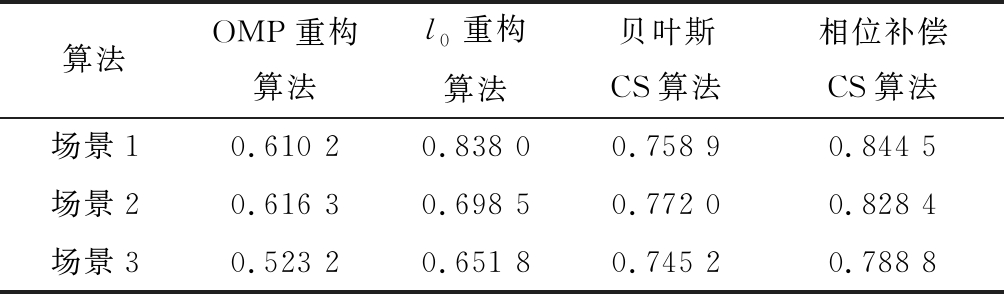
算法OMP重构算法l0重构算法贝叶斯CS算法相位补偿CS算法场景10.610 20.838 00.758 90.844 5场景20.616 30.698 50.772 00.828 4场景30.523 20.651 80.745 20.788 8
表5 MIMO为45时成像相对误差
Table 5 Imaging relative error when MIMO is 45
算法OMP重构算法l0重构算法贝叶斯CS算法相位补偿CS算法场景10.825 90.711 40.588 30.325 2场景20.921 40.917 80.621 40.444 9场景31.099 31.102 50.665 70.625 5
表6 MIMO为45时成像相关系数
Table 6 Imaging correlation coefficients when MIMO is 45
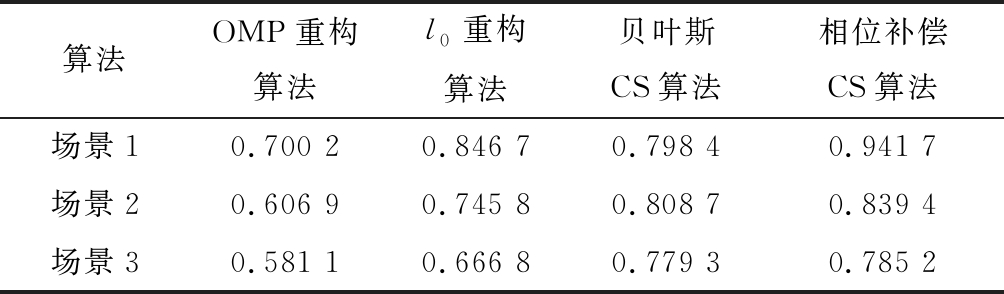
算法OMP重构算法l0重构算法贝叶斯CS算法相位补偿CS算法场景10.700 20.846 70.798 40.941 7场景20.606 90.745 80.808 70.839 4场景30.581 10.666 80.779 30.785 2
因此，基于相位补偿的压缩感知的图像重建算法能够较为理想地克服塌方体中心区域虚像较多、灵敏度较低对图像重建带来的不利影响，同时在UWB较少的回波数据下重构出较高质量的图像，故本文所提目标像重构算法具有高效性。
4 结 论
1)针对煤矿井下特殊的背景环境以及超宽带信号成像的特性，结合压缩感知成像理论，为解决超宽带信号在井下探测成像时目标回波数据不足的问题，提出了一种基于相位补偿的CS成像算法。
2)对井下超宽带成像的回波信号建立了系数向量模型，证明了回波信号是具有稀疏特性，并构造关于回波信号的测量矩阵，进而分析了对超宽带回波信号重建过程，针对相位误差补偿问题，采用了最小熵自聚焦等价计算的思路，利用一个最优化函数将相位误差估计与回波信号重构过程结合在一起，并采用迭代算法进行反复计算相位误差估计，最终得到较为理想的误差估计及图像重构结果。
3)通过不同仿真场景的试验结果也验证本文所提算法对回波具有良好的补偿效果，进一步针对不同程度噪声干扰以及天线阵列数对算法性能影响分析也验证了算法有效性。
[1] 孙继平.煤矿安全生产监控与通信技术[J]. 煤炭学报, 2010, 35(11):1925-1929.
SUN Jiping. Monitoring and communication technology for coal mine safety production [J].Journal of China Coal Society,2010, 35 (11):1925-1929.
[2] 郭继坤,孙继平. 超宽带无线接入系统在矿井通讯中应用的研究[J]. 煤矿机电,2004(5):87-91.
GUO Jikun, SUN Jiping. Application of UWB wireless access system in mine communication [J]. Coal Mine Mechanical and Electrical,2004(5):87-91.
[3] 王艳芬,于洪珍,张 申,等. 超宽带无线通信技术在煤矿井下的应用探讨[J]. 工矿自动化，2005(6):1-4.
WANG YanFen, YU Hongzhen, ZHANG Shen, et al. Discussion on the application of ultra wideband wireless communication technology in coal mine underground [J].Industrial and Mine Automation，2005(6):1-4.
[4] FCC.Revision of Part 15 the commission’s rules regarding ultra-wide band transmission systems[R]. FCC First Report and Order, Released，2002.
[5] 许 会,任 建,李邦宇,等.应用于超宽带呼吸检测的压缩感知算法研究[J].仪器仪表学报，2015，36 (1):56-62.
XU Hui, REN Jian, LI Bangyu,et al. Study of compressed sensing algorithm for ultra wide band respiration detection [J]. China Journal of Scientific Instrument，2015，36(1):56-62.
[6] DONOHO D L. Compressed sensing[J]. IEEE Transaction Information Theory,2006, 52 (4):1289-1306.
[7] JI S, XUE Y, CARIN L. Bayesian compressive sensing[J]. IEEE Transactions on Signal Processing,2008, 56(6):2346-2356.
[8] 杨海蓉, 张 成, 丁大为, 等. 压缩传感理论与重构算法[J]. 电子学报,2011, 39(1):142-148.
YANG Hairong, ZHANG Cheng, DING Dawei, et al. Compression sensing theory and reconstruction algorithm [J]. Chinese Journal of Electronics,2011,39(1):142-148.
[9] ZHENG Kai, JON P Longtin, HIMANSHU Gupta. Vibration control analysis on energy saving for data centers using Optical Wireless Communication (OWC)[C]//ASTFE Digital Library. Begel House Inc, 2017.
[10] PRICKET M J,CHEN C C. Principle of inverse synthetic aperture radar (ISAR) imaging [C]//Electronics and Aerospace Systems Conference record,Arlington.Ar-lington,1980:340-345.
[11] FRANCESCHETTI G, LANARI R. Synthetic aperture radar processing [M]. Boca Raton:CRC Press,1999.
[12] WARREN C, GIANNOPOULOS A,GIANNAKIS I.An advanced GPR modelling framework-the next generation of GprMax[C]//Proc 8th Int Workshop Advanced Ground Penetrating Radar,IEEE, 2015.
[13] 屈乐乐，方广有，杨天虹.压缩感知理论在频率步进探地雷达偏移成像中的应用[J].电子与信息学报, 2011, 33(1): 21-26.
QU Lele, FANG Guangyou, YANG Tianhong. The application of compressed sensing theory in frequency stepped ground penetrating radar [J].Journal of Electronics and Information,2011, 33 (1):21-26.
[14] 姬伟杰, 刘 平, 李 杰, 等. 一种应用于地下腔体成像的新超宽带成像算法[J]. 现代导航,2015,8(5):1674-7976.
JI Weijie, LIU Ping, LI Jie, et al. A new ultra-wideband imaging algorithm for underground cavity imaging [J]. Modern Navigation, 2015, 8 (5):1674-7976.
[15] DOBIGEON N, BASARAB A, KOUAME D, et al. Regularized bayesian com-pressed sensing in ultrasound imaging [C]//20th European Signal Processing Conference. Bucharest, Romania, 2012:2600-2604.
[16] 孙凤莲, 张 群, 罗 迎,等. 基于压缩感知的多目标认知成像方法[J]. 空军预警学院学报,2013, 27 (2):83-88.
SUN Fenglian, ZHANG Qun, LUO Ying, et al. A multi target cognitive imaging method based on compressive sensing [J].Journal of the Air Force Warning Institute,2013, 27 (2):83-88.
[17] 杨俊刚. 利用稀疏信息的正则化雷达成像理论与方法研究 [D]. 长沙:国防科学技术大学, 2013.
[18] 吴 敏, 邢孟道, 张 磊. 基于压缩感知的二维联合超分辨ISAR成像算法[J]. 电子与信息学报,2014 (1):187-193.
WU Min, XING Mengdao, ZHANG Lei. Two-dimensional joint super-resolution ISAR imaging algorithm based on compressive sensing [J]. Journal of Electronics and Information,2014 (1):187-193.
[19] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory,2007,53 (12):4655-4666.
