0 引 言
煤矿开采破坏了原有的应力平衡,最终导致地表产生开采沉陷,从而引发一系列工程技术问题,如何准确预计由于煤矿开采产生的地表移动变形是解决系列工程问题的前提。我国依据大量的工程实践与观测,提出了以典型曲线法、剖面函数法和概率积分法为代表的多种计算方法,并在工程实际中得到广泛应用[1-3]。地表移动计算中最为普遍的方法是影响函数法,而克诺特影响函数最为广泛,其基本原理是单元开采造成的地表沉降可用一影响函数表示,而对大面积开采造成的沉降可表述为单元影响函数对开采面积区域的积分,我国将这一方法称之为概率积分法。通过大量的地表沉降实测数据分析得到了不同矿区、不同开采方法、不同地质条件下概率积分法的计算参数,在开采沉陷领域得到了广泛应用[4-7]。
由于概率积分法采用的是单元影响的面积分计算方法,对于水平煤层的开采影响计算,其计算满足理论要求且较为符合实际,而对于倾斜煤层开采的影响计算往往采用近似计算方法。近似计算可概括为2种形式:①是将主断面沉降表示为2个不同采深(下山采深和上山采深)水平煤层的半无限开采的叠加;②是将倾斜工作面划分为不同采深的条状水平面进行叠加,实质是用多个平面替代斜面,从而造成计算误差。斜面的水平切割永远不能代替斜面,这种近似计算误差不能通过增加切割而消除,而且会随着倾角的增大而计算结果误差会增加[8]。如何消除这一计算误差是开采沉陷计算理论(概率积分计算方法)必须解决的问题,可以更精确计算得出工作面采动沉陷参数。
笔者通过等价的基本思路,解释了等价计算方法的实质,并通过计算实例分析了等价计算方法的优势,从等价的原理说明了半无限叠加计算下沉正确,变形计算存在误差,而切割计算存在难以消除的计算误差,从而表明了等价计算的优势,对提高概率积分法倾斜煤层的计算精度和适用范围均有一定的理论意义。
1 等价原理计算方法
若2个不同工作面的开采沉陷参数计算结果相同,则可以说这2个工作面等价。开采沉陷计算的等价原理基本思想如图1所示,在计算参数与充分开采条件下最大下沉相同的条件下,对于点P的下沉影响在任意区域PM和PN内,开采不同深度的水平煤层A,A′和A″是相同的[2,4],而且,与开采不同深度A1、A2和A3的煤层开采造成的下沉影响之和也是相同的,即A、A′、A″和A1+A2+A3煤层开采的下沉影响是等价的。该点可通过理论计算验证,也可被大量观测资料证实,在文献[5-7]中也有同样的论述。
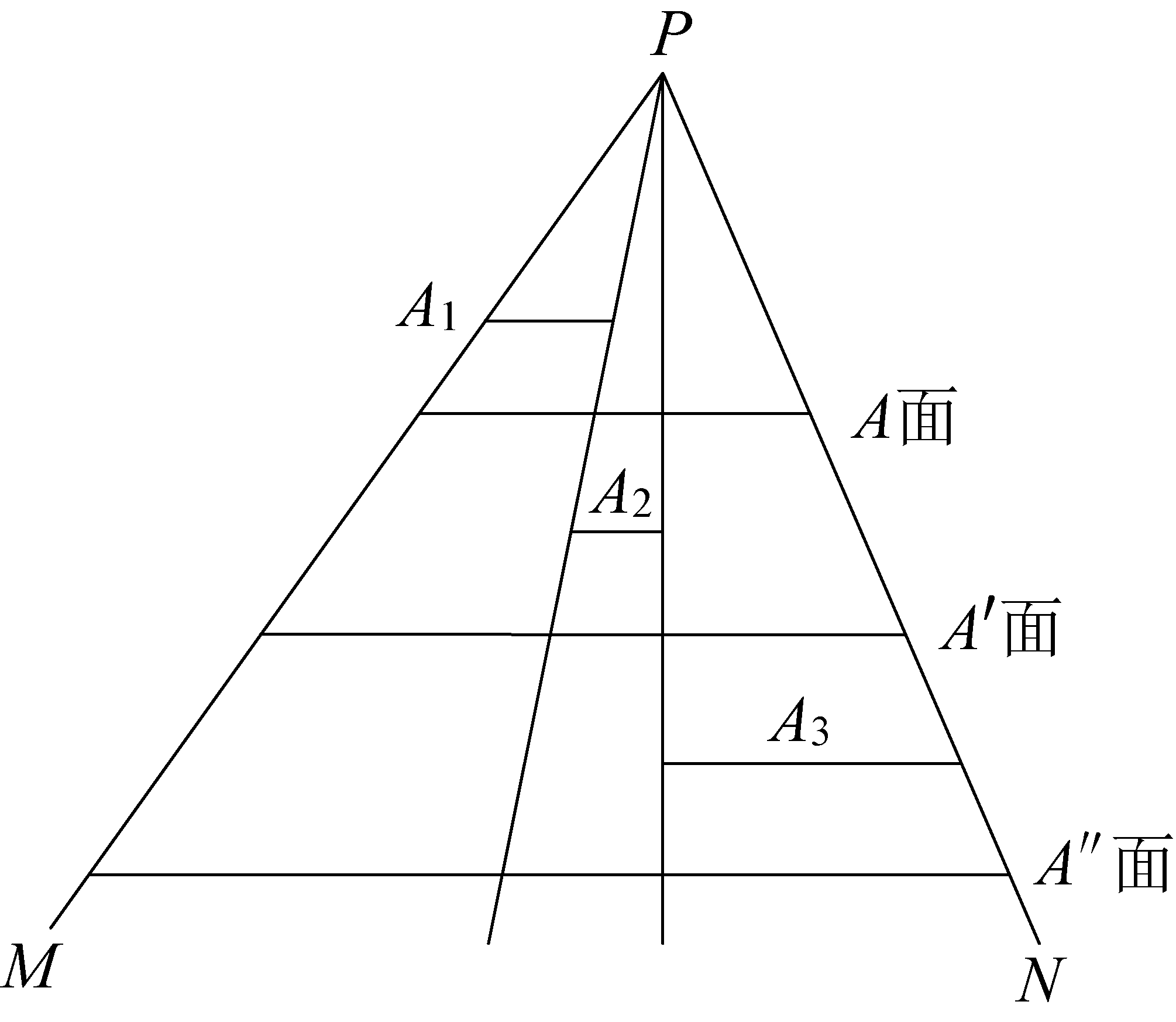
图1 等价原理计算示意
Fig.1 Basic Principle of equivalence caculation
对于倾斜煤层,也应该可寻求一个水平面与倾斜煤层的开采影响等价。实际上,只要计算参数相同,且水平煤层开采与倾斜煤层开采在充分采动条件下的最大沉降相同,其开采影响传播方向相同,影响区域内的任意开采面计算沉降都相同,这同样可通过理论计算加以验证,从而表明沉降计算的等价面有无数个,如图2所示。

图2 倾斜煤层等价示意
Fig.2 Sketch of equivalence for inclined seam
开采水平煤层A1和A2,倾斜煤层A′和A″,在开采影响传播方向和最大下沉相同的条件下,对于计算点P而言下沉相同,即它们等价。在开采沉陷计算中,除下沉量外,有倾斜、曲率和水平变形等其他计算参数,而这些参数与开采影响半径(开采深度)密切相关。图1中等价面的计算,虽然下沉量一致,但其他变形量却会因为影响半径的不同而造成计算结果的不同。因此,对于地表移动与变形计算而言,其计算面是唯一的。而对于倾斜煤层,只要寻求到一个影响半径与计算点相一致的水平面,倾斜煤层的开采影响计算就可通过水平面的计算而实现。因此,等价计算的实质是寻求能够反映计算点影响采深的等价水平面,以等价水平面的计算实现倾斜煤层开采影响的计算,如图3所示。
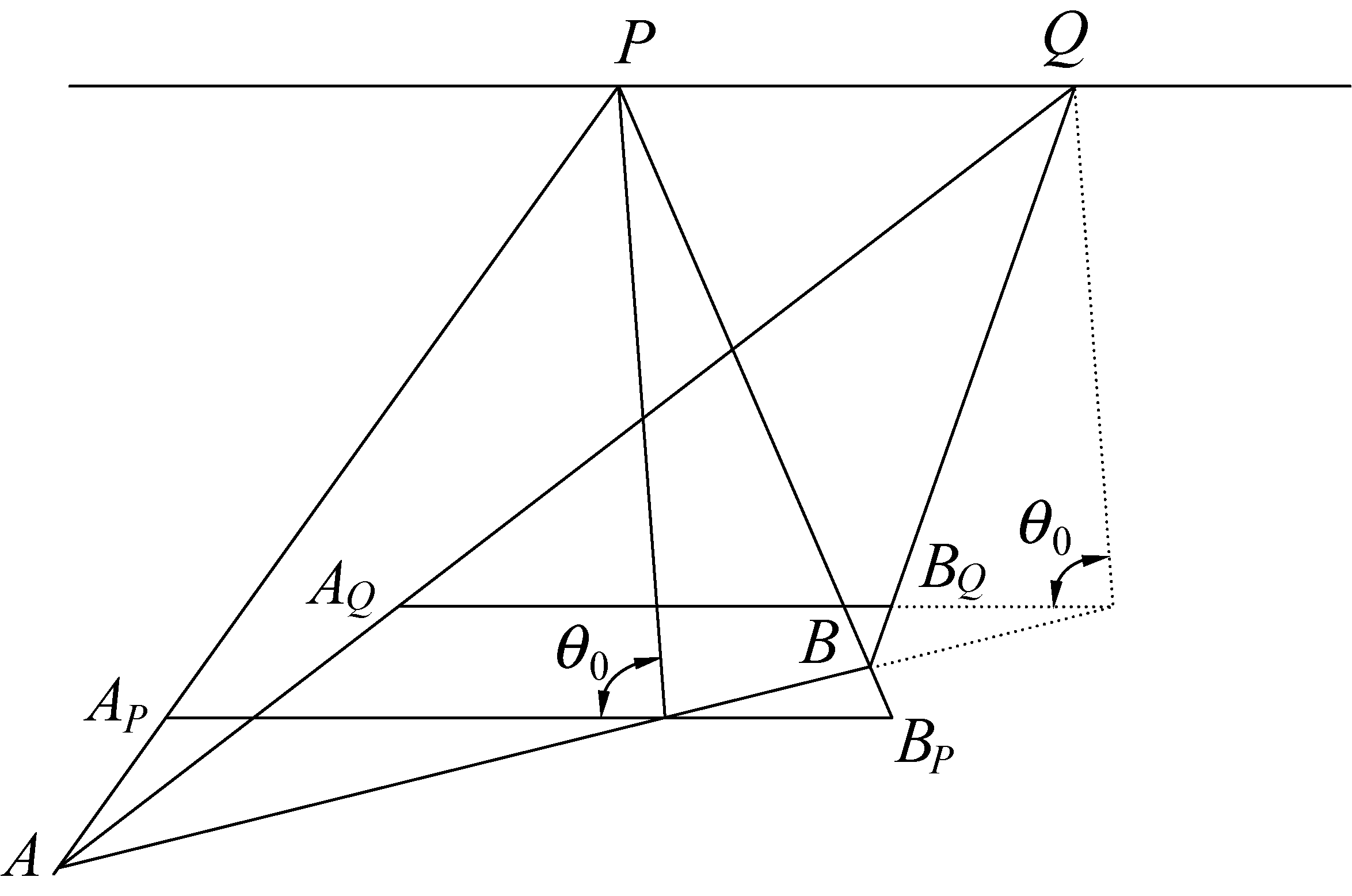
图3 等价工作面计算
Fig.3 Equivalence transform of mined inclined seam
依据计算点与工作面的相对位置,通过影响传播方向(开采影响传播角θ0)确定影响采深,并以这一采深确定的水平面为等价计算面。倾斜煤层AB的等价面对于点P是APBP,对于点Q是AQBQ。
综上所述,等价计算方法就是依据计算点与工作面的相对位置,通过影响传播角确定等价影响采深,并依据这一采深,通过计算点与工作面各角点连线的延长线在等价采深处的位置,确定等价影响计算工作面。即对于倾煤层开采的计算,每个点均存在一个唯一的等价计算水平面,并以这一水平面按倾斜煤层开采影响传播方向进行地表移动与变形的计算[9]。由于等价计算采用的是水平面计算,因此,切割计算将随切割密度的增加而趋近于理论结果,从而可避免倾斜煤层开采计算简化所带来的计算误差。这一方法已纳入2000年出版相关的“三下采煤规程”规范[10-11]。
2 计算结果分析
通过计算数据分析等价计算的可靠性,为便于计算,计算条件选取为工作面走向充分,倾向水平投影长度200 m,下山采深200 m,上山采深100 m,概率积分计算参数:下沉系数0.75,主要影响角正切tan β=2.0,水平移动系数0.3,开采影响传播角80°,充分采动条件下的最下沉量为1 500 mm。
对倾斜主剖面进行计算,计算分3种形式(5个方案):①是等价影响计算,如图4a所示;②是上、下山采深水平煤层半无限开采的叠加,如图4b所示;③是将倾斜面切割成不同采深的平面,分别为切割成2个平面、4个平面、8个平面,如图4c、图4d和图4e所示。

图4 计算方案工作面示意
Fig.4 Sketch of calculation schemes
各计算方案计算的主剖面下沉曲线如图5所示。

图5 下沉曲线
Fig.5 Sketch of subsidence
由计算结果可知,等价计算与半无限叠加计算的下沉基本相同(尽管存在一定差异),而切割计算出现明显差异。当切割为2个面时,盆地中央出现波浪下沉,局部下沉大于理论最大沉降量(误差2%),以等价原理分析,如图6所示,任意点P的下沉应与PM与PN连线范围内的任意水平面计算相同,与下山水平面MN′面相同,而下山水平面N′F′的下沉与上山水平面NF下沉相同,因此,等价面计算的下沉与下、上山半无限开采影响叠加影响计算的下沉相同。
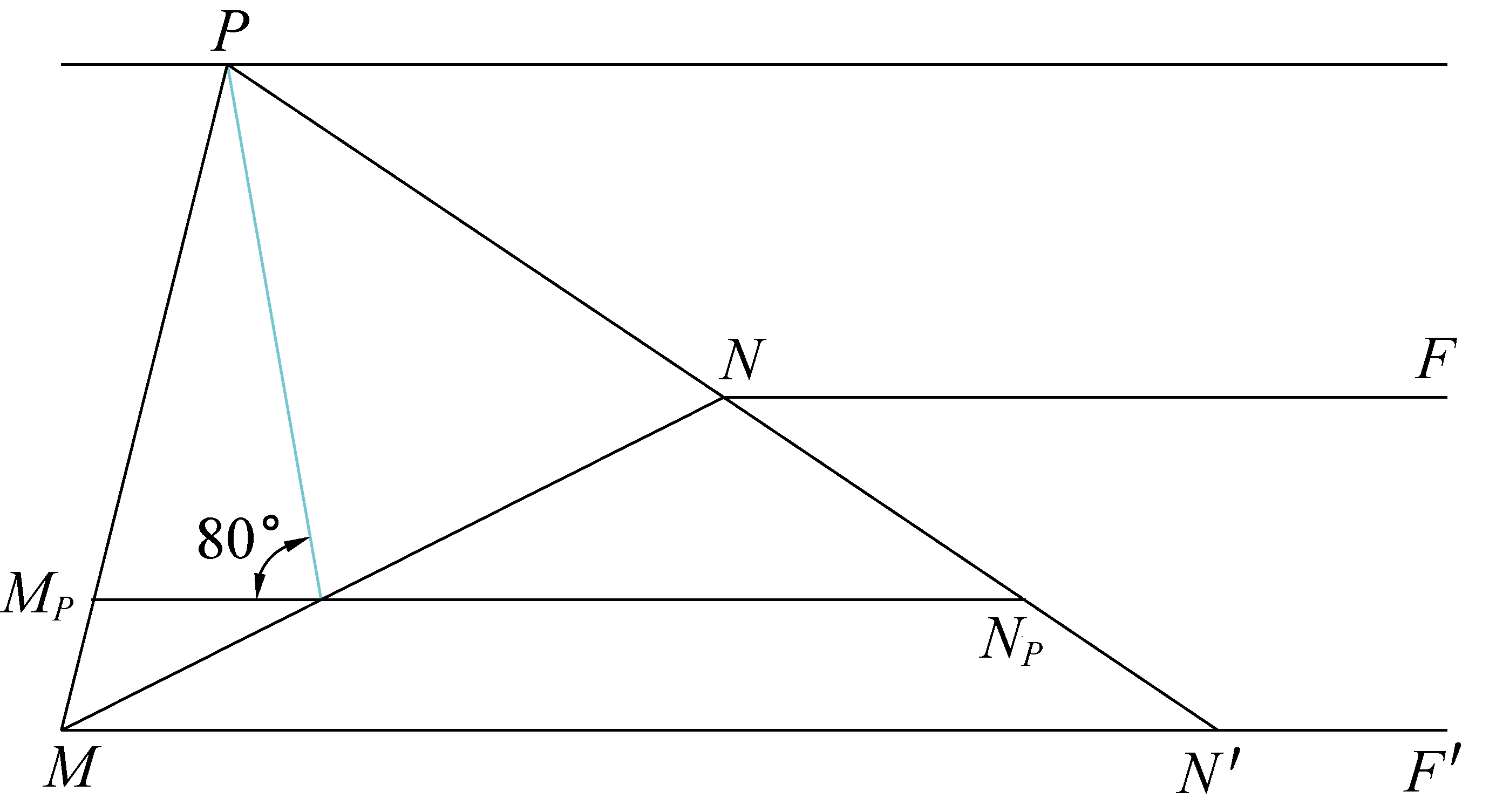
图6 计算结果等价分析示意
Fig.6 Sketch of equivalence analysis
当将工作面切割为2个面后,无论计算点在什么位置都无法实现等价,当计算点位于切割处上山工作面边界附近P时,中央出现了重叠的计算部分,即图7a中的CD段;当计算点位于切割点下山工作面附近P时,中央出现了缺失的计算部分,即图7b中的CD。虽然外侧有所不同,但中心处对下沉影响较大,从而产生了计算结果大于或小于理论最大值的情况。
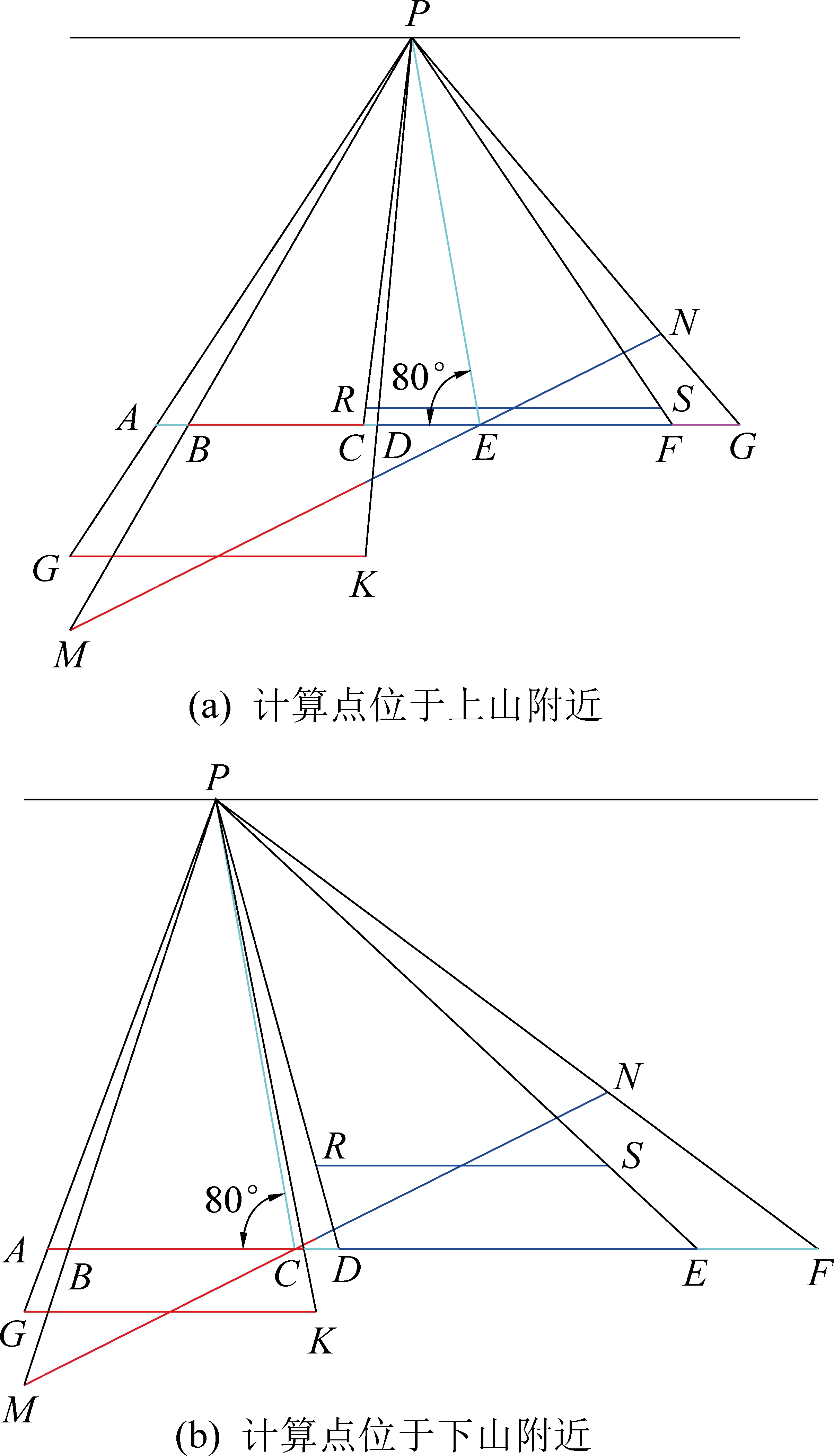
图7 计算结果等价分析示意
Fig.7 Sketch of equivalence analysis of calculation results
当切割成多个面后,盆地中央不再出现波浪,但最大值明显小于理论值。由于传播方向与切割的影响,对于任意点而言,其计算缺失了多个计算区域ΔL,如图8所示。

图8 计算结果等价分析示意
Fig.8 Sketch of equivalence analysis of calculation results
正如上文所述,水平切割永远不能等同于斜面,且由此产生的计算误差与倾角和开采影响传播角相关,计算条件下的系统误差约7.5%。
由于倾斜煤层开采中水平变形计算受开采影响传播角的影响,为消除开采影响传播角对计算结果的影响,将开采影响传播角设为90°,对倾向主剖面的水平变形进行计算,各方案计算的主剖面水平变形,如图9所示。
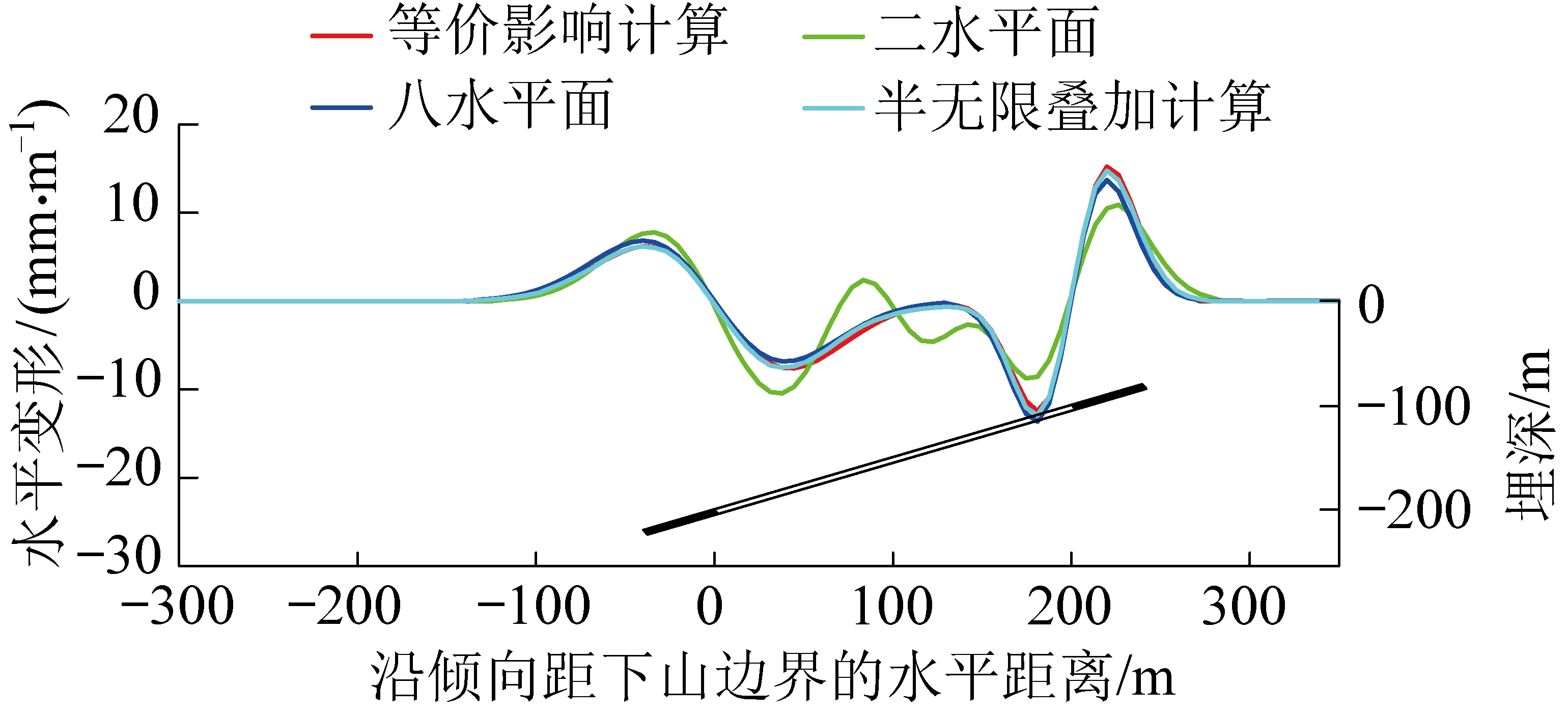
图9 水平变形曲线
Fig.9 Sketch of horizontal deformations
计算结果表明,半无限开采尽管在上、下山体现了采深对变形的影响,但上、下山边界两侧拉伸与压缩量值相同,未能充分体现变形与开采深度的密切关系,而等价计算方法更好地体现了这一点。当切割为两个面时,盆地中央现出了拉伸变形,这显然与实际和计算理论不符。随着切割面的增加,盆地中央拉伸变形消失,变形值也趋向于实际,但仍存在较大的系统误差,计算条件下的相对误差约为11%。
综上分析可知,半无限叠加计算结果对于下沉计算而言具有结果的一致性,对其他变形参数同样存在计算误差,而水平切割计算永远无法实现理论结果。在实际计算当中,半无限叠加简化计算方法仅能用于矩形工作面的倾斜主剖面计算,而对于任意工作面开采、任意点的计算往往采用切割方式。而这一计算产生的误差与切割宽度有关,与计算点的相对位置有关,而且永远无法消除这一简化方法带来的误差,误差的大小与倾角及开采影响传播角有关,倾角越大,误差越大,而采用等价计算方法可消除这一计算误差。
3 结 论
1)倾斜煤层开采半无限叠加下沉值计算结果与等价计算结果一致,但半无限迭加上、下山边界两侧拉伸与压缩量值相同,未能充分体现变形与开采深度的密切关系。
2)倾斜煤层开采水平划分在下沉值、水平变形值的计算结果误差较大,误差不会因水平划分数的增加而消除,这种简化计算的系统误差与煤层倾角和开采影响传播角有关,煤层倾角越大,误差越大。
3)倾斜煤层开采的地表移动计算可通过确定计算点影响采深,采用等价水平面进行计算,这一方法可消除倾斜工作面切割叠加计算带来的计算误差,实现计算结果与理论的完美契合。
参考文献(References):
[1] 何国清,杨 伦,凌赓娣,等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1991.
[2] 中国矿业学院,阜新矿业学院,焦作矿业学院.煤矿岩层与地表移动[M].北京:煤炭工业出版社,1981.
[3] 煤炭科学研究院北京开采研究所,煤矿地表移动与覆岩破坏规律及其应用[M].北京:煤炭工业出版社,1981.
[4] 崔希民,邓喀中.煤矿开采沉陷预计理论与方法研究评述[J].煤炭科学技术,2017,45(1):160-169.
CUI Ximin,DENG Kazhong.Research review of predicting theory and method for coal mining subsidence[J].Coal Science and Technology,2017,45(1):160-169.
[5] 许 冬,王临清,吴侃.任意形状工作面沉陷预计计算方法[J].金属矿山,2014,43(5):55-59.
XU Dong,WANG Linqing,WU Kan.Prediction method for subsidence of arbitrary shape working face[J].Metal Mine,2014,43(5):55-59.
[6] 刘玉成,戴华阳.近水平煤层开采沉陷预计的双曲线剖面函数法[J].中国矿业大学学报,2019,48(3):676-681.
LIU Yucheng,DAI Huayang.Hyperbolic function model for predicting the main section surface deformation curve due to approximate horizontal coal seam underground longwall mining[J].Journal of China University of Science &Technology,2019,48(3):676-681.
[7] 戴华阳,王金庄.非充分开采地表移动预计模型[J].煤炭学报,2003,28(6):583-587.
DAI Huayang,WANG Jinzhuang.Prediction model for surface movement and deformationinduced by sub-critical extraction[J].Journal of China Coal Society,2003,28(6):583-587.
[8] 张华兴,焦传武.地表移动精确预计法:线积分运算[J].矿山测量,1988,16(4):21-29.
ZHANG Huaxing,JIAO Chuanwu.An accurate predicting method of surface movement based on normal line integral operation[J].Mine Surveying,1988,16(4):21-29.
[9] 张华兴.井筒煤柱开采理论与技术的研究[D].北京:煤炭科学研究总院,1991.
[10] 胡炳南,张华兴,申宝宏.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南[M].北京:煤炭工业出版社,2017.
[11] 国家煤炭工业局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000.
