0 引 言
煤炭在我国能源发展规划中为主导能源。然而随着煤层采深加大,因煤体温度升高而引发的煤与瓦斯突出灾害事故不断增加。为防治灾害发生,众多学者从温度变化所导致的煤体孔裂隙渗透率、孔隙率、瓦斯压力等因素变化方面出发做了大量研究。张波等[1]建立了瓦斯渗流的THM耦合模型,考察了受采动影响下的工作面由于温度变化而导致的渗透率变化;徐达妮[2]用所构建的THM模型模拟了煤层气开采过程中,不同初始温度、地应力、裂缝发育程度等条件下的储层压力分布,并得出日产出速率曲线;冯雨实等[3]基于热流固耦合作用,利用THM模型对煤层气井壁失稳进行研究,并对井周的应力分布和变形情况进行数值模拟;张伟等[4]建立了适应于地热开发的THM耦合模型,并对高温地热开采不同方案的温度场进行模拟;张宁[5]对煤体进行热流固耦合分析表明,初始温度越高,由于内向吸附膨胀变形和内向热膨胀变形占据主导地位,使得钻孔周围煤体孔隙率和渗透率越小,所以随着煤体初始温度增大,瓦斯产气速率呈现降低趋势;秦涛等[6]测试了热流固耦合模型中,不同温度条件下,掘进工作面的瓦斯压力、瓦斯渗流速度、煤体位移的整体变化情况;马海峰[7]分析了流固耦合模型中,不同应力和不同连通情况下的煤体孔裂隙内瓦斯压力分布云图,并在不同孔裂隙内设置观测点,观察渗流速度变化曲线,从而判断出不同孔隙的流动优势性;马忠[8]运用热流固耦合模型,直接对抽采钻孔周围瓦斯压力、孔隙率、渗透率进行曲线模拟,分析了不同温度、载荷、钻孔间距以及初始渗透率条件下,瓦斯压力、瓦斯含量、煤体渗透率和孔隙率的变化情况。
许多学者对不同温度条件下煤体渗透率、孔隙率、煤裂隙中的瓦斯压力进行研究。但不同温度对热流固耦合模型中全贯通裂隙、部分连通裂隙以及孔隙瓦斯的相关参数的影响有待深入研究。笔者以鹤岗矿区地质构造演变[9-10]及构造应力变化参数[11-12]、煤储层特征参数[13-16]、煤体物性参数[11,13,17]以及煤瓦斯赋存[18-20]和地热参数[21]为基础,建立热流固多场耦合数值模型,分析不同温度条件下,煤体孔裂隙中瓦斯压力、瓦斯渗流速度以及煤体渗透率的变化规律,以期为含瓦斯煤体的动力灾害机理研究提供理论基础。
1 热流固耦合数值模型
热流固三相耦合是流体渗流、多孔介质弹塑性变形与温度场三者相互作用的过程,是温度、流体、固体三者通过流固交互界面进行的流体位移、固体形变以及热传导的相互作用过程。笔者根据达西渗流定律、质量守恒定律、多孔介质弹塑性理论、有效应力原理和传热学理论所建立的渗流方程、介质变形方程以及温度场方程,直接利用有限元软件COMSOL Mutiphysics中的Solid Mechanics(solid)、Darcy’s Law(dl)、Heat Transfer in Porous Media(ht)3个物理场接口将公式共用的参数变量作为衔接,建立起方程之间相互制约、相互影响的关系。并将这种关系套用在已经设定好的数值计算模型中,从而进行仿真模拟计算。
1.1 模拟假设前提条件
假设热流固耦合数值模型符合下列条件:①固体表面所覆盖的分子与固体表面所接触的介质两者间的气压关系符合朗格缪尔方程;②瓦斯在煤体中的流动符合达西定律;③瓦斯为理想气体;④煤体各向同性;⑤煤体变形为弹性变形;⑥煤体内的热量流动非常缓慢;⑦含瓦斯煤体在温度与外力的作用下发生变形,考虑非等温渗流,笔者将含瓦斯煤体看成由煤体骨架和瓦斯2个部分组成,并假设煤体与瓦斯的温度处处相同。
1.2 模型的建立
构建1 m×1 m的二维数值计算模型,根据裂隙特征参数,基于Monte-Carlo法构建二维模型中的模拟裂隙,数值模型如图1所示。
其中,pt1为上部孔隙观测点、pt2为部分连通裂隙观测点、pt3为全贯通裂隙观测点、pt4为下部孔隙观测点。图1中的直线为模拟裂隙的结构面迹线,由2种不同产状的裂隙组组成,其特征参数见表1。
Monte-Carlo法生成裂隙的本质是根据裂隙组控制的特征参数,基于结构面中裂隙倾角、迹长的概率分布函数,在模拟区域中生成大量随机单裂隙。其中,首尾交叉的单条裂隙在模拟裂隙生成的过程中形成闭合,构成部分连通裂隙。若部分连通裂隙的两端均与模型边界AD、BC边相连,就构成全贯通裂隙。若部分连通裂隙的一端与模型边界AD边相连,就构成半贯通裂隙。本次数值计算模型共模拟出27条单裂隙。其中单裂隙b1、b3、b4构成全贯通裂隙。b10、b11以及b5、b6、b25等单裂隙构成部分连通裂隙。模拟裂隙以外的模拟区域则构成孔隙。
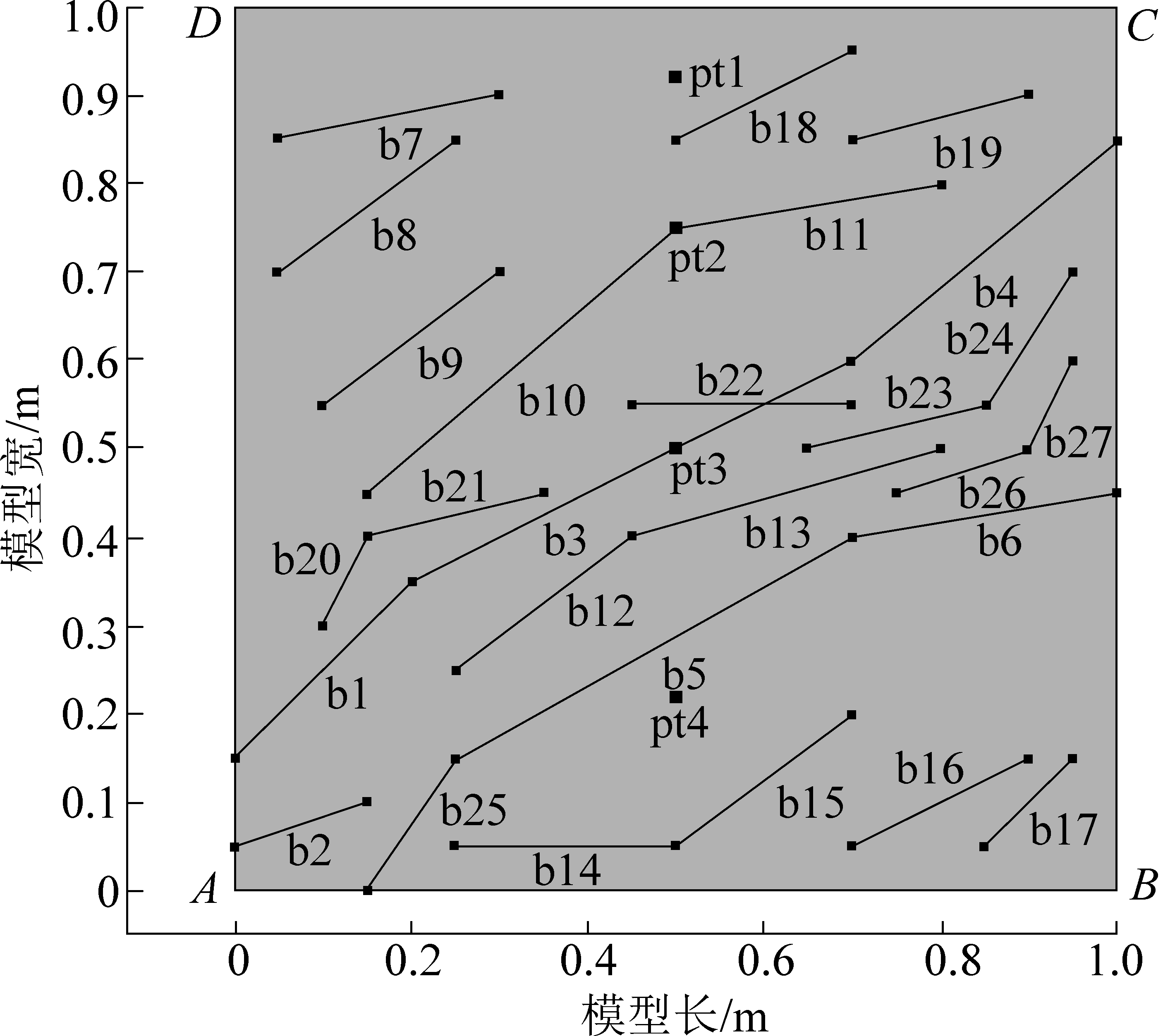
图1 数值计算模型
Fig.1 Numerical calculation model
表1 裂隙特征参数
Table1 Fracture characteristic parameters

裂隙组倾角/(°)迹长/m间距/m隙宽/mm均值标准差分布类型均值分布类型均值分布类型均值分布类型1153正态0.20负指数0.08负指数1负指数2505正态0.25负指数0.06负指数1负指数
1.3 模型的边界条件
选取预开采煤壁内的一块煤体区域作为模拟对象。依据地质隔离体所处位置及其与周围地质构造的连接关系,使模拟条件最大程度向实测地应力的大小和方向逼近。该研究中地应力、方位角以及倾角等物理参数参考鹤岗矿区地应力资料[19-20],设置模型边界条件如下:在模型AB边和BC边施加固定约束,模拟煤体在地下所处的约束状态。考虑上覆岩层质量、水平构造应力对煤体的作用,在CD边施加竖向载荷25.48 MPa、AD边施加横向载荷10.4 MPa。瓦斯压力参考鹤岗盆地煤层气资源参数:模型初始瓦斯压力设为1.7 MPa,AD边流入瓦斯压力设为3 MPa,BC边流出瓦斯压力设为1.7 MPa。
由于开采深度增加导致地温变化,因此需设置不同的试验温度条件。黑龙江省各矿区海拔在+100—+300 m、平均采掘深度在-600—-700 m,最深的近千米。矿区平均恒温深度为15~26 m,温度为6 ℃,且矿区平均地温梯度为2.7 ℃/hm,平均地热增温率为38.2 m/℃[21]。因此选取地表+300 m、恒温深度线15 m、采深1 000 m,计算出最大试验温度为313.15 K。选取采深600 m、恒温深度线26 m,计算出最小试验温度为293.15 K。
2 模拟结果分析
2.1 温度对孔裂隙瓦斯压力的影响
为对比不同试验温度对煤体孔裂隙内瓦斯压力的影响,选取293.15、299.15、305.15、313.15 K下,煤体孔裂隙内的瓦斯压力分布如图2所示。由图可知:全贯通裂隙内瓦斯压力明显大于孔隙内瓦斯压力,且越靠近AD侧,瓦斯压力越大;煤体裂隙与孔隙之间存在的瓦斯压力梯度会随两者间距的增大而减小;在不同温度条件下,煤体内瓦斯压力的二维分布沿贯通裂隙走向均呈现“尖突”形态,且裂隙内瓦斯压力高于周边孔隙内瓦斯压力。
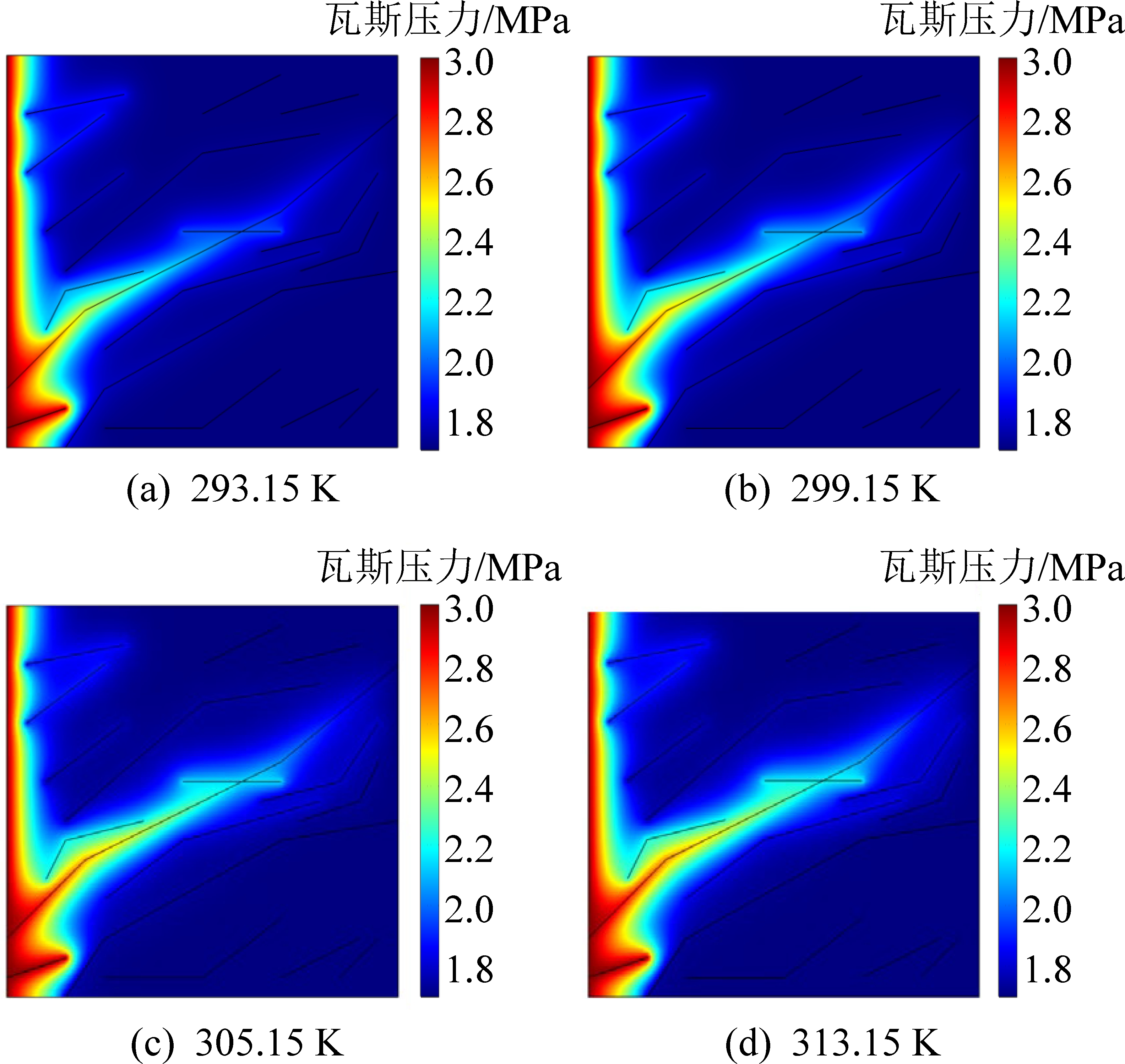
图2 不同温度下孔裂隙内瓦斯压力分布
Fig.2 Gas pressure distribution in holes and
fissures at different temperatures
4个观测点在不同试验温度条件下的瓦斯压力变化曲线如图3所示。对比可知:在相同试验温度条件下,全贯通裂隙内观测点pt3的瓦斯压力随时间增加而增大,且瓦斯压力增加值和增加速率均高于相同时刻观测点pt1、pt2、pt4的瓦斯压力增加值和增加速率。部分连通裂隙内观测点pt2的瓦斯压力增加值和增加速率均高于相同时刻孔隙中观测点pt1、pt4的瓦斯压力增加值和增加速率。
因受模型AD侧全贯通裂隙和部分连通裂隙的影响,导致流经观测点pt4的瓦斯流量减小,使此观测点处瓦斯对煤体孔裂隙的隙壁所产生的压应力减小。所以试验温度越高,观测点pt4处的瓦斯压力越低。因此在试验温度相同时,不同观测点瓦斯压力的大小顺序依次为:pt3>pt2>pt1>pt4。
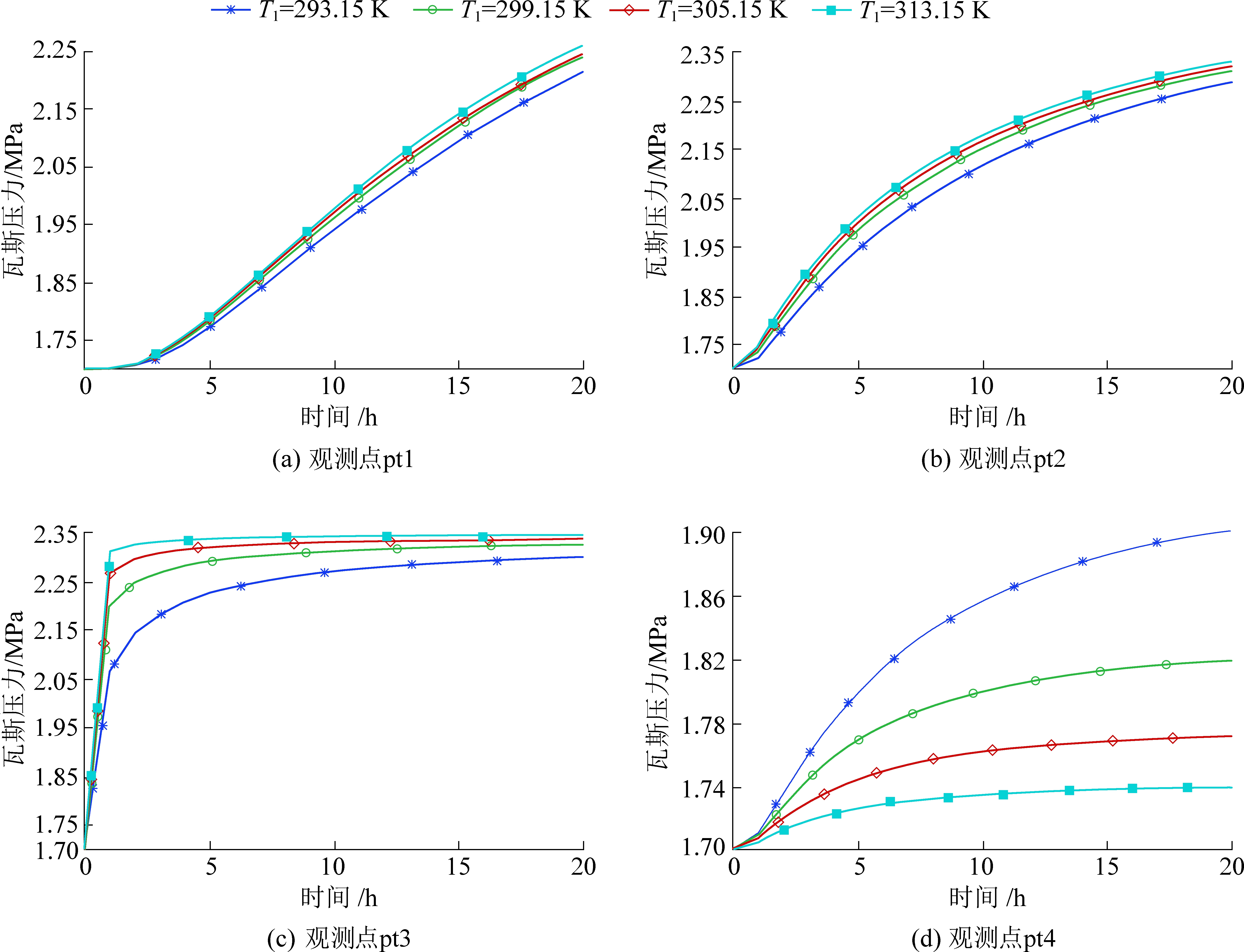
图3 不同温度下瓦斯压力变化曲线
Fig.3 Change curves of gas pressure at different temperatures
综合上述分析,全贯通裂隙、部分连通裂隙以及孔隙内瓦斯压力受试验温度的影响较大,但影响程度不同:全贯通裂隙>部分连通裂隙>孔隙。试验温度越高,不同煤体孔裂隙间的瓦斯压力梯度越大,瓦斯压力差值越大。瓦斯压力和瓦斯压力梯度较大的煤体孔裂隙相较于其他孔裂隙的流动优势性强。
2.2 温度对孔裂隙渗流速度的影响
不同试验温度条件下,沿水平方向(AD→BC)的渗流速度场变化云图如图4所示。由图可知:随试验温度升高,全贯通裂隙中的瓦斯渗流速度变大。因流体沿煤体裂隙从AD侧向BC侧传导,所以全贯通裂隙中靠近BC侧的渗流速度也逐渐变大。

图4 不同温度渗流速度场
Fig.4 Velocity field of seepage at different temperatures
单裂隙b2的始端与模型AD边相接,且与流体渗流速度方向呈19°,对瓦斯渗流方向有很强的引导作用。但单裂隙b2终端的裂隙消失并与四周孔隙相接,相当于流体流动通道的横截面面积大幅减小的同时流体压力梯度却不变,导致b2单裂隙终端处渗流速度较大,大于全贯通裂隙中的渗流速度,且以近圆形向四周扩散。因此,在b2单裂隙终端形成了一个较大的渗流速度场。随温度升高,b2单裂隙终端周围的渗流速度场半径范围增大,但由于孔隙渗透率低,因此渗流速度场的扩散范围较小。由b5、b6、b25组成的部分连通裂隙不仅没有和模型AD边相接,且b25单裂隙的展布方向与瓦斯渗流方向夹角大于45°。因此b2单裂隙终端的渗流速度场扩散范围以b25单裂隙为界,渗流范围不再扩大。
根据不同观测点在不同试验温度条件下渗流速度变化数值模拟结果可知:受模型AD侧全贯通裂隙及部分连通裂隙的影响,流经观测点pt4的流体流量减少,因此试验温度越高,观测点pt4的瓦斯渗流速度越小。试验温度越高,观测点pt1、pt2、pt3处的瓦斯渗流速度越大。又因为煤体裂隙初始渗透率为5×10-15 m2,煤体基质初始渗透率为3.82×10-17 m2,所以观测点pt2、pt3处的瓦斯渗流速度较大。在4个试验温度条件下,观测点pt1处瓦斯渗流速度变化范围是1.969 5×10-8~3.125 4×10-8 m/s到3.228 9×10-6~3.367 8×10-6 m/s;观测点pt2处瓦斯渗流速度变化范围是0.6×10-3~1.3×10-3 m/s到3.7×10-3~4.4×10-3 m/s;观测点pt3处瓦斯渗流速度变化范围是2.07×10-2~18.9×10-2 m/s到2.2×10-2~18.96×10-2 m/s。
分析结果表明:全贯通裂隙内瓦斯渗流速度>部分连通裂隙内瓦斯渗流速度>孔隙内瓦斯渗流速度,且试验温度越高,瓦斯渗流速度差值越大;渗透率和瓦斯渗流速度较大的煤体孔裂隙相较于其他孔裂隙的流动优势性强。
2.3 温度对孔裂隙渗透率变化的影响
根据不同试验温度条件下各观测点渗透率的变化数值模拟结果可知:观测点pt4的渗透率随试验温度升高而增大,但其孔隙瓦斯压力、流体渗流速度随试验温度升高而降低。其原因在于渗透率只与孔隙形状、大小及其排列方式有关,与流体性质无关。在模型受到恒定载荷以及不同温度热膨胀综合作用影响下,观测点pt4处的体积应变由293.15 K的-9.76×10-3变为313.15 K的-5.32×10-3,体积压缩量随温度升高而减小。因此,观测点pt4处的渗透率随温度升高而增大,观测点pt1、pt2、pt3处的渗透率同样因煤体裂隙体积压缩量变小而增大。
相同观测点在不同试验温度条件下的变化曲线趋势相同,参照时间点为1 h时的渗透率变化情况进行说明。由4个观测点渗透率在不同试验温度条件下的最大、最小值可以发现,全贯通裂隙无论处于高温或低温试验条件下,其初始及终值渗透率均大于部分连通裂隙,部分连通裂隙的初始及终值渗透率均大于孔隙。观测点pt1处体积应变从-9.76×10-3变为-5.36×10-3,压缩量大于观测点pt4,所以观测点pt4无论是在高温或低温试验条件下,其初始及终值渗透率均大于孔隙观测点pt1。综上所述,高温试验条件下,全贯通裂隙渗透率>部分连通裂隙渗透率>孔隙渗透率。
4个观测点在不同试验温度区间的渗透率差值不同。观测点pt1在3个试验温度区间293.15~299.15 K、299.15~305.15 K、305.15~313.15 K的渗透率差值分别为0.02×10-17、0.02×10-17、0.03×10-17 m2;观测点pt2在3个试验温度区间的渗透率差值为0.025×10-17、0.025×10-17、0.03×10-17 m2;观测点pt3在3个试验温度区间的渗透率差值为0.04×10-17、0.03×10-17、0.035×10-17 m2;观测点pt4在3个试验温度区间的渗透率差值为0.02×10-17、0.02×10-17、0.03×10-17 m2。综合上述4组数据可发现,不同试验温度条件下,温度越高所对应观测点处的渗透率变化值就越大,且在相同试验温度条件下呈现:全贯通裂隙渗透率变化>部分连通裂隙渗透率变化>孔隙观测点渗透率变化的特点。
根据不同试验温度条件下4个观测点渗透率变化数值模拟结果可知:
1)随试验温度升高,所有观测点处的渗透率均增大。
2)不同试验温度条件下,4个观测点在1~20 h时间段内的最大、最小渗透率变化幅度不同。渗透率的最大、最小变化幅度:观测点pt1为0.072 3×10-17、0.065 7×10-17 m2;观测点pt2为0.076 3×10-17、0.072 5×10-17 m2;观测点pt3为0.030 3×10-17、0.004 6×10-17 m2;观测点pt4为0.024 2×10-17、0.004 4×10-17 m2。由于全贯通裂隙与渗流瓦斯流体相连,导致观测点pt3处的煤体裂隙初始渗透率较大,所以观测点pt3在1~20 h内渗透率的最大、最小变化幅度均小于观测点pt1、pt2。
观测点pt2所在的部分连通裂隙虽没有与模型边界AD边相连,但裂隙方向与瓦斯渗流方向夹角小于45°,利于瓦斯渗流导向。所以试验温度越高,观测点pt2处的渗透率变化幅度越大,大于观测点pt1、pt3、pt4的渗透率变化幅度。观测点pt1的渗透率、渗透率变化幅度随试验温度升高而增大,但观测点pt1的渗透率变化幅度小于观测点pt2的渗透率变化幅度。由于观测点pt4受模型AD侧全贯通裂隙、部分连通裂隙对渗流瓦斯导向作用的影响,试验温度越高,观测点pt4处的渗透率越低、渗透率变化幅度越小,小于观测点pt1、pt2、pt3处渗透率变化幅度的最小值。
综合以上,观测点处渗透率变化幅度较小反而可以辅证此观测点处的渗透率较大。进而分析得出,全贯通裂隙渗透率>部分连通裂隙渗透率>孔隙渗透率。渗透率较大的煤体孔裂隙相较于其他孔裂隙的流动优势性强。
3 结 论
1)温度对含瓦斯煤体的瓦斯压力分布特征具有明显影响。试验条件下,温度越高,全贯通裂隙中的瓦斯压力越大。温差越大,全贯通裂隙所形成的瓦斯压力场越大、瓦斯压力梯度越大,部分连通裂隙次之,孔隙的瓦斯压力场以及瓦斯压力梯度最小。
2)温度对含瓦斯煤体的瓦斯优势流动方向具有明显影响。试验温度越高,煤体瓦斯更易沿着全贯通裂隙走向方向流动。温度对全贯通裂隙中瓦斯渗流速度的影响大于部分连通裂隙,孔隙内瓦斯渗流速度受温度的影响最小。
3)温度对含瓦斯煤体的渗透性具有明显影响。试验条件下,温度越高,煤体全贯通裂隙的渗透率越高。温度对全贯通裂隙渗透率的影响最大,部分连通裂隙次之,孔隙渗透率受温度影响最小。
[1] 张 波, 谢雄刚, 刘洋成. 基于热流固耦合工作面前方瓦斯渗流数值模拟[J]. 中国安全生产科学技术, 2018, 14(3):89-94.
ZHANG Bo, XIE Xionggang, LIU Yancheng. Numerical simulation on gas seepage in front of working face based on fluid-solid-heat coupling [J]. Journal of Safety Science and Technology, 2018, 14(3): 89-94.
[2] 徐达妮. 考虑热流固耦合的低渗透煤层气渗流理论及应用[D]. 西安: 西安石油大学, 2017.
[3] 冯雨实, 梁永昌. 煤层气水平井井周围岩热流固耦合数值分析[J]. 煤矿安全, 2018, 49(1): 206-209.
FENG Yushi, LIANG Yongchang. Numerical analysis of fluid-Solid-heat coupling of surrounding rock around coal bed methane horizontal wells [J]. Safety in Coal Mines, 2018, 49(1):206-209.
[4] 张 伟, 孙 江, 曲占庆, 等. 高温地热开采热流固耦合模型及综合评价方法[J]. 地球物理学进展, 2019, 34(2):668-675.
ZHANG Wei, SUN Jiang, QU Zhanqing, et al. Thermo-hydro-mechanical coupling model and comprehensive evaluation method of high temperature geothermal extraction[J]. Progress in Geophysics, 2019, 34(2): 668-675.
[5] 张 宁. 煤岩损伤演化与瓦斯渗流的热流固耦合分析[D]. 徐州: 中国矿业大学, 2017.
[6] 秦 涛, 张凯云, 刘永立. 不同温度下含瓦斯煤岩体的多场耦合数值模拟[J]. 黑龙江科技学院学报, 2014(4): 341-344.
QIN Tao, ZHANG Kaiyun, LIU Yongli. Multifold coupling numerical simulation of coal and rock containing gas under different temperature [J]. Journal of Heilongjiang University of Science and Technology, 2014(4): 341-344.
[7] 马海峰. 深部开采煤层瓦斯压力场特征研究与应用[D]. 北京: 中国矿业大学(北京), 2015.
[8] 马 忠. 基于热流固耦合的瓦斯抽采数值模拟研究[D]. 淮南: 安徽理工大学, 2014.
[9] 张宗宝, 翟世龙. 对鹤岗矿区峻德煤矿南三区F9断层发育规律的分析[J]. 山东煤炭科技, 2011(5): 124-125.
ZHANG Zongbao, ZHAI Shilong. Hegang coal mine on southern areas Junde F9 faults understanding of the law [J]. Shandong Coal Technology, 2011(5): 124-125.
[10] 赵德海, 苏循新. 鹤岗盆地构造特征及其演化[J]. 煤炭技术, 2008(6): 136-137.
ZHAO Dehai, SU Xunxin. Hegang basin′s conformation characteristics and itsevolvement [J]. Coal Technology, 2008(6):136-137.
[11] 蔡 超. 鹤岗矿区石头河子组层序地层格架与构造控煤分析[D]. 北京: 中国地质大学(北京), 2010.
[12] 蔡 超, 时 伟, 曹代勇. 鹤岗盆地断裂构造特征与地应力演化史分析[J]. 中国煤炭地质, 2016, 28(3): 8-11,25.
CAI Chao, SHI Wei, CAO Daiyong. Faulted structural features and crustal stress evolution history analysis in Hegangbasin [J]. Coal Geology of China. 2016, 28(3): 8-11, 25.
[13] 王 敏. 鹤岗、鸡西矿区原位煤层气藏开发类型判识研究[D]. 徐州: 中国矿业大学, 2017.
[14] 王晓永. 鹤岗盆地新一矿区煤层气资源特征分析[J]. 中国新技术新产品, 2016(5): 125.
WANG Xiaoyong. Characteristics of coal bed methane resources in the new mining area of Hegangbasin [J]. China’s New Technology and New Products, 2016(5):125.
[15] 王世辉, 王有智, 许承武, 等. 鹤岗盆地煤层气资源潜力分析[J]. 中国煤层气, 2012, 9(1): 18-22.
WANG Shihui, WANG Youzhi, XU Chengwu, et al. Study of potentials of CBM resources in Hegang basin [J]. China Coal Bed Methane, 2012, 9(1): 18-22.
[16] 张宗宝, 翟世龙. 鹤岗矿区峻德煤矿地质条件分类[J]. 山东煤炭科技, 2011(6): 102, 106.
ZHANG Zongbao, ZHAI Shilong. Classification of geological conditions of Junde coal mine in Hegang mining area [J]. Shandong Coal Technology, 2011(6): 102, 106.
[17] 毛 毳, 邹文斌, 孙世轩, 等. 主成分分析法在煤储层评价中的应用—以鹤岗煤矿为例[J]. 中国煤炭地质, 2016, 28(11): 15-18, 24.
MAO Cui, ZOU Wenbin, SUN Shixuan, et al. Application of principal component analysis in coal reservoir assessment—a case study of Hegang coal field [J]. Coal Geology of China, 2016, 28(11): 15-18, 24.
[18] 张 超. 鸡西、鹤岗盆地烃源岩“三史”及煤体结构控气特征分析[D]. 徐州: 中国矿业大学, 2018.
[19] 贾天让. 煤矿瓦斯赋存和运移的力学机制及应用研究[D]. 大连: 大连理工大学, 2014.
[20] 贾天让, 闫江伟, 王 蔚, 等. 辽宁省煤矿瓦斯赋存构造控制规律与瓦斯分带划分[J]. 中国安全生产科学技术, 2014, 10(4): 24-30.
JIA Tianrang, YAN Jiangwei, WANG Wei, et al. Tectonic-level-control rule and zone-dividing of coalmine gas occurrence in Liaoning province [J]. Journal of Safety Science and Technology, 2014, 10(4): 24-30.
[21] 周 静, 刘锡明, 张国华. 黑龙江省煤矿高温热害分析及防治措施[J]. 中国矿业, 2009, 18(5): 104-106, 109.
ZHOU Jing, LIU Ximing, ZHANG Guohua. Mine heat-harm analysis and prevention measures in Heilongjiang [J]. China Mining Magazine, 2009, 18(5): 104-106, 109.
