0 引 言
煤层渗透率的大小是制约瓦斯抽采和煤层气开发利用的关键因素。而我国绝大部分煤层的渗透率较低(小于0.1 m2/(MPa·d)),如何提高煤层的透气性是瓦斯防治中亟待解决的关键问题,也是煤层气开发利用研究的重点[1-5]。近年来,水力压裂作为一种大范围的增透措施被广泛使用在煤层增透领域,并取得了一定效果。然而,传统的长钻孔压裂存在着自身的不足:①文献[6]研究发现,长钻孔压裂时,裂纹在延展过程中,要经过钻孔所导致的应力集中区域,应力集中限制了裂纹的扩展,使压裂后所形成的裂纹沟通煤层自身裂纹的范围有限;②文献[7]认为长钻孔压裂时,一旦裂纹沿某一弱面开始延展以后,其余方向上的裂纹往往不再扩展,也就是说,不管压裂段有多长,所形成的大裂纹的量并不一定多。
围绕着怎么样使裂纹扩展得更长、更宽这一核心,煤层增透领域的一些学者开始探索采用定向射孔联合压裂的技术来提高增透效果[8-10]。这一技术的突出优势[11-13]主要体现在:①压裂前先射孔,来引导压裂裂纹在远离孔壁的地方起裂,从而消除应力集中对裂纹扩展的影响;②便于实现分段射孔压裂,将长钻孔分为若干段,在每一段的相对弱面上扩展形成大裂纹,从而增加整个钻孔范围内的大裂纹数量。实现定向射孔联合压裂的核心问题是裂纹在煤层中的扩展规律及如何控制裂纹扩展。针对裂纹在煤层中的扩展规律,近几年的研究和探索发现[14-16]:对于一个三维均匀体来说,当裂纹面垂直于最小水平主应力时,裂纹的导流性能最好。通常把垂直于最小水平主应力的裂纹面称为最佳裂纹面。但是对于在最佳裂纹面上,如何选择射孔方向,射孔深度对裂纹扩展的影响等方面的研究有待进一步加强。鉴于此,笔者采用基于ABAQUS平台的扩展有限元方法,模拟研究了定向射孔参数对裂纹扩展规律的影响,丰富了水力压裂裂纹在煤层中扩展规律的基础理论,以期为井下开展定向射孔联合压裂综合增透提供指导。
1 裂纹扩展有限元模型
1.1 应力平衡方程
假设煤岩为各向同性的弹性介质[17],根据虚功原理,可以得到煤岩受力平衡方程的弱积分形式[18]:
(1)
式中:Ω为二维扩展域;Γt为煤岩应力边界;Γc为裂纹边界;![]() 为单位体积力;
为单位体积力;![]() 为单位面积力;
为单位面积力;![]() 为有效应力;
为有效应力;![]() 为虚应变;
为虚应变;![]() 为虚位移;
为虚位移;![]() 为裂纹内的流体压力;β为边界Γc上的位移。
为裂纹内的流体压力;β为边界Γc上的位移。
式(1)中,左边表示煤岩单元变形所产生的虚应变能,右端第1项为体积力做功,第2项为水压力在裂纹面上的做功,第3项为外边界力做功。
1.2 应力平衡方程的扩展有限元近似
扩展有限元方法通过引入增强函数H(x)来处理裂纹位移场的不连续问题;裂尖增强函数Fl(x) 来处理裂尖位移场奇异问题,使得在模拟裂纹扩展过程中无需重新划分网格,且裂尖区域不需要加密。对于扩展有限元法,单元内任意高斯点x的位移可以表示为[19]
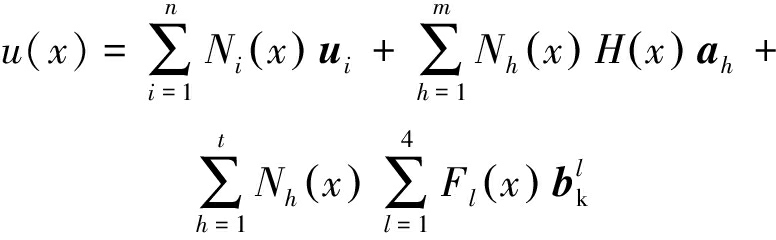
(2)
式中:n为单元常规有限元节点数;i为形函数和常规节点自由度向量编号;l为裂尖增强函数和裂纹尖端节点自由度向量编号;Ni(x)为形函数;u i为常规有限元节点自由度向量;h为裂纹单元节点;Nh(x)为单元中含有间断的节点形函数;m为被裂纹贯穿节点;ah为裂纹面两边增强节点自由度向量;t 为裂纹尖端节点数;![]() 为裂纹尖端节点自由度向量。
为裂纹尖端节点自由度向量。
增强函数在裂纹面的一侧取值为 1,另一侧取值为-1。裂尖增强函数Fl(x)在以裂尖为原点极坐标系下的表达式为
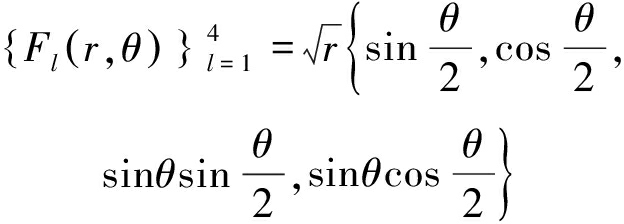
(3)
其中:(r, θ)分别为极坐标系中的半径和极角。裂纹上x点对应的裂纹面两侧的2个点分别记为x+和x-,而x+和x-点的位移由Heaviside增强函数和裂尖增强函数第1项![]() 的值决定。x点的裂纹开度w为
的值决定。x点的裂纹开度w为
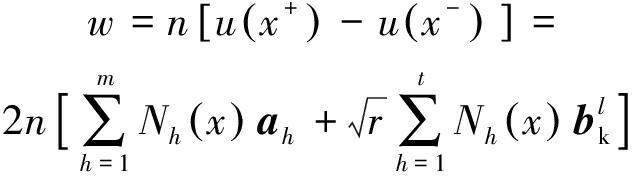
(4)
将扩展有限元近似位移函数式(2)代入式(1)中,可以得到煤岩变形总体刚度方程为
KU=F
(5)
式中:F为各单元节点等效载荷的集合;K为各单元节点刚度矩阵的集合;U为单元节点位移向量,包括传统有限元节点位移位移向量u、裂纹贯穿单元节点位移向量a和裂纹尖端单元节点位移向量b,即:U={u,a,b}T。
2 模型建立及参数选择
基于扩展有限元理论,在ABAQUS平台上建立如图1所示的计算模型。
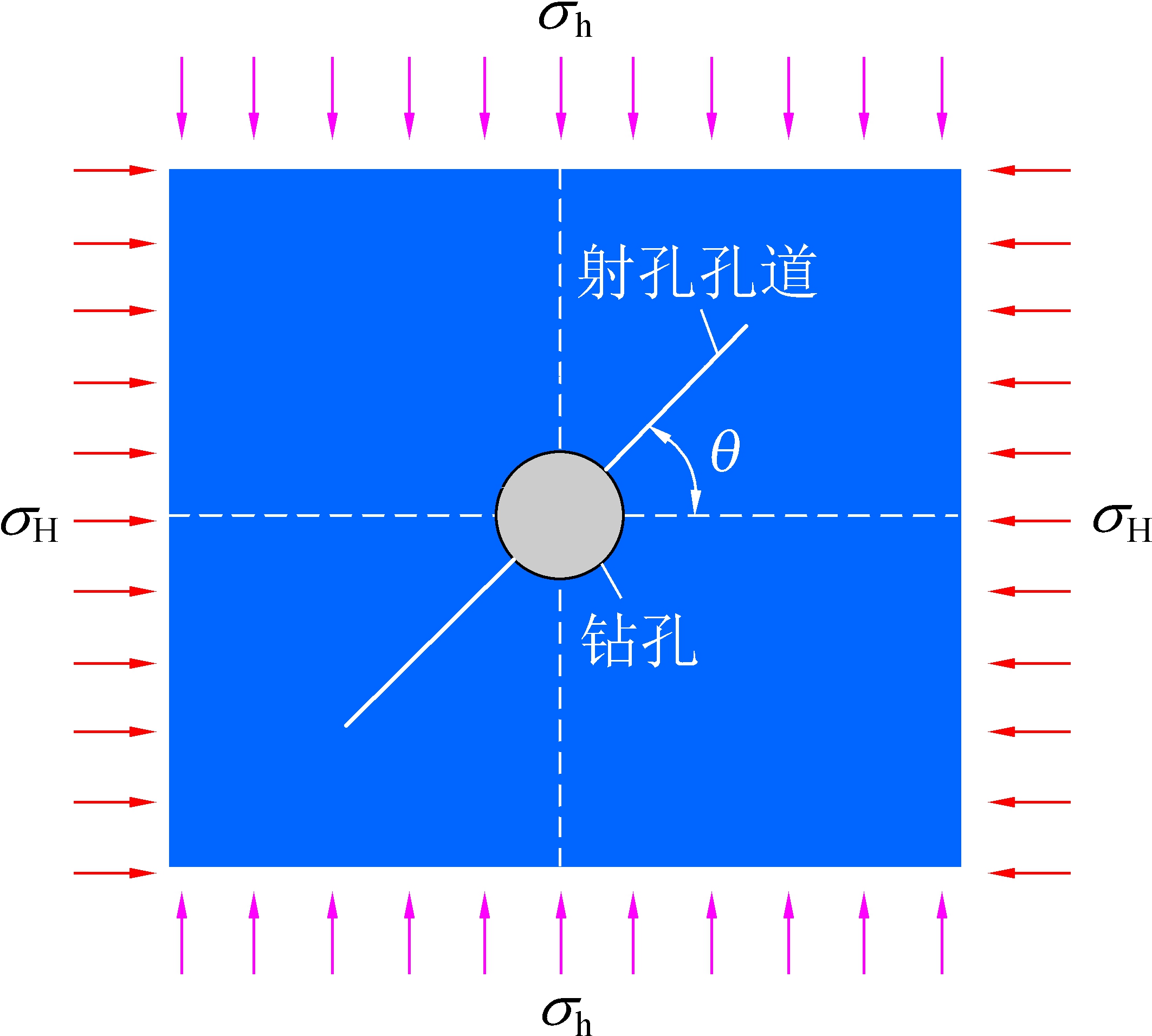
图1 数值模型示意
Fig.1 Numerical model
图1中σH为最大水平主应力,σh为最小水平主应力;θ为射孔方位角(射孔方向与最大主应力之间的夹角),其取值范围为0°~90°。通过 ABAQUS平台定义一条直线,代表射孔孔道[18],用直线的长度来表征射孔深度,直线与σH之间的夹角来反映射孔方位角。煤层基本参数选取谭鹏[15]的试验数据如下:

模型尺寸/(m×m)0.3×0.3钻孔半径/mm20弹性模量/GPa4.05泊松比0.25最小水平主应力/MPa4最大水平主应力/MPa9抗拉强度/MPa0.03孔隙率/%3.7
计算模型的边界为封闭固定边界,约束水平和竖直方向边界节点位移,以最大主应力准则作为判断裂纹起裂的依据;网格单元类型为CPE4RT。
3 模拟结果及分析
3.1 平面应力差对裂纹扩展的影响
取射孔方位角θ=45°,保持最小水平主应力σh=4 MPa不变,依次取最大水平主应力σH=6、7、8、9、10、11 MPa,模拟研究主应力差对裂纹扩展的影响。其中,平面应力差(σH-σh)为2、3、5、7 MPa时最终形成的裂纹形态如图2所示。不同平面应力差下裂纹的起裂压力及裂纹的宽度如图3所示。

图2 不同平面应力差下的裂纹扩展情况模拟结果
Fig.2 Simulation results of crack propagation under different stress in plane
由图2和图3可知:裂纹先在射孔的孔底处起裂,并最终转向了与最大水平主应力一致的方向上继续扩展。应力差越大,最终形成的裂纹越长。而从不同应力差下裂纹的起裂压力及最终形成的裂纹宽度来看,平面应力差由2 MPa增加到7 MPa的过程中,起裂压力增加了94.4%,裂纹宽度增加了375%。这说明,平面应力差最主要影响的是最终形成的裂纹长度和宽度。
设水平应力比为k=σH/σh,则k对裂纹转向半径的影响可利用裂纹的平面应变模型表示为[20]
(6)
式中:LR为裂纹转向的曲率半径;K1为应力强度因子。k越大,则裂纹转向曲率半径越小,即转向路径更短,裂纹扩展的阻力更小,易形成长而宽的裂纹。
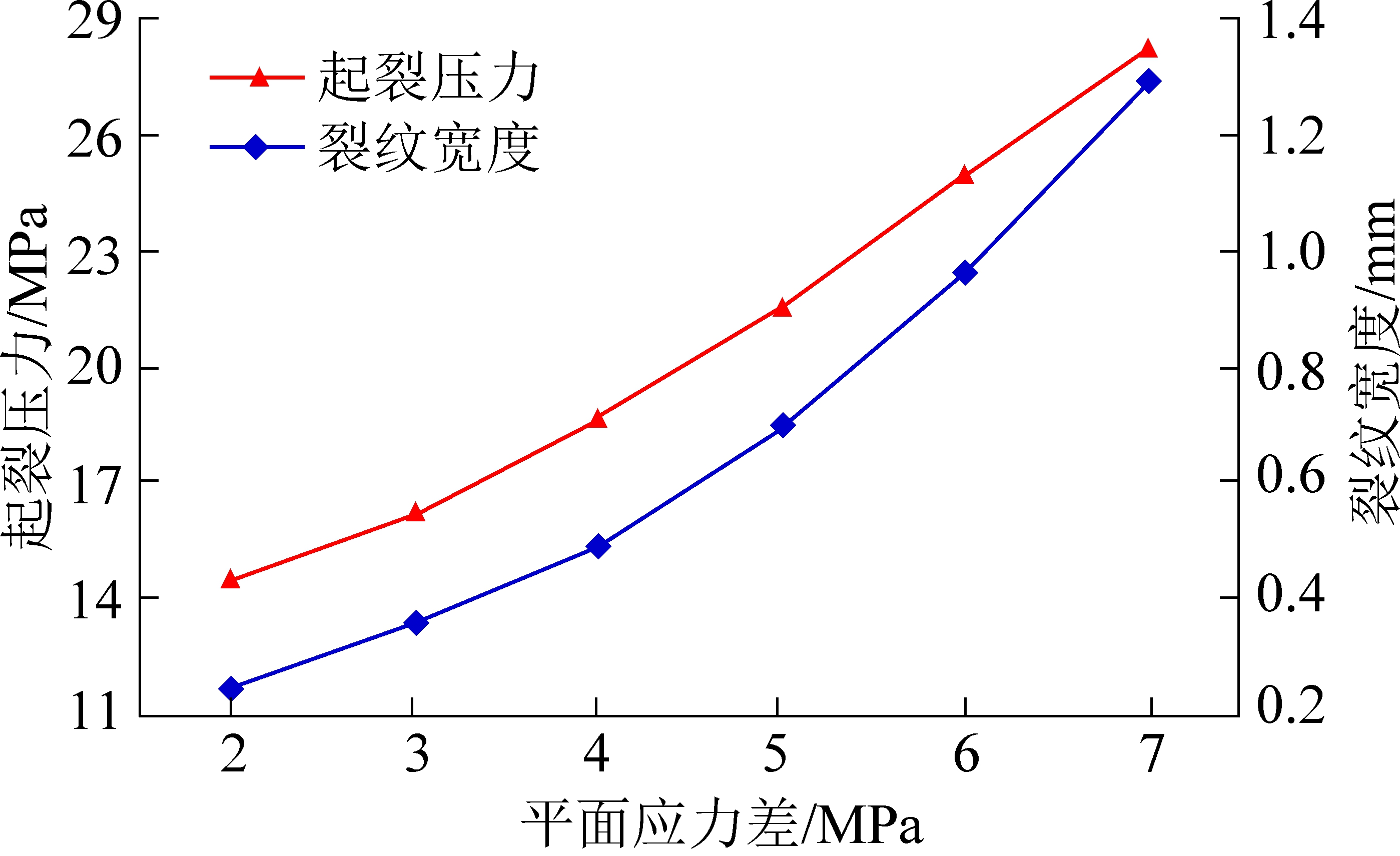
图3 起裂压力及裂纹宽度随平面应力差的变化关系
Fig.3 Relationship between initiation pressure and
crack width under difference plane stress
3.2 射孔方位角对裂纹扩展的影响
取最小水平主应力σh=4 MPa,最大水平主应力σH=10 MPa,射孔方位角分别取0°、15°、30°、45°及60°时形成的裂纹最终形态如图4所示。不同射孔方位角下裂纹的起裂压力及最终形成的裂纹宽度如图5所示。
由图4和图5可知:射孔方位角越大,裂纹由射孔方向转向最大主应力方向时,裂纹在转向处的扭曲程度越高,所形成的裂纹越短。而当射孔方位角等于0°时,也就是沿着与最大主应力一致方向的射孔,裂纹在扩展过程中不存在转向的问题,所形成的裂纹最长。从不同射孔方位角下裂纹的起裂压力及最终形成的裂纹宽度来看,射孔方位角从0°增加到60°的过程中,裂纹的起裂压力增加了187%,而裂纹宽度降低了84%。这说明射孔的方位角越大,裂纹在转向处流动路径越复杂,转向处的阻力和压降更大,使裂纹难以扩展形成更长更宽的大裂纹。因此,

图4 不同射孔方位角时裂纹扩展情况的模拟结果
Fig.4 Simulation results of crack propagation under different perforation azimuth angles
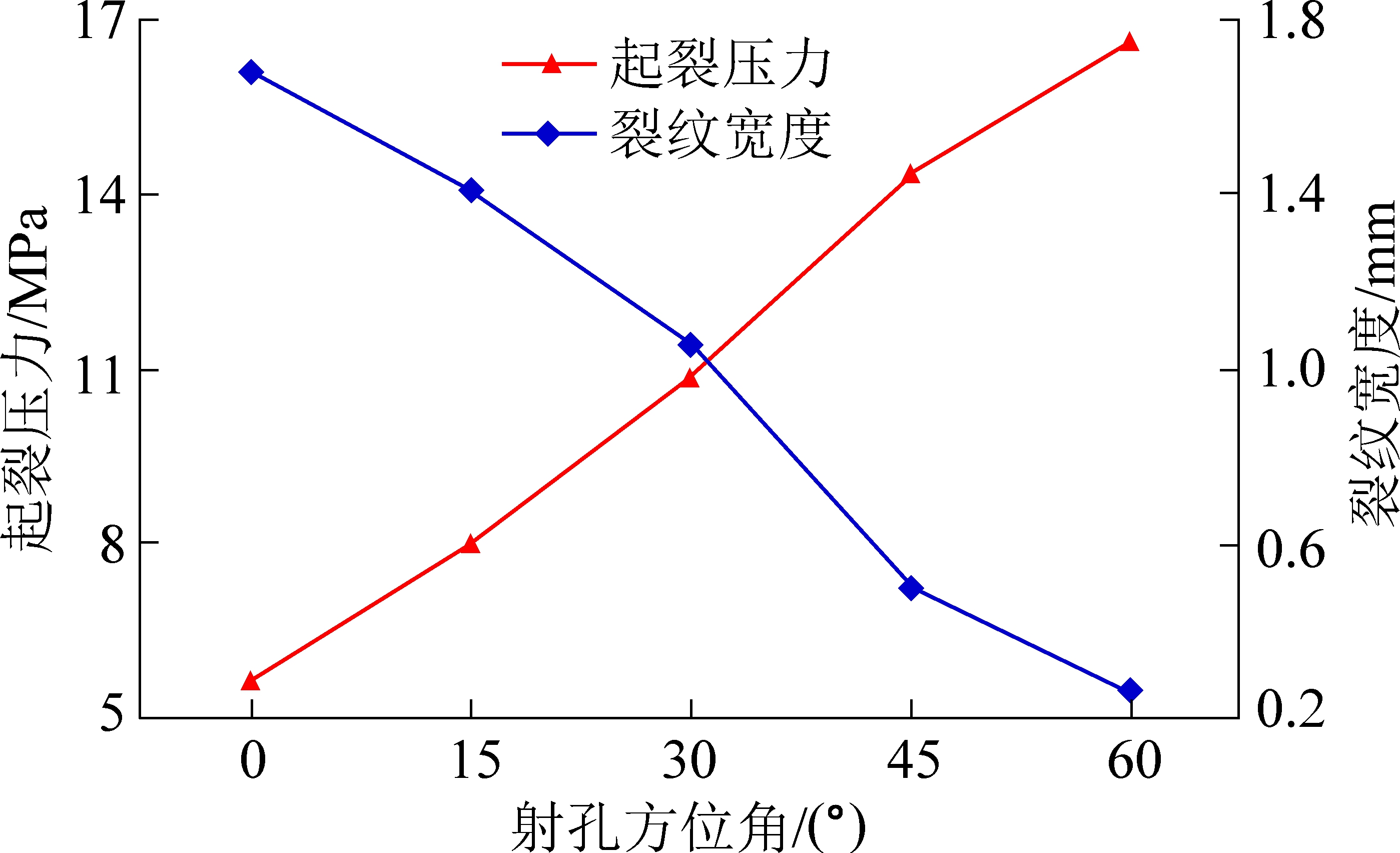
图5 不同射孔方位角时的起裂压力和裂纹宽度
Fig.5 Initiation pressure and crack width under
different perforation azimuth angles
在实际的施工中,要尽可能准确地取得煤层地应力分布情况,选择与最大主应力一致的方向上射孔。
在其他条件不变的情况下,裂纹的起裂压力随射孔方位角之间的关系可以表示为[20]
(7)
式中:Pf为裂纹的起裂压力,MPa;Pp为孔隙压力,MPa;μ为岩石的泊松比;σv 为垂向压力,MPa;σt为煤岩体的抗拉强度,MPa;α为孔隙弹性系数。
3.3 射孔深度对裂纹扩展的影响
令射孔方位角为45°,平面应力差为6 MPa,射孔深度L与钻孔半径r的比值分别取1.0、1.5、2.0、2.5、3.0、3.5。其中,L/r=1.0、1.5、2.0、3.0时最终形成的裂纹形态如图6所示。不同射孔深度下裂纹的起裂压力及最终形成的裂纹宽度如图7所示。
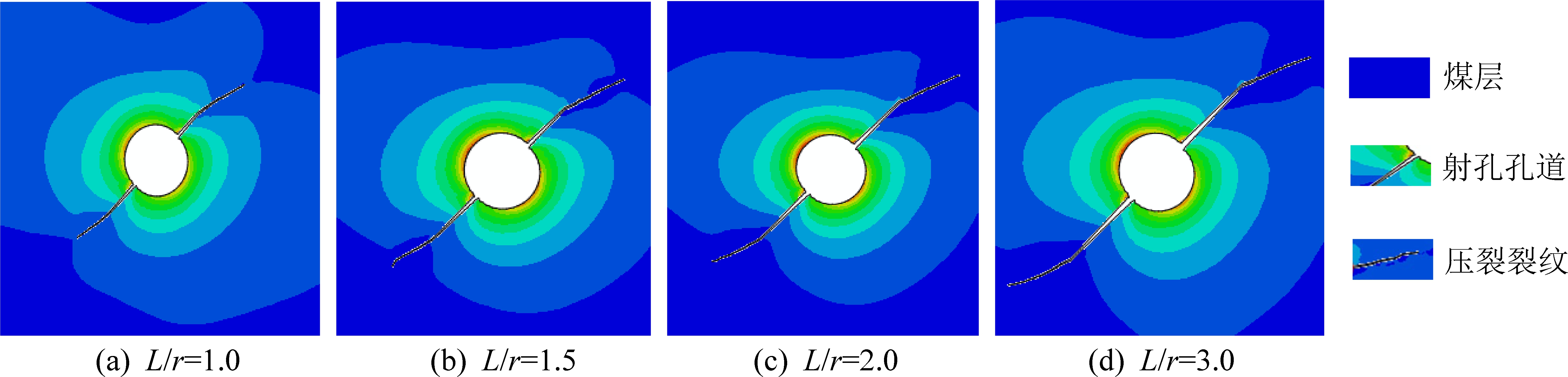
图6 不同射孔深度下的裂纹扩展情况模拟结果
Fig.6 Simulation results of crack propagation under different perforation depth

图7 起裂压力及裂纹宽度随L/r的变化关系
Fig.7 Relationship between initiation pressure and crack
width with L/r
由图6和图7可知,射孔深度对最终形成的裂纹长度有显著影响,射孔深度越深,最终形成的裂纹越长。而从不同射孔深度下裂纹的起裂压力及裂纹宽度来看,当射孔深度与钻孔半径的比值从1.0增加到3.5的过程中,起裂压力降低了51.4%,而裂纹的宽度增加了145%。这说明,射孔深度越深,离钻孔所导致的应力集中区域越远,越有利于裂纹的扩展。因此上,在实际的施工过程中,需要选择合适的射孔参数来到达较为理想的射孔深度。
3.4 模拟结果验证
为了验证数值模拟结果的正确性,选取射孔方位角为0°和60°模拟的裂纹几何形态与文献[15]物理试验结果进行对比,如图8所示。并将不同射孔方位角下的模拟的裂纹起裂压力与试验数据[15]进行对比,见表1。

图8 θ=0°和θ=60°物理试验裂纹与数值模拟裂纹几何形态对比
Fig.8 Comparison of crack geometry between physical
test and numerical simulation crack with θ=0°and θ=60°
表1 数值模拟的起裂压力与物理试验数据对比
Table 1 Comparison of numerical simulation results and
physical test data of crack initiation pressure
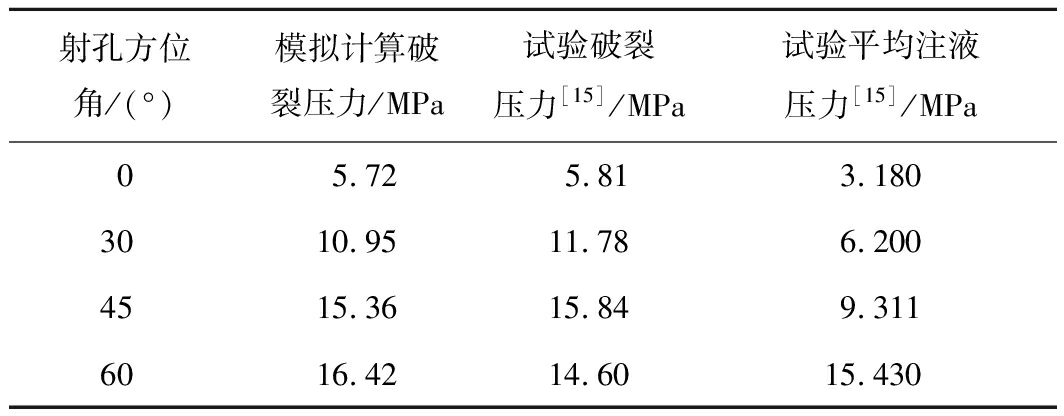
射孔方位角/(°)模拟计算破裂压力/MPa试验破裂压力[15]/MPa试验平均注液压力[15]/MPa05.725.813.1803010.9511.786.2004515.3615.849.3116016.4214.6015.430
由图8可知:模拟的裂纹的几何形态与文献[15]的物理试验结果有较好的匹配性:裂纹先在射孔的孔底处起裂,并最终转向与最大主应力一致的方向上继续扩展;而沿着最大主应力方向的射孔,裂纹起裂后一直沿着最大主应力的方向扩展,形成的裂纹更长更宽。
数值模拟的裂纹起裂压力与试验测得的数据基本一致。但在射孔方位角为60°时,模拟数据与试验数据之间误差较大,表明在实际的压裂过程中,煤岩的破裂压力除了受射孔方位角的影响以外,还受煤层割理走向及钻孔的空间布置等因素影响,取值范围变化大。但随着射孔方位角的增大,裂纹的起裂压力呈现增加趋势,引文中的平均注液压力也很好地反应了这一规律。
4 结 论
1)射孔转压裂时,裂纹首先在射孔的孔底处起裂,并最终转向了与最大水平主应力一致的方向上继续扩展。平面应力差对起裂压力和裂纹宽度有明显影响,增大平面应力差,起裂压力增加的同时裂纹宽度有了显著的增加,易形成长而宽的裂纹。
2)射孔方位角对起裂压力、最终形成的裂纹长度和宽度有显著影响。随着射孔方位角的增加,起裂压力呈现增大趋势,易形成较窄、较短的裂纹。在实际的施工过程中,要尽可能准确地取得煤层的地应力分布情况,选择与最大主应力一致的方向上射孔。
3)较长的射孔能减小裂纹的起裂压力,并能形成较长较宽的裂纹。在实际的施工过程中,要选择合适的射孔参数,达到较为理想的射孔深度。
[1] 张 义,鲜保安,孙粉锦,等. 煤层气低产井低产原因及增产改造技术[J].天然气工业,2010,30 (6):55-59,128.
ZHANG Yi,XIAN Bao’an,SUN Fenjin,et al.Reason analysis and stimulation measures of low coal bed methane gas production wells[J]. Natural Gas Industry,2010,30(6):55-59,128.
[2] 廖永远,罗东坤,李婉棣.中国煤层气开发战略[J].石油学报,2012,33(6):1098-1102.
LIAO Yongyuan,LUO Dongkun,LI Wandi.Development strategy analysis of China’s CBM[J].Acta Petrolei Sinica, 2012,33(6): 1098-1102.
[3] 王耀锋,何学秋,王恩元,等.水力化煤层增透技术研究进展及发展趋势[J].煤炭学报,2014,39(10):1945-1955.
WANG Yaofeng,HE Xueqiu,WANG Enyuan,et al.Research progress and development tendency of the hydraulic technology for increasing the permeability of coal seams[J].Journal of China Coal Society,2014,39(10):1945-1955.
[4] 张小东,张 鹏,刘 浩,等.高煤级煤储层水力压裂裂缝扩展模型研究[J].中国矿业大学学报,2013,42(4):573-579.
ZHANG Xiaodong,ZHANG Peng,LIU Hao,et al.Fracture extended model under hydraulic fracturing engineering for high rank coal reservoirs[J]. Journal of China University of Mining & Technology, 2013,42(4):573-579.
[5] 李 杰.特厚煤层综放工作面地面钻孔抽采治理瓦斯技术[J].煤炭科学技术,2019,47(3):150-155.
LI Jie. Gas control technology of ground drilling extraction in fully-mechanized caving face of extra thick coal seam[J]. Coal Science and Technology, 2019,47(3):150-155.
[6] 徐幼平,林柏泉,翟 成,等.定向水力压裂裂纹扩展动态特征分析及其应用[J].中国安全科学学报,2011,21(7):104-110.
XU Youping, LIN Baiquan, ZHAI Cheng,et al. Analysis on dynamic characteristics of cracks extension in directional hydraulic fracturing and its application[J]. China Safety Science Journal, 2011, 21(7):104-110.
[7] 康毅力,周来诚,池晓明,等.致密煤岩气藏压裂液损害实验评价[J].断块油气田,2014,21(2):269-272.
KANG Yili, ZHOU Laicheng, CHI Xiaoming,et al.Experimental evaluation on damage induced by fracturing fluids in tight coal rock gas reservoirs[J]. Fault-block Oil & Gas Field, 2014,21(2):269-272.
[8] LIU Da’an, SHI Xiaoshan, ZHANG Xin,et al. Hydraulic fracturing test with prefabricated crack on anisotropic shale: Laboratory testing and numerical simulation[J].Journal of Petroleum Science & Engineering, 2018.
[9] 王成旺,季 亮,车延前,等.煤层气井压裂波及邻井原因分析及防治措施研究[J].煤炭科学技术,2018,46(12):197-202.
WANG Chengwang,JI Liang,CHE Yanqian,et al. Study on cause analysis and prevention measures of fracturing in coalbed methane well affected to adjacent wells[J]. Coal Science and Technology,2018,46(12):197-202.
[10] 富 向.井下点式水力压裂增透技术研究[J].煤炭学报,2011, 36(8):1317-1321.
FU Xiang. Study of underground point hydraulic fracturing increased permeability technology[J].Journal of China Coal Society, 2011, 36(8):1317-1321.
[11] 王 利,张新生,曹运兴,等.定向射孔水力压裂平面裂缝形态数值研究[J].河南理工大学学报(自然科学版),2018,37(2): 124-132.
WANG Li,ZHANG Xinsheng,CAO Yunxing,et al. Numeric simulation of plane strain hydraulic fracturing under multi-oriented perforations[J]. Journal of Henan Polytechnic University (Natural Science),2018,37(2):124-132.
[12] 解经宇,蒋国盛,王荣璟,等.射孔对页岩水力裂缝形态影响的物理模拟实验[J]. 煤炭学报, 2018, 43(3):776-783.
XIE Jingyu,JIANG Guosheng,WANG Rongjing,et al. Experimental investigation on the influence of perforation on the hydraulic fracture geometry in shale[J]. Journal of China Coal Society, 2018, 43(3):776-783.
[13] PANG Yihui,WANG Guofa,DING Ziwei. Mechanical model of water in-rush from coal seam floor based on triaxial seepage experiments[J].International Journal of Coal Science & Technology, 2014,1 (4):428-433.
[14] CHANG Xin, WANG Huaidong, CHENG Yuanfang, et al. Experimental study of fracture propagation mechanisms by oriented perforation technology for SRV fracturing[J]. Advances in Petroleum Exploration and Development, 2015,10(2), 44-49.
[15] 谭 鹏,金 衍,侯 冰,等.煤岩定向井水力裂缝起裂及非平面扩展实验[J].石油勘探与开发,2017, 44(3): 439-445.
TAN Peng, JIN Yan, HOU Bing,et al. Experimental investigation on fracture initiation and non-planar propagation of hydraulic fractures in coal seams[J]. Petroleum Exploration and Development, 2017, 44(3): 439-445.
[16] 石欣雨,文国军,白江浩,等. 煤岩水力压裂裂缝扩展物理模拟实验[J]. 煤炭学报,2016,41(5):1145-1151.
SHI Xinyu,WEN Guojun,BAI Jianghao,et al. A physical simulation experiment on fracture propagation of coal petrography in hydraulic frac-turing[J].Journal of China Coal Society, 2016, 41(5):1145-1151.
[17] 陆沛青,李根生,黄中伟,等. 脉动水力压裂过程中煤层应力扰动特征的数值模拟分析[J].振动与冲击,2015,34(21):210-216.
LU Peiqing,LI Gensheng,HUANG Zhongwei,et al.Numerical simulation for stress disturbance features of coal beds during hydro-fracturing[J]. Journal of Vibration and Shock,2015,34(21):210-216.
[18] 曾青冬,姚 军.基于扩展有限元的页岩水力压裂数值模拟[J].应用数学和力学, 2014,35(11):1239-1248.
ZENG Qingdong, YAO Jun. Numerical simulation of shale hydraulic fracturing based on the extended finite element method[J].Applied Mathematics and Mechanics,2014,35(11):1239-1248.
[19] 陈军斌,魏 波,王汉青.定向射孔参数对压裂裂纹扩展规律的影响[J].断块油气田,2017,24(3):391-395.
CHEN Junbin,WEI Bo,WANG Hanqing. Influence of directional parameters on fracture propagation[J]. Fault-block oil & gas field,2017,24(3):391-395.
[20] 姜 浒,陈 勉,张广清,等.定向射孔对水力裂缝起裂与延伸的影响[J]. 岩石力学与工程学报,2009,28(7):1321-1326.
JIANG Hu,CHEN Mian,ZHANG Guangqing,et al. Impact of oriented perforation on hydraulic fracture initiation and propagation[J].Chinese Journal of Rock Mechanics and Engineering, 2009,28(7):1321-1326.
