0 引 言
岩石宏观破坏是由于细观结构的微裂隙的成核、扩展和贯通引起的，因而对岩石微裂隙进行细观尺度深入研究是揭示宏观破坏失稳规律的有效手段[1-3]。声发射(acoustic emission, AE)作为岩石破坏过程中的一种伴生现象，蕴含着岩石内部损伤过程的大量信息[4-7]。WANG等[8-9]将声发射参数演化突变特征作为判断岩石破坏失稳的前兆信息。张艳博等[10]通过在频域上分析岩石变形破裂全过程声发射波形信号，获得了岩石失稳主频前兆信息。左建平等[11]通过对单体岩石、单体煤和煤岩组合体进行单轴试验下的声发射测试，获得了三者之间声发射行为及时空演化机制的差异性。刘飞跃等[12]通过FLAC3D内嵌FISH语言二次开发将岩石破坏过程中的声发射损伤建立到力学模型中，获得了岩石破裂动态应力场，验证了岩石细观损伤表征方法的合理性。以上研究成果得出了很多有价值的结论，但未从破裂本质上从破裂源本质上揭示岩石破坏孕育演化的力学行为。
为更好地揭示微破裂特征，国内外诸多学者[13]运用矩张量来表示震源体力模型，研究岩石破坏演化过程。OHTSU等[14]通过设计一系列室内混凝土试件声发射试验研究来组合验证，提出了以MDC分量占矩张量的比重PDC来量化震源事件破裂类型的SiGMA矩张量分析方法。MANTHEI等[15]开展了三轴加载条件下岩盐声发射破裂损伤试验，获得了岩石破裂前期损伤特征。AKER等[16]对存在水平钻孔的砂岩试样进行了三轴加载声发射监测试验，证明了孔洞的存在严重影响声发射事件的定位和震源的破裂类型。刘培洵等[17]对远场P波反演声发射矩张量的适用条件和算法进行了较为详细的描述，并演算了矩张量反演结果的可靠性。任会兰等[18]基于SIGMA矩张量法揭示了混凝土宏观拉伸破坏的细观裂纹扩展机制，获得拉伸裂纹运动主导了宏观劈裂破坏的现象。因此，从震源本质上探究内部裂纹的演化规律，分析裂纹的产生类型和运动方向，能更好地了解微裂纹扩展与宏观破坏之间的演化关系。
基于此，利用声发射技术和高速摄像技术实时监测岩石变形失稳过程，结合声发射信息与岩石破裂的响应关系，分析岩石变形各阶段声发射参数特征和失稳前兆信息，并运用矩张量理论揭示岩石破裂孕育力学行为，探究微观破裂发展和宏观破坏孕育之间的演化关系。
1 单轴压缩下砂岩声发射试验
1.1 试样制备
试验所用砂岩试样均取自山西某矿煤层底板，该矿围岩存在弱冲击倾向性，部分巷道发生底鼓现象，为进一步评价围岩力学性能而开展此次综合力学试验。因试验应用绝对矩张量反演理论，为满足反演远场假设的尺寸要求将获取的样品加工成直径70 mm、高度140 mm的圆柱体试件。为提高试验结果的精确度和稳定性，每个试件两端面不平行度小于0.02 mm。各试件相应的实际尺寸和基本力学参数见表1。
表1 岩样尺寸及力学参数
Table 1 Sample size and mechanical parameters
编号直径/mm高度/mm密度/(g·cm-3)抗压强度/MPaP波波速/(m·s-1)S169.41139.562.45755.442 220S269.17139.632.45248.061 820S370.02139.152.45454.002 080S469.56139.222.42155.872 230S569.41138.872.31959.022 150S669.36139.112.35731.571 900S769.68139.422.33452.401 930
1.2 试验方法
试验所用加载设备为压力2 000 kN岩石三轴刚性压力试验机，采用单轴轴向位移控制加载，加载速率为0.1 mm/min，直至试样破坏。
AEwin声发射采集分析软件有2个采集模式：AE模式和TRA模式，AE模式为常规操作模式，各采集通道独立触发收集波形数据，当需要AE撞击数据、时间驱动数据和事件定位时选用该模式；TRA模式下系统只能采集波形数据，可实现同步触发采集，也只有根据此模式下采集的波形数据，才能较为准确地提取P波到时和初动振幅，实现震源机制的矩张量反演分析。试验采用2套PCI-II型声发射采集设备，分别在AE和TRA采集模式下采集数据，整个试验过程中，AE信号采集与加载过程实时同步进行。
同时，为实时记录岩石变形失稳的过程，试验采用千眼狼2F04M高速摄像仪拍摄记录，试验监测系统布置方式如图1所示。
图1 试验监测系统
Fig.1 Monitoring system of test
图2 AE传感器布置
Fig.2 Arrangement of AE sensors
为保证充分采集各传播方向上的P波，提高声发射事件定位精度并满足反演要求，试验将5个字母代表的AE传感器用于常规AE模式下数据采集，6个数字代表的AE传感器用于TRA模式下同步波形采集，布置方案如图2所示。将边缘传感器分别布置在离试样两端20 mm处，传感器与岩样表面之间涂抹适量耦合剂以保证接触充分，并用橡皮泥进行固定。将AE采集系统门槛值设定为45 dB，以减弱环境噪声影响，采样频率为1 MHz，前置放大器增益设为40 dB。试验开始前，先进行断铅试验，确保各通道信号采集良好；并调节采集硬件设置参数，提高AE定位精度，波速设置值见表1。
2 声发射试验结果及分析
2.1 岩石变形破坏声发射参数演化特征
声发射波形与岩石应力状态、内部结构、物质组成等信息存在相关性，当微裂纹开裂的方向、尺度及破裂类型不同时，波形上势必会有特征反映。如图3所示，撞击率、持续时间和AE主频3个参数的演化特征与各变形阶段有着较好的对应关系，撞击率为1 s内声发射撞击的累计数。在频域上存在3条极为明显的主频带，分别为低频带(90～130 kHz)、中高频带(250～280 kHz)、高频带(280～330 kHz)。在原始压密阶段Ⅰ，声发射活动较弱，且中高频带上数据分布较少。
图3 试样S4部分特征参数
Fig.3 Parameters of Sample S4
分析认为砂岩原始微裂纹和微孔洞等缺陷存在相对较少，尺度较小，致使声发射信号强度不高。在弹性变形阶段Ⅱ，声发射活动极少，而且各参数均处于较低水平。在加载时间550 s左右，Ⅲ阶段内试样开始发生塑性变形，裂纹稳定孕育扩展，中高频带数据开始增多，持续时间绝大多数处于500 μs以下。
试样在加载时间820 s左右进入屈服变形阶段IV，高强度声发射活动开始出现，各主频带明显加宽，且出现较为明显的中频带(130～250 kHz)，大量持续时间处于1 000 μs以上水平的活动出现。
在加载时间950 s左右试样达到峰值强度，出现宏观破坏，声发射活动极为活跃，撞击率达到最大值，4个主频带呈现上下贯通连接状态。在峰后残余变形阶段V，各声发射参数逐渐减弱，内部微裂纹急剧扩展，贯通形成宏观大尺度裂纹。因此，将声发射在中频带开始大量出现的现象作为砂岩破裂失稳前兆信息。
2.2 岩石微破裂强度时空分布特征
在岩石破裂孕育演化各阶段中，微观破裂起裂发展和宏观裂纹扩展贯通在波形参数尺度上必然存在着某些差异。对于由一定量裂纹单元组成的破裂，其孕育和扩展过程是时间与空间的函数。声发射作为伴随破裂起裂扩展而产生的弹性波，其远场波形可以当成是裂纹方向上无数裂纹单元所激发弹性波的叠加。在有限破裂尺度的情况下，监测点所记录到P波持续时间为裂纹破裂时间加上波的传播走时。然而，本试验试样尺寸有限，所以波形传播走时对波形持续时间产生的影响是有限的。
同时，由于裂纹开裂都是在瞬间完成，在不考虑破裂速度不均一，岩石不均匀性和传感器耦合效果等干扰因素的影响下，通道接收的波形持续时间与裂纹尺度存在正相关性。因此，可以根据波形信号持续时间参数的演化特征来定性地评价裂纹破裂孕育扩展过程。
为更好地表征破裂强度演化过程，将声发射能级取为Es=lg E，其中：E为声发射的能量，能量单位为aJ。图4为各变形阶段内事件空间分布特征，每个散点球代表一个定位事件，球的直径与持续时间呈同比例大小，颜色表示事件的能级，表征破裂强度(X、Y、Z为坐标轴)。由图4可以清晰地看出：试样屈服变形前内部损伤程度相对较小，微破裂和缺陷持续稳定发展，AE震源的破裂尺度相对较小，破裂间相互影响作用较小，处于微观稳定演化阶段。屈服阶段内，高能级高持续时间的事件分布相对集中，事件明显增多，微破裂间相互作用大幅增强，并且出现微裂纹局部归并、集结成核的现象，破裂尺度加大；达到峰值强度时，能量释放，微观裂纹相互贯通形成宏观裂纹。
图4 试样S4变形各阶段破裂尺度空间分布特征
Fig.4 Spatial distribution characteristics of crack scale in Sample S4 different deformation stage
峰后残余强度阶段V内，局部应变软化转移，大尺度裂纹分布相对分散，裂纹形成释放的能量与破裂尺度之间不再有正相关性。
结合图4d摄像仪采集结果可知，高强度、大破裂尺度的事件集中分布与宏观裂纹呈现区域较为一致。由图5可知，S6大尺度微破裂时空分布与宏观破坏部位对应较为一致。相比前人研究成果[9-10]，本次试验既从空间上分析了微观破裂的能量分布特征，也从波形特征上进一步探讨了破裂尺度与波形持续时间之间的响应关系。
图5 试样S6宏观裂纹扩展
Fig.5 Developing of Sample S6 macro-cracks
2.3 岩石微破裂机制在各变形阶段的分布特征
弹性波动力学认为当震源位于各向均匀介质内部一有限的体积元内时，对于震源而言，它所引起的总动量和总角动量必须守恒，如图6所示。引用力偶模型，并使用矩张量来表示震源的等效体力，能有效地描述震源的非弹性变形特征和弹性波的球面传播过程。基于震源点源假设和力偶模型，在监测点x处i方向上接收到的波形位移为
ui(x,t)=GijMij
(1)
其中：ui(x,t)为介质中震源在j方向的点力在点x处、t时刻、i方向上所产生的位移，是介质的脉冲响应；Gij为一个单力偶系激发的纯脉冲函数；Mij为震源等效体力的矩张量。
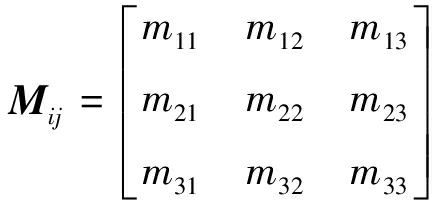
(2)
l—裂纹运动方向；n—破裂面法向；
1、2、3—空间直角坐标系的3个方向
图6 破裂面错动及矩张量模型
Fig.6 Crack face slipping and moment tensor model
KNOPOFF等[19]通过对角化求特征值将矩张量分解成各向同性部分(ISO)、纯双力偶成分(DC)和补偿线性矢量偶极成分(CLVD)3个部分，见式(3)。
(3)
其中，λ1、λ2、λ3为地震矩张量的3个特征值，相应的特征向量为各主轴方向。在主轴坐标系下，震源等价于3个互相垂直的力偶极子。当λ1 = λ2 = λ3时，Mij为纯膨胀源或纯压缩源；当λ1 = λ2，λ3 = 0时，Mij为纯剪切位错源。tr(M)= λ1 + λ2 + λ3为震源矩张量M的迹，在弹性波动学和角动量守恒的假设下，迹tr(M)在实际物理意义上可以反映点源的体积变化倾向；
式中第1项为各向同性部分(ISO)，第2项为纯剪切位错源(DC)，第3项为CLVD。
因此，一般的震源可以当成1个膨胀(压缩)中心、1个纯剪切位错和1个CLVD的线性叠加。OHTSU M[14]通过简化的SiGMA矩张量反演法，并采用优势判别方法对震源破裂类型进行识别。根据式(4)求解纯双力偶成分(DC)、补偿线性矢量偶极成分(CLVD)和各向同性部分(ISO)所占的比值A、B和C来对破裂分类进行量化处理。
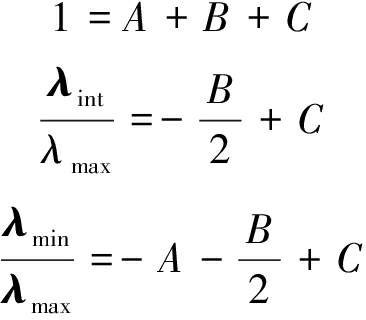
(4)
其中，λmax、λint、λmin分别为震源矩张量3个特征值中的最大特征向量、中间特征向量和最小特征向量。提出当A>60%时判定为剪切型破裂，当A<40%判定为张拉型破裂，当40%≤A≤60%判定为混合型破裂。同时，震源裂纹的运动方向向量l和破裂面的法线方向向量n可以表示为
(5)
式中：e1、e2、e3分别为λmax、λint、λmin所对应的单位特征向量，相互垂直，分别对应3个震源主轴方向。
为保证计算结果的误差尽可能小,保证选取的同步波形质量，首先通过设置门槛值55 dB以及聚类识别的方式进行整体滤波，这样各通道同步出的波形较为清晰且较为相似，排除了大量无效波形；再通过人工识别筛选各通道初动振幅都清晰波形的P波到时，利用SiGMA矩张量算法反演求得声发射震源机制演化特征。
试样S4各变形阶段微观破裂机制时空演化特征如图7所示。结合图4b和图7可知：在原始压密阶段I和弹性变形阶段II(图8)，破裂事件分布较少，大部分都集中分布在试样的下部和上部，且存在部分张拉破裂和混合破裂，破裂面法线方向和破裂运动方向均较为杂乱。
结合图8可知，进入塑性变形阶段Ⅲ，各种类型的破裂源无序杂乱分布，破裂源明显增多，剪切破裂开始成为主要破裂类型，整个试样都处于动态稳定无序的演化状态。屈服变形阶段Ⅳ内，破裂强度增加，微裂纹迅速扩展并集结成核，破裂源分布较为集中，多分布在试样上部，主要呈现为剪切破裂；微破裂破裂面法线方向和破裂运动方向由无序状态逐渐转化为有序行为状态，破裂方向大量倾向于轴向应力方向，直至宏观主裂纹出现，如图9所示。
图7 试样S4微破裂机制时空演化特征
Fig.7 Sample S4 micro-cracks evolution characteristic
图8 试样S4震源破裂特征
Fig.8 Behaviors of Sample S4 fracture sources
图9 试样S4微观破裂和最终宏观破裂
Fig.9 Sample S4 micro-cracks and macro-crac
前人研究[10]通过将声发射定位坐标嵌入到FLAC3D模型中，并对单元范围进行弱化处理，来反演岩石破裂应力场的演化特征，分析应力场弱化趋向，验证破裂结果；但未对声发射事件源的破裂模式进行分析探究。本次试验在前人的基础上，通过远场波形反演出微观破裂力学特征，从空间上分析了应变弱化的整体趋向。并结合高速摄像记录的试样破裂过程，发现试件整体表现为局部应力集中，宏观错动剪切破坏，与微观破裂主要破裂类型较为一致。由此可知，微观破裂机制演化特征与宏观破坏存在较为对应的响应关系，微观破裂状态从无序转化为有序的过程也是宏观破裂形成的过程。
3 结 论
1)在时序上，声发射参数演化特征与砂岩各变形阶段有着较好的对应关系，声发射频域上存在3条极为明显的主频带，分别为低频带(90～130 kHz)、中高频带(250～280 kHz)、高频带(280～330 kHz)；进入屈服变形阶段后，出现较为明显的中频带(130～250 kHz)，此现象可以作为破坏失稳前兆信息。
2)波形持续时间与裂纹尺度存在正相关性，可根据声发射持续时间的演化特征来定性地评价裂纹破裂孕育扩展演化过程；进入屈服阶段后峰值强度前，大破裂尺度、高破裂强度的微裂纹剧增，并呈现集结成核、局部弱化的现象。
3)试样达到屈服强度后，各微观破裂发展由无序状态逐渐转化为有序行为状态，剪切破裂成为主要的破裂方式，破裂方向大量倾向于轴向应力方向，此现象可作为岩石破坏失稳前兆特征。
[1] 何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803-2813.
HE Manchao, XIE Heping, PENG Suping,et al.Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803-2813.
[2] 彭瑞东, 谢和平, 鞠 杨.砂岩拉伸过程中的能量耗散与损伤演化分析[J]. 岩石力学与工程学报, 2007, 26(12): 2526-2531.
PENG Ruidong, XIE Heping, JU Yang. Analysis of energy dissipation and damage evolution of sandstone during tensile process[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2526-2531.
[3] 李庶林, 尹贤刚, 王泳嘉, 等. 单轴受压岩石破坏全过程声发射特征研究[J]. 岩石力学与工程学报, 2004, 23(15):2499-2503.
LI Shulin, YIN Xiangang, WANG Yongjia,et al.Studies on acoustic emission characteristics of uniaxial compressive rock failure[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2499-2503.
[4] CAI M, MORIOKA H, KAISER P K. Back-analysis of rock mass strength parameters using AE monitoring data[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(4): 538-549.
[5] 韩 兵, 杨宏伟. 不同围压下页岩三轴压缩声发射能量分布特性研究[J]. 煤炭科学技术, 2019, 47(4): 90-95.
HAN Bing, YANG Hongwei. Study on distribution characteristics of shale triaxial compression acoustic emission energy under different confining pressures[J]. Coal Science and Technology, 2019, 47(4): 90-95.
[6] 杜 帅, 王 炀. 基于声发射幅频分布的大理岩岩爆试验研究[J]. 煤炭科学技术, 2019, 47(11): 44-49.
DU Shuai，WANG Yang．Experimental study on rockburst test of marble based on acoustic emission amplitude-frequency distribution[J]. Coal Science and Technology, 2019, 47(11):44-49.
[7] 赵 程, 田加深, 松田浩, 等. 单轴压缩下基于全局应变场分析的岩石裂纹扩展及其损伤演化特性研究[J]. 岩石力学与工程学报, 2015, 34(4): 763-769.
ZHAO Cheng, TIAN Jiashen,SONG Tianhao,et al.Crack propagation and damage of rock under uniaxial compression based on global strain field analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 763-769.
[8] WANG Chunlai. Identification of early-warning key point for rockmass instability using acoustic emission/micro-seismic activity monitoring[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 71(5):171-175.
[9] WANG Chunlai. Evolution, monitoring and predicting models of rockburst[M].Singapore: Springer, 2017.
[10] 张艳博, 梁 鹏, 刘祥鑫, 等. 基于声发射信号主频和熵值的岩石破裂前兆试验研究[J]. 岩石力学与工程学报, 2015, 34(S1): 2959-2967.
ZHANG Yanbo, LIANG Peng, LIU Xiangxin,et al.Experimental study on precursor of rock burst based on acoustic emission signal dominant-frequency and entropy[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2959-2967.
[11] 左建平, 谢和平, 吴爱民, 等. 深部煤岩单体及组合体的破坏机制及力学特性研究[J]. 岩石力学与工程学报, 2011, 30(1):84-92.
ZUO Jianping, XIE Heping, WU Aimin,et al.Investigation on failure characteristics and mechanical behavior of deep coal-rock single body and combined body under different confining pressures[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(1): 84-92.
[12] 刘飞跃, 杨天鸿, 张鹏海, 等. 基于声发射的岩石破裂应力场动态反演[J]. 岩土力学, 2018, 39(4): 1517-1524.
LIU Feiyue, YANG Tianhong, ZHANG Penghai,et al.Dynamic inversion of rock fracturing stress field based on acoustic emission[J]. Rock and Soil Mechanics, 2018, 39(4): 1517-1524.
[13] 明华军, 冯夏庭, 张传庆,等. 基于微震信息的硬岩新生破裂面方位特征矩张量分析[J]. 岩土力学, 2013, 34(6):1716-1722.
MING Huajun, FENG Xiating, ZHANG Chuanqing,et al.Moment tensor analysis of attitude characterization of hard rock newborn fracture surface based on microseismic informations[J]. Rock and Soil Mechanics, 2013, 34(6):1716-1722.
[14] OHTSU M. Simplified moment tensor analysis and unified decomposition of acoustic emission source:application to in situ hydrofracturing test[J]. Journal of Geophysical Research: Solid Earth, 1991, 96(B4): 6211-6221.
[15] MANTHEI G. Characterization of acoustic emission sources in a rock salt specimen under triaxial compression[J]. Bulletin of the Seismological Society of America, 2005, 95(5): 1674-1700.
[16] AKER E, KÜHN D, 
V, et al. Experimental investigation of acoustic emissions and their moment tensors in rock during failure[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 70: 286-295.
[17] 刘培洵, 陈顺云, 郭彦双,等.声发射矩张量反演[J]. 地球物理学报,2014,57(3): 858-866.
LIU Peixun, CHEN Shunyun,GUO Yanshuang,et al.Moment tensor inversion of acoustic emission[J]. Chinese Journal of Geophysics,2014,57(3):858-866.
[18] 任会兰, 宁建国, 宋水舟,等. 基于声发射矩张量分析混凝土破坏的裂纹运动[J]. 力学学报, 2019, 51(6): 1830-1840.
REN Huilan, NING Jianguo, SONG Shuizhou,et al.Investigation on crack growth in concrete by moment tensor analysis of acoustic emission[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(6): 1830-1840.
[19] KNOPOFF L, RANDALL M J. The compensated linear-vector dipole:a possible mechanism for deep earthquakes[J]. Journal of Geophysical Research. 1970, 26(75): 4957-4963.
