0 引 言
冲击矿压是一种典型的煤矿动力灾害,严重威胁煤矿的高效生产和人员安全,因此,冲击矿压灾害的预防与预警至关重要[1]。 冲击矿压指在高应力作用下,聚集的能量突然释放,造成煤岩体的冲击,导致人员伤亡,建筑物破坏的现象[2]。 而微震是采矿活动引起的诱发地震,是煤岩介质在矿区应力作用下,聚集的弹性应变能释放,造成采掘空间周围岩体破裂的现象。 因此,通过监测煤矿微震来进行冲击矿压的预防预警是一种有效的手段[3]。 微震监测的主要技术包括:台网优化布置、微震信号识别、微震震源定位、震源机制分析和微震活动预测等[4]。 其中,震源位置是微震监测中需要确定的最关键和最基本的参数之一[5]。 目前,已有的微震定位方法有几何作图法、线性定位法(包括绝对定位法和相对定位法)和非线性定位法。 然而,受背景噪音、机械振动等因素干扰,煤矿微震信号非常复杂,上述方法定位性能较差。 因此,如何有效提升煤矿微震震源定位精度是目前面临的一个重大问题[6]。
目前,主要的煤矿微震震源定位方法是反演法。该方法通过震源检波探测器接收震源初至时刻来反演震源的位置,包括非启发式和启发式2 种[7]。 非启发式方法主要包括牛顿法、拟牛顿法和梯度下降法等。 杨俊峰等[8]提出了一种基于DTOA 和牛顿法的震源定位方法,发现该方法能有效地提高震源定位的准确性。 为解决远场震源定位问题,李月等[9]在基于无需测速的震源定位模型中,先利用遗传算法的全局优化能力缩小搜索范围,再通过拟牛顿法实现局部精确寻优。 试验结果表明,该混合算法定位速度更快、精度更高。 非启发式方法虽然可以通过一定的改进提升震源定位的精度,但是存在复杂的导数求解、局部搜索和收敛速度慢等问题[10],容易定位到错误的位置,导致定位精度较差。因此,启发式方法是目前研究的主流方法,主要包括模拟退火法、单纯形法、遗传算法和粒子群优化算法等。 王泉栋等[11]采用多种群遗传算法求解定位问题,通过2 个种群独立进化,提高遗传算法的全局搜索能力。 陈炳瑞等[12]利用粒子群优化算法,识别微震震源和速度模型,进一步提高了定位精度。 从上面的讨论和分析可以看出,大多数现有的微震震源定位方法是基于单目标优化方法或传统的非启发式方法,关于震源定位的多目标优化相关工作很少。分析发现,在震源定位问题中,能量较大的微震激发的检波探测器个数较多,选择哪些通道的震动信号进行定位可以获得更好的定位精度仍有待进一步研究[13]。 为此,笔者将震源定位问题转化为一个多目标优化问题,提出一种既考虑通道个数又考虑定位精度的多目标微震震源定位模型,并利用多目标粒子群优化算法进行求解。 考虑到粒子群优化算法易于早熟收敛,而模拟退火是一种易于跳出局部最优的全局搜索算法。 因此,将二者结合形成一种取长补短的混合算法,有利于提升震源定位精度。
1 微震震源的多目标定位模型
1.1 微震震源定位原理
要保证震源定位具有较高的准确性,通常选择比较容易辨认的P 波进行定位。 与其他波相比,P波初至时刻的误差较小,定位精度较高[14]。 假设煤岩体为均质、各向同性介质,即P 波在各个传播方向上速度保持不变。 矿震定位示意如图1 所示。
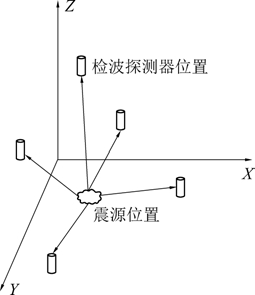
图1 矿震定位示意
Fig.1 Diagram of microseismic localization process
定位原理描述为:记P 波传播速度为V,则震源(x,y,z) 与第 i 个检波探测器 (xi,yi,zi) 的 P 波走时关系为
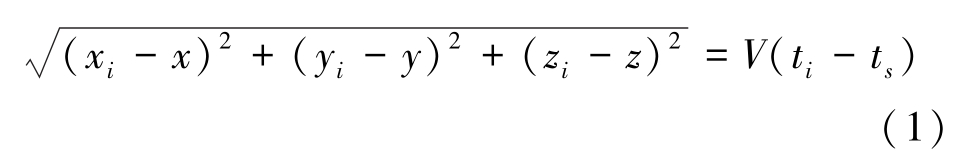
其中,ti 是编号为 i(i = 1,2,…,N) 的检波探测器接收到的初至时刻,ts 为震源起震时刻。 震源定位的解可以记为模拟震源 (x′,y′,z′) ,则对于同一模拟震源,第i 和j 个检波探测器的走时拟合误差为

其中,x′,y′,z′对应震源位置,为待解算量。 实现上述量的解算,至少需要4 个通道的震动信号参与。 显然,当 Δij= 0 时,震源定位误差最小。 基于此,震源定位的求解过程可转化成如下最优化问题:
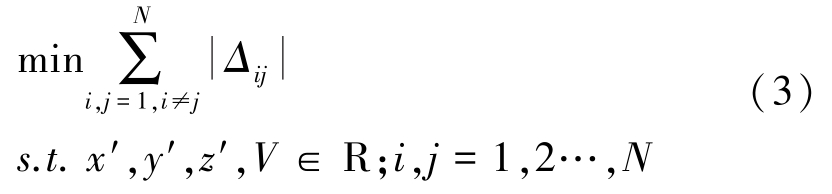
震源定位的目的就是通过求解式(3),得到未知震源的位置,即找到满足式(3)的最优坐标(x′,y′,z′) 。 但是,实际震源定位问题中,通常会有多于4 个通道的震动信号。 由于参与定位的通道数对定位精度有很大的影响,所以选择哪些通道的震动信号对式(3)进行求解至关重要。 为此,笔者给出一种既考虑检波探测器个数,又考虑定位精度的多目标微震震源定位模型。
1.2 多目标微震震源定位模型构建
微震震源多目标定位问题,旨在确定震源的坐标位置和检波探测器的个数,使检波探测器个数K最小,且震源的定位误差值最小。 设第j 个检波探测器的坐标记为(xj,yj,zj ) ,最多有N 个检波探测器,则该优化问题的决策变量,记为
其中,Xj=(xj,yj,zj) , j = 1,2,…,N ,代表第 j个检波探测器,则优化目标函数记为
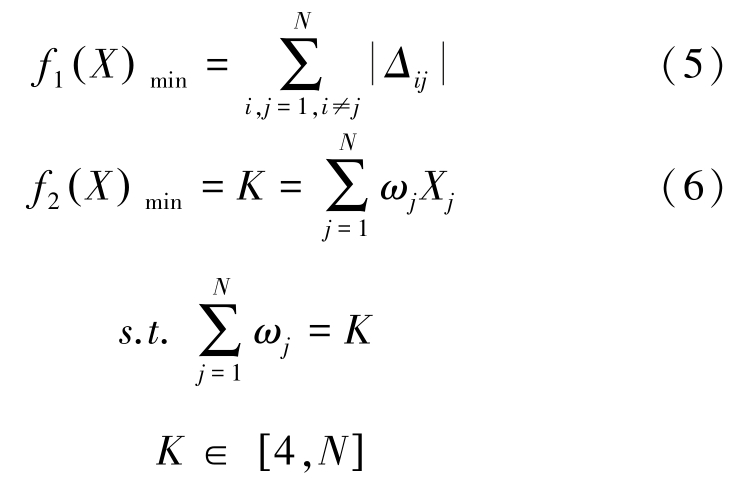
式中: ωj= 1 为检波探测器 j 有效; ωj= 0 为检波探测器j 无效; f1(X ) 为有效检波探测器的走时拟合误差值;f2(X ) 为有效检波探测器的个数;K 为检波探测器个数,最少为4 个[15]。
2 多目标粒子群-模拟退火混合定位方法
考虑到震源的通道个数和定位精度是2 个相互冲突的优化目标,因此,采用多目标粒子群优化算法进行求解。 但是,已有的多目标粒子群优化算法容易陷入局部最优,导致早熟收敛[18]。 为此,引入模拟退火算法,在确定的检波探测器个数条件下,进一步局部搜索具有最小定位误差的最优解。 由此,给出一种基于多目标粒子群-模拟退火的混合定位方法。
在该方法中,首先采用多目标粒子群优化算法对全局进行探索。 针对不同数目的检波探测器,采用模拟退火算法进行局部搜索,获得相应检测通道数目下的更精准定位。 由于模拟退火算法对初始解较为敏感,采用多目标粒子群优化算法获得的全局较优解,为基于模拟退火算法的局部搜索可以提供更有效的初始值,从而充分利用2 种算法的优势,提高定位精度和解算速度。 该混合定位方法的流程如图2 所示。

图2 多目标粒子群-模拟退火混合算法流程
Fig.2 Flow chart of MOPSO-SA hybrid algorithm
2.1 多目标粒子群优化定位算法
多目标粒子群算法(Multi-Objective Particle Swarm Optimization,MOPSO)是一种通过不断迭代,更新粒子的速度和位置,最终找到最优解的群体智能优化算法[16]。 其中,每个粒子具有多个评价目标值。 在多目标震源定位问题中,将定位精度和参与定位的通道个数作为评价粒子优劣的目标函数。
多目标粒子群优化算法的具体步骤如下:
1)初始化粒子的速度和位置,外部档案集。
2)评价粒子的适应度值。
3)对粒子进行非占优比较,选出个体最优解和全局最优解,并更新外部档案集。
4)更新粒子的位置和速度。
5)判断是否满足终止条件,若满足,则输出结果,否则,跳转到步骤3。
2.2 模拟退火局部搜索算法
模拟退火算法(Simulated Annealing,SA)是一种基于 Monte-Carlo 迭代求解策略的随机寻优算法[17]。 在优化过程中,以一定的概率接受次优的解,从而使寻优过程跳出局部极值解,收敛到全局最优解。 模拟退火算法步骤如下:
1)初始化参数,包括初始温度、初始状态和扰动次数等。
2)对当前状态产生扰动,获得新状态下的解。
3)评价新解,并比较2 个解的定位误差大小;如果新解的定位误差优于原始解,则新解替代原始解。
4)判断是否达到了最大扰动次数,如果不满足,则跳转步骤2。
5)判断是否达到了终止温度,如果不满足,则执行衰减过程,跳转到步骤2;如果满足,则输出最优解。
3 微震震源定位试验分析
为解决矿山微震震源定位问题,采用多目标粒子群-模拟退火混合算法实现震源定位最优解算。
假设P 波传播速度为2 500 m/s,起震时刻为0 s,震源位置为(71,167,-254),各个检波探测器的位置和初至时刻见表1[19]。 设定震源的每一维搜索范围为0~500 m。 算法中,每个粒子代表一种检波探测器的组合模式,最终获得的最优解具有最少的检测通道,且定位精度最高。
表1 微震检波探测器坐标及初至时刻
Table 1 Microseismic detectors location and first arrival time

编号 检波探测器位置/m初至时刻/ms x y z 1 210 399 -244 108.255 2 228 248 -202 73.663 3 54 95 -445 81.931 4 281 407 -121 138.211 5 51 205 -222 21.421 6 157 296 -461 103.449 7 64 172 -183 28.608 8 322 192 -61 127.043 9 416 478 -185 187.833 10 307 136 -231 95.654
算法参数设置如下:粒子群优化算法中,设置种群规模为20,最大迭代次数为100 代,学习因子c1=c2=1.494 5;模拟退火算法中,初始温度T 设置为1 000,衰减率 D=0.85,马尔科夫链长度 M =100,最大迭代次数为200 代。
3.1 微震震源定位误差分析
在微震震源定位模型中,主要存在以下2 个因素影响定位精度。 一方面,参与定位的通道个数会影响最终的定位精度;另一方面,通道个数相同时,采用不同的震动信号进行定位,获得的定位精度也存在一定差异。
为全面分析通道个数对定位精度的影响,在最大检波探测器个数为10 的条件下,分别设置K 为4、5、6、7、8、9 和 10,分别采用粒子群优化算法和模拟退火算法进行定位解算,获得其定位误差,如图3和表2(E 为定位误差)所示。 其中,图3 为不同通道个数下,2 个算法的定位误差变化趋势。 由图3可得,当采用粒子群优化算法实现定位解算时,随着K 从4 递增到6,对应的震源定位精度逐渐提高;在采用7 到10 个通道时,其定位误差逐渐增加。 同样,采用模拟退火算法在通道数为7 时,获得了最佳的定位精度。 分析上述现象,表明随着通道个数的增加,后加入的信号不仅贡献的信息越来越小,还可能引入了更多的到时标记误差,导致整体定位误差增加。 综上所述,通道个数的不同会对定位精度产生显著影响。
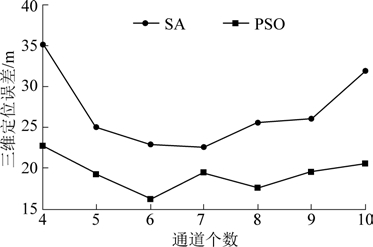
图3 通道个数对定位误差的影响
Fig.3 Influence of number of station on positioning error
表2 通道个数对定位性能的影响
Table 2 Influence of number of station on positioning performance

SA PSO K x/m y/m z/m E/m x/m y/m z/m E/m 4 68 202 -252 35 74 185 -240 22 5 87 177 -238 25 74 185 -250 19 6 75 189 -253 23 80 174 243 16 7 79 186 -246 22 82 178 -244 19 8 51 161 -238 25 85 177 255 17 9 53 148 -248 26 69 172 -235 20 10 70 140 -236 31 55 176 -243 20
由表2 可知,当K 等于6 时,2 种算法的定位误差都比较低。 在此基础上,每次选取6 个不同的通道参与定位,并在每种算法上各进行5 次试验,结果见表3。 其中,对于每个通道,1 代表参与定位,0 则代表未被选择。 由表3 可得,对于2 种不同的算法,每次试验得到的定位误差都具有较大的波动。 这是因为,不同检波探测器测量得到的数据中包含不同程度的噪声,改变参与定位的通道信号,定位性能自然会受到影响。 由此可见,即使通道个数确定,定位性能依然需要进一步优化。
表3 不同通道对定位性能的影响
Table 3 Influence of different station on positioning performance

注:对于每个通道,1 代表参与定位,0 代表未被选择。
通道是否被选择 震源位置算法 组别E/m 1 号2 号3 号4 号5 号6 号7 号8 号9 号10 号x y z 1 0 1 1 0 1 1 1 0 1 1 77 169 -231 23 SA 2 0 1 1 1 1 0 0 0 1 1 82 188 -262 25 3 0 0 1 0 1 0 1 1 1 1 82 181 -245 20 4 1 0 1 0 0 1 1 1 0 1 87 174 -257 19 5 1 0 1 0 1 1 1 1 0 0 93 153 -247 27 1 1 1 1 0 1 0 1 0 0 1 83 170 -240 18 PSO 2 1 1 1 0 1 1 1 0 0 0 81 177 -255 15 3 0 1 1 0 1 1 1 0 0 1 79 175 -254 12 4 1 1 1 0 1 0 1 1 0 1 83 181 -260 20 5 1 1 1 1 1 1 1 0 0 1 78 179 -250 14
3.2 多目标粒子群-模拟退火混合定位方法性能分析
笔者给出的多目标震源定位模型,改变了传统震源定位方法中只能解算震源位置的局限性,将通道个数也作为优化目标,在有效提高震源定位精度的同时,降低计算代价,降低井下布设检波探测器的难度。 多目标震源定位模型和单目标震源定位模型得到的定位误差,如图4 所示。
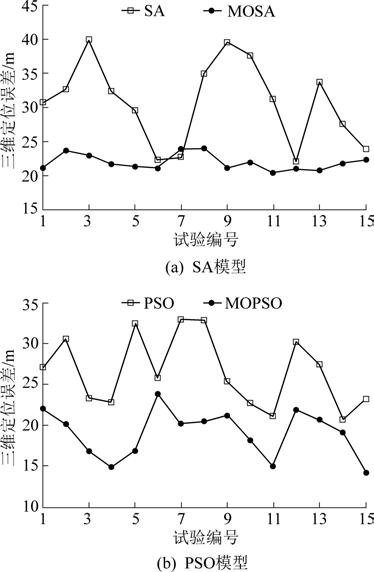
图4 定位模型对定位性能的影响
Fig.4 Influence of positioning models on accuracy
由图4 可得,采用多目标震源定位模型,可以显著减小定位误差。 对比多目标粒子群优化算法和多目标模拟退火算法的定位结果可知,前者的平均定位性能要优于后者,但是,多目标粒子群优化算法的定位结果波动比较大。 这是因为,如果该算法在定位过程中陷入局部搜索,则会导致比较低的定位精度。 相反,多目标模拟退火算法的定位性能比较鲁棒。 但是,由于采用初始值随机生成,导致其定位性能较差。 因此,为了综合两者的优点,将2 种算法进行有机结合,从而提高震源定位精度。 为了进一步分析多目标粒子群-模拟退火混合算法(MOPSOSA)的有效性,将其与 MOPSO[20]、MOGA[21]和 MOSA[22]进行对比,定位误差如图5 所示。

图5 4 种算法的定位误差
Fig.5 Positioning errors of four algorithms
可见,所提算法在3 个维度下的定位误差和总体误差上都明显优于其他3 种算法,更适合用于解决微震震源定位问题。
4 结 论
1)将传统微震震源定位模型非线性方程式的求解转化为一个优化问题,简化了求解过程。
2)针对不同的优化求解模型,多目标震源定位模型相比较于单目标震源定位模型,可以显著减小定位误差。
3)不同检波探测器测量得到的数据中包含不同程度的噪声,改变参与定位的通道信号,定位性能自然会受到影响。 参与定位的微震信号检测通道个数也是定位误差的主要影响因素之一,即使通道个数确定,定位性能依然需要进一步优化。
4)提出的一种基于多目标粒子群-模拟退火的混合定位方法,该方法利用多目标粒子群优化算法的全局探索性能,为实现局部搜索的模拟退火算法提供更优的初始解,同时也有效避免寻优过程陷入局部极值,能够实现多目标震源定位模型优化求解。
[1]曹安业,井广成,窦林名,等.孤岛面开采强矿震异常区的被动声波探测技术及应用[J].采矿与安全工程学报,2015,32(1):20-27.CAO Anye,JING Guangcheng,DOU Linming, et al.Seismic hazard assessment in complex island coalface by computed tomography[J].Journal of Mining & Safety Engineering,2015,32(1):20-27.
[2]程 健,杨凌凯,崔 宁,等.基于流形嵌入过采样的非平衡数据分类方法[J].中国矿业大学学报,2018,47(6):172-180.CHENG Jian,YANG Lingkai,CUI Ning, et al.A novel pattern classification method for imbalanced data set based on manifold embedded over-sampling[J].Journal of China University of Mining & Technology,2018,47 (6): 172-180.
[3]杨纯东,巩思园,马小平,等.基于微震法的煤矿冲击危险性监测研究[J].采矿与安全工程学报,2014,31(6):863-868.YANG Chundong,GONG Siyuan,MA Xiaoping,et al.Rock burst danger monitoring based on microseismic method[J].Journal of Mining & Safety Engineering,2014,31(6):863-868.
[4]程 健,杨凌凯,王全魁,等.基于半监督过采样非平衡学习的矿山微震信号识别[J].煤炭科学技术,2018,46(2):213-218,202.CHNEG Jian,YANG Lingkai,WANG Quankui, et al.Mine microseismic signal recognition based on semi-supervised over-sampling imbalanced learning[J].Coal Science and Technology,2018,46(2): 213-218,202.
[5]董陇军,李夕兵,唐礼忠.影响微震震源定位精度的主要因素分析[J].科技导报,2013,31(24):26-32.DONG Longjun,LI Xibing,TANG Lizhong.Main influencing factors for the accuracy of microseismic source location[J].Science &Technology Review,2013,31(24): 26-32.
[6]柳云龙,田 有,冯 晅,等.微震技术与应用研究综述[J].地球物理学进展,2013,28(4):1801-1808.LIU Yunlong,TIAN You,FENG Xuan, et al.Review of microseism technology and its application[J].Progress in Geophys,2013,28(4):1801-1808.
[7]陈 栋,王恩元,李 楠.千秋煤矿微震震源参数特征以及震源机制分析[J].煤炭学报,2019,44(7):2011-2019.CHEN Dong,WANG Enyuan,LI Nan.Analysis of microseismic source parameters and focal mechanism in Qianqiu coal mine[J].Journal of China Coal Society,2019,44(7):2011-2019.
[8]杨俊峰,张丕状.基于DTOA/DOA 和牛顿迭代法的震源定位方法研究[J].地震研究,2013,36(3): 324-329.YANG Junfeng,ZHANG Pizhuang.Research on source location method based on DTOA/DOA and Newton iteration[J].Earthquake Research,2013,36(3): 324-329.
[9]李 月,陈 卿,丁恩杰,等.基于遗传-拟牛顿混合算法的远场震源定位[J].河南理工大学学报:自然科学版,2018,37(2):109-115.LI Yue,CHEN Qing,DING Enjie, et al.Source localization of the far field based on GA-mixed quasi-newton algorithm[J].Journal of Henan Polytechnic University:Natural Science,2018,37(2):109-115.
[10]ZHANG Yong,GONG Dunwei,CHENG Jian.Multi-objective PSO approach for cost-based feature selection in classification[C].IEEE/ACM Transactions on Computational Biology and Bio-informatics,2017,14(1):64-75.
[11]王泉栋,李国和,吴卫江,等.多种群遗传算法在微震震源定位中的应用[J].计算机测量与控制,2015,23(4):1285-1288.WANG Quandong,LI Guohe,WU Weijiang, et al.Application of multi-population genetic algorithm in microseismic focal source location[J].Computer Measurement and Control,2015,23(4):1285-1288.
[12]陈炳瑞,冯夏庭,李庶林,等.基于粒子群算法的岩体微震源分层定位方法[J].岩石力学与工程学报,2009,28(4):740-749.CHEN Bingrui,FENG Xiating,LI Yilin, et al.Hierarchical localization of microseismic sources in rock mass based on particle swarm optimization[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(4):740-749.
[13]巩思园,窦林名,马小平,等.提高煤矿微震定位精度的最优通道个数的选取[J].煤炭学报,2010,35(12):2017-2021.GONG Siyuan,DOU Linming,MA Xiaoping, et al.Selection of the optimal number of channels to improve the accuracy of microseismic positioning of coal mines[J].Journal of China Coal Society,2010,35(12):2017-2021.
[14]巩思园,窦林名,曹安业,等.煤矿微震监测台网优化布设研究[J].地球物理学报,2010,53(2):457-465.GONG Siyuan,DOU Linming,CAO Anye, et al.Study on optimal configuration of seismological observation network for coal mine[J].Chinese Journal of Geophysics,2010,53(2):457-465.
[15]何世钧,黄智伟,黄星琪.一种基于TOA 测距的室内三维质心定位算法研究[J].测控技术,2017,36(10): 134-137.HE Shijun,HUANG Zhiwei,HUANG Xingqi.Research on an indoor three dimension centroid localization algorithm based on TOA ranging[J].Measurement & Control Technology,2017,36(10): 134-137.
[16]TSAI Shangjeng,SUN Tsungying,LIU Chancheng, et al.An improved multi - objective particle swarm optimizer for multi -objective problems[J].Expert Systems with Application,2010,37(8):5872-5886
[17]DANESHMAND Shabnam V,HEYDARI Hossein.A diversified multiobjective simulated annealing and genetic algorithm for optimizing a three-phase HTS transformer[J].IEEE Transactions on Applied Superconductivity,2016,26(2):1-10.
[18]LIU Dasheng,TAN K C,GOH C K,et al.A multiobjective memetic algorithm based on particle swarm optimization[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2007,37(1):42-50.
[19]吕进国,姜耀东,赵毅鑫,等.基于稳健模拟退火-单纯形混合算法的微震定位研究[J].岩土力学,2013,34(8):2195-2203.LYU Jinuo,JIANG Yaodong,ZHAO Yixin, et al.Microseismic localization based on a robust simulated annealing-simplex hybrid algorithm[J].Rock and Soil Mechanics,2013,34(8):2195-2203.
[20]COELLO Carlos A Coello,PULIDO Gregorio Toscano,LECHUGA Maximino Salazar.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2004,8(3): 256-279.
[21]DEB Kalyanmoy,PRATAP Amrit,AGARWAL Sameer, et al.A fast and elitist multi-objective genetic algorithm: NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[22]BANDYOPADHYAY Sanghamitra,SAHA Sriparna,MAULIK Ujjwal,et al.A simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA[J].IEEE Transactions on Evolutionary Computation,2008,12(3):269-283.
