0 引 言
煤矿粉尘给作业人员的身体健康造成极大危害，长时间接触会破坏肺部细胞，危害生命。 因此，加强煤矿中的粉尘质量浓度检测对煤矿粉尘防治、降低尘肺病发病率具有重要意义[1-3]。 国内外现有的粉尘检测方法有称重法、光散射法、 射线法等[4-5]。 称重法用于手动测量，不能在线检测；光散射法用于干烟气或者浓度大的场合，光学系统易污染、维护麻烦；射线法因辐射等原因用于在线监测的较少。
利用静电感应原理测量粉尘浓度近年来受到国内外学者的重视。 许传龙等[6-7]提出了阵列式静电传感器模型，并应用有限元法系统分析了阵列式传感器结构参数对传感器特性的影响；陈建阁等[8-9]建立了棒状电极与粉尘颗粒间的电荷感应数学模型，并对感应空间灵敏度的分布特性进行分析。 赵恩彪等[10-11]系统研究了3 种不同的探头在不同粉尘密度下产生电荷的关系，找出适合煤矿使用的探头。 静电感应法测量粉尘浓度，具有适应性强，维护成本低等优点，得到了广泛应用。
笔者所在团队在粉尘浓度测量方面做了很多研究。 针对煤矿粉尘质量浓度传感器测量窗口易受粉尘污染的问题[12]，借鉴空气幕的隔尘机理，文献[12]提出在光学测量窗口处改变气鞘的结构来提高粉尘质量浓度测量装置的精度；针对应用电荷感应法测量低浓度粉尘不够精确的问题[13]，依据文丘里效应，文献[13]减小测量传感器中间部分，依次形成收缩段、喉道段和扩散段，增大感应电荷量进而提高测量精度。 但是，文献[13]的改进装置仅对单一参数(喉道段直径)作了最优化求解，并没有考虑管路其他部分对结果的影响。 因此笔者在文献[13]改进装置的基础上，使用Fluent 软件对不同结构尺寸的装置进行数值模拟，基于响应曲面法(RSM)、利用统计软件Design-Expert，寻求使感应电荷量取得最大值时的收缩段长度、喉道段长度、喉道段直径和扩散段长度，以期提高基于静电感应原理测量粉尘浓度的感应电荷量。
1 静电感应法测量粉尘浓度
1.1 基本原理
图1 环状静电传感器的工作原理
Fig.1 Working principle of annular electrostatic sensor
基于静电感应法测量粉尘浓度的原理如图1 所示。 图中粉尘颗粒在运动过程中会摩擦带电，经过喉道段环状电极感应，通过信号处理电路得到感应带电量，进而求得粉尘浓度[14-15]。
1.2 环状静电传感器的数学模型
YAN Y 等[16-17]提出的环状静电传感器数学模型如图2 所示。 该模型主要由与管壁绝缘的金属环形电极和检测电路组成，并且认为传感器电极的轴向长度与管道尺寸相比较小。 该改进模型建立在点电荷的基础上，经过复杂的理论推导计算，最终获得了静电传感器上感应电荷的数学模型为
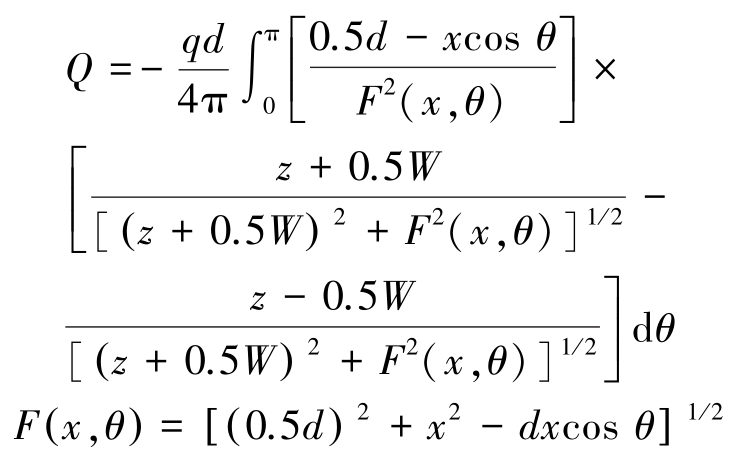
式中：Q 为极板上感应电荷量；z 为颗粒速度V 与时间T 的乘积；W 为极板宽度； q 为通过极板的点电荷；d 为环状电极直径，即喉道段直径； x 为点电荷与极板中轴线的距离；θ 为积分块与轴线的夹角；E为点电荷流动产生的电场强度。
图2 环状静电传感器数学模型
Fig.2 Mathematical model of annular electrostatic sensor
通过以上原理和模型分析可以看出，测量装置中的收缩段长度、喉道段长度、喉道段直径和扩散段长度对粉尘的带电量有影响，所以需要寻求一种方式求出测量装置的最优结构。
2 响应曲面法设计
2.1 响应曲面法
响应曲面法是利用数学和统计分析进行参数优化的方法，最早由 BOX 和 WILSON 于 1951 年提出[18-19]，基本过程是首先确定可能含有最佳区域的条件，然后拟合响应函数与影响因素之间的一阶或者二阶模型作为真实响应函数的一个近似，最后利用一阶或者二阶模型得到最优工艺参数。 而在本文中由于目标函数(传感器的数学模型)已知，只是借用响应曲面法对复杂目标函数寻找最大值以及取得最大值的条件，从而得出改进测量装置的最优结构。
响应曲面法经常使用的设计方法为中心复合设计和Box-Behnken 试验设计。 在因素相同时，Box-Behnken 试验设计比中心复合设计试验次数少，而且具有近似旋转性、无序贯性，没有试验因素同时为高水平的试验组合，尤为适应有安全要求的试验。因此笔者采用Box-Behnken 试验设计。
2.2 响应曲面法设计及CFD模型求解
2.2.1 响应曲面法设计
1)确定试验的变量。 选取喉道段直径d、收缩段长度X1、喉道段长度X2 和扩散段长度X3 为试验变量，给出4 个因素的取值范围，见表1。
表1 影响电荷量因素的取值范围
Table 1 Affects range of charge factors
影响因素 最大值Xih 最小值Xil X1 10 6 X2 20 10 X3 20 10 d 12 6
2)确定因素水平编码。 将所有变量按下式编码化：
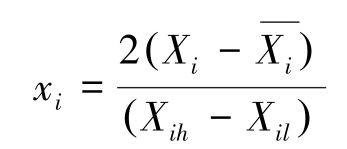
式中：Xi(i＝1，2，3)分别代表收缩段、喉道段、扩散段长度；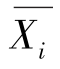
为 Xi 的均值；Xih 为第i 个变量xi 的最大值；Xil 为第i 个变量xi 的最小值。
3)CFD 模型求解。 笔者采用的四因素三水平的Box-Behnken 试验设计需 29 种不同的 CFD 模型。 模型中入口气体速度4 m/s，颗粒速度3 m/s，粒径10 μm，入口直径14 cm，空气密度1.225 mg/m3，黏度1.78×10-5Pa·s，传感器的数学模型中x 取1 cm [20]。
2.2.2 CFD 模型求解
CFD 模型求解步骤如下：
1)网格划分。 使用软件Gambit2.4 建立改进测量装置的结构模型，由于模型规则，仅由圆柱和圆台组成，因此不采用复杂网格划分，选择TGrid 格式作为网络化工具，并且设置Interval Size 为0.5，如图3所示，该图为CFD 模型中的一个，此时，收缩段长度10 cm，喉道段长度15 cm，扩散段长度15 cm，喉道段直径6 cm，入口直径14 cm。
图3 网格划分
Fig.3 Grid partition
2)计算方法。 使用CFD 软件Fluent6.3 对改进测量装置的内部流场进行数值模拟。 首先设置Multiphase Model 为欧拉模型，忽略动量方程中颗粒间的碰撞，气相流场计算时采用不可压缩、非稳态数学模型和标准k-ε 湍流模型，控制方程采用QUICK差分格式。
3) 边界条件。 改进测量装置入口采用VELOCITY INLET，出口采用 OUTFLOW，装置壁面默认设为WALL。
4)软件分析，显著性检验。 在Design-Expert 软件中仿真，分析仿真结果，得出显著影响静电传感器感应电荷量的因素，并得出使感应电荷量取得最大值的最优结构尺寸。
3 试验结果分析
3.1 显著性分析
由响应曲面法的Box-Behnken 设计方法，可以得到表2 的计算工况，再由CFD 模型得出喉道段速度V，最后由MATLAB 按照改进测量装置的数学模型计算得出感应电荷量Q，见表2。
表2 CFD 模型仿真及计算数据
Table 2 Simulation and data calculation of CFD model
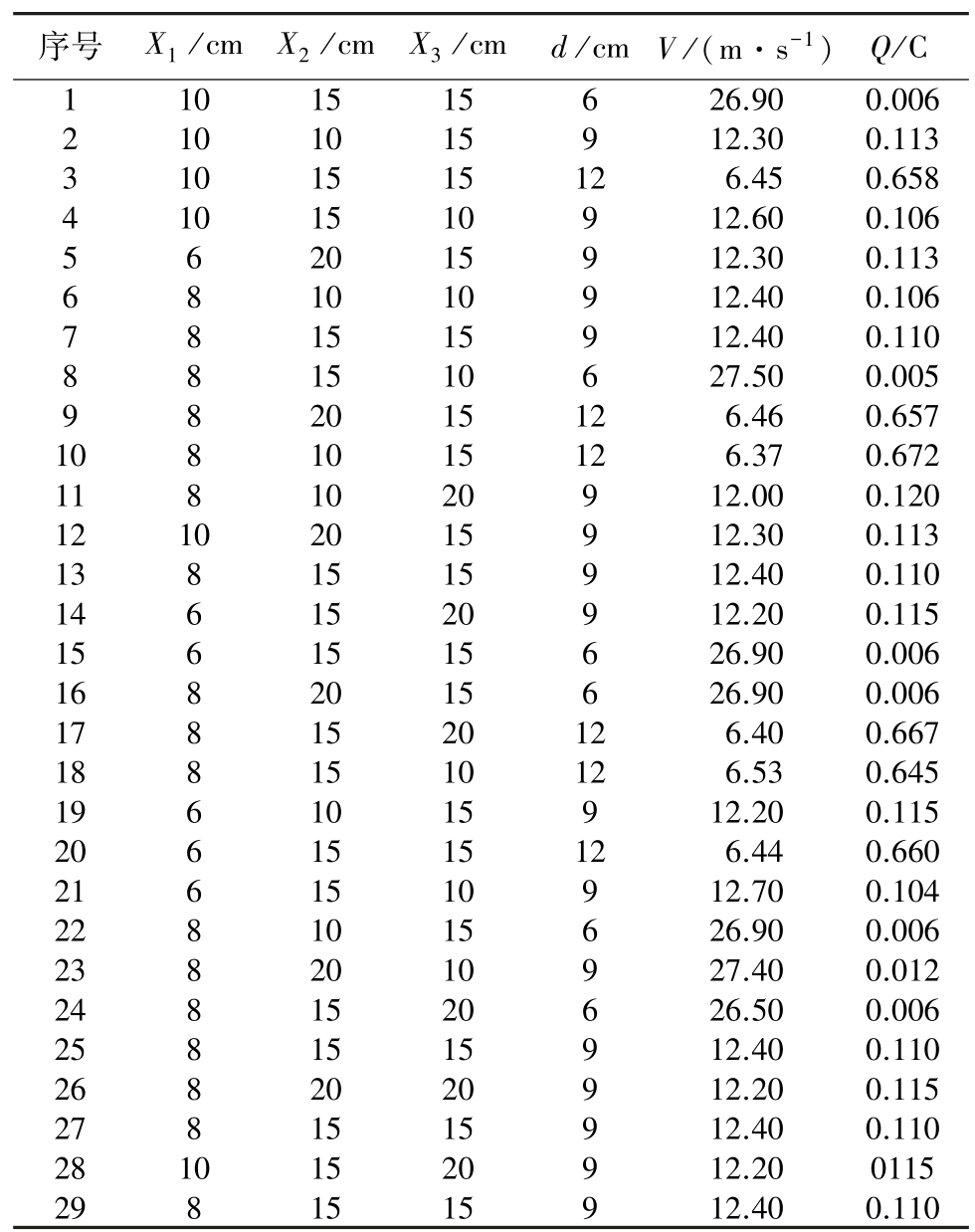
序号 X1 /cm X2 /cm X3 /cm d /cm V /(m·s-1) Q/C 1 10 15 15 6 26.90 0.006 2 10 10 15 9 12.30 0.113 3 10 15 15 12 6.45 0.658 4 10 15 10 9 12.60 0.106 5 6 20 15 9 12.30 0.113 6 8 10 10 9 12.40 0.106 7 8 15 15 9 12.40 0.110 8 8 15 10 6 27.50 0.005 9 8 20 15 12 6.46 0.657 10 8 10 15 12 6.37 0.672 11 8 10 20 9 12.00 0.120 12 10 20 15 9 12.30 0.113 13 8 15 15 9 12.40 0.110 14 6 15 20 9 12.20 0.115 15 6 15 15 6 26.90 0.006 16 8 20 15 6 26.90 0.006 17 8 15 20 12 6.40 0.667 18 8 15 10 12 6.53 0.645 19 6 10 15 9 12.20 0.115 20 6 15 15 12 6.44 0.660 21 6 15 10 9 12.70 0.104 22 8 10 15 6 26.90 0.006 23 8 20 10 9 27.40 0.012 24 8 15 20 6 26.50 0.006 25 8 15 15 9 12.40 0.110 26 8 20 20 9 12.20 0.115 27 8 15 15 9 12.40 0.110 28 10 15 20 9 12.20 0115 29 8 15 15 9 12.40 0.110
在Design-Expert 相应的工况Response 列填入计算所得的感应电荷Q，进行Analysis 分析，得到不同因素对因变量感应电荷Q 的响应曲面，如图4所示。
图4 各因素对电荷量的响应曲面
Fig.4 Response surface of each factor to amount of charge
由图4a 可知：当收缩段长度X1 不变时，感应电荷量Q 随着喉道段长度X2 增大而增大；喉道段长度X2 不变时，收缩段长度X1 对感应电荷量Q 影响很小；这表明喉道段长度X2 对感应电荷Q 影响显著。
由图4b 可知：当收缩段长度X1 不变时，感应电荷量Q 随着喉道段直径d 增大而增大；喉道段直径d 不变时，收缩段长度 X1 对感应电荷量Q 影响很小；这表明喉道段直径d 对感应电荷Q 影响显著。
由图4c 可知：扩散段长度X3 不变时，感应电荷量Q 随着喉道段直径d 增大而增大；喉道段直径d不变时，感应电荷Q 随着扩散段长度X3 增大而增大，但是幅度较小。
由图4d 可知：喉道段直径d 和喉道段长度X2对感应电荷量的影响比较复杂，组成的三维响应曲面近似于马鞍状，但是根据图4d 可知：喉道段直径d 和喉道段长度X2 对感应电荷量Q 的影响显著。
3.2 不同粒径对最优结构的影响
由Optimization 下的Numerical 选项卡可以得到在粒径为10 μm 改进测量装置的最优结构值，见表3。
表3 粒经10 μm 时的最优结构数据
Table 3 Optimal structure at particle size of 10 μm
参数项 X1 /cm X2 /cm X3 /cm d /cm参数值 7.21 14.46 16.66 9.370
改进测量装置此时的感应电荷量为0.190 74 C。 重复上述响应曲面及CFD 模型求解过程，得到5 μm 粒径下的最优结构数据，见表4。
表4 粒径5 μm 时的最优结构参数值
Table 4 Optimal structure parameters value at particle size of 5 μm
参数项 X1 /cm X2 /cm X3 /cm d /cm参数值 9.65 14.25 18.31 9.295
改进测量装置的感应电荷量为0.110 252 C。比较上述不同粒径的最优结构数据可知：在粒径不同时，求得的最优装置结构不同；粒径小时感应电荷量小，喉道段直径变小。 粒径减小感应到的电荷量变少，电荷量的减小会影响测量装置的精度，如果降低到测量装置的检测限之下，则不能精确测量出粉尘浓度。 结合第3.1 节可知，喉道段直径对感应电荷量影响显著，粒径降低，感应电荷量减小，改变喉道段直径，增加感应电荷量使之满足测量要求，符合改进测量装置改进思路。
3.3 改进测量装置改进前后感应电荷量对比
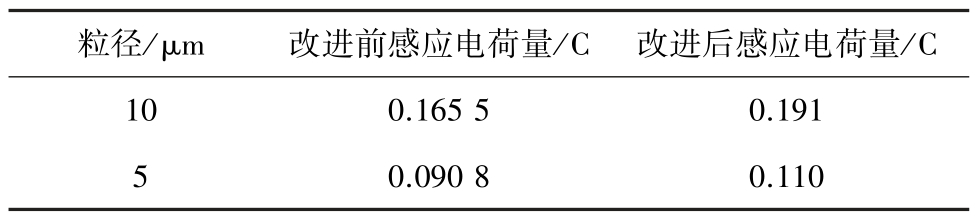
改进测量装置的改进前后感应电荷量见表5，其中，改进后感应电荷量为最优结构下求得的感应电荷量，改进前的管路长度与改进后最优结构时的长度相等。
表5 改进前后不同粒径的电荷量对比
Table 5 Comparison of charge volume of different particle sizes before and after improvement
粒径/μm 改进前感应电荷量/C 改进后感应电荷量/C 10 0.165 5 0.191 5 0.090 8 0.110
根据表5 可知：不论粒径大小，改进后感应电荷量大于改进前感应电荷量；对于粒径10 μm 时感应电荷量增加率为15.25%，而对于粒径为5 μm 时感应电荷量增加率为21.42%，由此可知，改进测量装置在小粒径时测量效果更好。
4 结 论
1)针对现有粉尘测量装置对低浓度粉尘测量不够精确的问题，收缩测量管路中间部分的改进模型可以增大感应电荷量，提高测量精度。
2)采用基于RSM 的方法研究改进测量装置各结构因素对感应电荷量的影响以及各因素间的交互作用，并通过对Design-Expert 软件三维响应曲面的分析，提取出对感应电荷量影响显著的结构因素为喉道段直径d 和喉道段长度X2，其与感应电荷的三维响应曲面为一近似马鞍状的曲面，最终得出使感应电荷量最大的结构参数。
3)分析不同粒径对最优结构以及对改进前后感应电荷量的影响，电荷量提高均在15%以上；分析结果可知，粒径不同最优结构不同、粒径减小、感应电荷量降低以及改进装置在小粒径时改进效果更好。
[1]张茂宇，贾福音.煤矿井下粉尘监测、防治技术的现状与趋势[J].中国安全生产科学技术，2011，7(12)：188-191.ZHANG Maoyu， JIA Fuyin.Current status and trends of coal mine dust monitoring and control technology[J].China Safety Science and Technology， 2011， 7(12)： 188-191.
[2]惠立锋.基于RSM 的呼吸性粉尘旋风分离器分离效能数值模拟研究[J].煤炭学报，2015，40(7)：1692-1697.HUI Lifeng.Numerical simulation of separation efficiency of respirable dust cyclone separator based on RSM[J].Journal of China Coal Society， 2015， 40(7)： 1692-1697.
[3]王 杰，郑林江.煤矿粉尘职业危害监测技术及其发展趋势[J].煤炭科学技术，2017，45(11)：119-125.WANG Jie， ZHENG Linjiang.Monitoring technology and development trend of coal mine dust occupational hazards[J].Coal Science and Technology，2017，45(11)：119-125.
[4]孟 君.综采工作面气水喷雾粉尘防治技术及管理研究[D].北京：中国矿业大学(北京)，2013.
[5]QIAN X， CHENG X， ZHANG L， et al.The sensitivity analysis and optimization design of the electrostatic inductive measuring device for weak charge measurement of coal mine dust [C]/ /Computer Science for Environmental Engineering and Informatics.Springer Berlin Heidelberg， 2011：83-90.
[6]高鹤明，许传龙，王式民.阵列式静电传感器灵敏场分布特性[J].中国电机工程学报，2010，30(5)：76-82.GAO Heming， XU Chuanlong， WANG Shimin.Sensitive field distribution characteristics of array electrostatic sensors[J].Proceedings of the CSEE， 2010， 30(5)： 76-82.
[7]付飞飞，许传龙，王式民，等.基于阵列式静电传感器的密相气力输送煤粉颗粒运动特性分析[J].东南大学学报：自然科学版，2013，43(3)：536-541.FU Feifei， XU Chuanlong， WANG Shimin， et al.Analysis of kinematic particle characteristics of dense phase pneumatic conveying pulverized coal particles based on array electrostatic sensor[J].Journal of Southeast University：Natural Science Edition，2013， 43(3)： 536-541.
[8]陈建阁，吴付祥，王 杰.电荷感应法粉尘浓度检测技术[J].煤炭学报，2015，40(3)：713-718.CHEN Jiange， WU Fuxiang， WANG Jie.Detection technology of dust concentration in charge induction method[J].Journal of China Coal Society， 2015， 40(3)： 713-718.
[9]陈建阁，王 杰，吴付祥.交流耦合式电荷感应法粉尘浓度检测技术研究[J].环境工程，2014，32(4)：131-134，147.CHEN Jiange，WANG Jie，WU Fuxiang.Study on the detection technology of dust concentration in AC-coupled charge induction method[J].Environmental Engineering， 2014， 32(4)： 131-134，147.
[10]赵恩彪，隋金君，王自亮，等.电荷法测量粉尘浓度技术研究[J].金属矿山，2009(S1)：757-760.ZHAO Enbiao， SUI Jinjun， WANG Ziliang， et al.Research on measurement of dust concentration by charge method[J].Metal Mine，2009(S1)：757-760.
[11]赵恩彪，李德文，王自亮，等.电荷法测量粉尘密度的试验研究[J].采矿与安全工程学报，2010，27(2)：269-272.ZHAO Enbiao， LI Dewen， WANG Ziliang， et al.Experimental study on measurement of dust density by charge method[J].Journal of Mining ＆ Safety Engineering， 2010， 27(2)： 269-272.
[12]刘丹丹，曹亚迪，汤春瑞，等.基于测量窗口气鞘多相流分析的粉尘质量浓度测量装置优化[J].煤炭学报，2017，42(7)：1906-1911.LIU Dandan，CAO Yadi，TANG Chunrui， et al.Optimization of dust mass concentration measuring device based on gas sheath monophase flow measurement in measurement window [J].Journal of China Coal Society， 2017， 42(7)： 1906-1911.
[13]刘丹丹，景 然，汤春瑞.基于电荷感应原理的粉尘质量浓度测量装置优化[J].煤炭学报，2018，43(3)：897-902.LIU Dandan， JING Ran， TANG Chunrui.Optimization of dust mass concentration measuring device based on charge induction principle[J].Journal of China Coal Society，2018，43(3)：897-902.
[14]施艳艳，董 峰，谭 超.两相流测量中环形电导传感器特性研究[J].中国电机工程学报，2010， 30(17)： 62-66.SHI Yanyan， DONG Feng， TAN Chao.Study on characteristics of annular conductance sensor in two-phase flow measurement[J].Proceedings of the CSEE， 2010， 30(17)： 62-66.
[15]赵 政.基于电荷感应法的金属粉尘浓度检测技术[J].煤炭科学技术，2017，45(12)：155-159.ZHAO Zheng.Detection technology of metal dust concentration based on charge induction method[J].Coal Science and Technology，2017，45(12)：155-159.
[16]YAN Y.Continuous measurement of particulate emission[J].IEEE Instrumentation Measurement Magazine，2005(4)：35-39.
[17]YAN Y， MA J.Measurement of particulate velocity under stackflow conditions[J].Measurement Science ＆ Technology， 2000，11(1)：59-62.
[18]邹全乐，林柏泉，郑春山，等.基于响应面法的钻割一体化喷嘴稳健性优化[J].中国矿业大学学报，2013，42(6)：905-910.ZOU Quanle， LIN Baiquan， ZHENG Chunshan， et al. Robust optimization of integrated drilling and cutting nozzle based on response surface method[J].Journal of China University of Mining＆ Technology， 2013， 42(6)： 905-910.
[19]赵健植，金保升，仲兆平，等.基于响应曲面法的除雾器叶片效率模拟[J].中国电机工程学报，2007，27(23)：61-65.ZHAO Jianzhi， JIN Baosheng， ZHONG Zhaoping， et al.Simulation of defogging blade efficiency based on response surface methodology[J].Proceedings of the CSEE，2007，27(23)： 61-65.
[20]刘丹丹，刘 衡，李德文，等.基于遗传算法的煤矿粉尘浓度测量装置优化[J].黑龙江科技大学学报，2018，28(1)：97-101，128.LIU Dandan， LIU Heng， LI Dewen， et al.Optimization of coal mine dust concentration measuring device based on genetic algorithm[J].Journal of Heilongjiang University of Science and Technology， 2018， 28(1)： 97-101，128.
