0 引 言
岩石介质在形成的过程中形成了各种尺寸、形状的裂隙结构。裂隙结构联系着材料宏、细观尺度,显著地影响着岩石介质的物理力学性质。学者针对岩石介质裂隙结构对物理力学性质的影响展开了一定研究。试验对象分为2种,一种是采取堆砌岩块来模拟的岩体裂隙结构,多见于早期国外学者的研究。如BROWN等[1-3]通过堆砌体三轴压缩试验,研究了节理方位、节理间距、节理组数、节理贯通程度变化对岩体强度、变形和破坏模式的影响。YOSHINAKA.R[4]通过岩块堆砌体的双轴压缩试验,研究了裂隙方位与结构面粗糙度对岩体力学特性的影响。现阶段主要采取预制裂纹的方法。如路亚妮等[5]对预制单裂隙岩体开展冻融试验,研究了预制单裂隙长度、倾角对试件单轴抗压强度和弹性模量的影响;靳瑾等[6]通过单轴压缩实验研究了类岩材料预制裂纹和岩桥倾角对破坏模式和单轴抗压强度的影响;杨圣奇等[7]的研究中表明预制裂隙大理岩与完整大理岩相比,峰值强度、弹性模量和峰值轴向应变显著降低,降低程度与裂隙长度、倾角、数目成正比;李树忱等[8]针对贯穿裂隙对岩石材料的峰后应力应变曲线、峰后残余强度、峰后泊松比的联系进行了探讨;陈新等[9]通过含预置裂隙石膏试件的单轴压缩试验,系统地研究了裂隙产状和裂隙连通率对断续裂隙岩体峰值强度和弹性模量的影响;韩建[10]选择含预置张开裂隙的类岩石材料模拟脆性岩石,进行压缩试验,研究了裂隙几何特征裂隙岩体力学参数的影响;腾俊洋等[11]研究结果表明,含孔岩石的破裂特征与裂隙几何形态密切相关。此外,数值建模也是一种常见的研究方法。如M.BAHAADDINI等[12]利用颗粒流的方法,模拟了裂隙几何参数对岩体破坏模式、无侧限抗压强度和变形模量的影响;XU等[13]通过物理试验和数值模拟的手段,研究了节理位置、迹长和取向对岩体单轴压缩特性的影响;张科等[14]运用RFPA数值模拟软件研究了含孔多裂隙岩体抗压强度受裂隙倾角的影响;李露露等[15]利用颗粒流原理研究了三叉裂隙岩体强度特征与α、β角的联系;明华军等[16]通过颗粒离散元数值模拟试验,分析了裂隙张开度对岩样破坏过程和破坏模式的影响;杨横涛等[17]采取FLAC建模计算方法研究了裂隙倾角、长度和张开度对岩样破坏强度的影响,其中关于裂隙倾角对岩样破坏强度的影响与张科等人的研究结论不同;韩建新等[18]提出一种计算模型用以计算多组贯穿裂隙几何参数对岩体等效弹性模量和等效泊松比的影响。以上研究在很大程度上揭示了岩石介质物理力学特性受裂隙结构的影响,进一步深化了对岩石断裂失效行为的认识,但也存在2点问题:①均是对材料裂隙结构的一种模拟,并非介质真实的裂隙结构,丢失了真实结构特征的有效信息,为研究带来一定的影响;②尤其是物理试验,多研究单一裂隙或几条裂隙,且形态简单。岩石介质宏观物理力学特性受各个尺度下,形态各异的裂隙结构的综合影响,一条或是几条形态简单的裂隙不足以说明问题。
因此本文选取不同冲击倾向性的煤岩介质,通过工业CT扫描试验,获取分辨率内的全部原生裂隙结构的信息,在煤岩原生裂隙结构三维重构的基础上,统计其整体和局部的三维几何特征。基于样本相关性分析原理和偏最小二乘回归分析原理,发现了煤岩物理力学特性与其原生裂隙结构几何特征的关联,将裂隙结构各个几何因子对物理力学参数的影响能力以及各物理力学参数受裂隙几何因子的影响程度做出了评估。
1 煤岩静态CT扫描试验
1.1 煤岩试样制备及岩石力学参数
煤样选自强、弱、无三个冲击倾向性矿井煤层,加工制备成尺寸为50 mm×50 mm×100 mm的标准试件,各2件。要求试件端面不平行度小于0.05 mm,轴向偏差小于0.25°。煤岩试件岩石力学参数见表1。
表1 煤岩介质岩石力学参数
Table 1 Coal rock medium rock mechanics parameter
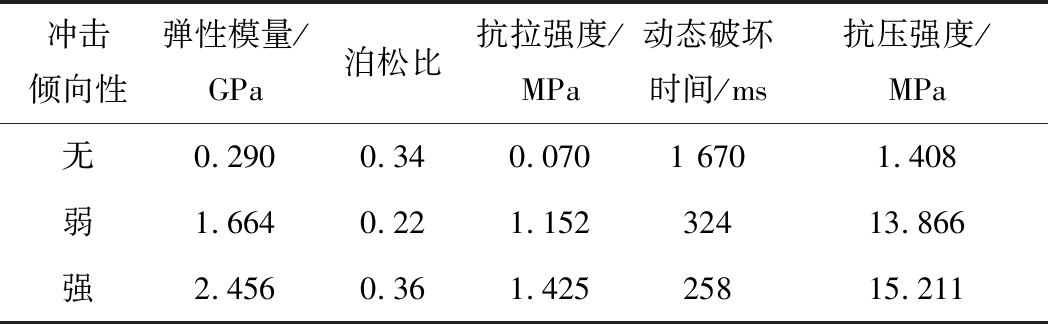
冲击倾向性弹性模量/GPa泊松比抗拉强度/MPa动态破坏时间/ms抗压强度/MPa无0.2900.340.0701 6701.408弱1.6640.221.15232413.866强2.4560.361.42525815.211
1.2 试验扫描方案
试验所使用的CT机为美国BIR公司生产的高级工业CT机,采用高精度16位微焦点X射线。扫描范围为整个试件高度,自上而下扫描1 000层,每层厚0.1 mm。每个试件可获得1 000张扫描图片。靠近试件顶部和底部的图片由于试件两端部干扰,图片残缺且不清晰,因此舍去靠近试件顶部和底部各50张图片,最终每个试件获得900张扫描图片。
2 煤岩原生裂隙结构特征
2.1 图像处理
由于机械切割的原因,试件边缘产生破裂。此部分裂隙非原生裂隙结构,因此首先剪除图像边缘部分。剪除图像边缘后,数字模型尺寸变为45 mm×45 mm×900 mm。由于煤岩介质密度不均匀,且CT扫描成像是一个极复杂的过程,这就容易导致部分CT扫描切片的灰度值整体偏高,部分CT扫描切片的灰度值整体偏低,直接影响后续阈值分割结果。因此对CT扫描图像做灰度均衡化处理,灰度均衡化可以使图像的像素在各个亮度区间均匀分布。同时经过均衡化处理后,目标和背景灰度值的差异被放大,便于后续识别、分割。为同一CT扫描切片,均衡化处理前后灰度直方图对比如图1所示。处理前后CT扫描切片效果如图2所示。

图1 某一切片均衡化处理前后灰度直方图
Fig.1 Grayscale histogram before and after a slice equalization process

图2 某一切片均衡化处理前后效果
Fig.2 Effect diagram before and after a slice equalization process
CT切片上存在一定数量的噪声、伪影,将影响最终原生裂隙结构三维重构和几何参数特征的分析,因此需要对其进行滤波处理。目前应用的滤波方法主要有中值滤波、均值滤波、高斯滤波、最大值和最小值滤波等。煤岩CT切片上存在的噪声、伪影以椒盐噪声和环状伪影为主,选用中值滤波效果较好。这是一种非线性滤波方法,它将每一像素点的灰度值设置为该点邻域内所有像素点灰度的中值。图像滤波过程,大多学者都基于二维CT切片进行处理,处理方式简单易行,视觉效果优越,但是会造成有效信息的缺失,部分二维切片上的“噪声”,在三维图像中实质是裂隙。因此在三维分析的前提下,应用中值滤波,噪声、伪影得到有效剔除,滤波效果如图3所示。

图3 某一切片滤波处理后效果图
Fig.3 The effect diagram of a slice after filtering process
2.2 图像分割与三维重构
处理后的图像,目标和背景的灰度差异变得明显,噪声、伪影得到有效剔除,为阈值分割带来便利。以往学者一般都是先进行二维图像分割,再进行三维重构。将阈值分割和三维重构独立操作的方法,虽然能够得到视觉效果优越的三维重构结果,但却丢失了部分有效信息,为后续分析带来误差。因此本文选择将三维重构和阈值分割同时进行的手段,分割的过程中,综合考虑煤岩试件空间各方向的分割结果,保证各个方向原生裂隙结构均被分割出来的前提下,尽可能选取小的阈值,保证分割结果中包含的噪声、孔隙等非目标结构最少。
三维重构后,煤岩介质原生裂隙结构的基本特征得到显现,但依然包含有部分孔隙结构以及很少的噪声和伪影,无法满足细观分析的要求,需要进一步筛选。根据相关研究[19],按裂隙的宽度W和长度L可划分为4种类型:A:W>5 μm且L>10 mm;B:W>5 μm且1 mm≤L≤10 mm;C:W<5 μm且300 μm≤L≤1 mm;D:W<5 μm且L≤300 μm。由于试验机分辨率的限制,本次试验中能探测的缺陷极限尺度为100 μm,因此只包含A、B两种类型的原生裂隙结构。根据裂隙长度进行筛选,得到最终三维重构结果如图4所示(3种冲击倾向性煤岩原生裂隙结构三维重构结果各出示1张)。
从重构结果看出,物理力学特性不同的煤岩介质原生裂隙结构整体特征差异明显,其发育程度与冲击倾向性成反比。无冲击倾向性煤岩,原生裂隙结构发育程度极高,以片状裂隙为主,分布于整个煤岩介质,且连通性强;弱冲击倾向性煤岩,原生裂隙结构发育程度较高,呈片状、条状,在介质中占据了较多空间;强冲击倾向性煤岩,原生裂隙结构发育程度很低,类似于“孤岛”状分布,有个别片状裂隙存在。
2.3 原生裂隙结构三维特征量化
现阶段对裂隙结构特征的量化以二维参数为主,包括迹长、倾角、间距、密度等。对于真实的三维空间特征的描述,尚无统一标准。借鉴二维几何参数,本文选取长度(Length3d)、宽度(Width3d)、最大主应力方向夹角(以下简称倾角,Angle)、表面积(Area3d)、体积(Volume3d)5种几何因子。通过以上5种几何因子可实现对裂隙几何形态的初步把握,但是考虑到原生裂隙不同于预制裂纹,其几何形态并不规则,因此增加空间分形维数(Fractal dimension3d)作为其几何特征的补充。根据分形理论可知,分形维数是对复杂结构形态的一种表述,其值越大表明形态特征越复杂,占有空间的有效性越高。故笔者认为,分形因子对损伤的描述显然比长度、宽度、体积、面积等因子更为科学,是对煤岩原生裂隙结构几何特征的深入刻画。并且可以推断,原生裂隙结构的分形因子越大,则煤岩体损伤越大,这在后文数据中得到印证。以上6种几何因子,其中长度为费雷特最大直径;宽度为费雷特最小直径;考虑到试件岩石力学参数均由实验室内单轴加载试验测得,故最大费雷特直径与z轴的夹角即为与最大主应力方向夹角。文中关注原生裂隙结构几何特征的两方面:一是全部原生裂隙结构三维几何参数呈现的统计学特征,为整体特征;二是原生裂隙结构中局部裂隙结构(空间贯通或体积最大的裂隙结构)的几何特征,为局部特征。3种冲击倾向性煤岩的原生裂隙结构几何特征的统计直方图各出示1组,如图5—图7所示。
从图5—图7可看出,长度、宽度、表面积、体积的数据范围跨度极大,在各个区间分布极不均匀,大部分数据分布在极小值附近,极大值附近仅有少量分布;倾角的数据在各个区间分布较为均匀。因此取长度、宽度、表面积、体积各自求和,倾角的平均值和空间分形维数作为对其整体特征的一个表述,计算结果保留两位小数,见表2。通过连通性和体积进行筛选,获得3种冲击倾向性煤岩介质的局部裂隙结构。取各个局部裂隙结构几何参数特征值作为局部特征的表述,3种冲击倾向性煤岩介质的局部裂隙结构几何因子见表3。

图4 原生裂隙结构三维重构图
Fig.4 3D reconstructiongraphs of primary fracture structure

图5 无冲击倾向性煤岩原生裂隙几何特征统计
Fig.5 Statistical histogram of geometric characteristics of coal rock primary fracture without outburst proneness

图6 弱冲击倾向性煤岩原生裂隙几何特征统计
Fig.6 Statistical histogram of geometric characteristics of coal rock primary fracture with weak outburst proneness

图7 强冲击倾向性煤岩原生裂隙几何特征统计
Fig.7 Statisticalhistogram of geometric characteristics of coal rock primary fracture with strong outburst proneness
表2 不同物理力学特性煤岩原生裂隙结构几何特征(整体特征)
Table 2 Geometric characteristics of original fracture structure of coal rock with different physical mechanical properties (integral characteristics)
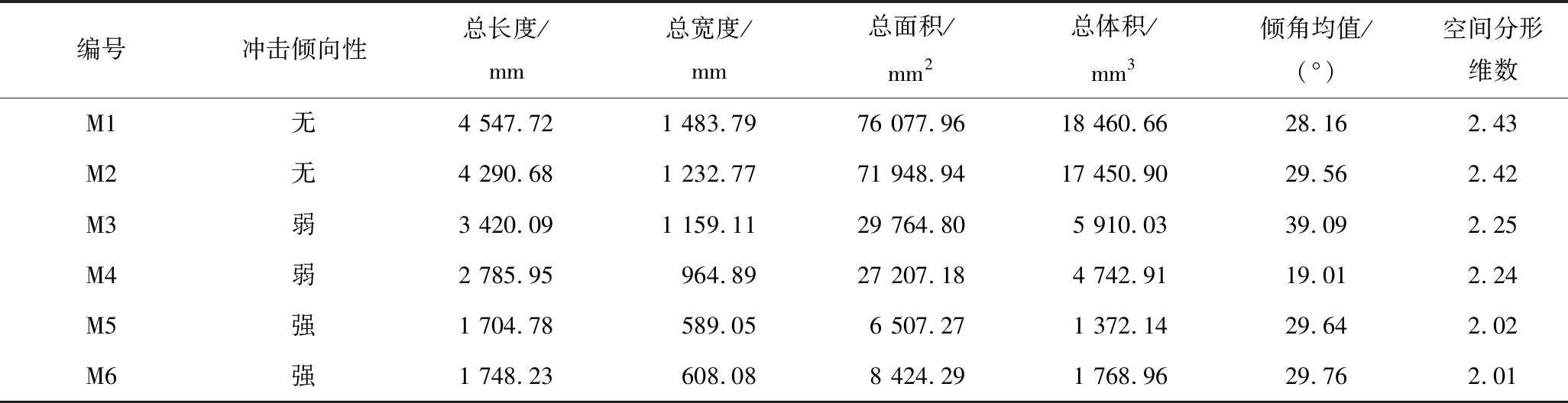
编号冲击倾向性总长度/mm总宽度/mm总面积/mm2总体积/mm3倾角均值/(°)空间分形维数M1无4 547.721 483.7976 077.9618 460.6628.162.43M2无4 290.681 232.7771 948.9417 450.9029.562.42M3弱3 420.091 159.1129 764.805 910.0339.092.25M4弱2 785.95964.8927 207.184 742.9119.012.24M5强1 704.78589.056 507.271 372.1429.642.02M6强1 748.23608.088 424.291 768.9629.762.01
表3 不同物理力学特性煤岩局部裂隙结构几何特征(局部特征)
Table 3 Geometric characteristics of local fracture structure of coal rock with different physical mechanical properties (local characteristics)
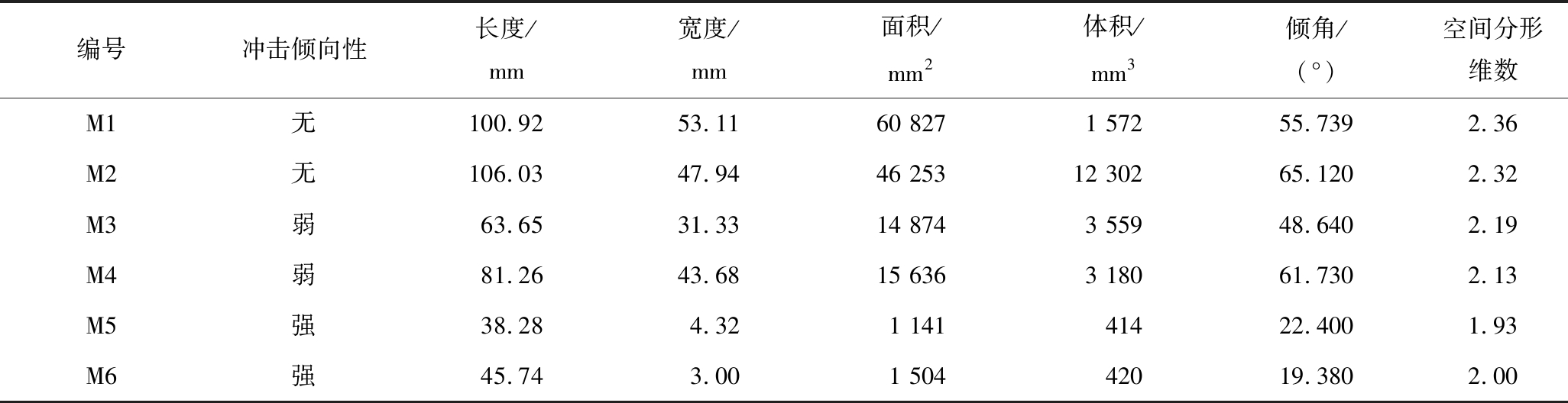
编号冲击倾向性长度/mm宽度/mm面积/mm2体积/mm3倾角/(°)空间分形维数M1无100.9253.1160 8271 57255.7392.36M2无106.0347.9446 25312 30265.1202.32M3弱63.6531.3314 8743 55948.6402.19M4弱81.2643.6815 6363 18061.7302.13M5强38.284.321 14141422.4001.93M6强45.743.001 50442019.3802.00
3 煤岩物理力学特性结构效应
理论上讲,煤岩介质的宏观物理力学特性在很大程度上受到材料原生裂隙结构的影响,文中将这种影响称为煤岩物理力学特性的结构效应。宏观物理力学特性相同的煤岩介质,其原生裂隙结构各个几何特征也不尽相同,因此考虑煤岩宏观物理力学特性与其原生裂隙结构特征的关联,不表现在原生裂隙结构的某一种几何特征上,而是多种几何特征综合影响的结果。文中采用样本相关性分析和偏最小二乘分析方法,其基本原理和技术步骤见文献[12],具体计算过程在MATALAB中完成。
3.1 原生裂隙结构整体特征与物理力学特性的关联
定义自变量系统X=[X1,X2,X3,X4,X5,X6],因变量系统Y=[Y1,Y2,Y3,Y4,Y5]。其中X1~X6分别代表原生裂隙结构的长度因子、宽度因子、面积因子、体积因子、倾角因子和分形因子,作为影响煤岩物理力学特性的几何因子;Y1~Y5分别表示煤岩介质的弹性模量、泊松比、抗拉强度、动态破坏时间和单轴抗压强度。原始数据矩阵S=[X,Y],矩阵S中各组变量之间量纲和数量级不同,因此首先进行标准化处理,然后分析各组变量之间的相关性,矩阵S相关系数矩阵C如下,结果保留两位小数。通常情况下,以绝对值大小判断变量的相关强度,分为4个等级,见表4。
参照表4,通过相关性系数判断,煤岩介质弹性模量、抗拉强度和单轴抗压强度与原生裂隙结构几何因子中的长度因子、宽度因子、面积因子、体积因子和分形因子均成明显的负相关关系;动态破坏时间与煤岩介质原生裂隙结构几何因子中的长度因子、宽度因子、面积因子、体积因子和分形因子有明显的正相关关系;泊松比几乎与原生裂隙结构几何因子无相关性。考虑自变量系统和因变量系统均存在严重的多重相关性,进行偏最小二乘回归分析。自变量系统中的倾角因子和因变量系统中的泊松比与系统其他参数相关性很弱,后续分析中不再考虑这两组变量,重新构造自变量系统X=[X1,X2,X3,X4,X6],因变量系统Y=[Y1,Y3,Y4,Y5]。
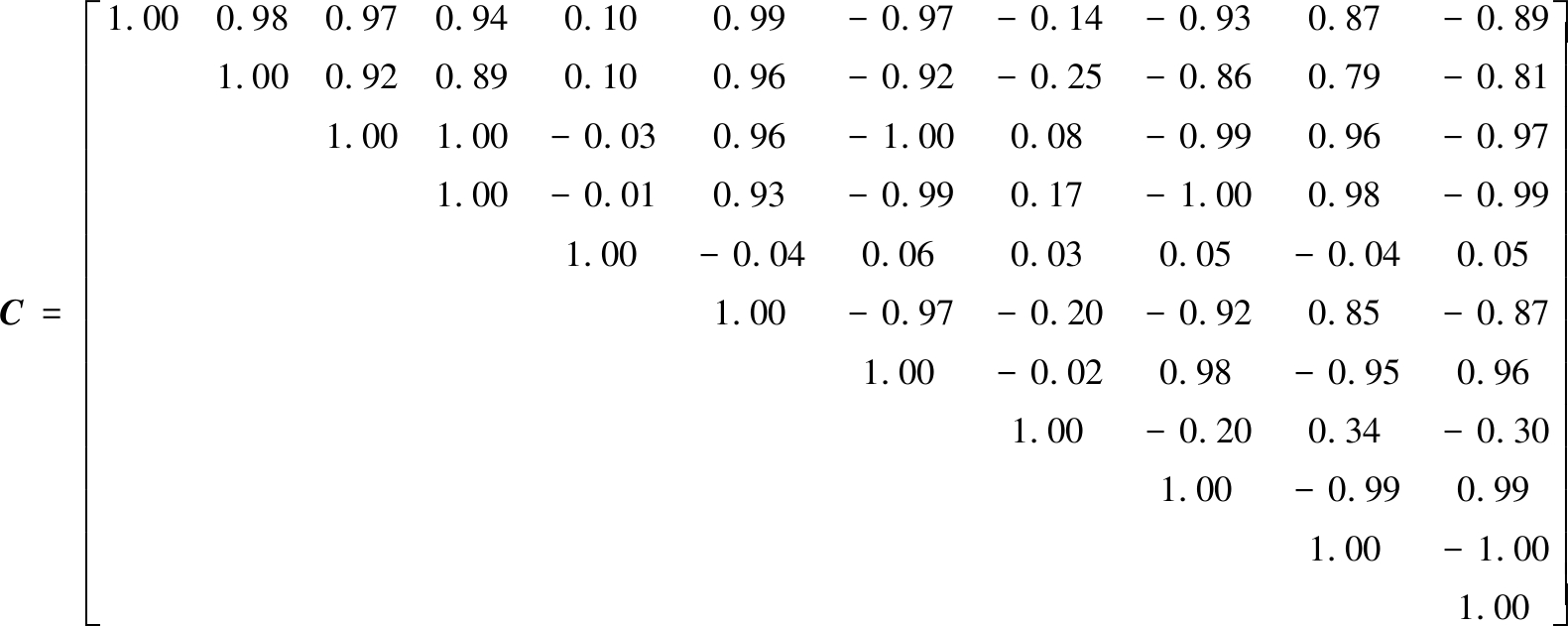
表4 相关强度参照
Table 4 The table of correlation strength reference

|rij|相关强度0.8~1.0极强相关0.6~0.8强相关0.4~0.6中等相关0.2~0.4弱相关0~0.2极弱相关或不相关
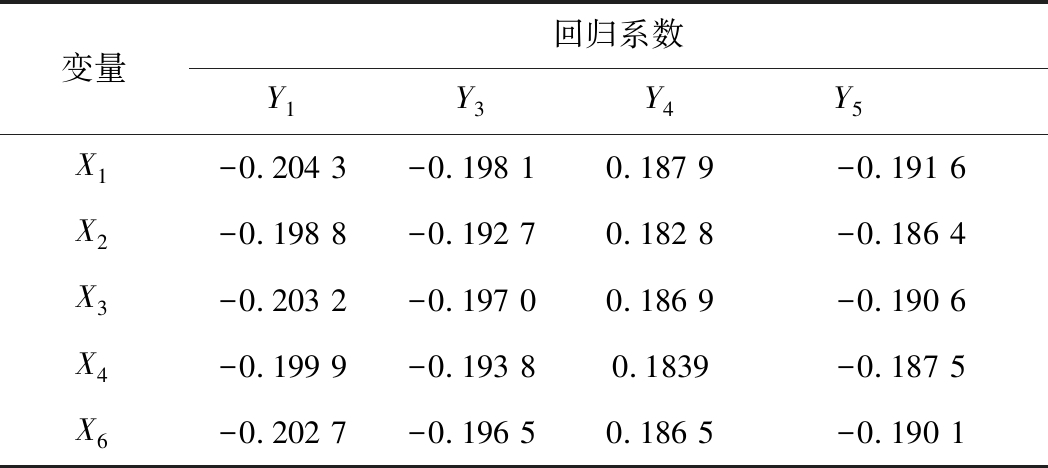
根据偏最小二乘分析原理,对标准化后的数据进行主成分提取,所有主成分及其复测定系数见表5。计算结果表明,当抽取1个主成分时,复测定系数已经达到0.912 4>0.850 0,且此时自变量系统变异信息的99.99%被提取,满足分析需求。表6列出了第一主成分t1对系统信息的解释能力,可以看出,t1对变量系统X1、X2、X3、X4、X6的解释能力均很强,所以可以将t1看作是X1、X2、X3、X4、X6的综合,解释了X系统96.28%的变异信息,Y系统89.81%的变异信息,能够代表自变量系统X。因此,在本次回归分析中,提取第1个主成分即可。通过计算第一主成分间的相关系数高达-0.955 8,兼顾主成分的解释能力及模型从简的原则,只选取第一主成分建模。标准化回归系数见表7,其绝对值大小反映了不同自变量对因变量的影响能力。
表5 复测定系数及自变量系统被提取变异信息量
Table 5 The table of complex measurement coefficient and independent variable system extracted variation information scale

主成分个数12345复测定系数0.912 41.013 21.015 51.015 61.016 0X系统被提取变异信息量0.999 91.031 41.037 31.038 61.038 6
表6 各个主成分对系统信息的解释能力
Table 6 The ability of each principal component to explain the information of the system

变量X1X2X3X4X6Y1Y3Y4Y5XYt10.986 7 0.934 0 0.976 5 0.945 0 0.971 6 0.980 1 0.921 2 0.829 2 0.861 7 0.962 80.898 1
表7 偏最小二乘回归后标准化的回归系数
Table 7 Standardizedregression coefficients estimated by partial least squares regression
变量回归系数Y1Y3Y4Y5X1-0.204 3 -0.198 1 0.187 9 -0.191 6 X2-0.198 8 -0.192 7 0.182 8 -0.186 4 X3-0.203 2 -0.197 0 0.186 9 -0.190 6 X4-0.199 9 -0.193 8 0.1839 -0.187 5 X6-0.202 7 -0.196 5 0.186 5 -0.190 1
3.2 局部裂隙结构特征与物理力学特性的关联
煤岩局部裂隙结构与其物理力学特性的关联的研究分析中,采取与3.1节同样的分析过程。自变量系统![]() 因变量系统
因变量系统![]() 其中
其中![]() 代表的几何因子分别是局部裂隙结构的长度、宽度、表面积、体积、倾角和空间分形维数;
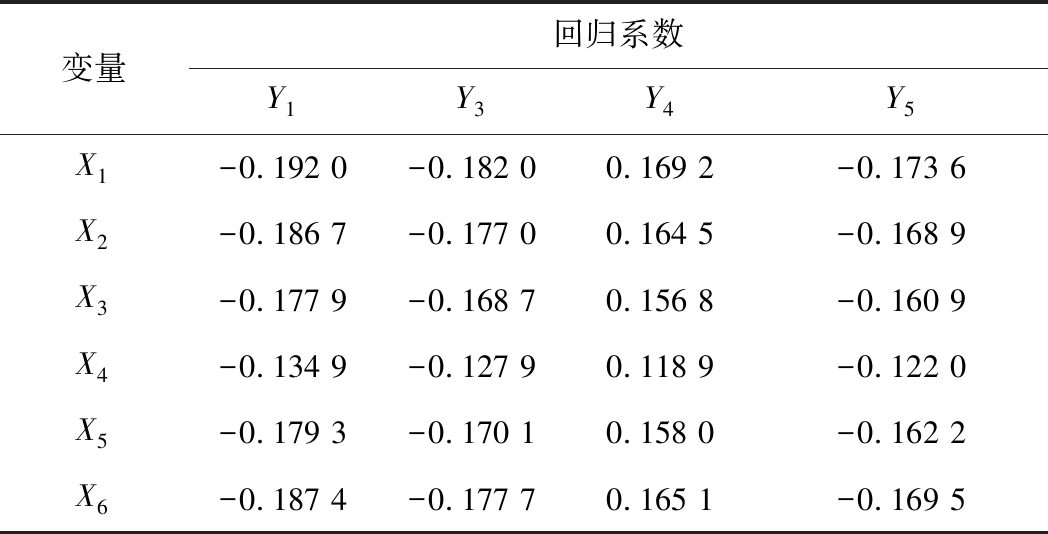
代表的几何因子分别是局部裂隙结构的长度、宽度、表面积、体积、倾角和空间分形维数;![]() 分别表示煤岩介质的弹性模量、泊松比、抗拉强度、动态破坏时间和单轴抗压强度。最终得到标准化回归系数见表8及样本相关系数矩阵C′。
分别表示煤岩介质的弹性模量、泊松比、抗拉强度、动态破坏时间和单轴抗压强度。最终得到标准化回归系数见表8及样本相关系数矩阵C′。
表8 偏最小二乘回归后标准化的回归系数
Table 8 Standardizedregression coefficients estimated by partial least squares regression
变量回归系数Y1Y3Y4Y5X1-0.192 0 -0.182 0 0.169 2 -0.173 6 X2-0.186 7 -0.177 0 0.164 5 -0.168 9 X3-0.177 9 -0.168 7 0.156 8 -0.160 9 X4-0.134 9 -0.127 9 0.118 9 -0.122 0 X5-0.179 3 -0.170 1 0.158 0 -0.162 2 X6-0.187 4 -0.177 7 0.165 1 -0.169 5

3.3 分析讨论
煤岩物理力学特性中,泊松比与介质原生裂隙结构整体和局部特征几乎均无相关性或相关性很弱,这一结论与先前李树忱等[6]的研究中的部分结论不同,这也恰恰说明通过类岩材料或是预制单一裂纹的方法无法真实反映介质某些物理力学性质受裂隙结构的影响。动态破坏时间与介质原生裂隙结构几何参数呈正相关关系,其余岩石力学参数与介质原生裂隙结构几何参数呈负相关关系。
煤岩介质原生裂隙结构整体特征的研究中,通过相关系数分析,发现原生裂隙结构倾角因子和煤岩物理力学特性几乎无相关关系。通过标准化回归系数可以看出,不同几何因子对煤岩物理力学特性的影响能力不同,依次为长度因子、面积因子、分形因子、体积因子、宽度因子;不同物理力学特性受几何因子的影响程度也不同,依次是弹性模量、抗拉强度、单轴抗压强度、动态破坏时间。
不同于煤岩介质原生裂隙结构整体特征的研究,局部裂隙结构倾角与煤岩弹性模量表现出极强的相关关系,与抗拉强度、动态破坏时间和单轴抗压强度有强相关关系。煤岩介质原生裂隙结构局部特征的讨论中,不同几何因子对煤岩物理力学特性的影响能力大小,依次是长度因子、分形因子、宽度因子、倾角因子、面积因子、体积因子,其中体积因子对其影响能力明显小于其他各因子;不同物理力学特性受几何因子的影响依次是弹性模量、抗拉强度、单轴抗压强度、动态破坏时间。
4 结 论
1)基于工业CT扫描成像技术,实现了煤岩原生裂隙结构三维重构。重构过程中,处理算法均在三维尺度下完成,较以往煤岩裂隙三维重构研究更为精确,煤岩原生裂隙结构信息更为全面。
2)采用三维空间指标,包括长度、宽度、表面积、体积、与最大主应力方向夹角和空间分形维数,完成了对煤岩原生裂隙结构整体和局部特征的量化描述。
3)研究发现煤岩原生裂隙结构发育程度与介质冲击倾向性成反比。无冲击倾向性煤岩,原生裂隙结构发育程度极高,有明显的片状裂隙分布于整个煤岩介质,且连通性强;弱冲击倾向性煤岩,原生裂隙结构发育程度较高,以片状、条状居多,在煤岩介质中占据了较多空间,连通性较弱;强冲击倾向性煤岩,原生裂隙结构发育程度很低,大多类似于“孤岛”状分布,无空间贯通裂隙。
4)选取煤岩原生裂隙结构三维空间几何特征,包括长度、宽度、表面积、体积、与最大主应力方向夹角和空间分形维数作为自变量系统,煤岩介质弹性模量、抗拉强度、动态破坏时间和单轴抗压强度作为因变量系统,二者之间有明显的相关性。整体特征对介质物理力学特性的影响能力大小依次为:长度因子、面积因子、分形因子、体积因子、宽度因子,与倾角因子无关;不同物理力学特性受几何因子的影响程度也不同,依次是弹性模量、抗拉强度、单轴抗压强度、动态破坏时间;局部特征对介质物理力学特性的影响能力大小依次为长度因子、宽度因子、分形因子、倾角因子、面积因子、体积因子,其中体积因子对其影响能力明显小于其他各因子;不同物理力学特性受几何因子的影响依次是弹性模量、抗拉强度、单轴抗压强度、动态破坏时间。
[1] BROWN E T,TROLLOPE D H.Strength of a model of jointed rock[J].Journal of the Soil Mechanics and Foundations Division,1970,96(2):685-704.
[2] BROWN E T.Strength of models of rock with intermittent joints[J].Journal of the Soil Mechanics and Foundations Division,1970,96(6):1935-1949.
[3] EINSTEIN H H,HIRSCHFELD R C.Model studies on mechanics of jointed rock[J].Journal of the Soil Mechanics and Foundations Division,1973,99(3):229-248.
[4] YOSHINAKA R.Joint stiffness and the deformation behaviour of discontinuous rock[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1986,23(1):19-28.
[5] 路亚妮,李新平,肖家双.单裂隙岩体冻融力学特性试验分析[J].岩石力学与工程学报,2014,10(3):593-649.
LU Yani,LI Xinping,XIAO Jiashuang.Experimental analysis on mechanical characteristic of single cracked rockmass under freeze-thaw condition[J].Chinese Journal of Rock Mechanics and Engineering,2014,10(3):593-649.
[6] 靳 瑾,曹 平,蒲成志.预制裂隙几何参数对类岩材料破坏模式及强度的影响[J].中南大学学报:自然科学版,2014,45(2):529-535.
JIN Jin,CAO Ping,PU Chengzhi.Influence of flaw parameters on damage mode andstrength of rock-like materials[J].Journal of Central South University:Science and Technology,2014,45(2):529-535.
[7] 杨圣奇,戴永浩,韩立军,等.断续预制裂隙脆性大理岩变形破坏特性单轴压缩试验研究[J].岩石力学与工程学报,2009,28(12):2391-2404.
YANG Shengqi,DAI Yonghao,HAN Lijun,et al.Uniaxial compression experimental research on deformation and failure properties of brittle marble specimen with pre-existing fissures[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(12):2391-2404.
[8] 李树忱,汪 雷,李术才,等.不同倾角贯穿节理类岩石试件峰后变形破坏试验研究[J].岩石力学与工程学报,2013,32(S2):3391-3395.
LI Shuchen,WANG Lei,LI Shucai,et al.Post-peak deformation and failure experimental study of rock-like specimens with different inclination angles persistent joints[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(S2):3391-3395.
[9] 陈 新,廖志红,李德建.节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J]岩石力学与工程学报,2011,30(4):781-789.
CHEN Xin,LIAO Zhihong,LI Dejian.Expreimentalsyudyof effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression[J].Journal of China Coal Society,2011,30(4):781-789.
[10] 韩 健.裂隙几何特征对岩体力学性质及裂纹扩展规律影响的试验研究[D].北京:中国地质大学(北京),2015.
HAN Jian.Experimental study of effects of fracture geometrical characteristics on mechanical properties and crack propagation laws of rock masses[D].Beiijng:China University of Geosciences (Beijing),2015.
[11] 腾俊洋,唐建新,李欣怡.含孔洞加锚岩石力学特性及裂纹扩展规律[J].岩石力学与工程学报,201,37(1):87-103.
TENG Junyang,TANG Jiangxin,LI Xinyi.Mechanical property and fracture propagation rule of anchored rock with a hole under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(1):87-103.
[12] BAHAADDINI M,Sharrock G,HEBBLEWHITE B K.Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression[J].Computers and Geotechnics,2013,49:206-225.
[13] XU T,RANJITH P G,WASANTHA P L P,et al.Influence of the geometry of partially-spanning joints on mechanical properties of rock in uniaxial compression[J].Engineering Geology,2013,167:134-147.
[14] 张 科,刘享华,李 昆,等.含孔多裂隙岩石力学特性与破裂分形维数相关性研究[J].岩石力学与工程学报,2018,37(1):1-11.
ZHANG Ke,LIU Xianghua,LI Kun,et al.Investigation on correlation between mechanical characteristic andfractal dimension of fracturing of rock containing ahole andmulti-flaws[J].Chinese Journal of Rock Mechanics and Engineering,2018,37(1):1-11.
[15] 李露露,高永涛,周 喻,等.单轴压缩条件下含三叉裂隙类岩石试样力学特性的细观研究[J].岩土力学,2018,39(10):1-9.
LI Lulu,GAO Yongtao,ZHOU Yu,et al.Meso research on the mechanical properties of rock-like material containing trident cracks under uniaxial compresssion[J].Rock and Soil Mechanics,2018,39(10):1-9.
[16] 明华军,徐小峰,梁 波.不同裂隙张开度下岩石材料破坏的颗粒离散元模拟[J].三峡大学学报:自然科学版,2013,35(6):63-66.
MING Huajun,XU Xiaofeng,LIANG Bo.Simulation of rock failure mechanism of different fracture apertures using particle flow code[J].Journal of China Three Gorges University:Natural Sciences,2013,35(6):63-66.
[17] 杨横涛,林 杭.岩样单裂隙几何参数对其破坏模式与强度的影响[J].长江科学院院报,2018,35(3):26-44.
YANG Hengtao,LIN Hang.Influence of flaw parameters on the failure mode and strength of single-flawed rock specimens[J].Journal of Yangtze River Scientific Research Institute,2018,35(3):26-44.
[18] 韩建新,李术才,李树忱,等.多组贯穿裂隙岩体变形特性研究[J].岩石力学与工程学报,2011,30(S1):3319-3325.
HAN Jianxin,LI Shucai,LI Shuchen,et al.Study of deformation characteristic of rock mass with multiple persistent crack sets[J].Journal of China Coal Society,2011,30(S1):3319-3325.
[19] 陈贞龙,王运海,王 宁,等.延川南地区煤储层孔裂隙特征研究[J].油气藏评价与开发,2013,3(3):67-71.
CHEN Zhenlong,WANG Yunhai,WANG Ning,et al.Research on the pore-fracture properties of coal reservoirs in South Yanchuan region.Reservoir Evaluationand Development,2013,3(3):67-71.
[20] 包研科.数据分析教程[M].北京:清华大学出版社,2011:184-189.
BAO Tanke.Data analysis tutorial[M].Beijing:Tsinghua University Press,2011:184-189.
