0 引 言
深部巷道围岩体除了受到上覆岩体的静载作用,还将受到爆破、矿震、机械振动等引起的动力扰动作用[1-4],此时深部巷道围岩处于初始高应力和动力扰动的复杂受力状态,在这种状态下,围岩的力学行为以及破坏程度较静力状态下有很大的不同[5-6]。因此,研究动力扰动下巷道围岩的力学特性有利于预测和治理深部开采引发的地质灾害,保证矿山安全生产。研究动力扰动下围岩巷道的变形破坏特征主要采用数值方法,包括离散元、有限元、解析法以及有限单元法等[7]。不少学者[8-11]分别采用RFPA、PFC2D和FLAC3D等数值模拟软件研究了不同侧压力系数、不同扰动幅值和扰动时间下巷道围岩的稳定性,结果表明随着扰动波应力幅值和扰动时间的增大,巷道围岩的变形增大,巷道顶、底板的应力、位移及裂纹数量也显著增加,巷道稳定性变差。温颖远等[12]认为动力扰动下巷道不同位置处的变形、应力和塑性区范围与煤层的软硬程度有关。唐礼忠等[13]研究了动力扰动下软弱夹层厚度对巷道围岩稳定性的影响,认为软弱夹层衰减了动力扰动的强度,弱化了爆破波的能量;此外,文献[14-16]研究了爆破扰动对巷道围岩稳定性的影响,认为爆破扰动增大了围岩裂纹扩展的速度,顶、底板围岩受拉严重。上述研究从不同方面揭示了动力扰动下巷道围岩的变形规律,但在研究影响围岩稳定性的因素时,都是在其他因素不变的情况下进行的,事实上动力扰动下巷道围岩的稳定性是由多种因素共同作用的结果。正交试验能在考虑各种因素情况下,在较少试验次数下,得出各个因素的影响。 笔者将通过正交试验,在正交优化组合的基础上,运用FLAC3D软件对影响巷道围岩变形的因素进行敏感性分析,寻找影响巷道稳定性的关键因素。
1 动力扰动下巷道围岩失稳机理
对于深部巷道围岩,在承受上覆岩层静载作用的情况下,周边叠加动力扰动易致其失稳。巷道受静载和动载的力学简化模型如图1所示,设上覆岩石垂直应力为σ1=γh,则水平应力σ2=λγh,至巷道中心距离为d处受到扰动力σd。根据基尔希公式,得圆形巷道在静力作用下,距巷道中心r处,与水平轴夹角为θ处的围岩应力与位移[17]为
(1)
(2)
(3)
(4)
(5)
式中:σr、σθ和σrθ分别为径向正应力、环向正应力和切向应力,MPa;ur和uθ分别径向位移和环向位移,m;λ为水平侧压力系数;a和r分别为圆形巷道半径和受力点距巷道中心的距离,m;γ为上覆岩层容重;h为模型上方覆岩层高度,m;θ为受力点与水平轴夹角;G为岩体的剪切模量,GPa;ν为泊松比。

图1 巷道受静载和动载的力学简化模型
Fig.1 Simplified mechanical models of roadway subjected to static and dynamic loads
由于缺乏精确的理论解,对于拱形巷道通常采用半径折算法计算巷道围岩的应力与位移[9]为
r0=b(S/π)1/2
(6)
式中:r0为拱形断面折算后半径,m;b为折算断面修正系数,拱形取1.1;S为拱形断面面积,m2。
在动力扰动下,应力波传播到巷道围岩表面时,将发生反射,反射界面满足速度和应力相等的条件,根据质量守恒和动量守恒,得出反射波应力强度为
(7)
式中:σdf为反射波应力强度,MPa;ηw和ηk分别为围岩表面波阻抗和空气表面波阻抗,g/(m2·s)。
由于空气的波阻抗很小,围岩波阻抗相对于空气为无穷大,则有σdf = -σd,此时围岩受到的反射力为拉应力,处于拉伸状态,通常情况下岩石抗压不抗拉,因此在受到扰动力后围岩极易发生变形,最终导致巷道失稳。
从式(1)—式(7)可以看出影响巷道稳定性的因素有扰动力σd,侧压力系数λ,扰动波至巷道中心距离d,影响扰动力σd的因素有应力峰值A、扰动频率f和扰动时间t。为了分析这些因素对巷道围岩变形的影响情况,采用数值模拟方法,研究埋深800 m,扰动波距巷道中心10 m处巷道围岩变形情况,运用正交试验分析巷道围岩移动对侧压力系数、扰动频率f、应力峰值A和扰动时间t的敏感性。
2 巷道围压动力响应数值模拟
根据某矿工程地质条件(巷道宽4 m,墙高2.6 m),采用FLAC3D中Dynamic模块对模型进行动力响应分析,设计模型尺寸为40 m ×40 m×40 m,每1 m3划分为1个计算单元格,共37 330个。采用理想弹塑性模型,屈服准则采用Mohr-Coulomb强度准则,其力学参数见表1,模型下部采用固定约束,上部采用均布荷载并距巷道中心10 m处再施加动荷载。在顶板和帮部其设置2个监测点,由于动荷载在巷道中心上方,且材料是均质的,因此两帮变形是一致的,只需要在帮部一侧布置1个监测点,模型及监测点布置如图2所示。
表1 岩石力学参数
Table 1 Petromechanical parameter

密度/(kg·m-3)体积模量/GPa剪切模量/GPa黏聚力/MPa内摩擦角/(°)2 6803.461.153.1032

图2 数值计算模型
Fig.2 Numeric calculation model
数值计算时取巷道受到扰动力为载荷波形中谐波的一段[18],其数学表达式:
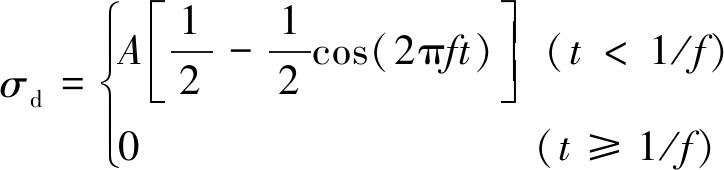
(8)
基于正交试验法,确定扰动频率f,应力峰值A,水平侧压力系数λ,扰动时间t为4个主要因素,分别设置4个水平,具体见表2。
表2 巷道稳定影响因素正交设计水平
Table 2 Orthogonal design level for influencing factor of roadway stability

水平应力峰值/MPa扰动频率/Hz侧压力系数扰动时间/s1510.80.221051.00.4315101.20.6420151.40.8
在考虑水平均匀性和配置均匀性的前提下,选用5因素4水平的正交设计方案,设置1列空列,用于误差分析,共16组配比,见表3;由于空列的主要作用是误差分析,表中并未列出。
表3 正交试验方案与数值模拟结果
Table 3 Orthogonal experimental scheme and numerical simulation results

试验影响因素最大变形量/mm应力峰值/MPa扰动频率/Hz侧压力系数扰动时间/s顶板两帮1510.80.24036.52551.00.4515435101.20.6606645151.40.8738751011.00.8555761050.80.64745710101.40.46483810151.20.2516191511.20.45966101551.40.259761115100.80.853461220151.00.65156132011.40.67087142051.20.863721520101.00.245511620150.80.44343
3 正交试验结果分析
3.1 方差分析
对于正交表Ln(mk),n为正交试验次数,m为影响指标结果的因素,k为水平。为了消除试验误差对结果的影响,需要在极差的基础上进行方差分析,计算数据的总偏差平方和SZ、各因素偏差平方和SY和误差偏差平方和SW,在此基础上构造统计量F,并将其与在给定显著性水平α下查出临界值Fα(m-1,n-m)进行比较(Fα值由F分布表查得),从而判断各因素的影响显著性。
一般情况下取显著性水平α=0.01和α=0.1,当F大于F0.01(m-1,n-m)时,称为因素影响显著;当F大于F0.1(m-1,n-m)并且小于F0.01,为因素影响较显著;当F小于F0.1(m-1,n-m)时,则为因素影响不显著。本次试验采用L16(45)型正交表,查表得F0.01(3,12)=5.95,F0.1(3,12)=2.61。
(9)
(10)
SW=SZ-SY
(11)
(12)
式中: Yi为第i次试验结果,![]() 为n次试验结果的平均值,mm;Kij为正交表中第j列的第i水平中Yi之和,mm;p为同一水平重复试验次数。
为n次试验结果的平均值,mm;Kij为正交表中第j列的第i水平中Yi之和,mm;p为同一水平重复试验次数。
1)顶板位移分析。将各个影响因素的水平模拟结果取平均值ki(i=1,2,3,4),并求出极差Ri(表4),平均值反映了同一因素的不同水平影响大小,极差反映了因素变化时试验结果的变化幅度。从表4可以看出影响顶板变形最大的组合为(4,1,4,4),即应力峰值20 MPa,频率1 Hz,侧压力系数1.4,扰动时间0.8 s,最小的组合为(1,4,1,1),即应力峰值5 MPa,频率15 Hz,侧压力系数0.8,扰动时间0.2 s。侧压力系数和扰动时间影响显著(表5),应力峰值和频率对围岩变形影响很小。将计算得出的F值与F0.01(3,12)和F0.1(3,12)比较,得出动力扰动下对顶板变形影响的敏感性顺序(由大到小)为侧压力系数、扰动时间、振幅、频率。
表4 顶板位移极差分析
Table 4 Range analysis of roof displacement 单位/mm

项目应力峰值扰动频率侧压力系数扰动时间k153.1056.0047.7554.25k254.2555.0050.5056.00k355.5055.0058.2555.65k456.5054.5066.5056.25极差Ri3.401.5020.752.00
2)两帮位移分析。影响两帮变形最大的组合为(4,1,4,4),即应力峰值20 MPa,频率1 Hz,侧压
表5 顶板位移方差分析
Table 5 Variance analysis of roof displacement

因素偏差平方和/mm2自由度F显著性应力峰值0.1431.52—扰动频率0.1730.40—侧压力系数1.95379.48显著扰动时间6.80325.40显著误差项1.425——
力系数1.4,扰动时间0.8 s(表6);最小的组合为(1,4,1,1),即应力峰值5 MPa,频率15 Hz,侧压力系数0.8,扰动时间0.2 s。侧压力系数和扰动时间影响显著,应力峰值和频率对两帮影响很小(表7)。 将计算得出的F值与F0.01(3,12)和F0.1(3,12)比较,动力扰动下对帮部变形影响的敏感性顺序(由大到小)为侧压力系数、扰动时间、振幅、频率。
表6 两帮位移极差分析
Table 6 Range analysis of two sides displacement
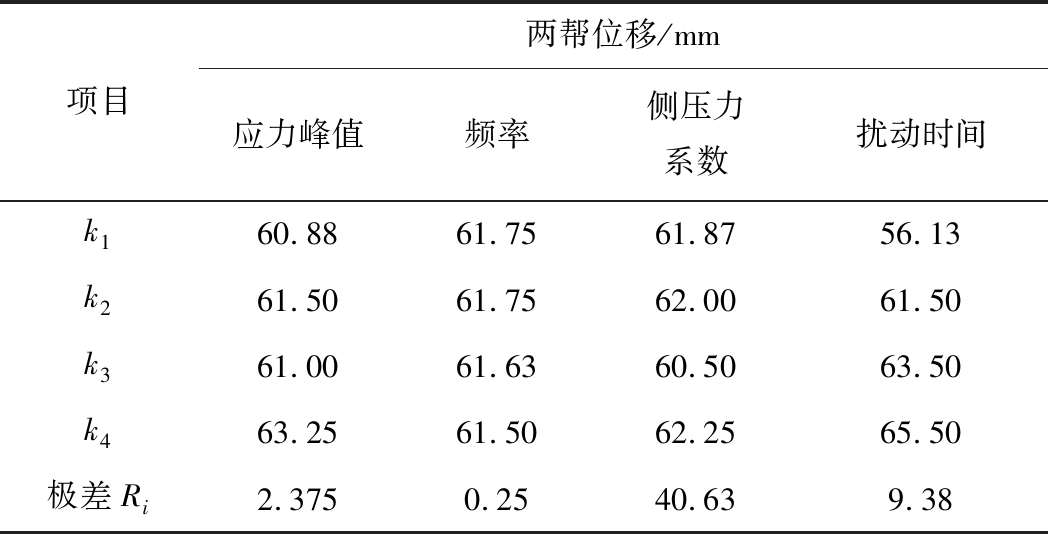
项目两帮位移/mm应力峰值频率侧压力系数扰动时间k160.8861.7561.8756.13k261.5061.7562.0061.50k361.0061.6360.5063.50k463.2561.5062.2565.50极差Ri2.3750.2540.639.38
表7 两帮位移方差分析
Table 7 Variance analysis of two sides displacement

因素偏差平方和/mm2自由度F显著性应力峰值0.18731.943—扰动频率0.18830.230—侧压力系数7.8003485.48显著扰动时间5.600326.297显著误差项0.6885——
3)数值模拟。选取影响巷道围岩变形程度最大的组合与最小的组合对比,即模拟应力峰值20 MPa和5 MPa,频率1 Hz和15 Hz,侧压力系数1.4和0.8,扰动时间0.8 s和0.2 s情况下围岩的变形(图3)及塑性区分布(图4),来验证敏感性分析结果。
由图3和图4可得,当应力峰值为5 MPa,扰动频率15 Hz,侧压力系数0.8,扰动时间0.2 s时,即影响巷道围岩变形程度最小的组合,塑性区范围较小,为1~2 m,顶板变形量0.032 m,两帮变形量0.024 m,比表3中任意组合值都小,说明该组合下围岩变形最小是成立的;应力峰值20 MPa,扰动频率1 Hz,侧压力系数1.4,扰动时间0.8 s时,即影响巷道围岩变形最大的组合,塑性区范围较大,为3~4 m,是最小组合的2~3倍,顶板变形量0.078 m,两帮变形量0.084 m,比表3中任意组合值都大,说明该组合下围岩变形最大是成立的。

图3 围岩变形
Fig.3 Deformation nephogram of surrounding rock

图4 塑性区分布
Fig.4 Distribution of plastic zone
3.2 回归分析
对正交试验结果进行回归分析,建立指标与因素之间的关系,影响因素为x1,x2,x3,…,xk,对应的试验结果y1,y2,…,yk,则指标与因素间的多元性回归模型[19]:
y=β0+β1x1+β2x2+…+βkxk+ε
(13)
相应多元线性回归方程为
(14)
式中:y为指标结果,mm;β0,β1,…,βk为回归模型参数;![]() 分别为对应的回归方程参数;
分别为对应的回归方程参数;![]() 为回归方程计算值,mm;ε为误差,mm。
为回归方程计算值,mm;ε为误差,mm。
回归方程能否能真实反映xi与yi的关系,要进行统计检验。构造统计量F 对多元线性回归方程进行显著性检验,将计算得到的F值与查表得到的显著性水平α下临界值Fα(k,n-k-1)比较。
(15)
式中:![]() 为回归平方和,mm2,由自变量xi变化引起;
为回归平方和,mm2,由自变量xi变化引起;![]() 为误差平方和,mm2,由实验误差及其他未加控制的因素引起;
为误差平方和,mm2,由实验误差及其他未加控制的因素引起;![]() 为yi的算术平均值,mm。
为yi的算术平均值,mm。
1)顶板位移回归分析。采用最小二乘法得到顶板最大位移试验结果的线性回归方程:
根据式(15)求得统计量F=89.81,当k=5,n-k-1=10时,取置信水平α=0.05,查F分布表得F0.05(5,10)=3.33,因此F >F0.05(5,10),表明巷道顶板位移试验结果与回归方程拟合很好,回归效果显著。
2)帮部位移回归分析。同理,对帮部最大位移试验结果进行多元线性回归计算,得:
根据式(15)求得统计量F=175.45,当k=5,n-k-1=10时,取α=0.05,查分位表F0.05(5,10)=3.33,表明巷道帮部位移试验结果与回归方程拟合很好,回归效果显著。
4 结 论
1)影响巷道顶板和帮部变形最大的组合为(1,1,4,4),最小的组合为(1,4,1,1)。方差分析结果表明,4个因素中对顶板和帮部围岩变形影响程度大小的因素依次为侧压力系数、扰动时间、应力峰值、频率。
2)采用数值模拟方式对敏感性分析结果进行了验证,结果表明:采用影响巷道围岩变形程度最小的组合模拟时,塑性区范围较小,为1~2 m,顶板变形量32 mm,两帮变形量24 mm;采用影响程度最大的组合模拟时,塑性区范围为3~4 m,是最小组合的2~3倍,顶板变形量78 mm,两帮变形量84 mm。
3)分别建立了应力峰值、扰动频率、侧压力系数及扰动时间与顶板变形和两帮变形多元线性回归方程,回归效果显著,研究成果为巷道围岩支护设计提供了参考依据。
[1] 何满潮,谢和平,彭苏萍.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16): 2803-2813.
HE Manchao, XIE Heping, PENG Suping. Study on mechanicsin deep mining engineering [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803-2813.
[2] 骆浩浩,李祥龙,王建国,等.井下大爆破直通巷道冲击波超压的预测研究[J].中国安全科学学报,2019,29(3):57-62.
LUO Haohao, LI Xianglong, WANG Jianguo,et al. Study on peak overpressure prediction of underground blasting shock waves on straight-through roadways[J]. Journal of Safety Science and Technology, 2019,29(3):57-62.
[3] 蔡美峰,冀 东,郭奇峰,等.基于地应力现场实测与开采扰动能量积聚理论的岩爆预测研究[J].岩石力学与工程学报, 2013, 32(10):1973-1980.
CAI Meifeng, JI Dong, GUO Qifeng,et al. Study of rock burst prediction based on in-situ stress measurement and theory of energy accumulation caused by mining disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10):1973-1980.
[4] 谢和平,高 峰,鞠 杨.深部岩体力学研究与探索[J].岩石力学与工程学报,2015,35(11):2161-2178.
XIE Heping, GAO Feng, JU Yang. Research and development of rock mechanics in deep ground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 35(11):2161-2178.
[5] 周小平,钱七虎.深埋巷道分区破裂化机制[J].岩石力学与工程学报,2007,26(5):877-885.
ZHOU Xiaoping, QIAN Qihu. Zonal fracturing mechanism in deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(5): 877-885.
[6] 李术才,王汉鹏,钱七虎,等.深部巷道围岩分区破裂化现象现场监测研究[J].岩石力学与工程学报,2008,27(8):1545-1553.
LI Shucai, WANG Hangpeng, QIAN Qihu, et al. In-situ monitoring research on zonal disinter- gration of surrounding rock mass in deep mine roadways[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(8): 1545-1553.
[7] SALMI E F,KARAKUS M,NAZEM M. Assessing the effects of rock mass gradual deterioration on the long-term stability of abandoned mine workings and the mechanisms of post-mining subsidence-A case study of Castle Fields mine[J]. Tunnelling and Underground Space Technology Incorporating Trenchless Technology Research, 2019,19(14):13-15.
[8] 朱万成,左宇军,尚世明,等.动态扰动触发深部巷道发生失稳破裂的数值模拟[J].岩石力学与工程学报,2007,26(5):915-921.
ZHU Wancheng, ZUO Yujun, SHANG Shiming, et al. Numerical simulation of instable failure of deep rock tunnel triggered by dynamic disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(5):915-921.
[9] 李夕兵,廖九波,赵国彦,等.动力扰动下高应力巷道围岩动态响应规律[J].科技导报,2012,30(22):48-54.
LI Xibing, LIAO Jiubo, ZHAO Guoyang, et al. Dynamic response of surrounding rock in highly-stressed tunnel under dynamic disturbance[J]. Science & Technology Review, 2012,30(22):48-54.
[10] 彭 瑞,赵光明,孟祥瑞.基于D-P准则的非均匀应力场受扰动轴对称巷道安全性分析[J].中国安全科学学报,2014,24(1):103-108.
PENG Rui, ZHAO Guangming, MENG Xiangrui. Analysis of safety of disturbed and axisymmetric roadway under non-uniform stress field based on D-P criterion[J]. Journal of Safety Science and Technology, 2014,24(1):103-108.
[11] 王如坤,梅甫定.高应力矿柱在动力扰动下力学响应研究[J].地下空间与工程学报,2016,12(2):349-355,419.
WANG Rukun, MEI Fuding. Study on mechanical response of highly-stressed pillars under dynamic disturbance[J]. Chinese Journal of Underground Space and Engineering, 2016,12(2):349-355,419.
[12] 温颖远,牟宗龙,易恩兵,等.动力扰动下不同硬度煤层巷道围岩响应特征研究[J].采矿与安全工程学报,2013,30(4):555-559.
WEN Yinyuan, MOU Zonglong, YI Enbing, et al. The response features of roadway surrounding rock in different hardness coal seams under dynamic disturbance [J]. Journal of Mining & Safety Engineering, 2013,30(4):555-559.
[13] 唐礼忠,高龙华,王 春,等.动力扰动下含软弱夹层巷道围岩稳定性数值分析[J].采矿与安全工程学报,2016,33(1):63-69.
TANG Lizhong, GAO Longhua, WANG Chun, et al. Numerical analysis of stability of roadway surrounding rock with weak interlayer under dynamic disturbance[J]. Journal of Mining & Safety Engineering, 2016,33(1):63-69.
[14] 贾 楠,吴 超,罗周全,等.动力扰动下采空区围岩非线性响应演化特性分析[J].爆破,2016,33(3):10-16.
JIA Nan, WU Chao, LUO Zhouquan, et al. Nonlinear response evolution characteristics of goaf surrounding rocks under dynamic disturbance[J]. Blasting, 2016,33(3):10-16.
[15] 高 魁,刘泽功,刘 健,等.爆破扰动松软煤层对巷道围岩稳定性的影响[J].振动与冲击,2018,37(15):136-142.
GAO Kui, LIU Zegong, LIU Jian,et al. Effects of blast disturbing soft coal seam on stability of roadway surrounding rock[J]. Journal of Vibration and Shock, 2018,37(15):136-142.
[16] 李春元,张 勇,张国军,等.深部开采动力扰动下底板应力演化及裂隙扩展机制[J].岩土工程学报,2018,40(11):2031-2040.
LI Chunyuan, ZHANG Yong, ZHANG Guojun, et al. Crack propagation mechanisms and stress evolution of floor under dynamic disturbance in deep coal mining[J]. Chinese Journal of Geotechnical Engineering, 2018,40(11):2031-2040.
[17] BRADY B H G, BROWN E T. Rock mechanics for under- ground mining[M]. Dordrecht: Springer, 2006.
[18] 龙 源,冯长根,徐全军,等.爆破地震波在岩石介质中传播特性与数值计算研究[J].工程爆破,2000,6(3):1-7.
LONG Yuan, FENG Changgen, XU Quanjun, et al. Study on propagation characteristics of blasting seismic waves in a rock medium and numerical calculation[J]. Engineering Blasting, 2000,6(3):1-7.
