0 引 言
近年来,由于地震作用的频繁发生,我国西南山区出现了一定规模的山体滑坡等现象[1-3]。现有边坡加固措施往往建设速度慢,成本投资大,稳定性系数较差,实际加固效果有限。因此,目前有关学者在研究新型的抗滑结构来加固边坡。曾海昌等[4]以某工程为背景,结合数值模拟和调研的方式,进行了框架式微型桩加固边坡的效果研究,并与多排式加固桩进行对比得出,桩身位移以及弯矩均有明显的减小,并满足相关设计规范要求;郑颖人等[5]通过研究在岩土边坡工程中的原理、失稳判定、强度准则等,选用了合适的抗滑支挡结构解决了多种滑坡问题;张志伟等[6]通过总结传统悬臂式和锚索式抗滑桩的优劣性,以及大量调研实际工程资料的基础上,提出了弧形间隔排桩+桩顶连系的抗滑结构。在理论、试验以及数值模拟的基础上,充分证明了这种新型支挡结构在边坡加固中的优越性;刘毅等[7]在针对传统悬臂式抗滑桩的缺点,采用弧形布置的抗滑桩,桩顶采用连系梁连接来共同受力,在理论的基础上,推导了这种组合式支挡结构的内力以及位移,计算结果表明弧形排列的支挡结构能有效的约束桩身的整体位移,并能将连系梁结构的抗压能力充分发挥;周德培等[8]针对不同形式抗滑桩结构,讨论并研究了这些结构在设计计算时的关键问题和适用条件,结合工程实际给出了设计计算方法。
从已有研究成果可以看出,以往学者对于抗滑桩的研究主要集中于理论推导、桩自身的力学参数和桩长等对横向与竖向承载能力的评估[9-11],以及群桩的不同布置下对于边坡整体稳定等方面的研究[12-14],而较少在新型的抗滑结构形式上进行研究。笔者基于上述研究,在弧形桩顶连系梁抗滑桩的基础上进行形式改进研究,并对不同型式下的抗滑结构进行参数化分析,为有关设计和工程提供参考。
1 理论分析
1.1 弧形桩顶连系梁抗滑结构理论分析
对于弧形布置跨距为L的连系梁抗滑结构的计算模型如图1所示,该计算模型为两铰拱模型,基本体系中共有n个未知力,其中X1表示右端拱铰处沿水平x轴负向的水平力,Xi表示连系梁上沿法向的集中力(i取偶数,i=2,4,…,n-1),Xj表示连系梁上沿轴向的集中力(j取奇数,j=3,5,7,…,n)。
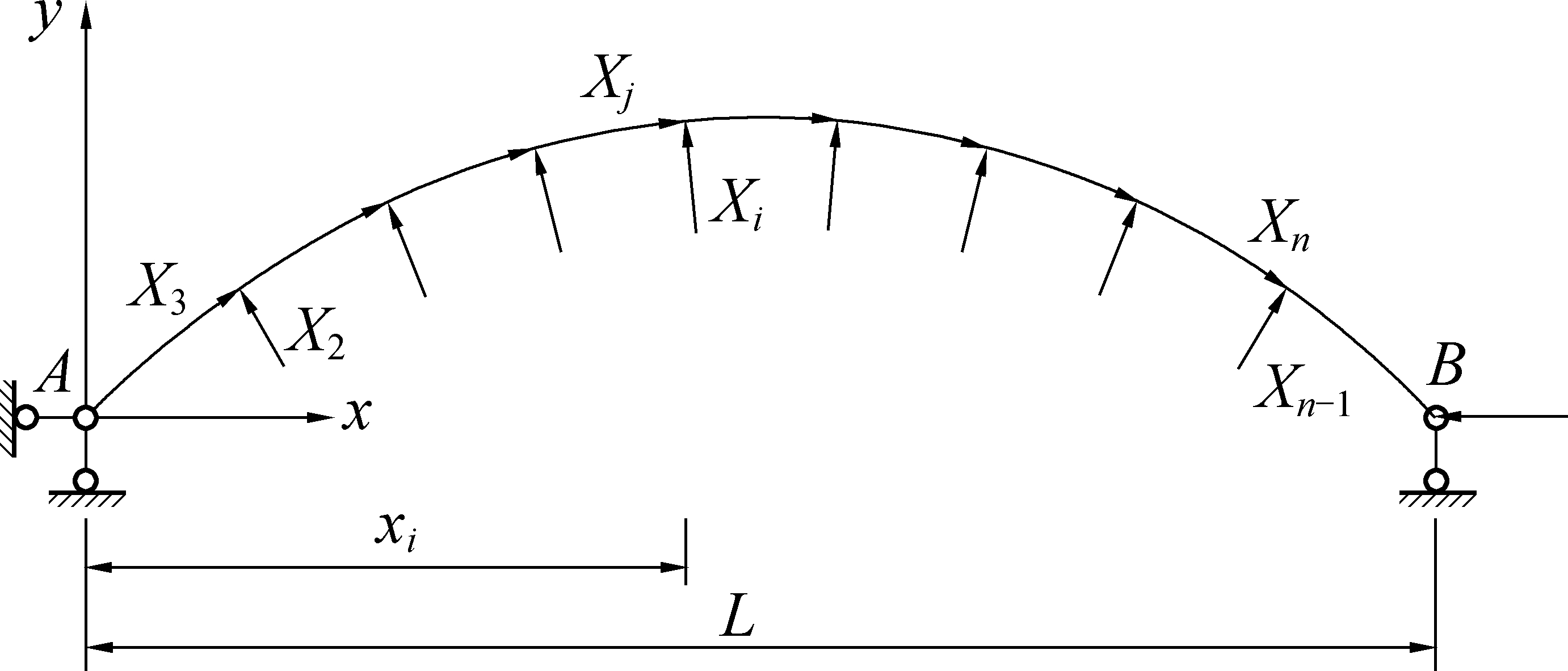
图1 弧形布置连系梁计算模型
Fig.1 Calculation Model of arc row piles with arc coupling beam on pile top
通过对计算模型施加上述单位未知力,通过叠加计算可得作用单位多余未知力的两铰拱的结构位移,即
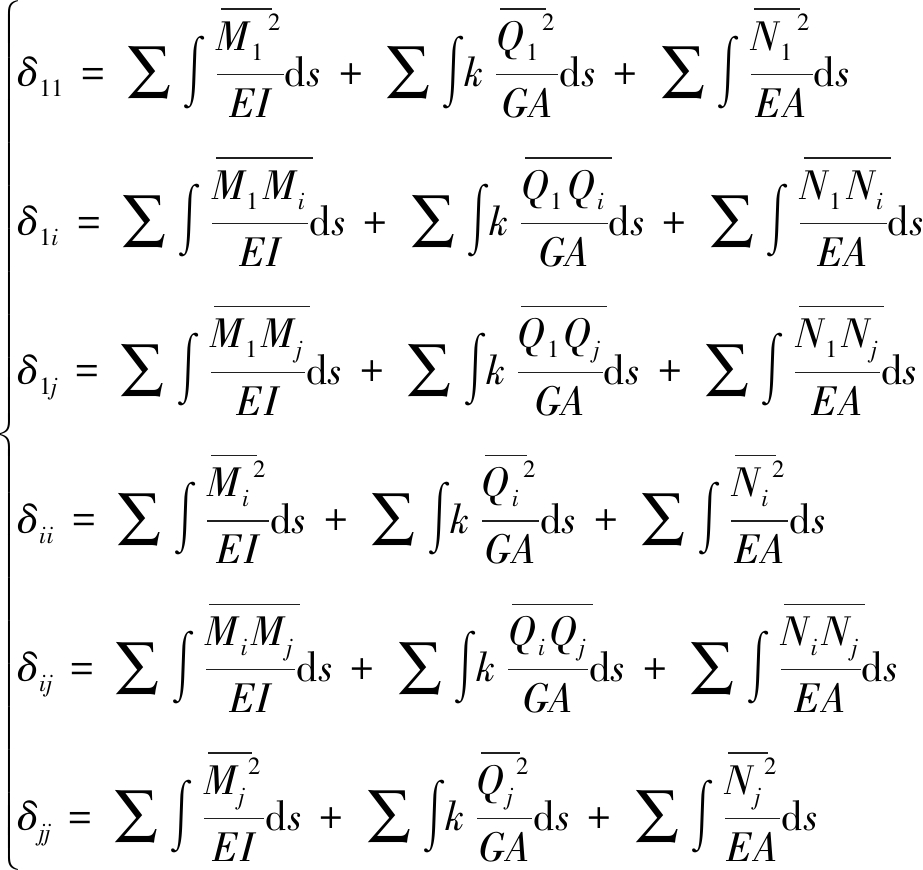
(1)
式中:δij为基本结构在单位未知力Xj单独作用沿Xi方向的位移(i为法向,j为轴向);![]() 和
和![]() 分别为基本结构在单位未知力Xi作用产生的弯矩、剪力和轴力;k为截面形状系数,圆形截面取10/9;E为结构弹性模量 ;I为截面惯性矩 ;A为截面面积 ;G为剪切模量 ; ds为连系梁的单位微分长度。
分别为基本结构在单位未知力Xi作用产生的弯矩、剪力和轴力;k为截面形状系数,圆形截面取10/9;E为结构弹性模量 ;I为截面惯性矩 ;A为截面面积 ;G为剪切模量 ; ds为连系梁的单位微分长度。
1.2 边坡安全性分析
基于有限元强度折减分析法来对边坡的稳定性进行分析[15],即在假定边坡整体所受外力荷载不变的情况下,通过将边坡岩土体的参数黏聚力c和内摩擦角φ同时除以一个折减系数Ftrial,从而获得折减之后的ctrial和φtrial,并将所得参数进行稳定性迭代求解运算。当边坡处于极限平衡状态时,折减系数Ftrial即为边坡的安全系数,即
φtrial=arctan(tan φ/Ftrial)
(2)
ctrial=c/Ftrial
(3)
2 工程概况
该露天边坡位于四川省九寨沟县境内,邻近特大铁路桥梁,所在岩堆大致呈扇形分布,岩堆体坡面较陡,坡度为38°~45°,该区域地形是我国起伏较为剧烈的深切陡峭的高山峡谷。该边坡地层岩性分布较为复杂,在该区域穿越了4条地震带,有大小不等的断裂活动。滑坡体主要为含角砾低液限黏土和块石土,滑坡体内裂隙发育,在天然降雨和地震作用下也容易引起滑坡,可能会对下部特大桥梁和列车的运行造成威胁。介于该边坡地理位置特殊,需对其进行整治加固,拟采用弧形布置的连系梁抗滑桩支挡结构对该边坡进行加固,并讨论不同形式支挡结构的加固效果。
3 模型建立和参数选取
3.1 数值模型的建立
采用有限元软件建立了边坡三维模型,如图2所示。该模型长×宽×高为40.0 m×15.5 m×22.0 m,边坡土层从上到下分别为含角砾低液限黏土、块石土和粉砂质泥岩。弧形布置连系梁抗滑桩布置在距离模型底部16.8 m的坡面上,抗滑桩直径为0.4 m,长度为8.0 m,沿弧形等间距分布,连系梁弧长为15.0 m,宽度为0.6 m,厚度为0.4 m。两端部为拱脚抗滑桩,为正方形截面,宽度为1.0 m,桩长8.0 m,矢跨比为0.14。

图2 边坡三维模型
Fig.2 Three-dimensional model of slope
3.2 参数取值
露天边坡岩土体本构模型采用的是Mohr-Coulomb模型,连系梁和拱脚抗滑桩采用的是钢筋混凝土。抗滑桩的材料参数的选取是直接影响边坡稳定的决定性因素,根据实际工程现场探测取样、试验,并结合现场边坡的地质情况以及施工的经验,选取了相应符合工程的岩土体和抗滑桩的材料力学参数见表1 。
表1 岩土体和抗滑桩参数
Table 1 Geotechnical and anti-slide pile parameters
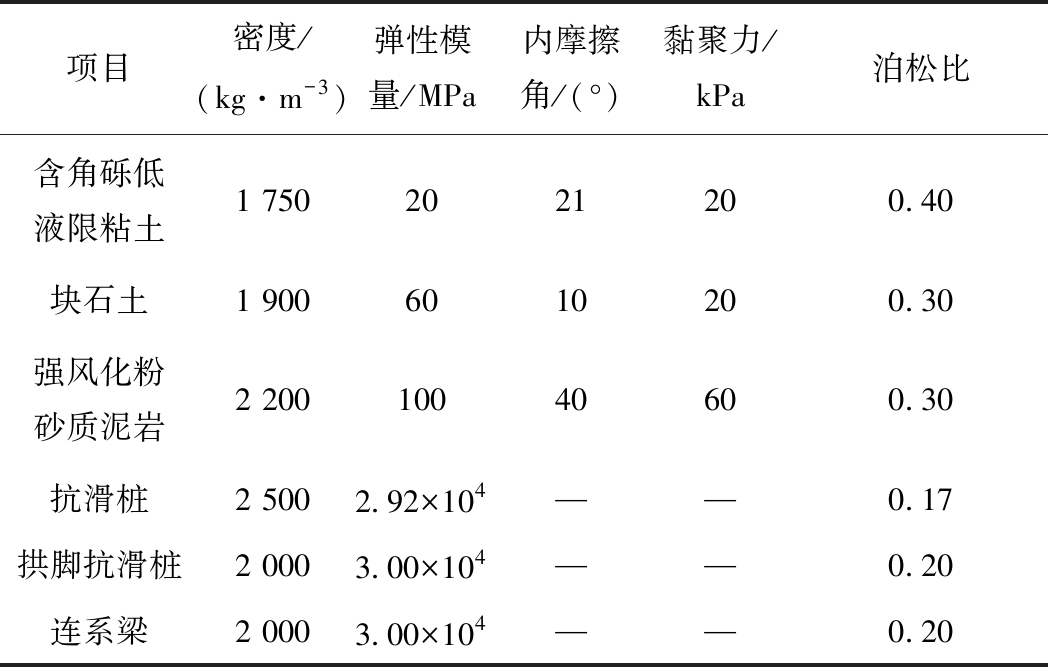
项目密度/(kg·m-3)弹性模量/MPa内摩擦角/(°)黏聚力/kPa泊松比含角砾低液限粘土1 7502021200.40块石土1 9006010200.30强风化粉砂质泥岩2 20010040600.30抗滑桩2 5002.92×104——0.17拱脚抗滑桩2 0003.00×104——0.20连系梁2 0003.00×104——0.20
3.3 接触约束的设置
岩土体、连系梁和抗滑桩等均采用三维实体单元建立,桩和土之间的摩擦接触采用的是摩尔-库伦准则,连系梁与抗滑桩顶端的连接为刚性连接。整体模型仅考虑在自重应力场下的作用,边界条件采用左右(X方向),前后(Y方向),底部(X,Y,Z方向)约束,如图3所示。

图3 边界约束
Fig.3 Diagram of boundary constraint
4 结果分析
4.1 边坡安全系数分析
不同排布型式下弧形抗滑桩的安全系数见表2,从表2中可知,自然边坡安全系数小于1,处于不稳定状态,在受到外部条件的影响,极易引发滑坡。通过设置抗滑桩,能使边坡趋向于稳定状态,但不同形式抗滑桩下的边坡安全系数不同。弧形和直线布置的安全系数要大于弧形布置(反向),弧形布置(8根)安全系数最高,随着桩数的减少,安全系数逐渐降低。
表2 边坡安全系数
Table 2 Slope safety factors
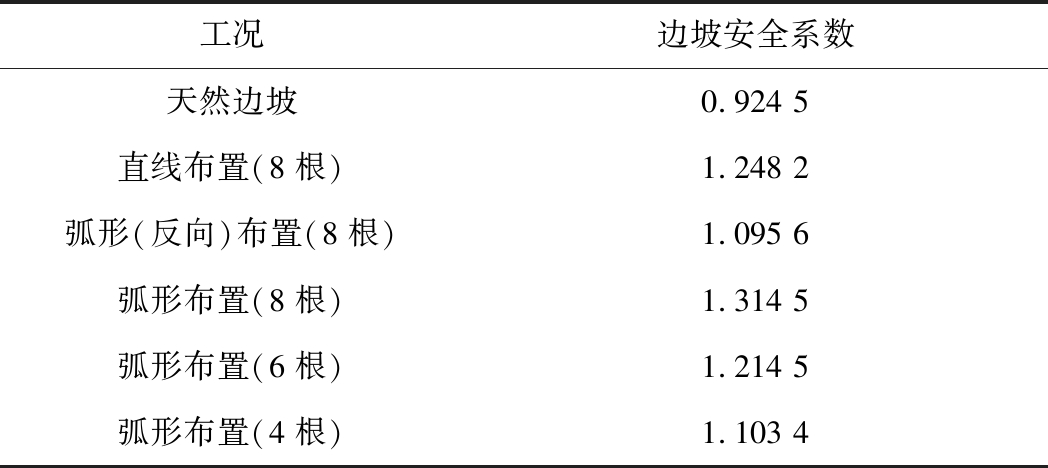
工况边坡安全系数天然边坡0.924 5直线布置(8根)1.248 2弧形(反向)布置(8根)1.095 6弧形布置(8根)1.314 5弧形布置(6根)1.214 5弧形布置(4根)1.103 4
4.2 边坡整体位移分析
边坡在不同型式抗滑桩下的整体位移云图如图4所示,从图4中可得出3条结论。
1)通过对比自然边坡和不同型式抗滑桩下的边坡位移可知,不同型式抗滑桩对边坡都具有一定的加固效果,能有效阻止抗滑桩后方土体滑动面的形成,保证边坡稳定。
2)通过对比相同桩数(8根)下的抗滑桩的加固效果可知,采用弧形布置(8根)的边坡位移(0.274 m)要小于直线布置(8根)的位移(0.417 m),这是由于弧形连系梁较直梁起到了一个承压的作用。而弧形(反向)布置抗滑桩的边坡位移(0.486 m)要大于直线布置抗滑桩的位移(0.417 m),说明弧形(反向布置)抗滑桩在限制边坡滑移方面的效果并不明显,因此,对相同桩数(8根)下的抗滑桩的加固效果进行比较可知,弧形布置抗滑桩加固效果最好,直线布置抗滑桩次之,弧形(反向)最小。
3)通过对比不同桩数(4、6、8根)的抗滑桩加固效果可知,抗滑桩数量的增加,能有效的限制边坡的滑移,也能提高连系梁抗滑桩整体的抗压性能,因此,可以有效的保障边坡的稳定性。

图4 不同型式抗滑桩下的整体边坡位移
Fig.4 Displacement of integral slope under different types of anti-slide piles
4.3 边坡塑性区分布
边坡在不同型式抗滑桩下的边坡塑性区如图5所示,从图5中可得出3条结论。
1)与自然边坡对比可知,抗滑桩能有效减少边坡塑性区的发展,能将边坡塑性区限制在一定范围之内,降低出现滑坡的风险。
2)通过对比相同抗滑桩数(8根)下的塑性区可知,三者塑性区面积大小依次为:直线布置>弧形(反向)布置>弧形布置,通过对比可以发现,弧形布置抗滑桩较直线布置区域要大,且更靠近坡角位置,能有效减小边坡塑性区面积,为了边坡安全考虑,建议抗滑桩布置尽量靠近坡角位置。而从最大剪切应变增量数值上来看,弧形(反向)布置(0.459 m)>直线布置(0.303 m)>弧形布置(0.209 m), 反映出弧形布置抗滑桩在空间上的分布较前两者能有效的减小边坡剪切应变增量。
3)通过对比不同桩数(4、6、8根)的抗滑桩的塑性区可知,弧形布置抗滑桩数的增加,能有效的减小塑性区的分布和剪应变增量的数值,保持边坡的整体稳定性。

图5 不同型式抗滑桩下的边坡塑性区
Fig.5 Plastic zone of slope under different types of anti-slide piles
4.4 抗滑桩位移分析
不同型式抗滑桩下的桩体位移如图6所示,从图6中可知,各个抗滑桩在边坡滑移作用下出现了不同程度的变形,且最大位移与变形状态有关。直线型布置的抗滑桩最大位移出现在连系梁顶部,为2.75 mm。弧形(反向)布置抗滑桩桩身所受压力较大,最大位移出现在连系梁下部桩体(图6b ),最大位移为3.30 mm。弧形布置(4、6、8根)抗滑桩的最大位移均出现在连系梁底部位置,分别为5.23、3.59和3.01 mm。

图6 不同型式抗滑桩下的桩体位移
Fig.6 Pile displacement under different types of anti-slide piles
通过提取连系梁中部抗滑桩沿深度的位移数据,并绘制如图7所示。由图7可知,不同型式抗滑桩的位移都随着深度的增加而逐渐减小,仅弧形(反向)抗滑桩在桩深为1.75 m出现最大位移。各抗滑桩在桩深达到6.00 m时,抗滑桩位移基本趋于稳定。弧形(4根)抗滑桩的整体位移均远大于其他抗滑桩,说明其加固边坡的效果小于其他形式抗滑桩。
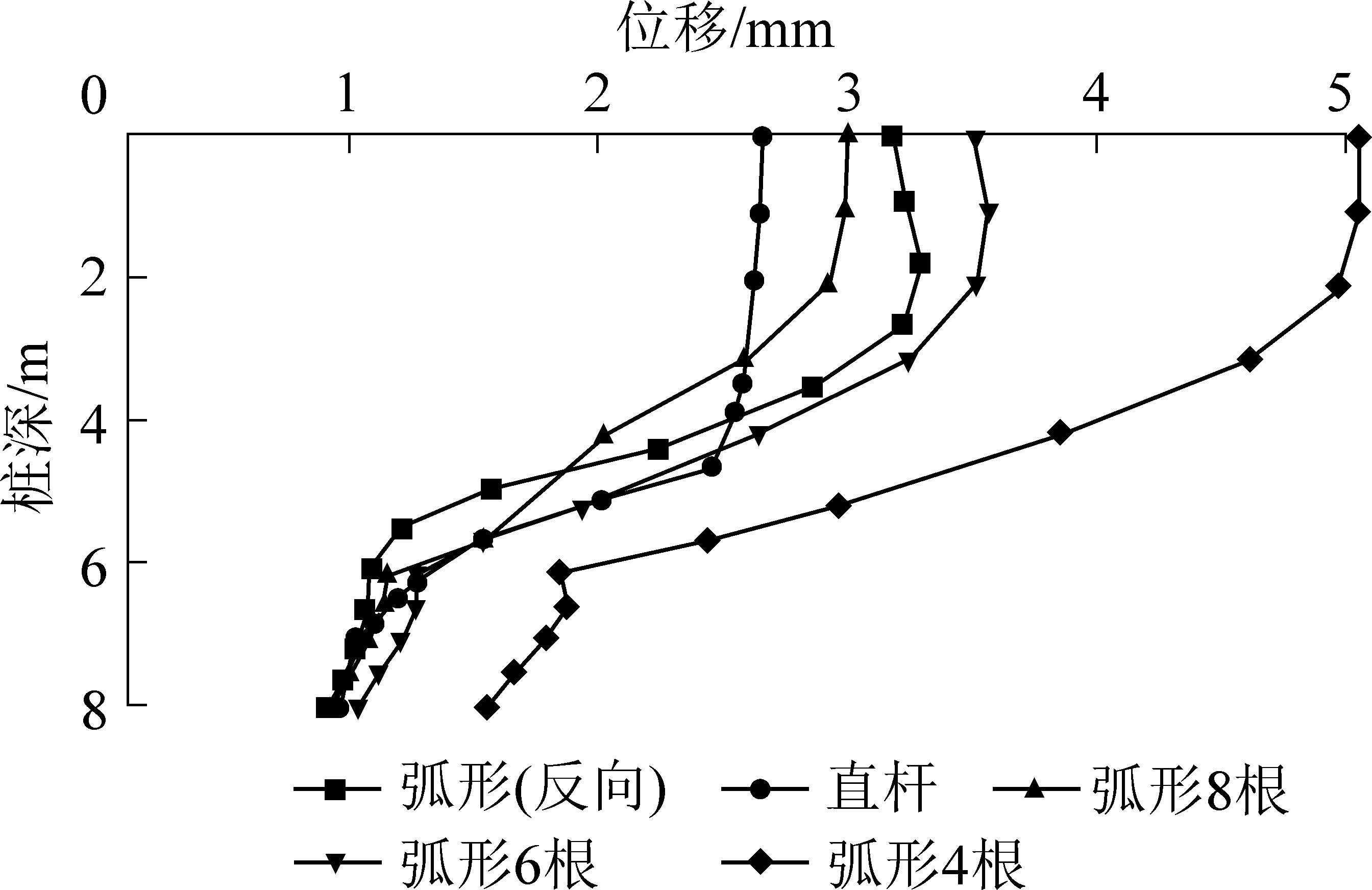
图7 不同型式中部抗滑桩沿桩深的位移
Fig.7 Displacement of anti-slide piles along pile depth with different types
4.5 连系梁位移分析
不同型式抗滑桩下的连系梁水平位移云图如图8所示 ,为分析连系梁在边坡滑移作用下的位移情况,分别在连系梁顶部从左到右等间距布置10个监测点,并将提取的数据绘制如图9所示。
从图9中可知,各种型式连系梁的位移都大致呈现弧形分布,最大位移出现在梁中部附近。通过对比相同桩数(8根)连系梁的位移可知,由于直杆分布的连系梁离坡脚有一定距离,故整体位移偏小,其最大位移仅为2.36 mm。弧形(反向)布置抗滑桩限制边坡滑移的作用没有直线布置抗滑桩明显,其连系梁最大位移较直线布置连系梁大,为3.11 mm。弧形布置抗滑桩的中部桩基离坡脚较近,承受压力较大,故其连系梁在中部位置处的位移较大,为2.83 mm。

图8 不同型式抗滑桩下的连系梁水平位移云图
Fig.8 Nephogram of coupling beam displacement under different types of anti-slide Piles
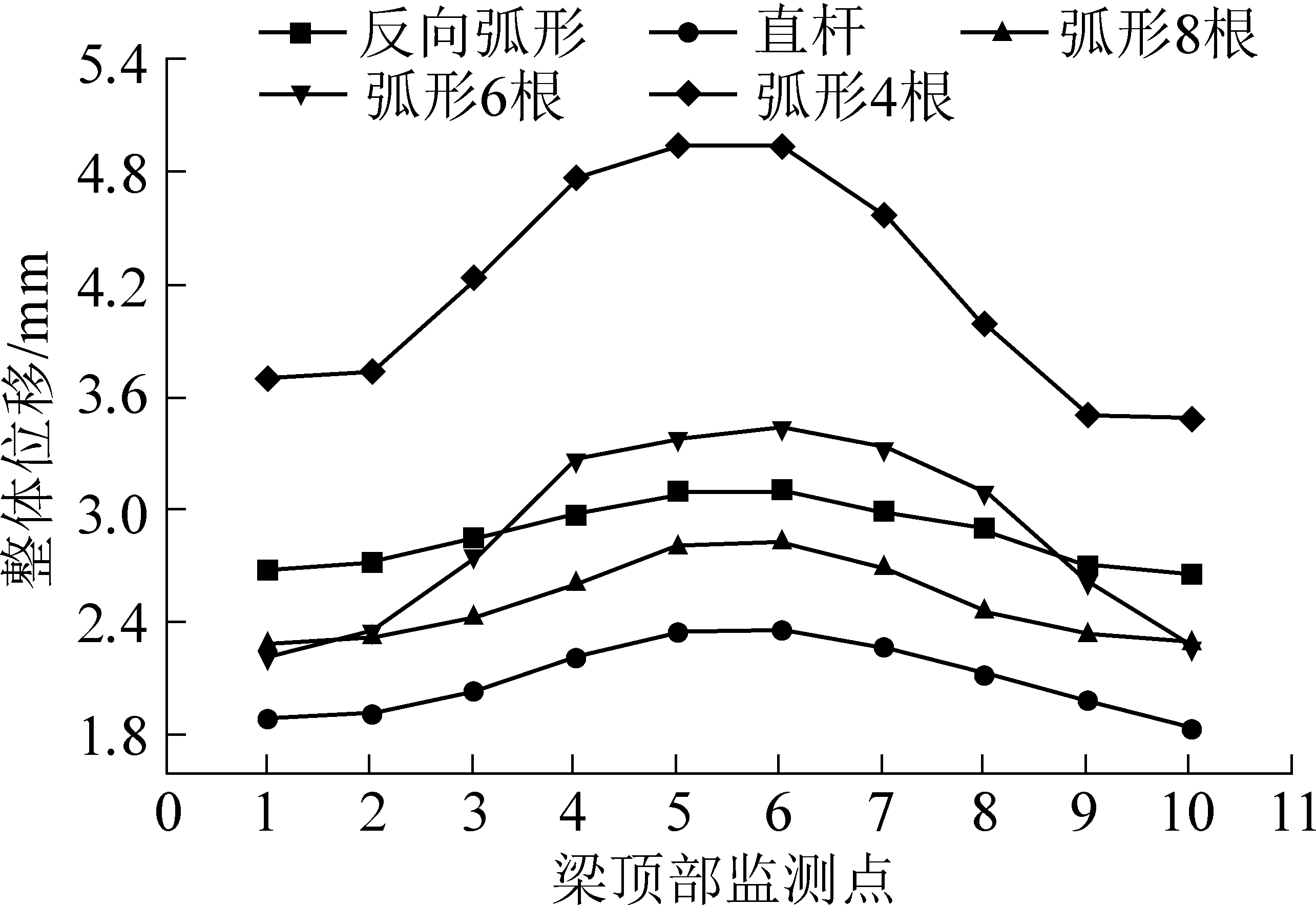
图9 不同型式抗滑桩下的连系梁水平位移
Fig.9 Diagram of coupling beam displacement under different types of anti-slide Piles
通过对比不同桩数(4、6、8根)抗滑桩的连系梁的位移可知,弧形布置(4根)抗滑桩的连系梁的全梁位移要远大于弧形布置(6、8根)抗滑桩所对应的连系梁的位移,说明前者限制边坡滑移的作用明显削弱。弧形布置(6根)与(8根)连系梁的全梁位移分布较为近似,前者仅在梁中部位置附近的位移较后者略大,说明二者抗滑桩支挡结构整体受力较为稳定,对边坡加固效果显著。
4.6 弧形连系梁抗滑结构优化选取分析
为了对弧形连系梁抗滑结构进行优化分析,选取弧形布置(8根)连系梁抗滑结构在不同混凝土等级、连系梁矢跨比以及抗滑桩长度的情况下的边坡,通过计算并统计得到边坡安全性系数见表3 。
从表3中可知,随着弧形连系梁抗滑结构混凝土等级的增大,边坡的安全系数逐渐增大,但增加的趋势逐渐变缓,说明当混凝土等级达到一定程度后,对边坡的加固作用减弱。通过对比不同连系梁矢跨比可知,随着矢跨比的增加,边坡的安全系数逐渐增大,说明增大连系梁的矢跨比能有效对边坡进行加固。对于不同抗滑桩长度而言,增加抗滑桩的长度在一定范围内能有效的限制边坡滑移,但随着长度的继续增大,这种限制效果逐渐减小。
表3 不同参数下边坡的安全系数
Table 3 Safety factor of slope under different parameters
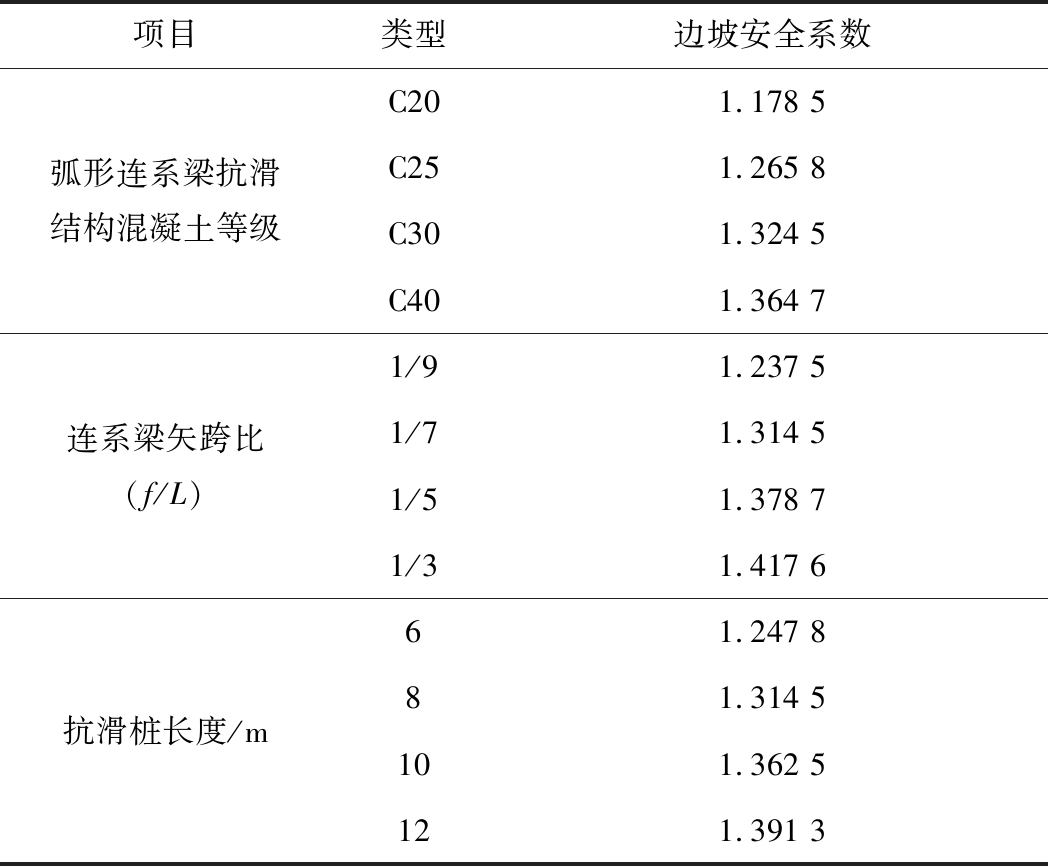
项目类型边坡安全系数弧形连系梁抗滑结构混凝土等级C201.178 5C251.265 8C301.324 5C401.364 7连系梁矢跨比(f/L)1/91.237 51/71.314 51/51.378 71/31.417 6抗滑桩长度/m61.247 881.314 5101.362 5121.391 3
5 结 论
通过对以往悬臂梁抗滑桩的加固效果进行研究,提出一种新型的弧形布置的连系梁抗滑桩支挡结构,并对比分析在不同型式下连系梁抗滑桩的加固效果,得到以下结论:
1)通过对比自然边坡和不同型式抗滑桩下的边坡位移可知,不同型式抗滑桩对边坡都具有一定的加固效果,其中弧形布置的抗滑桩的加固效果最好,能有效阻止抗滑桩后方土体滑动面的形成,保证边坡稳定。
2)由于弧形连系梁较直梁有一个拱效应的作用,能起到良好的承压效果,所以加固效果大于其他支挡结构,且随着抗滑桩数量的增加,能有效的限制边坡的滑移,也能提高连系梁抗滑桩整体的抗压性能。
3)弧形布置抗滑桩在空间上的分布较其他支挡结构能有效的减小边坡塑性区域和剪切应变增量的数值,能有效保护边坡的稳定。
4)不同型式抗滑桩的位移都随着深度的增加而逐渐减小,各抗滑桩在桩深达到6 m时,抗滑桩位移基本趋于稳定。
5)连系梁与抗滑桩顶部连接,能有效加强抗滑桩之间的联系作用,提高结构整体的刚度,约束结构整体变形。连系梁在边坡滑移作用下仅在梁部中间出现较大的位移,两端部较为稳定,起到了良好承压作用。
6)随着弧形连系梁抗滑结构混凝土等级的增大,边坡的安全系数逐渐增大,但混凝土等级增加到一定程度时,对边坡的加固作用减弱。增大连系梁的矢跨比能有效对边坡进行加固。增加抗滑桩的长度在一定范围内能有效的限制边坡滑移,但随着长度的继续增大,这种限制效果逐渐减小。
[1] 王根龙,张军慧,梁永朵.中国地震灾害现状及地震灾害系统工程研究[J].灾害学, 2006, 21(3):15-19.
WANG Genlong, ZHANG Junhui, LIANG Yongduo. Research on present situation of earthquake disaster and systems engineering of earthquake disaster in China[J]. Journal of Catastrophology, 2006, 21(3):15-19.
[2] 曹兰柱,李广贺,王 东,等.露天矿顺倾软弱基底内排土场边坡空间形态优化[J].煤炭科学技术,2018,46(2):163-167.
CAO Lanzhu, LI Guanghe,WANG Dong, et al.Optimization on spatial morphology slope of in pit dumping site at inclined weak-basement of surface mine[J].Coal Science and Technology,2018, 46(2):163-167.
[3] 王 东,姜聚宇,韩新平,等.基于强度折减法的露天矿压煤区复合边坡稳定性研究[J].煤炭科学技术,2019,47(3):234-238.
WANG Dong, JIANG Juyu, HAN Xinping, et al. Study on stability of composite slope in unexploited coal area of open-pit mine based on Strength Reduction Method[J]. Coal Science and Technology, 2019, 47(3):234-238.
[4] 曹兰柱,王 珍,王 东,等.露天煤矿端帮逆倾软岩边坡稳定性研究[J].煤炭科学技术,2017,45(3):1-6.
CAO Lanzhu, WANG Zhen, WANG Dong, et al. Study on stability of reversed inclined soft rock slope at end slope of surface mine[J]. Coal Science and Technology, 2017,45(3):1-6.
[5] 郑颖人,赵尚毅,邓楚键,等.有限元极限分析法发展及其在岩土工程中的应用[J].中国工程科学,2006,8(12):39-61.
ZHENG Yingren, ZHAO Shangyi, DENG Chujian, et al. Development of finite element limit analysis method and its applications in geotechnical engineering [J]. Engineering Science, 2006, 8(12):39-61.
[6] 张志伟,邓荣贵.弧形间隔排桩-桩顶拱梁空间抗滑结构理论研究[J].岩土力学,2013,34(12):3403-3409,3430.
ZHANG Zhiwei, DENG Ronggui. Theoretical study of spatial anti-slide structure of arc interval row piles with coupling beam on pile top[J]. Rock and Soil Mechanics, 2013,34(12):3403-3409,3430.
[7] 刘 毅. 弧形排列抗滑桩综合支挡结构研究[D].成都:西南交通大学,2014.
[8] 周德培,王唤龙,孙宏伟.微型桩组合抗滑结构及其设计理论[J].岩石力学与工程学报,2009,28(7):1353-1362.
ZHOU Depei, WANG Xuelong, SUN Hongwei. Micro-pile composite structure and its design theory [J]. Journal of Rock Mechanics and Engineering, 2009,28(7):1353-1362.
[9] 陈 冲,王 卫,吕华永.基于复合抗滑桩模型加固边坡稳定性分析[J].岩土力学,2019,40(8):1-12.
CHEN Chong, WANG Wei, LYU Huayong. Stability analysis of slope reinforced with solid- structural pile model[J].Rock and Soil Mechanics, 2019,40(8):1-12.
[10] 邵巧希,胡 蓉.基于强度折减法的抗滑桩加固路基稳定性分析[J].土工基础,2018,32(6):620-624.
SHAO Qiaoxi, HU Rong. Stability analysis of embankments strengthened by sliding resistant caissons using Strength Reduction Method[J]. Soil Engineering and Foundation, 2018,32(6):620-624.
[11] 李 松,喻丹萍,杨 杰.一种新型的小尺寸抗滑桩力学特性研究[J].科学技术与工程,2007,21(7):5720-5722,5735.
LI Song, YU Danping,YANG Jie. Study on Bayesian model of risk evaluation about industry transform anon for the resources city[J]. Science Technology and Engineering, 2007,21(7):5720-5722,5735.
[12] 曹文昭,郑俊杰,薛鹏鹏.抗滑桩-加筋土挡墙组合支挡结构开发[J].中南大学学报:自然科学版,2019,50(1):118-129.
CAO Wenzhao, ZHENG Junjie, XUE Pengpeng. Development of combined retaining structure composed of anti-slide pile and reinforced earth retaining wall[J]. Journal of Central South University:Science and Technology, 2019,50(1):118-129.
[13] 储召军,石少卿,孙建虎,等.基于模型试验的桩间距对组合式钢管抗滑桩抗滑效果的影响分析[J].岩土力学,2018,39(3):848-853,862.
CHU Zhaojun, SHI Shaoqing, SUN Jianhu, et al. Analysis of anti-sliding mechanism of steel tube piles with different spacings based on model test[J]. Rock and Soil Mechanics, 2018,39(3):848-853,862.
[14] 时步炯,郑 静,吕昌明,等.组合板抗滑桩抗滑特性模型试验研究[J].铁道建筑,2017,57(10):96-100.
SHI Bujing, ZHENG Jing, LYU Changming, et al. Model test study on anti-sliding characteristics for anti-slide piles of composite slabs[J]. Railway Engineering, 2017,57(10):96-100.
[15] 陈祖煜.土质边坡稳定分析—原理、方法、程序[M].北京:中国水利水电出版社, 2005.
