0 引 言
国内外大型露天矿为了达到多采矿、少剥岩的目的,普遍采用高台阶、陡帮开采,形成了大量高陡边坡。同时爆破作为破岩的主要方式,在提高生产效率的同时,也会对边坡的稳定性构成威胁。因此,研究爆破振动对边坡稳定性的作用效应,减小爆破振动造成的灾害具有较强的社会和经济效益[1]。
目前露天矿边坡的监测方法较多[2],露天矿边坡受爆破作用影响的监测以现场爆破振动监测仪测试和试验数据分析方法为主。郭学彬等[3]提出高程放大效应是一种坡面效应,根据不同爆破振动测试实例,分析了不同类型坡面的高程放大效应;万鹏鹏等[4]通过对台阶地形爆破振动进行现场实测,得出了鞭梢效应和坡面效应是影响台阶地形放大效应的主要因素;许红涛等[5]根据爆破振动峰值速度衰减规律得到边坡的稳定性安全系数时程。近年来,数值模拟技术也应用到高程放大效应研究当中,陈明等[6]得出爆破振动速度随着边坡坡度增加以衰减为主,但存在高程放大效应占主导的现象;唐海等[7-8]的研究表明,凸形和凹形地形、地貌对爆破振动波垂直向的放大效应大于水平向,放大效应具有方向性;蒋楠等[9]对不同坡度边坡进行数值计算,得到存在高程放大效应占主导的结果。同时有不少学者进行了高程放大效应的机理研究,石崇等[10]利用平面射线理论和方法,推导出单面边坡地震的高程放大效应理论解;杨风威等[11]得到坡体内质点振动速度放大系数的表达式,从理论角度揭示均质岩石边坡质点速度放大效应的机制。
目前,利用数值计算方法在爆破振动作用下同时对迎波坡面和背波坡面响应情况进行对比的研究较少,而且大部分学者在进行数值计算时只关注了边坡表面质点的振动情况,并未关注边坡内部质点的振动情况,但实际上很多边坡事故都是由于破坏从边坡内部发生,所以应当关注边坡内部质点峰值振速的情况。笔者利用FLAC3D动力分析模块,分析了台阶边坡坡面在迎波和背波情况下的动力响应。并对台阶边坡表面和内部质点的高程放大效应进行了研究,以期加深对台阶边坡高程放大效应的认识,同时有利于对哈尔乌素露天矿边坡台阶参数优化,提高产出,具有一定的社会和经济意义。
1 边坡爆破数值模拟及验证
1.1 模型和参数
利用FLAC3D数值模拟软件,建立以哈尔乌素露天矿北端帮边坡工程为背景的边坡数值模型。根据现场工程地质条件,得到边坡以砂岩为主,并对边坡进行简化。如图1所示,坡高135 m,各台阶高度分别为30 、30 、45 、30 m。

图1 边坡数值模型
Fig.1 Slope numerical model
在模拟计算过程中,假设模型材料是连续、均质、各向同性的。模型顶面及坡面为自由面,左、右、下3个面均采用安静边界,结合现场试验与室内试验,哈尔乌素北端帮边坡砂岩的物理力学参数见表1。
表1 岩石力学参数
Table 1 Rock mechanics parameters

密度/(g·cm-3)弹性模量/MPa泊松比剪切模量/GPa黏聚力/MPa2.326 549.850.387.027.2
采等效荷载法施加爆破荷载,爆炸荷载采用三角波荷载,作用时间假设为7 ms,其中上升波时间1 ms,下降波时间6 ms。荷载峰值σm由式(1)确定[13],即
σm=Pw(1-r)α
(1)
Pw=ρwD2/(1+K)
(2)
式中:Pw为药包中心处爆轰波产生的平均初始压力,N/m2;r为比例半径,r=R/Rw,R为离药包轴线的距离,m;Rw为药包横切面半径,m;α为与岩石及炸药种类有关的常数,对于大多数岩石,α≈1.5;K为等熵指数,与装药密度相关,根据表2[14],当装药密度ρw<1.2 g/cm3时,K=2.1,ρw>1.2 g/cm3时,K=3;D为炸药的爆轰速度,m/s。
表2 爆破荷载峰值相关参数
Table 2 Relevant parameters of peak value of blasting load

等熵指数比例半径炸药密度/(kg·m-3)爆轰速度/(m·s-1)装药直径/mm31201 5003 20050
FLAC3D动力计算中应考虑阻尼,瑞利阻尼其理论与常规动力分析方法类似,计算得到的速度响应规律比较符合实际,所以采用瑞利阻尼。使用瑞利阻尼必须确定最小中心频率fmin,和最小临界阻尼比ξmin。瑞利阻尼是与频率相关的,采用对模型做无阻尼动力计算的方法确定中心频率,通过对模型进行无阻尼的自振计算,得到一个振荡周期需要的时间约为0.2 s,据此可以计算出模型的自振频率fmin,约为5 Hz。利用经验方法,直接选取岩土体的阻尼比ξmin为0.5%[15]。
1.2 计算分析和验证
通过现场监测和数值模拟的方法,得到哈尔乌素北端帮各个台阶测点的振动速度,模拟得到的各监测点振速波形如图2所示,由图2可知,各台阶监测点切面处竖直方向峰值振速分别为1.80 、1.75 、2.08 、2.08 cm/s。计算结果表明:上部2个台阶振速整体大于下部台阶。

图2 数值模拟各监测点波形
Fig.2 Waveform of each monitoring point in numerical simulation
为了验证数值模拟结果是否合理,结合哈尔乌素北端帮的现场监测结果进行对比,现场监测与数值模拟振速峰值对比如图3所示。

图3 现场监测与数值模拟对比
Fig.3 Comparison of field monitoring and numerical simulation
由图3可以看出,数值模拟与3次现场监测振动速度数值和趋势一致,现场监测结果略微小于数值模拟结果。结果表明:数值计算能够较好地反映边坡岩体受爆破振动影响程度。
2 高程放大效应分析
通过简单一般化台阶边坡模型分析边坡在背波和迎波情况下的高程放大效应。建立台阶高度为15 m,宽度为15 m的边坡数值模型,并从不同方向施加爆破荷载如图4和图7所示。
2.1 台阶边坡在背波情况下的高程放大效应
边坡共有4个台阶,由下到上分别为台阶一、二、三、四,每个台阶布置12个监测点,由台阶边坡自由面向边坡内部依次分为第1、2、3列,每列为4个监测点,由下到上依次编号Ⅰ、Ⅱ、Ⅲ、Ⅳ,测点布置如图4所示。

图4 监测点布置
Fig.4 Layout of monitoring points
提取数值计算后各监测点竖直方向峰值振速如图5所示。由图5可知,台阶四的振速范围是8.53~16.05 cm/s,台阶一的振速范围是6.22 ~13.16 cm/s。说明台阶状坡面在背波情况下,台阶四至台阶一的整体峰值振速减小,台阶表面和内部质点峰值振动速度总体呈现随着距离的增加逐渐衰减的趋势。
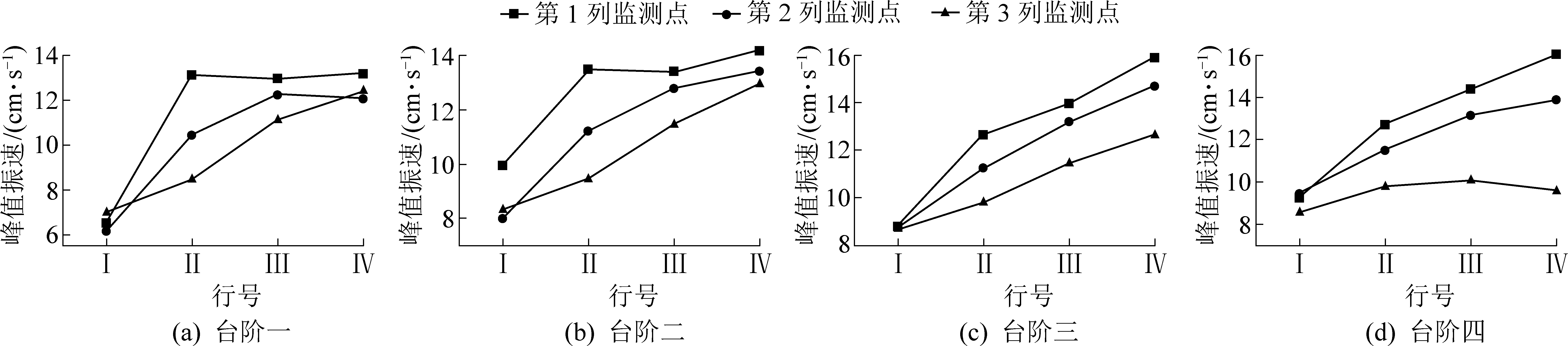
图5 背波台阶坡面峰值振速
Fig.5 Peak velocity of back wave step slope
同一高程情况下(即峰值振速图中同一横坐标下),峰值振速大致呈现由第1列监测点向第3列监测点递减的趋势,例如,台阶二行号为Ⅱ、1、2、3列测点峰值振速分别为13.52 、11.23 、9.46 cm/s。虽然各台阶的第3列监测点距离爆源相比第1列监测点较近,但是峰值振速却明显较小,原因可能是由于第1列监测点靠近台阶边坡自由面,端部自由度较多。
监测点与爆源同一水平距离情况下(即同一列监测点情况下),峰值振速大致由下部监测点行号Ⅰ到上部监测点行号Ⅳ逐渐变大,呈现高程放大效应。例如台阶三第1列行号Ⅰ—Ⅳ的监测点峰值振速分别为8.9 、12.7 、13.97 、15.94 cm/s。
振动速度放大系数如图6所示(振动速度放大系数为各列行号Ⅳ与行号Ⅰ监测点的峰值振动速度之比)[9],由图6可知,台阶状坡面在背波情况下呈现出明显高程放大效应。峰值振速的放大系数由第1列监测点向第3列监测点逐渐减弱,即高程放大效应由边坡自由面向内部逐渐减弱。
同时从台阶一至台阶四,边坡表面和内部质点高程放大效应整体上呈现减弱的趋势。峰值振速放大系数最大值为台阶一的第1列监测点,最大值为2.03。
2.2 台阶边坡在迎波情况下的高程放大效应
迎波坡面情况下监测点的布置与背波坡面情况时同理,监测点布置如图7所示,模拟所得各监测点竖直方向峰值振速如图8所示。
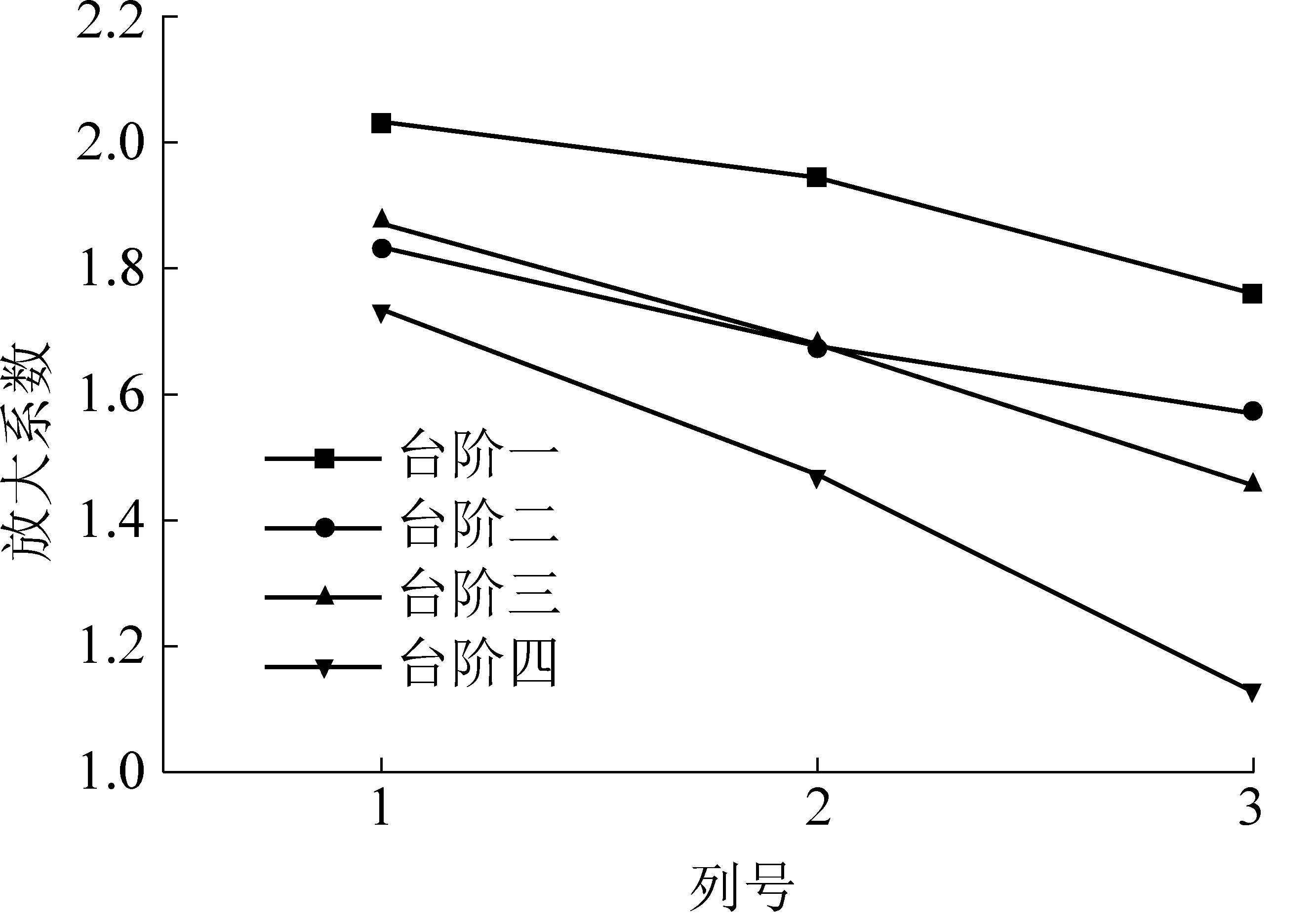
图6 各列监测点的放大系数
Fig.6 Amplification coefficient of each monitoring point
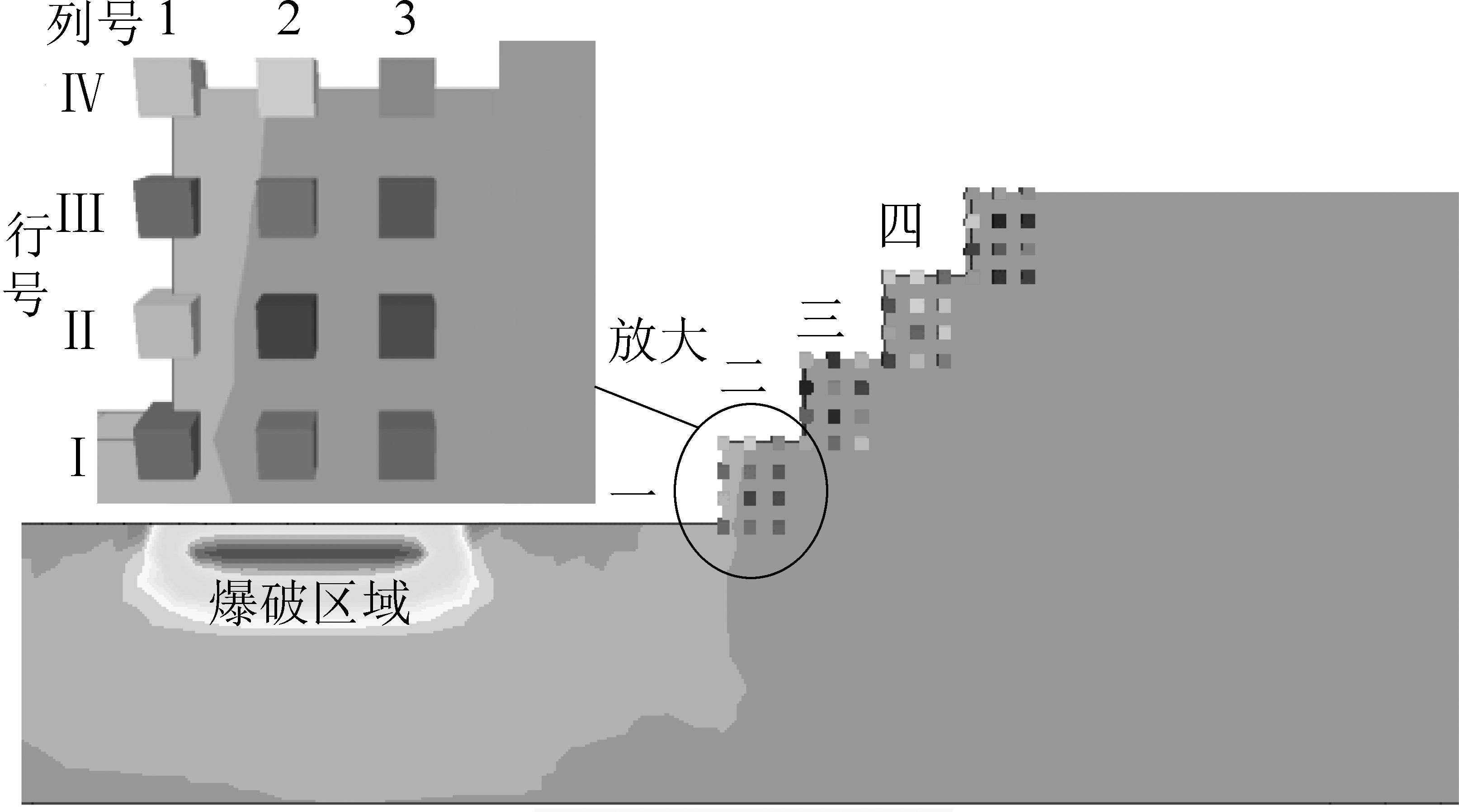
图7 监测点布置
Fig.7 Layout of monitoring points

图8 迎波台阶坡面峰值振速
Fig.8 Peak velocity on slope of wave front step
由图8可以得到台阶边坡在迎波情况下,台阶一内各列质点的峰值振动速度向台阶四逐渐衰减,台阶表面和内部质点峰值振动速度总体呈现随着距离的增加逐渐衰减的趋势。
同一高程情况下(即峰值振速图中同一横坐标下),各台阶监测点大致呈现出由第1列向第3列递减,例如台阶二监测点行号为Ⅳ时,1、2、3列Ⅳ监测点的峰值振速分别为3.19、2.94、2.43 cm/s,即越靠近爆源和自由面的监测点峰值振速越大。
监测点与爆源同一水平距离情况下(即同一列监测点情况下),大致呈现出峰值振速由下部监测点行号Ⅰ到上部监测点行号Ⅳ逐渐变大,呈现高程放大效应。例如台阶二第1列监测点行号Ⅰ—Ⅳ的峰值振速分别为1.28、1.51、2.33、3.19 cm/s。

图9 各列监测点的放大系数
Fig.9 Amplification coefficient of each monitoring point
图9为各列监测点振速放大系数,由图可知,台阶一未出现高程放大效应,原因可能是台阶一在坡脚处,质点距离爆源最近,与爆源的距离是爆破振动衰减的主导因素。台阶二、三、四呈现明显高程放大效应,但台阶二、三、四高程放大系数并未呈现出明显规律。放大系数最大值为台阶四的第3列测点,最大值为2.88。
3 高程放大效应机理分析
坡底是地形的突变区,振动波在坡面底角处将产生绕射,形成新的振源,坡面使振动波的强度和频率发生变化。
图10说明了台阶边坡的绕射现象[16]。平面波AB垂直入射到边坡台阶上,当它以t=t0时刻到达台阶表面时,波前的位置是COD。当t=t0+Δt时,O点下面的平面波会继续下传至GH的位置,而O点上面的波前在台阶表面反射到达线段EF。

图10 绕射波示意
Fig.10 Schematic diagram of diffraction wave
根据惠更斯原理作图法可以把CO和OD上各点作为圆心,并以VΔt为半径做圆弧(V为波速),这些圆弧的包络线就是GH和EF的波前面,其中以断点O为圆心的点构成左行波波前面GH和右行波波前面EF之间的转换点,而圆弧EFG就是以O点为新震源产生的绕射波波前,它在t=t0+Δt时刻把EF和GH两个波前联系起来。因此在O点下侧虽无弹性界面存在,但仍可观测到FPG绕射波波前面构成的波动[18-20]。
在波的传播过程中,波前面将不断推进而扫过边坡的全部,因此边坡中任何一个点都有一个波面,波面是同相、等时和静止的。根据射线理论,边坡内任意质点的位移(速度、加速度)都由入射波、反射波和绕射波叠加而成,不同波场相位相同或相近时,则导致边坡质点振速的变大。由于坡面自由面具有较多的自由度、各波场相位变化共同导致边坡内高程放大效应呈现节律性变化。
4 结 论
根据上述数值模拟、现场监测及动力响应机理,对爆破振动作用下迎波坡面和背波坡面的表面质点、内部质点响应情况的对比,得到以下结论:
1)哈尔乌素露天矿台阶边坡1100和1130台阶峰值振速明显高于1025和1055台阶。
2)台阶边坡存在高程放大效应。台阶表面和内部质点峰值振动速度总体呈现随着距离的增加逐渐衰减的趋势。同一台阶的质点振速由边坡表面向内部递减,越靠近自由面,质点的振动速度越大。
3)在背波情况下,高程放大效应最显著的在边坡底部台阶;越靠近边坡自由面,放大系数越大,同一台阶的质点高程放大效应由边坡表面向边坡内部逐渐减弱。
4)在迎波情况下,高程放大效应最显著的则在边坡顶部台阶。即远离爆源台阶的高程放大效应明显;同一台阶的质点的高程放大效应未呈现出明显的变化趋势。
5)背波坡面峰值振速放大系数整体大于迎波坡面,背波坡面的高程放大效应较迎波坡面明显。
[1] 李浩荡,佘长超,周永利,等.我国露天煤矿开采技术综述及展望[J]. 煤炭科学技术, 2019,47(10):24-35.
LI Haodang, SHE Changchao, ZHOU Yongli, et al. Summary and prospect of open-pit coal mining technology in China[J]. Coal Science and Technology, 2019,47(10):24-35.
[2] 丁 震. 露天煤矿边坡实时监测技术应用对比分析[J]. 煤炭科学技术, 2017, 45(S1):194-197.
DING Zhen. Comparative analysis on application of real-time monitoring technology of slope in open pit coal mine[J]. Coal Science and Technology,2017, 45(S1):194-197.
[3] 郭学彬,肖正学,张志呈.爆破振动作用的坡面效应[J]. 岩石力学与工程学报, 2001, 20(1):83-87.
GUO Xuebin, XIAO Zhengxue, ZHANG Zhicheng. Slope effect of blasting vibration[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(1):83-87.
[4] 万鹏鹏, 璩世杰, 许文耀,等. 台阶爆破质点振速的高程效应研究[J]. 爆破, 2015, 32(2):29-32,63.
WAN Pengpeng, QU Shijie, XU Wenyao, et al. Study of elevation effect of bench blasting particle vibration velocity[J].Blasting,2015, 32(2):29-32,63.
[5] 许红涛, 卢文波, 周创兵,等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法[J]. 岩石力学与工程学报, 2006, 25(11):2213-2213.
XU Hongtao, LU Wenbo, ZHOU Chuangbing, et al. Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11):2213-2213.
[6] 陈 明,卢文波,李 鹏,等.岩质边坡爆破振动速度的高程放大效应研究[J]. 岩石力学与工程学报, 2011, 30(11):2189-2195.
CHEN Ming,LU Wenbo,LI Peng, et al. Elevation amplification effect of blasting vibration velocity in rock slope[J].Chinese Journal of Rock Mechanics and Engineering,2011, 30(11):2189-2195.
[7] 唐 海, 李俊如. 凸形地貌对爆破震动波传播影响的数值模拟[J]. 岩土力学, 2010, 31(4):1289-1294.
TANG Hai, LI Junru. Numerical simulation of influence of protruding topography on blasting vibration wave propagation[J]. Rock and Soil Mechanics, 2010, 31(4):1289-1294.
[8] 唐 海, 李海波, 周青春,等. 凹形地貌对爆破振动波传播影响的数值模拟[J]. 岩土力学, 2008, 29(6):1540-1544.
TANG Hai, LI Haibo, ZHOU Qingchun, et al. Numerical simulation of influence of concave landform on blasting vibration wave propagation[J]. Rock and Soil Mechanics, 2008, 29(6):1540-1544.
[9] 蒋 楠,周传波,平 雯,等. 岩质边坡爆破振动速度高程效应[J]. 中南大学学报:自然科学版, 2014,45(1):237-243.
JIANG Nan, ZHOU Chuanbo, PING Wen, et al. Altitude effect of blasting vibration velocity in rock slopes[J].Journal of Central South University:Science and Technology, 2014,45(1):237-243.
[10] 石 崇, 周家文, 任 强,等. 单面边坡高程放大效应的射线理论解[J]. 河海大学学报:自然科学版, 2008, 36(2):238-241.
SHI Chong , ZHOU Jiawen, REN Qiang, et al.Ray theory solution of the elevation amplification effecton a single-free-face slope[J]. Journal of Hohai University:Natural Science,2008, 36(2):238-241.
[11] 杨风威, 李海波, 齐三红,等. 平面应力波在岩质边坡中的传播规律研究[J]. 岩石力学与工程学报, 2015,34(S1):2623-2631.
YANG Fengwei,LI Haibo,QI Sanhong, et al Study of regularity of plane stress wave transmitting in rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2015(S1):2623-2631.
[12] 武 旭, 张云鹏, 郭奇峰. 台阶地形爆破振动放大与衰减效应研究[J]. 爆炸与冲击, 2017(6):128-133.
WU Xu, ZHANG Yunpeng, GUO Qifeng. Amplification and attenuation effect of blasting vibration on step topography[J]. Explosion and Shock Waves, 2017(6):128-133.
[13] HAO Hong, WU Chengqing. Scaled-distance relationships for chamber blast accidents in underground storage of explosives[J]. International Journal of Blasting and Fragmentation, 2001, 5(1/2):57-90.
[14] 夏 祥,李俊如,李海波,等.爆破荷载作用下岩体振动特征的数值模拟[J]. 岩土力学, 2005,26(1):50-56.
XIA Xiang, LI Junru, LI Haibo, et al. Udec mode ling of vibration characteristics of jointed rock mass under explosion[J]. Rock and Soil Mechanics, 2005,26(1):50-56.
[15] 李胜林, 刘志远, 张会歌,等. 基于FLAC3D对爆破振动下某土坝的安全振速预测[J]. 北京理工大学学报, 2018, 38(10):20-25.
LI Shenglin, LIU Zhiyuan, ZHANG Huige, et al. Prediction of safe blasting vibration velocity of an earth dam based on FLAC3D[J]. Transactions of Beijing Institute of Technology,2018, 38(10):20-25.
[16] 王观石, 胡世丽, 李贵荣,等.爆破地震波在结构面的传播特性与结构面倾角判断[J]. 岩石力学与工程学报, 2010, 29(9):1790-1798.
WANG Guanshi, HU Shili, LI Guirong, et al. Transmission attributes of blasting seismic wave in interface and judgement of interface obliquity[J].Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9):1790-1798.
[17] 周 剑. SH波作用下岩质边坡响应规律的解析探讨[J]. 工程地质学报, 2011, 19(4):570-576.
ZHOU Jian. Analytical analysis on rock slope dynamic response under action of SH wave[J].Journal of Engineering Geology, 2011, 19(4):570-576.
[18] 车 伟, 罗奇峰. 复杂地形条件下地震波的传播研究[J]. 岩土工程学报, 2008, 30(9):1333-1337.
CHE Wei, LUO Qifeng. Seismic wave propagation in complex topography[J].Chinese Journal of Geotechnical Engineering, 2008, 30(9):1333-1337.
[19] 范留明, 黄润秋,林 峰. 基于射线理论的边坡地震反应分析[J]. 成都理工大学学报,2000,27(1):72-75.
FAN Liuming, HUANG Runqiu,LIN Feng. Ray theory for the seismic response analysis of slope[J]. Journal of Chengdu University of Technology, 2000,27(1):72-75.
[20] 曹统仁. 绕射波的叠加效应分析[J]. 西南石油学院学报, 1987(3):13-18.
CAO Tongren. Analysis of stack effect of diffracted waves[J].Journal of Southwestern Petroleum Institute, 1987(3):13-18.
