0 引 言
三软煤层煤质松软,巷道围岩强度低,在巷道掘进时顶煤容易冒落[1],掘进工作面预注浆是治理顶板冒落的有效手段[2]。掘进工作面预注浆技术是在巷道掘进工作面打注浆孔,通过注浆对顶板进行加固,使下个掘进进尺内的巷道处在预加固的顶板之下。合理的钻孔布置与注浆参数能有效改善顶板煤体力学性能,进而有效预防掘进漏顶事故[3]。
当前注浆材料主要包括有机材料和无机材料2类,有机注浆材料凝胶时间短,凝结强度高[4]。有关专家对无机注浆材料也进行了深入研究,开发了以超细硫铝酸盐水泥为主料,辅以各种外加剂的注浆材料,通过改变配比,可以达到早期加固强度高,凝结时间可控的目的[5]。根据浆液的扩散方式[6],形成了渗透、压密和劈裂注浆理论,其中渗透注浆理论较为成熟,但是3种注浆理论均不能完整揭示浆液扩散规律。地下煤岩体注浆效果与被注介质特征、浆体特性、运移规律、浆液与被注介质相互作用关系等因素有关[7]。而三软托顶煤巷道掘进工作面注浆效果不但与上述因素有关,而还与掘进工作面所处的力学环境、空间位置存在较大联系[8],因此实验室模拟结果还需要在实际工程中进一步验证。赵家寨矿煤层属于典型三软煤层,煤质松软,裂隙发育充分,根据实揭地质资料及钻孔资料可知,煤厚变化1.42~9.11 m,平均厚4.70 m,属于缓倾斜煤层。回采巷道沿煤层底板布置,顶板托顶煤厚度2~5 m厚度不等,随掘随冒现象比较严重,难以安装锚杆和金属支架,即使勉强安装巷道。变形量也很大且难以维护。为了验证浆液扩散理论在实际工程中的应用效果,论文将实验室试验所得参数用于浆液扩散半径的理论计算,并与数值模拟结果对比确定了浆液的扩散半径,最后将结果运用于赵家寨煤矿掘进巷道施工现场。
1 煤块注浆基础参数试验
1.1 煤块渗透系数试验
煤的渗透性是指流体在压力作用下,通过煤体的难易程度[9]。利用TST-55渗透仪测试煤样渗透性。
测试原理基于达西渗流定律。测试煤样分A、B、C三组,分别取自掘进巷道顶板煤体的左帮、中线位置和右帮。渗透系数测试示意渗透系数为
(1)
其中:a为变水头管内截面积,cm2;A为测试煤样截面积,cm2;l为试样长度,cm;t1、t2分别为起始时刻与终了时刻;h1、h2分别为起始水头与终止水头,cm。渗透系数测试如图1所示,图中h为水头变化过程中某时刻测压管水头。
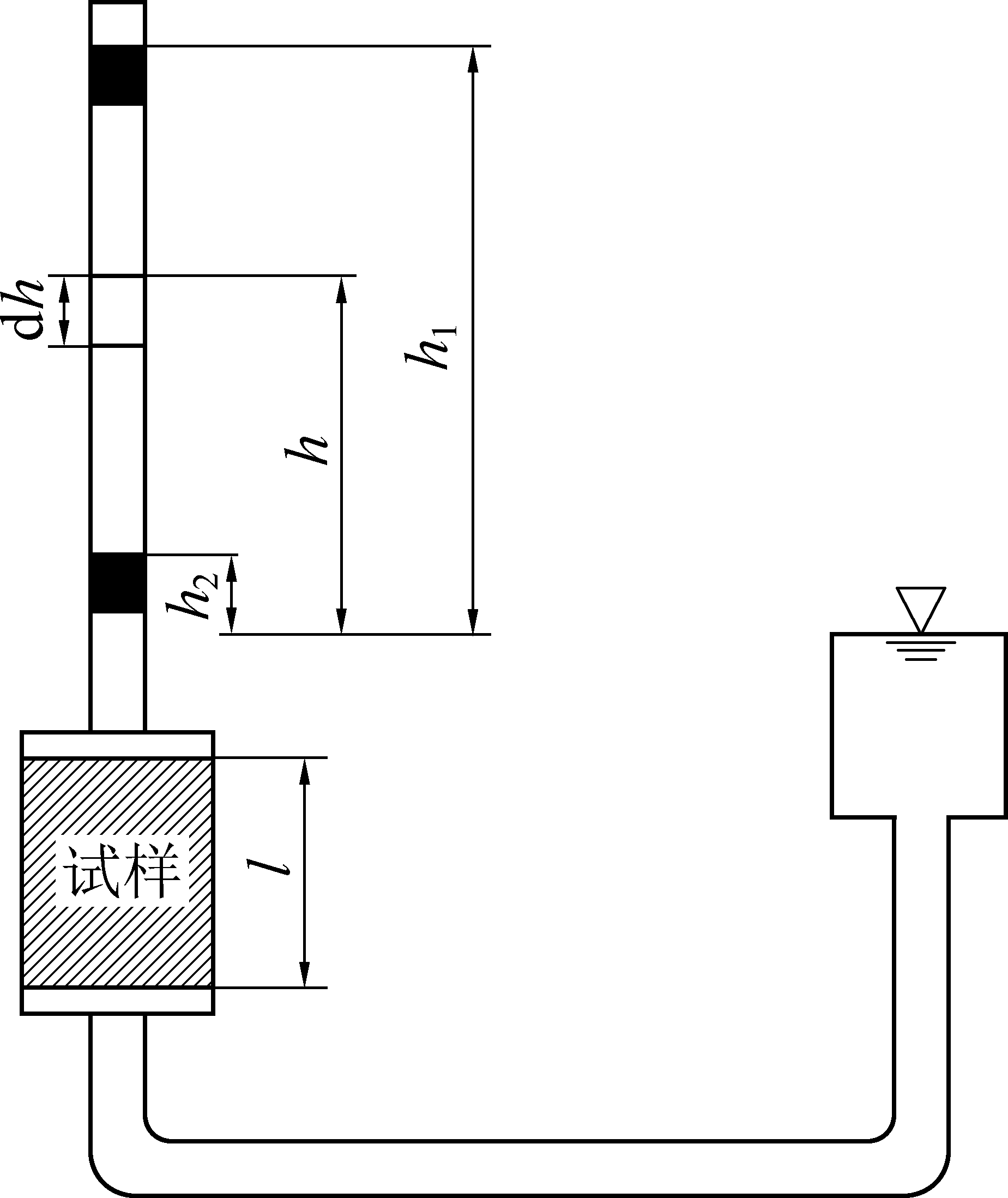
图1 渗透系数测试示意
Fig.1 Principle of measurement for permeability coefficient
表1 渗透系数测试结果
Table 1 Measurement results of permeability coefficient

试验编号测记次数时间/s起始水头/cm终止水头/cm水温/℃kT/(10-4 cm·s-1)单值均值温度修正系数ηT/η20k20/(10-4 cm·s-1)单值均值A145.01144.0124.0292.28123.0103.03167.44102.082.04264.6281.061.05378.4960.040.0292.961.711.160.969.561.200.8152.421.400.950.780.780.98B131.25149.0129.02116.95125.0105.03277.37103.583.54275.8281.061.05380.6658.038.0284.121.331.020.920.991.070.8333.431.110.850.760.830.89C187.47148.0128.02121.87127.0107.03142.49107.087.04205.7186.066.05250.3865.045.0301.481.251.011.151.311.240.7981.181.000.810.921.050.99
渗透系数测试结果见表1,其中:k20为标准温度的渗透系数,cm/s;kT为温度T时的渗透系数,cm/s; k20=kT(ηT/η20),其中:ηT为温度T时水的动力黏滞系数,kPa·s; η20为温度20 ℃时水的动力黏滞系数,kPa·s。计算可得k20=9.533×10-5 cm/s。
1.2 煤块孔隙率测定
孔隙率是煤体中孔隙体积与总体积之比,是影响浆液扩散性能的重要指标。孔隙率按式(2)计算:
(2)
式中:![]() 为20 ℃时煤的视相对密度;
为20 ℃时煤的视相对密度;![]() 为20 ℃时煤的真相对密度;n为孔隙率,结果见表2。
为20 ℃时煤的真相对密度;n为孔隙率,结果见表2。
表2 煤的孔隙率测试结果
Table 2 Measurement results of porosity
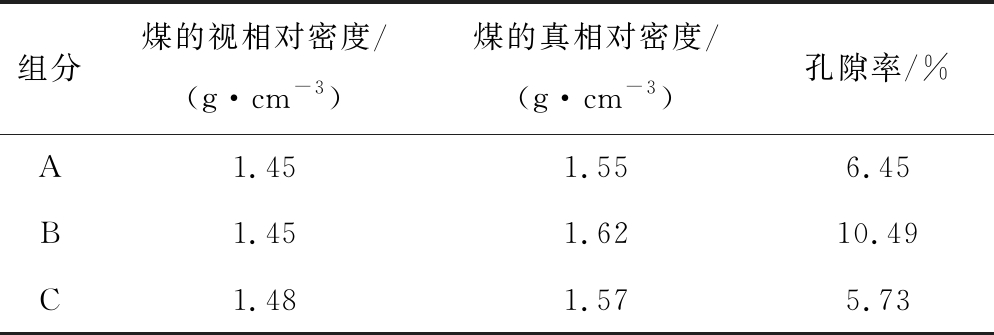
组分煤的视相对密度/(g·cm-3)煤的真相对密度/(g·cm-3)孔隙率/%A1.451.556.45B1.451.6210.49C1.481.575.73
孔隙率取3组测试结果的平均值为7.56%。通常煤的孔隙率为5%,试验煤样孔隙率大于5%,为浆液扩散预留了丰富空间。
1.3 浆液黏度与密度测试
浆液以超细硫铝酸盐水泥为主料,辅以外加剂配置而成,利用ZNN-D6II型六速旋转黏度计测量浆液的表观黏度,并计算液表观黏度,塑性黏度,动、静切力等参数,见表3。同时,利用XYM-1型液体密度计测量浆液密度。
表3 浆液黏度测试结果
Table 3 Measurement results of viscosity
转速/(r·min-1)600300200100黏度/(MPa·s)7.54.02.51.5
表观黏度按式(3)计算:
ηb=w1/2
(3)
塑性黏度按式(4)计算:
ηs=w1-w2
(4)
动切力按式(5)计算:
τ0=0.511(w2-ηs)
(5)
其中:w1为转速600 r/min时黏度计的读数;w2为转速300 r/min时黏度计的读数。将表3中的读数代入式(3)—式(5),得浆液的表观黏度为3.75 MPa·s,塑性黏度为3.5 MPa·s,动切力为0.255 5 Pa。
取多次密度测量结果的算术平均值,测得浆液密度为1.23 g/cm3。
2 软煤层预注浆液扩散理论分析
2.1 浆液扩散理论基础
注浆理论主要是建立压力、流量、扩散半径、注浆时间之间的关系[10-12],将浆液在煤体中的扩散过程理想化为流体在介质中做层流运动[13-15]。层流达西定律由法国学者根据沙土试验结果得到[16],其广义表达如公式(6)。达西定律假设流体在介质中做一维运动,即渗流速度和水力坡度的大小和方向沿程恒定。
(6)
式中:k为渗透系数;i为水头梯度;L′为水头空间中的方向。
2.2 浆液柱形扩散规律
赵家寨煤矿煤质松软,裂隙充分,所需注浆压力较小,宜采用渗透注浆理论分析浆液在煤体中的扩散规律。现场采用注浆锚杆进行注浆,浆液流经杆体喷射孔,注浆源可简化为线性浆源,利用柱形扩散理论对浆液扩散进行定量分析[17-18]。浆液柱形扩散如图2所示。
单位时间内的浆液流量为
q=A′v=A′ki
(7)
式中:A′为浆液扩散柱体的截面积。
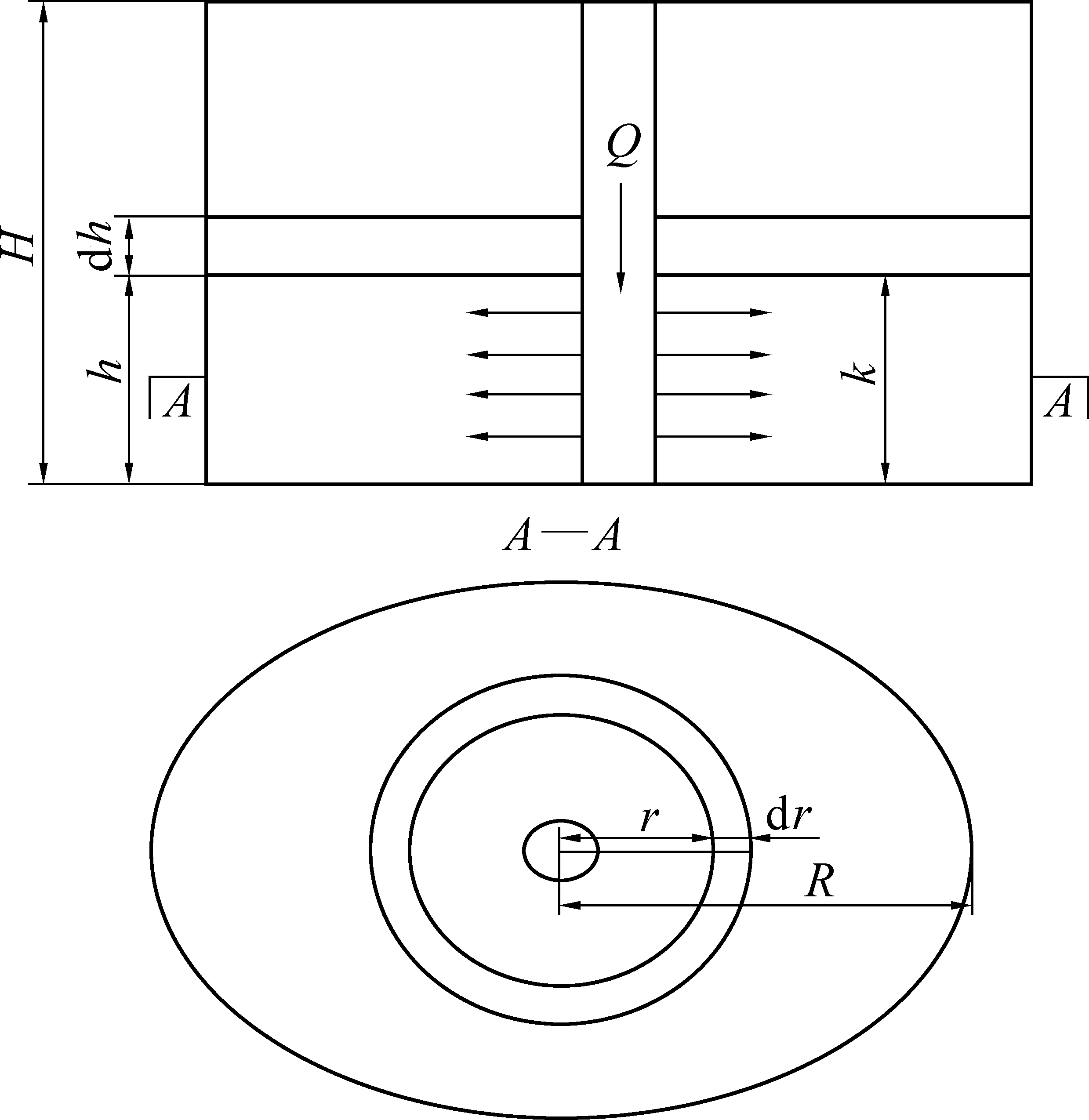
图2 浆液柱形扩散示意
Fig.2 Cylindrical diffusion of slurry
不考虑地下静水压力对注浆压力造成的影响,将浆液扩散沿注浆孔径向和轴向进行二重积分,积分域r[r0,R],h[0,H],由此可得:
(8)
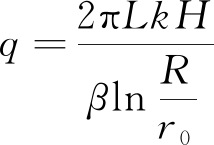
(9)
由Q=πR3Ln和Q=qt得:
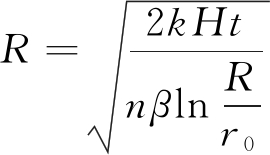
(10)
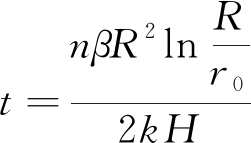
(11)
其中:Q为浆液流量,cm;β为浆液黏度与水的黏度比;R为浆液的扩散半径,cm;r为至注浆中心的距离;L为柱状注浆的长度,cm;H为注浆压力水头之和,cm;r0为注浆管半径,cm;t为注浆时间,s。
3 三软煤层巷道掘进预注浆模拟分析
3.1 数值模型构建
以赵家寨煤矿12204工作面运输巷为研究对象,采用流固耦合模块对浆液在煤体中的扩散规律进行研究。注浆孔与掘进工作面空间关系模型如图3所示。
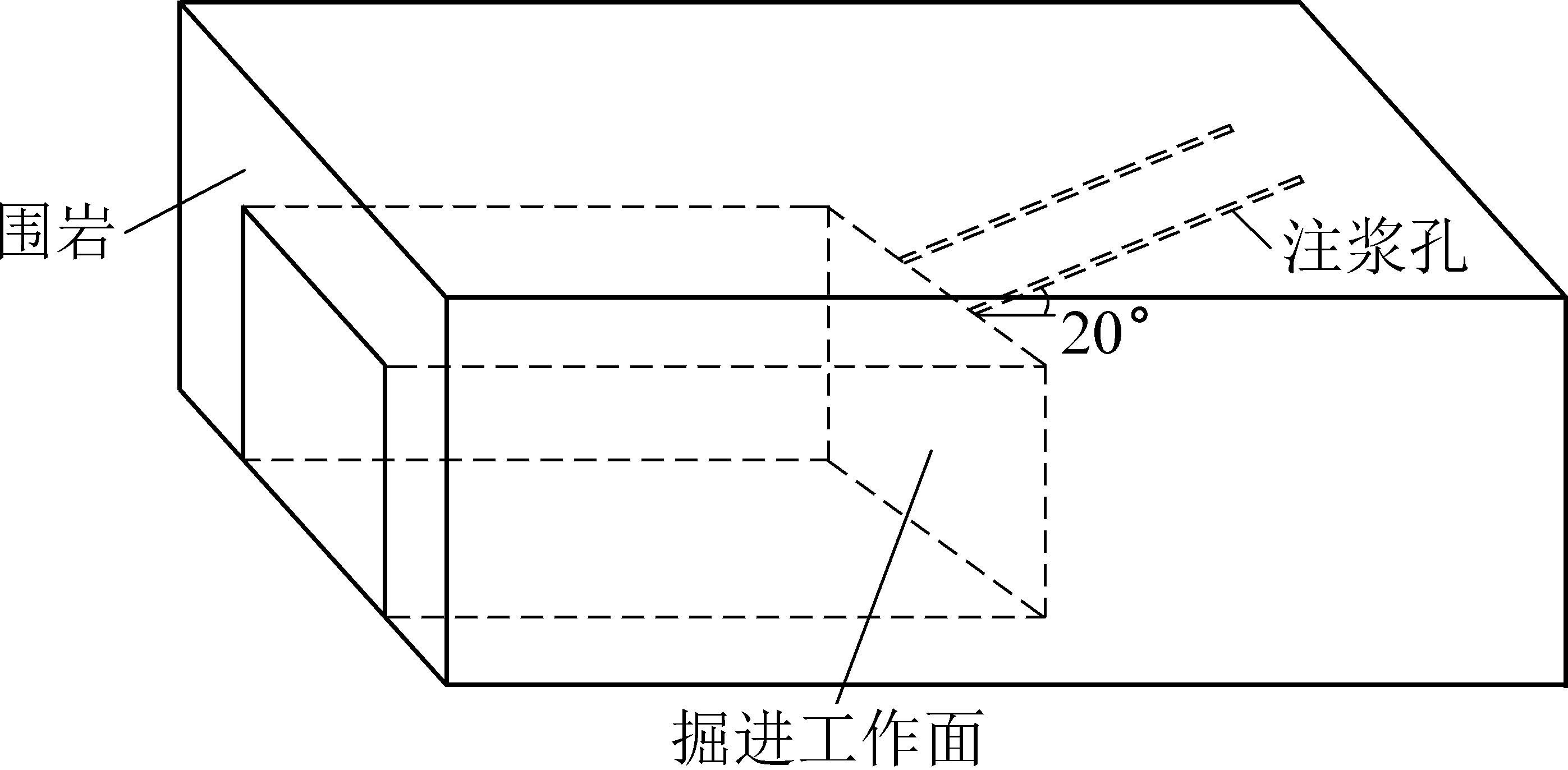
图3 注浆孔与掘进工作面层位关系
Fig.3 Stratigraphic relation between grouting hole and heading face
3.2 边界条件及数值计算参数
掘进巷道沿煤层底板推进,顶煤厚度2~5 m,浆液在煤体中的扩散半径一般小于3 m,将掘进工作面设为自由面,其余5个面固定。渗透系数与土力学中渗透系数之间的换算[19]后的渗透系数为9.72×10-11,孔隙率7.56%。浆液密度1.2 g/cm3,注浆量60 L/min。
3.3 注浆压力对浆液扩散的影响
3.3.1 浆液扩散机理
孔隙压力即饱和土体中孔隙水承担或传递的压力[20]。距离注浆孔壁较近的围岩体内裂隙或孔隙首先被浆液充满,然后浆液向距离注浆孔壁更远的围岩体扩散[21]。先充满浆液的孔隙或裂隙中孔隙压力会瞬间降低,但是浆源不断涌入,使得降低的孔隙压力瞬间恢复。因此一定位置的孔隙压力变化趋势为“增大-降低-恢复”型,如图4所示。
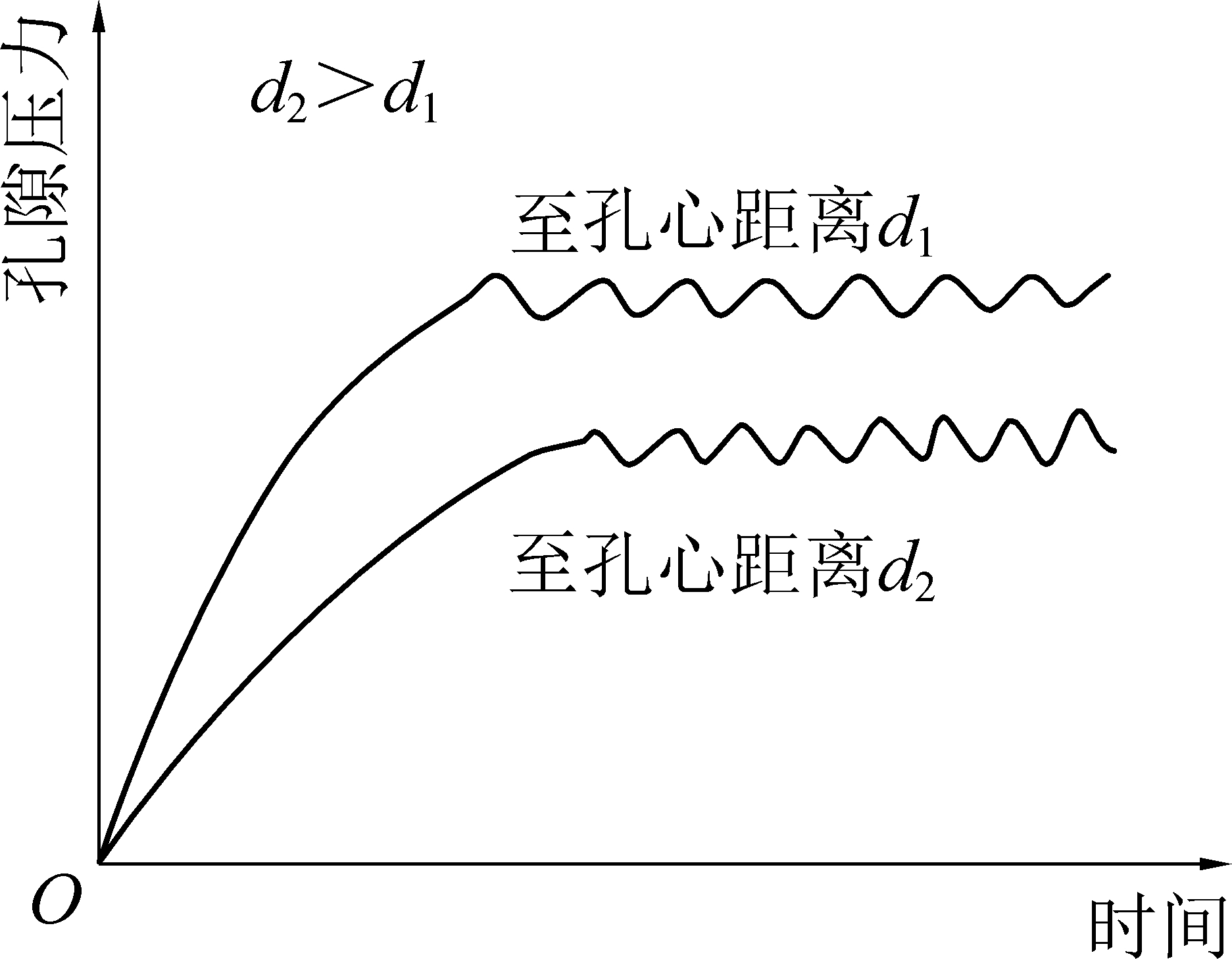
图4 一定点处孔隙压力随时间变化曲线
Fig.4 Pore pressure curve with time
3.3.2 注浆压力与孔隙压力关系分析
模拟了注浆压力分别为2.0、2.5、3.0、3.5、4.0 MPa时孔隙压力的变化,如图5所示,注浆压力对浆液扩散的影响随着与孔距离的增加越来越小,注浆10 min与注浆15 min的孔隙压力分布曲线差别很小,注浆15 min时距孔中心2 m处,注浆压力降为0。因此,在相同注浆时间下提高注浆压力能适当提高浆液的扩散效率,但对提高浆液的最大扩散半径不明显。

图5 不同注浆压力下孔隙压力分布曲线
Fig.5 Distribution curves of pore pressure under different grouting pressure
3.3.3 注浆压力与饱和度关系分析
饱和度为流体所占体积与孔隙体积之比。若一点处饱和度小于1,则认为该处孔隙尚未被浆液填满,则该点孔隙压力不足以压迫浆液继续扩散,因此孔隙压力为1的点为扩散有效区,小于1的点则表示浆液不能有效扩散。
不同注浆压力下饱和度分布曲线如图6所示,注浆5 min时5条曲线变化趋势及点坐标值近似重合,说明在注浆刚开始的一段时间内,不同注浆压力下浆液扩散速度及扩散半径相近。主要是起始阶段,注浆孔围岩破坏,裂隙充分,且浆液中的固相颗粒尚未充填孔隙及裂隙,浆液不需过高压力即可克服流动阻力。
当注浆10 min时,随着注浆压力的增大,浆液的扩散半径增大,扩散半径有效值达到1.5 m。其中3.5 MPa和4.0 MPa两条曲线近似重合,说明注浆压力达到3.5 MPa时,若继续提高注浆压力,对浆液扩散意义不大。
当注浆15 min,注浆压力为2.0 MPa和2.5 MPa时,浆液扩散半径仍然在1.5 m左右。但是注浆压力为3.0、3.5、4.0 MPa时,浆液扩散半径增大到1.8 m,此后饱和度迅速降低。因此,注浆15 min时,注浆压力达到3.0 MPa及以上,对浆液扩散半径增加并不明显,而且浆液饱和度出现降低现象,可能是压力增加导致孔内煤体出现突然破坏所致。因此,不论继续延长注浆时间,还是提高注浆压力,煤体中的有效扩散半径及最大扩散半径均不能得到显著提高,故最佳注浆压力范围在2.5~3.0 MPa。

图6 不同注浆压力下饱和度分布曲线
Fig.6 Distribution curves of saturation under different grouting pressure
3.4 应力状态对浆液扩散的影响
为保证浆液有效扩散,避免浆液在高压作用下造成煤体破坏,单孔浆液扩散时注浆压力取2.5 MPa,通过观测注浆孔周围的孔隙压力分布,确定浆液有效扩散范围,由于各种影响因素的相互作用对浆液扩散的影响无法定量计算,根据理论公式计算结果与现场注浆实例,注浆孔周围围岩体取孔隙压力1.0 MPa为临界值,孔隙压力高于该值认为浆液在该范围内有效扩散,孔隙压力低于该值认为浆液在该范围内扩散较差。为分析应力状态对浆液扩散的影响,设计了侧压系数分别为1.0、1.2和1.5的三种模拟方案。
3.4.1 应力状态对扩散速率的影响
浆液扩散轨迹呈“正多边形”,随着侧压系数增大,“正多边形”扩散轨迹更加明显,如图7所示。由于煤体为不均匀介质,因此浆液扩散速率不断变化,可用“平均扩散速率”衡量扩散快慢,“平均扩散速率”即单位时间内浆液的扩散半径。当注浆时间15 min,侧压系数为1.0时,扩散半径达1.41 m,当侧压系数为1.2时,扩散半径减少到1.15 m;当侧压系数为1.5倍时,扩散半径为0.90 m。因此,随着侧压系数增大,浆液扩散速率减小。

图7 注浆时间15 min时不同侧压下孔周围孔隙压力分布
Fig.7 Distribution of pore pressure around the grouting hole when grouting 15 minutes
3.4.2 应力状态与孔隙压力及饱和度关系分析
图8为3种应力状态下注浆5 min到15 min内,注浆孔周围孔隙压力分布特征。曲线的零点出现在距孔中心约2 m处,且零点位置未随时间增加而前移,说明在注浆压力一定时,浆液最大扩散范围相对固定。在相同注浆时间内,侧压系数越大,孔隙压力越小。
对比注浆5、10、15 min的孔隙压力分布曲线可知,前期延长注浆时间能在一定范围内增大浆液扩散半径,但随着注浆时间继续延长,浆液扩散速率会下降,注浆进入低扩散阶段,此时,如果继续延长注浆时间则对浆液的扩散影响不大。
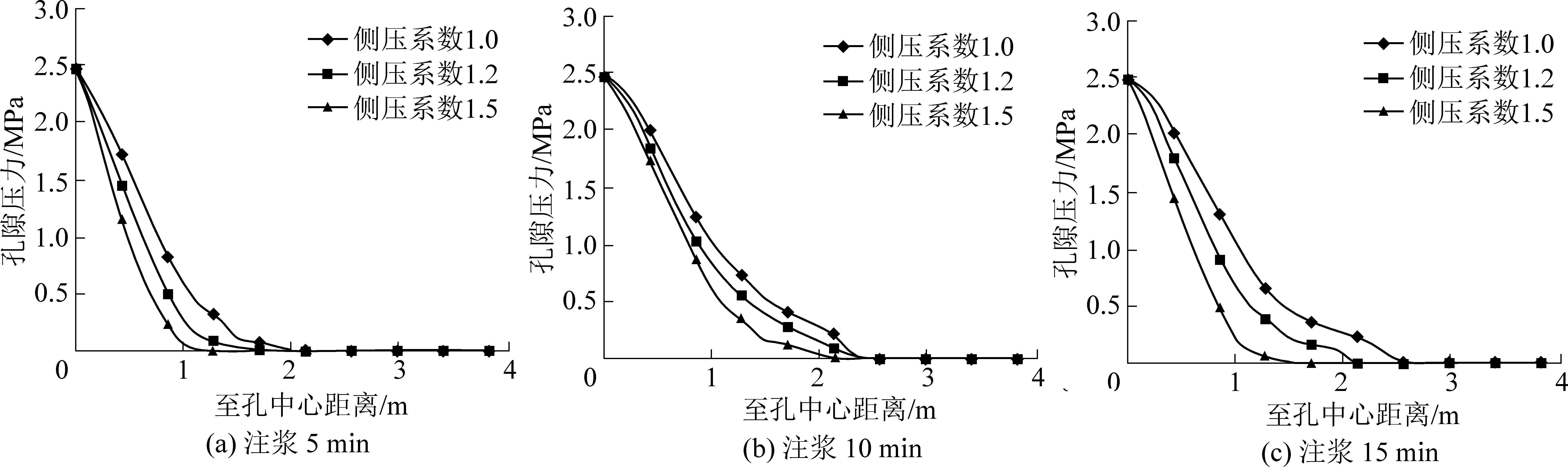
图8 不同侧压系数时孔隙压力变化曲线
Fig.8 Variation curves of pore pressure under different lateral pressure
图9为3种应力状态下注浆5~15 min,注浆孔周围饱和度分布特征。与孔隙压力变化曲线不同,随着距孔中心距离的增大,饱和度降低率增大,距孔越远,浆液扩散衰减越快。注浆时间由5 min增加到10 min再到15 min时,饱和度临界值均出现在距孔中心约2 m处,并没有发生明显的变化,这与前文分析所得的浆液最大扩散范围结果基本一致。

图9 不同侧压系数时孔周围饱和度分布曲线
Fig.9 Variation curves of saturation under different lateral pressure
4 赵家寨掘进工作面注浆现场应用分析
4.1 浆液扩散半径确定
注浆量0.06 m3/min,注浆压力为2.5 MPa,依据实验室参数进行理论计算,与数值模拟计算结果比较见表4,理论与数值计算结果较接近,因此扩散半径确定为1.4 m。
4.2 工程布置与注浆参数
选赵家寨煤矿12204工作面运输巷掘进工作面为试验现场,巷道沿煤层底板掘进,巷道宽4 m,高度3 m,顶煤厚度1~3 m。注浆参数的确定基于数值计算与理论计算的总和分析结果。①注浆时间:注浆持续15 min左右,浆液已经进入低扩散阶段,
表4 理论计算与数值模拟扩散半径对比
Table 4 Comparation of diffusion radius under theoretical calculation and numerical calculation

注浆压力/MPa不同注浆时间的扩散半径/m5 min 10 min15 min2.50.81、0.67*1.07、1.14*1.40、1.49*
注:*表示前者为公式半径,后者为模拟半径。
因此注浆时间定为20 min能保证浆液充分扩散。②注浆压力:为防止浆液对软煤造成破坏,同时保证浆液扩散充分,注浆压力定为2.5 MPa。③注浆量:注浆量设定为0.06 m3/min。④注浆孔布置:注浆孔布置如图10所示,注浆孔深4 m,上仰角20°。
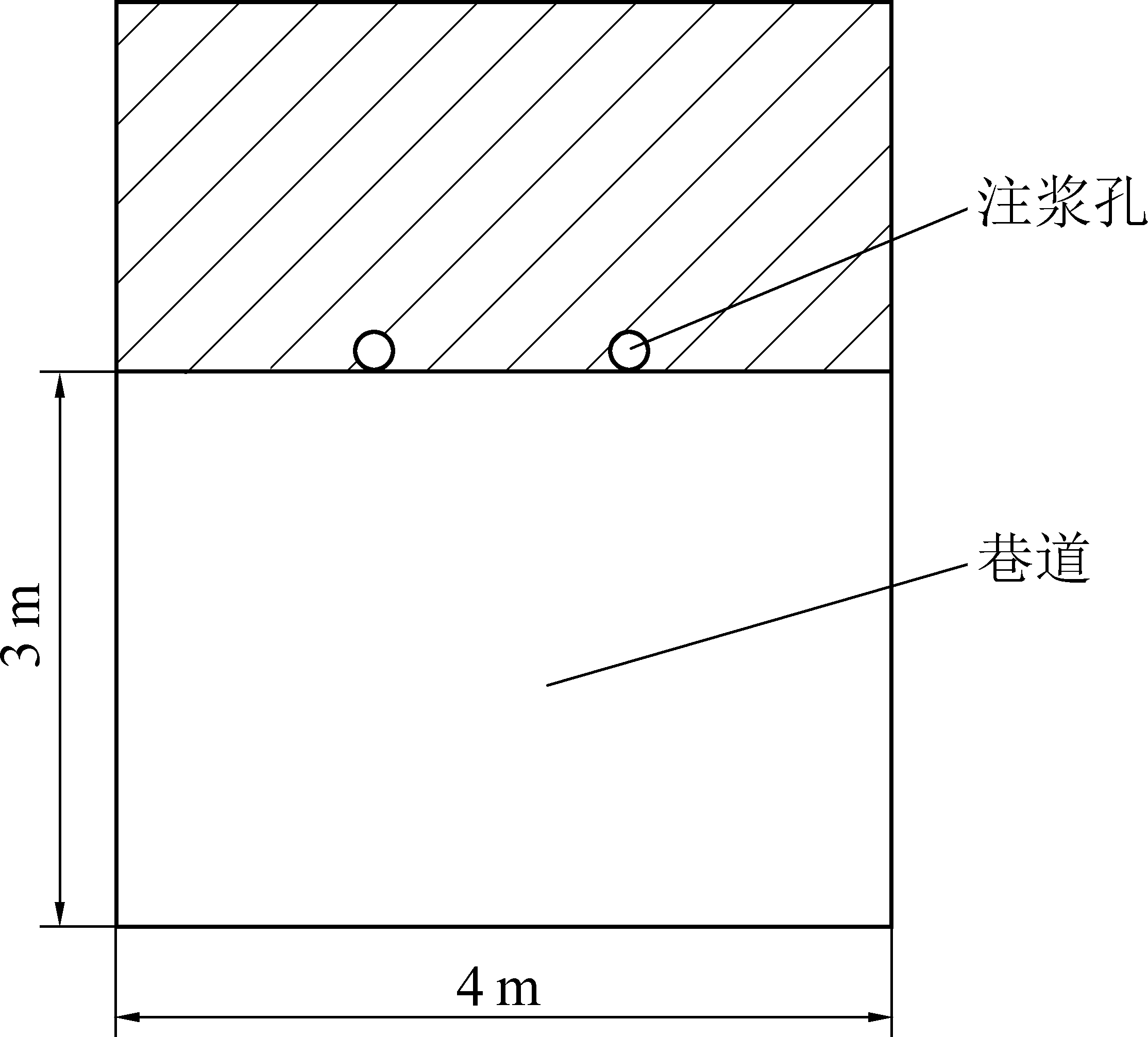
图10 注浆孔布置
Fig.10 Distibution of grouting holes
4.3 注浆效果检验
为检验浆液扩散效果,注浆24 h后沿巷道顶板进行岩心取样,取心钻孔深4 m,上仰角20°。取心钻孔分A(顶板左帮),B(顶板中部),C(顶板右帮)3组,每组在孔深1、4 m处取样2次(A组记为A1、A2、B组记为B1、B2、C组记为C1、C2),如图11所示。

图11 顶板取心样品
Fig.11 Samples extracted from the roof
观察图11的3组图片,发现注浆后的岩心质地致密,裂隙少,完整度明显提高。通过对比每组内两取样点的不同岩心发现,注浆孔浅部比注浆孔深部浆液扩散效果好。综合以上可以确定,在设计半径内,浆液扩散与预期分析结果吻合良好。
5 结 论
1)通过改变侧压系数,分析了不同应力状态下浆液扩散半径及扩散速率,在注浆压力一定时,侧压越大,浆液扩散速率越小,一定时间内浆液的扩散半径越小。浆液扩散范围有最大值,且最大值点不随应力状态改变而变化,即应力状态影响浆液扩散的有效范围,并不影响浆液的最大扩散范围。
2)通过改变注浆压力,分析了5种注浆压力下浆液扩散规律,增加注浆压力在一定范围内能提高浆液的扩散效率(即扩散速率和扩散半径),但并不能明显提高浆液的最大扩散半径。且较高的注浆压力作用可能破坏煤体。
3)无论延长注浆时间还是提高注浆压力,都不能显著提高浆液的最大扩散半径。
[1] 侯朝炯团队.巷道围岩控制[M].徐州:中国矿业大学出版社,2013:546-550.
[2] 边 强,金煜皓.综采工作面复合顶板失稳机理及深孔注浆控制技术[J].煤炭科学技术,2018,46(8):57-62.
BIAN Qiang,JIN Yuhao.Instability mechanism and deep hole grouting control technology of composite roof in fully-mechanized mining face[J].Coal Science and Technology,2018,46(8):57-62.
[3] 卢海军.管棚囊袋注浆超前支护技术在巷道过采空区中的应用[J].煤炭科学技术,2018,46(3):49-53.
LU Haijun.Application of advance supporting technology with pipe-shed and capsular bag grouting in roadway through goaf[J].Coal Science and Technology,2018,46(3):49-53.
[4] 刘永文,王新刚.注浆材料与施工工艺[M].北京:中国建材工业出版社2008:1-3.
[5] 彭英华,华攸金,李希建,等.破碎煤岩巷道注浆加固材料试验与应用研究[J/OL].煤炭科学技术:1-6[2020-04-04].http://kns.cnki.net/kcms/detail/11.2402.TD.20200207.1444.017.html.
PENG Yinghua,HUA Youjin,LI Xijian,et al.Experiment and application of grouting reinforcement material for broken coal and rock in roadway[J/OL].Coal Science and Technology:1-6[2020-04-04].http://kns.cnki.net/kcms/detail/11.2402.TD.20200207.1444.017.html.
[6] 李术才,张 霄.地下工程涌突水注浆止水浆液扩散机制和封堵方法研究[J].岩石力学与工程学报,2011,30(12):2377-2396.
LI Shucai,ZHANG Xiao.Research on mechanism of grout diffusion of dynamic grouting and plugging method in water inrush of underground engineering[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(12):2377-2396.
[7] 李树刚,成小雨,刘 超,等.破碎围岩动压巷道锚索支护与注浆加固技术研究[J].煤炭科学技术,2016,44(1):67-72.
LI Shugang,CHENG Xiaoyu,LIU Chao,et al.Research on technology of anchor cable supporting and grouting reinforcement for dynamic pressurized tunnel with crushed surrounding rock[J].Coal Science and Technology,2016,44(1):67-72.
[8] 任海强,陶广美.受动压影响巷道注浆加固技术研究[J].煤炭科学技术,2016,44(3):22-25.
REN Haiqiang,TAO Guangmei.Study on grouting reinforced technology of roadway affected by dynamic pressure[J].Coal Science and Technology,2016,44(3):22-25.
[9] 董世举.赵固二矿大采高工作面煤壁片帮机理及注水防治技术研究[D].焦作:河南理工大学,2012.
[10] 孙斌堂,凌贤长.渗透注浆浆液扩散与注浆压力分布数值模拟[J].水利学报,2007,37(11):1402-1406.
SUN Bintang,LING Xianchang.Numerical simulation of slurry diffusion of penetration grouting and distribution of grouting pressure[J].Journal of Hydraulic Engineering,2007,37(11):1402-1406.
[11] 张忠苗,邹 健.黏土中压密注浆及劈裂注浆室内模拟试验分析[J].岩土工程学报,2009,31(12):1818-1824.
ZHANG Zhongmiao,ZHOU Jian.Laboratory tests on compaction grouting and fracture grouting of clay[J].Chinese Journal of Geotechnical Engineering,2009,31(12):1818-1824.
[12] 刘 健,刘人太.水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J].岩石力学与工程学报,2012,31(12):2445-2452.
LIU Jian,LIU Rentai.Diffusion law model test and numerical simulation of cement fracture grouting[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2445-2452.
[13] 刘泉声,卢超波.深部巷道注浆加固浆液扩散机理与应用研究[J].采矿与安全工程学报,2014,31(3):333-339.
LIU Quansheng,LU Chaobo.Research on the grouting diffusion mechanism and its application of grouting reinforcement in deep roadway[J]. Journal of Mining & Safety Engineering,2014,31(3):333-339.
[14] 钱自卫,姜振泉.渗透注浆浆液扩散半径计算方法研究及应用[J].工业建筑,2012 ,42(7):100-104.
QIAN Ziwei,JIANG Zhenquan.Research and application penetration radius calculation method for permeation grouting[J].Industrial Construction,2012,42(7):100-104.
[15] 李慎举,王连国.破碎围岩锚注加固浆液扩散规律研究[J].中国矿业大学学报,2011,40(6):874-879.
LI Shenju,WANG Lianguo.Slurry diffusion within cracked wall rock during the bolt-grouting process[J].Journal of China University of Mining & Technology,2011,40(6):874-879.
[16] 赵树德.土力学[M].北京:高等教育出版社,2001:44-46.
[17] 王 乾,曲立清.青岛胶州湾海底隧道围岩注浆加固技术[J].岩石力学与工程学报,2011,30(4):790-802.
WANG Qian,QU Liqing.Grouting reinforcement technique of qingdao jiaozhou bay subsea tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(4):790-802.
[18] 湛铠瑜,隋旺华.单一裂隙动水注浆扩散模型[J].岩土力学,2011,32(6):1659-1663.
ZHAN Kaiyu,SUI Wanghua.A model for grouting into single fracture with flowing water[J].Rock and Soil Mechanics,2011,32(6):1659-1663.
[19] 刘汉龙.FLAC3D基础与工程实例[M].北京:中国水利水电出版社2008:234-237
[20] 柳昭星,靳德武,尚宏波,等.矿区岩溶裂隙岩体帷幕截流注浆参数确定研究[J].煤炭科学技术,2019,47(6):81-86.
LIU Zhaoxing, JIN Dewu, SHANG Hongbo,et al.Study on determination of curtain closure grouting parameters of fractured rock mass in karst mining area[J].Coal Science and Technology, 2019,47(6):81-86.
[21] 赵万里,杨战标.深部软岩巷道强力锚注支护技术研究[J].煤炭科学技术,2018,46(12):92-97.
ZHAO Wanli,YANG Zhanbiao.Study on strength bolt grouting support technology in deep soft rock roadway[J].Coal Science and Technology,2018,46(12):92-97.
