0 引 言
随着我国对煤炭资源的勘探深入,地震勘探所面临的对象与开采的环境也越来越复杂[1]。传统的煤田地震勘探技术一般是研究各向同性介质,而煤层裂缝介质实际上都是各向异性介质。因此,当研究煤层地震波传播时,需要选择更加复杂的各向异性介质地震勘探技术。目前研究的煤层各向异性介质主要是横向各向同性介质(Transversely isotropic medium,TI)和正交各向异性介质(Orthogonal anisotropic medium,OA)。TI介质有一个无穷重对称轴,称为主对称轴,根据对称轴的特征将TI介质分为3类[2]:①具有水平对称轴的TI介质称HTI(TI with a Horizontal symmetry axis)介质;②具有垂直对称轴的TI介质称VTI(TI with a vertical symmetry axis)介质;③具有倾斜对称轴的TI介质称TTI(TI with a tilted symmetry axis)介质。正交各向异性介质具有3个相互正交的对称面。煤层中存在一种常见的裂隙近似为正交裂隙,对此通常可以用OA介质来描述,将存在正交裂隙的煤层近似为OA型煤层[3],并可将单组裂隙等效为HTI介质,将2组正交裂隙等效为OA介质,并推导出等效正交各向异性参数表达式[4]。HUDSON[5]在一定假设条件下,给出了裂隙介质弹性张量和近似表达式,描述单组裂缝的另一种等效理论;THOMSEN等[6]提出各向异性参数,得出横向各向异性介质中各向异性参数的物理意义;SCHOENBERG等[7]基于柔度矩阵,应用线性滑动理论进行裂隙介质模拟;BAKULIN等[8]将THOMSEN各向异性参数、法向柔度和切向柔度联系起来,分析了填充物裂隙中弱各向异性介质弱度变化规律;刘财等[9-10]对多组等效裂隙各向异性模型展开研究;刘东洋等[11]研究了裂隙等效介质模型对煤层裂隙参数的影响;裴正林等[12]研究了不同裂隙密度煤层弹性波场及其方位各向异性特征。TSVANKIN等[13]引入各向异性弱度,推导出OA介质对称面上的P波、SV波相速度表达式;BERRYMAN[14]基于相速度指出对称面内群速度、群角的标量表达式;熊金良等给出了任意各向异性介质条件下,群角与相角的对应关系;唐志远等[16]建立了一种煤层气储层地震波速度预测方法,并且提高煤层气储层速度预测准确性,证明了地震波速度差异受煤层气储层气体含量影响。
笔者针对OA型煤层,利用裂隙的等效介质模型模拟了裂隙参数变化对各向异性参数的影响,同时分析了正交各向异性介质中地震波传播产生的各种波形的不同速度响应,对煤储层裂隙介质的参数研究和地震波响应研究有重要意义。
1 裂缝等效模型理论及OA各向异性参数
1.1 裂缝等效模型理论
根据Schoenberg线性滑动理论将裂隙等效为地层中的一个柔性面,此柔性面满足线性滑动边界条件,该理论本质是将含裂隙岩石的柔度分解为裂隙柔度与围岩柔度的和,其中围岩是各向同性的[17-18]。即有
S=Sb+Sf
(1)
式中:S为含有裂隙地层的柔度矩阵,Sb为围岩地层的柔度矩阵,Sf为裂隙的柔度矩阵。
令C=S-1,裂隙的柔度矩阵转化为弹性参数矩阵,对于OA介质,具有3个相互正交的对称面,2个拉梅常数用λ和μ表示,裂隙介质的弹性系数矩阵是围岩弹性矩阵与裂隙的弹性矩阵之和,其中围岩介质的弹性矩阵[4]Cb为
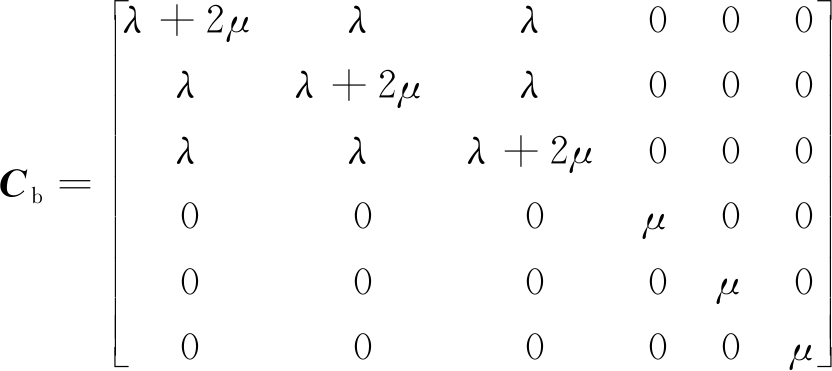
(2)
基于BAKULIN[4]提出的裂隙等效公式,可知位于各向同性介质两组正交裂缝可以等效为正交各向异性介质,2组正交裂隙模型如图1所示。
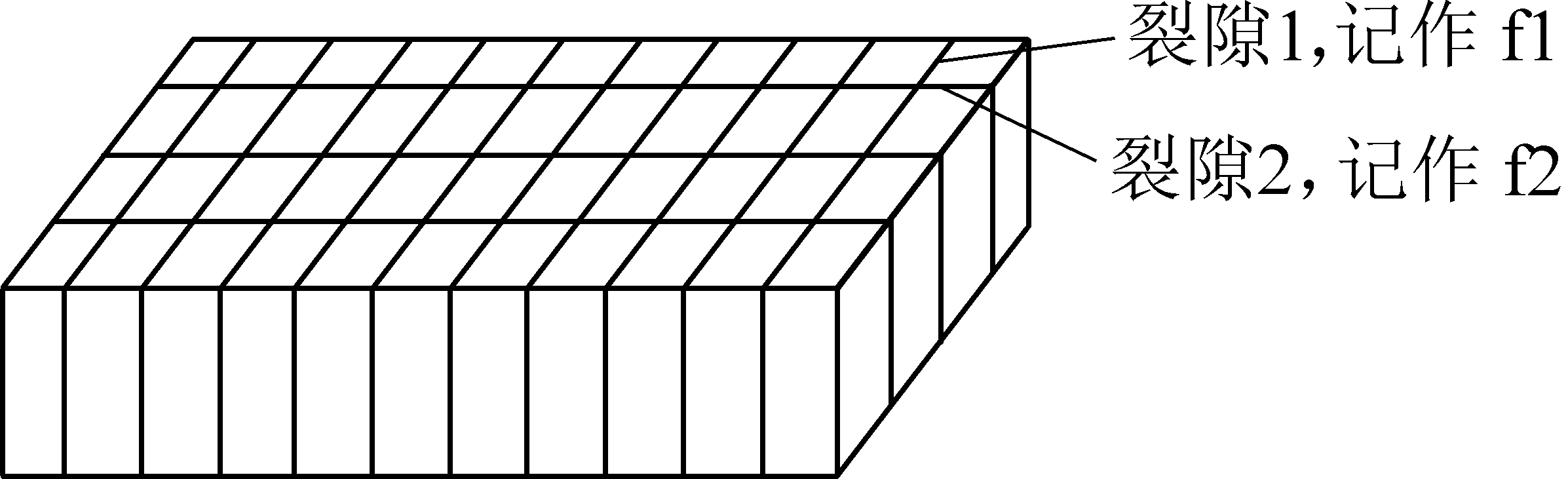
图1 两组正交裂隙模型
Fig.1 Two sets of orthogonal fracture models
令:af1=(λ+2μ)(1-ΔN1)、af2=(λ+2μ)(1-ΔN2)、bf1=μ(1-ΔN1)、bf2=μ(1-ΔN2),则裂隙1、裂隙2的柔度矩阵[4]Sf1、Sf2分别为

(3)

(4)
式中:ΔN1、ΔN2为裂缝1、裂缝2的法向柔度;ΔT1、ΔT2为裂缝1、裂缝2的切向柔度。
根据围岩矩阵与柔度矩阵求取裂隙介质的弹性矩阵[3],即
![]() =Cb(1+CbSf1+CbSf2)-1
=Cb(1+CbSf1+CbSf2)-1
(5)
裂隙的高宽之比及充填物和裂隙线密度表示裂隙的形态,含有裂隙岩层的弹性矩阵等于围岩的弹性矩阵、单个裂隙的弹性矩阵及裂隙相互作用的弹性矩阵之和。结合 式(3)—式(5) 可得2组正交裂隙弹性矩阵参数[3]。根据实际裂隙介质通常满足切向柔度与法向柔度远远小于1(THOMSEN弱各向异性假设),即ΔT1<<1、ΔT2<<1、ΔN1<<1、ΔN2<<1,2组正交裂隙弹性矩阵参数弱各向异性近似等效后的弹性矩阵内元素{cij}的表达式[3]为
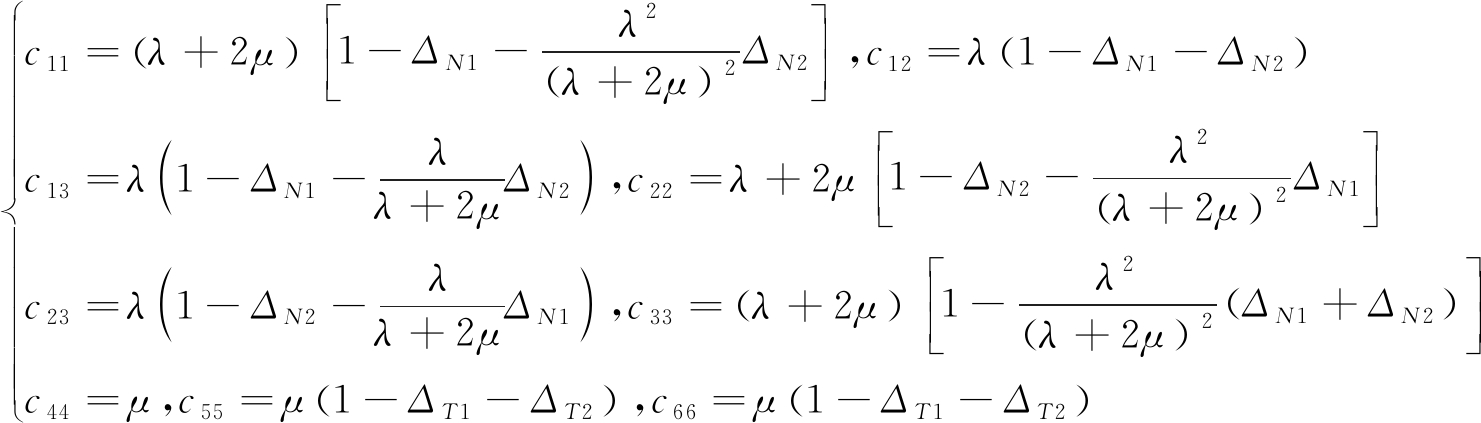
(6)
式(6) 为正交裂隙弹性矩阵参数表达式,其中每个弹性参数不仅与背景拉梅常数有关,还与ΔT1、ΔN1、ΔT2、ΔN2有关。
根据线性滑动理论与Hudson理论相结合的等效理论,裂隙切向柔度、法向柔度表达式 [3]分别为
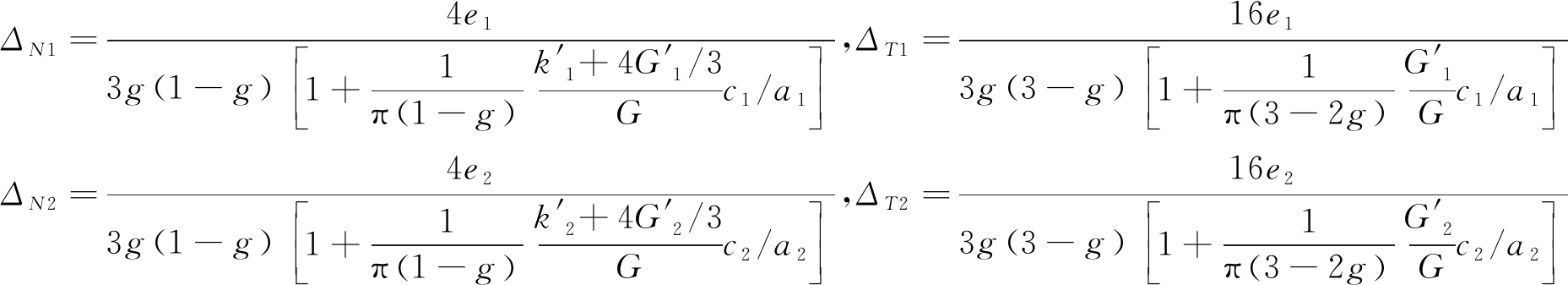
(7)
式中:e1、e2为裂隙1、裂隙2的裂隙密度,均表示裂隙单位体积内所占总体积的比例,且都是无量纲参数;k′1、G′1、k′2、G′2分别为裂隙1、裂隙2充填物的体积模量与剪切模量;G为背景介质的剪切模量;a1、a2为裂隙1、裂隙2的高度;c1、c2为裂隙1、裂隙2的宽度;![]() 和Vp分别为围岩介质的横波和纵波速度。
和Vp分别为围岩介质的横波和纵波速度。
1.2 OA介质各向异性参数
正交各向异性介质具有3个相互正交的对称面。在沉积盆地中广泛存在周期性薄互层(Periodic Thin Layers,PTL),如果在此背景上发育有垂直的定向裂隙(Extensive Dilatancy Anisotropy,EDA),一般将这种介质视为正交各向异性介质[19]。3种实际各向异性介质模型如图2所示,实际各向异性介质的弹性矩阵为

(8)
正交各向异性介质中的弹性系数由9个独立的弹性常数来描述:c11、c12、c13、c22、c23、c33、c44、c55、c66。式(8)一直被用于传统弹性参数的分析,TSVANKIN根据正交各向异性介质与 VTI 介质相似性与相异性,定义了OA介质各向异性参数,让各参数有更准确的物理意义,具体定义如下[13]:
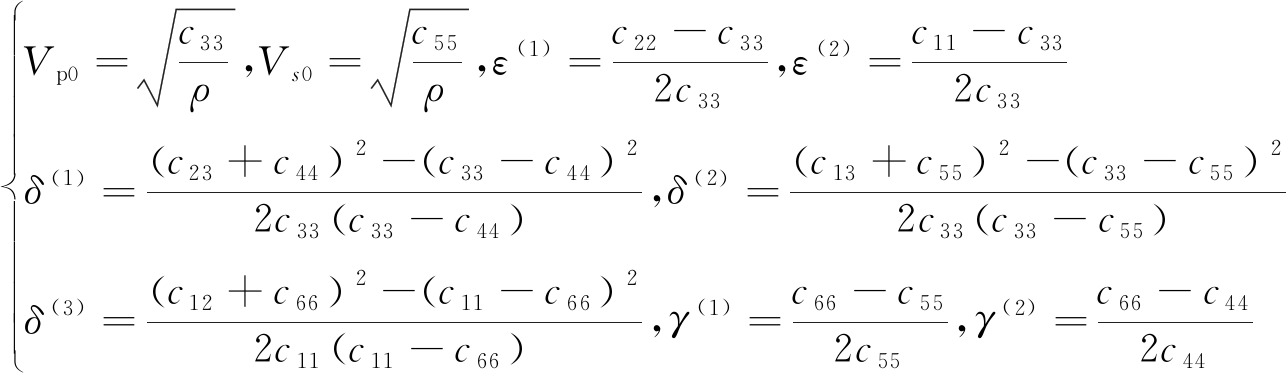
(9)
式中:ε(1)、ε(2)、δ(1)、δ(2)、γ(1)、γ(2)为OA介质各向异性参数,与TI 介质 Thomsen 参数中的意义相同,均为无量纲,上标(1)、(2)、(3)分别表示对应面的法线方向为x、y、z 方向;ε(1)、ε(2)表示P波各向异性程度;δ(1)、δ(2)是影响垂直介质对称轴方向附近的P波速度大小的参数;γ(1)、γ(2)表示横波分裂强度或横波各向异性参数强度的参数;Vp0表示qP波的垂向速度;Vs0表示极化方向在x方向的qS波的垂向速度。

图2 实际各向异性介质模型
Fig.2 Actual anisotropic medium model
OA介质中,在裂隙平面内传播的地震波速度与传播角度有关。当正交各向异性介质的对称轴与坐标轴重合时,地震波沿坐标轴传播时的偏振方向与传播方向平行或垂直,为纯P波、纯SV 波。THOMSEN推导了弱各向异性近似解,用Vp0、Vs0、ε(d)、δ(d)分别描述纯P波、纯SV波在对称面的相速度与相角θ关系[13]分别为
![]()
(10)
其中,![]()
在式(10)中,当d分别取值1、2时,Vp(θ)和VSV(θ)分别表示在垂直对称面和水平对称面上的P波、SV波的相速度。
BERRYMAN[14]指出对称面内群速度Vgr、群角ψ的标量表达式为
(11)
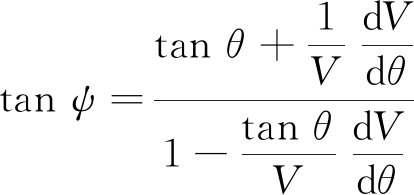
(12)
Thomsen基于弱各向异性近似,用ε(2)、δ(2)在对称面上描述群角与相角关系[15]为
tan ψ=tan θ[1+2δ(2)+4(ε(2)-δ(2))sin2θ]
(13)
相速度是相角的函数,由于在各向异性介质中,射线方向与波矢量的方向不同,群角与相角也就有一个对应关系[3]为
ψ=θ+f(θ)
(14)
其中
(15)
2 不同裂隙参数对煤层裂隙各向异性参数的影响
为了说明Thomsen各向异性参数与裂隙密度、裂隙纵横比的关系,结合式(6)、式(7)、 式(9),计算出OA型裂隙煤层的Thomsen各向异性参数( 表1)。将OA型裂隙煤层干裂隙(气充填)充填物设为气(0.02 GPa)、饱和水(2.25 GPa),裂隙密度变化范围为0.10~0.15、裂隙纵横比变化范围为0.001~0.100;再根据式(9)计算出OA型裂隙煤层各向异性参数,并分析各向异性参数随不同裂隙充填物及其裂隙参数的变化情况(图3)。
OA煤层垂直对称面各向异性参数随裂隙密度、裂隙纵横比变化曲线如图3所示,实线、虚线和点划线分别表示ε(2)、γ(2)和δ(2)曲线,其中图3a、图3c分别为气充填和饱和水裂隙时各向异性参数与裂隙密度关系图,图3b、图3d分别为气充填和饱和水裂隙时各向异性参数与裂隙纵横比关系图。
表1 不同裂隙参数OA型煤层模型裂隙参数
Table 1 OA coal seam model parameter with different fracture parameters

OA煤层裂隙密度介质密度/(g·cm-3)a/c体积模量/GPaε(1)δ(1)γ(1)ε(2)δ(2)γ(2)干裂隙0.10~0.151.310.001~0.1000.02-0.36~-0.28-0.35~-0.040.15~0.13-0.34~-0.23-0.43~-0.30-0.34~-0.23饱水裂隙0.10~0.151.310.001~0.1002.250-0.13~-0.150.13~0.15-0.24~-0.15-0.34~-0.27-0.33~-0.24

图3 OA煤层垂直对称面各向异性参数随裂隙密度、裂隙纵横比变化
Fig.3 Anisotropy of OA coal seam variety with fracture density and fracture aspect ratio
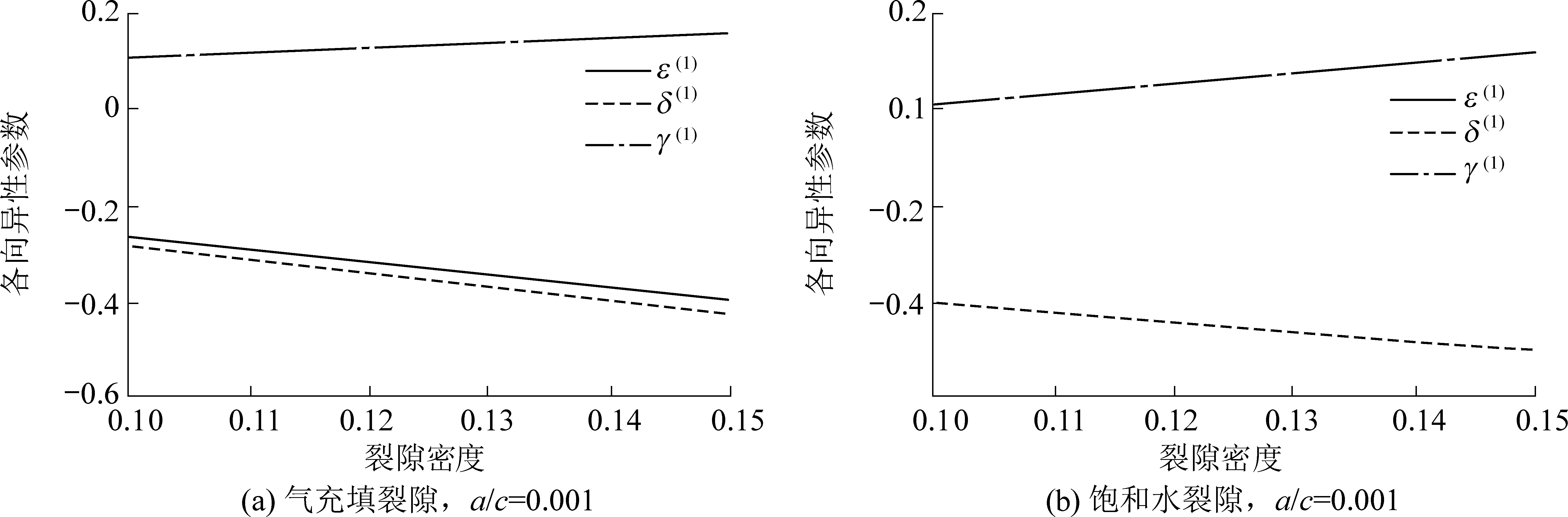
图4 OA煤层水平对称面各向异性参数随裂隙密度变化
Fig.4 Anisotropy of horizontal symmetry plane of OA coal seam variety with fracture density
从图3a可以看出,随着裂隙密度增加,煤层的各向异性参数曲线总体呈单调下降趋势,δ(2)、γ(2)值下降趋势几乎相同,ε(2)值相比前者下降趋势更大,可见随着裂隙密度增大,P波在横向和垂向之间的各向异性程度减弱更明显;从图3b可以看出,随着裂隙纵横比的增加,煤层的各向异性参数ε(2)、δ(2)曲线下降趋势明显,γ(2)曲线基本不变,可见随着裂隙纵横比增大,P波各向异性程度明显减弱;对比图3a和图3b,假设裂隙都是气充填时,可见各向异性参数随着裂隙密度、裂隙纵横比的增大而减小;从图3c可知,随着裂隙密度增加,煤层的各向异性参数曲线总体呈单调下降趋势,γ(2)和δ(2)曲线下降幅度较大,横波各向异性程度随裂隙密度增强;从图3d可知,随着裂隙的纵横比增大,煤层的各向异性参数ε(2)、δ(2)曲线趋势更明显,可见水饱和煤层中,裂隙纵横比增大,煤层各向异性程度更弱;对比图3b和图3d可知,当裂隙纵横比在0.001~0.010变化时,煤层充气裂隙的各向异性程度变化更明显。
OA煤层水平对称面各向异性参数随裂隙密度变化曲线如图4所示,其中,图4a、图4b分别为干裂隙(气充填)、饱和水裂隙各向异性参数与裂隙密度关系 ;从图4a可知,各向异性参数ε(1)、δ(1)随裂隙密度增大而减小,且ε(1)、δ(1)变化曲线相近,可见P波的各向异性程度随裂隙密度增大而减弱;从图4b可知,当裂隙密度增大时,各向异性参数δ(1)、γ(1)分别减小和增大,且ε(1)和裂隙密度无关,可见横波各向异性程度随裂隙密度增大而增强;对比图3a、图3c、图4a可知,当裂隙纵横比比一定时,干裂隙(气充填)和饱和水裂隙煤层中,纵波的各向异性程度都随裂隙密度增大而减弱。
3 OA煤层裂隙等效介质模型速度响应
通过本文的两组裂隙正交等效公式可知:煤层中裂隙密度变化不仅对OA介质的各向异性参数有影响,也对OA介质的群相速度有影响,为了探明煤层裂隙密度变化与OA型煤层速度之间的规律,利用Schoenberg线性滑动模型模拟研究裂隙法向柔度ΔN和切向柔度ΔT变化、速度变化特征和趋势,得到(气充填)干裂隙、饱和水裂隙OA型煤层群、相速度随裂隙密度变化曲线。
根据等效介质模型理论的小裂隙密度假设[20],故纵横比取值为0.001~0.010,基质拉梅系数取值分别为:λ=3.86×109 N/m2、μ=5.5×109 N/m2,而充填OA煤层裂隙气体和液体的体积模量分别为kg=0.02 GPa、kw=2.25 GPa。
表2 不同纵、横波速度的OA煤层模型裂隙参数
Table 2 OA coal seam model parameters with different longitudinal and transverse wave velocities

岩性速度/(m·s-1)纵波横波介质密度/(g·cm-3) 裂隙密度各向异性参数e1e2ε(1)ε(2)δ(1)δ(2)γ(1)γ(2)OA煤层干裂隙1干裂隙2裂隙饱水20151068198768920316891.310.010.1-0.10-0.01-0.04-0.17-0.10-0.130.10.2-0.21-0.11-0.08-0.39-0.10-0.130.10.2-0.002-0.001-0.001-0.36-0.003-0.34
地震波的相速度可以通过解Christoffel方程得到,群速度决定地震射线的分布[21]。群速度又称射线速度,在一定程度上反映波传播的动力学特征[2]。相速度和群速度是认识各向异性地震波传播规律的主要参数,对表2中不同纵、横波速度的OA煤层裂隙模型进行相、群速度进行分析,得到相、群速度关系图,如图5—图9所示:
OA煤层垂直对称面干裂隙(气充填)模型地震波速度如图5所示,对比图5a、图5b、图5c、图5d可知,当煤层裂隙密度e1=0.01,e2=0.1时,群相速度图椭圆率较小,此时OA型煤层垂直对称面干裂隙(气充填)的各向异性程度不强烈;由图6a、图6b、图6c、图6f可知,当煤层裂隙密度e1=0.1,e2=0.2时,P波波前的形状椭圆率较大,且沿长轴方向的速度最大,沿短轴方向的速度小,在90°和270°附近,变化较快,SV波变化比较剧烈。因此,裂隙密度是影响裂隙模型地震波速度各向异性的重要参数,即在实际地层中裂隙诱导是地层各向异性产生的主要成因之一。
OA煤层垂直对称面饱水裂隙模型地震波速度如图8所示,当煤层裂隙密度e1=0.1,e2=0.2时,P波波前的形状为近似菱形,SV波变化剧烈,在45°和135°,出现三分叉区,群速度取值表现为多值现象;对比图6a、图6b、图6c、图6d、图7可知,干裂隙(气充填)模型与饱和水裂隙模型中P波都表现为较强的各向异性,扁率都较大;然而对于SV波,当裂隙充填物为饱和水时,SV波波形剧烈变化,出现明显的三叉区,表现出更强的各向异性。
OA煤层水平对称面干裂隙(气充填)模型地震波速度如图8所示,当煤层裂隙密度e1=0.01,e2=0.10时,P波波前的形状椭圆率较大,且沿长轴方向的速度大,沿短轴方向的速度小,在0°和180°附近,变化较快。
OA煤层水平对称面饱和水裂隙模型地震波速度如图9所示,当煤层裂隙密度e1=0.1,e2=0.01时,群相关系速度图近似为圆形,此时OA煤层水平对称面干裂隙(气充填)模型各向异性程度不强烈;对比图5、图9可知,OA煤层垂直对称面和OA煤层水平对称面,P波、SV波各向异性都表现为弱各向异性。因此,P波对OA煤层裂隙中干裂隙(气充填)、饱水都比较敏感,SV波对OA煤层含水裂隙更敏感,而对气体却不敏感。

图5 OA煤层垂直对称面干裂隙(气充填)模型地震波速度(e1=0.01,e2=0.1)
Fig.5 Seismic wave velocity diagram of vertically symmetrical surface dry fracture (air fill) model in OA coal (e1=0.01,e2=0.1)

图6 OA煤层垂直对称面干裂隙(气充填)模型地震波速度(e1=0.1、e1=0.2)
Fig.6 Seismic wave velocity of vertically symmetrical surface dry fracture (air fill) model in OA coal seam(e1=0.1、e1=0.2)

图7 OA煤层垂直对称面饱水裂隙模型地震波速度(e1=0.1、e1=0.2)
Fig.7 Saturated fracture model of vertically symmetrical plane in OA coal seam & seismic wave velocity(e1=0.1、e1=0.2)
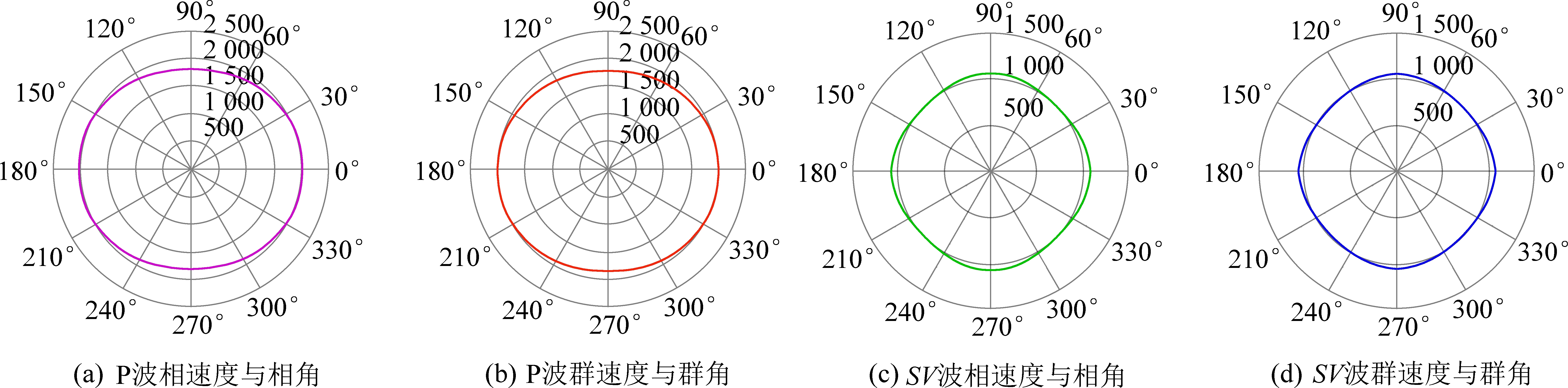
图8 OA煤层水平对称面干裂隙(气充填)模型地震波速度(e1=0.1、e1=0.2)
Fig.8 Seismic wave velocity of horizontal symmetrical surface dry fracture (air fill) model in OA coal seam(e1=0.1、e1=0.2)

图9 OA煤层水平对称面饱和水裂隙模型地震波速度(e1=0.1、e1=0.2)
Fig.9 Seismic wave velocity of saturated water fracture model of horizontal symmetric plane in OA coal seam(e1=0.1、e1=0.2)
4 结 论
通过在OA煤层裂隙模型中引入Schoenberg线性滑动模型,分析了各向异性参数在不同裂隙流体充填、不同裂隙密度以及不同裂隙纵横比情况下的变化特征,并通过地震波速度研究了裂隙特征与地震波各向异性的关系,可得到如下结论:
1)在给定理论模型中,当裂缝纵横比一定时,煤层裂缝中充填不同流体时,各向异性参数随着充填流体体积模量的增大而减小;当裂隙密度一定时,煤层裂缝中充填不同流体时,各向异性参数随着充填流体体积模量的增大而增大。
2)OA煤层干裂隙(气充填)和饱和水裂隙模型中P波都表现出较强的各向异性;干裂隙(气充填)模型SV波波前的形状近似为方形,饱水裂隙模型SV波波前出现三叉区变化剧烈。即此类介质中P波对OA煤层裂隙中干裂隙(气充填)、饱水都比较敏感,SV波对OA煤层含水裂隙更敏感,而对气体却不敏感。
3)论文通过正交等效裂隙方法,从地震波速度方面分析了不同裂隙煤层的地震波速度响应特征,论证了对煤层裂隙利用两组正交裂隙等效模型分析是可行的,并为地震波正交各向异性分析提供数据选择建议。
[1] 戴世鑫.基于物理模型的煤田地震属性响应特征的关键技术研究[D].北京:中国矿业大学(北京),2012.
[2] 李 娜.正交各向异性介质正演模拟方法及波场特征分析[D].青岛:中国石油大学(华东),2014.
[3] BAKULIN A,GRECHKA V,TSVANKIN I.Estimation of fracture parameters from reflection seismic data(Part I): HTI model due to a single fracture set[J].Geophysics,2000,65(6):1788-1802.
[4] 秦海旭.基于各向异性理论的裂隙介质正反演方法研究[D].青岛:中国石油大学(华东),2015.
[5] HUDSON J A.Wave speeds and attenuation of elastic waves in material containing cracks[J].Geophysical Journal International,1981,64(1):133-150.
[6] THOMSEN L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966.
[7] SCHOENBERG M,DOUMA J.Elastic wave propagation in media with parallel fractures and aligned cracks[J].Geophysical Prospecting,1988,36(6):571-590.
[8] BAKULIN A,GRECHKA V,TSVANKIN I.Estimation of fracture parameters from reflection seismic data,Part I:HTI model due to a single fracture set[J].Geophysics,2000,65(6):1788-1802.
[9] 刘 财,迟唤昭,高 炜,等.裂缝诱导双相HTI介质地震波场错格伪谱法模拟与波场特征分析[J].地球物理学报 ,2016,59(5):1776-1789.
LIU Cai,CHI Huanzhao,GAO Wei,et al. The cracks induced bipolar HTI medium seismic wave field anacoluthon pseudo-spectral method of simulation and analysis of characteristics of wave field[J].Journal of Geophysics,2016,59(5):1776-1789.
[10] 刘 财,兰慧田,郭智奇,等.基于改进BISQ 机制的双相HTI介质波传播伪谱法模拟与特征分析[J].地球物理学报,2013,56(10):3461-3473.
LIU Cai,LAN Huitian,GUO Zhiqi et al.Simulation and characteristic analysis of dual-phase HTI dielectric wave propagation pseudo-spectral method based on improved BISQ mechanism[J].Journal of Geophysics,2013,56(10):3461-3473.
[11] 刘东洋,师素珍,赵太郎.裂隙等效介质模型对煤层裂隙参数的影响[J].矿业科学学报,2017,2(1):7-16.
LIU Dongyang,SHI Suzhen,ZHAO Tailang.The influence of fracture effective model to the parameters of coal fracture[J].Journal of Mining Science and Techology,2017,2(1):7-16.
[12] 裴正林,董玉珊,彭苏萍.裂隙煤层弹性波场方位各向异性特征数值模拟研究[J].石油地球物理勘探,2007,42(6):665-672.
PEI Zhenglin,DONG Yushan,PENG Suping.Numerical simulation of azimuthal anisotropy of elastic wave field in fractured coal seam[J].Petroleum Geophysical Exploration,2007,42(6):665-672.
[13] TSVANKIN I.Anisotropic parameters and P-wave velocity for orthorhombic media[J].Geophysics,1997,62(4):1292-1309.
[14] BERRYMAN J G.Long-wave elastic anisotropy in transversely isotropic media[J].Geophysics,1979,44(5): 896-917.
[15] 熊金良,刘 洋,侯伯刚.任意各向异性介质方位旅行时正演[J].石油地球物理勘探,2005,40(3):300-304.
XIONG Jinliang,LIU Yang,HOU Bogang.Forward modeling for travel in any anisotropic medium[J].Petroleum Geophysical Exploration,2005,40(3):300-304.
[16] 唐志远,杨延强,刘国昌.基于双重孔隙结构的煤层气储层震波速度预测研究[J].煤炭科学技术,2018,46(12):187-191.
TANG Zhiyuan,YANG Yanqiang,LIU Guochang.Study on prediction on seismic wave velocity in coalbed methane reservoir based on dual pore structure[J].Coal Science and Technology,2018,46(12):187-191.
[17] SCHOENBERG M.Elastic wave behavior across linear slip interfaces[J].The Journal of the Acoustical Society of America,1980,68(5):1516-1521.
[18] SCHOENBERG M,SAYERS C M.Seismic anisotropy of fractured rock[J].Geophysics,1995,60(1):204-211.
[19] 桂俊川,陈 平,马天寿.正交各向异性岩石弹性参数的空间展布[J].西南石油大学学报:自然科学版,2019,41(3):13-28.
GUI Junchuan,CHEN Ping,MA Tianshou.The spatial distribution of elastic parameters of orthotropic rocks[J].Journal of Southwest Petroleum University:Science & Technology Edition,2019,41(3):13-28.
[20] 帅 达,魏建新,狄帮让,等.等效介质理论中裂缝密度的适用性研究[J].地球物理学报,2019,62(7):2697-2710
SHUAI Da,WEI Jianxin,DI Bangrang et al.Physical modeling of the influence of crack density on the accuracy of effective medium theory[J].Journal of Geophysics,2019,62(7):2697-2710.
[21] 杜丽英,刘国明,杜丽娟.VTI介质中地震波反射波合成记录的方法研究[J].地球物理学进展,2001(2):58-64.
DU Liying,LIU Guoming,DU Lijuan,et al.Synthetic recording method of seismic wave reflection inVTI medium[J].Progress in Geophysics,2001(2):58-64.
