0 引 言
破碎机主要应用于矿山开采、建筑、煤炭开采、冶金、热电等行业中,其中双齿辊式破碎机以其结构简单、工作可靠、成本低廉等特点得到了广泛应用。矿用破碎设备对各种石材或者煤炭等完成破碎操作,依照破碎的机制以及破碎后相关颗粒物尺寸的差异能够划分成多种类型[1]。在破碎煤炭时通常使用的破碎机型式包括反击式、颚式、立式冲击型、锤式型、辊式、环锤式、圆锥式、旋回式、移动式等[2]。不同型式的破碎机工作原理也不尽相同。
双齿辊破碎机作为一种较新型的矿用破碎机,主要适用于矿石的中细碎作业,对于中等硬度以下的脆性材料具有较好的破碎效果。双齿辊破碎机中有2个平行安装的破碎辊,其中间的下方装有破碎棒,当2个破碎辊进行相对转动时,物料由于受到剪切力和拉伸力作用而发生破碎。刘伯元等[3]对新型双齿辊破碎机的矿石破碎理论研究发现,由于双齿辊破碎机主要对物料进行剪切和拉伸作用,因而相比其他只依靠挤压破碎的破碎机,双齿辊破碎机充分利用了脆性材料抗拉应力低的特点。双齿辊破碎机适合大粒度物料的破碎,破碎后的物料粉末率较低,并能有效控制产品粒度;且其运转速度较低,工作部件磨损较小,运转噪声低、灰尘少[4],因而在工程中得到越来越广泛的应用。
离散单元方式是CUNDALL P A等[5]在20世纪70年代以分子动力原理为基础提出的对颗粒物相互作用进行探究的一种方法,该方法中颗粒之间的内部作用力在任何时候均处于平衡状态,对单个颗粒运动轨迹进行追踪,可获得整个聚集体的位移大小与力的具体数值。OTSUBO M等[6]讨论了离散元仿真的时间步长在不同情况下的求解方法。田震等[7]利用离散元技术,通过跟踪和统计装煤过程中颗粒速度、质量计算出螺旋滚筒的转给效率。张科芬等[8]改进了三维离散元模型在破碎过程中的破碎准则,并证明了考虑应力集中效应的点载荷破碎准则,相比基于平均应力Mohr-Coulomb理论的颗粒破碎准则,更能真实反应颗粒材料的破碎现象。AKIMOV P等[9]则通过离散元和有限元结合的方法对实际的结构问题进行求解。贺安民[10]采用EDEM离散元软件模拟截齿液压冲击与截割联合破煤岩的过程,分析有无冲击预裂的破煤岩性能。
目前离散单元法在解决颗粒破碎相关的实际工程问题时得到了越来越广泛的应用[11-15],但对于颗粒直径、齿辊转速等影响因素对破碎过程及结果的规律性探究还有待补充。笔者采用离散单元法分析双齿辊破碎机对物料的破碎过程,将颗粒的接触模型简化为振动运动模型,推导各分力的计算式。采用网格法对颗粒接触模型中颗粒位置进行检索,判断其接触状态。对最新设计制造的双齿辊式破碎机的燃煤颗粒粉碎过程进行仿真,获得破碎齿在整个过程的受力情况,并分析颗粒直径、齿辊转速对破碎齿受力的影响规律。
1 离散单元法仿真分析模型与算法
1.1 模型基本假设
对双齿辊破碎机的仿真模型建立均基于如下假设:
1)颗粒接触模式为软颗粒接触。
2)所有颗粒在每一个接触处的变形之和等效为整体颗粒系统的变形。
3)颗粒间的接触面积忽略不计,每一个接触均视为在一点处产生。
4)在每个周期范围中,搅动很难从任意一个颗粒同时扩散到同它紧邻的颗粒中。
1.2 接触模型的建立
颗粒经过运动产生碰撞作用并迅速借助运动完成传播,离散单元法能够明确阐述碰撞发生时的整个过程。接触形式能够被划分成2类,一种是硬颗粒接触,另一种是软颗粒接触。前者可以看作是设定某个颗粒表层接受的应力相对偏低的时候,颗粒彼此间不存在明显的变形情况,而且假定颗粒彼此间发生的碰撞是短暂的,该方式重点使用在稀疏快速颗粒流领域;后者可以看作是允许存在某个接触位置有重叠的区域,借助弹性变量以及阻尼变量针对颗粒间接触情况完成简化操作,一般设定在整个接触时期的所有变量都是恒定的,不关注个别细节问题,依据颗粒之间存在的重叠情况运算出相关的接触力大小,运算总量显著降低。在仿真双齿辊破碎机的破碎情况时采用软颗粒接触模型。
软颗粒接触模型一般借助一对大小一致方向相反的力,将受力位置的重叠部分、冲击速率、接触粒子的物理特性以及时间幅度等有关数据进行合理整合,运算出对应颗粒上的合力。并以牛顿第二运动定律为基础,计算相关加速度、速度以及位移信息。
软颗粒接触模型依据两颗粒之间接触位置的重叠区域来计算作用力大小,将两颗粒记作P1、P2,并定义P1、P2质心的连线为法线,将重叠区域产生的作用力分解为法向力和切向力,法向力简化为弹簧和阻尼器的组合,切向力简化为弹簧、阻尼器和滑动器的组合[16]。通过上述分解便可在计算时将颗粒之间的接触化为振动运动过程进行模拟,如图1a和图1b所示。

图1 接触模型简化为振动运动模型
Fig.1 Contact model is simplified to vibration motion model
接触模型转化为振动运动模型后,以块体或颗粒为单元,通过循环计算,对颗粒的移动状态进行追踪。基于牛顿运动定律的更迭,对动态进程里各颗粒之间在每一时间步长的彼此受力情况进行计算,以评估离散群体的行为。针对离散单元法的迭代过程, COETZEE C J等[17-18]对颗粒在该过程中材料参数的标定方法及这些参数对仿真接触模型的影响进行总结。对在每一时间步长计算开始前,需要从前处理输入或从上一时间步长结果提取颗粒属性参数。之后将两颗粒间的作用力分解为颗粒间法向力F、法向阻尼力![]() 切向力Ft、切向阻尼力
切向力Ft、切向阻尼力![]() 和滚动摩擦力矩T,如图1所示。
和滚动摩擦力矩T,如图1所示。
在求解上述力之前,通过初始条件参数依次计算中间变量。法向重叠量α为
α=R1+R2-r1-r2
(1)
式中:R1、R2为两球形颗粒半径,r1、r2为两颗粒球心位置矢量。
等效粒子半径R*为
(2)
粒子接触半径a为
(3)
切向重叠量δ为
δ=2a
(4)
等效弹性模量E*为
(5)
式中:E1、E2分别为两颗粒的弹性模量;υ1、υ2分别为两颗粒的泊松比。
等效剪切模量G*为
(6)
式中:G1、G2分别为两颗粒的剪切模量。
阻尼系数β为
(7)
式中:е为颗粒间恢复系数。
法向刚度Sn为
(8)
切向刚度St为
(9)
在获得上述中间变量值之后,结合初始参数计算颗粒间作用力各分力的值。颗粒间法向力为
(10)
法向阻尼力为
(11)
其中:m*为两颗粒等效质量;![]() 为两颗粒相对速度的法向分量。颗粒间切向力为
为两颗粒相对速度的法向分量。颗粒间切向力为
Ft=-Stδ
(12)
切向阻尼力为
(13)
在上述公式中,![]() 为2个颗粒相对速度的分量(切向)。滚动摩擦力矩为
为2个颗粒相对速度的分量(切向)。滚动摩擦力矩为
T=-μrFnRωi
(14)
式中:μr为粒子之间的滚动摩擦因数;R为粒子的质心与接触点之间的间距;ωi为粒子在前一步中的转动速度分量。
假设在时间步长Δt内颗粒间作用力不变,将上一步中计算出的颗粒间作用力分量合成为合力F(t)和合力矩T(t),再将其分解为沿x、y、z(其中z为齿辊轴向,垂直于z轴的平面内水平向右为x轴正方向,竖直向上为y方向)三个坐标方向的分量Fi(t)和Ti(t)(其中i=1、2、3,分别表示沿x、y、z三个坐标方向的分量)。
根据牛顿第二定律,可得出以下方程,反应了粒子的运动状态,公式运用了欧拉算法。
(15)
(16)
式中:vi(t)为颗粒在t时刻的平动速度分量;ωi(t)为颗粒在t时刻的转动速度分量;m为颗粒质量;gi为重力加速度分量(其中i=1、2、3,分别表示沿x、y、z三个坐标方向的分量);I为颗粒的转动惯量。
将式(15)、式(16)转换为时间步长Δt的迭代形式,得
(17)
(18)
则速度及角速度迭代公式为
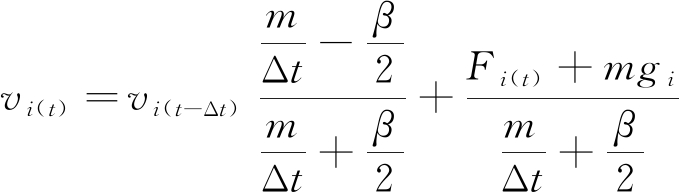
(19)
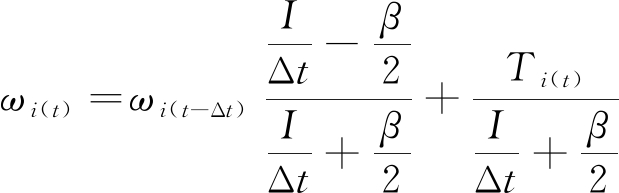
(20)
t时刻颗粒的平动位移ui(t)和转动位移θi(t)为
ui(t)=ui(t-Δt)+vi(t)Δt
(21)
θi(t)=θi(t-Δt)+ωi(t)Δt
(22)
将t时刻颗粒的平动位移和转动位移作为下一时间步长的初始参数,继续循环上述过程直至求解完毕。
1.3 颗粒接触检索方法
对颗粒物质的行为进行模拟,应考虑颗粒之间因重叠而产生的接触力,根据重叠的量计算出接触力,再根据运算出的结果依次对各颗粒的位置和速率进行修正,进而实现明确优化整体颗粒架构的目标。颗粒之间有没有产生重叠,应根据各颗粒的所在位置进行多次运算,运算量很大,所以,明确地判断颗粒之间有没有存在接触是首先要关注的问题。
如何提升颗粒离散单元模拟的运算效率,其最重要的技术就是接触快速检索技术。在现有的离散单元法模型中,对于颗粒接触的检索分为粗略判别和详细判别2个阶段。在进行粗略判别时,把全部占用的空间规划成三维的立体网格,所有颗粒都有特定的相关立方体网格对应,将颗粒所在的网格位置与其相邻的网格之间可能存在的接触关系的识别建立相应的方法;在详细判别阶段,对紧邻网格当中的颗粒之间距离进行检索操作,明确其是否发生接触。
将全部运算部分规划成若干正方体或者正方形网格,网格每边的长度lbox和粒子直径最大值dmax依照下式确定:
dmax<lbox<2dmax
(23)
根据颗粒物占用的区域,将相关颗粒完成分配工作,划分到具体的网格中,如图2所示。
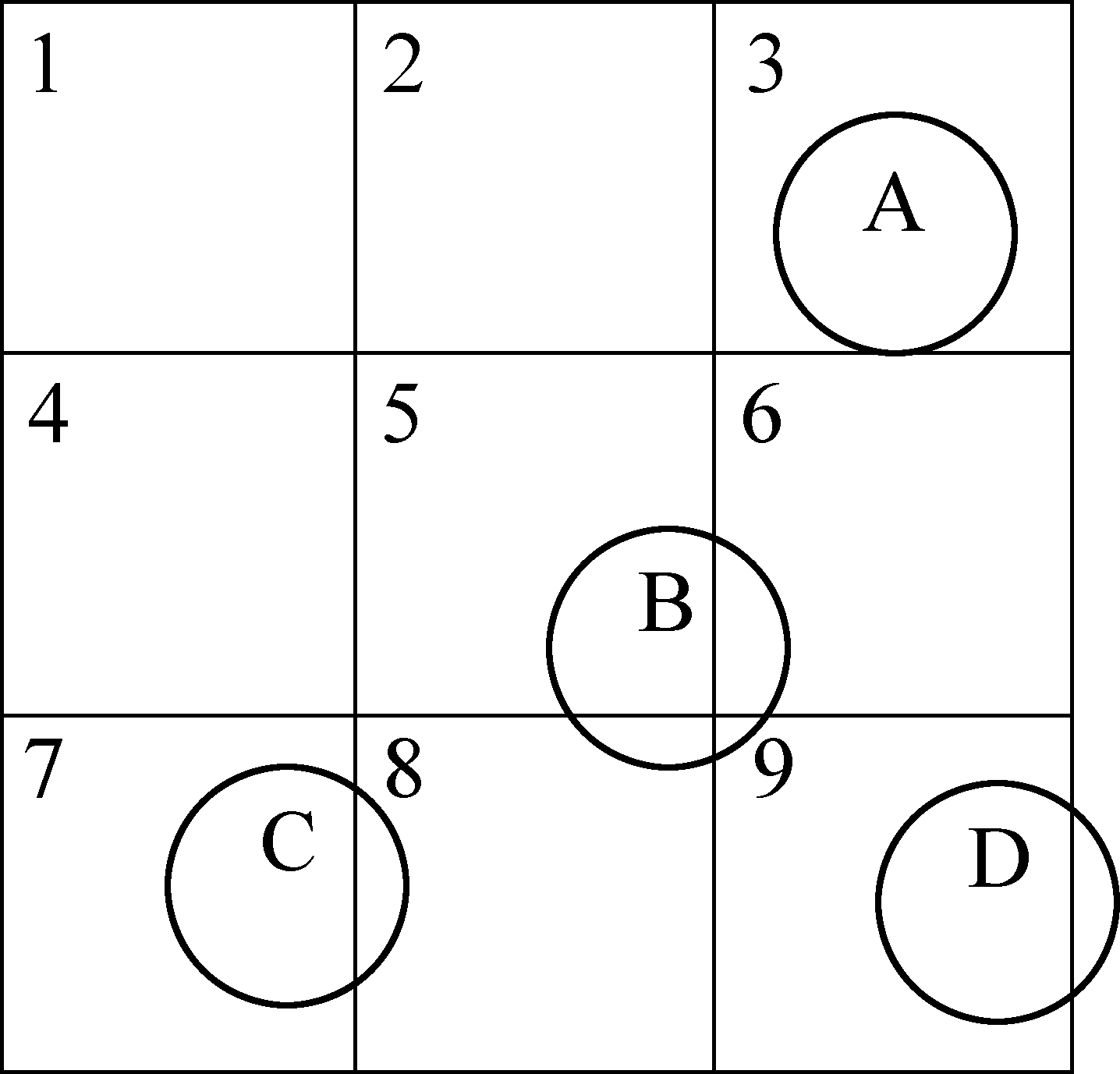
图2 网格法搜索颗粒接触状态
Fig.2 Searching contact particles state by mesh method
图2中的所有颗粒均保证至少有1个网格进行对应,在二维项目中运行某个颗粒最多占用4个网格(比如颗粒B)。在关于某个颗粒是否存在同其余颗粒有对应接触关系的判别中,仅需要针对这个网格中的其余颗粒完成运算判别即可,如图2所展示的颗粒B和C,都处在网格8中,就有可能会发生接触,而颗粒C和A则不会发生接触。上述网格探索方式简单快捷,能够满足相关程序的要求。
网格尺寸过大易导致误检,而过小则运算时间长。假定最小颗粒直径为30 mm,且存在多种不同直径的颗粒,将网格边长在30~69 mm区间内每增大3 mm作为1组,对每组网格进行仿真对比,得出运算时间与网格尺寸大小的关系,如图3所示。
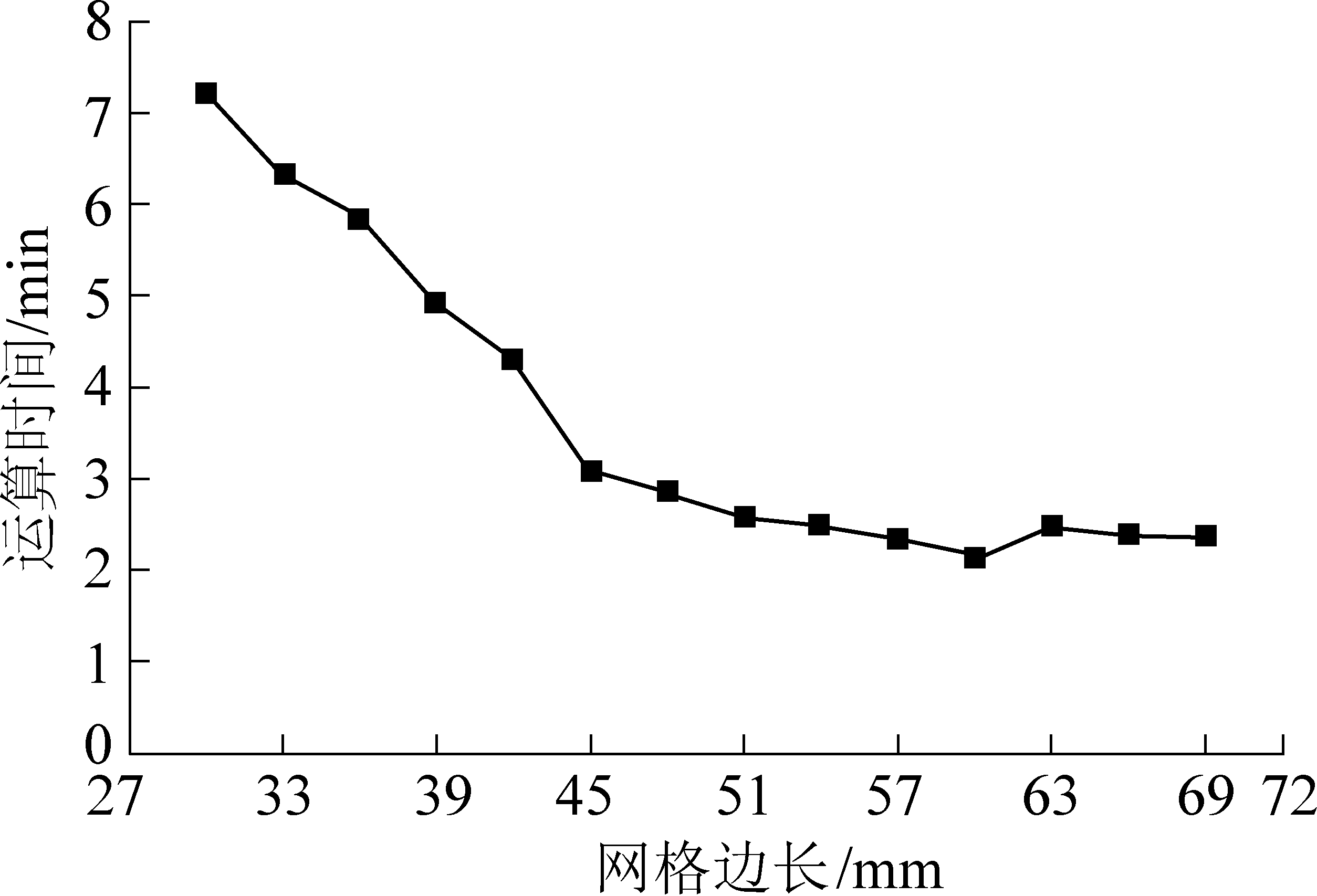
图3 运算时间随网格边长变化
Fig.3 Operation time varies with mesh size
运算时间随网格尺寸的增大而减少。网格边长为60 mm,即2倍最小颗粒直径尺寸时运算用时较短。当尺寸继续变大时,运算时间变化不大,且在理论上有出现漏算接触的可能。因此计算时将网格边长定为2倍最小颗粒直径。
2 双齿辊破碎机仿真模型建立
双齿辊破碎机在破碎过程中破碎的物料是燃煤,对应的破碎机制是一个相对复杂的受力分析过程。赵丽梅等[19-20]对反击式破碎机使用数值仿真的方法分析了破碎机在破碎时的受力,并对破碎机的尺寸进行了参数优化。笔者将通过数值仿真的方式,采用离散单元法对新型双齿辊式破碎机在破碎过程中的受力进行分析。
2.1 破碎机实体模型
双齿辊破碎机来自大唐环境产业集团股份有限公司为大唐平罗火电工程输煤项目提供的无尘筛碎一体机,该机器的一级破碎段模型如图4所示。

图4 破碎机实体模型正视图
Fig.4 Front elevation of crusher model
破碎机的外部带式输送机把燃煤输送到破碎机入料漏斗顶部,燃煤沿漏斗进入机体内,燃煤的入料粒度要求为颗粒直径小于300 mm。大块燃煤因重力作用落入由主破碎辊、导料板与反击辊组成的破碎腔。通过一级粗破碎辊高速转动破碎,将大尺寸燃煤破碎成30 mm以下粒径的燃煤颗粒。
两齿辊中心距为683.63 mm,主破碎辊沿顺时针方向旋转,转速为41.65 rad/s;反击辊沿逆时针方向旋转,转速为128.73 rad/s。燃煤颗粒在入料漏斗最顶部的平面生成,在重力作用下沿漏斗落入破碎腔中。
2.2 模型材料参数
燃煤和破碎机钢材的材料参数见表1。
表1 材料参数
Table 1 Material parameters

材料密度/(kg·m-3)剪切模量/MPa弹性模量/MPa泊松比 燃煤2.5×1031.953.50×1030.25钢材7.9×1037.94×1042.06×1050.30
燃煤与钢结构之间的恢复系数为0.5,静摩擦因数为0.4,滚动摩擦因数为0.05。燃煤颗粒之间的恢复系数为0.5,静摩擦因数为0.6,滚动摩擦因数为0.05。
煤炭自身的平均孔隙率为33.43%,内摩擦角为38.1°,内部黏聚力为0.36 MPa,平均耐崩解指数为81.1%,抗压强度为1.95 MPa。
2.3 颗粒破碎过程设置
在用离散单元法仿真破碎问题时,通常采用的方法有绑定法和替代法,其中替代法使用更为广泛,如LUO T等[21]使用了无黏结介质的颗粒破碎模型替代原模型的方法仿真颗粒的破碎过程。笔者使用的替代法是在仿真颗粒破碎时将颗粒模型替换为许多破碎后的小颗粒的集合,替换后在小颗粒之间生成Hertz-Mindlin黏结接触模型。该接触模型能绑定2个小颗粒之间的相对位移,使其以一个整体的形态运动来仿真破碎前煤炭颗粒的运动方式。在受到外力作用时,该接触模型会不断累积受到的法向应力和切向应力。当接触累积的法向应力或切向应力到达预设的崩解值时,该接触将被破坏,使自身绑定的2个小颗粒分离。通过这种方式来仿真煤炭颗粒在破碎机内不断积累损伤最终被破碎的过程,如图5所示。
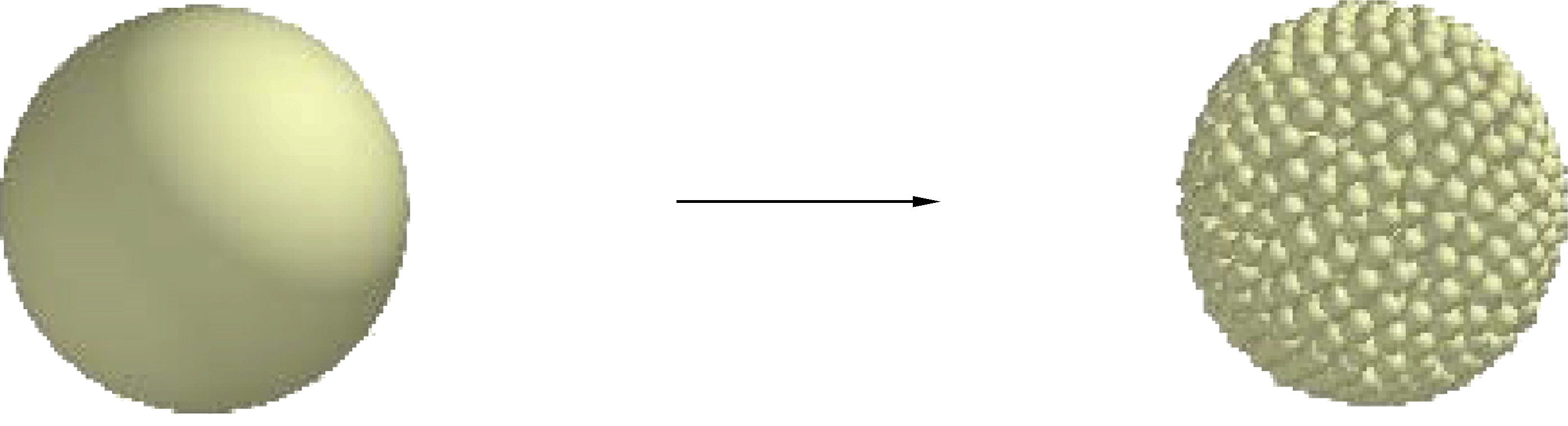
图5 颗粒模型替换
Fig.5 Replacement of particle model
在破碎机的入料漏斗顶部平面内的随机位置生成500颗煤炭颗粒,并让其在重力作用下落入破碎腔。在煤炭颗粒进入破碎腔前完成对煤炭颗粒的替换,并仿真替换之后的颗粒模型在破碎腔内的破碎过程,如图6所示。

图6 破碎机破碎过程仿真
Fig.6 Crushing process of the crusher
3 双齿辊破碎机仿真结果
分析破碎过程中单排破碎齿的受力,并研究燃煤颗粒直径和齿辊转速对单排破碎齿受力大小的影响,对不同尺寸颗粒直径和不同齿辊中心距进行仿真分析,研究尺寸变化时受力的影响。
3.1 双齿辊破碎机破碎力仿真结果
仿真完成后,在后处理界面中选取破碎机实体模型中的单排破碎齿,提取该排破碎齿在整个破碎过程中所受到的破碎力随时间变化曲线,如图7所示。
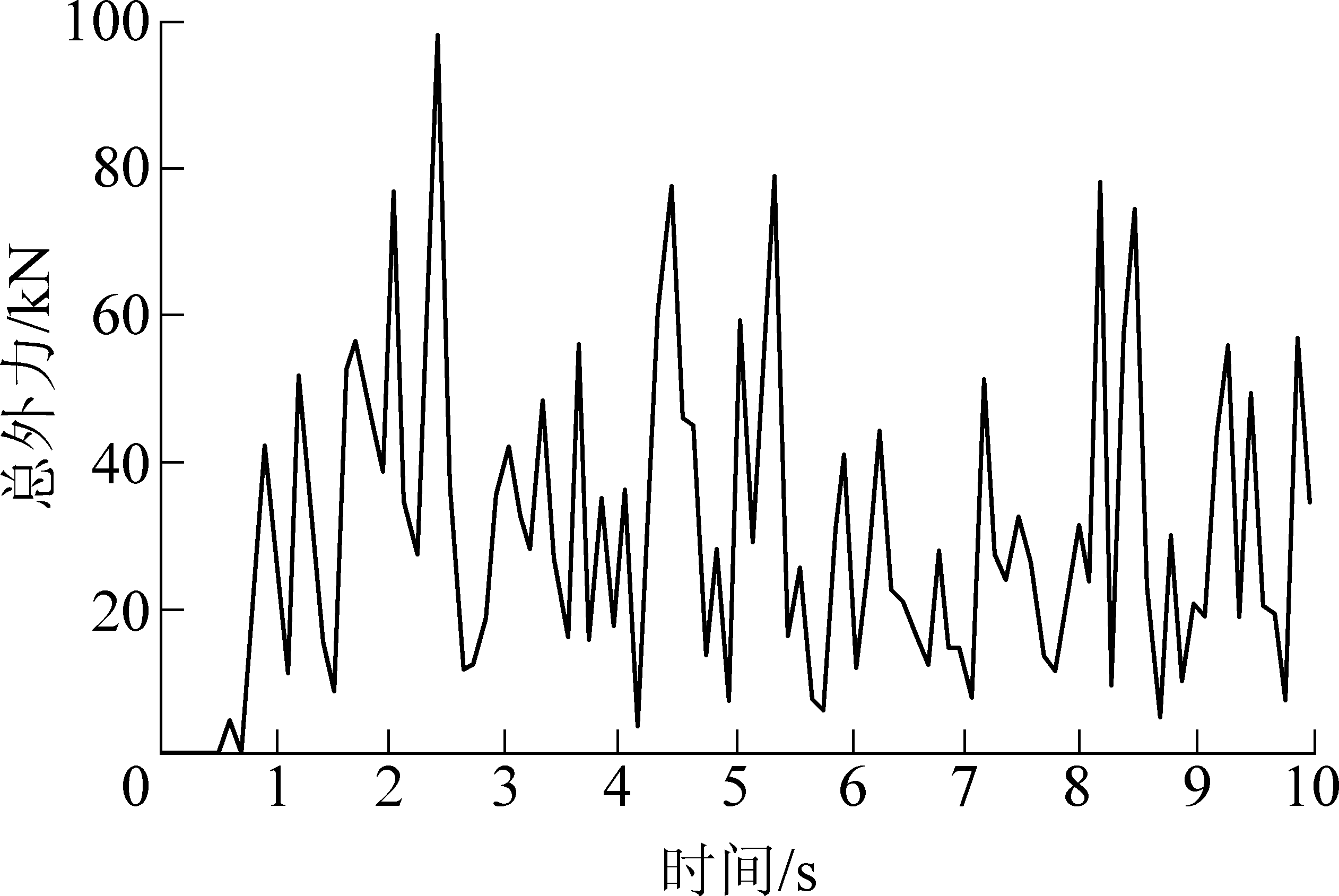
图7 单排破碎齿破碎力仿真结果
Fig.7 Simulation results of crushing force on single row crushing teeth
根据仿真结果得到,双齿辊破碎机在正常运转过程中,单排的破碎齿所受的破碎力载荷在不断变化,其中受力的最大值为98 457 N。将破碎力仿真结果的最大的10个极大值进行记录,这10组数据的最小值为76 918 N,10组数据的平均值为81 967 N。因此,单排破碎齿在正常运转过程中承受的最大载荷为98 457 N,平均载荷为81 967 N。
为了验证仿真结果,这里使用经验公式对其进行验证。根据文献[22]总结的双齿辊破碎机破碎齿在破碎过程中的受力计算公式,单个破碎齿在破碎过程中的受力F为
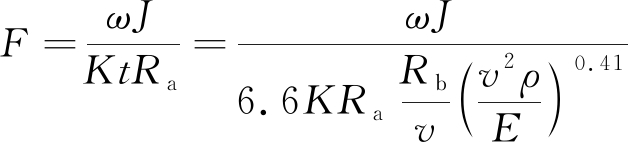
(24)
其中:ω为齿辊角速度;J为破碎齿转动惯量;Ra为齿尖轨迹半径;Rb为颗粒破碎前平均半径;v为齿尖线速度;ρ为颗粒密度;E为颗粒弹性模量;K为修正系数,通常取值为0.5。由第2.1节中的实体模型参数及第2.2节中的材料参数可知,齿辊角速度为41.65 rad/s,破碎齿转动惯量为39.4×10-3 kg/m2,齿尖轨迹半径为0.51 m,颗粒破碎前平均半径为0.06 m,齿尖线速度为21.26 m/s,颗粒密度为2.5×103 kg/m3,颗粒弹性模量为3.5×109 Pa。将以上数据代入式(24)可算得单个破碎齿受力为9 326.3 N。
由笔者仿真所得单排破碎齿平均载荷为81 967 N,破碎机单排共含有8个破碎齿,因此每个破碎齿所受的平均载荷为10 246 N,仿真计算结果比上述经验公式计算值大9%。
3.2 燃煤颗粒直径的影响
由于入料漏斗的出口尺寸限制,若颗粒过大,则不能进入破碎区域;若颗粒过小,则在重力作用下无法完成在破碎区域的堆积,因此仿真颗粒直径范围设定为35~80 mm。将颗粒直径以5 mm为间隔分为10组。考虑到仿真时颗粒生成位置具有一定的随机性,因此每组做10次仿真并取平均值,得到单排破碎齿在破碎时所受的反作用力随颗粒直径变化规律,如图8所示。
由图8可以看出,随着颗粒直径的增大,单排破碎齿受力也逐渐增大,并且单排破碎齿在破碎期间受力的最大值与最小值之间的差值也逐渐增大。
3.3 齿辊转速的影响
由于笔者所用的破碎机模型在实际应用中的额定转速为397 r/min,所以将齿辊转动速度的数值设置为100~900 r/min,以100 r/min为间隔分为9组。由于反击辊在设计时被要求与齿辊转速相同,所以齿辊转速增大时,反击辊转速也随齿辊转速一同增大。考虑到仿真时颗粒生成位置具有一定的随机性,因此每组做10次仿真并取平均值。得到单排破碎齿受力随齿辊转速变化规律,如图9所示。
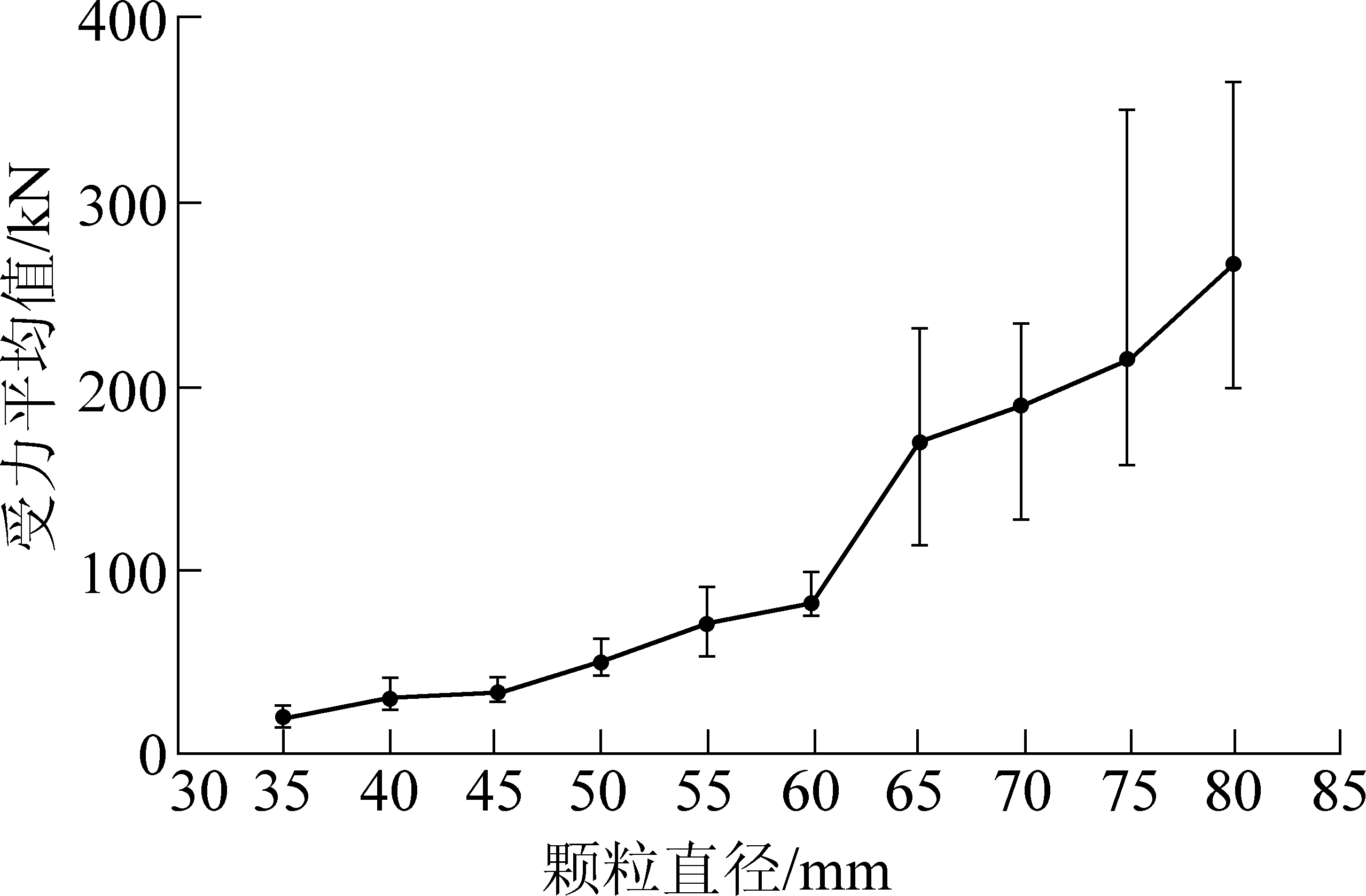
图8 单排破碎齿受力随颗粒直径变化
Fig.8 Crushing force of one row teeth varies with particle diameter
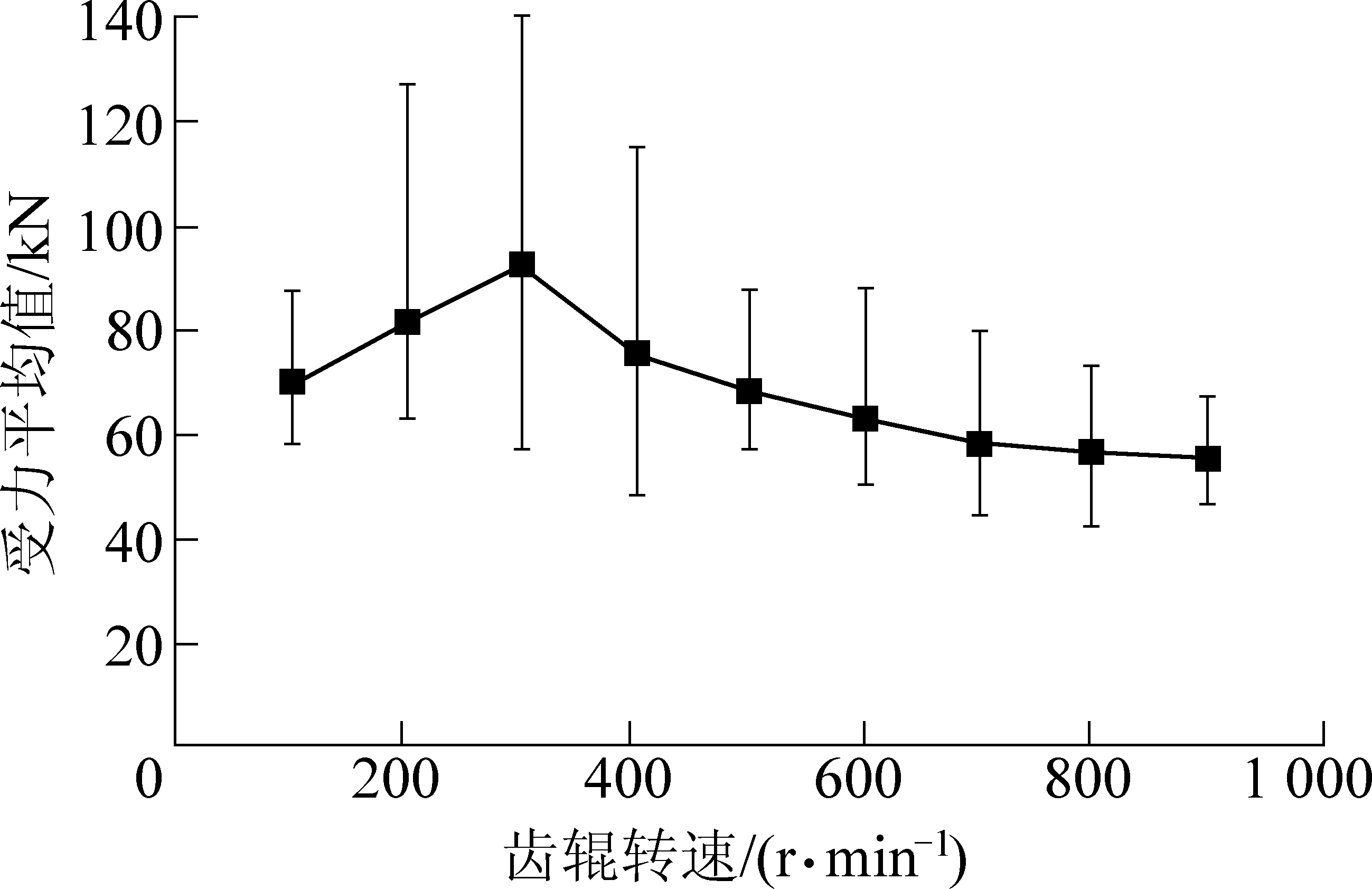
图9 单排破碎齿受力随齿辊转速变化
Fig.9 Crushing force of single row teeth varies with roller speed
由图9可以看出,随着齿辊转速的增大,单排破碎齿受力先增大后减小,并且单排破碎齿在破碎期间受力的最大值与最小值之间的差值也先增大后减小。单排破碎齿受力的峰值出现在齿辊转速为300 r/min时。当转速小于该值时,单排破碎齿受力随转速增加而增大;但当转速大于该值时,转速增加导致齿与颗粒未能充分接触,破碎力随之有所下降,因此,采用适当的转速会有较高的破碎效率。但在破碎齿受力大的区域破碎力差值也大,即破碎力的稳定性降低,因此该破碎机在实际应用中使用397 r/min作为其额定转速。
4 结 论
应用Hertz-Mindlin无滑动接触模型以及Hertz-Mindlin黏结接触模型相结合的离散单元法,对大唐环境产业集团股份有限公司所提供的无尘筛碎一体机中一级破碎段的破碎过程进行仿真分析。讨论了2种主要参数对齿辊在破碎过程中受力的影响。主要结论如下:
1)当破碎颗粒含有多种颗粒尺寸时,将网格的边长尺寸定为最小颗粒直径的2倍。可以在保证尽量不漏算接触的前提下使运算时间较短。
2)对YLWP+S1000-1500WX新型双齿辊破碎机进行了破碎过程的数值仿真,得到其一级粗破碎辊上的单排破碎齿在破碎正常煤矿时中承受的最大破碎力载荷为98 457 N,平均破碎力载荷为81 967 N。
3)燃煤颗粒直径增大,单排破碎齿受力也逐渐增大。破碎过程中单排破碎齿受力的最大值和最小值之间的差值,也随着颗粒直径的增大逐渐变大。
4)齿辊转速增大,单排破碎齿受力趋势为先增大后减小。破碎过程中单排破碎齿受力的最大值和最小值之间的差值也随之先增大后减小。
[1] 蔡 鹏.基于离散元的双齿辊破碎机破碎性能分析与齿形优化[D].长沙:湖南大学,2014.
[2] 田文剑.矿用双齿辊破碎机结构设计与强度分析[D].鞍山:辽宁科技大学,2015.
[3] 刘伯元,杨传忠.MMD型轮齿式破碎机:矿石破碎理论的突破[J].中国非金属矿工业导刊,2003(2):36-38,41.
LIU Boyuan,YANG Chuanzhong.MMD gear crusher:a breakthrough in the theory of ore crushing[J].China Non-Metallic Mining Industry Herald,2003(2):36-38,41.
[4] 孙成林.破碎机的最新发展[J].中国粉体技术,2000(2):32-39.
SUN Chenglin.The latest development of crusher[J].China Powder Science and Technology,2000(2):32-39.
[5] CUNDALL P A,STRACK O D L.A discrete numerical model for granular assemblies[J].Géotechnique,1979,30:331-336.
[6] OTSUBO M,O'SULLIVAN C,SHIRE T.Empirical assessment of the critical time increment in explicit particulate discrete element method simulations[J].Computers & Geotechnics,2017,86:67-79.
[7] 田 震,赵丽娟,周文潮,等.离散元技术在螺旋滚筒装煤性能研究中的应用[J].煤炭科学技术,2018,46 (8):135-139.
TIAN Zhen,ZHAO Lijuan,ZHOU Wenchao,et al.Application of discrete element technology to study on coal loading performances of spiral cutting drum[J].Coal Science and Technology,2018,46(8):35-139.
[8] 张科芬,张 升,滕继东,等.颗粒破碎的三维离散元模拟研究[J].岩土力学,2017,38(7):2119-2127.
ZHANG Kefen,ZHANG Sheng,TENG Jidong,et al.3D numerical simulation of particle breakage using discrete element method[J].Rock and Soil Mechanics,2017,38(7):2119-2127.
[9] AKIMOV P,NEGROZOV O A.Semianalytical solution of multipoint boundary problems of structural analysis with the use of combined application of finite element method and discrete-continual finite element method[C]// International Conference on Information and Digital Technologies,IEEE,2017.
[10] 贺安民.基于单截齿的液压冲击与截割联合破煤岩过程研究[J].煤炭科学技术,2018,46(8):119-124.
HE Anmin.Study on the process of breaking coal based on single pick hydraulic impact and cutting[J].Coal Science and Technology,2018,46(8):119-124.
[11] 周 博,黄润秋,汪华斌,等.基于离散元法的砂土破碎演化规律研究[J].岩土力学,2014,35(9):2709-2716.
ZHOU Bo,HUANG Runqiu,WANG Huabin,et al.Study of evolution of sand crushability based on discrete elements method[J].Rock and Soil Mechanics,2014,35(9):2709-2716.
[12] 陈宇龙,张宇宁,李科斌,等.单轴压缩下软硬互层岩石破裂过程的离散元数值分析[J].采矿与安全工程学报,2017,34(4):795-802.
CHEN Yulong,ZHANG Yuning,LI Kebin,et al.Distinct element numerical analysis of failure process of interlayered rock subjected to uniaxial compression[J].Journal of Mining & Safety Engineering,2017,34(4):795-802.
[13] 方 刚,杨圣奇,孙建中,等.深部厚煤层巷道失稳破裂演化过程离散元模拟研究[J].采矿与安全工程学报,2016,33(4):676-683.
FANG Gang,YANG Shengqi,SUN Jianzhong,et al.Study on instability fracture evolution of deep thick coal seams based on discrete element simulation[J].Journal of Mining & Safety Engineering,2016,33(4):676-683.
[14] DU Y,GAO J,JIANG L,et al.Numerical analysis on tractive performance of off-road wheel steering on sand using discrete element method[J].Journal of Terramechanics,2017,71:25-43.
[15] BOEMER D,PONTHOT J P.A generic wear prediction procedure based on the discrete element method for ball mill liners in the cement industry[J].Minerals Engineering,2017,109:55-79.
[16] 王国强,郝万军,王继新.离散单元法及其在EDEM上的实践[M].西安:西北工业大学出版社,2010.
[17] COETZEE C J.Review:calibration of the discrete element method[J].Powder Technology,2017,310:104-142.
[18] COETZEE C J.Calibration of the discrete element method and the effect of particle shape[J].Powder Technology,2016,297:50-70.
[19] 赵丽梅,陈伦军,苏 明,等.反击式破碎机破碎过程建模与仿真分析[J/OL].煤炭学报,2013,38(8):1496-1502.
ZHAO Limei,CHEN Lunjun,SU Ming,et al.Modeling and simulation on crushing process of impact crusher[J/OL].Journal of China Coal Society,2013,38(8):1496-1502.
[20] 赵丽梅,陈伦军,何 锋,等.基于响应面法的反击式破碎机板锤多目标优化[J].煤炭学报,2013,38(S1):243-248.
ZHAO Limei,CHEN Lunjun,HE Feng,et al.Multi-objective optimization of impact crusher hammers based on reponse surface methodology[J].Journal of China Coal Society,2013,38(S1):243-248.
[21] LUO T,OOI E T,CHAN A H C,et al.The combined scaled boundary finite-discrete element method:Grain breakage modelling in cohesion-less granular media[J].Computers & Geotechnics,2017,88:199-221.
[22] 张见宝,苏 凯,王 磊,等.轮齿式双齿辊破碎机破碎齿冠受力计算及有限元分析[J].矿山机械,2013,41(6):72-74.
ZHANG Jianbao,SU Kai,WANG Lei,et al.Force computation and FEA of tooth crown of double toothed-roll crusher[J].Mining & Processing Equipment,2013,41(6):72-74.
