0 引 言
目前随着浅部资源的逐渐枯竭和深部资源勘探力度的加强,我国越来越多的煤矿已经进入深井开采阶段[1]。深井或超深井开采高温热害问题日渐严重,已成为制约矿井安全开采的重大问题[2-4]。热害的存在制约了采矿效率、影响矿工身心健康、威胁了矿山生产安全[5-6]。要进行有效的热害治理,研究热害产生原因和机理是十分必要的。
导致井下空气高温的主要因素是地热引起的围岩放热、机电设备放热、运输中的矿石放热、风流自压缩放热、矿井内高温水涌出以及人员照明散热等,这些热源的放热机理目前研究较多,并有较成熟的计算方法[7]。国内外深井矿山开采实践表明,充填采矿法是深部开采的主要采矿法之一[8-9],但是造成充填采矿法的深井热害的热源不同于其他采矿方法的深井的热源,其特殊性在于热源中还需考虑充填体的放热。目前对充填体放热的计算直接利用充填体水泥的水化热进行计算。
NASIR等[10]开发了基于FLAC的数值模型来预测和分析充填体的水化热。GHIRIAN等[11]通过试验研究了7 d内充填体热-水力-机械-化学强耦合过程,测试了包括导热率等的一系列物理和微观结构特征。尹博等[12]应用等温微量热仪测定充填材料的水化放热速率和放热量,模拟了充填材料在不同水化程度下的水化过程。陈蛟龙等[13]采用测试手段研究赤泥基似膏体充填材料的水化特性。毋林林等[14]对8种配比的粉煤灰膏体充填材料的水化放热速率和水化热进行了微量热测试与分析。刘鹏亮[15]对井下充填体温度场进行了为期50 d的实测试验,研究结果表明,水化温度持续时间约30 d。魏丁一等[16]现场实测胶结充填体分布,研究结果表明,充填作业完成后3 d内放热量达到最大。黄山果等[17]提出深井采矿的热贡献率概念,确定了不同热源(包括充填体放热)放热热源贡献率的变化。
事实上,深井充填体放热是经过复杂的传热过程将热量传递到矿井风流中,充填体水泥的水化热仅是这一传热过程的内热源,最终传递到矿井空气的热量还会受到充填体热物性、初始条件和边界条件等的影响。为了能够给出深井充填体定量的传热结果,需要研究充填体传热模型,并给出传热的基本方程,从而可以比较精确地描述与计算深井充填体传热过程。格林函数法可以利用叠加原理解析求出含内热源的温度场[18],并成功应用于环形翅片传热[19]、平壁热传导问题[20]以及移动边界热传导问题[21]等。因此,笔者采用格林函数法研究深井充填体的传热问题,推导出深井充填体温度场分布的解析表达式,在这一解析表达式的基础上,利用傅里叶导热定律,获得深井充填体传递给矿井风流的热流密度。此外,笔者的研究结果可为充填体热应用和热应力的研究提供借鉴。
1 深井充填体传热数学模型
1.1 基本假设条件
对深井充填体传热问题,可做以下的假设:
1)忽略其他2个方向的导热,充填体的热量传递是沿垂直方向传递的一维非稳态导热过程。
2)充填体均质且为各向同性,充填体的物理成分、热物性参数不随着充填体温度的变化而变化。
3)充填体中水分形态不发生变化,不考虑水分迁移对热量传递的影响。
4)充填体内部初始温度均相等。
5)忽略充填体与围岩以及硬化顶的接触热阻。
6)矿井风流风温及风速不变,且围岩与风流的对流换热系数不变。
1.2 物理模型
忽略充填体渗流,充填体内部以热传导的方式向风流传递热量,因此充填体内温度分布服从导热微分方程。基于上述假设,可将充填体传热问题简化为有内热源的一维非稳态导热微分方程,内热源为充填体中水泥的水化热,深井充填体传热物理模型如图1所示。

图1 深井充填体传热模型示意
Fig.1 Schematic diagram of the model for calculating heat transfer in filling body of deep mines
1.3 数学模型
根据导热微分方程式,充填体传热的数学模型表示如下:

(1)
式中:t为充填体温度,℃;τ为传热时间,s;α为充填体热扩散系数,m2/s;x为充填体距充填体底部的距离,m; qv为单位面积充填体中水泥的水化热,W/m2;ρ为充填体的密度,kg/m3;c为充填体的比热容,kJ/(kg•℃);H为充填体的高度,m;t0为原始岩温,℃;λ为充填体的导热系数,W/(m•℃);q0为充填体下部岩石向充填体传入的热流密度,W/m2;h为风流与充填体的对流换热系数,W/(m2·℃)。
令充填体的过余温度θ=t-tf,原始岩温的过余温度θ0= t0-tf,式(1)可转换为

(2)
2 深井充填体传热数学模型的求解
式(2)是非齐次导热方程,用格林函数法进行求解。在特定几何条件下的导热系统中,格林函数法将导热问题形成的温度场看成由许多瞬时热源引起的温度场叠加。针对式(2)的充填体导热方程,格林函数考虑为瞬时点热源在齐次边界条件和零初始条件下引起的温度分布[22],其中,δ的表达式为:
(3)
其中:b为任意有限值,在τ′时刻作用在空间中任意一点x′的瞬时点热源相应的充填体导热方程的格林函数G满足以下辅助问题:
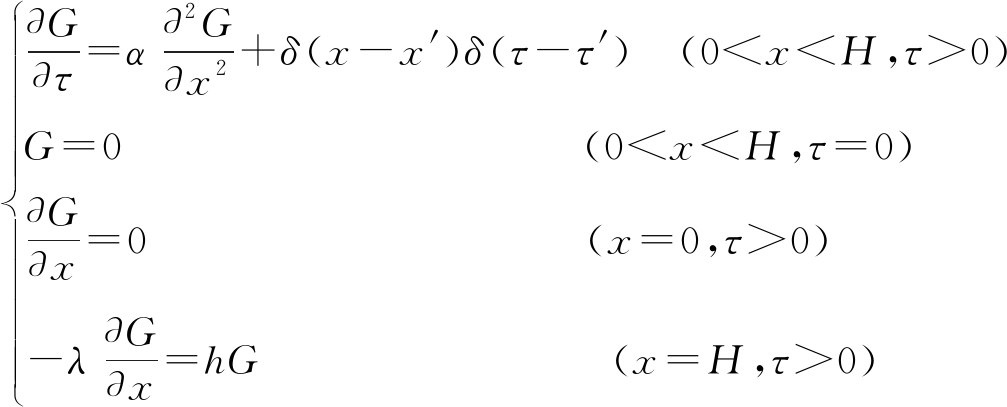
(4)
由于热源是瞬时热源,τ′时刻前充填体内部无热源的作用,故由瞬时点热源δ(x-x′)δ(τ-τ)′产生的温度分布也应维持为0,而τ′时刻的瞬时点热源就可看成τ′时刻的初始温度分布,即式(4)可转化为

(5)
显然式(5)为齐次方程,可采用分离变量法求出式(5)的解[22]。则式(5)的解为
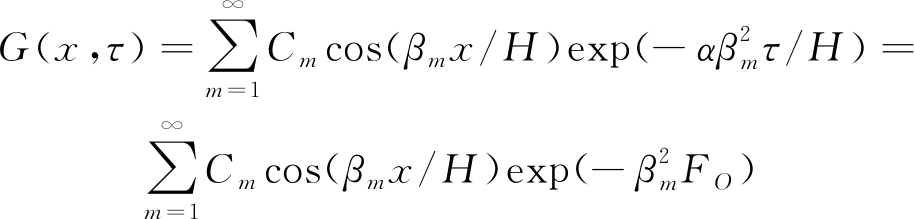
(6)
其中:FO=ατ/H2为傅里叶数;βm(m=1,2,3,…)为超越方程cot(βm)=βm/Bi的正根,Bi为毕渥数,Bi=hH/λ。
系数Cm由式(5)的初始条件确定,则
(7)
应用余弦函数的正交性可求得
![]()
exp(αβm2τ′/H)
(8)
则式(5)的解,即式(2)的格林函数为
cos(βmx/H)exp[-αβm2(τ-τ′)/H2]
(9)
利用格林函数法,充填体过余温度可表示为
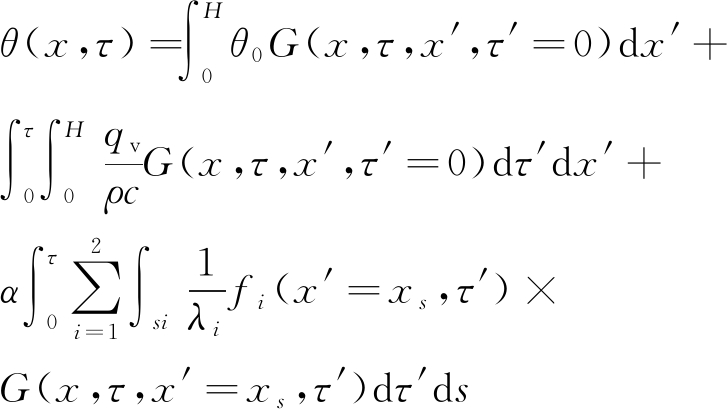
(10)
其中:si为边界面;xs为边界在x方向的值。式(10)等号右边第1项为充填体初始过余温度θ0对温度场θ(x,τ)的影响;第2项为充填体水泥水化热qv对温度场θ(x,τ)的影响;第3项表示边界条件对温度场θ(x,τ)的影响,其中,i=1时表示边界条件x=0,此时fi=q0;i=2时表示边界条件x=H,此时fi=hθ。
因此,经积分后,充填体过余温度可表示为
![]()
exp(-![]() FO)+
FO)+![]()
[1-exp(-![]() FO)]+
FO)]+![]()
[1-exp(-![]() FO)]
FO)]
(11)
式(11)是深井充填体传热的解析表达式,解析表达式是初始条件、边界条件及充填体水泥水化热对温度场影响的叠加,其中,充填体初始温度分布可表达为距离和时间的函数;充填体水泥水化热可表达为距离和时间的函数;边界条件可表达为第二类和第三类齐次或非齐次边界边界条件,该式适用充填体传热的一般情况。
式(11)中βm由毕渥数(Bi)决定,因此,式(11)的解析表达式反映出充填体的温度分布是位置(x)、毕渥数(Bi)及傅里叶数(FO)的函数。
3 深井充填体传热解析解的简化模型
为了方便工程应用,式(11)无穷级数中取前2项,其他各项均可忽略不计,得到深井充填体传热的解析解的工程简化模型。

(12)
式(12)是深井充填体传热的解析解的工程简化式。式(12)中的β1、β2由毕渥数![]() 确定,已知充填体的导热系数和充填体与对流换热系数h即可求出
确定,已知充填体的导热系数和充填体与对流换热系数h即可求出![]() 可由强制对流换热中的迪图斯-贝尔特公式[22]得出。因此,在实际应用中利用式(12)可很方便地求出充填体在不同时间、不同深度下的过余温度。
可由强制对流换热中的迪图斯-贝尔特公式[22]得出。因此,在实际应用中利用式(12)可很方便地求出充填体在不同时间、不同深度下的过余温度。
利用傅里叶定律,由深井充填体传热的解析解的工程简化式(12),可以进一步求得充填体向风流释放的热流密度q。
4 深井充填体传热解析解的简化模型应用
4.1 工程概况
某矿充填体由水泥、尾砂和水按1∶23∶29比例拌合,充填体尺寸为60 m×60 m×20 m,其中20 m为充填体的厚度。该充填体的密度为2 400 kg/m3,比热容为1 100 J/(kg·℃),导热系数为1.80 W/(m·℃)。
充填体下部岩石为砂岩,导热系数为1.84 W/(m·℃),岩石的温度梯度为0.015 K/m;充填体上部工作面的风速为2 m/s,工作面的风流温度为30 ℃;充填体初始温度为40 ℃。对流换热系数h计算为5.11 W/(m2·℃),水泥水化热由经验公式确定[23]。
以该矿的充填体为例,应用笔者提出的深井充填体传热解析解的工程简化式进行不同工况条件下充填体温度场的计算,工况参数见表1。
表1 充填体温度场计算工况参数
Table 1 Different states parameters for studying temperature distribution of filling body
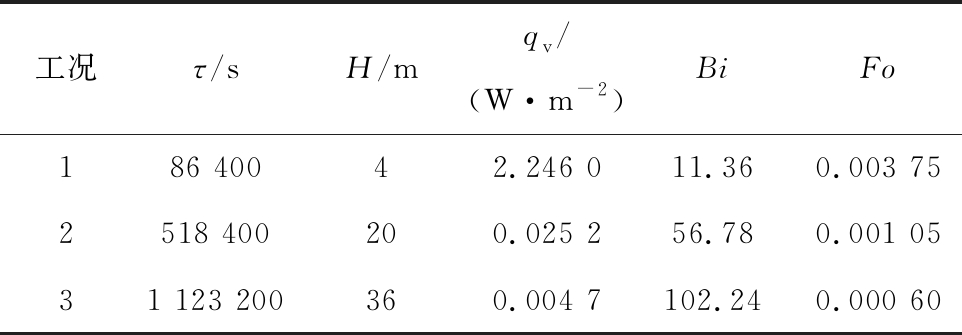
工况τ/sH/mqv/(W·m-2)BiFo186 40042.246 011.360.003 752518 400200.025 256.780.001 0531 123 200360.004 7102.240.000 60
4.2 温度场分布
应用公式(18),可得到充填体温度场分布,该充填体温度场分布如图2所示。
从图2可以看出,随着充填体在x方向位移的增加,温度逐渐降低,在充填体底部(x=0 m)温度最高,达到峰值(情况1:47.91 ℃;情况2:46.86 ℃;情况3:46.83 ℃),在充填体顶部(x=20 m)温度最低,达到最低值(情况1:30.32 ℃;情况2:30.01 ℃;情况3:30.01 ℃)。充填体底部温度较高的原因在于来自岩石的传热以及水泥水化热的共同作用。充填体顶部温度接近工作面风流温度的原因在于,当毕渥数较大时,充填体表面对流换热热阻相对于充填体的导热热阻可以忽略,因此,传热一开始,充填体顶部的表面温度就立即接近工作面风流温度。

图2 充填体温度场分布曲线
Fig.2 Temperature distribution curves in CPB
4.3 热流密度
利用傅里叶定律,由深井充填体传热的解析解的工程简化式,可以进一步求得该矿充填体传热的热流密度q。
(13)
CPB中的热流密度分布如图3所示。可以看出qv、Bi和FO的变化对热流密度分布的影响更大。当Bi数增加并且FO减少时,热流密度分布范围减小。热流密度基本成对称分布,在分布曲线的中心处达到峰值(情况1:12.68 W/m2;情况2:2.67 W/m2;情况3:1.49 W/m2)。 CPB顶部的热流密度是从CPB向工作面释放热流密度(情况1:1.65 W/m2;情况2:0.052 W/m2;情况3:0.034 W/m2),该热流密度会造成工作面温度升高,是充填采矿热害形成的来源之一。

图3 充填体热流密度分布曲线
Fig.3 Heat flux density curves in CPB
5 结 论
深井充填体的传热过程是一个复杂的、非稳态的传热过程。为了解决深井充填体的传热计算问题,推导出深井充填体温度场的解析解表达式及工程简化表达式,给深井充填体传热问题的计算提供了一个快速、准确且有效的方法。
1)建立了深井充填体有内热源的非稳态一维的传热模型,内热源为充填体中水泥的水化热,充填体传热的初始条件可表达为距离和时间的函数,充填体传热的上下2个边界上的边界条件分别是第3类边界条件和第2类边界条件。
2)采用格林函数法,对建立的深井充填体有内热源的非稳态一维的传热模型进行求解,推导出充填体温度分布的理论解析表达式,解析表达式是初始条件、边界条件及充填体水泥水化热对温度场的影响的叠加,解析表达式反映出充填体的温度分布是位置(x)、毕渥数(Bi)及傅里叶数(FO)的函数。
3)为了方便工程应用,对求解出的理论解析表达式中无穷级数取前2项,其他各项均可忽略不计,得到深井充填体传热的解析解的工程简化式。利用傅里叶定律,由深井充填体传热的解析解的工程简化式,可以很方便地求得充填体传热的热流密度q。
4)以某矿的充填体为例,应用笔者提出的深井充填体传热解析解的工程简化式进行了充填体温度场的计算分析,计算结果表明:随着充填体在x方向位移的增加,温度逐渐降低,充填体内部温度均高于风流温度,说明来自岩石的传热量以及水泥水化热对充填体传热的影响较大。充填体顶部温度接近工作面风流温度的原因在于,工程实例中毕渥数较大,充填体表面的对流换热热阻相对于充填体的导热热阻可以忽略。
[1] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005, 24(16):2803-2813.
HE Manchao, XIE Heping, PENG Suping, et al. Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(16): 2803-2813.
[2] LOWNDES I S, YANG Z Y, JOBING S, et al. A parametric analysis of a tunnel climatic prediction and plannling modes[J]. Tunnelling and Underground Space Technology, 2006,21(5):520-532.
[3] 何满潮,郭平业.深部岩体热力学效应及温控对策[J].岩石力学与工程学报,2013,32(12):2377-2393.
HE Manchao, GUO Pingye. Deep rock mass thermodynamic effect and temperature control measures [J].Chinese Journal of Rock Mechanics and Engineering, 2013,2(12):2377- 2393.
[4] 谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思考[J].煤炭学报,2012,37(4):535-542.
XIE Heping, ZHOU Hongwei, XUE Dongjie, et al. Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2012,37(4):535-542.
[5] 何满潮,徐 敏.HEMS深井降温系统研发及热害控制对策[J].岩石力学与工程学报,2008,27(7):1353-1361.
HE Manchao, XU Min. Research and debelopment of HEMS cooling system and heat-harm control in deep mine[J].Chinese Journal of Rock Mechanics and Engineering, 2008,27 (7):1353-1361.
[6] 马冬娟,唐一博.高地温对不同变质程度煤自燃微观结构影响试验研究[J].煤炭科学技术,2019,47(12):109-115.
MA Dongjuan, TANG Yibo. Experimental investigation on microstructure influence of high temperature on spontaneous combustion of coal with different ranks[J].Coal Science and Technology, 2019,47(12):109-115.
[7] 杨德源,杨天鸿.矿井热环境及其控制[M].北京:冶金工业出版社,2009.
[8] 古德生,周科平.现代金属矿业的发展主题[J].金属矿山,2012(7):1-8.
GU Desheng, ZHOU Keping. Development theme of the modern metal mining[J].Metal Mine,2012(7):1-8.
[9] 陈 勇,孟宁康,杨玉贵,等.沿空留巷巷旁充填体稳定性控制技术研究[J].煤炭科学技术,2019,47(9):273-278.
CHEN Yong, MENG Ningkang, YANG Yugui, et al. Research on stability control technology of filling body in gob-side entry retaining [J].Coal Science and Technology, 2019,47(9): 273-278.
[10] NASIR O, FALL M. Modeling the heat development in hydrating CPB structures[J]. Computers and Geotechnics, 2009, 36(7): 1207-1218.
[11] GHIRIAN A, FALL M . Coupled behavior of cemented paste backfill at early ages[J]. Geotechnical and Geological Engineering, 2015, 33(5):1141-1166.
[12] 尹 博,康天合,康健婷,等.粉煤灰膏体充填材料水化动力过程与水化机制[J].岩石力学与工程学报,2018,37(S2):4384-4394.
YIN Bo, KANG Tianhe, KANG Jianting, et al. The research of the hydration kinetics process and hydration mechanism of fly ash paste filling materials[J].Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S2): 4384-4394.
[13] 陈蛟龙,张 娜,李 恒,等.赤泥基似膏体充填材料水化特性研究[J].工程科学学报,2017, 39(11):1640-1646.
CHEN Jiaolong, ZHANG Na, LI Heng, et al. Hydration characteristics of red-mud based paste-like backfill material[J].Chinese Journal of Engineering, 2017, 39(11): 1640-1646.
[14] 毋林林,康天合,尹 博,等.粉煤灰膏体充填材料水化放热特性的微量热测试与分析[J].煤炭学报,2015,40(12):2801-2806.
WU Linlin, KANG Tianhe, YIN Bo, et al. Microcalorimetric test and analysis of hydration heat of fly ash paste-filling material[J].Journal of China Coal Society, 2015, 40(12): 2801-2806.
[15] 刘鹏亮.胶结充填体水化温度场特征及对煤自燃特性的影响[J].煤炭科学技术, 2017,45(11):74-80.
LIU Pengliang. Characteristics on hydrated temperature field of cementing filling body and affected to coal spontaneous combustion features[J].Coal Science and Technology,2017, 45(11):74-80.
[16] 魏丁一,杜翠凤,张宏光,等.胶结充填体水化放热规律及其影响研究[J].中国安全生产科学技术,2018,14(10):138-143.
WEI Dingyi, DU Cuifeng, ZHANG Hongguang, et al. Study on hydration heat release laws of cemented backfill body and its influence[J].Journal of Safety Science and Technology, 2018,14(10):138-143.
[17] 黄山果,吴 超,邱冠豪,等.深井采矿热贡献率计算方法研究与实践[J].中国安全生产科学技术,2015,11(1):91-96.
HUANG Shanguo, WU Chao, QIU Guanhao, et al. Study on calculation method of thermal contribution rate in deep mining and its application[J].Journal of Safety Science and Technology,2015,11(1):91-96.
[18] BECK J V, COLE K D, HAJI-SHEIKH A,et al. Heat conduction using Green’s functions[M]. Washington D C, Hemisphere, 1992.
[19] MOSAFFA A H, TALATI F, ROSEN M A, et al. Green′s function solution for transient heat conduction in annular fin during solidification of phase change material[J].Applied Mathematics and Mechanics(English Edition), 2012,33(10):1265-1274.
[20] CHEN E L, ANG W T. Special Green’s function boundary element approach for steady-state axisymmetric heat conduction across low and high conducting planar interfaces[J].Applied Mathematical Modelling, 2013, 37(4):1948-1965.
[21] 赵国昌,杜 霞,宋丽萍,等.格林函数法求解含移动介质轴向导热的稳态温度场[J].航空动力学报,2014,29(6):1249-1260.
ZHAO Guochang, DU Xia, SONG Liping, et al. Solving steady-state temperature fields with axial conduction in moving media using Green′s function method[J].Journal of Aerospace Power,2014,29(6):1249-1260.
[22] 孙德兴.高等传热学—导热与对流的数理解析[M].北京:中国建筑工业出版社, 2005.
[23] 马 峰,孟稳权.冬瓜山铜矿二步骤回采采场热源调查与分析[J].现代矿业,2010,26(10):7-9.
MA Feng,MENG Wenquan.Investigation and analysis concerning heat sources in two-step mining zone of Dongguashan copper mine[J]. Modern Mining, 2010, 26(10): 7-9.
