0 引 言
煤层瓦斯含量不仅是我国煤矿瓦斯危险程度评价、瓦斯灾害治理及煤层瓦斯资源开发利用不可或缺的基础参数,还是煤与瓦斯突出危险性预测、区域防突措施效果检验的主要指标[1]。因此,瓦斯含量测值的可靠性和准确性至关重要。目前,井下煤层瓦斯含量的测定方法主要有直接法和间接法[2]。间接法由于煤层原始瓦斯压力测定工艺复杂且周期较长、成功率低、成本高等原因,煤矿现场较少采用,主要采用井下直接测定法[3-5]。GB/T 23250—2009《煤层瓦斯含量井下直接测定方法》规定煤矿井下瓦斯含量测定须采用取心管取心法或其他验证有效的定点取样方法[6]。而在钻孔取心过程中,利用取心管采集煤心会存在所取煤样一端长时间暴露,取心钻头与煤壁切削产热以及取心管管壁与孔壁摩擦生热导致取心管和管内煤样温度升高而加速煤样解吸瓦斯并使煤产生变质的问题,这一点在工程实践中已达成共识。
基于煤的瓦斯放散速度随温度升高而加快的性质[7-10],文献[11-12]提出了冷冻(0 ℃及以下)取心方法,以期通过降温抑制瓦斯放散来提高瓦斯含量测值的准确性。近年来,一些学者亦开展了低温环境下(0 ℃以下)煤的吸附/解吸试验。陈昌国[13]研究了-21、0 ℃两个低温点无烟煤的瓦斯吸附性能,发现随温度降低,瓦斯吸附量增加,吸附平衡时间随之增长;文献[14-15]试验研究了低温条件下煤中瓦斯解吸规律,证明低温下煤中瓦斯解吸速度比常温和高温下慢许多,煤体冷冻取样技术的使用能够实现对煤体瓦斯解吸的抑制,验证了冷冻取心技术的合理性;文献[16-17]通过搭建高/低温瓦斯吸附解吸试验平台,开展了低温、常温环境下煤中瓦斯吸附/解吸特性研究,发现低温环境下温度对煤的瓦斯吸附影响明显,温度越低,煤的瓦斯吸附量越大,而解吸量、解吸率和解吸速度均越小,从理论上证实了低温取心的可行性;文献[18-19]进行了不同加热功率下冷冻取心过程瓦斯解吸试验模拟,发现变温过程中煤心瓦斯解吸量变化分为:前期增加、中期稳定和后期增长3个阶段,但该程序变温条件缺乏现场实测温度依据,与冷冻取心过程的温度边界条件相差较大。以上学者对低温环境下煤心吸附/解吸瓦斯做了一定的研究工作,但冷冻取心过程是在既有外部热源又有内部冷源的变温环境中进行的,针对此过程取心管壁与煤壁摩擦的产热量、促使煤心降温所需合理冷冻剂量并未进行考察。基于此,采用自主研制的取心管自动测温装置,开展钻孔取心过程中取心管管壁温度变化特性研究至关重要。
确定取心管管壁温度分布有一定的困难。由于取心过程中取心管管壁与煤壁的剧烈摩擦影响,直接在取心管表面放置热电偶传感器会使温度测量结果有较大的误差。传热学反问题方法为此类问题提供了新思路。因此,本研究通过在取心管管壁内部布置k型热电偶传感器,实现对管壁温度的实时测定,并基于顺序函数法[20]求解导热反问题,以取心管内部测点处温度作为输入,直接反演取心管表面热流密度,从而获得随时间和空间变化的取心管表面温度分布。
1 试验装置
为了实时测定取心过程中取心管管壁及煤心温度,自主研制了一套取心管自动测温装置,如图1所示。该装置主要包括测温电路板和定制取心管。测温电路板主要由微控制单元模块、测温模块、数据存储模块、实时时钟模块、电源模块等5个模块组成;定制取心管和常规取心管形状相似,均为中空圆筒状,直径75 mm,长500 mm,其前端可以通过螺纹连接直径75 mm的取心钻头,定制取心管安装钻头后长度为570 mm,如图2所示。与常规取心管相比,不同点如下:
1)末端通过螺纹连接测温电路板的外壳,而不是普通钻杆。
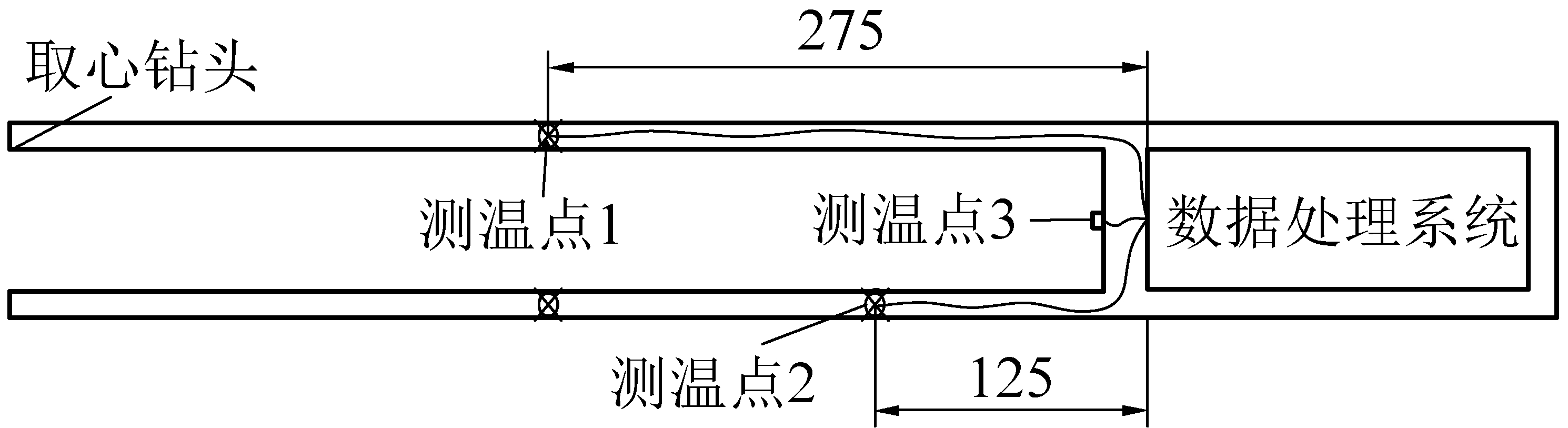
图1 取心管自动测温装置示意
Fig.1 Schematic diagram of coring tube automatic temperature measuring device

图2 定制取心管
Fig.2 Customized coring tube
2)定制取心管管壁略微加厚,使用电脉冲沿取心管轴向方向打了2个深孔(长度分别为275、125 mm,直径为1 mm),可以分别插入同孔深的k型热电偶传感器T1和T2(测温范围0~600 ℃),用以测量取心过程中取心管管壁不同位置处的温度。
3)取心管末端预留一个带有螺纹的孔,可以固定一个k型传感器T3,用以测量取心过程进入取心管中的煤心温度。
2 取心管管壁温度测定试验
2.1 试验场及钻孔布置
试验点选在焦煤集团九里山煤矿15091回风巷道。考虑到钻孔测温深度宜超出巷道调热圈深度及测温装置的续航时间等两方面,分别设计了取心深度为5、20、40 m的测温钻孔,在15091回风巷进行顺层钻孔施工,钻孔间距为1 m,如图3所示。
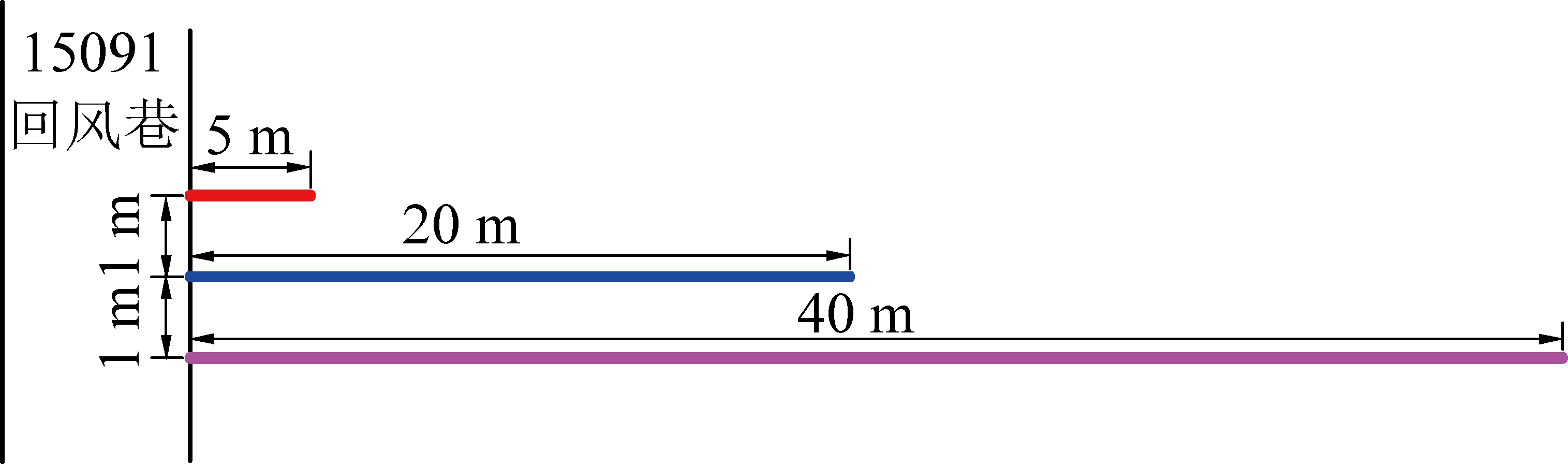
图3 取心钻孔施工示意
Fig.3 Construction schematic of core drilling
2.2 试验过程
1)在测温地点,使用ø93 mm钻头、ø73 m钻杆施工取心钻孔,待钻孔施工至4.5 m时,停止钻进并利用压风清理钻孔,退出钻杆。
2)迅速取下ø93 mm钻头,同时安装好取心管自动测温装置,钻机工作,下管至钻孔底部,开始切削孔底煤体进行取样测温,正常推进一个取心管长度(0.5 m)。
3)取心结束后,将钻杆退出并卸下取心管,倒出取心管中煤样,至此,取心深度为5 m下取心管管壁温度测试工序结束。
4)待取心管冷却至环境温度后,在相邻位置(1 m)处,钻机以相同转速,重复步骤1)—3),进行钻孔深度分别为20、40 m的取心管管壁温度测试作业。
3 测温结果及分析
对本研究所进行的3组取心深度测温试验数据整理分析,温度传感器T1、T2和T3的温度变化曲线如图4所示,不同取心深度下各取心阶段测定的具体数值见表1。
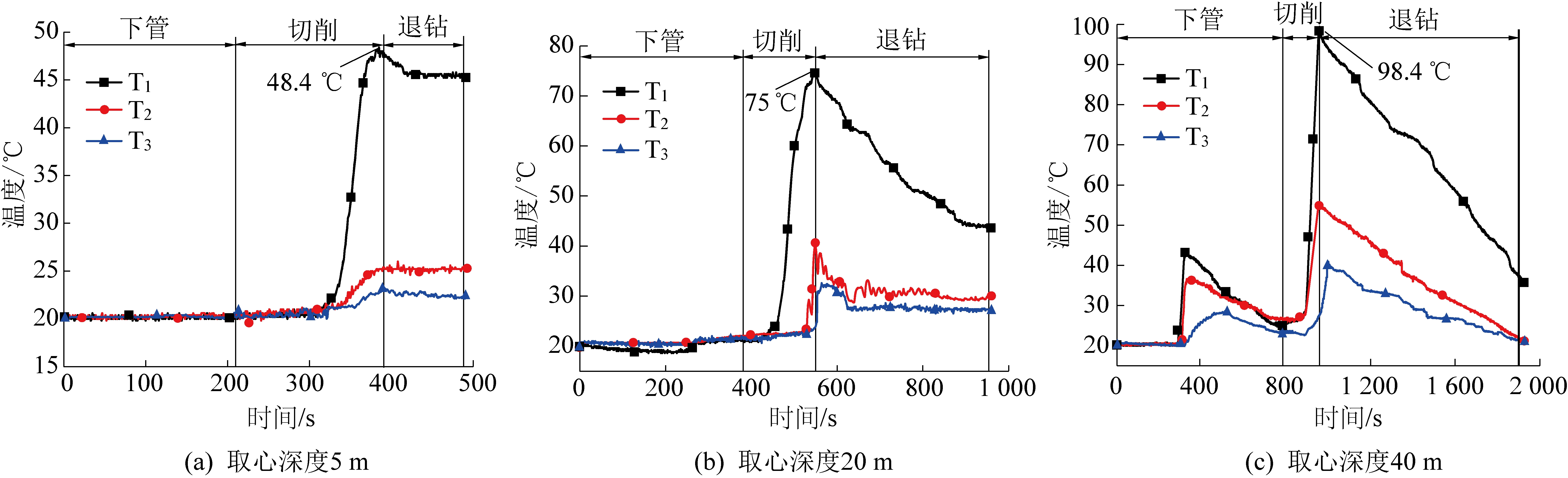
图4 取心过程中取心管温度变化曲线
Fig.4 Temperature variation curves of coring tube during coring process
表1 取心过程中各阶段测温数据
Table 1 Temperature measurement data in each stage of coring process

取心深度/m 见煤温度(下管阶段)切削结束时温度(切削阶段)出孔温度(退钻阶段)全程最高温度时长/sT1/℃T2/℃T3/℃时长/sT1/℃T2/℃T3/℃时长/sT1/℃T2/℃T3/℃T1/℃T2/℃T3/℃521020.220.120.017948.425.023.39945.225.422.448.425.023.42038022.121.821.017075.040.323.840543.429.827.175.040.332.64078825.426.423.316698.455.327.294637.422.021.398.455.340.9
注:T1、T2、T3为温度传感器T1、T2、T3的温度读数。
由图4及表1可以看出,不同取心深度下,温度传感器T1、T2和T3温度变化规律基本趋于一致。以取心深度40 m为例分析,在下管阶段,温度传感器T1、T2、T3在进钻分别进行290、301、318 s后开始升温,至334、342、523 s时达到极大值。
此后开始降低;在切削阶段,切削开始时温度传感器T1、T2、T3均缓慢升温,在取心管与孔底煤体分别切削94、107、116 s后开始快速升温,T1、T2均在切削结束时(954 s)升至最高值98.4、55.3 ℃,而T3在切削结束一段时间后(1 000 s)升至最高值40.9 ℃;在退钻阶段,T1、T2及T3温降速度基本相同,处于同步缓慢降低状态。
笔者认为,当取心深度不大(5、20 m)时,下管阶段取心管管壁与钻孔壁的摩擦产热量较小,对取心管温度影响不明显,表明下管过程中,钻孔变形不大;当取心深度较大(40 m)时,下管阶段T1、T2及T3存在明显升温现象,表明在下管过程中取心管受到了孔洞变形的影响,取心管管壁与孔壁发生了剧烈摩擦,导致取心管温度迅速升高。当取心深度为20、40 m时,切削开始阶段T1、T2存在缓慢升温现象,其主要原因是,当取心钻头刚开始旋转切削孔底煤体时,钻孔底存在有残留的破碎煤屑,孔底煤体不平整且较松软,无法卡紧取心钻头,导致取心管及钻杆抖动,使得取心管与孔壁发生撞击及摩擦并产生热量,造成取心管管壁温度缓慢升高。T3温度变化滞后于T1和T2的主要原因是,一方面,传感器T3处于取心管末端,与T1、T2相比距离取心钻头较远,取心钻头切削孔底煤体产热需经热传导过程依次作用于T1、T2和T3,存在时间差效应;另一方面,T1、T2布置于取心管管壁内部,而传感器T3处于取心管末端靠中心位置,距取心管管壁较T1、T2长,则取心管管壁与钻孔壁摩擦生热会先作用于T1、T2,然后才能传导至T3。
4 取心管管壁温度分布数值模拟结果及讨论
为了获得随时间和空间变化的取心管表面温度分布,本研究通过建立取心管管壁传热模型,基于顺序函数法求解导热反问题,并分析了模拟温度与实测温度的误差。
4.1 取心管管壁传热模型
对取心管管壁传热模型作如下假设:①取心管内壁与末端均绝热;②取心管外壁均匀受热;③假设取心管外壁前34 cm受热相同,后23 cm受热相同。以取心管半剖面为研究对象,如图5所示。
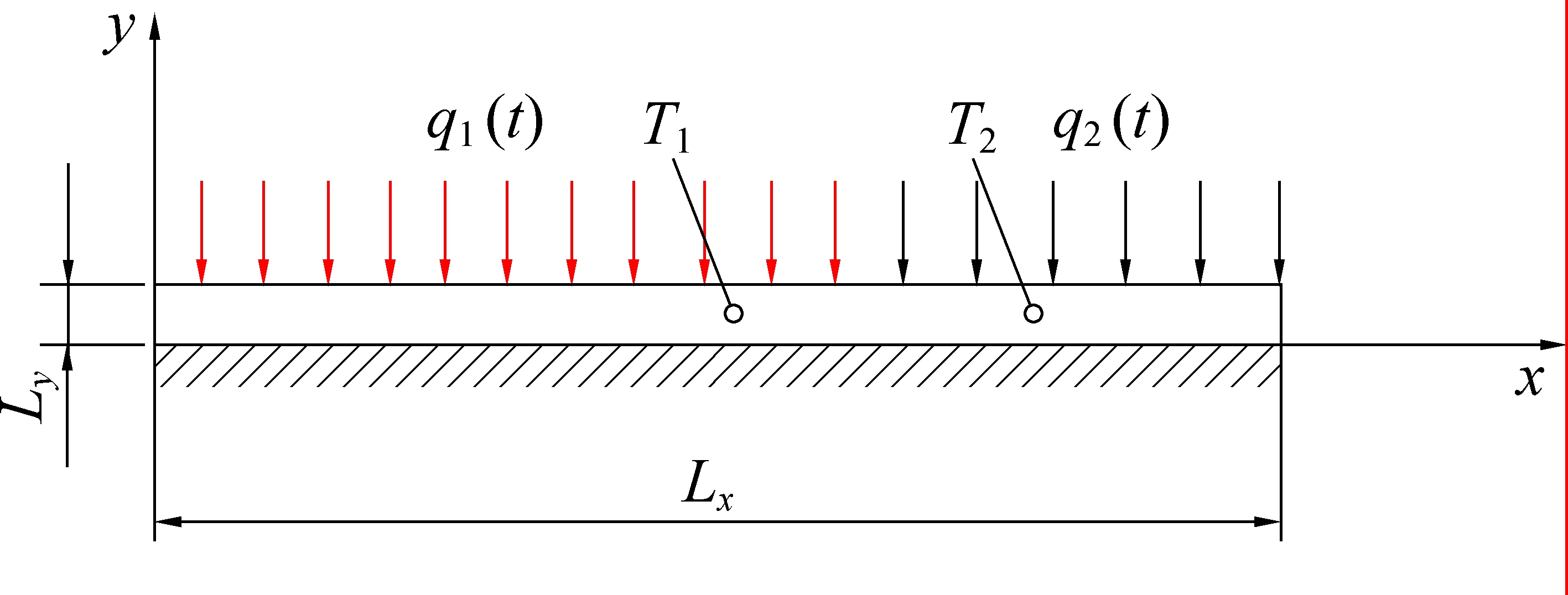
图5 取心管传热半剖面示意
Fig.5 Half section heat transfer diagram of coring tube
取心管温度分布T(x,y,t)满足如下二维非稳态导热控制方程[21]:
0≤x≤Lx,0≤y≤Ly,t>0
(1)
边界条件:
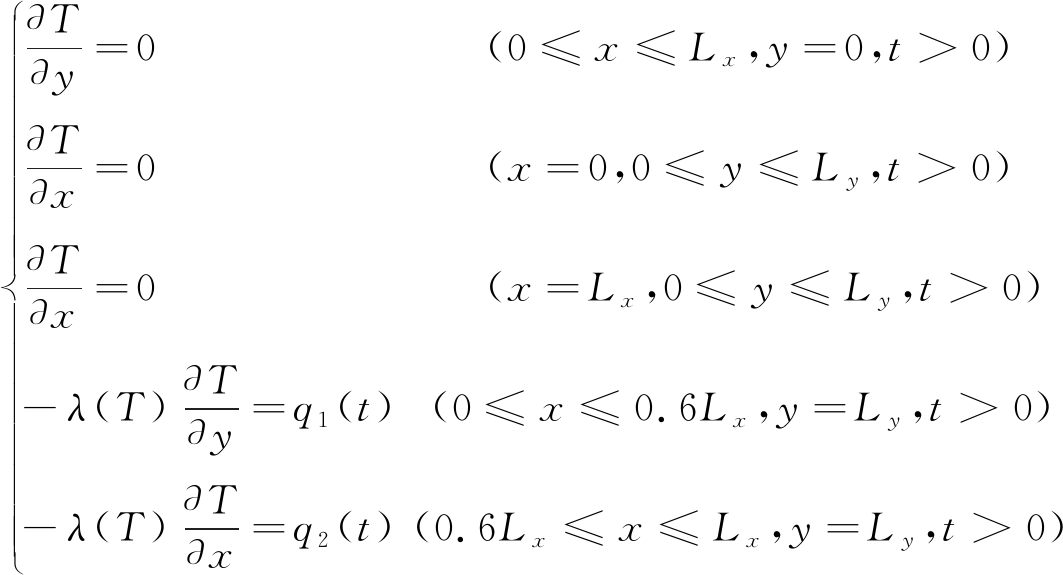
(2)
初始条件:
T(x,y,t0)=T0(x,y)
(3)
式中:ρ为取心管材料密度,kg/m3;c(T)为随温度变化的比热容,J/(kg·℃);∂T/∂t为温度随着时间的变化率;λ(T)为随温度变化的热导率,W/(m·K);∂T/∂x为温度在x方向上的变化率;∂T/∂y为温度在y方向上的变化率;x为长度方向上某点至原点的距离,cm;y为厚度方向上某点距原点的距离,cm;t为时间,s;Lx和Ly分别为取心管的长度和厚度,cm;q1(t)和q2(t)分别为取心管外壁前34 cm和后23 cm的热流密度,J/(m2·s);T0(x,y)为取心管的初始温度分布,℃。
4.2 反演取心管表面热流的顺序函数法
顺序函数法求解传热反问题是利用取心管内部的N个测点在K个时刻的测量温度Yj,k(j=1,2,3,…,N,k=1,2,3,…,K)反演q1(t)和q2(t)。这里取N=2,温度测点T1和T2位置如图5所示。
采用顺序函数法[20]依次反演各个时刻的表面热流,设tm时刻前m-1个时刻的热流密度估计值q1,q2,…,qm-1和tm-1时刻的温度分布已知,估计边界热流qm时,首先假定(tm,tm+r-1)内的热流密度变化满足:
qm=qm+1=…=qm+r-1
(4)
定义向量qj:
n=1,2,…,p
式中:p为每个时刻的待反演热流数;r为预先选择的未来时间步。
定义qm的目标函数J(qm),选择[tm,tm+r-1]时间区间内的测量温度和计算温度之差的平方和作为目标函数。
(5)
式中:Yj,m+i-1和Tj,m+i-1(qm)分别为测点j在tm+i-1时刻的温度测量值和计算值。
假定在求解区间(tm,tm+i-1)内热物性保持不变,且λ=λ(tm-1),c=c(tm-1)。将测点j的计算温度在![]() 处泰勒展开,得:
处泰勒展开,得:
(6)
式中:Zj,i,n=∂Tj,m+i-1/∂qm(n)为热流分量qm(n)单位扰动下的测点温度响应值。
将式(6)代入式(5),并令
∂J(qm)/∂qm(n)=0
可得qm的求解表达式,整合为矩阵形式如下:
(7)
4.3 取心管表面热流反演及温度预测
利用Matlab软件并基于顺序函数法对取心管管壁传热模型求解,其中计算参数如下:

取心管管壁导热系数/(W·m-1·K-1)21.5取心管管壁恒压热容/(J·kg-1·K-1)500取心管管壁密度/(kg·m-3)7 900取心管管壁长度/m0.57取心管管壁厚度/m0.01长度方向上网格数50厚度方向上网格数20
不同取心深度下取心管表面热流密度反演结果如图6所示;基于反演的取心管表面热流密度,并在此基础上重构了取心管表面温度,获得整个取心过程中的取心管管壁温度分布,如图7所示。
4.4 误差分析
为验证所建立取心管管壁传热模型的有效性,对取心管管壁温度观测点模拟值与实测值进行百分比误差分析,计算公式为
(8)
式中:δ为百分比误差;Tm为模型计算的模拟温度,℃;Tz为取心现场实测温度,℃。
对图7中模拟温度与实测温度进行百分比误差分析,结果如图8所示。

图6 不同取心深度下取心管表面热流密度的反演结果
Fig.6 Inversion results of density of heat flow rate on the surface of coring tube at different coring depths

图7 取心管管壁温度分布
Fig.7 Temperature distribution of coring tube wall

图8 不同取心深度下温度观测点温度模拟值与实测值百分比误差
Fig.8 Temperature percentage error between simulated value and measured value of temperature observation points at different coring depths
由图8可以看出,当取心深度为5 m时,取心管T1和T2的模拟温度与实测温度的百分比误差基本保持在3%以内;当取心深度分别为20、40 m时,取心管T1和T2的模拟温度与实测温度的百分比误差基本保持在2%以内。证明了本研究所建立取心管管壁传热模型的可靠性及反演求得取心管表面温度分布的准确性。
5 结 论
1)开展了钻孔取心过程中取心管管壁温度测试试验,试验发现,在下管阶段,当取心深度较大(40 m)时,存在取心管温度快速升高的现象;在切削阶段,不同取心深度下,取心管温度均呈现出切削进行一段时间后开始迅速升高,切削结束时升至最高值的规律;在退钻阶段,取心管温降速度基本相同,处于一个缓慢降低的状态。
2)建立了预测取心管表面温度分布的传热模型,基于顺序函数法求解导热反问题,以取心管测点处温度作为输入,可以准确反演出整个取心过程中取心管表面的热流分布情况。
3)通过现场实测取心管温度与模型计算模拟温度对比分析,结果表明,实测管壁温度变化曲线与模拟结果吻合良好,误差小,证明了取心管管壁传热模型的可靠性及反演所得取心管表面温度的准确性。
4)本研究不仅为确定冷冻取心过程所需合理冷冻剂量提供了充实的试验基础,也为冷冻取心煤心瓦斯解吸规律的研究提供了可靠的温度变化依据。
[1] 王兆丰,刘 军.我国煤矿瓦斯抽放存在的问题及对策探讨[J].煤矿安全,2005,36(3):29-32.
WANG Zhaofeng,LIU Jun.Probe into the problems of methane drainage in Chinese coal mines and its counter measures [J].Sa-fety in Coal Mines,2005,36(3):29-32.
[2] 林柏泉.矿井瓦斯防治理论与技术[M].徐州:中国矿业大学出版社,2010.
[3] 姜海纳,程远平,安丰华.淮北矿区煤层瓦斯含量直接测定法中有效取样时间研究[J].采矿与安全工程学报,2013,30(1):143-148.
JIANG Haina,CHENG Yuanping,AN Fenghua.Research on ef- fective sampling time in direct measurement of gas content in Huaibei coal seams[J].Journal of Mining & Safety Engineering, 2013,30(1):143-148.
[4] CHEN Shaojie,CHENG Genyin,XU Ameng,et al.New technolo-gy of deterrmining coalbed gas content by reversion seal coring [J].Journal of Coal Science and Engineering,2012,18(1):35-38.
[5] 张淑同.井下瓦斯含量直接法测定关键技术研究[J].采矿与安全工程学报,2014,31(2):328-332.
ZHANG Shutong.Key technology for gas content direct deter- mination methodin underground mine[J].Journal of Mining & Safety Engineering,2014,31(2):328-332.
[6] GB/T 23250—2009,煤层瓦斯含量井下直接测定方法[S].
[7] WANG Jikun,CUI Xia. Infrared measurement of temperatu refield in coal gas desorption[J].International Journal of Mining Science and Technology,2014,24(1):57-61.
[8] NODZENSKI A.Sorption and desorption of gases on hard c- oal and active carbon at elevated pressure[J].Fuel,1998,77(11):1243-1246.
[9] 聂百胜,杨 涛,李祥春,等.煤粒瓦斯解吸扩散规律实验[J].中国矿业大学学报,2013,42(6):975-981.
NIE Baisheng,YANG Tao,LI Xiangchun,et al.Research on diff- usion of methane in coal particles[J].Journal of China Universi- ty of Mining & Technology,2013,42(6):975-981.
[10] 刘彦伟,魏建平,何志刚,等.温度对煤粒瓦斯扩散动态过程的影响规律与机理[J].煤炭学报,2013,38(S1):100-105.
LIU Yanwei,WEI Jianping,HE Zhigang,et al.Influence rules a- nd mechanisms of temperature on dynamic progress of gas dif- fusion from coal particles[J].Journal of China Coal Society,2013,38(S1):100-105.
[11] WANG Zhaofeng,TANG Xu,YUE Gaowei,et al.Physical s- imulation of temperature influence on methane sorption and ki-netics in coal:Benefits of temperature under 273.15K[J]. Fuel, 2015,158:207-216.
[12] 岳高伟,王兆丰,谢 策,等.降温促进煤体对瓦斯吸附效应的试验研究[J].煤炭科学技术,2016,44(4):45-49.
YUE Gaowei,WANG Zhaofeng,XIE Ce,et al.Experiment study on gas adsorption effect promoted by temperature reducing of coal mass[J].Coal Science and Technology,2016,44(4):45-49.
[13] 陈昌国,鲜晓红,张代均,等.无烟煤及其炭化样吸附甲烷的动力学研究[J].重庆大学学报,1995,18(3):76-79.
CHEN Changguo,XIAN Xiaohong,ZHANG Daijun,et al.The kinetic study of adsorption of methane on anthracite and its ch- arring samples[J].Journal of Chongqing University,1995,18(3): 76-79.
[14] 王轶波,李红涛,齐黎明.低温条件下煤体瓦斯解吸规律研究[J].中国煤炭,2011,37(5):103-104.
WANG Yibo,LI Hongtao,QI Liming.Study on gas desorption l- aw of coal mass at low temperatures[J].China Coal,2011,37(5): 103-104.
[15] 王 晗.冰冻取样煤体瓦斯解吸规律研究[D].重庆:重庆大学,2018.
[16] 康 博.低温环境煤的瓦斯解吸特性研究[D].焦作:河南理工大学,2013.
[17] 谢 策,王兆丰,康 博.低温下温度对无烟煤瓦斯吸附能力的影响[J].煤炭技术,2015,34(4):164-166.
XIE Ce,WANG Zhaofeng,KANG Bo.Influence in environment of low temperature to adsorption capacity of anthracite coal [J].Coal Technology,2015,34(4):164-166.
[18] 马向攀.低温取芯过程煤芯瓦斯解吸特性研究[D].焦作:河南理工大学,2017.
[19] 马向攀,王兆丰,任浩洋.基于吸附势理论的低温环境煤甲烷吸附等温线预测[J].煤矿安全,2017,48(5):22-25.
MA Xiangpan,WANG Zhaofeng,REN Haoyang.Prediction for CH4 isothermal adsorption curve of coal at low temperature ba- sed on adsorption potential theory[J].Safety in Coal Mines,2017,48(5):22-25.
[20] 张丽慧,王广军,罗兆明,等.利用二维导热反问题预测钢坯温度分布[J].工程热物理学报,2013,34(11):2136-2139.
ZHANG Lihui,WANG Guangjun,LUO Zhaoming,et al. Estim-ation of the steel slab temperature distribution using 2-D inver- se heat conduction problem[J].Journal of Engineering Thermo- physics,2013,34(11):2136-2139.
[21] OSMAN A M,DOWDING K J.Numerical solution of the general two-dimensional inverse heat conduction problem (IHCP)[J].Heat Transfer,1997,38(1):38-45.
