0 引 言
劈裂注浆是硬塑状黏土、风化岩和破碎带等不良地质体加固的有效手段,目前已广泛应用于建筑地基、地铁隧道、矿山巷道和水利等各项工程中,如高层建筑地基基础的加固和沉降防治、高速铁路软硬夹层不良地质体的改良、坝基砂卵石层地基承载力的提高和防渗治理、地铁及矿山隧道富水区的涌水突泥预防、高填方机场跑道脱空塌陷病害处理及填方坡体的加固、挡土墙支护结构和深基坑坑底的锚固及钻孔灌注桩后注浆的处理等[1-5]。劈裂注浆在加固体内可以形成纵横交错的网状浆脉,浆脉起到骨架支撑和“加筋”作用,能显著提高加固体的整体强度和刚度。目前劈裂注浆的机理研究远滞后于工程建设的需要,鉴于劈裂注浆技术在工程实践中不可替代的重要作用,越来越多的科研工作者对这一重要研究领域投入了关注。劈裂注浆的物理力学机制非常复杂,需要结合理论推导、模型试验和数值计算等多种分析方法进行深入研究。笔者首先厘清了劈裂注浆的发展过程和能量消耗方式,然后基于弹塑性理论、模型试验和数值计算等方法对劈裂注浆技术的最新研究成果进行阐释和述评,期望能为工程技术人员和科研人员提供有益启示和新见解。
1 劈裂机理
劈裂注浆需要较高的注浆压力,首次劈裂产生后注浆压力呈脉冲状变化,继而在土体内会产生新的劈裂通道。劈裂注浆过程中伴随有压密注浆和渗透注浆等多种复杂作用方式,常需要结合球形或柱形扩孔理论及能量分析的方法进行分析计算[6-8]。
1.1 劈裂过程
根据注浆压力的变化和能量的耗散规律,可将劈裂注浆过程划分为能量积聚、劈裂流动和浆液能量转移3个阶段:①能量积聚阶段。浆液在注浆孔附近积聚形成浆泡,对塑性影响区范围的土体产生压密作用,土体受挤密作用以塑性应变能的形式积蓄能量。②劈裂流动阶段。注浆压力升高至土体的启劈压力,浆液沿着最薄弱面将土体劈裂,注浆压力回升后产生二次劈裂(图1)。③浆液能量转移阶段。劈裂通道形成后浆液不断向周边扩展,锋面压力降低,浆液转而以渗透形式扩散,所携带能量向土体转移。

σ1、σ2、σ3—最大主应力、中间主应力、最小主应力; rc—注浆管半径;P0—周围压力;r—扩散半径;Pr—扩散半径r处的注浆压力;Rmax—浆液最大扩散半径;δ0—劈裂厚度
图1 劈裂注浆机理分析
Fig.1 Analysis of splitting grouting mechanism
1.2 能量消耗
劈裂注浆过程中浆液劈裂土体需消耗一部分能量,剩余的能量则储存在土体内部。根据能量守衡原理可得
ΔE=(ΔEs+ΔEf)+(ΔEic+ΔEip+ΔEiv+ΔEis+ΔEit)
(1)
式中:ΔE为劈裂注浆消耗总能量;ΔEs和ΔEf分别为土体和浆液的弹性应变能;ΔEic为启劈土体消耗的能量;ΔEip为土体塑性变形消耗的能量;ΔEiv为浆土介质摩擦作用消耗的能量;ΔEis为浆体克服剪切作用所耗能量;ΔEit为注浆系统各种摩擦作用产生的能量消耗[9]。
1.3 劈裂半径及压力衰减规律
在孔内注浆压力的作用下,浆液将在土层一定范围内产生平面径向流动。若浆液为牛顿流体,则其流动规律遵从Navier-Stokes方程
(2)
其中:x,y分别为横纵坐标;ρ为流体的质量密度;u为浆液的流速;p为注浆压力;v为流体平均流速;t为注浆时间。根据边界条件和定解条件,当x=0时,p(x,t)=pc;当x=Rmax时,t=0,p(x,t)=ps;当y=±δ0/2时,u(y,t)=0。pc为注浆孔内的注浆压力;ps为土体的启劈注浆压力;可求得
(3)
(4)
式中:Q为注浆量;μ0为浆液初始黏度。
2 劈裂注浆研究进展
2.1 理论计算与机理分析
邹金锋等[10]基于Hoek-Brown非线性强度准则,利用断裂力学理论对裂隙岩体的劈裂注浆机理进行分析。研究表明地质强度指标GSI、材料参数mi和裂纹长度a是影响裂隙岩体启劈注浆压力的主要因素,启劈注浆压力随地质强度指标GSI增加而增加,GSI等于50时达到峰值,材料参数mi和裂纹长度a增加时岩体的完整性提高,启劈注浆压力随之增大。
张淼等[11]基于扩孔理论和统一强度准则分析非对称荷载作用下的启劈压力,计算表明非对称荷载作用下的启劈压力较对称荷载作用下的值明显偏小。研究同时表明土的黏聚力c、内摩擦角φ和侧压力系数k是决定启劈压力的关键因素,启劈压力与黏聚力、内摩擦角呈正相关关系,与侧压力系数的关系则存在分界点,当k<1时启劈压力与k呈正相关, k>1时负相关(图2)。

p1—周围土压力;k—侧压力系数;p2—初始注浆压力
图2 非对称荷载下劈裂注浆力学机制分析
Fig.2 Mechanical mechanism analysis of splitting grouting under asymmetric load
郭炎伟等[12]将劈裂注浆后的复合土体视为各向同性均匀介质,采用横向各向同性理论对复合体进行力学分析和推导,得出三维单元体模型等效弹性模量和等效泊松比的解析解。
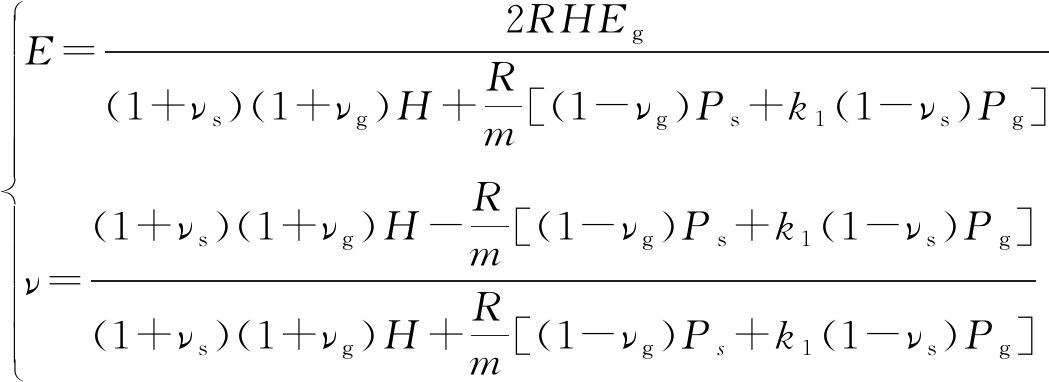
(5)
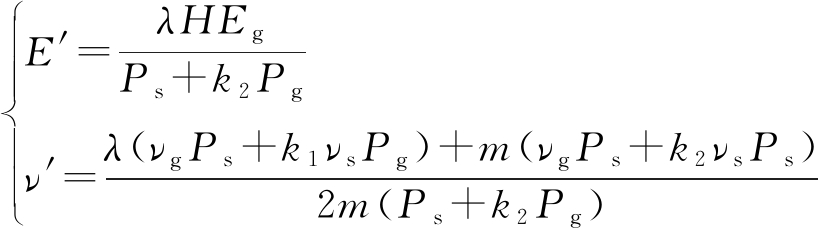
(6)
式中:E、E′分别为各向同性平面及垂直于该平面的弹性模量;R、H为等效参数,表示式为R=m(1+νs)+(Es/Eg)(1-m)(1+νg),H=Ps+k1k2Pg+k1Psg+k2Pgs;m为侧面等效注入率;νs、νg分别为土体和浆体的泊松比;Es、Eg分别为土体和浆体的弹性模量;Ps、Pg、Psg、Pgs则分别为土体、浆体、复合土体、复合介质的泊松比转换系数,其中Ps=1-νs-2![]() ,Pg=1-νg-2
,Pg=1-νg-2![]() ,Psg=1-νs-2νsνg,Pgs=1-νg-2νgνs;ν为泊松比;k1、k2为模量计算参数, k1=(Es/Eg)(1-λ)/λ,k2=(Es/Eg)(1-m)/m;λ为浆液的实际注入率;ν′为垂直于各向同性平面方向上的应力引起的各向同性平面方向上的应变。
,Psg=1-νs-2νsνg,Pgs=1-νg-2νgνs;ν为泊松比;k1、k2为模量计算参数, k1=(Es/Eg)(1-λ)/λ,k2=(Es/Eg)(1-m)/m;λ为浆液的实际注入率;ν′为垂直于各向同性平面方向上的应力引起的各向同性平面方向上的应变。
欧阳进武等[13]假定劈裂通道为椭球体,采用一般力学的分析方法推导脉动注浆时浆液的扩散方程(式(7)—式(9)),分析得到脉动注浆条件下浆液的扩散规律。研究表明脉动注浆条件下浆液的扩散距离与脉动频率有关,脉动注浆条件下浆液的扩散距离远小于稳压注浆方式下浆液的扩散距离。
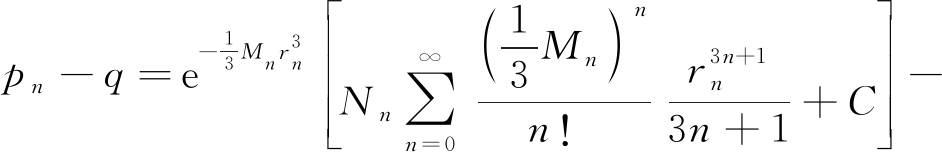
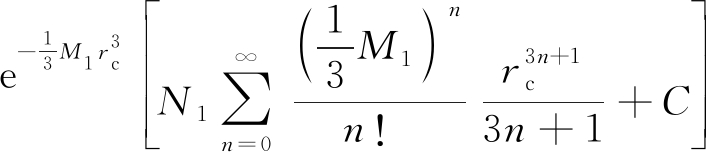
(7)
(8)
(9)
式中:pn、q分别为第n(n=1,2,3……)次脉动后的注浆压力和孔口注浆压力; rn为第n次脉动后的浆液扩散距离;rc为注浆孔半径;μ为动力黏度;μB为浆液的塑性黏度;Mn、Nn为第n次脉动注浆参数;T为脉动注浆间隔时长;τs为浆液剪切屈服强度;bn为第n次脉动后劈裂通道宽度。
张乐文等[14]根据浆土应力耦合特性推导劈裂过程中浆液压力的时空分布方程,分析得出劈裂半径和劈裂缝宽度的动态变化规律。研究显示基床系数、浆液黏度及土性的差别均会对劈裂效果产生影响,浆液的扩散半径与基床系数标准值呈正相关,而与浆液黏度呈负相关,黏性土中浆液的扩散半径小于砂土中的扩散半径;浆液压力与基床系数标准值和浆液黏度呈正相关,黏性土中浆液压力小于砂土中浆液压力;劈裂缝宽度与基床系数标准值呈负相关而与浆液黏度呈正相关,黏性土中的劈裂缝宽度大于砂土中的劈裂缝宽度等。
2.2 试验探索和劈裂机制探究
李鹏等[15-16]通过模型试验发现劈裂注浆过程中注浆压力呈脉冲状变化,浆液在注浆压力起伏变化的过程中依次经历扩散形式转换(渗透→压密→劈裂)、主次生劈裂通道饱和、新劈裂通道形成和后续次劈裂区域饱和4个阶段。充填介质凝固后开挖显示,浆脉宏观上呈现为环注浆孔多区域分布,细观则呈现为一条骨架浆脉衍生多条分支脉络分布,主次浆脉在劈裂注浆过程中同步发展、共生共存。
张庆松等[17]分析认为浆液流场与土体应力场的耦合效应对黏土劈裂机制及劈裂规律存在较大影响,理论推导表明受浆液流场的限制注浆孔及浆液锋面附近注浆压力衰减较快,劈裂通道宽度随注浆压力衰减而呈现出非线性衰减特征;一定注浆压力下浆液扩散半径与土体的弹性模量及浆液的塑性黏度呈反比例关系,一定扩散半径下劈裂通道宽度则与浆液的塑性黏度呈正比例关系,与土体的弹性模量呈反比例关系(图3)。

D—注浆影响极限范围;b—劈裂通道宽度
图3 劈裂注浆机理分析
Fig.3 Analysis of splitting grouting mechanism
王凯等[18]指出浆液在全风化花岗岩地层中以劈裂扩散模式为主,注浆压力提高则主次浆脉生长扩展,加固效果增强,试验表明劈裂区和压密区岩体抗压强度分别提高152.4%和95.2%,抗剪强度则分别提高348.6%(σn=200 kPa,σn为直剪试验法向压力)和149.6%(σn=400 kPa);浆液的挤密、充填作用降低了介质的孔隙率和渗透性,浆脉的骨架作用则提高了岩体的水稳定性。
李相辉等[19]发现非均质断层破碎带的物质组分对浆液的扩散方式影响非常显著,松散型和软弱型介质中浆液主要以渗透和压密扩散方式为主,而密实型介质中浆液则以劈裂扩散方式为主,注浆压力在介质结构分界面处存在突变点。针对松散型和软弱型不良地质区域的特点及浆液扩散规律提出定域注浆控制技术,可有效实现不良地质区域的重点注浆处治。
张家奇等[20]指出分层界面两侧浆液的扩散路径迥然不同,分层介质的层间突变性导致浆液发生渗透-界面式、劈裂-渗透式和渗透-界面-劈裂式这3种不同的扩散模式,加固效果上分别呈现“界面浆脉黏结”、“贯穿浆脉连接”和“并行浆脉架构”3种特征;为提高劈裂注浆的效果,可采用注浆材料动态调节、同孔多序梯度注浆和分层界面控域注浆等多种灵活的注浆方式。
杨磊等[21]发现水泥浆液的黏度对劈裂注浆效果有较大影响,浆液黏度小时主劈裂浆脉呈“三叉形”分布,浆液相对黏度(计算方法为浆液从漏斗式黏度计下端全部流出的秒数)超过18.8 s后主劈裂浆脉呈“折线形”分布,浆脉的宽度也在一定程度上增加(图4)。

图4 主劈裂浆脉形态
Fig.4 Shape of main cleavage plasma vein
强度测试则表明,水泥浆液黏度对结石体的抗压强度、黏聚力和内摩擦角等也有较明显影响,24.6 s的浆液相对黏度对应的高幅度分别达87%、220%和46.6%等。
2.3 数值模拟计算
近年来基于离散元(DEM)和有限元(FEM)商业软件的异军突起,为劈裂注浆机理探究也提供了新的途径。郑刚等[22]通过PFC2D数值试验发现注浆压力是注浆过程中的决定性因素,注浆压力对浆液的扩散半径、土体的孔隙率及应力状态均有显著的影响。数值试验表明浆液的扩散半径随注浆压力的增加先增后减,存在最优注浆压力,测量圈的记录则显示距注浆孔越近,土体的孔隙率、主应力等力学参数变化越复杂(图5)。

图5 注浆数值计算图示
Fig.5 Graphic illustration of grouting numerical calculation
朱旻等[23]基于弥散裂缝模型模拟劈裂缝的产生和发展,采用流体体积函数法(VOF)对劈裂注浆过程进行了有限元分析。结果表明注浆孔埋深对浆液扩散形态和浆脉数量、宽度等有明显影响,埋深较浅时易产生次生浆脉,浆脉数量和分支较多,埋深大时浆脉长度减小宽度增加;注浆量相同的条件下,注浆速率越大浆脉宽度越大,注浆效果越好。数值分析的结果与模型试验结果基本一致,具有较高的工程应用价值。
王晓玲等[24]指出单裂隙岩体劈裂注浆过程中浆液与岩壁存在流固耦合作用,这种流固耦合作用随注浆压力的增加而增大,随裂隙宽度的增大而减小,但基本不随裂隙倾角的变化而变化。
程少振等[25]基于有限元(FEM)和流体体积函数法(VOF)对劈裂注浆规律进行深层探索。研究显示初次劈裂阶段地层的整体性和结构性改变较小,二次劈裂后斜向浆脉则迅速产生并扩展,其对土体的结构性改变较大,地层竖向位移随之增加(图6);注浆孔深度和土体的压缩模量对浆脉的宽度和劈裂缝的扩展形态影响较为显著,注浆深度增加和土体压缩模量增大则劈裂注浆效果变差。

图6 劈裂注浆发展形态
Fig.6 Development form of splitting grouting
3 结 语
作为注浆技术研究的一个重要分支,劈裂注浆技术研究取得了许多重要成果,有力地推动了注浆技术在工程项目建设中的应用。笔者分析了劈裂注浆的发展过程、能量消耗方式和劈裂压力衰减规律,并从裂隙岩体注浆、脉动注浆等理论方面对劈裂注浆的力学机理进行分析,然后从浆土应力耦和特性等方面对劈裂注浆试验研究进行探索分析,最后结合离散元和有限元数值计算对劈裂注浆机制进行了进一步揭示。劈裂注浆技术一系列重要研究成果的取得,将推动注浆技术在工程建设应用中的发展。
[1] YANG Z Q,HOU K P,GUO T T. Research on time-varying behavior of cement grouts of different water-cement ratios[J]. Applied Mechanics and Materials,2011,75:4398-4401.
[2] GUSTAFSON G,CLAESSON J,FRANSSON Å. Steering parameters for rock grouting[J]. Journal of Applied Mathematics,2013(1):1-9.
[3] BIRDSELL, DANIEL T,RAJARAM, et al. Imbibition of hydraulic fracturing fluids into partially saturated shale[J]. Water Resources Research,2015 (8):112-119.
[4] KITAZUME M,MARUYAMA K.Collapse failure of group column type deep mixing improved ground under embankment[C]/ /Proceedings of the International Conference on Deep Mixing 2005.US: ASCE,2005: 245-254.
[5] 张忠苗,邹 健.桩底劈裂注浆扩散半径和注浆压力研究[J].岩土工程学报,2008,30 (2):181-184.
ZHANG Zhongmiao,ZOU Jian.Penetration radius and grouting pressure in fracture grouting[J].Journal of Geotechnical Engineering,2008,30 (2):181-184.
[6] GUSTAFSON G,CLAESSON J,FRANSSON Å. Steering parameters for rock grouting[J]. Journal of Applied Mathematics,2013(1):1-9.
[7] 朱光轩,张庆松,刘人太,等.基于渗滤效应的沙层劈裂注浆扩散规律分析及其ALE算法[J].岩石力学与工程学报,2017,36(S2): 4167-4176.
ZHU Guangxuan, ZHANG Qingsong, LIU Rentai, et al. Analysis of fracturing grouting diffusion in sand considering filtration effects and its ALE algorithm[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(S2): 4167-4176.
[8] 李术才,刘人太,张庆松,等.基于黏度时变性的水泥-玻璃浆液扩散机制研究[J].岩石力学与工程学报,2013,32(12):2415-2421.
LI Shucai, LIU Rentai, ZHANG Qingsong, et al.Research on c-s slurry diffusion mechanism with time-dependent behavior of viscosity[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(12):2415-2421.
[9] 石明生.高聚物注浆材料特性与堤坝定向劈裂注浆机理研究[D].大连:大连理工大学,2011.
[10] 邹金锋,童无欺,罗 恒,等.基于Hoek-Brown强度准则的裂隙岩体劈裂注浆力学机理[J].中南大学学报:自然科学版,2013,44 (7):2889-2896.
ZOU Jinfeng,TONG Wuqi,LOU Heng,et al.Mechanics mechanism of split grouting in fractured rock mass based on Hoek-Brown strength criterion [J].Journal of Central South University:Natural Science Edition,2013,44 (7): 2889-2896.
[11] 张 淼,邹金锋,陈嘉祺,等.非对称荷载作用下土体劈裂注浆压力分析[J].岩土力学,2013 ,34(8):2255-2263.
ZHANG Miao,ZOU Jinfeng,CHEN Jiaqi,et al.Analysis of soil fracture grouting pressure under asymmetric load[J].Geotechnical Mechanics,2013,34(8):2255-2263.
[12] 郭炎伟,贺少辉,张安康,等.劈裂注浆复合土体三维等效弹性模型理论研究[J].岩土力学,2016,37 (7):1877-1886.
GUO Yanwei,HE Shaohui,ZHANG Ankang,et al.A three-dimensional equivalent elastic model of composite soils with fracturing grouting[J].Rock and Soil Mechanics,2016,37(7):1877-1886.
[13] 欧阳进武,张贵金,刘 杰.劈裂灌浆扩散机理研究[J].岩土工程学报,2018,40(7): 1328-1336.
OUYANG Jinwu, ZHANG Guijin, LIU Jie. Diffusion mechanism of split grouting[J].Journal of Geotechnical Engineering,2018,40(7): 1328-1336.
[14] 张乐文,辛冬冬,丁万涛,等.基于基床系数法的劈裂注浆过程分析[J].岩土工程学报,2018,40(3): 399-407.
ZHANG Lewen, XIN Dongdong, DING Wantao, et al.Process analysis of split grouting based on foundation bed coefficient method[J].Journal of Geotechnical Engineering,2018,40(3): 399-407.
[15] 李 鹏,张庆松,张 霄.基于模型试验的劈裂注浆机制分析[J].岩土力学,2014,35(11): 3221-3230.
LI Peng, ZHANG Qingsong, ZHANG Xiao.Analysis of fracture grouting mechanism based on model test[J].Geotechnical Mechanics,2014,35(11): 3221-3230.
[16] 李 鹏,张庆松,王 倩,等.隧道泥质断层多序注浆动态劈裂扩散规律[J].中国公路学报,2018,31(10): 328-338.
LI Peng, ZHANG Qingsong, WANG Qian, et al. Dynamic splitting and diffusion law of multi sequence grouting in tunnel mud fault [J]. Journal of China Highway, 2018, 31 (10): 328-338.
[17] 张庆松,张连震,刘人太,等.基于“浆-土”界面应力耦合效应的劈裂注浆理论研究[J].岩土工程学报,2016,38(2):323-330.
ZHANG Qingsong, ZHANG Lianzhen, LIU Rentai, et al. Split grouting theory based on slurry-soil coupling effects[J].Journal of Geotechnical Engineering,2016,38(2): 323-330.
[18] 王 凯,李术才,杨 磊,等.全风化花岗岩加固特性注浆模拟试验[J].天津大学学报:自然科学与工程技术版,2017,50(11): 1219-1229.
WANG Kai, LI Shucai, YANG Lei, et al. Grouting simulation experiment on reinforcement characteristics of completely decomposedGranite[J].Journal of Tianjin University:Science and Technology,2017,50(11): 1219-1229.
[19] 李相辉, 张庆松, 张 霄,等.非均质断层破碎带注浆扩散机理[J].工程科学与技术,2018,50(2):67-76.
LI Xianghui, ZHANG Qingsong, ZHANG Xiao, et al. Grouting diffusion mechanism in heterogeneous fault-fracture zone[J].Advanced Engineering Sciences,2018,50(2): 67-76.
[20] 张家奇,李术才,张 霄,等.土石分层介质注浆扩散的试验研究[J].浙江大学学报,2018,52(5): 914-924.
ZHANG Jiaqi, LI Shucai, ZHANG Xiao, et al. Model test on grouting diffusion in rock and soil layered medium[J].Journal of Zhejiang University,2018,52(5): 914-924.
[21] 杨 磊,林荣峰,李召峰,等.水泥浆液黏度对全风化花岗岩注浆加固效果的影响[J].中国公路学报,2018,31(10):246-254.
YANG Lei, LIN Rongfeng, LI Zhaofeng, et al. Influence of grout viscosity on the grouting reinforcement effect of completely weathered Granite[J]. China Journal of Highway and Transportation, 2018,31(10): 246-254.
[22] 郑 刚,张晓双.劈裂注浆过程的二维颗粒流的模拟研究[J].厦门大学学报:自然科学版,2015,54(6): 905-912.
ZHENG Gang, ZHANG Xiaoshuang. Meso-mechanical simulation of fracture grouting using particle flow code in two dimensions[J]. Journal of Xiamen University:Natural Science, 2015,54(6): 905-912.
[23] 朱 旻,龚晓南,高 翔,等.基于流体体积法的劈裂注浆有限元分析[J].岩土力学,2019,40 (11):1-11.
ZHU Min, GONGXiaonan, GAO Xiang,et al.FEM/VOF analysis of fracture grouting[J].Rock and Soil Mechanics,2019,40(11):1-11.
[24] 王晓玲,刘长欣,李瑞金,等.大坝基岩单裂隙灌浆流固耦合模拟研究[J].天津大学学报:自然科学版,2017,50(10):1037-1046.
WANG Xiaoling, LIU Changxin, LI Ruijin, et al.Fluid-solid coupling simulation of single fracture grouting in dam bedrock[J]. Journal of Tianjin University:Science and Technology, 2017, 50(10): 1037-1046.
[25] 程少振,陈铁林,郭玮卿.土体劈裂注浆过程的数值模拟及浆脉形态影响因素分析[J].岩土工程学报,2019,41(3):1667-1676.
CHENG Shaozhen, CHEN Tielin, GUO Weiqing. Numerical simulation of fracture grouting and analysis of influencing factors of grout vein morphology[J].Journal of Geotechnical Engineering,2019,41(3): 1667-1676.
