0 引 言
矿井涌水量是矿井水害防治工作的一个十分关键基础数据,伴随矿井整个生产周期,是矿井生产系统特别是防排水系统设计及其水害防治技术方案与技术路线选择的基础[1]。在矿井水害防治技术进程中,形成了多种关于矿井涌水量预测计算的理论和方法[2-3],随着绿色、高效矿井建设的持续推进,煤矿对于涌水预测的结果精细度、预测方法的适用性等要求也在逐步提高。而相关理论研究和防治水实践中关于矿井涌水量的定义、预测方法有待改进,缺乏完善的矿井涌水量预测结果的准确性判定方法,难以实现矿井涌水量的预测、实际涌水量的统计、结果准确性判定等涌水量计算全过程的闭环,进而提升涌水量预测的技术水平。
笔者针对以上问题,综合当前各类规范以及科研成果和前人的论述,探讨矿井涌水量的定义,阐述矿井涌水量的主要计算方法在实际应用中的改进方案,分析矿井正常涌水量、最大涌水量在各类定义和煤矿实践过程中的统计差异,论述矿井涌水量预测结果准确性判定的基本方法。从而促进矿井涌水量预测方法、理论的不断完善,预测精度的持续提高,为煤矿的安全、绿色开采提供支撑。
1 矿井预测涌水量与实际涌水量差异性
矿井涌水量一般分为正常涌水量和最大涌水量,《煤矿防治水细则》[4]中(以下简称《细则》)对矿井正常涌水量的定义为:指矿井开采期间,单位时间内流入矿井的平均水量。一般以年度作为统计区间[4]。该定义强调了涌水量的时间段特征,为平均水量。矿井最大涌水量,是指矿井开采期间,正常情况下矿井涌水量的高峰值[5]。最大涌水量主要与采动影响或降水量有关,不包括矿井灾害水量,一般也以年度作为统计区间取最大值。而对于矿井预测涌水量也是如此,将正常涌水量和最大涌水量分别预测。不同之处在于:预测正常涌水量和预测最大涌水量针对的是某一生产阶段或时间节点,而且为了保障所预测的水量包含了整个生产过程,各项参数会取在阶段性生产过程完成时,采用各类计算方法得到的涌水量值,一般多属于预测生产阶段内正常涌水量的峰值,尤其是解析法计算的涌水量。但该预测值属于瞬时量,而非《细则》中计算的平均量(如矿井实际涌水量处在稳定增长阶段,则平均量接近生产阶段中期的水量),强调了生产的空间过程。由于《细则》定义的矿井正常涌水量强调了时间过程(1年内),而预测的正常涌水量则强调了空间过程(某个水平或者盘区、工作面),两者一般不能完全对应起来(图1,表1)。
此外,预测最大涌水量一般在预测正常涌水量的基础上乘以一个最大系数所得(一般取1.2~3.0)。其意义在于计算出该生产阶段涌水量的上限值,目的在于保障计算误差处在矿井可接受的范围之内。预测最大涌水量也属于瞬时涌水量,而与《细则》中所定义的某一个时间段内的峰值量的意义不同,则有: 矿井涌水量一直处在稳定增长阶段,则2个数值才有可能重合;矿井实测涌水量的依据为井下涌水量台账,每个生产节点都只会有一个涌水量数据,而该数据是唯一的,该节点不可能存在有最大涌水量。但从整个年度来看,会有最大涌水量,该涌水量数值与《细则》中定义的最大涌水量值相对应。
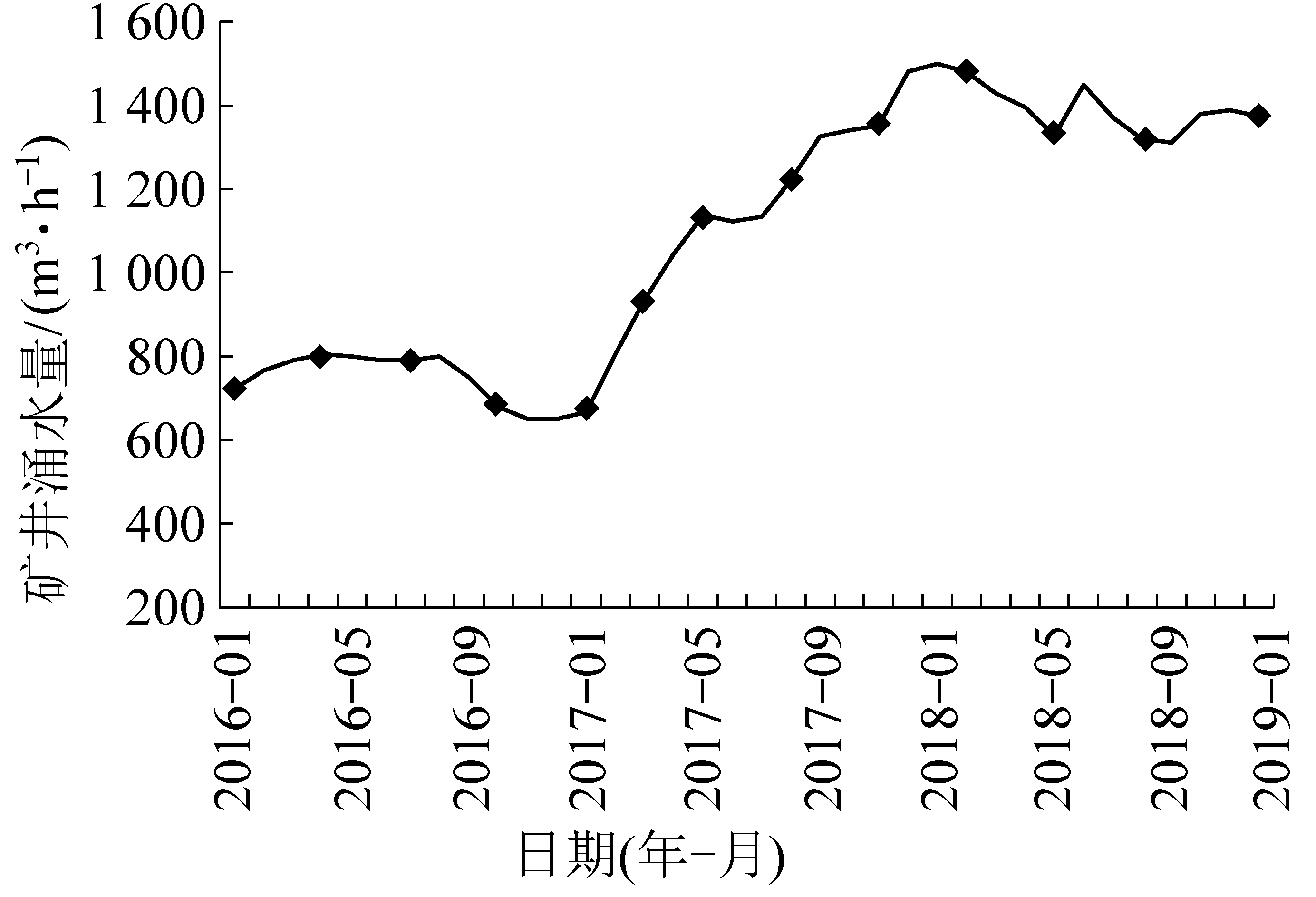
图1 蒙陕地区某矿井涌水量历时曲线
Fig.1 Duration curve of water inflow from a
mine in Inner Mongolia-Shaan Area
表1 蒙陕地区某煤矿不同定义下矿井涌水量对比
Table 1 Comparison of mine water inflow under different
definitions of a coal mine in Inner Mongolia-Shaan Area
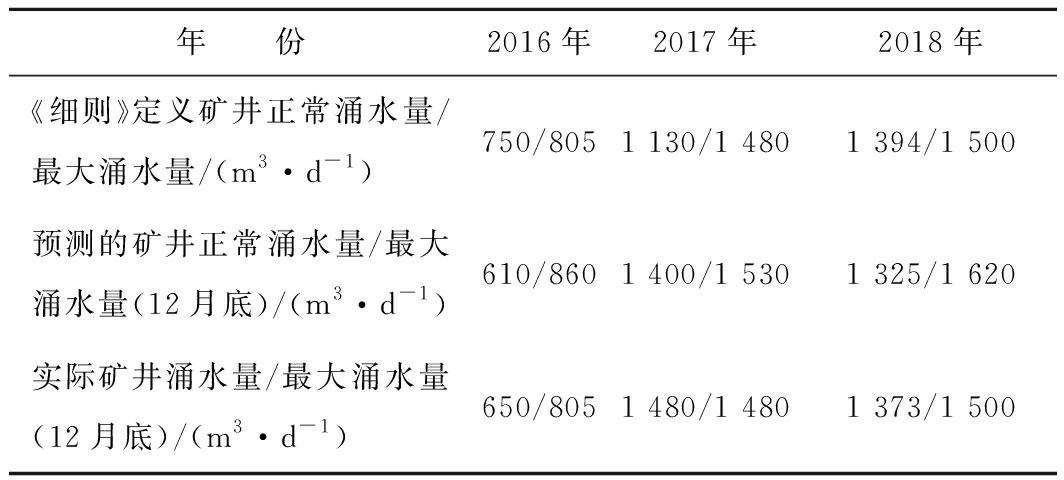
年 份2016年2017年2018年《细则》定义矿井正常涌水量/最大涌水量/(m3·d-1)750/8051 130/1 4801 394/1 500预测的矿井正常涌水量/最大涌水量(12月底)/(m3·d-1)610/8601 400/1 5301 325/1 620实际矿井涌水量/最大涌水量(12月底)/(m3·d-1)650/8051 480/1 4801 373/1 500
综合来看,矿井涌水量的预测与实践,必须以涌水量台账为根本。①涌水量台账的记录应尽量详细,除了记录观测时间外,还应详细记录各观测点的位置以及采掘进尺变化情况;②涌水量预测前,引用涌水量台账过程中,在利用“大井法”和“廊道法”等各类确定性分析方法时,应以不同回采距离对应的瞬时水量台账值为准,而非《细则》中所定义的矿井涌水量值(统计意义上的数值,忽略了涌水量数据随回采距离变化的规律性)。③对于煤矿来说,从年度角度出发,可以参考《细则》进行正常涌水量和最大涌水量的统计,但在具体实践过程中,应当以台账为基础,结合当前矿井所处的开采阶段,来阐述矿井的涌水情况。
2 矿井涌水量的概念与计算方法
2.1 矿井涌水量概念
在《煤矿防治水细则》中将矿井涌水量定义为:矿井开采期间,单位时间流入矿井的水量。虎维岳等[1]认为以上定义对矿井涌水量概念定义不清,使得预测结果对生产实际的指导性不足,并重新提出了矿井涌水量的定义:“在矿井建设或生产过程中,矿井采掘工程直接或间接揭露或导通某种充水水源的水,使其在特定时段和区段单位时间内流入矿井的总水量,特定的时间段是指矿井所处的特定生产期间(如井筒建设期、首采面回采期、一水平开采期等),特定的区段是指矿井某个生产区域(如水平、采区、工作面等)”。主要特点为:①强调了矿井涌水量是因矿井采掘活动诱发的,充水水源的水自然地、无法控制地流入矿井,没有把人为的、通过专门的疏放水工程疏放出来的水量归结为矿井涌水量。②强调了流入矿井的水总量是特定生产阶段的对应水量,因此必须是个一个动态变化值[6]。以上论述值得商榷:在生产实际的涌水量统计、预测过程中,一般矿井涌水量主要为排水系统设计及水害防治提供直接依据,对于疏放水量和井下生产用水等人为流入水量,如果不计入矿井涌水量,则可能对矿井的系统设计造成严重的误判(比如,部分煤矿的井下疏放水水量超过其他所有水量之和),进而威胁矿井安全。此外,矿井疏放水的目的、方法以及结果评价均属于矿井水害防治的范畴,不将疏放水量纳入到矿井涌水量之中,难以真正使得涌水量统计、预测工作有效服务于矿井安全生产。
笔者认为,矿井涌水量的定义,应当从服务生产实际出发,不应仅考虑矿井的水文地质特征以及采掘实际,而忽略了疏放水工程、井下生产用水等产生的水量。与此同时,矿井涌水量的概念应该是从发生事实角度的定义,其还有统计意义:分析涌水量的总体水平及矿井水文地质条件,总结水量预测结果的准确性,优化排水系统布置,与矿井涌水量预测有着十分明显的区别:由于矿井的生产是个长期、缓慢的发展过程,因此每个矿井涌水量必然对应着特定的时间和生产阶段,也导致了矿井涌水量本身具备了特定时间、特定生产阶段的属性。相应地,矿井涌水量预测则面向的是未来的长期过程,在进行预测时尤其需要考虑或强调采掘阶段性特征来满足生产实践。通过这两者的计算可做明显对比:矿井涌水量计算当前主要通过井下水泵房的排水记录来推断或者井下各涌水点的水量实测值相加,其目的还在于进行水量的总体统计分析;而矿井涌水量预测的计算方法则包含了解析法、数值法、水文地质比拟法等各类方法。但综合来看,虎维岳等对于矿井涌水量的定义更多是结合了矿井涌水量预测的要求,而非矿井涌水量本身意义。进而从广义属性特征来说,矿井涌水量应该同时具备统计属性、水文属性和生产属性。基于以上分析,笔者对矿井涌水量进行了重新定义:矿井涌水量是指矿井在某一生产阶段,单位时间内井下各出水点涌水量总和。该定义方式可以体现涌水量的统计属性之外,也说明了矿井的涌水量是在不同生产阶段或者不同生产区域的水量叠加的总和,兼有了上述3重属性。
2.2 矿井涌水量预测计算方法改进
如前文所述,矿井涌水量是井下各个涌水点的水量之和,矿井涌水量预测实际上是结合生产规划,在分析矿井涌水量各组成的前提下,运用水文地质、数学地质方法,针对井下一个或多个涌水点,开展水量预测,并将水量结果进行叠加分析,进而得到矿井涌水量的过程。因此,下文所述的矿井涌水量预测方法皆是针对涌水点(重点是回采工作面)的计算方法,不再赘述。
2.2.1 涌水量预测的基本要求
为了使预测涌水量也能够具备统计属性、水文属性和生产属性。提出涌水量的预测结果应该包含了3个数值:①矿井预测正常涌水量,取该生产阶段结束时的预测矿井涌水量;②矿井预测最大涌水量,一般取矿井预测正常涌水量的1.2~3.0倍,具体倍数值可参考以往最大涌水量与实际正常涌水量的比值确定;③矿井预测平均涌水量,取该生产阶段内典型节点(年初、年终、年底)处进行正常涌水量预测,结合生产进度、充水通道的变化特征以及含水层与采动空间之间的补给关系进行涌水量的精细预测,绘制涌水量预测曲线,利用该曲线求取矿井的平均涌水量。
2.2.2 矿井涌水量预测改进方法
通过统计多个煤矿的工作面和开采年代久远的矿井涌水量曲线发现,工作面的最大涌水量多不会出现在工作面回采结束或者闭坑时,而这与传统的水文地质理论计算结果相矛盾:无限边界条件下,采动影响的范围越大,则涌水量越大[7-8]。为此,提出以下涌水量预测的改进方法以使得涌水量预测结果满足实际需求。
2.2.2.1 解析法
将矿井涌水量概化为充水水源与充水通道综合作用的结果,重点结合充水通道的动态变化特征以及含水层与充水通道间的补给关系,说明“解析法”的改进方法。
1)“大井法”的理论基础是井壁四周进水模型,概化为抽水井,水井内部不含水[9]。但作为井下主要涌水点的回采工作面,当前现代化高效回采方式下,单个工作面的走向长度一般为2 000~6 000 m,倾向长度120~400 m,因此工作面内部的静储量Qj无法忽略。而大井法实际上计算的是工作面回采后的动态补给量Qd1。此外,对于导水裂隙带未直接导通但其与直接充水含水层间无稳定隔水层的巨厚含水层,其垂向动态补给量Qd也不可忽略。这部分水量可以按照“顶板+井壁”的出水模式计算[10],顶板出水面概化为圆形,通过圆形补给周长与垂向渗透系数、水位降深之积得到Qd2。则工作面的实测涌水量应该是:Q=Qj+Qd1+Qd2,其中静储量Qj以重力释水为主,可以用重力给水度、开采冒落面积和充水含水层厚度的乘积求得;导水裂隙带直接导通范围内的含水层厚度按照实际厚度计算,而对于未直接导通但中间无稳定隔水层的其他部分含水层厚度,也可引入抽水“有效带”的概念[11-12],将非完整井群涌水量计算转化为等效完整井群涌水量计算。
2)对于“大井法”而言,关键在于确定参数,尤其是渗透系数K和含水层厚度M,这2个对涌水量计算结果敏感度最高的参数[13]。一般渗透系数是通过抽水试验或者井下放水试验得到,但地面抽水试验得到的参数结果普遍偏小,而井下放水试验的结果却普遍偏大。为此,为了能够得到较为准确的K,应该以实际回采过的工作面涌水量进行K的反算,并结合地面和井下的水文孔进行综合计算,而该方法得到的数值较为准确。对于未进行过工作面回采的矿井,可以参考周边矿井的反算渗透系数和本矿井的水文试验数据综合得到。如前文所述,不同的导水裂隙带发育高度下,对应着不同的涌水模式。但对于一个工作面来说,导水裂隙带是逐步发育的,因此含水层的厚度值也应当是动态变化的。如一个倾向长度300 m的工作面,其导水裂隙带一般在一次见方附近发育到顶界面,因此对于前300 m的涌水量预测,应该通过预测导水裂隙带的动态发育特征来确定不同的充水含水层厚度值来进行计算[14-15]。
2.2.2.2 水文地质比拟法
水文地质比拟法属于当前矿井涌水量预测中最为简单、直接的一类方法,可以规避大量的参数计算,默认部分参数相似或者相等来进行计算[16]。对于开采程度较高的矿井,预测的准确性也较高。除了常用的“富水系数比拟法”、“单宽流量比拟法”等比拟方法外[17],还可以用以下方法进行计算:
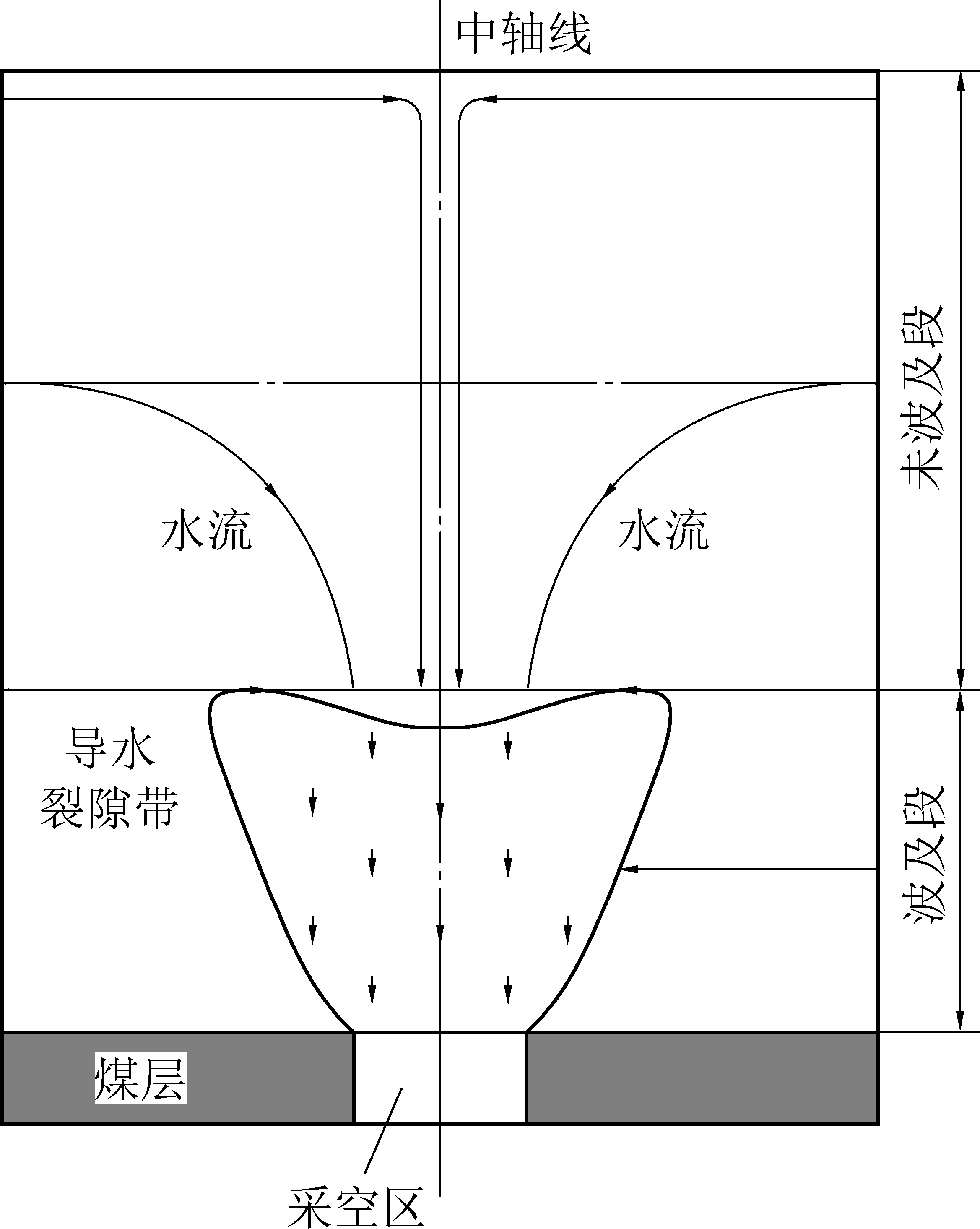
图2 巨厚含水层“顶板+井壁”涌水模式[10]
Fig.1 Water irushing model diagram of “roof + sidewall”in
thick aquifer[10]
1)相邻次采工作面“同频率放大法”。对于次采的相邻工作面涌水量精细预测,由于难以直接判定首采工作面回采对次采工作面的影响,因此预测的精准程度较低。可以参考工程水文学中对于“洪水过程线”计算时采用的“同频率放大法”[18]进行计算:依据首采工作面的单宽流量(双侧进水)比拟计算出未采面的总体水量(单侧进水)。将2个水量的比值记作k,即
k=Q2/Q1
(1)
式中:Q1为首采工作面采空涌水量,m3/h;Q2为次采工作面采空区涌水量,m3/h。
在此基础之上,将首采工作面的涌水量曲线放大(缩小)k倍,即可得到次采工作面涌水量与进尺的曲线图。
2)远距离次采工作面多因素综合比拟法。比拟计算的前提是2个工作面参数相近,但受到回采以及工作面距离远的影响,工作面的水文地质参数发生变化,尤其是含水层的水位、厚度与已采工作面有较大差异,因此还需要考虑多因素进行比拟[19]。多因素比拟所采取的公式为
(2)
式中:Q为待采工作面的预测涌水量;Q0、F0、S0为已知的工作面涌水量、开采面积和相应的水位降深;F、S为预测工作面的开采面积和水位降深;X、Y为待定系数,据已采工作面涌水量进行拟合确定。
2.2.2.3 时间序列分析法
其基本思想是利用分段线性化的方法来处理非线性动态数据[20]。由于门限值的控制作用,门限自回归模型对于模拟类似跳跃、共振等非线性特征有较强大的功能,适用于开采年代久远的矿井涌水量预测[21]。涌水量的时间序列{Qt}自相关可用如下数学模型表示为
![]()
rj-1<Qt-d<rj j=1,2,…,l
(3)
式中:rj为门限值;d为延迟步长;kj为第j个分段的阶;![]() 均为模型的系数;
均为模型的系数;![]() 为第j个门限自回归模型的白噪声;l为模型的个数。
为第j个门限自回归模型的白噪声;l为模型的个数。
但受限于。因上述方法受限于模型的预测步长(SETAR模型的预测步长不能超过延迟步长d),通过自激励门限回归建立的模型并不能够预测较长时间段内的矿井涌水量。而是对于矿井的生产建设来说,必须要将短期及时性预测与长期总体性预测相结合,才能更好的指导矿井的安全生产。
通过有效利用矿井多年来的涌水量资料,可采用水文地质比拟法进行矿井涌水量的长期总体性预测;应用自激励门限自回归进行矿井即时预测,两者配合使用,实现对矿井涌水量预测周期的延长和预测精度的提高[22-23];该预测方法可以有效减少一般回归分析对于其他相关因素数据的依赖,更适应于水文地质条件复杂或者水文资料相对匮乏矿井的涌水量预测。
3 矿井涌水量预测准确性判定
在进行涌水量预测过程中难以避免地要出现模型误差、观测误差、截断误差、舍入误差[24]。导致预测结果与实际涌水量存在一定的偏差,对这种偏差或者涌水量准确性的判定,不仅可以评价相关预测成果的科学性和可靠程度,更是煤矿及相关科研单位不断优化科研成果,开展后续防治水工作的基本。
3.1 当前涌水量预测准确性判定存在的问题
如前文所述,当前对涌水量的认识存在分歧以及忽视技术背景条件使得对矿井预测涌水量准确性判定中存在明显不足。
3.1.1 涌水量预测结果认识存在分歧
煤矿要判定某个回采工作面的涌水量预测结果是否准确,当前判定方法多如下:将该工作面预测最大涌水量(解析计算以及比拟法计算的最大涌水量多出现在回采结束时)与整个工作面回采过程中的最大涌水量进行对比(该最大涌水量一般多不出现在回采结束时,图3、图4),如果两者相差较小,则认为计算较为准确,反之则认为计算结果差距较大。
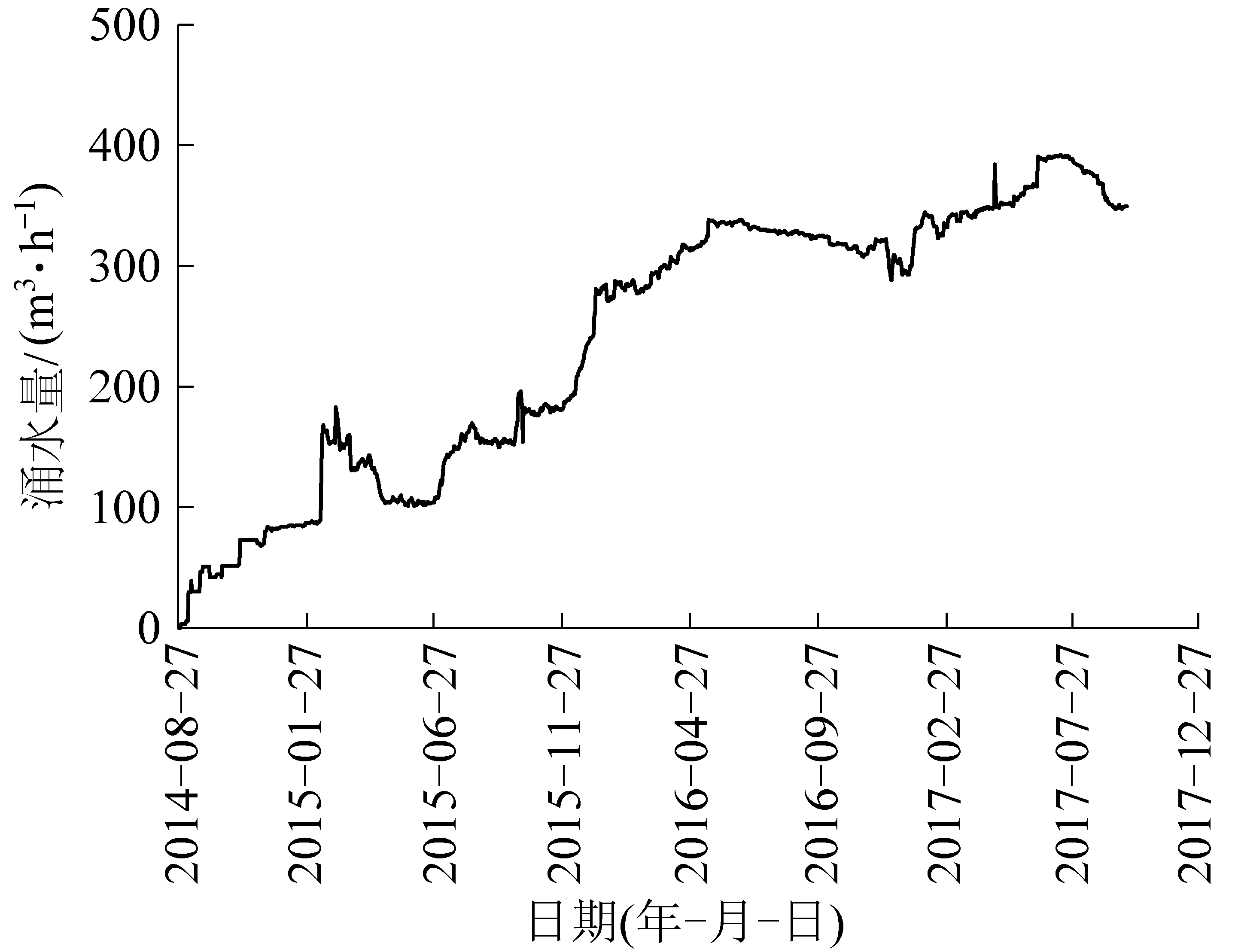
图3 某矿3101工作面涌水量历时曲线
Fig.3 Duration curve of water inflow in No.3101 working face
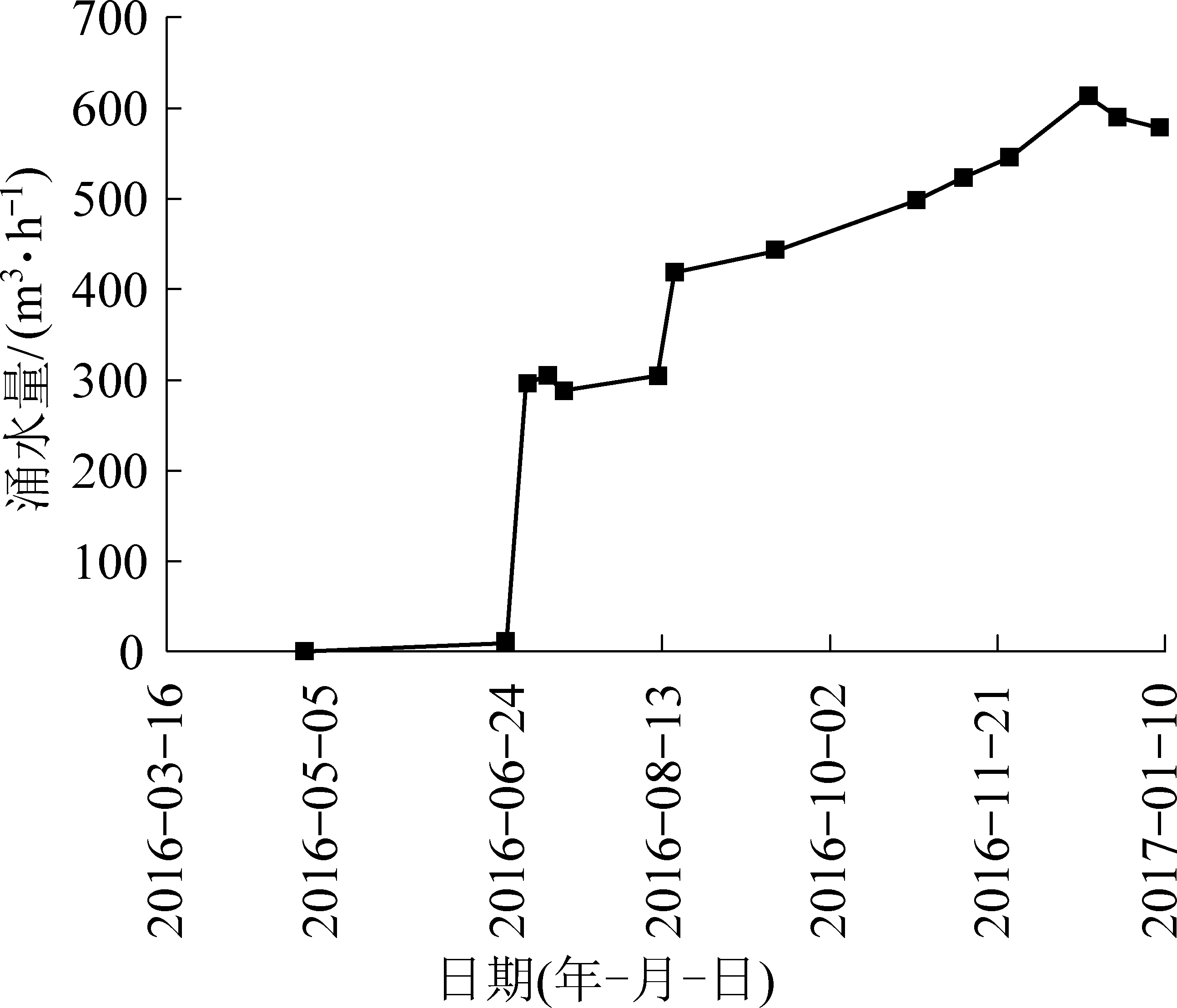
图4 某矿201工作面涌水量历时曲线
Fig.4 Duration curve of water inflow in No.201 working face
这样的比较方法,没有将涌水量预测与实际水量的预测固定在同一参数背景下(同一个生产节点),也使得矿井涌水量的预测结果准确性判定存在有明显的错误,对于矿井防治水工作存在严重的误导。
3.1.2 忽视了涌水量预测的技术条件
经过多年的技术发展,矿井涌水量预测已经朝着精细化方向发展,也使得矿井涌水量预测多以煤矿的采掘规划为依据,这个采掘规划包含了回采区的范围、面积、接续方法、回采方式等技术参数。而由于井下施工条件的复杂性,回采范围以及接续方式等涌水量计算的基础参数可能发生变化,但煤矿易忽略技术条件的变化,此时依然用改变前的预测结果去与现有技术参数下的实际涌水量进行对比,进而使得预测结果多与实际差距较大。
3.2 涌水量预测结果准确性判定方法
文献[25-26]依据GB15218—94《地下水资源分类分级标准》与GB 12719—91《矿区水文地质工程地质勘探规范》,根据不同的勘查研究程度和计算方法求得的矿井涌水量,可以认定为不同的精度级别。但其针对的是勘探阶段的矿井涌水量预测,预测的范围多为整个井田或者盘区,难以真正有效指导生产。而当前的生产实践要求涌水量预测须结合不同阶段的采掘规划进行精细计算,并在同一生产节点下,与实际水量值进行对比分析,从而确定同一生产阶段涌水量预测值的准确性。当前的准确性对比判定主要有如下2种方法。
1)涌水量绝对差值判定法:按照预测的正常涌水量的与实际涌水量差值的绝对值进行确定。如某矿在某一具体的生产阶段涌水量为:Qs,而对应生产阶段的预测涌水量结果为Qy,则Qc=Qy-Qs为预测涌水量Qy的绝对差值。当Qc<0时,Qc为亏预测量或者弱预测涌水量,当Qc>0时,Qc为盈预测量或者强预测涌水量。而为了保障矿井的排水安全,多出现了的是盈预测量或强预测量。而对于具体绝对差值为多少才算是偏差大,难以指导实践,尚没有可以确定的标准。主要在于用绝对差值来判定预测涌水量的准确程度存在较大的局限性,在不同水文条件的矿井,其难以具备普遍适用的特征。如实际涌水量为1 000和100 m3/h的2个矿井,若其预测涌水量和实际涌水量绝对差值均为10 m3/h,但显然前者的准确程度要高于后者。由此可知,决定涌水量预测准的确程度,除了要计算绝对差值,还有考虑该矿井实际涌水量本身的大小,进而提出涌水量的相对差值判定法。
2)涌水量相对差值判定法:该方法按照预测的矿井涌水量和实际涌水量差值与实际值的比值确定。如某矿在确定的生产阶段的涌水量为:Qs,而对应生产阶段的预测涌水量结果为Qy,则Qr=(Qy-Qs)/Qs为预测涌水量Qy的相对差值。根据上述定义可知,实际涌水量为1 000和100 m3/h的2个矿井,预测涌水量和实际涌水量绝对差值都为10 m3/h的预测结果,前者的相对误差为1%,而后者的相对误差为10%,可见前者的准确程度要远高于后者。类似与绝对差值限,为了使得涌水量预测结果可以指导实践,须确定相对差值限或者相对差值上限δ,使得|Qr|=|(Qy-Qs)/Qs|≤δ。δ 越小,则预测的精度越高。在实践中如何确定δ至关重要。笔者提出以矿井排水安全为根本,δ判定方法为:考虑到煤矿设置排水系统时要求能在20 h内排出24 h的水,即:排水系统设置仅高于预测水量值的20%。因此涌水量的预测相对差值最大不超过-20%,否则威胁矿井安全。考虑0.5的保险系数,则认为该涌水量预测值弱相对差值最大不超过-10%,而强相对差值则主要考虑涌水量预测过大带来的防治水工程建设投入过大,将强相对差值限设置为20%。此外,按照涌水量预测的相对差值,进一步将涌水量预测的准确程度按照准确至不准确或偏离,以涌水量预测的主要功能为导向,可以细分经济型(Ⅰ)、安全型(Ⅱ)和偏离型(Ⅲ)3个等级,具体见表2。
事实上,相对差值可以转化为绝对差值的表达方式。参考上述标准,可以根据矿井水文地质条件的不同,尤其是涌水量的不同,采用涌水量绝对差值进行准确等级的判定,如水文地质条件中等,涌水量小于且接近600 m3/h的矿井,其涌水量预测结果的准确程度判定标准可如表3,其他水文条件的矿井,也可以参考表2进行预测水量准确性的判定。
表2 以相对差值计算的涌水量预测准确性等级判定标准
Table 2 Criteria for determining the accuracy of water
inflow prediction calculated by relative difference

序号相对差值/%预测准确性等级1-10~10经济型(Ⅰ)210~20安全型(Ⅱ)3<-10或>20偏离型(Ⅲ)
表3 以绝对差值计算的涌水量预测准确性等级判定标准
Table 3 Criteria for determining accuracy of water in
flow prediction calculated by absolute difference

序号绝对差值/%预测准确性等级1-60~60经济型(Ⅰ)260~120安全型(Ⅱ)3<-60或>120偏离型(Ⅲ)
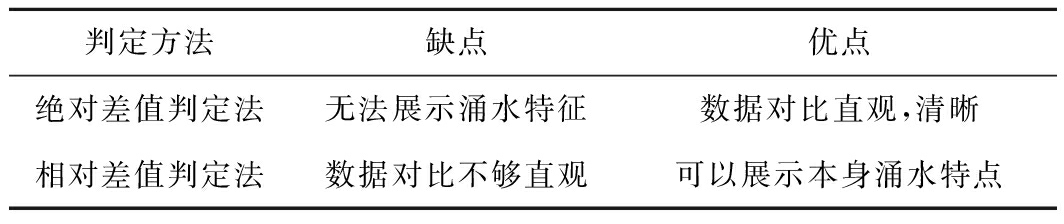
总体而言,采用绝对差值和相对差值判定这两种方法各有优缺点(表4),可以将两者结合使用。
但需要注意的是,对于预测涌水量准确性的判定,其主要针对的是涌水量中等及以上的情况,而对于正常涌水量小于50 m3/h,最大涌水量小于100 m3/h的矿井,由于难以避免的要出现模型误差、观测误差、截断误差、舍入误差等因素存在,因而实际值与预测值必然有一定差值。而当实际值较小时,绝对差值小,但相对差值大,进而使得两者判定方法得出完全不同的结论,此时必须结合矿井实际的排水系统设置进行准确性判定,而非仅依靠某一种判定方法。
表4 涌水量准确性判定方法对比
Table 4 Comparison of methods for determining
the accuracy of water inflow
判定方法缺点优点绝对差值判定法无法展示涌水特征数据对比直观,清晰相对差值判定法数据对比不够直观可以展示本身涌水特点
4 结 论
1)提出了矿井涌水量的属性特征包含统计属性、水文属性和生产属性,矿井涌水量可以定义为:矿井在某一生产阶段时,单位时间内井下各涌水点涌水量之和。
2)阐述了“大井法”计算矿井涌水量应当包含静储量Qj和导水裂隙带直接导通含水层的动态补给量Qd1和巨厚含水层未直接导通部分的动态补给量Qd2三部分,提出了利用“同频率放大法”改进水文地质比拟法,得到预测涌水量的动态曲线;将时间序列分析和水文地质比拟相结合提高预测步长(周期),增强时间序列分析的适用性,从而实现涌水量的精细、动态预测。
3)提出采用“绝对差值法”和“相对差值法”进行矿井预测涌水量准确性判定,并以涌水量预测的主要功能为导向,将预测结果的准确性由高到低分成经济型、安全型、偏离型3种不同等级,并建立了对应的分级标准。
4)通过统一技术背景(生产节点或阶段),可以实现矿井涌水量的统计、预测计算和结果准确性判定在技术上的闭环。
5)建议在相关规范、《细则》中加入矿井涌水量准确性的判定标准,对于提高涌水量预测精度,推动矿井水害防治技术进步具有重要意义。
[1] 虎维岳,闫 丽.对矿井涌水量预测问题的分析与思考[J]. 煤炭科学技术,2016,44(1):13-18.
HU Weiyue,YAN Li. Analysis and consideration on prediction problems of mine water inflow volume[J]. Coal Science and Technology,2016,44(1):13-18.
[2] 陈酩知,刘树才,杨国勇. 矿井涌水量预测方法的发展[J]. 工程地球物理学报,2009,6(1):68-72.
CHEN Mingzhi,LIU Shucai,YANG Guoyong. The develop ment of mining water inflow predict method[J].Chinese Journal of Engineering Geophysics,2009,6(1):68-72.
[3] 杜敏铭,邓英尔,许 模. 矿井涌水量预测方法综述[J]. 四川地质学报,2009,29(1):70-73.
DU Minming,DENG Yinger,XU Mo. Review of methodo- logy for prediction of water yield of mine[J].Acta Geologica Sichuan,2009,29 (1):70-73.
[4] 国家煤矿安全监察局.煤矿防治水细则[M]. 北京:煤炭工业出版社,2018.
[5] 邵震杰,任文忠,陈家良 .煤田地质学[M].北京:煤炭工业出版社,1993.
[6] 虎维岳,周建军. 煤矿水害防治技术工作中几个易混淆概念的分析[J]. 煤炭科学技术,2017,45(8):60-65.
HU Weiyue,ZHOU Jianjun. Discussion on some confused key concepts used in mine water disaster control and protection[J]. Coal Science and Technology,2017,45(8):60-65.
[7] 靳德武,乔 伟,李 鹏,等.煤矿防治水智能化技术与装备研究现状及展望[J].煤炭科学技术,2019,47(3):10-17.
JIN Dewu,QIAO Wei,LI Peng,et al.Research status and prospects on intelligent technology and equipment for mine water hazard prevention and control[J].Coal Science and Technology,2019,47(3):10-17.
[8] 李超峰,虎维岳. 回采工作面顶板复合含水层涌水量时空组成及过程预测方法[J]. 水文地质工程地质,2018,281(3):7-19.
LI Chaofeng,HU Weiyue. Prediction method of mine water inflow regime from a layered extra-thick aquifer[J]. Hydro geology & Engineering Geology,2018. 281(3):7-19.
[9] 陈思佳,骆祖江. “分段大井法”预测矿井工作面涌水量[J]. 中国煤炭地质,2016,25(1):41-43.
CHENSijia,LUO Zujiang . Mine working face water inflow prediction through“ segmental virtual large diameter well method”[J]. Coal Geology of China,2016,25(1):41-43.
[10] 罗安昆,王 皓,郭小铭. 巨厚含水层采动影响下矿井涌水量预测[J]. 煤矿安全,2017,48(9):182-185.
LUOAnkun ,WANG Hao,GUO Xiaoming. Prediction of water inflow under the influence of mining of thick aquifer[J]. Safety in Coal Mines,2017,48(9):182-185.
[11] 刘俊龙. 潜水含水层中的非完整井降水设计计算探讨[J]. 岩土工程技术,2002(5):297-301.
LIU Junlong. Research on the simplified method of design for dewatering by annular partially penetrated wells in phreatic aquifer[J]. Geotechnical Engineering Technique,2002(5):297-301.
[12] 张惠昌. 大厚度含水层“有效带”和滤水管合理长度的探讨[J]. 兰州大学学报(自然科学版),1989,25(4):118-123.
ZHANGHuichang. Discussion on the effective zone in large thiCk water bearing strata and the rational length of filter tube[J]. Journal of Lanzhou University(Natural Sciences),1989,25(4):118-123.
[13] 王科奇,刘佩贵,陶月赞,等. 矿坑涌水量预测模型参数灵敏度分析[J]. 合肥工业大学学报(自然科学版),2017,40(4):502-505.
WANGKeqi,LI Peigui,TAO Yuezan,et al. Sensitivity analysis for forecasting model parameters of mine water inflow[J]. Journal of Hefei University of Technology(Natural Science),2017,40(4):502-505.
[14] 周振方,靳德武,虎维岳,等.煤矿工作面推采采空区涌水双指数动态衰减动力学研究[J]. 煤炭学报,2018,43(9):225-232.
ZHOU Zhenfang,JIN Dewu,HU Weiyue,et al. Double-exponential variation law of water-inflow from roof aquifer in goaf of working face with mining process[J]. Journal of China Coal Society,2018,43(9):225-232.
[15] 刘英锋,郭小铭. 导水裂缝带部分波及顶板含水层条件下涌水量预测[J]. 煤田地质与勘探,2016,44(5):97-101.
LIU Yingfeng,GUO Xiaoming. Prediction of water inflow in roof aquifer affected by water-flowing fracture zone[J]. Coal Geology & Exploration,2016,44(5):97-101.
[16] 甘圣丰,乔 伟,雷利剑,等. 招贤煤矿水文地质特征及涌水量预测研究[J]. 煤炭科学技术,2018,46(7):210-217.
GAN Shengfeng,QIAO Wei,LEI Lijian,et al.Study on hydro- geological features and mine water inflow prediction in Zhaoxian Mine[J]. Coal Science and Technology,2018,46(7):205-212.
[17] 张人权 .水文地质学基础[M]. 6版.北京:地质出版社,2011.
[18] 姚瑞虎,覃光华,丁 晶,等. 基于概化洪水过程的水库防洪安全计算[J]. 中国农村水利水电,2018(1):75-80.
YAO Ruihu,QIN Guanghua,DING Jing,et al. Estimation of safety for reservoir flood prevention based on generalized flood hydrograph[J]. China Rural Water & Hydropower,2018(1):75-80.
[19] 郑 纲,何 渊.深埋矿井超大工作面顶板砂岩含水层涌水量预测方法[J].煤矿安全,2015,46(S1):76-80.
ZHENG Gang,HE Yuan.Prediction of roof sandstone water discharge at super large working face in deep mine[J]. Safety in Coal Mines,2015,46(S1):76-80.
[20] 安 欣,贾进章. 矿井涌水量时间序列ARIMA预测模型[J]. 辽宁工程技术大学学报,2015,34(7):785-790.
ANXin,JIA Jinzhang. Time serie prediction of mine water inflow of ARIMA model[J]. Journal of Liaoning Technical University(Natural Science),2015,34(7):785-790..
[21] 何 保,李振南,赵世杰. 基于多元非线性回归分析的露天煤矿涌水量预测[J].煤炭科学技术, 2018, 46(5):125-129.
HE Bao,LI Zhennan,ZHAO Shijie. Prediction on water inflow of surface mine based on multi-elementnonlinear regression analysis[J].Coal Science and Technology, 2018, 46(5):125-129.
[22] 苗霖田,贺晓浪,张建军,等. 矿井涌水量的时间序列分析-水文地质比拟法预测[J]. 中国煤炭,2017,43(3):32-35.
MIAO Lintian,HE Xiaolang,ZHANG Jianjun.Time series analysis hydrogeological analogy method for mine water inflow forecast[J].China Coal,2017,43(3):32-35.
[23] 刘启蒙,胡友彪,张宇通,等. 矿井涌水量预测方法探讨[J]. 安徽理工大学学报(自然科学版),2017,37(6):1-7.
LIU Qimeng,HU Youbiao,ZHANG Yutong,et al. Exploration on the Prediction Methods of Coal Mining Water Inflow[J]. Journal of Anhui University of Science and Technology(Natural Science),2017,37(6):1-7.
[24] 丁丽娟,程杞元. 数值计算方法[M].2版.北京理工大学出版社,2005.
[25] 吴 英,兰 伟,于海波,等.多开采水平矿井涌水量预测方法及精度级别分析:以中煤能源新疆分公司106团准南煤矿改扩建工程项目水资源论证为例[J]. 中国农村水利水电,2010(12):57-59.
WU Ying, LAN Wei,YU Haibo. Prediction method and accuracy level analysis of water inflow in multi-mining level mine:taking the water resources demonstration of the reconstruction and expansion project of the 106th regiment of Zhunnan Coal Mine of China Coal Energy Xinjiang Branch as an example[J].China Rural Water and Hydropower, 2010 (12):57-59.
[26] 钱学溥.预测矿井涌水量的计算级别与精度评述[J]. 中国煤炭地质,2007,19(5):48-50.
QIAN Xuepu.Estimation rating and precision comment on mine inflow prediction[J].Coal Geology of China,2007,19(5):48-50.
