0 引 言
煤是一种复杂的天然多孔介质,孔径分布从毫米级到纳米级不等[1-2],不同尺度的孔隙结构控制着煤层气的吸附-解吸(孔隙表面)、扩散(纳米级孔隙)与渗流(微米-毫米级孔隙)等过程[3-4],孔隙结构特征与上述过程密切相关。构造煤的孔隙结构具有较强的非均质性,不同类型构造煤的构造变形差异性使得构造煤的孔隙结构变得极为复杂,难以用传统的欧氏几何理论描述其复杂性和不规则性[5-6]。分形理论作为一种描述复杂现象的工具,为研究构造煤复杂的孔隙结构提供了一种新的科学方法。研究表明煤的孔隙结构在一定尺度范围内表现出自相似性,其空间展布形态介于二维和三维之间,和绝大多数天然岩石一样具有分形特征[7-8]。煤中的吸附-解吸、扩散及渗流等物理现象受其影响,也表现出一定的分形特征[9]。分形维数是定量表征多孔介质分形特征的重要参数,能够反映孔隙结构的非均质性和表面的复杂程度,分形维数越大则孔隙结构越复杂,形态越不规则[10]。因此,研究构造煤孔隙结构的分形维数计算方法,进而利用分形维数对构造煤孔隙结构的分形特性进行定量表征,具有重要的意义。构造煤分形维数的计算方法众多,有基于扫描电镜法、小角度散射法等图像方法的孔隙表面分形维数计算方法;有基于气体吸附等温曲线的粒径法、FHH(Frenkel-Halsey-Hill)模型及NK模型等计算方法[11];还有基于介质渗流过程的热力学方法、Menger海绵模型等计算方法[12]。其中FHH模型、NK模型、热力学模型及Menger海绵模型由于测试过程简单、测试精度高、测试范围广等优点,在煤孔隙分形研究中应用广泛[11]。但是上述方法受测试原理和基础数据的限制,单一方法所获得的分形维数仅能反映一定尺度范围内孔隙的分形特征。根据国内外应用较广的IUPAC孔隙分类方案,煤中孔隙按照孔径分为大孔(>50 nm)、介孔(2~50 nm)及微孔(<2 nm)等3个主要尺度[13]。低温N2吸附法和压汞法主要用于测试介孔和大孔尺度的孔隙结构,对应的FHH模型、NK模型及Menger海绵模型等方法也仅能够表征相应尺度的孔隙分形特征,而利用低温CO2吸附法数据计算微孔分形维数的方法较少。目前,大多数研究仍是采用单一方法对局部尺度的孔隙分形特征进行研究,对于构造煤多尺度孔隙分形特征的研究尚少见报道。
基于此,笔者基于IUPAC孔隙分类方案,对构造煤不同尺度孔隙的分形特征进行分析,就构造煤不同尺度孔隙的分形特性综合表征方法进行研究与探讨,进而探索一种可靠的构造煤孔隙结构多尺度综合分形表征方法,并在此基础上采用灰色关联的方法对构造煤孔隙分形特征的影响因素进行分析,以期为研究不同类型构造煤的多尺度孔隙分形特征提供参考。
1 试验样品与孔隙测试
试验所用4个煤样均采集自潞安矿区二叠系下统山西组3号煤层。潞安矿区整体为向西倾斜的单斜构造,并伴随发育宽缓褶曲及小型断层,区域性的文王山断褶带和二岗山断褶带则将矿区分割成不同区块,区内构造煤普遍发育[14]。按照GB/T 30050—2013《煤体结构分类》中的相关方案,所研究的煤样分别为原生结构煤(Ⅰ类)、碎裂煤(Ⅱ类)、碎粒煤(Ⅲ类)和糜棱煤(Ⅳ类)。依据相关标准,样品的基础参数测试结果见表1。
根据IUPAC的孔隙分类方案,联合使用压汞法、低温N2吸附法及CO2吸附法对不同尺度的孔隙结构进行测试。在此基础上,将基于各测试方法的研究数据进行插值处理,从而获得构造煤孔隙结构的全孔径段分布数据。受限于篇幅,测试数据分析过程见文献[2],孔隙结构分布特征见表2和表3。
2 不同尺度孔隙结构的分形表征
构造煤孔隙分形维数计算必须以孔隙结构测试数据为前提,不同孔隙结构测试方法对应不同的分形维数计算模型,对应不同尺度的孔隙分形特征。笔者基于低温CO2吸附法、低温N2吸附法和压汞法等孔隙测试方法,分别探讨了不同尺度孔隙的分形维数计算方法和分形特征。
表1 煤样基础参数测试结果
Table 1 Basic parameters of coal samples

样品编号结构类型工业分析/%水分Mad灰分Aad挥发分VdafPS-1糜棱结构1.4610.9711.80PS-2碎粒结构0.284.9711.84PS-3碎裂结构2.046.1712.44PS-4原生结构0.429.0713.30
表2 构造煤全孔径段孔容分布特征
Table 2 Characteristics of pore volume distribution in full pore size section of tectonic coal

样品编号中值孔径rz/nm最可几孔径rj/nm总孔容V/(cm3·g-1)孔容/(cm3·g-1)孔容比例/%微孔V1介孔V2大孔V3V1/VV2/VV3/VPS-10.821 60.573 20.084 590.064 320.001 780.018 4976.032.1021.86PS-20.785 50.500 80.080 470.062 550.001 480.016 4477.731.8420.43PS-30.656 10.500 80.067 280.060 120.001 180.005 9889.361.758.89PS-40.627 20.548 00.062 700.056 890.001 080.004 7390.731.727.55
注:V=V1+V2+V3。
表3 构造煤全孔径段孔比表面积分布特征
Table 3 Characteristics of specific surface area distribution in full pore size section of tectonic coal

样品编号平均孔径rp/nm总孔比表面积S/(cm2·g-1)孔比表面积/(cm2·g-1)孔比表面积比例/%微孔S1介孔S2大孔S3S1/SS2/SS3/SPS-10.001 67203.567 93202.760 000.529 190.278 7499.600.260.14PS-20.001 66194.501 41193.880 000.438 840.182 5799.680.230.09PS-30.001 46185.113 73184.520 000.513 440.080 2999.680.280.04PS-40.001 52165.819 83165.300 000.411 970.107 8699.680.250.07
注:S=S1+S2+S3。
2.1 微孔结构的分形表征
对于微孔尺度的孔隙主要采用低温CO2吸附法进行测试,CO2气体分子直径为0.33 nm,CO2气体分子受强吸附作用影响,主要以微孔填充的形式吸附在微孔尺度孔隙内[15],不会产生毛细凝聚现象[16]。因此,基于传统多层吸附模型的FHH模型和热力学模型等方法不再适用于微孔分形维数的计算,需要从孔隙大小分布的标度关系出发,将Jaroniec定义的微孔分布密度函数与孔隙大小之间的标度关系[16-17]推广到构造煤微孔结构中,按照盒维数方法两边取对数可得煤中微孔分布的幂律关系:
ln J(r)=(2-d1)ln r+C
(1)
式中:J(r)为孔隙分布密度函数;r为孔隙的孔径,nm;d1为微孔分形维数;C为常数。
结合STOECKLI等[18]关于0.44 nm以上孔隙的吸附特征能E0和孔径r关系的经验公式,可以得到孔隙分布密度函数J(r)的数学表达式为

(2)
式中:ρ为尺度参数,kJ/mol,ρ>0;ν为形状参数,ν>0;Г为伽马函数;x为特征能E0的倒数。
对于式(2),x可以直接由低温CO2吸附测试给出,不同大小的孔径γ对应不同的x,参数ν和ρ可根据CO2气体在煤中微孔的相对吸附量方程[17,19]拟合得出,将其代入式(2),则可以得到孔隙分布密度函数J(r),利用式(1)对J(r)和r数据进行回归(图1),根据所得直线斜率即可计算出微孔分形维数(表4)。
表4 构造煤微孔分形维数
Table 4 Fractal dimension of tectonic coal micropores

样品编号斜率k计算公式微孔分形维数d1相关系数R2PS-1-0.93k=2-d12.930.97PS-2-0.86k=2-d12.860.97PS-3-0.46k=2-d12.460.99PS-4-0.38k=2-d12.380.91
由表4可知,微孔分形维数d1为2.38~2.93,R2均在0.9以上,分形特征较为明显。对比不同构造煤的分形维数发现,随着构造变形程度的增强,微孔分形维数d1也相应增大,如图2所示。煤的构造变形程度越高,微孔分形维数就越大,微孔尺度的孔隙结构也愈加复杂。

图1 CO2吸附数据分形维数拟合
Fig.1 Fractal dimension fitting of CO2 adsorption data

图2 构造煤孔隙分形维数变化特征
Fig.2 Evolution characteristics of pore fractal
dimensions of tectonic coal
2.2 介孔结构的分形表征
对于介孔的表征主要以低温N2吸附法测试数据为基础,基于低温N2吸附数据的分形维数计算方法主要有NK模型[20]和FHH模型2种[21],其中FHH模型在具体计算中根据毛细凝聚现象的强弱还细分为2种不同的计算方法[22-23]。研究中分别采用基于上述2种模型的3种计算方法对试验样品的分形维数进行计算,相关拟合曲线如图3和图4所示。
基于NK模型的拟合方程相关系数均达到0.99,但是NK模型计算的分形维数中存在大于3的情况(表5),而构造煤的孔隙结构实际上是一种嵌置在三维空间的分形结构,其分形维数高于二维平面的维数2,低于三维空间的维数3。因此,大于3或小于2的分形维数在孔隙分形上均无意义,故NK模型不能完全适用构造煤介孔分形维数的计算。
表5 基于NK模型的构造煤介孔分形维数计算
Table 5 Fractal dimension of tectonic
coal mesoporous based on NK model

样品编号斜率k计算公式介孔分形维数d2R2PS-1-0.51d2=2-k2.510.99PS-2-0.71d2=2-k2.710.99PS-3-1.32d2=2-k3.320.99PS-4-0.69d2=2-k2.690.99
利用FHH模型计算分形维数时,回归图中数据点的分布趋势在气体分压p/p0为0.5前后出现较为明显的分段现象(图4),不同压力阶段的数据点分布趋势存在较大差异,针对不同压力阶段的数据分别进行拟合,拟合直线斜率也不相同,计算出的分形维数也不同,见表6。基于FHH模型计算的分形维数均在2~3,相关系数为0.95~0.99,故选择FHH模型对构造煤的介孔分形维数进行计算。
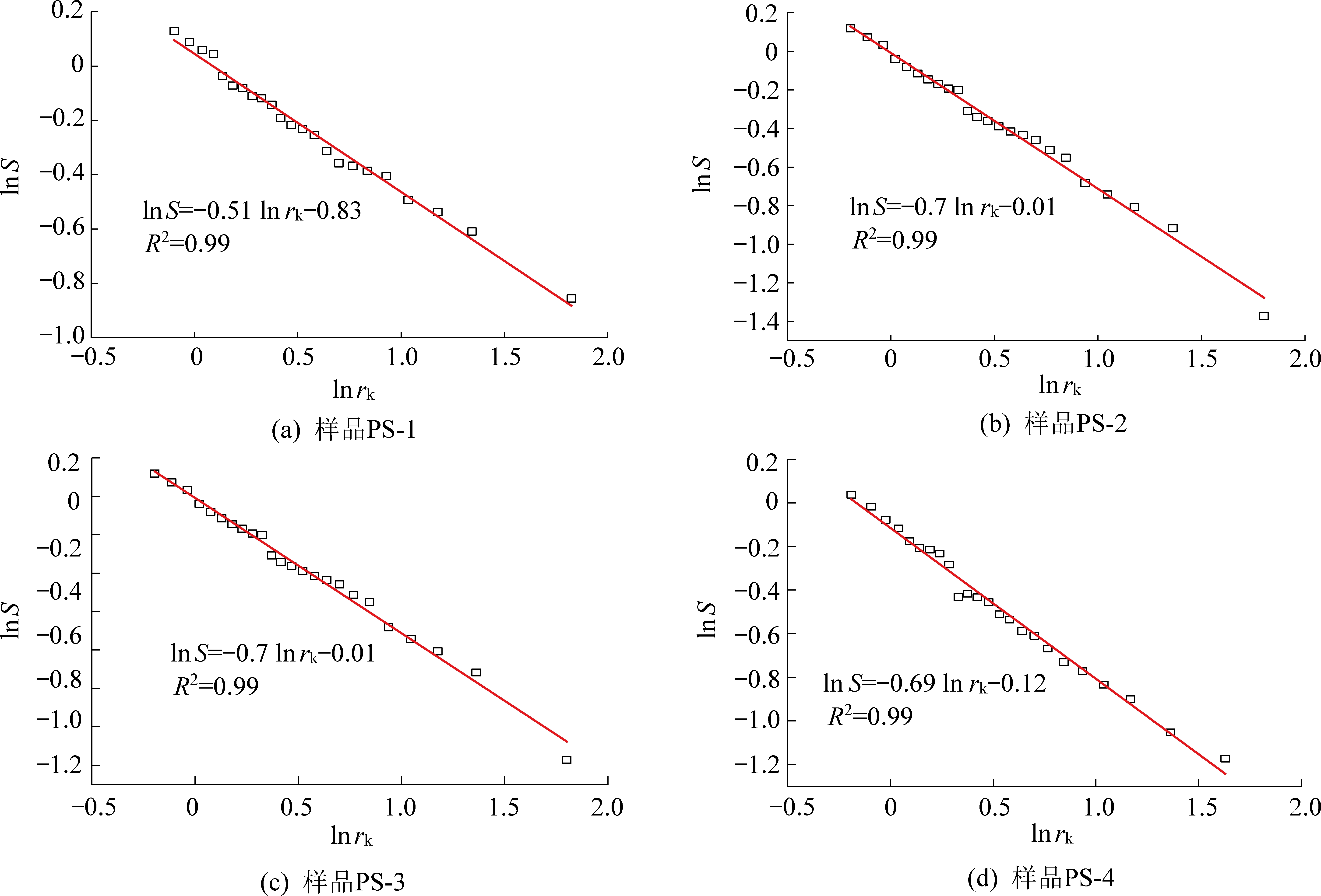
S—孔隙比表面积,cm2/g;γk—吸附膜平均曲率半径,nm
图3 基于NK模型的吸附数据分形维数拟合
Fig.3 Fractal dimension fitting of adsorption data based on NK model
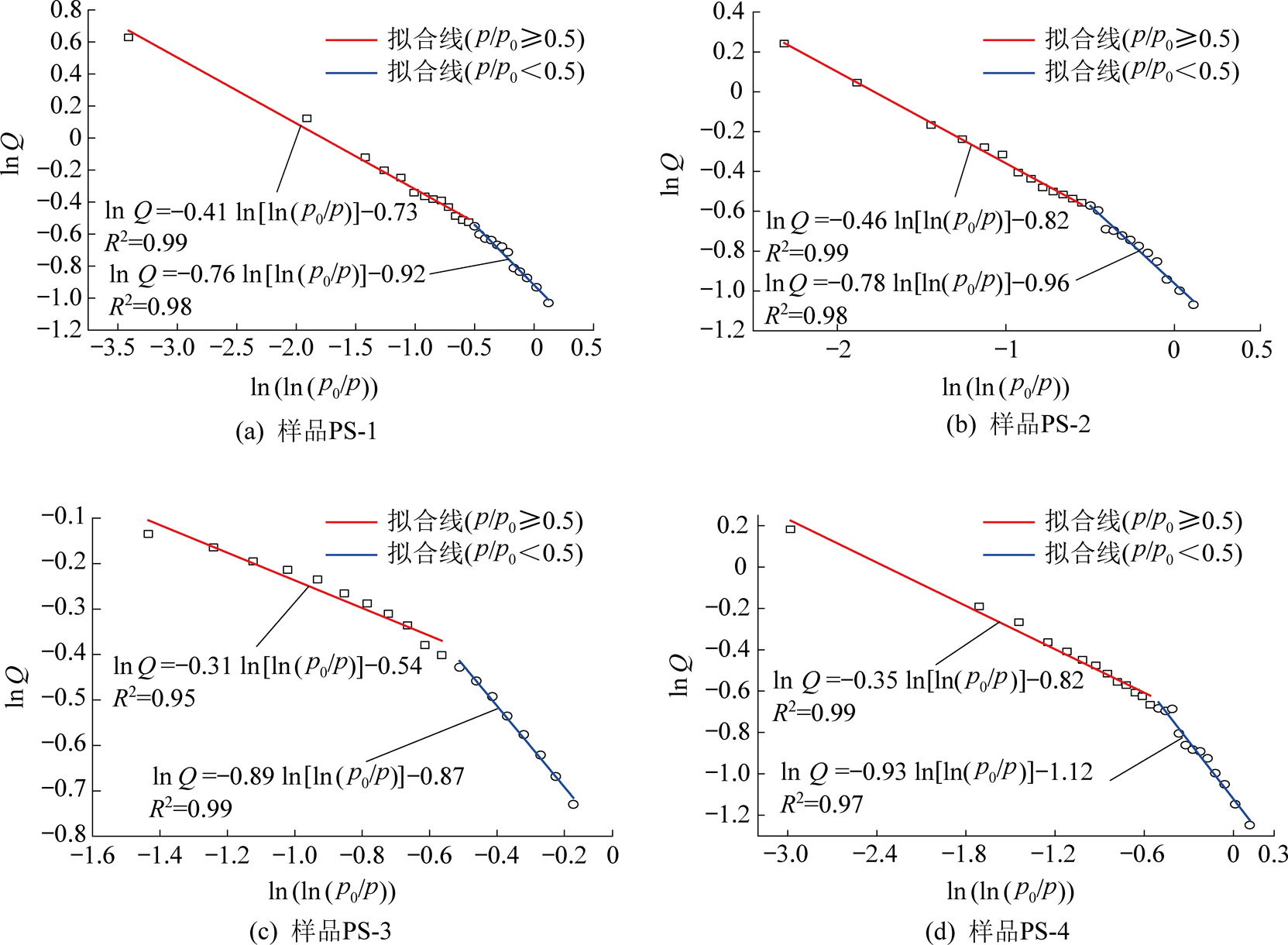
Q—吸附平衡压力p下的气体吸附量,cm3/g;p0—气体饱和蒸气压,MPa
图4 基于FHH模型的吸附数据分形维数拟合
Fig.4 Fractal dimension fitting of adsorption data based on FHH model
表6 基于FHH模型的构造煤介孔分形维数
Table 6 Fractal dimension of tectonic coal mesoporous based on FHH model

样品编号相对压力p/p0≥0.5相对压力p/p0<0.5k计算公式d2R2k计算公式d2R2PS-1-0.41d2=k+32.590.99-0.76d3=k+32.240.98PS-2-0.46d2=k+32.540.99-0.78d3=k+32.220.98PS-3-0.30d2=k+32.700.95-0.89d3=k+32.110.99PS-4-0.35d2=k+32.650.99-0.93d3=k+32.070.97
不同分压阶段的介孔分形维数也不相同,当气体分压p/p0≥0.5时,对应的孔径段为6~50 nm,分形维数为2.54~2.70,平均2.62;当气体分压p/p0<0.5时,对应的孔径段为2~6 nm,分形维数为2.07~2.24,平均2.16。对于同一煤样,6~50 nm孔径段的分形维数总是大于2~6 nm孔径段的分形维数(图4),说明介孔尺度孔隙中6~50 nm孔径段的孔隙结构更为复杂,形态更加不规则。对比不同结构类型煤的介孔分形维数发现,随着构造变形程度的增强,2~6 nm孔径段的分形维数也不断增大;而6~50 nm孔径段的分形维数的变化则较为复杂,出现增大—减小—增大的波动(图2),表明构造变形作用对不同孔径阶段孔隙的分形特征影响程度不同。
2.3 大孔结构的分形表征
压汞数据能够较好地对构造煤中的大孔进行表征,因此大孔阶段孔隙分形维数主要依靠压汞法数据进行计算。Washburn方程是压汞法分形维数的计算基础[12],在此之上发展出了Menger海绵模型[24]和热力学模型[25]等2种较为常用的计算模型,其中在Menger海绵模型的基础上又可以细分出2种不同的计算模型[12]。采用上述方法分别对试验煤样的孔隙分形维数进行计算,在双对数坐标上对相应的数据进行线性回归(图5和图6),利用所得直线的斜率计算分形维数,见表7。
对比图5和图6中相关数据点的分布情况和拟合曲线的形态,可以发现同一煤样的相关回归数据点在各自的双对数坐标系内分布趋势基本一致,孔隙分形没有明显的分段现象。分形数据对应的孔径下限为50 nm,但孔径上限没有明显的规律,一般在3 000 nm以下。

Wn—第n次进汞增量Qn对应的表面能,J/m2;γn—第n次进汞对应的孔半径,nm
图5 构造煤热力学模型分形维数拟合
Fig.5 Fractal dimension fitting of thermodynamic model of tectonic coal samples


pi—进汞压力,MPa;pt—进汞突破压力,MPa
图6 构造煤Menger海绵模型分形维数拟合
Fig.6 Fractal dimension fitting of tectonic coal Menger sponge model
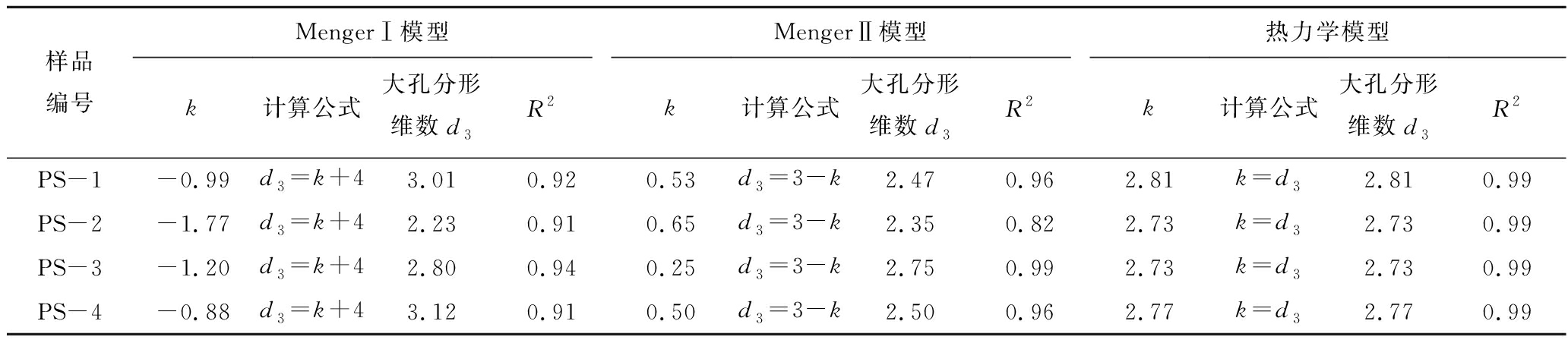
表7 基于Menger模型和热力学模型的构造煤大孔分形维数计算
Table 7 Fractal dimension of tectonic coal macropore based on Menger model and thermodynamics model
样品编号MengerⅠ模型MengerⅡ模型热力学模型k计算公式大孔分形维数d3R2k计算公式大孔分形维数d3R2k计算公式大孔分形维数d3R2PS-1-0.99d3=k+43.010.920.53d3=3-k2.470.962.81k=d32.810.99PS-2-1.77d3=k+42.230.910.65d3=3-k2.350.822.73k=d32.730.99PS-3-1.20d3=k+42.800.940.25d3=3-k2.750.992.73k=d32.730.99PS-4-0.88d3=k+43.120.910.50d3=3-k2.500.962.77k=d32.770.99
对比表7中数据发现,利用Menger模型Ⅰ计算的分形维数存在大于3的结果,这与构造煤孔隙分形维数为2~3的实际情况不符;Menger模型Ⅱ拟合公式的决定系数R2最小为0.82,在计算精度方面相对偏低,而热力学模型不仅计算的分形维数在正常范围内,且R2均为0.99,计算精度高。综合考虑上述因素,采用热力学模型对大孔分形维数进行计算。基于热力学模型计算的大孔分形维数为2.73~2.81,平均为2.76。如图2所示,随着构造变形程度的增强,大孔分形维数出现先减小后增大的变化特征,演化趋势相对更为复杂。
3 构造煤孔隙结构的多尺度分形特征
采用不同方法对构造煤微孔、介孔及大孔孔隙的分形维数进行了计算,分析了不同尺度孔隙分形维数随煤体结构类型变化的特征。由于不同的分形维数计算方法受测试原理限制,所能表征的孔隙尺度范围有限,难以对构造煤孔隙结构的多尺度分形特征进行描述。因此,需要借助其他方法将不同尺度的孔隙分形维数统一起来,从而实现构造煤孔隙结构分形特性的多尺度综合表征。
3.1 构造煤孔隙多尺度综合分形维数
构造煤的分形孔隙结构实质上是大量不规则微小孔隙对构造煤颗粒内部整体空间不完全填充的结果,如果孔隙网络完全填充了内部的空间,则孔隙结构转化为三维欧式空间;如果孔隙网络分布足够扁平光滑,则会退化为二维平面。因此,孔隙的孔容对孔隙结构的分形特征有着重要的影响。根据计算孔隙分形维数时所使用的CO2微孔填充模型、FHH模型及热力学模型,可以发现用于拟合直线的双对数数据点均与孔容直接相关,说明分形维数除了与孔隙的具体结构相关外,还与孔容的分布具有密切的联系。
综合上述分析,孔容比例能够反映不同孔径段孔隙的分形特征对构造煤整体分形特征的影响程度。因此,以各孔径段孔隙的孔容比例为权重,对不同尺度孔隙的分形维数进行加权计算,所得即为构造煤多尺度综合分形维数,即
(3)
式中:dz为构造煤多尺度综合分形维数;Bi为第i个孔隙尺度的孔容占总孔容的比例,i=1,2,…,m,m为划分出的孔隙尺度阶段数量,为正整数;dij为第i个孔隙尺度中第j个孔径段的分形维数,j=1,2,…,n,n为第i个孔隙尺度中划分出的孔径段数量,为正整数;bij为第i个孔隙尺度中第j个孔径段孔容占该尺度孔容的比例。
分别采用CO2微孔填充模型、N2吸附FHH模型和压汞热力学模型对微孔、介孔及大孔的分形特性进行表征。根据各尺度、各孔径段分形维数和孔容比例,按照式(3)分别计算了不同煤样的孔隙多尺度综合分形维数,结果见表8。
表8 构造煤多尺度综合分形维数
Table 8 Multi-scale comprehensive fractal dimension of tectonic coal

样品编号dz微孔介孔大孔B1/%d1B2/%b21/%d21b22/%d22B3/%d3PS-12.8976.032.932.1031.182.2468.822.5921.862.81PS-22.8277.732.861.8444.092.2255.912.5420.432.73PS-32.4889.362.461.7567.712.1132.292.708.892.73PS-42.4190.732.381.7242.022.0757.982.657.552.77
注:B1为微孔孔容比例,B2为介孔孔容比例,B3为大孔孔容比例;b21为介孔中6~50 nm孔径段孔容比例,b22为介孔中2~6 nm孔径段孔容比例;d1为微孔分形维数,d21为介孔6~50 nm孔径段的分形维数,d22为介孔2~6 nm孔径段的分形维数,d3为大孔分形维数。
通过对不同尺度孔隙分形维数的加权平均计算,使得分布无序、无明显规律的不同尺度孔隙分形维数按照一定的趋势统一起来,所得综合分形维数与构造煤结构变化表现出一定的关联性。随着构造煤变形程度的增强,多尺度综合分形维数也不断增大,表明孔隙结构的不规则性、非均质性也相应增强(图7)。

图7 构造煤多尺度综合分形维数变化特征
Fig.7 Evolution characteristics of multi-scale comprehensive
fractal dimension of tectonic coal
3.2 构造煤分形维数的影响因素
目前,已经有学者运用回归分析的方法研究了不同参数与分形维数之间的联系,如煤的灰分、水分等工业分析参数[26],煤的孔径分布、孔容、孔比表面积等孔隙参数等[27]。但是,分形维数的影响因素众多,各因素对分形维数的影响程度不同,传统方法难以对其影响程度进行比较。笔者采用灰色关联度方法[28-29]对孔隙分形维数的影响因素进行分析,以判断不同因素对分形维数的影响程度。
灰色关联度方法是判断多种因素与变量之间关联程度的一种方法,该方法能够计算出系统中各因素之间的灰色关联度,从而定量判断不同因素对于目标值的影响程度[28]。参考灰色关联度方法,将不同煤样的多尺度综合分形维数作为参考序列,将灰分、挥发分、孔容、阶段孔容、阶段孔容比例、孔比表面积、阶段孔比表面积、阶段孔比表面积比例、平均孔径、最可几孔径、中值孔径等19个参数作为比较序列。由于煤体结构类型属于定性参数,不易量化,且前文的分析已经说明煤体结构类型是多尺度综合分形维数的重要影响因素。因此,本次灰色关联度分析中不包含该因素。利用表1—表3中的数据,按照灰色关联度方法计算了不同比较序列与参考序列的关联度,结果见表9。
根据灰色关联度值域范围所代表的意义[30]对各因素进行分析,其中灰色关联度γ>0.9的有中值孔径rz、微孔孔容V1、总比表面积S、微孔比表面积S1等,表明上述参数对多尺度综合分形维数的影响最大;0.9≥γ>0.8的因素有最可几孔径rj、总孔容V、介孔比表面积S2、微孔比表面积比例S1/S等,说明上述参数是多尺度综合分形维数的重要影响因素;0.8≥γ>0.7的因素有灰分Aad、挥发分Vdaf、介孔孔容V2、介孔比表面积比例S2/S等,说明上述因素对多尺度综合分形维数具有一定的影响;其余灰色关联度γ≤0.7的参数可以忽略。
表9 构造煤分形维数影响因素的灰色关联度
Table 9 Grey relational grade of tectonic coal fractal dimensional factors

分形维数影响因素AadVdafrprjrzVV1V2V3V1/V灰色关联度γ0.710.750.920.850.910.880.910.710.610.70分形维数影响因素V2/VV3/VSS1S2S3S1/SS2/SS3/S—灰色关联度γ0.900.660.930.930.810.550.810.760.57—
4 结 论
1)基于CO2吸附数据的微孔填充模型,基于N2吸附数据的FHH模型和基于压汞数据的热力学模型能够分别对构造煤微孔、介孔、大孔尺度孔隙的分形特性进行有效表征,NK模型和Menger模型存在计算精度低和分形维数大于3的情况,不能有效反映构造煤孔隙的分形特征。
2)不同尺度孔隙的分形维数随构造煤破坏程度增大而变化的规律不同,其中微孔分形维数及介孔中2~6 nm孔径段的分形维数随构造煤的破坏程度增大而增高,其余尺度孔隙的分形维数变化则没有明显规律。
3)提出了描述构造煤全孔径段孔隙分形结构特征的多尺度综合分形维数,即以阶段孔容比例为权重对构造煤不同尺度的孔隙分形维数加权平均,所得的多尺度综合分形维数与煤体结构密切相关,随着煤体构造变形程度的增强,构造煤多尺度综合分形维数不断增大,孔隙结构的不规则性、非均质性也相应增强。
4)运用灰色关联度方法分析了构造煤分形维数的影响因素,中值孔径、微孔孔容、总比表面积、微孔比表面积等因素对多尺度综合分形维数的影响最大,最可几孔径、总孔容、介孔比表面积、微孔比表面积比例等因素也是重要的影响因素,灰分、挥发分、介孔孔容、介孔比表面积比例等因素对分形维数的影响次之。
[1] 王 聪,江成发,储 伟.煤的分形维数及其影响因素分析[J].中国矿业大学学报,2013,42(6):1009-1014.
WANG Cong,JIANG Chengfa,CHU Wei.Fractal dimension of coals and analysis of its influencing factors [J].Journal of China University of Mining & Technology,2013,42(6):1009-1014.
[2] 李 阳,张玉贵,张 浪,等.基于压汞、低温N2吸附和CO2吸附的构造煤孔隙结构表征[J].煤炭学报,2019,44(4):1188-1196.
LI Yang,ZHANG Yugui,ZHANG Lang,et al.Characterization on pore structure of tectonic coals based on the method of mercury intrusion,carbon dioxide adsorption and nitrogen adsorption[J].Journal of China Coal Society,2019,44(4):1188-1196.
[3] LI Y,TANG D,ELSWORTH D,et al.Characterization of coalbed methane reservoirs at multiple length scales:a cross-section from southeastern Ordos Basin,China[J].Energy & Fuels,2014,28(9):5587-5595.
[4] 王 凯,乔 鹏,王壮森,等.基于二氧化碳和液氮吸附、高压压汞和低场核磁共振的煤岩多尺度孔径表征[J].中国矿业,2017,26(4):146-152.
WANG Kai,QIAO Peng,WANG Zhuangsen,et al.Multiple scale pore size characterization of coal based on carbon dioxide and liquid nitrogen adsorption,high-pressure mercury intrusion and low field nuclear magnetic resonance[J].China Mining Industry,2017,26(4):146-152.
[5] ALEXEEV A D,VASILENKO T A,ULYANOVA E V.Closed porosity in fossil coals[J].Fuel,1999,78(6):635-638.
[6] JU Yiwen,JIANG Bo,HOU Quanlin.Relationship between nanoscale deformation of coal structure and metamorphic deformed environments[J].Chinese Science Bulletin,2005,50(16):1785-1796.
[7] 童宏树,胡宝林.鄂尔多斯盆地煤储层低温氮吸附孔隙分形特征研究[J].煤炭技术,2004,23(7):1-3.
TONG Hongshu,Hu Baolin.Research on the fractal characteristics of pore of coal reservoirs tested with cryogenic nitrogen adsorption in the Ordos Basin [J].Coal Technology,2004,23(7):1-3.
[8] 秦跃平,傅 贵.煤孔隙分形特性及其吸水性能的研究[J].煤炭学报,2000,25(1):57-61.
QIN Yueping,FU Gui.Study on fractal characteristic of pore in coal and moisture-absorbing property of coal [J].Journal of China Coal Society,2000,25(1):57-61.
[9] 蒋晓芸,徐明瑜.分形介质分数阶反常守恒扩散模型及其解析解[J].山东大学学报:理学版,2003,38(5):29-32.
JIANG Xiaoyun,XU Mingyu.Fractional anomalous conservation diffusion model and its analytic solution in fractal media [J].Journal of Shandong University:Science Science Edition,2003,38(5):29-32.
[10] 李留仁,赵艳艳,李忠兴,等.多孔介质微观孔隙结构分形特征及分形系数的意义[J].石油大学学报:自然科学版,2004,28(3):13-14,120.
LI Liuren,ZHAO Yanyan,LI Zhongxing,et al.Fractal characteristics of micropore structure of porous media and the meaning of fractal coefficient [J].Journal of Petroleum University:Natural Science Edition,2004,28(3):13-14,120.
[11] 戴方尧.川东—湘西地区龙马溪组与牛蹄塘组页岩孔隙与页岩气赋存机理研究[D].武汉:中国地质大学,2018.
DAI Fangyao.The study of Pores Characteristics and shale gas occurrence of Longmaxi and Niutitang Formation in east of Sichuan and west of Hunan Area [D].Wuhan:China University of Geosciences,2018.
[12] 覃生高.储层孔隙分布及流体渗流特征的分形描述与应用[D].大庆:大庆石油学院,2010.
TAN Shenggao.Study of the reservoir fluid flow by fractal method and its application[D].Daqing:Daqing Petroleum Institute,2010.
[13] THOMMES M.Physisorption of gases,with special reference to the evaluation of surface area and pore size distribution(IUPAC Technical Report)[J].Pure Applied Chemistry,2015,87(9/10):1051-1069.
[14] 李 阳,张 浪,舒龙勇,等.潞安矿区煤储层特征及瓦斯含量分布规律研究[J].煤炭科学技术,2014,42(12):65-69.
LI Yang,ZHANG Lang,SHU Longyong,et al.Sudy on coal reseroir features and cas distibution law in Lu’an Mining Area[J].Coal Science and Technology,2014,42(12):62-66.
[15] 张哲泠,杨正红.微介孔材料物理吸附准确性分析的理论与实践[J].催化学报,2013,34(10):1797-1810.
ZHANG Zheleng,YANG Zhenghong.Theoretical and practical discussion of measurement accuracy for physisorption with micro-and mesoporous materials [J].Chinese Journal of Catalysis,2013,34(10):1797-1810.
[16] PFEIFER P,AVNIR D.Chemistry in noninteger dimensions between two and three.I.fractal theory of heterogeneous surfaces[J].The Journal of Chemical Physics,1983,79(7):3558-3565.
[17] JARONIEC M,GILPIN R K,CHOMA J.Correlation between microporosity and fractal dimension of active carbons [J].Carbon,1993,31(31):325-331.
[18] STOECKLI H F,BALLERINI L,DEBERNARDINI S.On the evolution of micropore widths and areas in the course of activation[J].Pergamon,1989,27(3):501-502.
[19] CHOMA J,JARONIEC M,PIOTROWSKA J.On the mesopore correction of adsorption data used for characterizing microporous structure of activated carbons[J].Materials Chemistry & Physics,1987,18(4):409-421.
[20] LOWELL S,SHIELDS J,THOMAS M,et al.Characterization of porous solids and powders:surface area,pore size and density[M].Dordrecht:Springer Science & Business Media,2012:158-165.
[21] PFEIFER P,OBERT M,COLE M W.Fractal bet and FHH theories of adsorption:a comparative study[J].Proceedings of the Royal Society of London,1989,423:169-188.
[22] AVNIR D,JARONIEC M.An isotherm equation for adsorption on fractal surfaces of heterogeneous porous materials[J].Langmuir,1989,5(6):1431-1433.
[23] PFEIFER P,WU YJ,COLE M W,et al.Multilayer adsorption on a fractally rough surface[J].Physical Review Letters,1989,62(17):1997.
[24] XIE Heping,WANG Jinan,QAN Pinggao.Fractal characters of micropore evolution in marbles[J].Physics Letters A,1996,218(3):275-280.
[25] ZHANG Baoquan,LI Shaofen.Determination of the surface fractal dimension for porous media by mercury porosimetry[J].Industrial & Engineering Chemistry Research,1995,34(4):1383-1386.
[26] YAO Y,LIU D,TANG D.Fractal characterization of adsorption-pores of coals from North China:aninvestigation on CH4 adsorption capacity of coals[J].International Journal of Coal Geology,2008,73(1):27-42.
[27] 张晓辉,要惠芳,李 伟,等.韩城矿区构造煤纳米级孔隙结构的分形特征[J].煤田地质与勘探,2014,42(5):4-8.
ZHANG Xiaohui,YAO Huifang,LI Wei,et al.Fractal characteristics of nano-pore structure in tectonically deformed coals in Hancheng Mining Area [J].Coal Geology & Exploration,2014,42(5):4-8.
[28] DENG J L.Control problems of grey systems[J].Systems & Control Letters,1982,1(5):288-294.
[29] WANG Z,MENG H,FU J.Novel method for evaluating surface roughness by grey dynamic filtering[J].Measurement,2010,43(1):78-82.
[30] FU Chaoyang,ZHENG Jiashen,ZHAO Jingmao.Application of grey relational analysis for corrosion failure of oil tubes[J].Corrosion Science,2001,43(5):881-889.
